Effects of Movement for High Time-Bandwidths in Batched Pulse Compression Range-Doppler Radar
Abstract
1. Introduction
2. Challenges of Pulse Compression with High Time-Bandwidth Products
2.1. Stationary Pulse Compression Principle
2.2. Batched Processing Scheme Implementation for Range-Doppler Analysis
2.3. Evolution of Radar Waveforms and Reasons for High Instantaneous Time-Bandwidth Products
2.4. Bistatic Geometry Relations on the Effectively Measurable Velocity
2.5. Limits Introduced by the Bistatic Velocity and the Time-Bandwidth Product
3. Doppler Effect Modelled in Its Scaling Relation
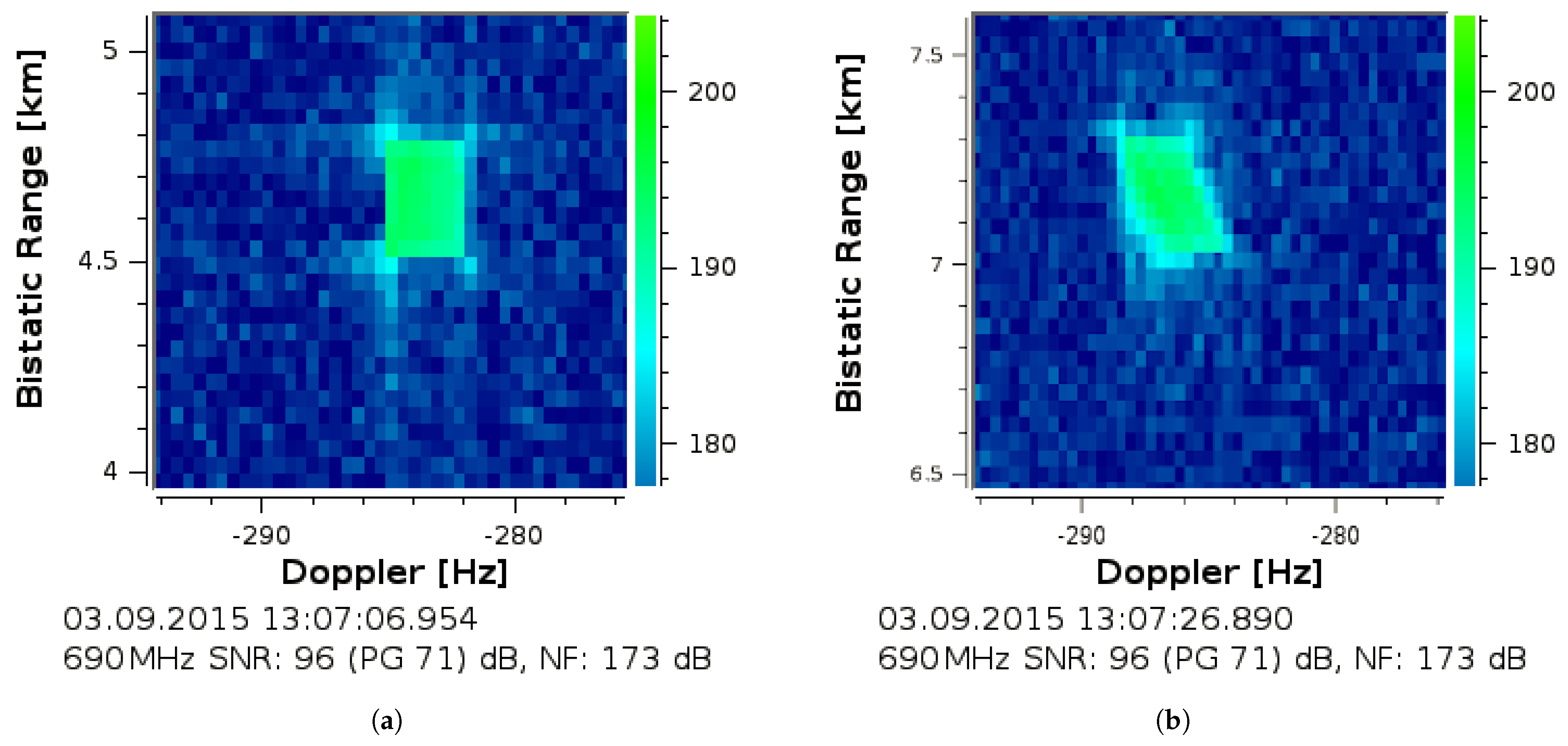
3.1. Exemplary Processed Targets from Measurement Campaign Datasets
3.2. Effect of a Constant Effective Velocity on an Instantaneous Broadband Waveform Processing
3.3. Doppler as an Instantaneous Relation
4. Implication of a Linear Target Movement in Batched Range-Doppler Processing
- (a)
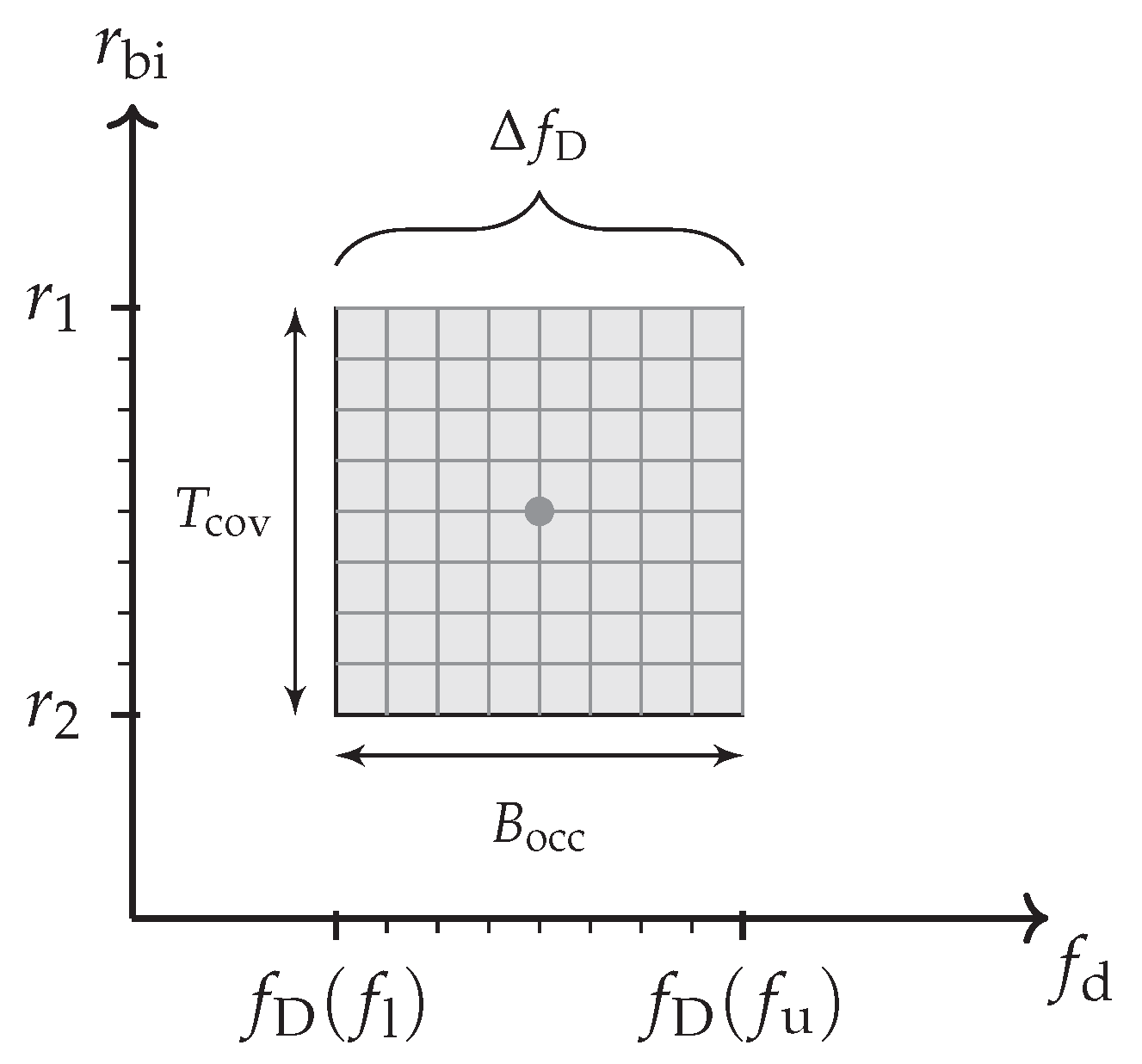
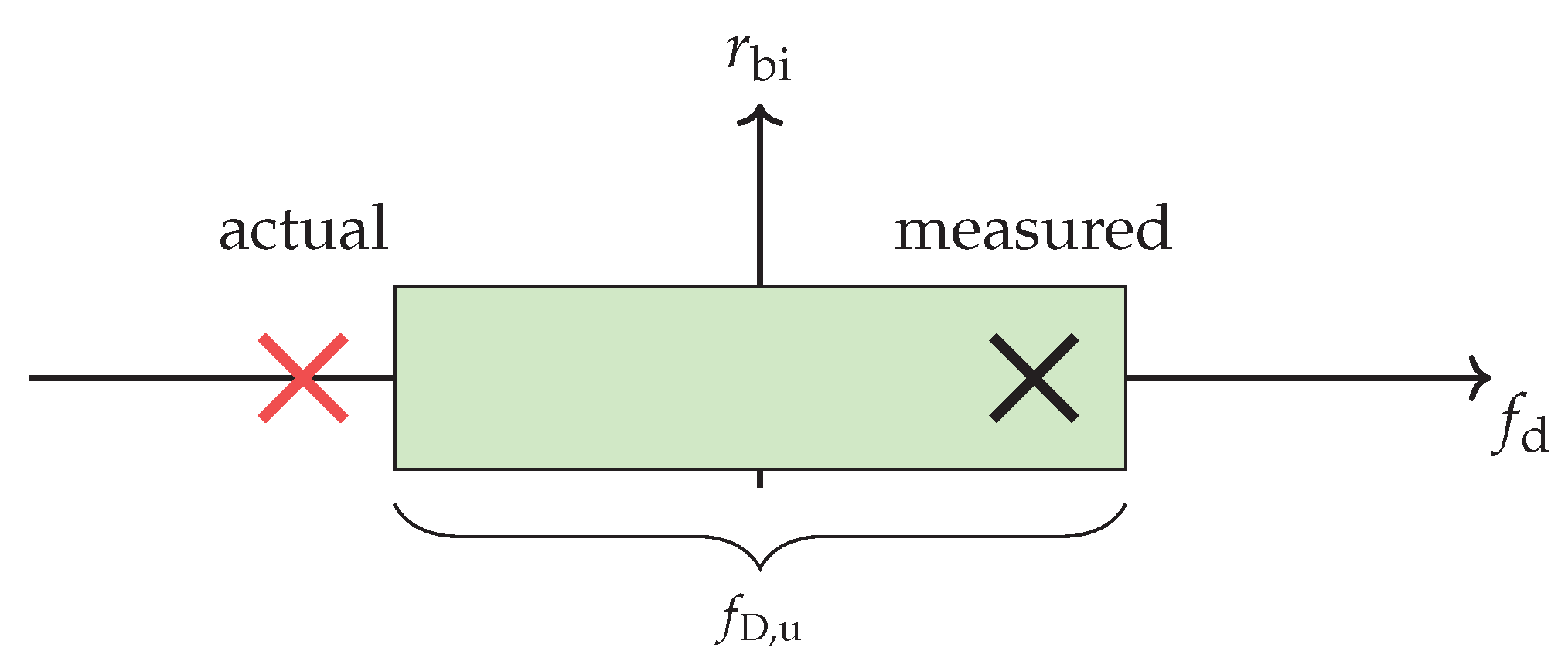
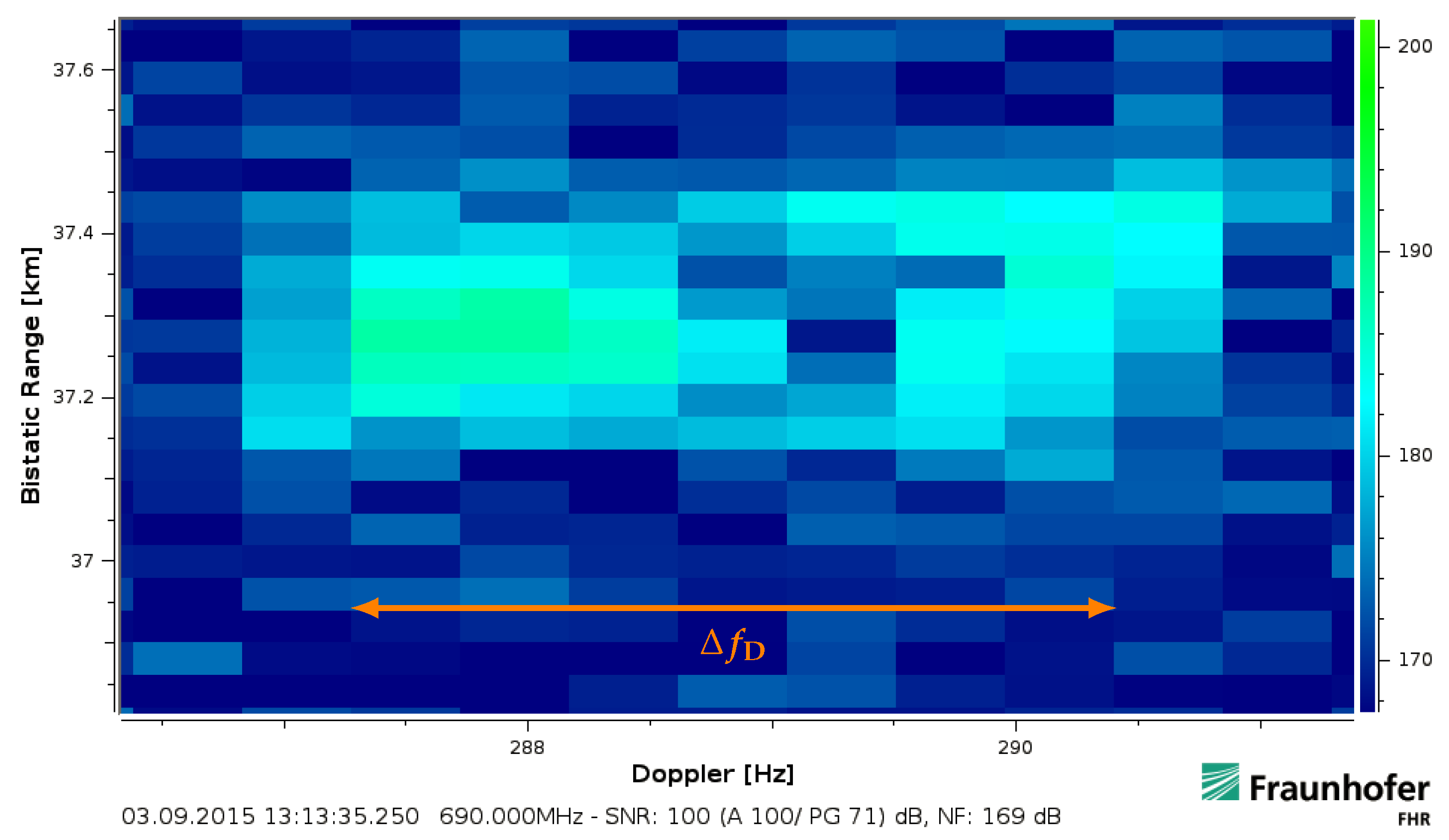
- introduce a frequency sensitivity [14,24] due to the Gross Doppler displacement . This is caused by its intra-pulse phase approximation [9] over the block duration . If a cyclic prefix waveform with guard duration is considered, this will lead to a sensitivity degradationThe relation (18) is thereby only range () dependent with outside of the guard duration [25]. Its derivation is given in Appendix A.In addition, only ambiguously measurable parameters are determined by a batched processing. This will impact subsequent processing stages like the tracking. In particular multi-carrier waveforms with long symbol durations and a low Doppler tolerance might result in a limited unambiguous Doppler processing from the radar perspective [26]. The unambiguity window in the analysed frequency domain is as illustrated in Figure 8. This gives an unambiguously measurable velocity span of . If the resulting fold-over effect was not considered, it would have a severe impact on tracking because the wrong radial direction and speed would be determined. For chirped signals the ambiguity impact is often worsen by a strong range-Doppler coupling of the waveform [13]. The directly unambiguously measurable range is . This influence can be resolved by pulse staggering or similar modifications to the transmit waveform.
- (b)
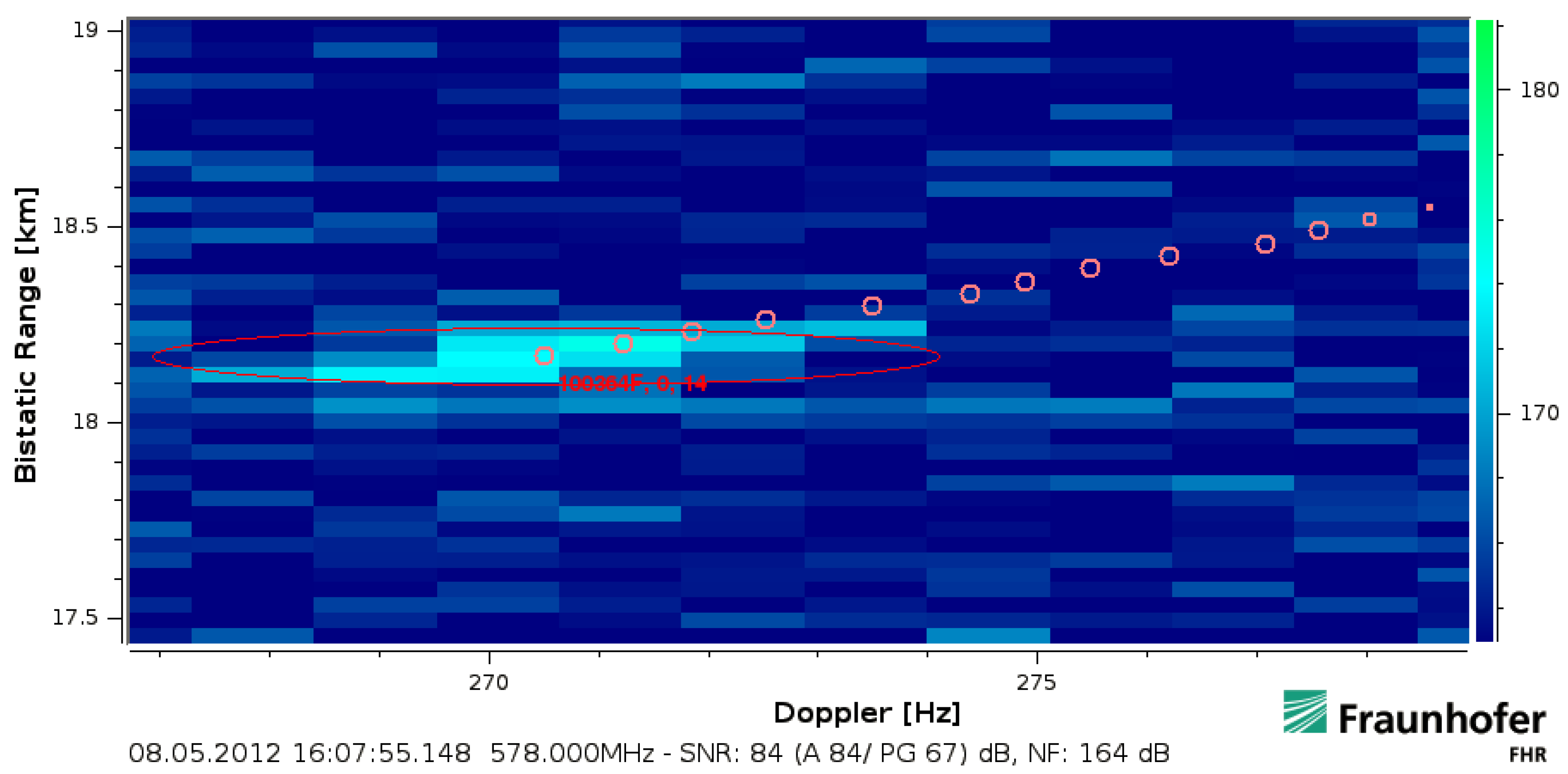
- a temporary impact on a moving scatterer’s maximum that is inherent from the DSP architecture. This leads to an DFT scalloping [27] and range straddling [13] loss whenever a point scatterer is time-dependently displaced over multiple discretised range (ft) or Doppler (st) cells.A single point can be split over up to four processed range-Doppler cells as illustrated in Figure 9. This gets in particular worse for quadrature sampled signals, confined and point scatterer like target returns and rectangular high effective instantaneous bandwidth waveforms. The range straddling impact will increase for high ratios up to . The DFT scalloping depends on the relation of signal displacement to the frequency bins and the number of processed samples. The scalloping loss can reach another for quadrature sampling. Despite this effect is in principle widely known in digital signal processing, it is rarely considered in radar processing schemes [28,29]. This is unrelated to the previously described bandwidth extension spread but the involved challenge might occur for re-focused point scatterer returns as it had been indicated in Figure 7 as well. Particular stationary DSP effects further introduced by sampling, the analogue to digital conversion and deviations from these relations will be addressed in separate publications.
- (c)
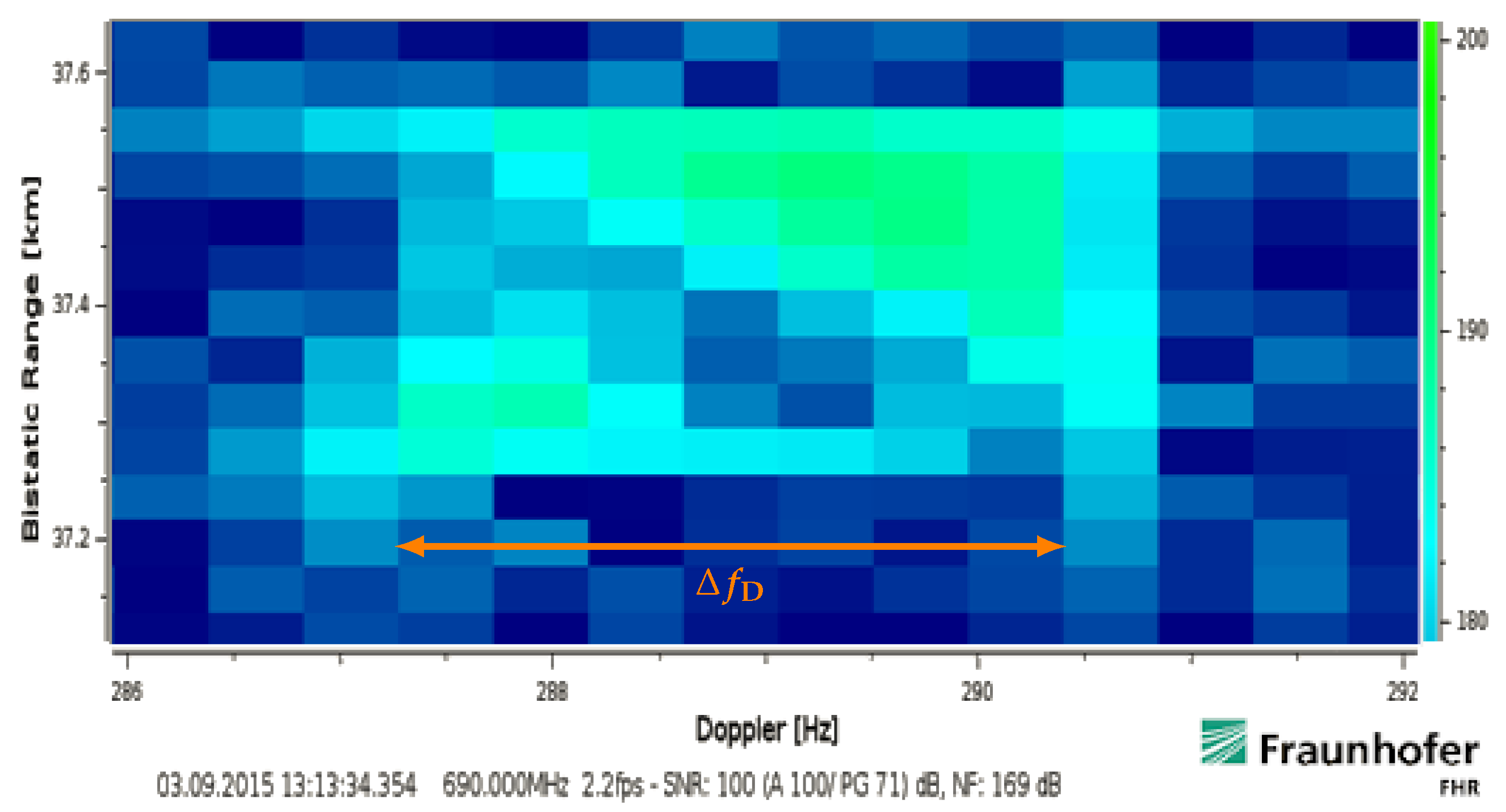
- be determined by the in total occupied bandwidth and the target motion within the covered timespan . The Doppler’s bandwidth dependent influence relates directly to the target movement but it is at first independent of for example a batched range-Doppler implementation. A high instantaneous bandwidth will hereby lead to the spread previously illustrated in Figure 7. Due to many distinct impacts, their influence will be addressed in the following section in more detail.
5. Influence of Linear Movement within the Signal Bandwidth due to Doppler
5.1. Spread over Multiple Range-Doppler Cells
5.2. Analysis of Decreased Range-Frequency Accuracy
5.3. Impact of a Constant Speed on the Achievable Coherent Integration Gain
5.4. Bandwidth Paradox in Multi-Channel Processing with a High Instantaneous Bandwidth
5.5. Target Response Coherency over and from Measurement Datasets
5.6. Higher-Order Motion Aspects
6. Discussion of Findings and Consideration for Processing Approaches
6.1. Preface
6.2. Constant Effective Velocity Detection in a Time-Scale Analysis Approach
6.3. Common Time-Scale Analysis Implementation Techniques for Batched Schemes
6.4. Constrains of Actual Non-Uniform and Non-Rectangular Target Returns
6.5. Remaining Limitations of Velocity Spread Compensation on the Achievable Integration Gain
6.6. Summary
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Frequency Sensitivity from Equation (18)
References
- Weiss, L. Wavelets and wideband correlation processing. IEEE Signal Process. Mag. 1994, 11, 13–32. [Google Scholar] [CrossRef]
- Stewart, J.; Westerfield, E. A Theory of Active Sonar Detection. Proc. IRE 1959, 47, 872–881. [Google Scholar] [CrossRef]
- Remley, W. Doppler dispersion effects in matched filter detection and resolution. Proc. IEEE 1966, 54, 33–39. [Google Scholar] [CrossRef]
- DiPietro, R.; Fante, R.; Perry, R. Space-based bistatic GMTI using low resolution SAR. In Proceedings of the 1997 IEEE Aerospace Conference, Snowmass, CO, USA, 13 February 1997; Volume 2, pp. 181–193. [Google Scholar] [CrossRef]
- Perry, R.; DiPietro, R.; Fante, R. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Perry, R.; DiPietro, R.; Fante, R. Coherent Integration With Range Migration Using Keystone Formatting. In Proceedings of the IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 863–868. [Google Scholar] [CrossRef]
- Griffiths, H.; Baker, C. Passive coherent location radar systems. Part 1: Performance prediction. IEE Proc. Radar Sonar Navig. 2005, 152, 153–159. [Google Scholar] [CrossRef]
- Kuschel, H.; Cristallini, D.; Olsen, K.E. Tutorial: Passive radar tutorial. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 2–19. [Google Scholar] [CrossRef]
- Berger, C.; Demissie, B.; Heckenbach, J.; Willett, P.; Zhou, S. Signal Processing for Passive Radar Using OFDM Waveforms. IEEE J. Sel. Top. Signal Process. 2010, 4, 226–238. [Google Scholar] [CrossRef]
- Searle, S.; Palmer, J.; Davis, L.; O’Hagan, D.; Ummenhofer, M. Evaluation of the ambiguity function for passive radar with OFDM transmissions. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1040–1045. [Google Scholar]
- Haimovich, A.; Blum, R.; Cimini, L. MIMO Radar with Widely Separated Antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Schwark, C.; Cristallini, D. Advanced multipath clutter cancellation in OFDM-based passive radar systems. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 1–6 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Skolnik, M. Introduction to Radar Systems; McGraw Hill: Boston, MA, USA, 2001; ISBN 978-0-07-288138-7. [Google Scholar]
- Moscardini, C.; Petri, D.; Capria, A.; Conti, M.; Martorella, M.; Berizzi, F. Batches algorithm for passive radar: A theoretical analysis. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1475–1487. [Google Scholar] [CrossRef]
- Proakis, J.; Salehi, M. Digital Communications; McGraw-Hill: Boston, MA, USA, 2008; ISBN 978-0-07-295716-7. [Google Scholar]
- Frigo, M.; Johnson, S. The Design and Implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]
- Howland, P.; Griffiths, H.; Baker, C. Passive Bistatic Radar Systems. In Bistatic Radar; John Wiley & Sons, Ltd.: England, UK, 2008; pp. 247–313. [Google Scholar]
- Middleton, R. Dechirp-on-Receive Linearly Frequency Modulated Radar as a Matched-Filter Detector. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2716–2718. [Google Scholar] [CrossRef]
- Willis, N. Bistatic Radar; SciTech Pub.: Chennai, India, 2005; ISBN 978-1-891-12145-6. [Google Scholar]
- Malanowski, M.; Kulpa, K. Analysis of integration gain in passive radar. In Proceedings of the International Conference on Radar, Adelaide, Australia, 2–5 September 2008; pp. 323–328. [Google Scholar] [CrossRef]
- IEEE “Standard for Radar Definitions”. IEEE Std 686-2017 2017, 1–54. [CrossRef]
- Doppler, C. Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels. Abhandlungen der k. böhm. Gesellschaft der Wissenschaften; V Folge, Bd. 2. Prag; In Commission bei Borrosch & André. 1842. Available online: https://nbn-resolving.org/urn:nbn:de:bvb:210-09-014047463-0 (accessed on 13 March 2020).
- Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Phys. 1905, 322, 891–921. [Google Scholar] [CrossRef]
- Franken, G.; Nikookar, H.; Genderen, P.V. Doppler Tolerance of OFDM-coded Radar Signals. In Proceedings of the 2006 European Radar Conference, Manchester, UK, 13–15 September 2006; pp. 108–111. [Google Scholar] [CrossRef]
- Bok, D. Reconstruction and Reciprocal Filter of OFDM Waveforms for DVB-T2 Based Passive Radar. In Proceedings of the International Conference on Radar (RADAR), Brisbane, Australia, 27–30 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Tigrek, R.; Heij, W.D.; Van Genderen, P. OFDM Signals as the Radar Waveform to Solve Doppler Ambiguity. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 130–143. [Google Scholar] [CrossRef]
- Lyons, R. Reducing FFT Scalloping Loss Errors Without Multiplication [DSP Tips and Tricks]. IEEE Signal Process. Mag. 2011, 28, 112–116. [Google Scholar] [CrossRef]
- Cann, A. Range gate straddling loss and joint probability with partial correlation. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1054–1058. [Google Scholar] [CrossRef]
- Glass, J.; Blair, W. Detection of rayleigh targets using adjacent matched filter samples. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1927–1941. [Google Scholar] [CrossRef]
- Garry, J.; Smith, G. Distributed multipath effects with passive radar. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 1–6 May 2016; pp. 1–6. [Google Scholar]
- Malanowski, M.; Kulpa, K.; Misiurewicz, J. Acceleration estimation for Passive Coherent Location radar. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Bok, D.; Heckenbach, J. OFDM Waveform Synchronisation for Multistatic Radar and DVB-T2 Illumination. In Proceedings of the International Conference on Radar (RADAR), Toulon, France, 23–27 September 2019; pp. 1–6. [Google Scholar]
- Misiurewicz, J. Resampling methods for stretch processing in PCL radars. In Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2007; SPIE, International Society for Optics and Photonics: Bellingham, WA, USA, 2007; Volume 6937, pp. 896–901. [Google Scholar] [CrossRef]
- Malanowski, M.; Kulpa, K. Correction of range cell migration with FIR filter for passive radar. In Proceedings of the IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 1123–1128. [Google Scholar] [CrossRef]
- Crouse, D. A time-shift model for OFDM radar. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; pp. 0841–0846. [Google Scholar] [CrossRef]
- Richards, M. The Keystone Transformation for Correcting Range Migration in Range-Doppler Processing. Available online: https://radarsp.weebly.com/supplemental-tech-notes.html (accessed on 16 March 2020).
- Barott, W.; Engle, J. Single-antenna ATSC passive radar observations with remodulation and keystone formatting. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0159–0163. [Google Scholar] [CrossRef]
- Kirkland, D. Linear and Second Order Keystone Transforms and Their Applications. Available online: https://cradpdf.drdc-rddc.gc.ca/PDFS/unc131/p538213_A1b.pdf (accessed on 10 March 2020).
- Scott, K.; Barott, W.; Himed, B. The keystone transform: Practical limits and extension to second order corrections. In Proceedings of the IEEE Radar Conference (RadarConf), Arlington, VA, USA, 27–30 October 2015; pp. 1264–1269. [Google Scholar] [CrossRef]
- Digital Video Broadcasting (DVB). Frame Structure Channel Coding and Modulation for a Second Television Broadcasting System (DVB-T2); European standard ETSI EN 302 755, Rev. V1.4.1 (2015-07); European Telecommunications Standards Institute: Sophia Antipolis, France, 2015. [Google Scholar]
- Shan, T.; Liu, S.; Zhang, Y.; Amin, M.; Tao, R.; Feng, Y. Efficient architecture and hardware implementation of coherent integration processor for digital video broadcast-based passive bistatic radar. IET Radar Sonar Navig. 2016, 10, 97–106. [Google Scholar] [CrossRef]
- Martelli, T.; Filippini, F.; Pignol, F.; Colone, F.; Cardinali, R. Computationally effective range migration compensation in PCL systems for maritime surveillance. In Proceedings of the IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 1406–1411. [Google Scholar] [CrossRef]
- Pignol, F.; Colone, F.; Martelli, T. Lagrange–Polynomial-Interpolation-Based Keystone Transform for a Passive Radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1151–1167. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, T.; Long, T.; Wang, Z. Range Migration Compensation and Doppler Ambiguity Resolution by Keystone Transform. In Proceedings of the 2006 CIE International Conference on Radar, Shanghai, China, 16–19 October 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Strange, A.; Barott, W.; Roberts, B.; Himed, B. A Time-Domain Keystone Transform Filter. In Proceedings of the IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Stolt, R. Migration by Fourier Transform. Geophysics 1978, 43, 23–48. [Google Scholar] [CrossRef]
- Xie, J.; Luo, Y. Comments on “Range Gate Straddling Loss and Joint Probability with Partial Correlation”. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 773–775. [Google Scholar] [CrossRef]









| Time | Bandwidth | Max. Resolution | Frequency | |
|---|---|---|---|---|
| /s | /MHz | /m | /Hz | dB |
| 1 | 0.77 | 194.8 | 1 | 58.8 |
| 0.5 | 1.50 | 100.0 | 2 | 58.8 |
| 0.1 | 7.70 | 19.5 | 10 | 58.8 |
| 0.05 | 15.40 | 9.7 | 20 | 58.8 |
| 0.02 | 37.93 | 4.0 | 50 | 58.8 |
| 0.01 | 75.86 | 2.0 | 100 | 58.8 |
| 7.59 × | 1000 | 0.15 | 1318 | 58.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bok, D.; O’Hagan, D.; Knott, P. Effects of Movement for High Time-Bandwidths in Batched Pulse Compression Range-Doppler Radar. Sensors 2021, 21, 2492. https://doi.org/10.3390/s21072492
Bok D, O’Hagan D, Knott P. Effects of Movement for High Time-Bandwidths in Batched Pulse Compression Range-Doppler Radar. Sensors. 2021; 21(7):2492. https://doi.org/10.3390/s21072492
Chicago/Turabian StyleBok, Dominik, Daniel O’Hagan, and Peter Knott. 2021. "Effects of Movement for High Time-Bandwidths in Batched Pulse Compression Range-Doppler Radar" Sensors 21, no. 7: 2492. https://doi.org/10.3390/s21072492
APA StyleBok, D., O’Hagan, D., & Knott, P. (2021). Effects of Movement for High Time-Bandwidths in Batched Pulse Compression Range-Doppler Radar. Sensors, 21(7), 2492. https://doi.org/10.3390/s21072492







