Real-Time Compression for Tactile Internet Data Streams †
Abstract
1. Introduction
2. Materials and Methods
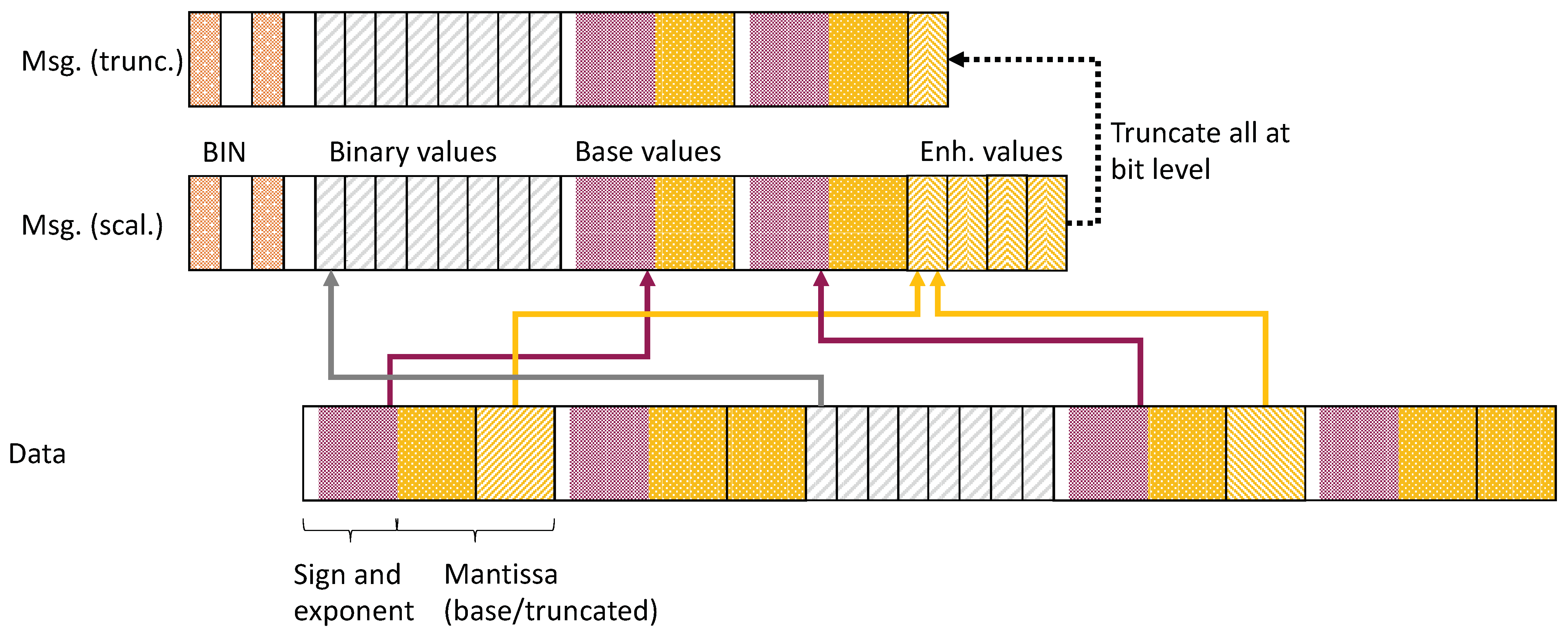
2.1. Bit-Level Integrated Scalability Support (BINBLISS)
2.2. Configuration
| Algorithm 1: Perceptual change incorporation into BINBLISS. |
 |
2.3. TU Munich Kinesthetic Traces
2.4. JIGSAWS Traces
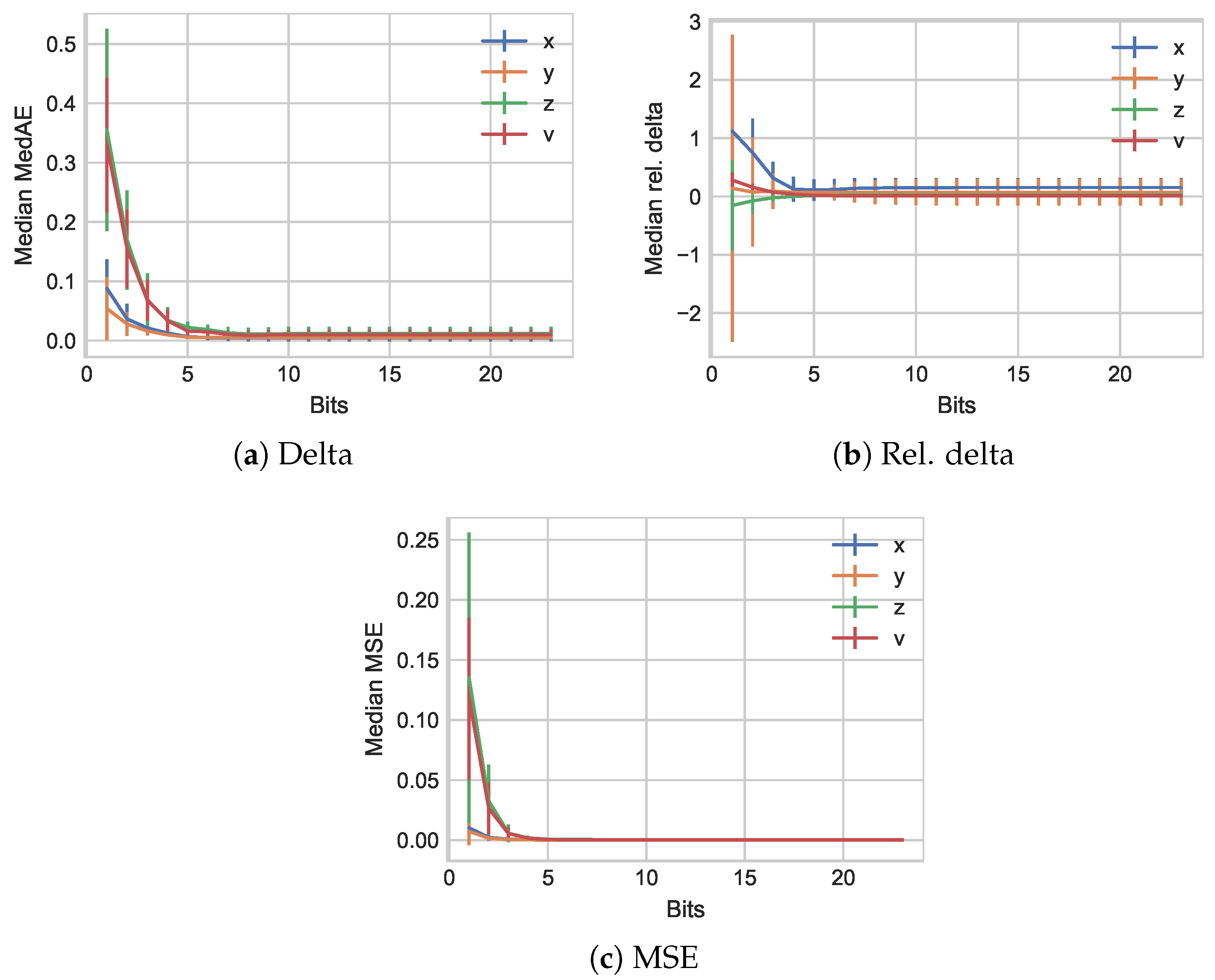
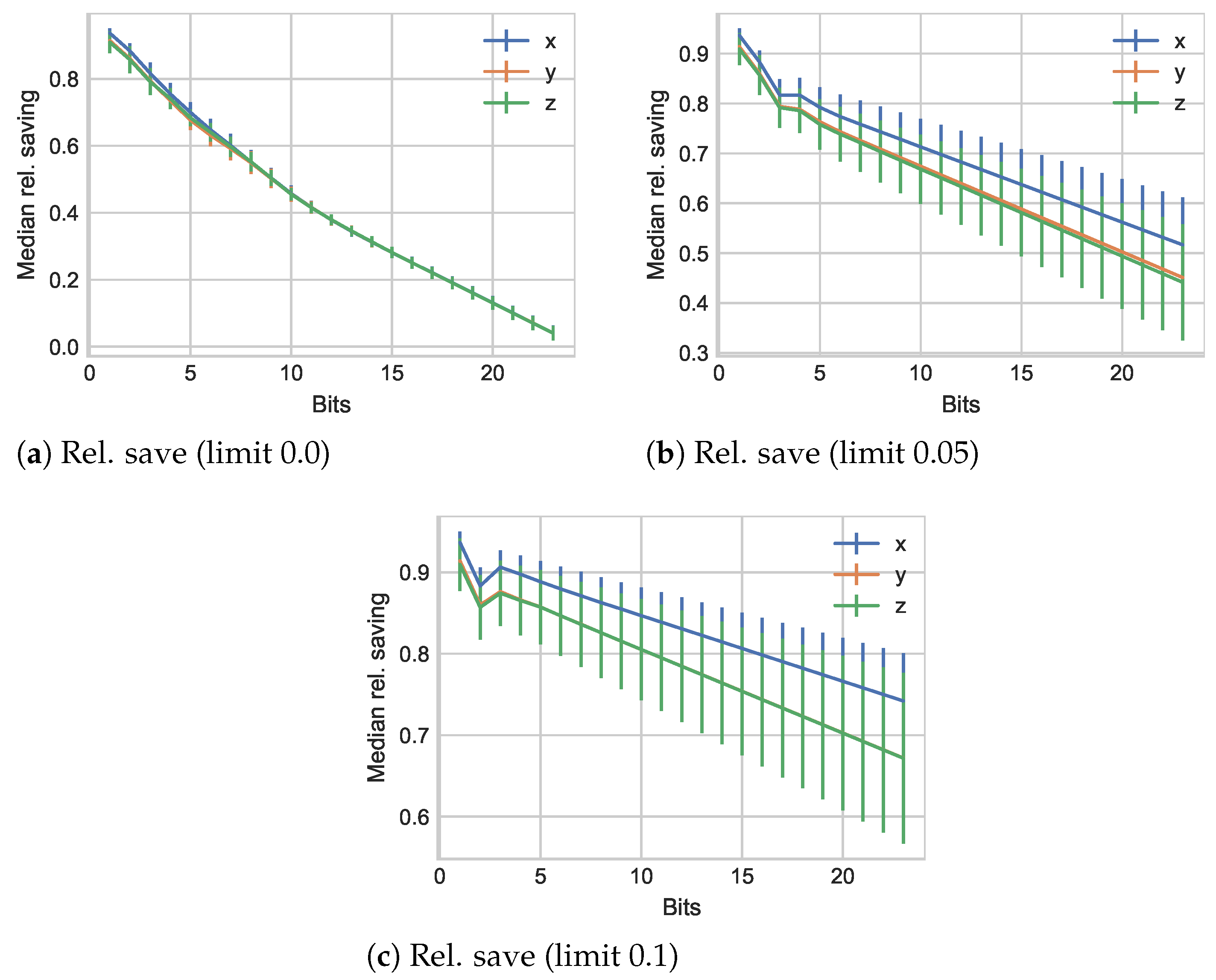
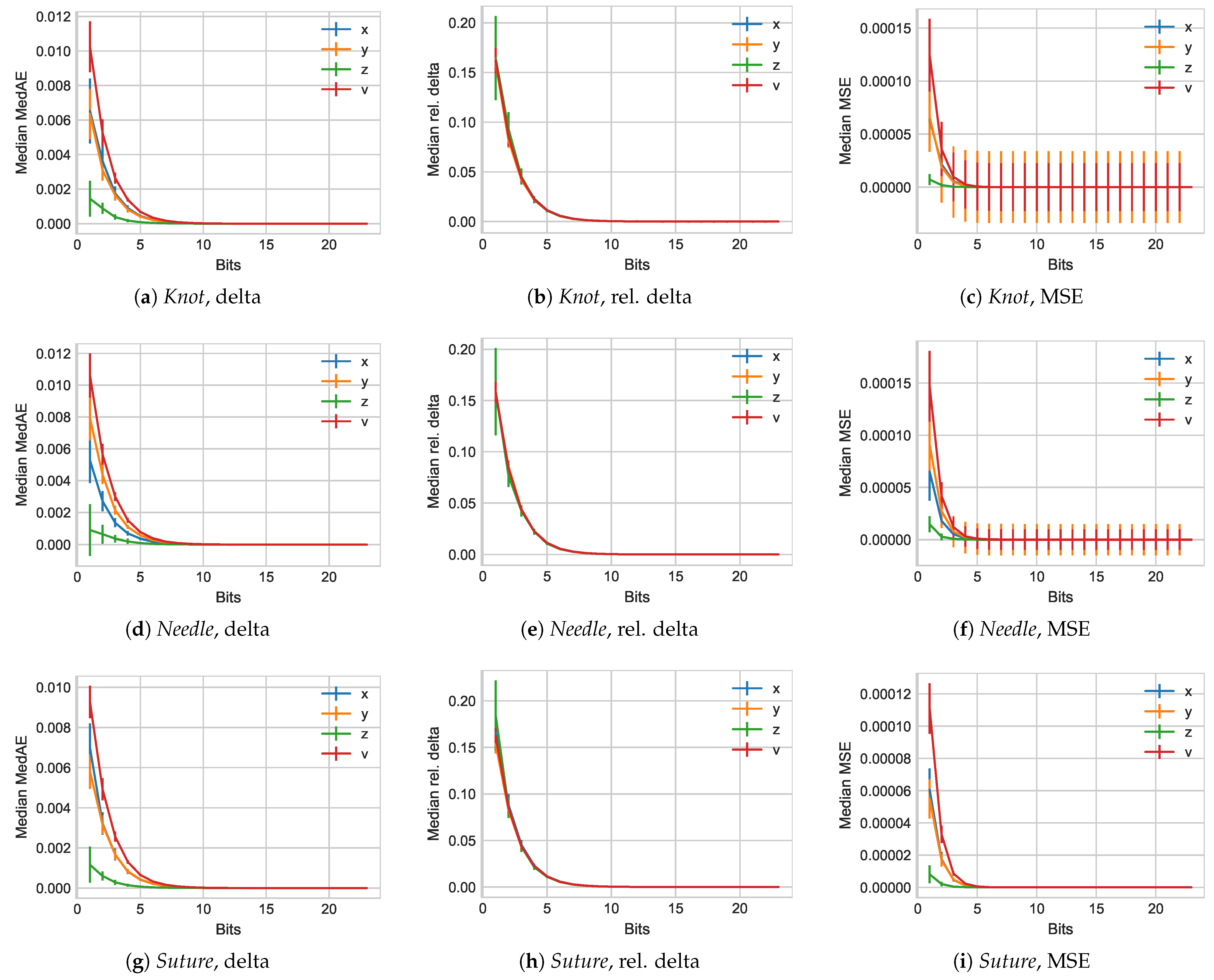
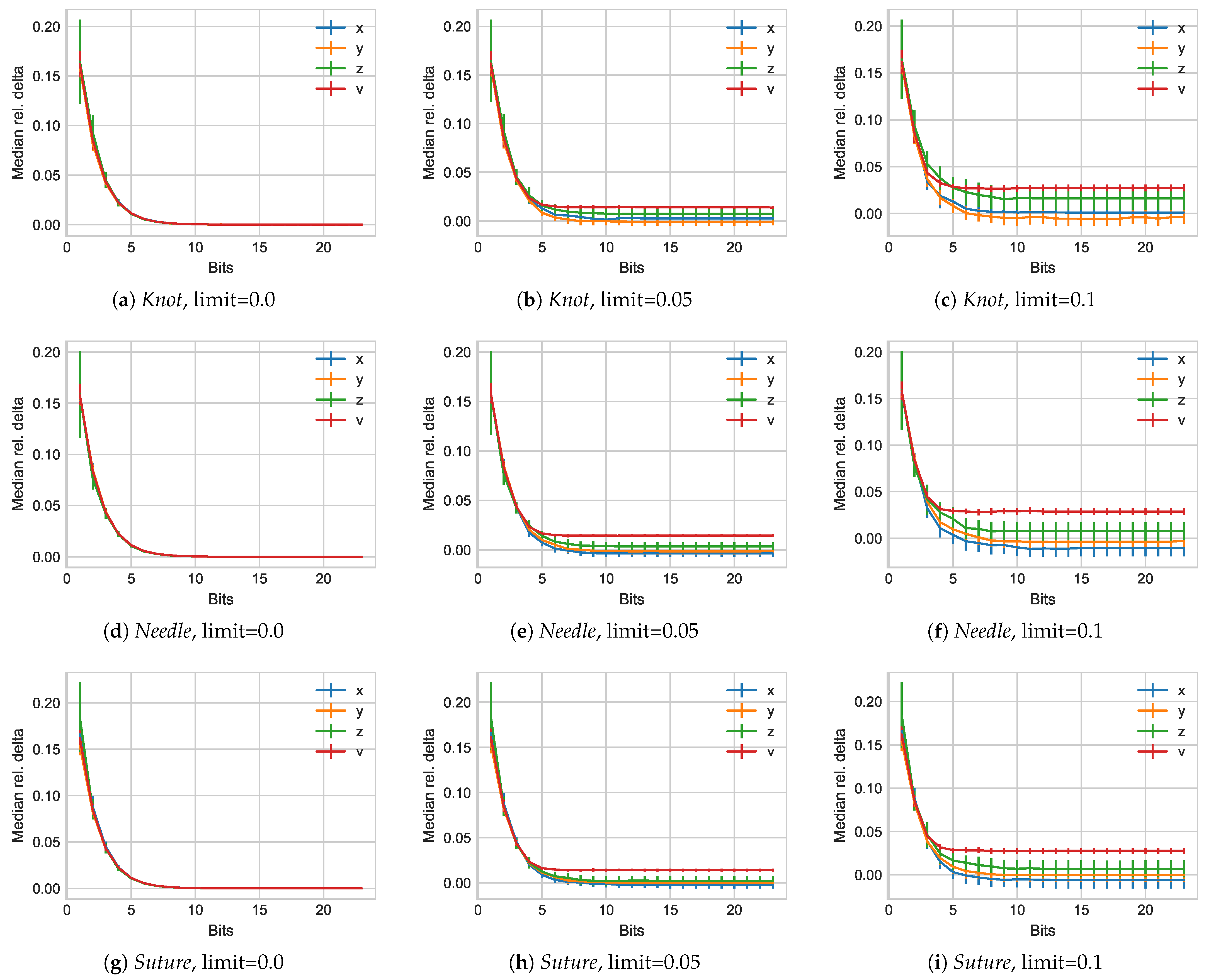
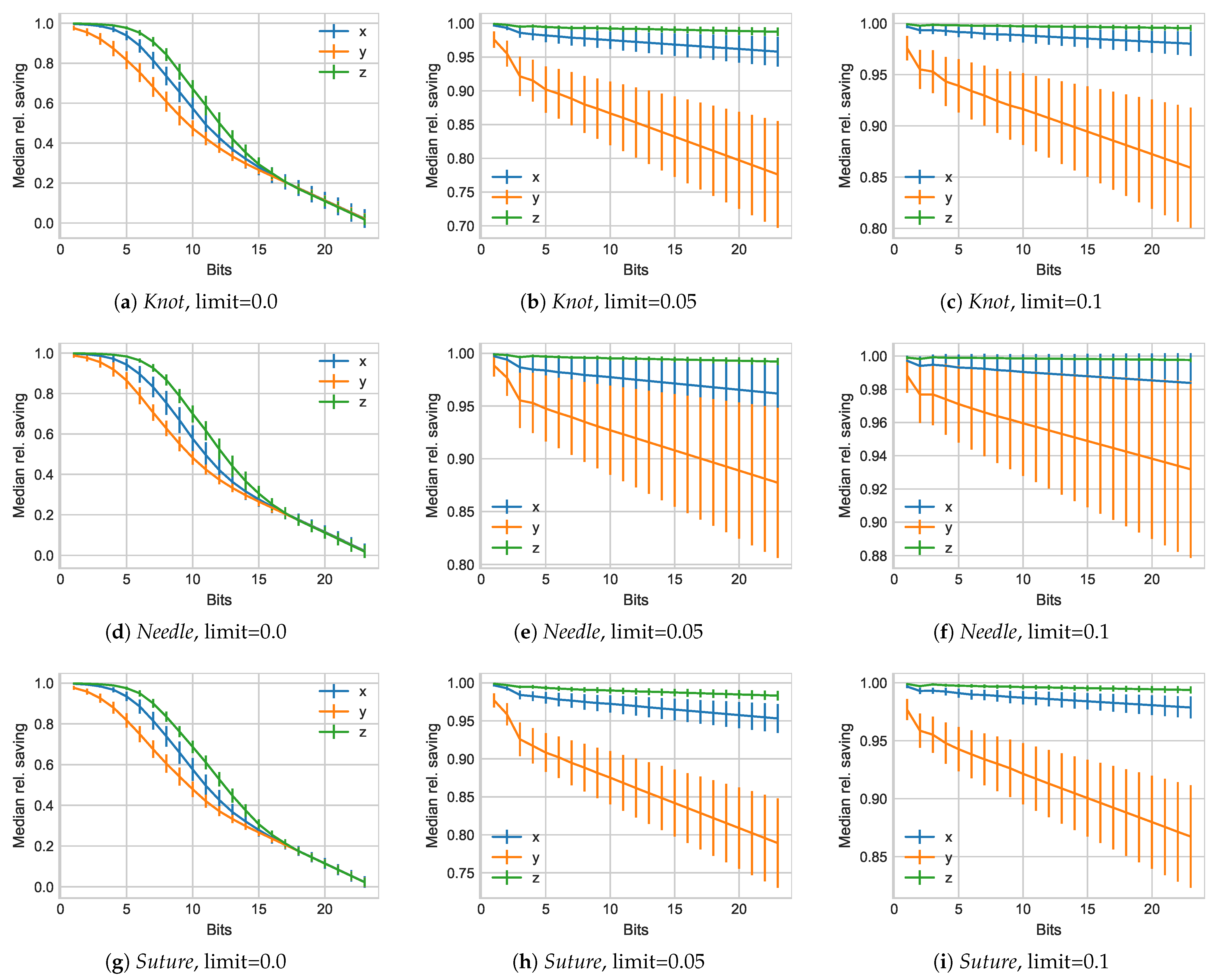
3. Compression Results
3.1. TU Munich Kinesthetic Traces
3.2. JIGSAW
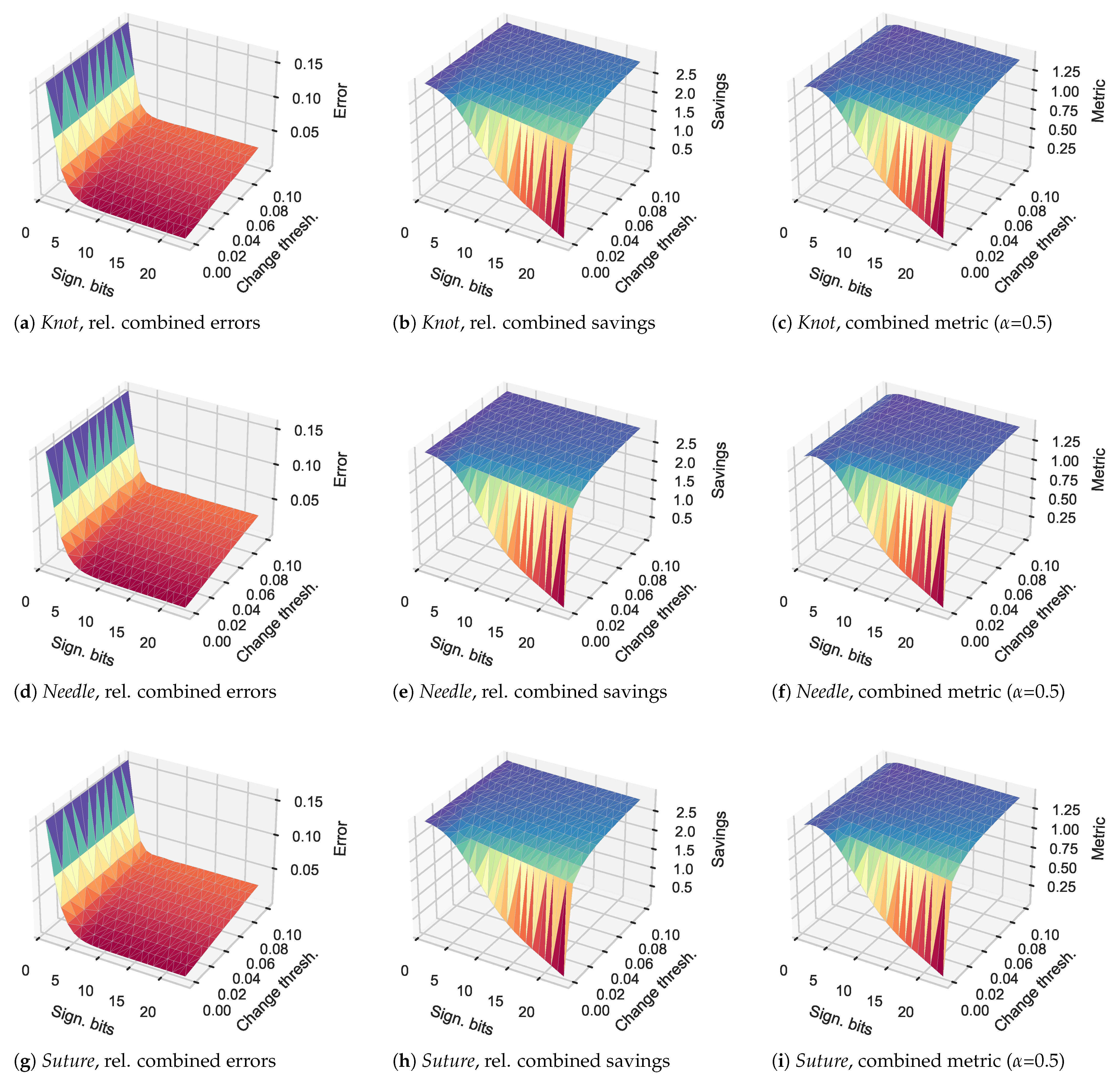
4. Combined Performance Metric
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Forge, S.; Vu, K. Forming a 5G Strategy for Developing Countries: A Note for Policy Makers. Telecommun. Policy 2020, 44, 101975.1–101975.24. [Google Scholar] [CrossRef]
- Hoeschele, T.; Dietzel, C.; Kopp, D.; Fitzek, F.; Reisslein, M. Importance of Internet Exchange Point (IXP) Infrastructure for 5G: Estimating the Impact of 5G Use Cases. Telecommun. Policy 2021, 45, 102091.1–102091.18. [Google Scholar] [CrossRef]
- Maternia, M.; Ayoubi, S.E.E.; Fallgren, M.; Spapis, P.; Qi, Y.; Martin-Sacristan, D.; Óscar, C.; Fresia, M.; Payaro, M.; Schubert, M.; et al. 5G PPP use cases and performance evaluation models. 2016. Available online: https://5g-ppp.eu/wp-content/uploads/2014/02/5G-PPP-use-cases-and-performance-evaluation-modeling_v1.0.pdf (accessed on 8 March 2021).
- Navarro-Ortiz, J.; Romero-Diaz, P.; Sendra, S.; Ameigeiras, P.; Ramos-Munoz, J.J.; Lopez-Soler, J.M. A survey on 5G usage scenarios and traffic models. IEEE Commun. Surv. Tutor. 2020, 22, 905–929. [Google Scholar] [CrossRef]
- Rendon Schneir, J.; Ajibulu, A.; Konstantinou, K.; Bradford, J.; Zimmermann, G.; Droste, H.; Canto, R. A Business Case for 5G Mobile Broadband in a Dense Urban Area. Telecommun. Policy 2019, 43, 101813.1–101813.19. [Google Scholar] [CrossRef]
- Verde, S.; Marcon, M.; Milani, S. Advanced Assistive Maintenance Based on Augmented Reality and 5G Networking. Sensors 2020, 20, 7157. [Google Scholar] [CrossRef]
- Fettweis, G.P. The Tactile Internet: Applications and Challenges. IEEE Veh. Technol. Mag. 2014, 9, 64–70. [Google Scholar] [CrossRef]
- Fitzek, F.; Li, S.C.; Speidel, S.; Strufe, T.; Simsek, M.; Reisslein, M. Tactile Internet with Human-in-the-Loop; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Bello, L.L.; Steiner, W. A Perspective on IEEE Time-Sensitive Networking for Industrial Communication and Automation Systems. Proc. IEEE 2019, 107, 1094–1120. [Google Scholar] [CrossRef]
- Finn, N. Introduction to time-sensitive networking. IEEE Commun. Stand. Mag. 2018, 2, 22–28. [Google Scholar] [CrossRef]
- Gavriluţ, V.; Pop, P. Traffic-type Assignment for TSN-based Mixed-criticality Cyber-physical Systems. ACM Trans. Cyber Phys. Syst. 2020, 4, 1–27. [Google Scholar] [CrossRef]
- Nasrallah, A.; Thyagaturu, A.S.; Alharbi, Z.; Wang, C.; Shao, X.; Reisslein, M.; ElBakoury, H. Ultra-Low Latency (ULL) Networks: The IEEE TSN and IETF DetNet Standards and Related 5G ULL Research. IEEE Commun. Surv. Tutor. 2019, 21, 88–145. [Google Scholar] [CrossRef]
- Varga, P.; Peto, J.; Franko, A.; Balla, D.; Haja, D.; Janky, F.; Soos, G.; Ficzere, D.; Maliosz, M.; Toka, L. 5G Support for Industrial IoT Applications—Challenges, Solutions, and Research gaps. Sensors 2020, 20, 828. [Google Scholar] [CrossRef]
- Antonakoglou, K.; Xu, X.; Steinbach, E.; Mahmoodi, T.; Dohler, M. Towards haptic communications over the 5G Tactile Internet. IEEE Commun. Surv. Tutor. 2018, 20, 3034–3059. [Google Scholar] [CrossRef]
- Steinbach, E.; Strese, M.; Eid, M.; Liu, X.; Bhardwaj, A.; Liu, Q.; Al-Ja’afreh, M.; Mahmoodi, T.; Hassen, R.; El Saddik, A.; et al. Haptic codecs for the Tactile Internet. Proc. IEEE 2018, 107, 447–470. [Google Scholar] [CrossRef]
- Hinterseer, P.; Hirche, S.; Chaudhuri, S.; Steinbach, E. Perception-based data reduction and transmission of haptic data in telepresence and teleaction systems. IEEE Trans. Signal Process. 2008, 56, 588–597. [Google Scholar] [CrossRef]
- Weber, E.H. Die Lehre vom Tastsinne und Gemeingefühle auf Versuche gegründet; Friedrich Vieweg und Sohn: Braunschweig, Germany, 1851. [Google Scholar]
- Mohammadi Amin, F.; Rezayati, M.; van de Venn, H.; Karimpour, H.A. A Mixed-Perception Approach for Safe Human–Robot Collaboration in Industrial Automation. Sensors 2020, 20, 6347. [Google Scholar] [CrossRef] [PubMed]
- Fiedler, M.; Hossfeld, T.; Tran-Gia, P. A generic quantitative relationship between quality of experience and quality of service. IEEE Netw. 2010, 24, 36–41. [Google Scholar] [CrossRef]
- Reichl, P.; Tuffin, B.; Schatz, R. Logarithmic laws in service quality perception: Where microeconomics meets psychophysics and quality of experience. Telecommun. Syst. 2013, 52, 587–600. [Google Scholar] [CrossRef]
- Maier, M.; Ebrahimzadeh, A. Towards Immersive Tactile Internet Experiences: Low-Latency FiWi Enhanced Mobile Networks with Edge Intelligence. J. Opt. Commun. Netw. 2019, 11, B10–B25. [Google Scholar] [CrossRef]
- Meli, L.; Pacchierotti, C.; Prattichizzo, D. Experimental evaluation of magnified haptic feedback for robot-assisted needle insertion and palpation. Int. J. Med Robot. Comput. Surg. 2017, 13, e1809. [Google Scholar] [CrossRef]
- Xu, X.; Schuwerk, C.; Cizmeci, B.; Steinbach, E. Energy prediction for teleoperation systems that combine the time domain passivity approach with perceptual deadband-based haptic data reduction. IEEE Trans. Haptics 2016, 9, 560–573. [Google Scholar] [CrossRef]
- Wong, E.; Dias, M.P.I.; Ruan, L. Predictive resource allocation for Tactile Internet capable passive optical LANs. IEEE/OSA J. Light. Technol. 2017, 35, 2629–2641. [Google Scholar] [CrossRef]
- Rico, D.; Merino, P. A Survey of End-to-End Solutions for Reliable Low-Latency Communications in 5G Networks. IEEE Access 2020, 8, 192808–192834. [Google Scholar] [CrossRef]
- Ferrer, A.J.; Marquès, J.M.; Jorba, J. Towards the decentralised cloud: Survey on approaches and challenges for mobile, ad hoc, and edge computing. ACM Comput. Surv. (CSUR) 2019, 51, 111.1–111.36. [Google Scholar] [CrossRef]
- Fitzek, F.; Granelli, F.; Seeling, P. Computing in Communication Networks; Academic Press Books: Cambridge, MA, USA, 2020. [Google Scholar]
- Mehrabi, M.; You, D.; Latzko, V.; Salah, H.; Reisslein, M.; Fitzek, F.H. Device-Enhanced MEC: Multi-Access Edge Computing (MEC) Aided by End Device Computation and Caching: A Survey. IEEE Access 2019, 7, 166079–166108. [Google Scholar] [CrossRef]
- Junior, J.C.; Torquato, M.F.; Mahmoodi, T.; Dohler, M.; Fernandes, M.A. Reconfigurable Computing Applied to Latency Reduction for the Tactile Internet. arXiv 2020, arXiv:2003.12463. [Google Scholar]
- Linguaglossa, L.; Lange, S.; Pontarelli, S.; Rétvári, G.; Rossi, D.; Zinner, T.; Bifulco, R.; Jarschel, M.; Bianchi, G. Survey of performance acceleration techniques for network function virtualization. Proc. IEEE 2019, 107, 746–764. [Google Scholar] [CrossRef]
- Niemiec, G.S.; Batista, L.M.; Schaeffer-Filho, A.E.; Nazar, G.L. A Survey on FPGA Support for the Feasible Execution of Virtualized Network Functions. IEEE Commun. Surv. Tutor. 2019, 22, 504–525. [Google Scholar] [CrossRef]
- Shantharama, P.; Thyagaturu, A.S.; Reisslein, M. Hardware-Accelerated Platforms and Infrastructures for Network Functions: A Survey of Enabling Technologies and Research Studies. IEEE Access 2020, 8, 132021–132085. [Google Scholar] [CrossRef]
- Xiang, Z.; Gabriel, F.; Urbano, E.; Nguyen, G.T.; Reisslein, M.; Fitzek, F.H. Reducing latency in virtual machines: Enabling tactile Internet for human-machine co-working. IEEE J. Sel. Areas Commun. 2019, 37, 1098–1116. [Google Scholar] [CrossRef]
- Freund, E.; Rossmann, J. Projective virtual reality: Bridging the gap between virtual reality and robotics. IEEE Trans. Robot. Autom. 1999, 15, 411–422. [Google Scholar] [CrossRef]
- Guivant, J.; Cossell, S.; Whitty, M.; Katupitiya, J. Internet-based operation of autonomous robots: The role of data replication, compression, bandwidth allocation and visualization. J. Field Robot. 2012, 29, 793–818. [Google Scholar] [CrossRef]
- Kelly, A.; Chan, N.; Herman, H.; Huber, D.; Meyers, R.; Rander, P.; Warner, R.; Ziglar, J.; Capstick, E. Real-time photorealistic virtualized reality interface for remote mobile robot control. Int. J. Robot. Res. 2011, 30, 384–404. [Google Scholar] [CrossRef]
- Tsokalo, I.A.; Kuss, D.; Kharabet, I.; Fitzek, F.H.P.; Reisslein, M. Remote Robot Control with Human-in-the-Loop over Long Distances Using Digital Twins. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, X.; Cizmeci, B.; Schuwerk, C.; Steinbach, E. Model-mediated teleoperation: Toward stable and transparent teleoperation systems. IEEE Access 2016, 4, 425–449. [Google Scholar] [CrossRef]
- Qie, Y.; Hao, C.; Song, P. Wireless Transmission Method for Large Data Based on Hierarchical Compressed Sensing and Sparse Decomposition. Sensors 2020, 20, 7146. [Google Scholar] [CrossRef]
- Pirozzi, S. Tactile Sensors for Robotic Applications. Sensors 2020, 20, 7009. [Google Scholar] [CrossRef] [PubMed]
- Junior, J.C.V.S.; Torquato, M.F.; Noronha, D.H.; Silva, S.N.; Fernandes, M.A.C. Proposal of the Tactile Glove Device. Sensors 2019, 19, 5029. [Google Scholar] [CrossRef]
- Sayem, M.; Sadat, A.; Hon Teay, S.; Shahariar, H.; Fink, P.L.; Albarbar, A. Review on Smart Electro-Clothing Systems (SeCSs). Sensors 2020, 20, 587. [Google Scholar] [CrossRef]
- Wilson, S.; Laing, R. Fabrics and Garments as Sensors: A Research Update. Sensors 2019, 19, 3570. [Google Scholar] [CrossRef]
- Seeling, P.; Fitzek, F.H.P. Binary Indicated Numbers with Bit-Level Integrated Scalability Support (BINBLISS). In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020. [Google Scholar]
- Seeling, P.; Reisslein, M. Video Traffic Characteristics of Modern Encoding Standards: H.264/AVC with SVC and MVC Extensions and H.265/HEVC. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Liu, S. Recent Advances in Video Coding Beyond the HEVC Standard. APSIPA Trans. Signal Inf. Process. 2019, 8, e18-1–e18-10. [Google Scholar] [CrossRef]
- Zhang, T.; Mao, S. An Overview of Emerging Video Coding Standards. ACM GetMobile: Mob. Comput. Commun. 2019, 22, 13–20. [Google Scholar] [CrossRef]
- Sanchez-Gomez, J.; Gallego-Madrid, J.; Sanchez-Iborra, R.; Santa, J.; Skarmeta, A. Impact of SCHC Compression and Fragmentation in LPWAN: A Case Study with LoRaWAN. Sensors 2020, 20, 280. [Google Scholar] [CrossRef] [PubMed]
- Hough, D.G. The IEEE Standard 754: One for the History Books. Computer 2019, 52, 109–112. [Google Scholar] [CrossRef]
- Kirsch, J.; Noll, A.; Strese, M.; Liu, Q.; Steinbach, E. A Low-Cost Acquisition, Display, and Evaluation Setup for Tactile Codec Development. In Proceedings of the 2018 IEEE International Symposium on Haptic, Audio and Visual Environments and Games (HAVE), Dalian, China, 20–21 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, Y.; Vedula, S.S.; Reiley, C.E.; Ahmidi, N.; Varadarajan, B.; Lin, H.C.; Tao, L.; Zappella, L.; Bejar, B.; Yuh, D.D.; et al. JHU-ISI gesture and skill assessment working set (JIGSAWS): A surgical activity dataset for human motion modeling. In Proceedings of the Fifth Workshop on Modeling and Monitoring of Computer Assisted Interventions (M2CAI), BOSTON, MA, USA, 14–18 September 2014; Volume 3, pp. 1–10. [Google Scholar]
- Hektner, J.M.; Schmidt, J.A.; Csikszentmihalyi, M. Experience Sampling Method: Measuring the Quality of Everyday Life; SAGE: Thousand Oaks, CA, USA, 2007. [Google Scholar]
- Migabo, E.; Djouani, K.; Kurien, A. An Energy-Efficient and Adaptive Channel Coding Approach for Narrowband Internet of Things (NB-IoT) Systems. Sensors 2020, 20, 3465. [Google Scholar] [CrossRef]
- Nguyen, V.; Tasdemir, E.; Nguyen, G.T.; Lucani, D.E.; Fitzek, F.H.; Reisslein, M. DSEP Fulcrum: Dynamic Sparsity and Expansion Packets for Fulcrum Network Coding. IEEE Access 2020, 8, 78293–78314. [Google Scholar] [CrossRef]
- Peralta, G.; Cid-Fuentes, R.G.; Bilbao, J.; Crespo, P.M. Homomorphic Encryption and Network Coding in IoT Architectures: Advantages and Future Challenges. Electronics 2019, 8, 827. [Google Scholar] [CrossRef]
- Tanjung, D.; Byeon, S.; Huh, J.; Kim, D.; Kim, J. Opportunistic and On-Demand Network Coding-Based Solutions for LPWAN Forwarding. Sensors 2020, 20, 5792. [Google Scholar] [CrossRef]
- Chukhno, O.; Chukhno, N.; Araniti, G.; Campolo, C.; Iera, A. Optimal Placement of Social Digital Twins in Edge IoT Networks. Sensors 2020, 20, 6181. [Google Scholar] [CrossRef]
- Gu, X.; Ji, C.; Zhang, G. Energy-Optimal Latency-Constrained Application Offloading in Mobile-Edge Computing. Sensors 2020, 20, 3064. [Google Scholar] [CrossRef]
- Hamdan, S.; Ayyash, M.; Almajali, S. Edge-Computing Architectures for Internet of Things Applications: A Survey. Sensors 2020, 20, 6441. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L. Privacy-Preserving Distributed Analytics in Fog-Enabled IoT Systems. Sensors 2020, 20, 6153. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seeling, P.; Reisslein, M.; Fitzek, F.H.P. Real-Time Compression for Tactile Internet Data Streams. Sensors 2021, 21, 1924. https://doi.org/10.3390/s21051924
Seeling P, Reisslein M, Fitzek FHP. Real-Time Compression for Tactile Internet Data Streams. Sensors. 2021; 21(5):1924. https://doi.org/10.3390/s21051924
Chicago/Turabian StyleSeeling, Patrick, Martin Reisslein, and Frank H. P. Fitzek. 2021. "Real-Time Compression for Tactile Internet Data Streams" Sensors 21, no. 5: 1924. https://doi.org/10.3390/s21051924
APA StyleSeeling, P., Reisslein, M., & Fitzek, F. H. P. (2021). Real-Time Compression for Tactile Internet Data Streams. Sensors, 21(5), 1924. https://doi.org/10.3390/s21051924







