Abstract
Carbon nanomaterials, such as carbon nanotubes (CNTs), graphene sheets (GSs), and carbyne, are an important new class of technological materials, and have been proposed as nano-mechanical sensors because of their extremely superior mechanical, thermal, and electrical performance. The present work reviews the recent studies of carbon nanomaterials-based nano-force and nano-mass sensors using mechanical analysis of vibration behavior. The mechanism of the two kinds of frequency-based nano sensors is firstly introduced with mathematical models and expressions. Afterward, the modeling perspective of carbon nanomaterials using continuum mechanical approaches as well as the determination of their material properties matching with their continuum models are concluded. Moreover, we summarize the representative works of CNTs/GSs/carbyne-based nano-mass and nano-force sensors and overview the technology for future challenges. It is hoped that the present review can provide an insight into the application of carbon nanomaterials-based nano-mechanical sensors. Showing remarkable results, carbon nanomaterials-based nano-mass and nano-force sensors perform with a much higher sensitivity than using other traditional materials as resonators, such as silicon and ZnO. Thus, more intensive investigations of carbon nanomaterials-based nano sensors are preferred and expected.
1. Introduction
During the last several decades, since the fast development of observation instruments for nanotechnology such as scanning electron microscopy (SEM), transmission electron microscopy (TEM), scanning tunneling microscopy (STM), and atomic force microscopy (AFM), a variety of carbon nanomaterials, e.g., fullerene [1], carbon nanotubes (CNTs) [2,3,4], graphene sheets (GSs) [5], and carbyne [6] were discovered (or predicted) and investigated by scholars (as shown in Figure 1). For instance, according to the invention of STM, which won the Nobel Prize in Physics in 1986, Kroto et al. [1] first produced and observed a soccer ball-like C60 fullerene and were awarded the 1996 Nobel Prize in Chemistry, and Iijima [3] synthesized and measured double-walled, five-walled, and seven-walled CNTs with diameters of 5.5, 6.7 and 6.5 nm, respectively. CNTs with one wall are often called single-walled CNTs (SWCNTs), with two walls are named as double-walled CNTs (DWCNTs), and with more than two walls are named as multi-walled CNTs (MWCNTs). Using SEM and AFM, Novoselov et al. [5] first produced and observed single-layered GSs. Similar to the naming of CNTs, GSs with one layer are often called single-layered GSs (SLGSs), with two layers are named as double-layered GSs (DLGSs), and with more than two layers are named as multi-layered GSs (MLGSs). The present work focuses on the carbon nanomaterials of CNTs and GSs, which are usually adopted as components of nanoelectromechanical systems (NEMS) because of their outstanding material properties.
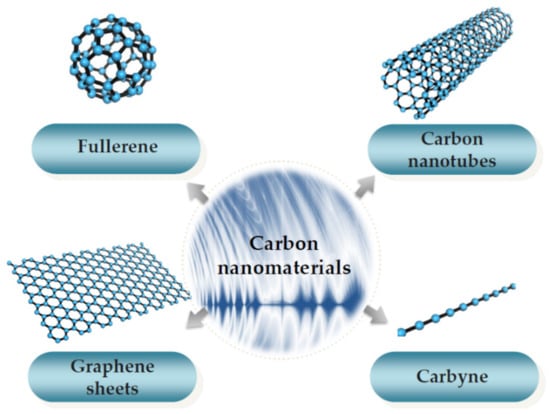
Figure 1.
Kinds of carbon nanomaterials.
Regarding the material properties of carbon nanomaterials, the representative one-dimensional (1D) CNTs and two-dimensional (2D) GSs exhibit extremely superior mechanical, thermal, electrical, and optical performance almost on the same level (e.g., [7,8,9,10,11,12,13]). For example, Shokrieh and Rafiee [7] concluded mechanical properties of CNTs determined from both theoretical and experiments methods, and indicated that Young’s modulus of CNTs could reach to the TPa range. Kumar et al. [8] made a review work of material properties of GSs, where they summarized that GSs own Young’s modulus of 1 TPa, thermal conductivity of 1500~5000 W m−1K−1, electrical conductivity of 104 S/cm, and optical transmittance of 97.7%. Because of their exceptionally high electronic conductivities, the application of CNTs and GSs on transistors [9], nanoelectronics [10], and supercapacitor [11] were also reviewed by scholars. In addition, more detail of their thermal and optical properties could also refer to some of previous review works [12,13]. According to their outstanding material properties introduced above, CNTs and GSs have been proposed and applied as sensing elements in biosensors [14,15,16], strain sensors [17,18,19], and gas sensors [20,21,22]. Besides these three kinds of sensors, carbon nanomaterials are also expected to contribute to the fields of nano-mass and nano-force sensors, which are considered in the present work.
When a mass is too tiny to be detected by a normal measure method, mass sensors using mechanical resonators belonging to micro-electromechanical systems (MEMS), even NEMS, need to be developed. It is well known that mechanical resonators can be used as inertial balances to detect tiny mass by measuring oscillation frequency shifts [23]. Abadal et al. [24] proposed a simple electromechanical model using polysilicon as a cantilevered resonator, which had the sensitivity to detect attogram scales (10−18 g) of mass. By means of a complementary metal-oxide-semiconductor (CMOS) circuitry, this model could calculate dynamic quantities of the current flowing through the resonator at the resonance frequency as well as static magnitudes of the collapse voltage and deflection of the resonator, so that the unknown mass could be detected from the feedback of the electrical specifications of the CMOS circuitry as well as the resonance frequency of the resonator. Using the similar approach, silicon-based mass sensors have been investigated and developed further [25,26,27,28,29,30,31,32,33,34,35,36,37]. However, silicon-based mass sensors have their limitations of mass detection due to their relatively lower material properties (e.g., Young’s modulus of 180 GPa [24]) and larger cross-section (e.g., thickness of 1 µm [24]) compared to carbon nanomaterials. Poncharal et al. [38] firstly produced a nano-mass sensor using a cantilevered MWCNT as the resonator and observed the electrically induced dynamic deflections of the resonator attached by a carbon particle. From calculating the resonance frequency as revealed by the deflected contours, they measured the mass of the attached carbon particle to be 22 ± 6 fg (1 fg = 10−15 g). After that, plenty of experimental and theoretical investigations of CNTs/GSs-based nano-mass sensors were carried out (e.g., [39,40,41,42,43,44,45,46,47,48]), which owned much higher sensitivity (>10−21 g) than silicon-based mass sensors.
Regarding force sensors, for manipulating nano particles, biomolecular or cells, development of high sensitivity force sensors with mechanical types [49,50,51,52,53,54,55,56], electrical types [57,58,59,60,61,62,63,64], and optical types [65,66,67,68], it has been a great challenge for advanced micro/nano-assembly and bio-engineering. Willemsen et al. [49] summarized the works of the detection of biomolecular interaction forces using AFM with silicon nitride probes by that time, in which the AFM probes were considered as force sensors that could detect the interaction forces between individual molecules in nN (10−9 N) range by mechanical evaluations, such as strain change or frequency shift. They pointed out that though AFM was a versatile and high enough instrument to discern individual molecules, it could only detect force in one direction, and it would be interesting to be able to measure lateral and torsional forces. Wang et al. [57] demonstrated a piezoelectric field effect transistor (i.e., a nano-force sensor) composed of a ZnO nanowire bridging across two electrodes, which could detect a force in nanonewton range acted on the nanowire by evaluating the decrease of conductance. Hong et al. [66] developed a CNTs-based nano-force sensor composed a CNTs-based transistor suspended with dual-trap optical tweezers, which could detect external forces by monitoring the morphology changes of the transistor using three-dimensional (3D) scanning photocurrent microscopy. This developed nano-force sensor had ability to detect mechanical coupling between individual DNA molecules and the transistor in pN (10−12 N) range, which was much more sensitive than silicon nitride/ZnO-based nano-force sensors. More detail of the difference among the three types of force sensors can be found in two previous review works [69,70]. The present work mainly discusses the frequency-based nano-force sensors, i.e., using carbon nanomaterials as resonators for detecting tiny forces from the evaluation of the resonant frequency shifts [71].
Whether for nano-mass or nano-force sensors, the determination of the resonance frequency from the vibration analysis is very important work. Theoretical analysis of the vibration behavior of carbon nanomaterials-based resonators can measure or predict the precisions of proposed nano-mass and nano-force sensors. In the mechanical analysis (e.g., vibration analysis) of carbon nanomaterials, the most essential thing is considering their analytical models. Up to now, there are generally two categories of theoretical model approaches for analyzing the mechanical properties of carbon nanomaterials. The first is the atomistic modeling techniques, such as first-principles calculation (e.g., [72,73,74,75]) and molecular dynamics (MD) simulation (e.g., [76,77,78,79]). Though any mechanical analysis of carbon nanomaterials can be simulated by the atomistic modeling techniques, due to the huge computational tasks, practical execution of the atomistic modeling techniques is often limited to atomistic models with a relatively small number of carbon atoms and a relatively short-lived phenomenon. The second is continuum mechanical modeling approaches, such as beam and shell models of carbon nanomaterials (e.g., [80,81,82,83]), where the appropriate evaluation of material properties is very essential.
The present work aims to review and discuss the recent works about carbon nanomaterials (CNTs/GSs/carbyne)-based nano-mass and nano-force sensors based on vibration analysis using continuum mechanical approaches. In Section 2, we introduce the mechanism of frequency-based nano-mass and nano-force sensors, where we point out the importance of determining the material properties of carbon nanomaterials. In Section 3, we introduce and discuss some representative works for the determination of material properties of continuum models of CNTs, GSs, and carbyne, respectively. In Section 4, we conclude the representative works of CNTs/GSs/carbyne-based nano-mass and nano-force sensors, and propose some challenge works in the future. At last, we summarize the remarkable conclusions.
2. Mechanism of Frequency-Based Nano-Mass and Nano-Force Sensors
As described in the introduction, the detection mechanism of frequency-based nano-mass and nano-force sensors is generally based on vibration analysis of the sensor systems for determining the resonant frequency shift, which is sensitive to the resonator force or mass. When an additional mass or an extra force is attached on the resonator of a nano sensor system, the resonant frequency of the resonator changes, so the accurate determination of the variation of the resonant frequency (i.e., the resonant frequency shift) can measure the additional mass or the unknown extra force exactly [41,44,69,71].
2.1. Nano-Mass Sensor
In natural vibration (also named as free vibration) analysis of a nano-mass sensor system, the typical governing equation of vibrational motion of resonators for determining its fundamental frequency can be given as [71]:
where and denote the mass and stiffness matrices of the analytical system, and are the displacement and acceleration vectors, respectively.
Here, we show the mechanism of the nano-mass sensor as following: According to Equation (1), if the dimension (e.g., thickness, diameter, and length and width) and density of resonator related to the mass matrix and the materials properties of resonators (e.g., Young’s modulus, shear modulus, and Poisson’s ratio) related to stiffness matrix are known, the fundamental frequency of the sensor system without attached mass can be calculated at first. Next, a tiny mass with mass matrix is added on the resonator to generate a different mass matrix of the total sensor system and a new fundamental frequency can be determined, so the frequency shift can be determined. Repeating this process by alternating the mass matrix of the tiny mass, the correlation curve between the additional mass and the frequency shift of the total sensor system performs one-to-one correspondence, which is used to measure an unknown tiny mass at last. However, when the tiny mass becomes smaller and smaller, the frequency shift shows a tiny change that cannot be recognized clearly, the nano-mass sensor reaches its limitation of mass detection.
2.2. Nano-Force Sensor
For governing equation of a nano-force sensor system that detecting unknown external forces, a loading vector is added on the right side of Equation (1), shown as
We introduce the mechanism of the nano-force sensor as following, which is similar with that of the nano-mass sensor. At first, the frequency of the resonator without external force (i.e., shown as Equation (1)) should be theoretically calculated. Then, a given external force related to the loading matrix is added on the resonator to generate a new frequency from Equation (2) for determining the frequency shift or the relationship between the external force and the frequency. Accordingly, the correlation curve between the external force and the frequency shift (or the frequency) of the total sensor system can be drawn, which can be used to measure an unknown external force at last. Additionally, when the external force becomes smaller and smaller until the frequency shift shows an extremely tiny change that cannot be recognized, the nano-force sensor reaches its measure limitation of force detection.
From Section 2.1 and Section 2.2, we can find that, if we want to use Equations (1) and (2) for vibration analysis of carbon nanomaterials-based nano-mass and nano-force sensors, the dimensions (e.g., thickness, diameter or width, and length) and densities of carbon nanomaterials-based resonators and the materials properties of the resonators (e.g., Young’s modulus, shear modulus, and Poisson’s ratio) should be determined coinciding with the analytical models of nano-mass and nano-force sensors. Thereby, plenty of works have been carried out for determining the material properties of continuum models of carbon nanomaterials.
3. Continuum Models of Carbon Nanomaterials
Up to now, different continuum models have been adopted for carbon nanomaterials. According to Equations (1) and (2), material properties (e.g., Young’s modulus, shear modulus, and Poisson’s ratio) as well as the dimensions (e.g., thickness, diameter or width, and length) of different continuum models of carbon nanomaterials should be determined appropriately. Here, we introduce some representative works for determining the material properties and corresponding dimensions of continuum models of CNTs, GSs, and carbyne, respectively.
3.1. Carbon Nanotubes and Graphene Sheets
Among carbon nanomaterials, CNTs and GSs have been attracted the most interest of scholars. In general, there are two equivalent continuum models, which are shell and beam models, usually adopted in theoretical analysis of CNTs and GSs. Generally, perfect GSs are 2D materials and CNTs can be considered as tubes rolled from GSs, so both of CNTs and GSs are often analyzed based on classical plate/shell theories (e.g., [84,85,86,87,88]). Additionally, CNTs are 1D materials, so beam theories can be adopted for mechanical analysis of CNTs (e.g., [89,90,91,92]), which is used the most in theoretical evaluation of CNTs-based nano-mass and nano-force sensors. Moreover, graphene nanoribbons (GNRs) are special kinds of GSs owning 1D structures, so mechanical behavior of GNRs can be also analyzed by beam theories (e.g., [93,94,95,96]). Whether using shell theories or beam theories for mechanical analysis of CNTs and GSs, their material properties should be evaluated matching with atomistic modeling techniques.
With respect to CNTs, Yakobson et al. [76] performed MD simulation of SWCNTs subjected to axial compressive forces and estimated Young’s modulus and thickness of shell model of SWCNTs as 5.5 TPa and 0.066 nm, which could be used for theoretical analysis of mechanical behaviors of SWCNTs. However, this work was discussed as the well-known “Yakobson’s paradox” because of the contradicting results of Young’s modulus of SWCNTs compared with other studies (around 1 TPa) [97,98,99].
In 2003, Li and Chou [100] proposed a notable continuum mechanical approach, named as molecular structural mechanics (MSM), for modeling CNTs and GSs with frame-like structures by establishing a linkage between the molecular mechanics (MM) and the structural mechanics. Detail of this approach was shown in Figure 2, where the total steric potential energy of each C–C chemical bond with a summation of the bond stretching interaction energy , the bond angle bending energy , and the equivalent torsion energy were expressed as shown in Equation (3).
and each potential energy was given as:
where , , and indicated the bond stretching resistance constant, the bond bending resistance constant, and the bond torsion resistance of a C–C chemical bond, respectively, which were determined based on MM [101]. , , and were the stretching deformation, the bending rotational angle, and the torsion rotational angle, respectively.
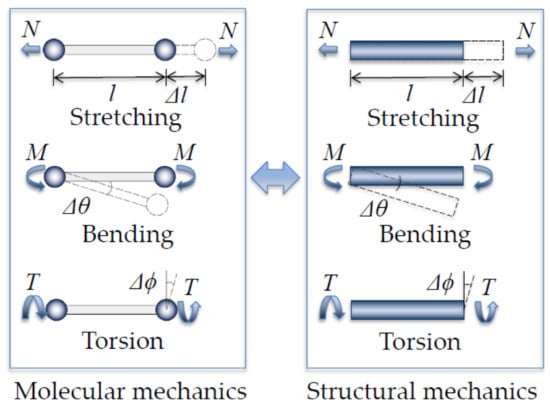
Figure 2.
Continuum mechanical approach for modeling C–C chemical bond as an equivalent continuum beam from a linkage between molecular mechanics and structural mechanics.
On the other hand, each C–C chemical bond could be also assumed as an equivalent continuum beam with the tensile resistance , the flexural bending rigidity , and the torsion stiffness . Accordingly, each potential energy in terms of stretching, bending, and torsion energy of the equivalent continuum beam could also be determined from structural mechanics, shown as:
where is the length of the C–C chemical bond.
Using the direct relationship between Equations (4)–(6) and Equations (7)–(9), the material properties and sectional stiffness parameters of the equivalent continuum beam could be calculated and adopted in FEM for mechanical analysis of CNTs and GSs. With this approach, Li and Chou calculated Young’s moduli and shear moduli of GSs and SWCNTs with different diameters, which were 0.85~1.05 TPa and 0.2~0.5 TPa, respectively, as shown in Figure 3. Up to now, the approach of MSM has been widely adopted for calculating the material properties (e.g., Young’s modulus and shear modulus) of CNTs (e.g., [102,103,104,105,106,107,108,109]) and GSs (e.g., [106,107,108,109,110,111,112,113,114,115,116]) for mechanical analysis with continuum shell and beam models.
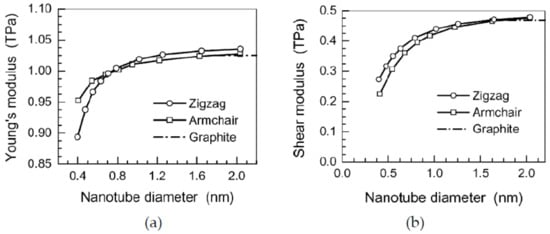
Figure 3.
(a) Young’s moduli and (b) shear moduli of carbon nanotubes versus tube diameter. Adapted with permission for [100], copyright Elsevier, 2003.
Along with the Young’s modulus and shear modulus, the thickness of the continuum models of CNTs and GSs was also an essential dimensional parameter in theoretical analysis. 0.34 nm, the interlayer distance between each graphene layer in graphite, was commonly assumed for mechanical analysis of CNTs and GSs (e.g., [117,118,119,120]. However, for the mechanical analysis of CNTs and GSs using continuum mechanics theories, the appropriate thickness should be determined matching with different analytical conditions. For example, in the “Yakobson’s paradox”, the thickness of CNTs was calculated as 0.066 nm (paired with Young’s modulus 5.5 TPa) matching with MD simulation under loading condition of axial compression. Shi et al. [112] calculated Young’s modulus and thickness of GSs as 2.81 TPa and 1.27 Å considering bending and stretching loading conditions simultaneously. However, both works did not consider the density term, so they are difficult to be adopted in vibration analysis of CNTs and GSs. Hence, we should note here that, in vibration analysis of CNTs and GSs, the density term related to the mass matrix usually should be determined simultaneously matching with Young’s modulus, shear modulus, and thickness, which will be an essential work in development of CNTs and GSs-based nano sensors using continuum mechanical approaches in the future.
3.2. Carbyne
Carbyne is a chain of carbon atoms linked with double chemical bonds (…C=C=C…) or alternating single and triple chemical bonds (…C–C≡C…). Liu et al. [121] investigated the mechanical behavior of carbyne by means of first-principles calculations, where they modeled the carbyne as an elastic beam and established a link between the molecular model and the continuum beam model of carbyne under tension, bending, and torsion loading conditions. In this landmark study, they calculated the diameter, Young’s modulus, shear modulus, and Poisson’s ratio of the equivalent continuum beam model of carbyne as 0.772 Å, 32.71 TPa, 11.8 TPa and 0.386, respectively (The authors corrected the shear modulus and Poisson’s ratio as 47.2 TPa and –0.65 later [122]). These material properties have been adopted for most of the theoretical studies of carbyne using continuum mechanical approaches (e.g., [123,124,125]).
For the density of carbyne that can be used in vibration analysis, Shi et al. [123] calculated it as 32.21 g/cm3 from the following equation:
where is the total mass of a carbyne with 12 carbon atoms, is the diameter of the equivalent continuum carbyne beam, is the length of the carbyne with 12 carbon atoms.
4. Nano-Mass Sensor
With the material properties determined from Section 3, carbon nanomaterials-based nano-mass sensors can be investigated by continuum mechanical approaches using the mechanism shown in Section 2.1. Here, we introduce and summarize representative works of CNTs, GSs, and carbyne-based nano-mass sensors, respectively, by vibration analysis based on their continuum models.
4.1. Carbon Nanotubes-Based Nano-Mass Sensor
CNTs-based nano-mass sensors have been studied using variety of theoretical mechanical approaches, such as FEM (e.g., [126,127,128,129,130,131,132]) and continuum beam theories (e.g., [127,129,131,133,134,135,136,137,138,139,140,141,142,143,144]). Though shell theories of CNT were adopted in vibration analysis of CNTs (e.g., [84,85,86,87,88]), they usually treated CNTs with small aspect ratio (length/diameter) and have been seldom used for study of CNTs-based nano-mass sensor to our knowledge. The reason can be considered as that only the first vibrational mode can be evaluated for the application of nano-mass sensor and most of the CNTs-based resonators have large aspect ratio (length/diameter). Thereby, using beam models of CNTs is simple and sufficient to evaluate the efficiency of CNTs-based nano-mass sensors.
Li and Chou [126] studied CNTs-based nano-mass sensors by adopting the approach of MSM for modeling CNTs and GSs that just proposed by themselves [100]. In this study, SWCNTs with length 10 nm and diameters of 0.8, 1.0 and 1.2 nm were proposed as the resonators, and two boundary conditions, cantilevered and bridged, were considered as shown in Figure 4. From their results, as shown in Figure 5, the resonant fundamental frequencies of both cantilevered and bridged CNTs decreased with the increase of attached mass, and when the attached mass was larger than 10−6 fg (i.e., 10−21 g), a logarithmically linear relationship between the resonant frequency and the attached mass could be found, which means that the proposed CNTs-based nano-mass sensor had ability to measure a tiny mass larger than 10−21 g. In addition, the frequency shift increased with the increase of attached mass, and shorter (as shown in Figure 6a) or thicker (as shown in Figure 6b) CNTs resonator owned higher mass sensitivity. However, comparing with Figure 6a,b, the effect of tube length was much bigger than that of tube diameter on the sensitivity.
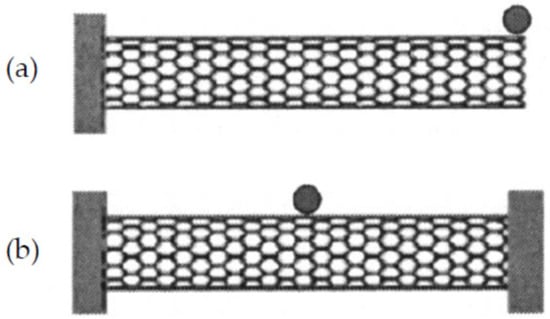
Figure 4.
(a) Cantilevered and (b) simply supported carbon nanotube resonators with an attached mass. Adapted with permission for [126], copyright AIP Publishing, 2004.
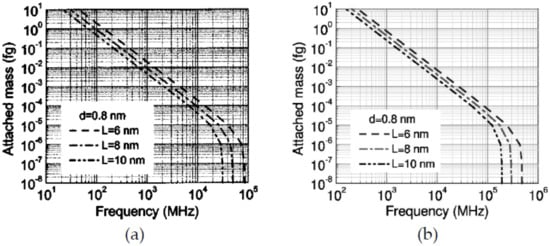
Figure 5.
Fundamental frequency of (a) cantilevered and (b) bridged carbon nanotube resonators with different length L vs. attached mass. Adapted with permission for [126], copyright AIP Publishing, 2004.
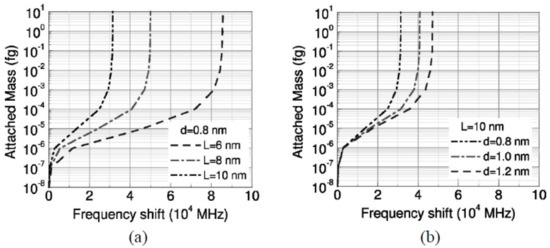
Figure 6.
Frequency shift of cantilevered carbon nanotube resonators with (a) different lengths L or (b) different diameters d vs. attached mass. Adapted with permission for [126], copyright AIP Publishing, 2004.
We summarize some of the representative works with respect to CNTs-based nano-mass sensor adopting FEM [126,127,128,129,130,131,132], Euler–Bernoulli beam theory (EBT) [127,129,131,135,138,140], nonlocal EBT [133,134,136,139,142,143,144], Timoshenko beam theory (TBT) [141], nonlocal TBT [137] for studying CNTs-based nano-mass sensors as shown in Table 1, from which we can see that though the work considering thermal and nonlocal effects could make sensitivity to atom mass of 6.65 × 10−24 g and 0.218 × 10−24 g under special thermal conditions [143,144], most of the works indicated that the CNTs-based nano-mass sensor could detect tiny mass larger than 10−21 g. Moreover, detail of CNTs-based nano-mass sensor can be also found in some previous review works [18,145].

Table 1.
Summarization of studies on carbon nanotubes-based nano-mass sensors.
4.2. Graphene Sheets-Based Nano-Mass Sensor
The study of GSs-based nano-mass sensors using continuum mechanical approaches is also popular among scholars. In contrast to 1D CNTs, GSs own 2D structures in general. Hence, using the material properties introduced in Section 3.1, continuum plate/shell theories are often adopted by scholars, such as FEM (e.g., [146,147,148]) and elasticity plate theory (EPT) (e.g., [149,150]). Tsiamaki et al. [146] proposed a circular GSs-based nano-mass sensor and simulated its vibration behavior using FEM for calculating the frequency shift. They discussed different boundary conditions of the GSs resonators and compared their results with other works to demonstrate the reasonable accuracy of the results. Their results showed that the proposed nano-mass sensor had sensitivity of 10−22 g level. Natsuki et al. [149] presented a frequency-based nano-mass sensor using rectangular DLGSs as resonators, where a continuum EPT was adopted for vibration analysis and sensitivity of the presented nano-mass sensor could also reach 10−22 g level. Furthermore, nonlocal EPT that considering nonlocal effects is also popular for the studies of GSs-based nano-mass sensors (e.g., [151,152,153,154,155,156,157]). Shen et al. [151] modeled a simply supported SLGSs-based nano-mass sensor and calculated its frequency shifts using the nonlocal Kirchhoff plate theory. The mass sensitivity of the SLGSs-based nano-mass sensor could reach at least 10−21 g. They also pointed out that the frequency shifts became smaller when the nonlocal effect was considered. In addition, as special kinds of GSs that own 1D structures, GNRs-based nano-mass sensors were also investigated using EBT (e.g., [158]) or nonlocal EBT (e.g., [159]).
To show a clear comparison, the results of GSs-based nano-mass sensors are summarized in Table 2. The summarization shows that most works indicated GSs-based nano-mass sensors have ability to detect tiny mass from 10−24 g to 10−22 g at least, which is more sensitive than CNTs-based nano-mass sensors.

Table 2.
Summarization of studies on graphene sheets-based nano-mass sensors.
4.3. Carbyne-Based Nano-Mass Sensor
Though carbyne really exists or not was a subject of great interest among some scholars several decades ago [160,161,162], carbyne has been proposed with a higher stiffness than CNTs and GSs [121]. It is also expected that resonators made by carbyne can perform higher sensitivity in nano-mass sensors.
Using the material properties determined by Liu et al. [121], Shi et al. [123] predicted the sensitivity of a carbyne-based nano-mass sensor. Considering the difficulty of preparation of long carbyne chain, carbyne resonators with 12 carbon atoms and 17 carbon atoms were investigated in this work, where they adopted the nonlocal TBT for studying the two kinds of carbyne resonators with low aspect ratios. Moreover, they also performed the Rayleigh energy method and MD simulation to confirm the feasibility of the nonlocal TBT, where the results obtained from the three methods coincided each other very well. To obtain the highest sensitivity of the carbyne-based nano-mass sensor, initial stressed carbyne resonators were also studied, where they found that a higher initial stress could obtain higher fundamental frequency of the resonator as well as higher sensitivity of mass detection. According to their results, carbyne-based nano-mass sensor could detect tiny mass reaching to the range of 10−26 g.
Just after the above-mentioned work was published, Agwa and Eltaher [124] studied the carbyne-based mass-sensor considering the influence of surface effects (i.e., surface stress and surface elasticity) on the vibration behavior of a carbyne resonator with 12 carbon atoms, where they adopted the TBT in this work. According to their results, the surface stress and surface elasticity had considerable effect on vibration behavior of the carbyne resonator, and the proposed carbyne-based nano-mass sensor had ability to detect a tiny mass below 10−23 g.
Hence, we can confirm that carbyne-based nano-mass sensors own the highest sensitivity of detecting tiny mass among the three kinds of carbon nanomaterials.
5. Nano-Force Sensor
Similar to the nano-mass sensors, using the mechanism shown in Section 2.2 and the material properties determined from Section 3, carbon nanomaterials-based nano-force sensors can also be investigated by continuum mechanical approaches. However, up to now, the studies of theoretical analysis about carbon nanomaterials-based nano-force sensors are only a few to our knowledge (e.g., [71,92,163]).
To interest more scholars in devoting themselves to the study of carbon nanomaterials-based nano-force sensors using theoretical analysis, we emphasize a previous study of CNTs-based nano-force sensors carried out by Natsuki and Urakami to show its feasibility [92]. This study was performed based on vibration analysis of CNTs using a continuum mechanical approach. In detail, a SWCNT with diameter = 2 nm and length = 40 nm as shown in Figure 7 was considered as the probe of an AFM (i.e., the resonator of a nano-force sensor). The CNT probe was partial embedded in epoxy resin with embedded length and exposed length for detecting an unknown external compressive force .
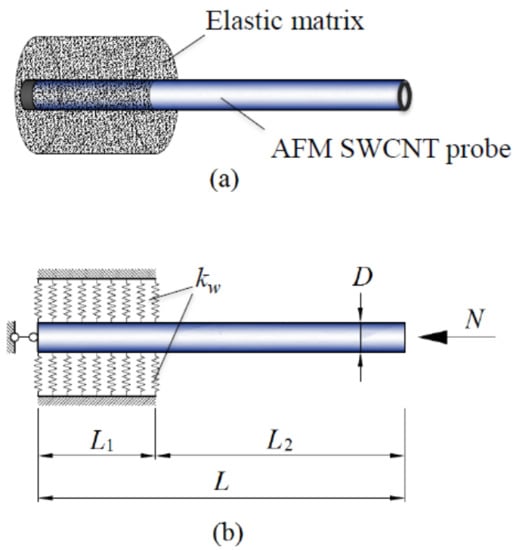
Figure 7.
(a) A proposed carbon nanotubes-based nano-force sensor, and (b) the analytical model of the partial embedded carbon nanotubes resonator [92].
Considering the large aspect ratio of the CNT probe, it was schemed as a continuum beam model and the epoxy resin was described as an elastic medium. When the CNT beam generated flexural deflection , the interaction pressure between the CNT beam and the surrounding elastic medium was described by springs with constant of according to the Whitney–Riley model, shown as:
For vibration analysis, the governing equation was expressed as Equation (12) based on EBT.
where and indicate Young’s modulus and moment of inertia of the CNT beam, respectively. and denote the longitudinal coordinate and time, respectively. Hence, the vibration motion of the embedded part and exposed part of the CNT beam were performed as Equations (13) and (14), respectively.
where are the flexural deflections of the embedded part and the exposed part of the CNT beam.
Then, using a mathematical technique to solve the two differential equations and considering the boundary conditions at , a simultaneous equation was obtained as:
where is a 8 × 8 matrix in terms of the external compressive force , the embedded length , and the exposed length of the CNT beam. are integration constants that can be determined from the governing equations of vibration motion of the CNT beam by considering boundary conditions. From the non-trivial solution of Equation (15), when the eigenvalue of becomes 0, i.e., , the relationship between the external compressive force and the frequency can be obtained.
According to the non-trivial solution of Equation (15), the first three vibrational modes of the partial embedded CNT beam under an external compressive force were obtained and expressed in Figure 8 as a result. Furthermore, the relationship between the external compressive force and the frequency of vibrational modes 1 and 2 were drawn in Figure 9, the results showed that the fundamental frequency of the CNT beam decreased clearly as the external compressive force increased. Hence, by calculating the frequency shift from the obtained relationship curve of mode 1, the unknown compressive force can be detected theoretically. However, for the compressive loading condition, critical force of 2.5 nN appeared in mode 1, which means the proposed CNTs-based nano-force sensor had its upper limitation of 2.5 nN of force detection.
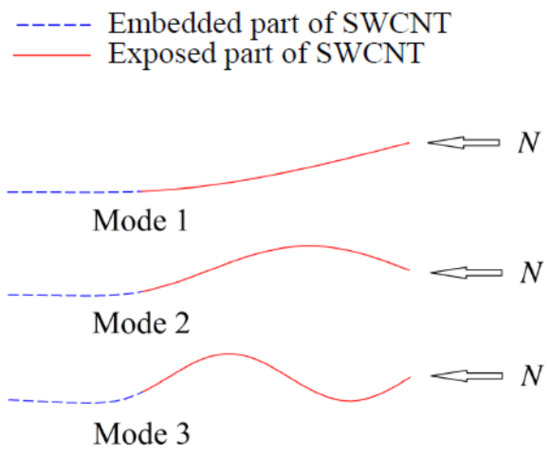
Figure 8.
The first three vibrational modes of the partial embedded carbon nanotubes resonator under an external compressive force [92].
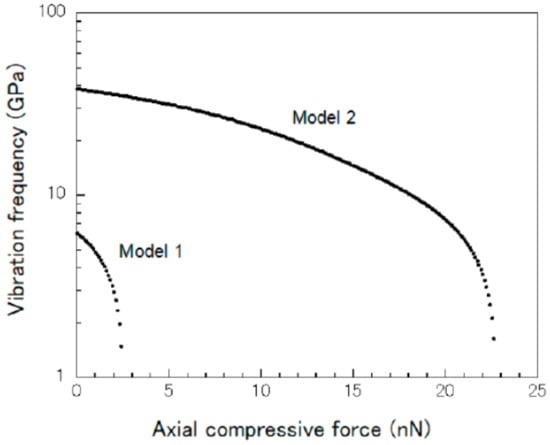
Figure 9.
Relationship between the external compressive force and the frequency of the partial embedded carbon nanotubes resonator [92].
In the future, just like the representative works of theoretical analysis of nano-mass sensors summarized in Section 4, because of their extremely excellent material properties, CNTs/GNRs/carbyne-based nano-force sensors investigated by approaches of FEM, EBT, etc., and GSs-based nano-force sensors investigated with FEM, EPT, etc., are expected for the development of carbon nanomaterials-based nano-force sensors. Additionally, nonlocal elasticity theory is preferred to be considered for deep investigation with theoretical analysis. Moreover, the measurement of external forces acting in different directions is also an important challenge for real application of nano-force sensors, where the vibration behavior of carbon nanomaterials resonators will become more complicated.
6. Conclusions
In summary, due to the high-speed development of nanotechnology in the field of nano sensors, the present work reviewed recent studies of frequency-based carbon nano-mass and nano-force sensors using carbon nanomaterials as resonators by continuum mechanical approaches. Three kinds of carbon nanomaterials, CNTs, GSs (including GNRs), and carbyne were considered as resonators of sensors, and the efficiency of each carbon nanomaterial was summarized and discussed. We have listed the highlights of this review work as the following:
- The mechanism of nano-mass and nano-force sensors based on vibration analysis were introduced theoretically.
- The methods of modeling CNTs, GSs, and carbyne as continuum structures were reviewed in detail. Especially, we have proposed that, in the vibration analysis of CNTs and GSs, besides Young’s modulus, shear modulus, and thickness, their densities should be determined simultaneously, which will be an essential work for studying CNTs/GSs-based nano sensors in the future.
- By summarizing the recent studies of carbon nanomaterials-based nano-mass sensors, CNTs, GS, and carbyne-based nano-mass sensors owned the minimum sensitivity of 10−23 g, 10−24~10−22 g, and 10−26~10−23 g, respectively. Hence, nano-mass sensors using carbyne resonators can provide the highest sensitivity among the three kinds of carbon nanomaterial resonators.
- Carbon nanomaterials-based nano-force sensors are seldom investigated. However, because of their extremely excellent material properties, CNTs/GSs/carbyne-based nano-force sensors should be studied further by vibration analysis. Moreover, discussion of detecting external forces acting in different directions would also be a deserved work toward the real application of nano-force sensors in the future.
- At present, the nanobalance technique for measuring the frequency shift of CNTs was demonstrated that could be applied to measure the mass of a tiny particle of light as 22 × 10−15 g [38]. Fifty-one gold atoms loaded on CNTs resonators could be experimentally measured using the relationship between the resonance frequency and atom numbers [40]. However, the real-time application of the nano-testing techniques would be a big challenge due to the small size and weight of carbon nanomaterials. New methods and approaches should be well established to reduce the measurement uncertainly and increase testing accuracy.
Author Contributions
Conceptualization, T.N. and J.-X.S.; investigation, J.-X.S., X.-W.L., and T.N.; writing—original draft preparation, J.-X.S. and X.-W.L.; reviewing and editing, T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kroto, H.W.; Heath, J.R.; O Brien, S.C.; Curl, R.F.; E Smalley, R. C60: Buckminsterfullerene. Nat. Cell Biol. 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Oberlin, A.; Endo, M.; Koyama, T. Filamentous growth of carbon through benzene decomposition. J. Cryst. Growth 1976, 32, 335–349. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nat. Cell Biol. 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Iijima, S.; Ichihashi, T. Single-shell carbon nanotubes of 1-nm diameter. Nat. Cell Biol. 1993, 363, 603–605. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Heimann, R.B.; Kleiman, J.; Salansky, N.M. A unified structural approach to linear carbon polytypes. Nat. Cell Biol. 1983, 306, 164–167. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Rafiee, R. A review of the mechanical properties of isolated carbon nanotubes and carbon nanotube composites. Mech. Compos. Mater. 2010, 46, 155–172. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, K.; Dixit, A.R. A review of the mechanical and thermal properties of graphene and its hybrid polymer nanocomposites for structural applications. J. Mater. Sci. 2019, 54, 5992–6026. [Google Scholar] [CrossRef]
- Sun, D.-M.; Liu, C.; Ren, W.-C.; Cheng, H.-M. A review of carbon nanotube- and graphene-based flexible thin-film transistors. Small 2013, 9, 1188–1205. [Google Scholar] [CrossRef]
- Che, Y.; Chen, H.; Gui, H.; Liu, J.; Liu, B.; Zhou, C. Review of carbon nanotube nanoelectronics and macroelectronics. Semicond. Sci. Technol. 2014, 29, 1–17. [Google Scholar] [CrossRef]
- Yang, Z.; Tian, J.; Yin, Z.; Cui, C.; Qian, W.; Wei, F. Carbon nanotube- and graphene-based nanomaterials and applications in high-voltage supercapacitor: A review. Carbon 2019, 141, 467–480. [Google Scholar] [CrossRef]
- Kumanek, B.; Janas, D. Thermal conductivity of carbon nanotube networks: A review. J. Mater. Sci. 2019, 54, 7397–7427. [Google Scholar] [CrossRef]
- Yamashita, S. A tutorial on nonlinear photonic applications of carbon nanotube and graphene. J. Light. Technol. 2011, 30, 427–447. [Google Scholar] [CrossRef]
- Wang, J. Carbon-nanotube based electrochemical biosensors: A review. Electroanalysis 2005, 17, 7–14. [Google Scholar] [CrossRef]
- Fam, D.; Palaniappan, A.; Tok, A.; Liedberg, B.; Moochhala, S. A review on technological aspects influencing commercialization of carbon nanotube sensors. Sens. Actuators B Chem. 2011, 157, 1–7. [Google Scholar] [CrossRef]
- Castillo-Henríquez, L.; Brenes-Acuña, M.; Castro-Rojas, A.; Cordero-Salmerón, R.; Lopretti-Correa, M.; Vega-Baudrit, J.R. Biosensors for the detection of bacterial and viral clinical pathogens. Sensors 2020, 20, 6926. [Google Scholar] [CrossRef] [PubMed]
- Mahar, B.; Laslau, C.; Yip, R.; Sun, Y. Development of carbon nanotube-based sensors—a review. IEEE Sens. J. 2007, 7, 266–284. [Google Scholar] [CrossRef]
- Li, C.; Thostenson, E.T.; Chou, T.-W. Sensors and actuators based on carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2008, 68, 1227–1249. [Google Scholar] [CrossRef]
- Her, S.-C.; Hsu, W.-C. Strain and temperature sensitivities along with mechanical properties of CNT buckypaper sensors. Sensors 2020, 20, 3067. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Cui, H.; Gui, Y.; Tang, J. Mechanism and application of carbon nanotube sensors in sf6 decomposed production detection: A review. Nanoscale Res. Lett. 2017, 12, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Pandhi, T.; Chandnani, A.; Subbaraman, H.; Estrada, D. A review of inkjet printed graphene and carbon nanotubes based gas sensors. Sensors 2020, 20, 5642. [Google Scholar] [CrossRef]
- Nikolic, M.V.; Milovanovic, V.; Vasiljevic, Z.Z.; Stamenkovic, Z. Semiconductor gas sensors: Materials, technology, design, and application. Sensors 2020, 20, 6694. [Google Scholar] [CrossRef] [PubMed]
- Sauerbrey, G. Verwendung von Schwingquarzen zur Wägung Dünner Schichten und zur Mikrowägung. Eur. Phys. J. A 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Abadal, G.; Davis, Z.J.; Barniol, N.; Helbo, B.; Borrisé, X.; Ruiz, R.; Boisen, A.; Campabadal, F.; Esteve, J.; Figueras, E.; et al. Electromechanical model of a resonating nano-cantilever-based sensor for high-resolution and high-sensitivity mass detection. Nanotechnology 2001, 12, 100–104. [Google Scholar] [CrossRef]
- Davis, Z.; Abadal, G.; Helbo, B.; Hansen, O.; Campabadal, F.; Perez-Murano, F.; Esteve, J.; Figueras, E.; Verd, J.; Barniol, N.; et al. Monolithic integration of mass sensing nano-cantilevers with CMOS circuitry. Sens. Actuators A Phys. 2003, 105, 311–319. [Google Scholar] [CrossRef]
- Ono, T.; Li, X.; Miyashita, H.; Esashi, M. Mass sensing of adsorbed molecules in sub-picogram sample with ultrathin silicon resonator. Rev. Sci. Instrum. 2003, 74, 1240–1243. [Google Scholar] [CrossRef]
- Forsén, E.; Abadal, G.; Ghatnekar-Nilsson, S.; Teva, J.; Verd, J.; Sandberg, R.; Svendsen, W.E.; Perez-Murano, F.; Esteve, J.; Figueras, E.; et al. Ultrasensitive mass sensor fully integrated with complementary metal-oxide-semiconductor circuitry. Appl. Phys. Lett. 2005, 87, 043507. [Google Scholar] [CrossRef]
- Zhang, W.; Turner, K.L. Application of parametric resonance amplification in a single-crystal silicon micro-oscillator based mass sensor. Sens. Actuators A Phys. 2005, 122, 23–30. [Google Scholar] [CrossRef]
- Naik, A.K.; Hanay, M.S.; Hiebert, W.K.; Feng, X.L.; Roukes, M.L. Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Barton, R.A.; Ilic, B.; Verbridge, S.S.; Cipriany, B.R.; Parpia, J.M.; Craighead, H.G. Fabrication of a nanomechanical mass sensor containing a nanofluidic channel. Nano Lett. 2010, 10, 2058–2063. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Ramos, D.; Martínez, J.; Fernández-Regúlez, M.; García, R.; San Paulo, Á.; Calleja, M.; Tamayo, J. Nanomechanical mass sensing and stiffness spectrometry based on two-dimensional vibrations of resonant nanowires. Nat. Nanotechnol. 2010, 5, 641–645. [Google Scholar] [CrossRef]
- Hanay, M.S.; Kelber, S.; Naik, A.K.; Chi, D.; Hentz, S.; Bullard, E.C.; Colinet, E.; Duraffourg, L.; Roukes, M.L. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602–608. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Airborne engineered nanoparticle mass sensor based on a silicon resonant cantilever. Sens. Actuators B Chem. 2013, 180, 77–89. [Google Scholar] [CrossRef]
- Olcum, S.; Cermak, N.; Wasserman, S.C.; Manalis, S.R. High-speed multiple-mode mass-sensing resolves dynamic nanoscale mass distributions. Nat. Commun. 2015, 6, 7070. [Google Scholar] [CrossRef] [PubMed]
- Hanay, M.S.; Kelber, S.I.; O’Connell, C.D.; Mulvaney, P.; Sader, J.E.; Roukes, M.L. Inertial imaging with nanomechanical systems. Nat. Nanotechnol. 2015, 10, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Cermak, N.; Olcum, S.; Delgado, F.F.; Wasserman, S.C.; Payer, K.R.; Murakami, A.M.; Knudsen, S.M.; Kimmerling, R.J.; Stevens, M.M.; Kikuchi, Y.; et al. High-throughput measurement of single-cell growth rates using serial microfluidic mass sensor arrays. Nat. Biotechnol. 2016, 34, 1052–1059. [Google Scholar] [CrossRef]
- Sader, J.E.; Hanay, M.S.; Neumann, A.P.; Roukes, M.L. Mass spectrometry using nanomechanical systems: Beyond the point-mass approximation. Nano Lett. 2018, 18, 1608–1614. [Google Scholar] [CrossRef]
- Poncharal, P.; Wang, Z.L.; Ugarte, D.; De Heer, W.A. Electrostatic deflections and electromechanical resonances of carbon nanotubes. Science 1999, 283, 1513–1516. [Google Scholar] [CrossRef]
- Bunch, J.S.; Van Der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef]
- Jensen, K.H.; Kim, K.; Zettl, A. An atomic-resolution nanomechanical mass sensor. Nat. Nanotechnol. 2008, 3, 533–537. [Google Scholar] [CrossRef] [PubMed]
- Eom, K.; Park, H.S.; Yoon, D.S.; Kwon, T. Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles. Phys. Rep. 2011, 503, 115–163. [Google Scholar] [CrossRef]
- Chaste, J.; Eichler, A.; E Moser, J.; Ceballos, G.; Rurali, R.; Bachtold, A. A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 2012, 7, 301–304. [Google Scholar] [CrossRef]
- Chen, H.-J.; Zhu, K.-D. Graphene-based nanoresonator with applications in optical transistor and mass sensing. Sensors 2014, 14, 16740–16753. [Google Scholar] [CrossRef]
- Wang, Q.; Arash, B. A review on applications of carbon nanotubes and graphenes as nano-resonator sensors. Comput. Mater. Sci. 2014, 82, 350–360. [Google Scholar] [CrossRef]
- Asadi, E.; Askari, H.; Khamesee, M.B.; Khajepour, A. High frequency nano electromagnetic self-powered sensor: Concept, modelling and analysis. Measurements 2017, 107, 31–40. [Google Scholar] [CrossRef]
- Duan, K.; Li, L.; Hu, Y.; Wang, X. Pillared graphene as an ultra-high sensitivity mass sensor. Sci. Rep. 2017, 7, 14012. [Google Scholar] [CrossRef] [PubMed]
- Kwon, S.H.; Kim, H.J.; Choi, W.S.; Kang, H. Development and performance analysis of carbon nanowall-based mass sensor. J. Nanosci. Nanotechnol. 2018, 18, 6552–6554. [Google Scholar] [CrossRef]
- Ricci, F.; Cuairan, M.T.; Conangla, G.P.; Schell, A.W.; Quidant, R. Accurate mass measurement of a levitated nanomechanical resonator for precision force-sensing. Nano Lett. 2019, 19, 6711–6715. [Google Scholar] [CrossRef]
- Willemsen, O.H.; Snel, M.M.; Cambi, A.; Greve, J.; De Grooth, B.G.; Figdor, C.G. Biomolecular interactions measured by atomic force microscopy. Biophys. J. 2000, 79, 3267–3281. [Google Scholar] [CrossRef]
- Stampfer, C.; Helbling, T.; Obergfell, D.; Schöberle, B.; Tripp, M.K.; Jungen, A.; Roth, S.; Bright, A.V.M.; Hierold, C. Fabrication of single-walled carbon-nanotube-based pressure sensors. Nano Lett. 2006, 6, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Gopal, A.; Luo, Z.; Kumar, K.; Lee, J.Y.; Hoshino, K.; Li, B.; Schmidt, C.; Ho, P.S.; Zhang, X. Nano-grating force sensor for measurement of neuron membrane characteristics under growth and cellular differentiation. In Proceedings of the TRANSDUCERS 2007-2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lion, France, 10–14 June 2007; pp. 1239–1242. [Google Scholar]
- Abadie, J.; Piat, E.; Oster, S.; Boukallel, M. Modeling and experimentation of a passive low frequency nanoforce sensor based on diamagnetic levitation. Sens. Actuators A Phys. 2012, 173, 227–237. [Google Scholar] [CrossRef]
- Piat, E.; Abadie, J.; Oster, S. Nanoforce estimation based on Kalman filtering and applied to a force sensor using diamagnetic levitation. Sens. Actuators A Phys. 2012, 179, 223–236. [Google Scholar] [CrossRef]
- Li, T.; Li, L.; Song, W.; Zhang, G.; Li, Y. Design and modeling of a novel two dimensional nano-scaled force sensor based on silicon photonic crystal. ECS Trans. 2014, 58, 65–73. [Google Scholar] [CrossRef]
- Yu, N.; Nakajima, M.; Shi, Q.; Yang, Z.; Wang, H.; Sun, L.; Huang, Q.; Fukuda, T. Characterization of the resistance and force of a carbon nanotube/Metal side contact by nanomanipulation. Scanning 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Mata-Hernandez, D.; Fernández, D.; Banerji, S.; Madrenas, J. Resonant mems pressure sensor in 180 NM cmos technology obtained by BEOL isotropic etching. Sensors 2020, 20, 6037. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Song, J.; Liu, J.; Xu, A.N.; Wang, Z.L. Piezoelectric field effect transistor and nanoforce sensor based on a single zno nanowire. Nano Lett. 2006, 6, 2768–2772. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.-S.; Choi, J.-H.; Park, Y.-K.; Kim, J.-H. Atomic force microscope cantilever calibration device for quantified force metrology at micro- or nano-scale regime: The nano force calibrator (NFC). Metrologia 2006, 43, 389–395. [Google Scholar] [CrossRef]
- Duc, T.C.; Creemer, J.F.; Sarro, P.M. Lateral nano-Newton force-sensing piezoresistive cantilever for microparticle handling. J. Micromech. Microeng. 2006, 16, S102–S106. [Google Scholar] [CrossRef]
- Mandal, D.; Yoon, S.; Kim, K.J. Origin of piezoelectricity in an electrospun poly(Vinylidene fluoride-trifluoroethylene) Nanofiber web-based nanogenerator and nano-pressure sensor. Macromol. Rapid Commun. 2011, 32, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.S.; Hinchet, R.; Mouis, M.; Wang, Z.L.; Yang, Y.; Ardila, G.; Songmuang, R.; Zhang, F.; Zhang, Y.; Han, W.; et al. Nano-newton transverse force sensor using a vertical gan nanowire based on the piezotronic effect. Adv. Mater. 2012, 25, 883–888. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, Y.; Liu, Y.; Zhang, K.; Liu, W.; Zhai, J. Nano-force sensor based on a single tellurium microwire. Semicond. Sci. Technol. 2017, 32, 074001. [Google Scholar] [CrossRef]
- Paul, S.J.; Sharma, I.; Elizabeth, I.; Gahtori, B.; Titus, S.S.; Chandra, P.; Gupta, B.K. A comparative study of compressible and conductive vertically aligned carbon nanotube forest in different polymer matrixes for high-performance piezoresistive force sensors. ACS Appl. Mater. Interfaces 2020, 12, 16946–16958. [Google Scholar] [CrossRef]
- Mahata, C.; Algadi, H.; Lee, J.; Kim, S.; Lee, T. Biomimetic-inspired micro-nano hierarchical structures for capacitive pressure sensor applications. Measurement 2020, 151, 107095. [Google Scholar] [CrossRef]
- Bahadoran, M.; Noorden, A.F.A.; Chaudhary, K.; Aziz, M.S.; Ali, J.; Yupapin, P. Nano force sensing using symmetric double stage micro resonator. Measurement 2014, 58, 215–220. [Google Scholar] [CrossRef]
- Hong, T.; Wang, T.; Xu, Y.-Q. Direct measurement of π coupling at the single-molecule level using a carbon nanotube force sensor. Nano Lett. 2018, 18, 7883–7888. [Google Scholar] [CrossRef]
- Lu, H.; Zheng, Y.; Jiang, J.; Yin, W.; Meng, Y.; Tian, Y. A shadow-based nano scale precision force sensor. IEEE Sens. J. 2018, 19, 2072–2078. [Google Scholar] [CrossRef]
- Yoo, J.-Y.; Seo, M.-H.; Lee, J.-S.; Choi, K.-W.; Jo, M.-S.; Yoon, J.-B. Industrial grade, bending-insensitive, transparent nanoforce touch sensor via enhanced percolation effect in a hierarchical nanocomposite film. Adv. Funct. Mater. 2018, 28. [Google Scholar] [CrossRef]
- Hierold, C.; Jungen, A.; Stampfer, C.; Helbling, T. Nano electromechanical sensors based on carbon nanotubes. Sens. Actuators A Phys. 2007, 136, 51–61. [Google Scholar] [CrossRef]
- Zang, H.; Zhang, X.; Zhu, B.; Fatikow, S. Recent advances in non-contact force sensors used for micro/nano manipulation. Sens. Actuators A Phys. 2019, 296, 155–177. [Google Scholar] [CrossRef]
- Li, C.-Y.; Chou, T.-W. Strain and pressure sensing using single-walled carbon nanotubes. Nanotechnology 2004, 15, 1493–1496. [Google Scholar] [CrossRef]
- Kürti, J.; Kresse, G.; Kuzmany, H. First-principles calculations of the radial breathing mode of single-wall carbon nanotubes. Phys. Rev. B 1998, 58, R8869–R8872. [Google Scholar] [CrossRef]
- Liu, H.J.; Chan, C.T. Properties of4Åcarbon nanotubes from first-principles calculations. Phys. Rev. B 2002, 66, 115416. [Google Scholar] [CrossRef]
- Gillen, R.; Mohr, M.; Thomsen, C.; Maultzsch, J. Vibrational properties of graphene nanoribbons by first-principles calculations. Phys. Rev. B 2009, 80, 155418. [Google Scholar] [CrossRef]
- Muller, S.E.; Nair, A.K. Carbyne as a fiber in metal-matrix nanocomposites: A first principle study. Comput. Mater. Sci. 2019, 159, 187–193. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of carbon tubes: Instabilities beyond linear response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef] [PubMed]
- Prylutskyy, Y.; Durov, S.; Ogloblya, O.; Buzaneva, E.; Scharff, P. Molecular dynamics simulation of mechanical, vibrational and electronic properties of carbon nanotubes. Comput. Mater. Sci. 2000, 17, 352–355. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Arash, B. Vibrations of single- and double-walled carbon nanotubes with layerwise boundary conditions: A molecular dynamics study. Curr. Appl. Phys. 2012, 12, 707–711. [Google Scholar] [CrossRef]
- Jing, N.; Xue, Q.; Ling, C.; Shan, M.; Zhang, T.; Zhou, X.; Jiao, Z. Effect of defects on Young’s modulus of graphene sheets: A molecular dynamics simulation. RSC Adv. 2012, 2, 9124–9129. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput. Mater. Sci. 2012, 51, 303–313. [Google Scholar] [CrossRef]
- Arash, B.; Jiang, J.-W.; Rabczuk, T. A review on nanomechanical resonators and their applications in sensors and molecular transportation. Appl. Phys. Rev. 2015, 2, 021301. [Google Scholar] [CrossRef]
- Eltaher, M.; Khater, M.; Emam, S.A. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Appl. Math. Model. 2016, 40, 4109–4128. [Google Scholar] [CrossRef]
- Askari, H.; Younesian, D.; Esmailzadeh, E.; Cveticanin, L. Nonlocal effect in carbon nanotube resonators: A comprehensive review. Adv. Mech. Eng. 2017, 9, 1–24. [Google Scholar] [CrossRef]
- Lei, X.-W.; Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. Radial breathing vibration of double-walled carbon nanotubes subjected to pressure. Phys. Lett. A 2011, 375, 2416–2421. [Google Scholar] [CrossRef]
- Lei, X.-W.; Ni, Q.-Q.; Shi, J.-X.; Natsuki, T. Radial breathing mode of carbon nanotubes subjected to axial pressure. Nanoscale Res. Lett. 2011, 6, 492. [Google Scholar] [CrossRef]
- Fazelzadeh, S.; Ghavanloo, E. Nonlocal anisotropic elastic shell model for vibrations of single-walled carbon nanotubes with arbitrary chirality. Compos. Struct. 2012, 94, 1016–1022. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, H.; Sahmani, S. Free vibration analysis of single- and double-walled carbon nanotubes based on nonlocal elastic shell models. J. Vib. Control. 2012, 20, 670–678. [Google Scholar] [CrossRef]
- Avramov, K. Nonlinear vibrations characteristics of single-walled carbon nanotubes by nonlocal elastic shell model. Int. J. Non-Linear Mech. 2018, 107, 149–160. [Google Scholar] [CrossRef]
- Lei, X.-W.; Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. Surface effects on the vibrational frequency of double-walled carbon nanotubes using the nonlocal Timoshenko beam model. Compos. Part B Eng. 2012, 43, 64–69. [Google Scholar] [CrossRef]
- Shi, J.-X.; Natsuki, T.; Lei, X.-W.; Ni, Q.-Q. Buckling instability of carbon nanotube atomic force microscope probe clamped in an elastic medium. J. Nanotechnol. Eng. Med. 2012, 3, 020903. [Google Scholar] [CrossRef]
- Natsuki, T.; Ni, Q.-Q.; Elishakoff, I. Influence of the axial compression on the natural frequency of AFM probes using double-walled carbon nanotubes with different wall lengths. Appl. Phys. A 2012, 110, 1–7. [Google Scholar] [CrossRef]
- Natsuki, T.; Urakami, K. Analysis of vibration frequency of carbon nanotubes used as nano-force sensors considering clamped boundary condition. Electronics 2019, 8, 1082. [Google Scholar] [CrossRef]
- Shi, J.-X.; Ni, Q.-Q.; Lei, X.-W.; Natsuki, T. Nonlocal elasticity theory for the buckling of double-layer graphene nanoribbons based on a continuum model. Comput. Mater. Sci. 2011, 50, 3085–3090. [Google Scholar] [CrossRef]
- Shi, J.-X.; Ni, Q.-Q.; Lei, X.-W.; Natsuki, T. Wave propagation in embedded double-layer graphene nanoribbons as electromechanical oscillators. J. Appl. Phys. 2011, 110, 84321. [Google Scholar] [CrossRef]
- Shi, J.-X.; Ni, Q.-Q.; Lei, X.-W.; Natsuki, T. Nonlocal vibration of embedded double-layer graphene nanoribbons in in-phase and anti-phase modes. Phys. E Low-Dimens. Syst. Nanostruct. 2012, 44, 1136–1141. [Google Scholar] [CrossRef]
- Nazemnezhad, R.; Kamali, K.; Hosseini-Hashemi, S. Study on tensile-compressive and shear effects of van der Waals interactions on free vibration of bilayer graphene nanoribbons. Meccanica 2016, 52, 263–282. [Google Scholar] [CrossRef]
- Shenderova, O.A.; Zhirnov, V.V.; Brenner, D.W. Carbon nanostructures. Crit. Rev. Solid State Mater. Sci. 2002, 27, 227–356. [Google Scholar] [CrossRef]
- DiBiasio, C.M.; Cullinan, M.A.; Culpepper, M.L. Difference between bending and stretching moduli of single-walled carbon nanotubes that are modeled as an elastic tube. Appl. Phys. Lett. 2007, 90, 203116. [Google Scholar] [CrossRef]
- Pine, P.; Yaish, Y.E.; Adler, J. Vibrational analysis of thermal oscillations of single-walled carbon nanotubes under axial strain. Phys. Rev. B 2014, 89, 115405. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.-W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef]
- Natsuki, T.; Tantrakarn, K.; Endo, M. Prediction of elastic properties for single-walled carbon nanotubes. Carbon 2004, 42, 39–45. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.-W. Single-walled carbon nanotubes as ultrahigh frequency nanomechanical resonators. Phys. Rev. B 2003, 68, 073405. [Google Scholar] [CrossRef]
- Xiao, J.; Gama, B.; Gillespie, J. An analytical molecular structural mechanics model for the mechanical properties of carbon nanotubes. Int. J. Solids Struct. 2005, 42, 3075–3092. [Google Scholar] [CrossRef]
- Meo, M.; Rossi, M. Prediction of Young’s modulus of single wall carbon nanotubes by molecular-mechanics based finite element modelling. Compos. Sci. Technol. 2006, 66, 1597–1605. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Rafiee, R. Prediction of Young’s modulus of graphene sheets and carbon nanotubes using nanoscale continuum mechanics approach. Mater. Des. 2010, 31, 790–795. [Google Scholar] [CrossRef]
- Rafiee, R.; Moghadam, R.M. On the modeling of carbon nanotubes: A critical review. Compos. Part B Eng. 2014, 56, 435–449. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Agwa, M.; Kabeel, A. Vibration analysis of material size-dependent CNTs using energy equivalent model. J. Appl. Comput. Mech. 2018, 4, 75–86. [Google Scholar] [CrossRef]
- Mohamed, N.; Mohamed, S.A.; Eltaher, M.A. Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Reddy, C.D.; Rajendran, S.; Liew, K.M. Equilibrium configuration and continuum elastic properties of finite sized graphene. Nanotechnology 2006, 17, 864–870. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M. Nonlinear bending and stretching of a circular graphene sheet under a central point load. Nanotechnology 2009, 20, 075702. [Google Scholar] [CrossRef]
- Shi, J.-X.; Natsuki, T.; Lei, X.-W.; Ni, Q.-Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104, 223101. [Google Scholar] [CrossRef]
- Yeh, Y.-K.; Hwu, C. A modified molecular-continuum model for estimating the strength and fracture toughness of graphene and carbon nanotube. Eng. Fract. Mech. 2017, 176, 326–342. [Google Scholar] [CrossRef]
- Korobeynikov, S.; Alyokhin, V.; Babichev, A. On the molecular mechanics of single layer graphene sheets. Int. J. Eng. Sci. 2018, 133, 109–131. [Google Scholar] [CrossRef]
- Yeh, Y.-K.; Hwu, C. Molecular-continuum model for the prediction of stiffness, strength and toughness of nanomaterials. Acta Mech. 2017, 230, 1451–1467. [Google Scholar] [CrossRef]
- Mokhalingam, A.; Ghaffari, R.; Sauer, R.A.; Gupta, S.S. Comparing quantum, molecular and continuum models for graphene at large deformations. Carbon 2020, 159, 478–494. [Google Scholar] [CrossRef]
- Dresselhaus, M.; Dresselhaus, G.; Saito, R. Physics of carbon nanotubes. Carbon 1995, 33, 883–891. [Google Scholar] [CrossRef]
- Lu, J.P. Elastic properties of single and multilayered nanotubes. J. Phys. Chem. Solids 1997, 58, 1649–1652. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, J.; Hwang, K.C. Thickness of graphene and single-wall carbon nanotubes. Phys. Rev. B 2006, 74, 245413. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Artyukhov, V.I.; Lee, H.; Xu, F.; Yakobson, B.I. Carbyne from first principles: Chain of C atoms, a nanorod or a nanorope. ACS Nano 2013, 7, 10075–10082. [Google Scholar] [CrossRef]
- Liu, M.; Artyukhov, V.I.; Lee, H.; Xu, F.; Yakobson, B.I. Correction to carbyne from first-principles: Chain of C atoms, a nanorod or a nanorope. ACS Nano 2017, 11, 5186. [Google Scholar] [CrossRef]
- Shi, J.-X.; Liu, Y.; Shimoda, M. Vibration analysis of a carbyne-based resonator in nano-mechanical mass sensors. J. Phys. D Appl. Phys. 2015, 48, 115303. [Google Scholar] [CrossRef]
- Agwa, M.A.; Eltaher, M.A. Vibration of a carbyne nanomechanical mass sensor with surface effect. Appl. Phys. A 2016, 122, 335. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, Q.; Wu, J.; Sui, C.; Tong, L.; He, X.; Wang, C. Mechanical properties of helically twisted carbyne fibers. Int. J. Mech. Sci. 2020, 186, 105823. [Google Scholar] [CrossRef]
- Li, C.; Chou, T.-W. Mass detection using carbon nanotube-based nanomechanical resonators. Appl. Phys. Lett. 2004, 84, 5246–5248. [Google Scholar] [CrossRef]
- Wu, D.H.; Chien, W.T.; Chen, C.S.; Chen, H.H. Resonant frequency analysis of fixed-free single-walled carbon nanotube-based mass sensor. Sens. Actuators A Phys. 2006, 126, 117–121. [Google Scholar] [CrossRef]
- Li, Y.; Qiu, X.; Yang, F.; Wang, X.-S.; Yin, Y. Ultra-high sensitivity of super carbon-nanotube-based mass and strain sensors. Nanotechnology 2008, 19, 165502. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, R.; Adhikari, S.; Mitchell, J. Vibrating carbon nanotube based bio-sensors. Phys. E Low-Dimens. Syst. Nanostruct. 2009, 42, 104–109. [Google Scholar] [CrossRef]
- Georgantzinos, S.; Anifantis, N. Carbon nanotube-based resonant nanomechanical sensors: A computational investigation of their behavior. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 1795–1801. [Google Scholar] [CrossRef]
- Joshi, A.Y.; Harsha, S.; Sharma, S.C. Vibration signature analysis of single walled carbon nanotube based nanomechanical sensors. Phys. E: Low-Dimens. Syst. Nanostruct. 2010, 42, 2115–2123. [Google Scholar] [CrossRef]
- Cho, S.-H.; Choi, M.-S.; Kang, D.-K.; Lee, J.H.; Kim, C.-W. Analysis on mass sensing characteristics of SWCNT-based nano-mechanical resonators using continuum mechanics based finite element analysis. J. Mech. Sci. Technol. 2015, 29, 4801–4806. [Google Scholar] [CrossRef]
- Lee, H.-L.; Hsu, J.-C.; Chang, W.-J. Frequency shift of carbon-nanotube-based mass sensor using nonlocal elasticity theory. Nanoscale Res. Lett. 2010, 5, 1774–1778. [Google Scholar] [CrossRef]
- Aydogdu, M.; Filiz, S. Modeling carbon nanotube-based mass sensors using axial vibration and nonlocal elasticity. Phys. E Low-Dimens. Syst. Nanostruct. 2011, 43, 1229–1234. [Google Scholar] [CrossRef]
- Mehdipour, I.; Barari, A.; Domairry, G. Application of a cantilevered SWCNT with mass at the tip as a nanomechanical sensor. Comput. Mater. Sci. 2011, 50, 1830–1833. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Tang, G.-J.; Zhang, L.; Li, X.-F. Vibration of double-walled carbon nanotube based nanomechanical sensor with initial axial stress. Comput. Mater. Sci. 2012, 58, 51–58. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Li, D.-K.; Li, N.; Tang, G.-J. Frequency shift of a nanomechanical sensor carrying a nanoparticle using nonlocal Timoshenko beam theory. J. Mech. Sci. Technol. 2012, 26, 1577–1583. [Google Scholar] [CrossRef]
- Natsuki, T.; Matsuyama, N.; Shi, J.-X.; Ni, Q.-Q. Vibration analysis of nanomechanical mass sensor using carbon nanotubes under axial tensile loads. Appl. Phys. A 2014, 116, 1001–1007. [Google Scholar] [CrossRef]
- Natsuki, T.; Matsuyama, N.; Ni, Q.-Q. Vibration analysis of carbon nanotube-based resonator using nonlocal elasticity theory. Appl. Phys. A 2015, 120, 1309–1313. [Google Scholar] [CrossRef]
- Bouchaala, A.; Nayfeh, A.H.; Younis, M.I. Frequency shifts of micro and nano cantilever beam resonators due to added masses. J. Dyn. Syst. Meas. Control. 2016, 138, 091002. [Google Scholar] [CrossRef]
- Eltaher, M.; Agwa, M. Analysis of size-dependent mechanical properties of CNTs mass sensor using energy equivalent model. Sens. Actuators A Phys. 2016, 246, 9–17. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Agwa, M.A.; Mahmoud, F.F. Nanobeam sensor for measuring a zeptogram mass. Int. J. Mech. Mater. Des. 2015, 12, 211–221. [Google Scholar] [CrossRef]
- Ghaffari, S.S.; Ceballes, S.; Abdelkefi, A. Effects of thermal loads representations on the dynamics and characteristics of carbon nanotubes-based mass sensors. Smart Mater. Struct. 2019, 28, 074003. [Google Scholar] [CrossRef]
- Ghaffari, S.S.; Ceballes, S.; Abdelkefi, A. Nonlinear dynamical responses of forced carbon nanotube-based mass sensors under the influence of thermal loadings. Nonlinear Dyn. 2020, 100, 1013–1035. [Google Scholar] [CrossRef]
- Natsuki, T. Carbon nanotube-based nanomechanical sensor: Theoretical analysis of mechanical and vibrational properties. Electronics 2017, 6, 56. [Google Scholar] [CrossRef]
- Tsiamaki, A.; Georgantzinos, S.; Anifantis, N. Monolayer graphene resonators for mass detection: A structural mechanics feasibility study. Sens. Actuators A Phys. 2014, 217, 29–38. [Google Scholar] [CrossRef]
- Xu, C.; Rong, D.; Tong, Z.; Zhou, Z.; Hu, J.; Deng, Z. Analytical modeling of a magnetically affected cantilever nanoplate-based mass detector. Superlattices Microstruct. 2020, 137, 106338. [Google Scholar] [CrossRef]
- Xu, C.; Qu, J.; Rong, D.; Zhou, Z.; Leung, A. Theory and modeling of a novel class of nanoplate-based mass sensors with corner point supports. Thin-Walled Struct. 2021, 159, 107306. [Google Scholar] [CrossRef]
- Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. Vibration analysis of nanomechanical mass sensor using double-layered graphene sheets resonators. J. Appl. Phys. 2013, 114, 094307. [Google Scholar] [CrossRef]
- Lei, X.-W.; Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. An atomic-resolution nanomechanical mass sensor based on circular monolayer graphene sheet: Theoretical analysis of vibrational properties. J. Appl. Phys. 2013, 113, 154313. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Tang, H.-L.; Li, D.-K.; Tang, G.-J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Lee, H.-L.; Yang, Y.-C.; Chang, W.-J. Mass detection using a graphene-based nanomechanical resonator. Jpn. J. Appl. Phys. 2013, 52, 25101. [Google Scholar] [CrossRef]
- Jalali, S.K.; Naei, M.H.; Pugno, N.M. A mixed approach for studying size effects and connecting interactions of planar nano structures as resonant mass sensors. Microsyst. Technol. 2014, 21, 2375–2386. [Google Scholar] [CrossRef]
- Zhou, S.-M.; Sheng, L.-P.; Shen, Z.-B. Transverse vibration of circular graphene sheet-based mass sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2014, 86, 73–78. [Google Scholar] [CrossRef]
- Natsuki, T. Theoretical analysis of vibration frequency of graphene sheets used as nanomechanical mass sensor. Electronics 2015, 4, 723–738. [Google Scholar] [CrossRef]
- Natsuki, T.; Yiwada, A.; Natsuki, J. Influence of temperature on vibrational frequency of graphene sheet used as nano-scale sensing. C J. Carbon Res. 2017, 3, 4. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Jiang, R.-W.; Zhang, L.; Tang, G.-J. Nonlocal galerkin strip transfer function method for vibration of double-layered graphene mass sensor. Acta Mech. Solida Sin. 2018, 31, 94–107. [Google Scholar] [CrossRef]
- Rajabi, K.; Hosseini-Hashemi, S. Effect of the interparticle interactions on adsorption-induced frequency shift of nano-beam-based nanoscale mass-sensors: A Theoretical study. J. Solid Mech. 2018, 10, 864–873. [Google Scholar]
- Li, H.; Wang, X.; Wang, H.; Chen, J. The nonlocal frequency behavior of nanomechanical mass sensors based on the multi-directional vibrations of a buckled nanoribbon. Appl. Math. Model. 2020, 77, 1780–1796. [Google Scholar] [CrossRef]
- Whittaker, A.G. Carbon: A new view of its high-temperature behavior. Science 1978, 200, 763–764. [Google Scholar] [CrossRef]
- Whittaker, A. Carbon: Occurrence of carbyne forms of carbon in natural graphite. Carbon 1979, 17, 21–24. [Google Scholar] [CrossRef]
- Smith, P.P.K.; Buseck, P.R.; Pettengill, G.H.; Ford, P.G.; Nozette, S. Carbyne forms of carbon: Do they exist? Science 1982, 216, 984–986. [Google Scholar] [CrossRef] [PubMed]
- Menacer, F.; Kadr, A.; Dibi, Z. Modeling of a smart nano force sensor using finite elements and neural networks. Int. J. Autom. Comput. 2018, 17, 279–291. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).