On the Speech Properties and Feature Extraction Methods in Speech Emotion Recognition
Abstract
1. Introduction
2. Materials and Methods
2.1. Time–Frequency Distributions, Spectrograms
2.2. Auditory Filter Banks and Psychoacoustic Scales
2.3. Linear Model of Speech Production
2.4. Phase Information
2.5. Cepstral Features Using Psychoacoustic FBs (MFCC and GFCC)
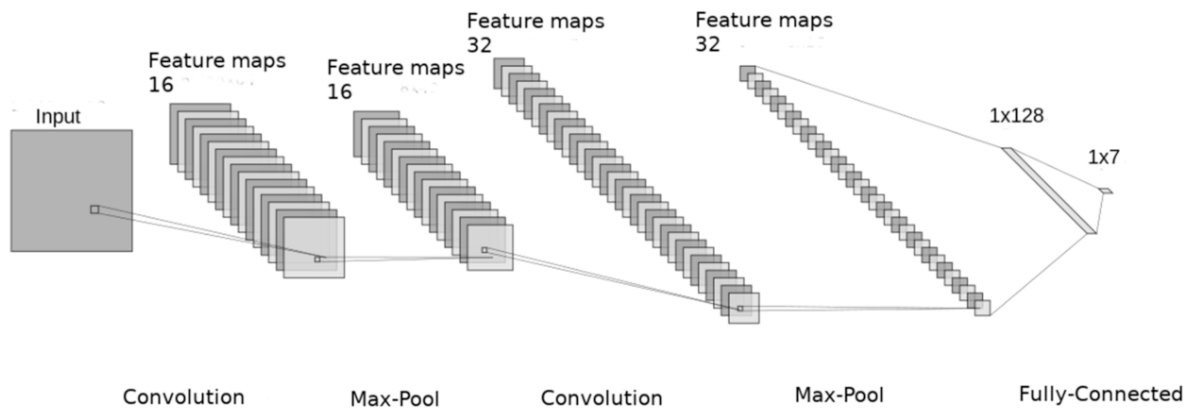
2.6. Convolutional Neural Networks
2.7. Statistical Evaluation of Results
2.8. Databases
3. Results
3.1. Time and Segmentation
3.2. Frequency Ranges and Frequency Scales
3.3. Vocal Tract Spectra Estimated by FB and LPC
3.4. Excitation Signal Spectra
3.5. Phase Processing
3.6. Cepstrum Based Features
3.7. Database and Classification Method Dependency Tests
3.8. Most Successful Methods and Settings
4. Discussion
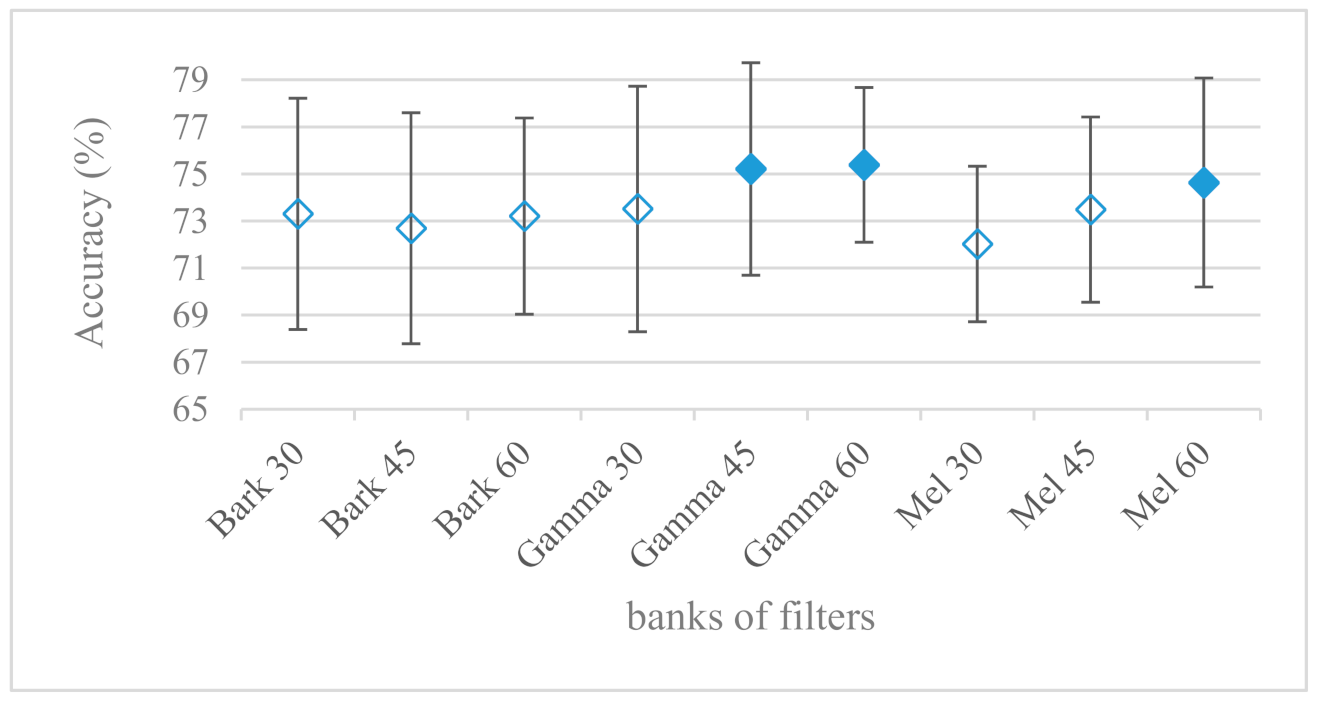
- As listed in Table 2, the most successful methods were derived from FBs using Gammatone, Mel, and Bark shape filters and scales. This means vocal tract features (spectral envelope) are very important, and the manner they are extracted and expressed, e.g., LPC model based features were proven to be statistically worse while extracting and representing the same sort of information. Even though the rank correlation is only 0.38, these findings mostly apply to the IEMOCAP database as can be seen in Table 3, i.e., the best methods are also GFB based.
- Other successful methods cover spectral based features (spectrograms) derived from the whole speech signals, i.e., containing both excitation and vocal tract signals. However, to do so they use significantly more parameters than FB features, e.g., 160 vs. 60, see Table 2. The settings proved to be important again, especially when frequency ranges in combination with magnitude modifying methods are regarded.
- The least successful methods were based on phase signals. However, neither of the tested settings failed, i.e., all were able to extract some SER relevant information so that the performance was significantly better than the one provided by a random classifier, i.e., 14.3% (seven classes). Thus they can still act as auxiliary features in some systems.
- In general the same ranking of methods, i.e., vocal tract based expressed by GFB, vocal tract and excitation signals using spectrograms and the least successful utilizing phases were observed on both databases. They however differ in some particular settings and ranges. This is mostly caused by differences in databases, e.g., by listening to some recordings it was noticed that the Berlin database consists mostly of genuine speech whereas in IEMOCAPS there were many recordings containing more background or speech artifacts. Thus some segments might not even contain a speech and a proper speech detection algorithm should be used. Moreover there was reported a significant difference between actors and native evaluators [37] in the perception of emotions for some scenarios.
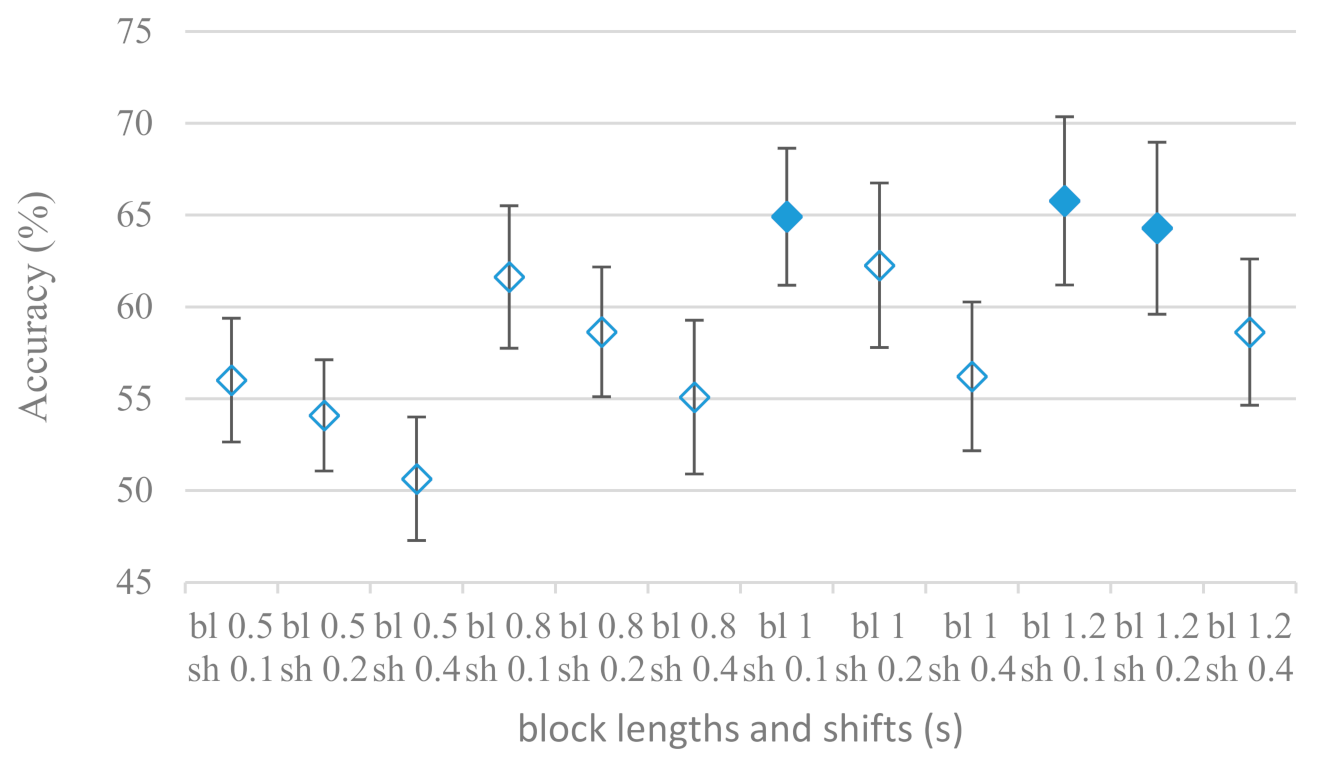
- The time span of speech blocks (spectrograms) that were used for SER (classification) could significantly improve the accuracy. It is natural as more speech provides more valuable information. However, the increase becomes mild at around 1.2 s (Figure 4). The shift of adjacent speech blocks showed to be an important parameter as well, i.e., the shorter the shift the higher the accuracy. Nevertheless, this phenomenon is rather related to the increase of available data for CNN at the cost of increased redundancy across speech blocks. The same observations were made also for IEMOCAP database (rank correlation 0.7) however this time the shift (more data) was a more dominant factor.
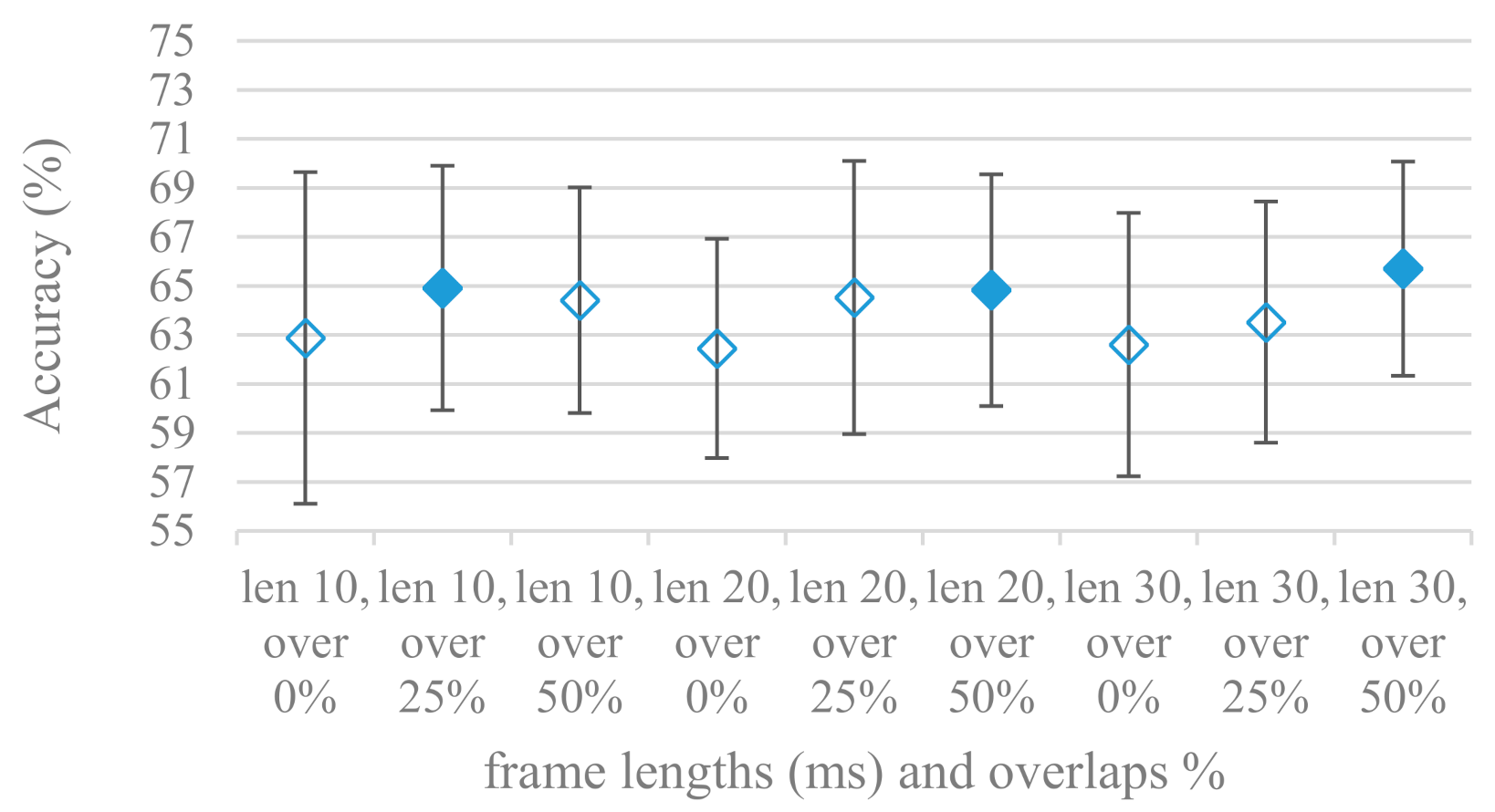
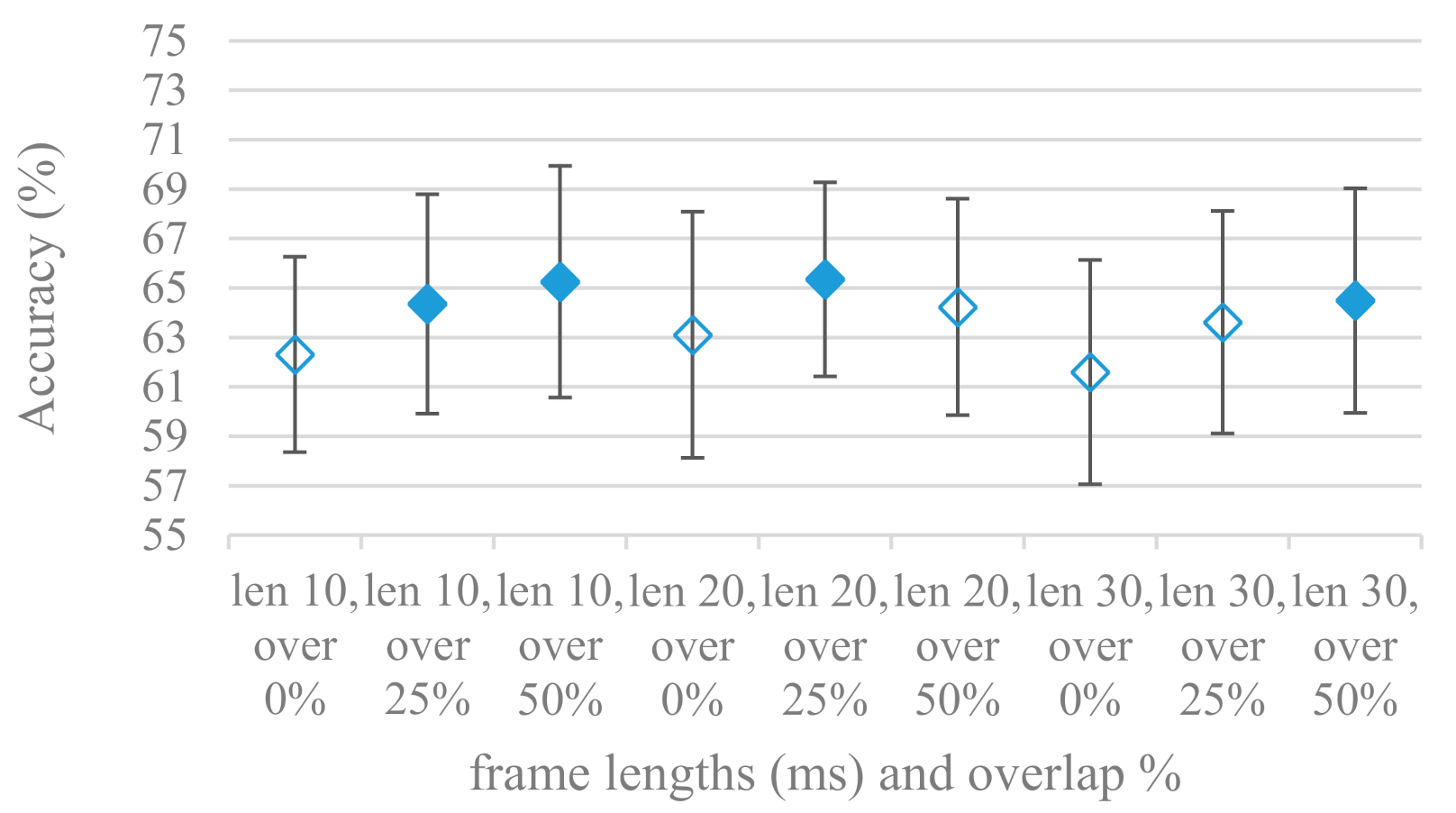
- The effect of speech segmentation is documented in Figure 2 and Figure 3. As in the previous case longer overlaps (shorter shifts) of adjacent segments are preferred. However, in this case the bigger overlaps do not increase the number of training–testing samples (this effect is negligible) as the spectrograms are of a fixed time duration. It increases the number of frames in spectrograms, i.e., time resolution at the expense of increased redundancy, resulting in bigger FVs. The frame lengths (from which short time spectra were constructed) in the tested range were not a decisive factor, i.e., all lengths proved to be statistically equal (Figure 2). This means the frequency resolution resulting from 10 to 30 ms windows was adequate for SER.
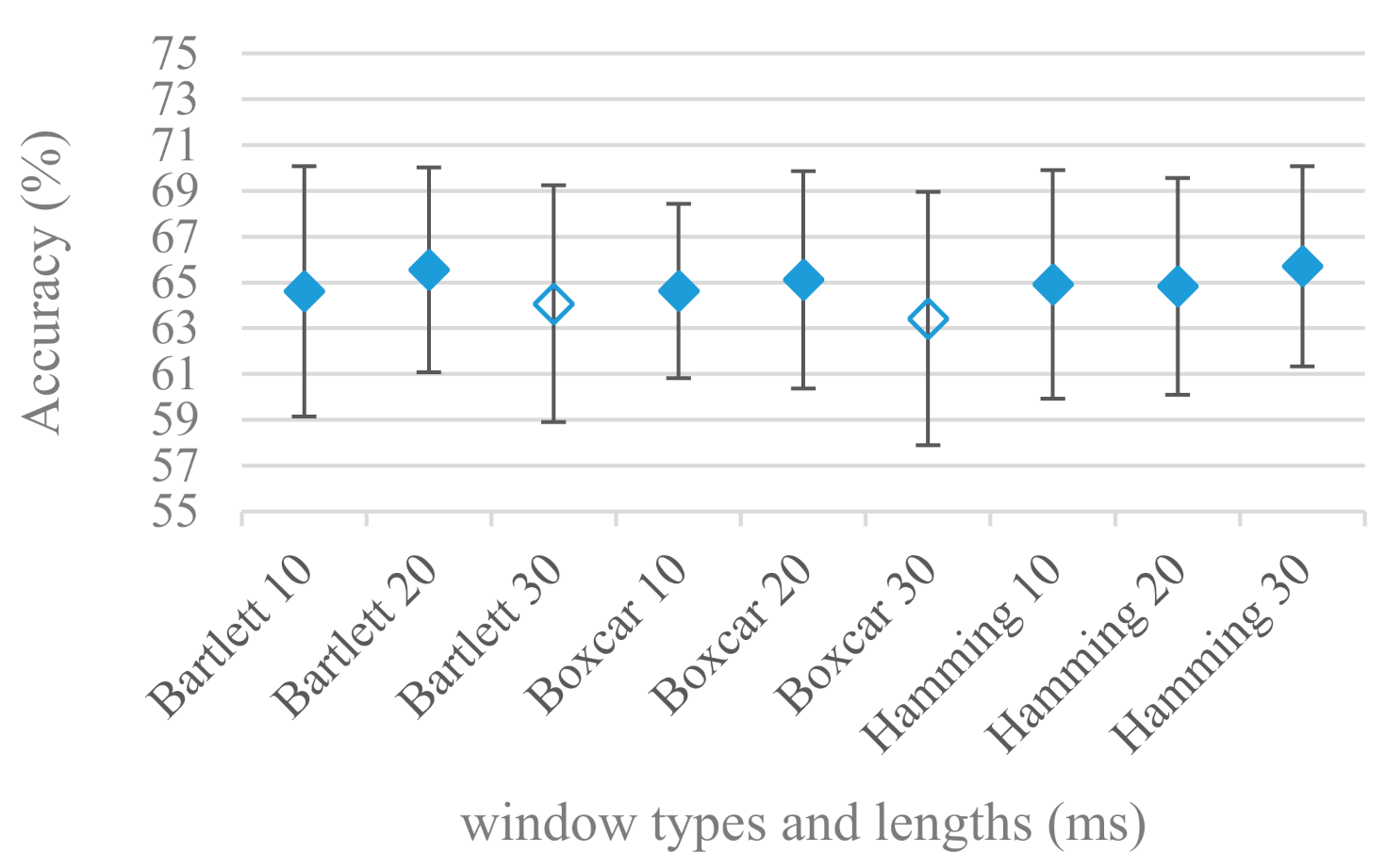
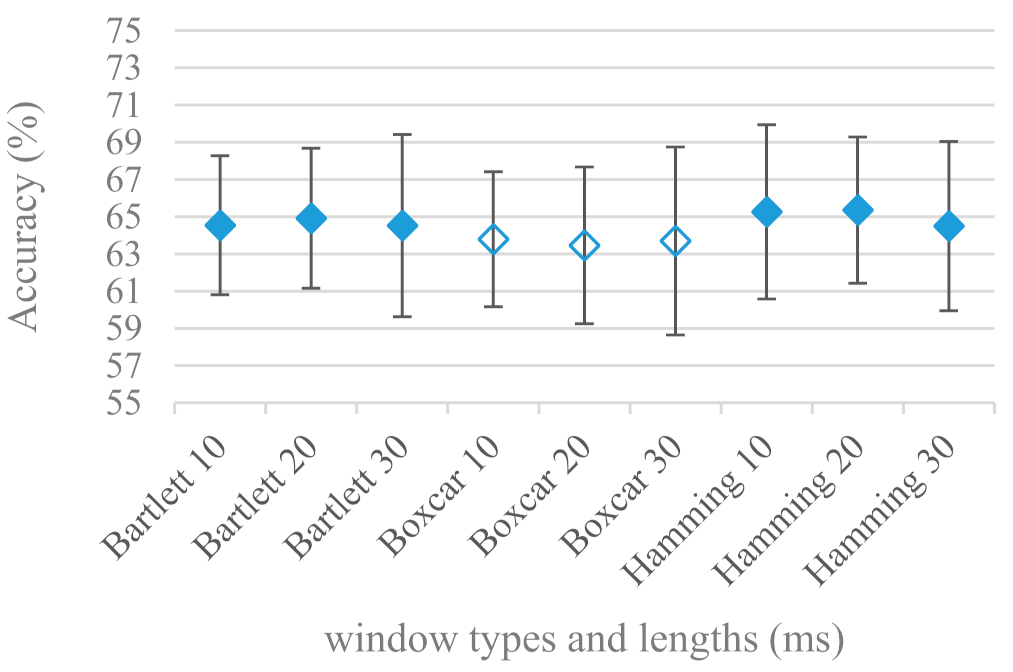
- Windows types, e.g., Boxcar, Barttlet, and Hamming showed slightly different behavior depending on the used frequency range. For the 4 kHz upper frequency they acted equally from a statistical point of view (Figure 5). However, for the 8 kHz upper bound (Figure 6) Boxcar proved to be inferior in all cases. Boxcar is the least decaying window in the frequency meaning it causes frequency aliasing among distant frequencies. This probably proved to be more important for higher frequencies that got contaminated by lower frequencies having much higher energies. This phenomenon was not that critical in the 4 kHz limit as the “noise” from higher frequencies was presumably negligible compared to low frequency energies. Nevertheless this segmentation related setting in the tested ranges did not prove to be very decisive and robust as there was only negligible positive correlation (0.11) between databases.
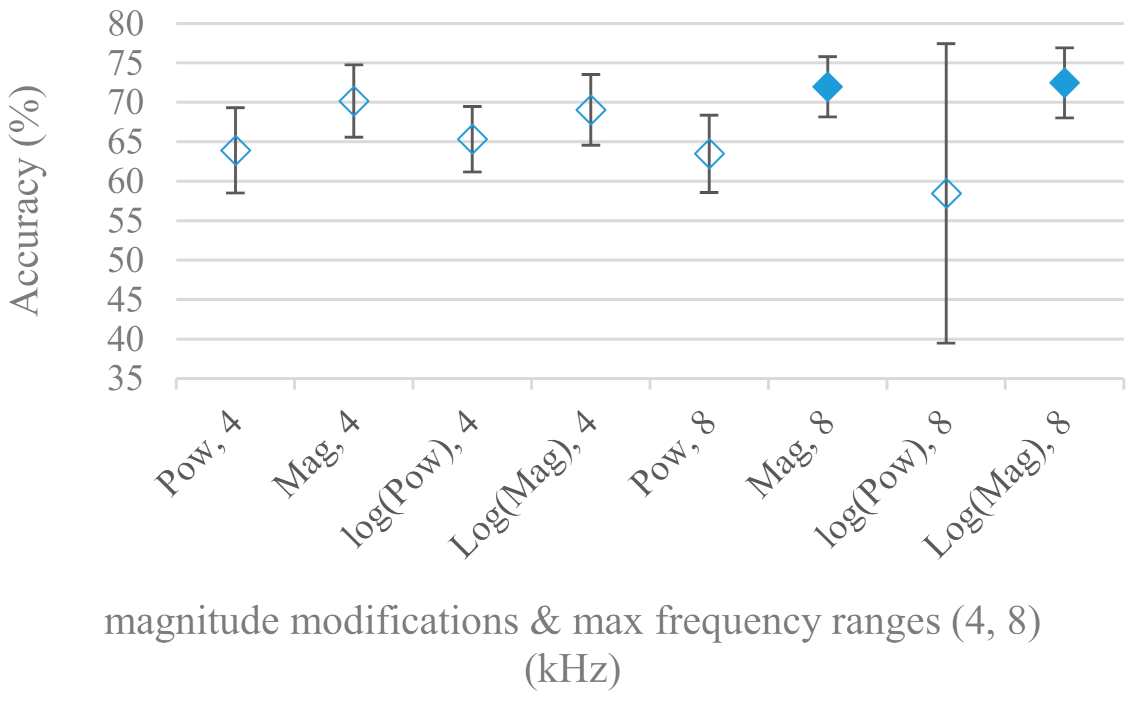
- Very interesting and apparent was the effect of magnitude manipulation, i.e., power, magnitude, and logarithm of power and magnitude in connection with a frequency upper bound and the application of pre-emphasis. The magnitude processing is significantly dependent on the frequency ranges and pre-emphasis. Even though magnitudes scored better both for 4 and 8 kHz ranges (Figure 11), a quite substantial deterioration in the case of log energy and energy in combination with pre-emphasis was recorded for the 8 kHz range. These observations led to the following possible explanation. Higher frequencies are known to have rather small magnitudes for speech signals especially voiced ones. By the additional application of power these values get even smaller that is critical for a logarithm, e.g., if X~R(0,1) and y = ln(x), then D{y} = 12D{x} (D is dispersion), if power of x is used, the dispersion is further amplified by factor 4, i.e., D{2ln(x)} = 4*12D{x}. The application of a logarithm is a known practical problem, so to avoid singularities an energy threshold is applied, e.g., using a minimal positive number at a given precision. Nevertheless, high variations persist for low energies (high frequencies). Such amplified variations that are not caused by genuine speech naturally deteriorate the accuracy. This effect is crucial for spectrograms and vanishes when, e.g., a bank of filters are applied that average (dispersion reduction) energies over frequency bands. It should be noted that some of the deterioration may have been caused by the applied classification method; in our case CNN, which uses convolution (weighted combination of samples) and logarithm turns it into a multiplication of original samples powered to filter weights, which in general may be rather difficult to interpret. Thus the designers must be aware of this phenomenon and take into consideration magnitude modifications, frequency ranges, and pre-emphasis in connection with spectrograms and classification methods. An automatic application of logarithmic power, so common in speech processing, may not be optimal in such cases. Even though these phenomena show only a small positive correlation (0.07) between databases, a closer inspection of IEMOCAP results revealed that for an 8 kHz frequency range, all except a magnitude spectra modification, i.e., log power and log magnitude recorded a dramatic accuracy drop from approximately 40% to only 19%. So, this is strictly in line with the observations and explanations inferred from the Berlin database.
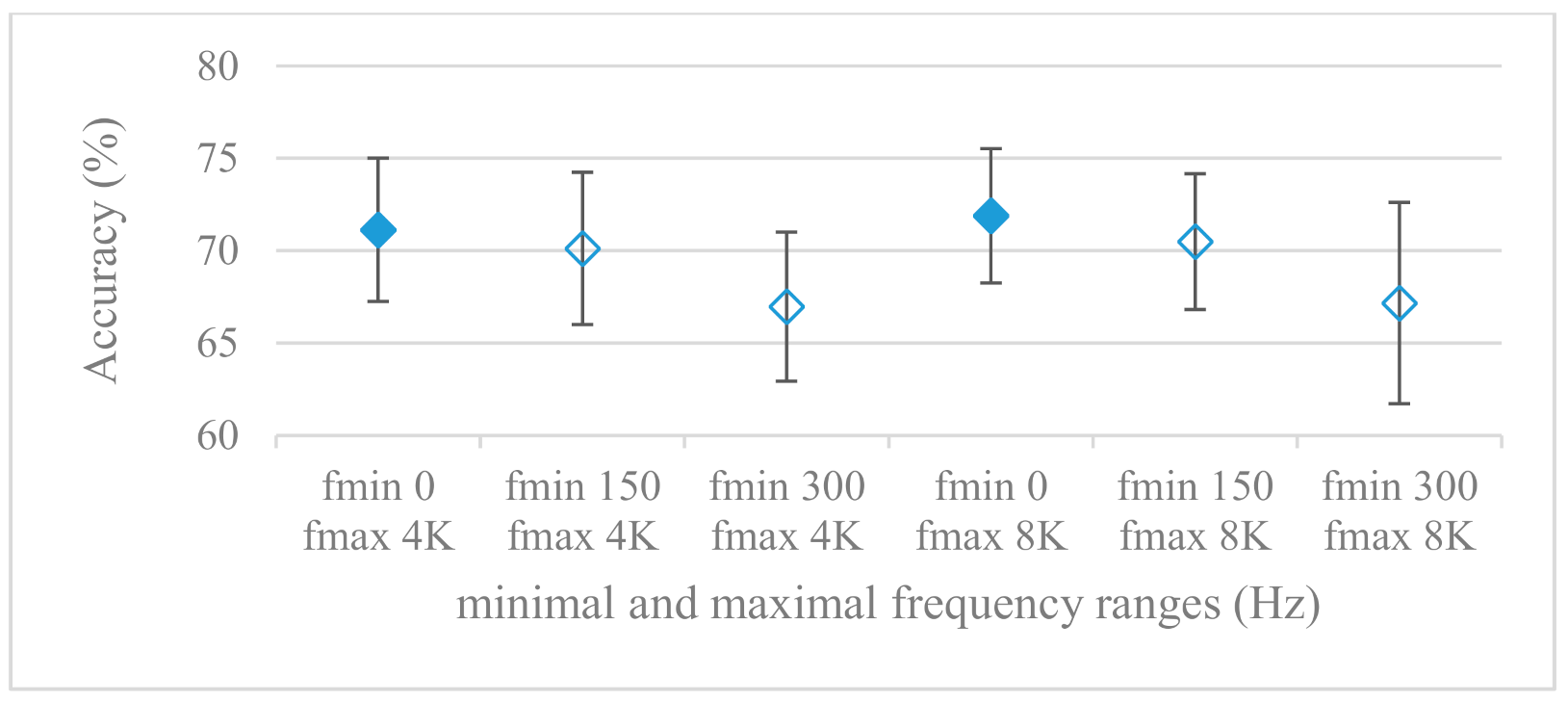
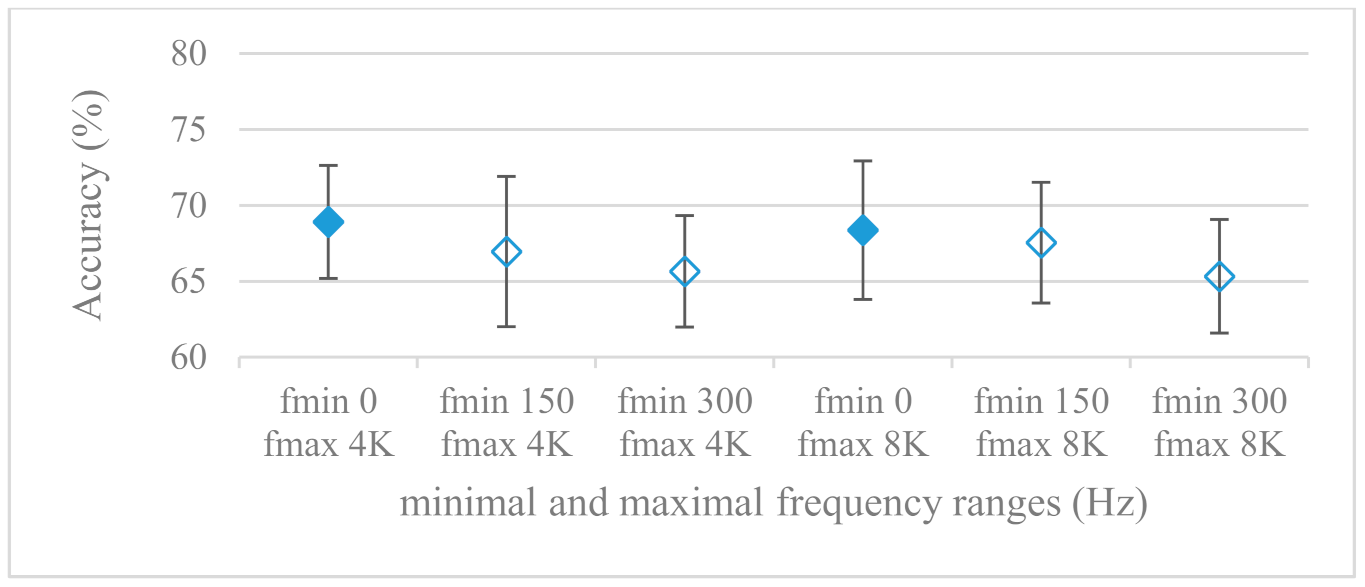
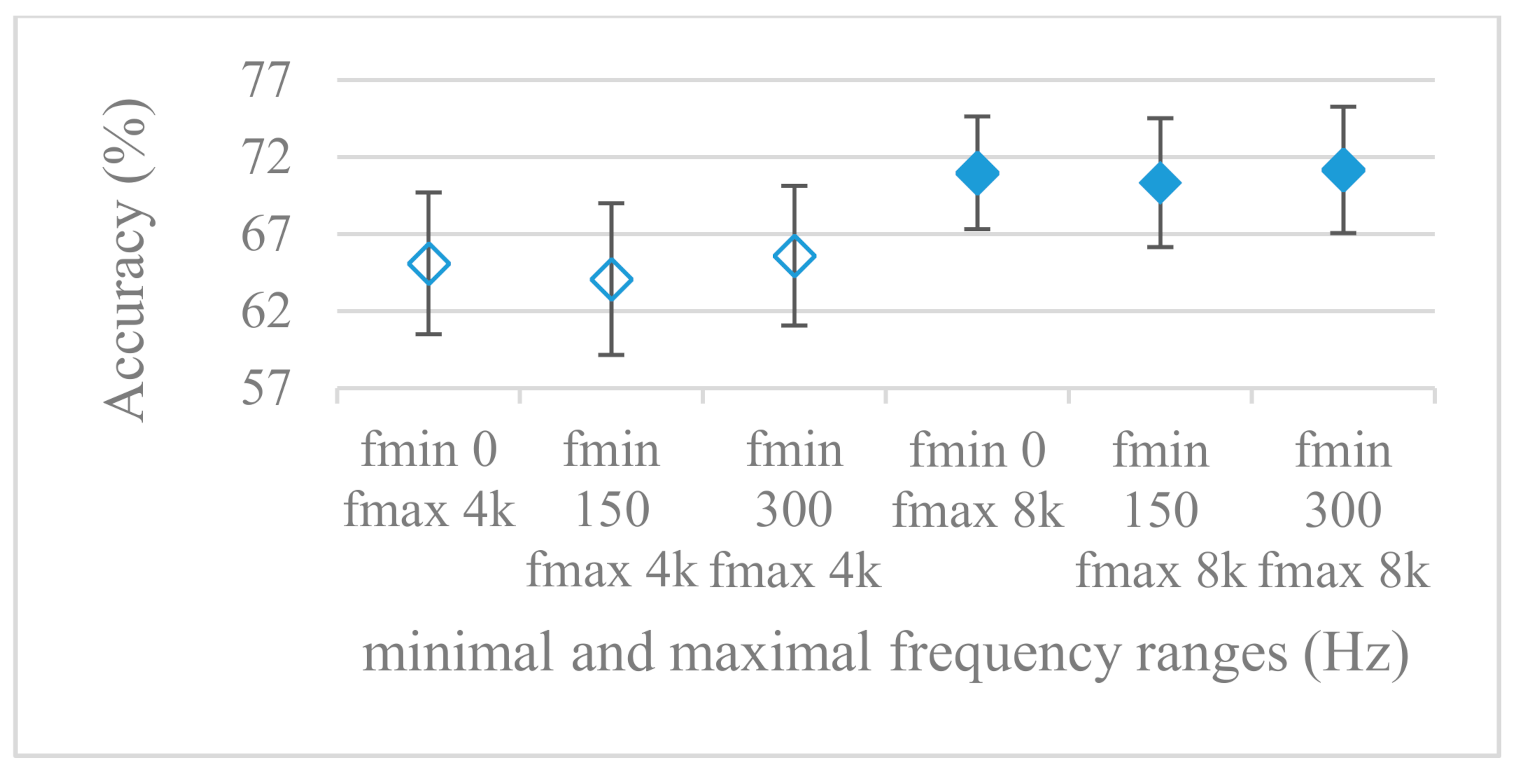
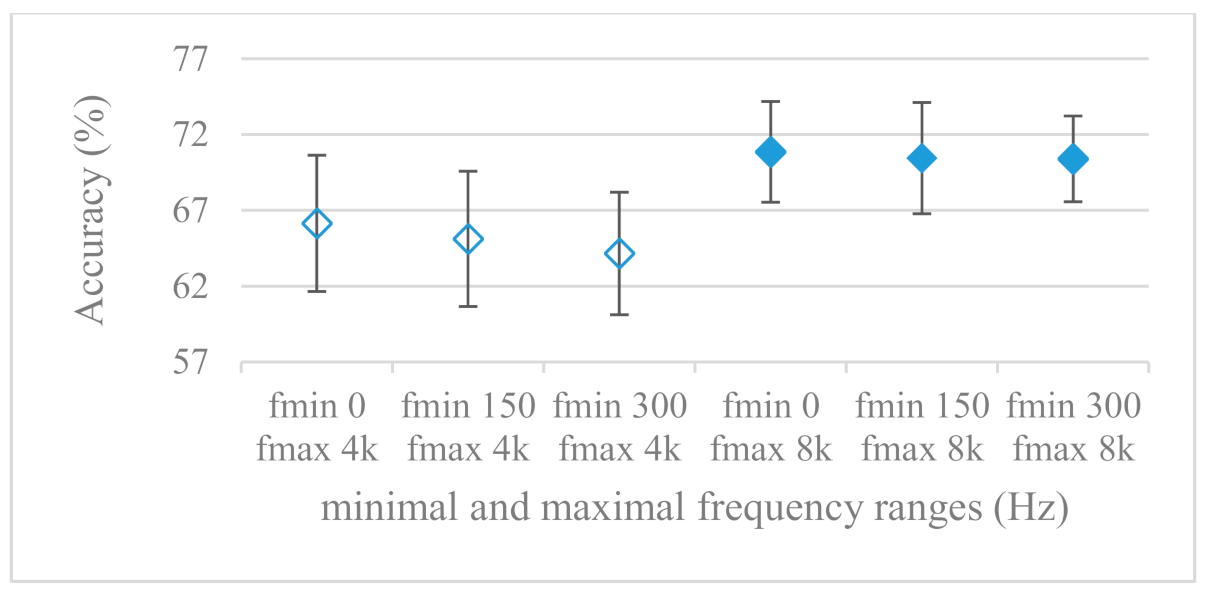
- While testing frequency ranges a positive effect of low frequencies, less than 300 Hz was found (Figure 7 and Figure 8). Likewise, higher frequencies, i.e., 8 kHz recorded better scores (Figure 11). It differs from the speech recognition systems that mostly operate in the 300 Hz to 4 kHz range. However, these systems aim to extract minimal lexical information, which increases their robustness in real environments. The benefit of a higher frequency limit (over 4 kHz) is in the line with our previous research on speaker recognition [41]. It shows the speaker specific information is also located in higher frequencies. Nevertheless, these findings favoring the (0+, 8 kHz) range hold true for clean recordings, and taking into account the previous discussion, the effect of an upper bound significantly depends on magnitude modifications when spectrograms are regarded. The positive effect for 0+ lower bound was confirmed also for IEMOCAP database (correlation 0.43), however the higher frequency bond had a slightly adverse effect compared to the Berlin database.
- When testing linear and nonlinear frequency scales in the construction of spectrograms (Figure 9 and Figure 10), it was observed that on average the linear scale slightly outperformed the non-linear Mel scale both for 4 and 8 kHz frequency limits. A non-linear scale may disrupt the clear trace of a fundamental frequency in a spectrum that is presented by sharp minima located at integer multiplications of a fundamental frequency. The course of fundamental frequency in time is known to reflect speech prosody, which is definitely controlled by emotions. On the other hand, the Mel scale significantly improved the performance for the 8 kHz frequency limit, which was not observed for the linear scale. Such a behavior can be attributed to the increased precision for lower frequencies over the higher ones (nonlinear scale) as the amount of frequency samples (FV size) in both cases was kept the same. It should be noted that the experiments regarding the Mel scale were highly correlated (0.92) to the IEMOCAP database.
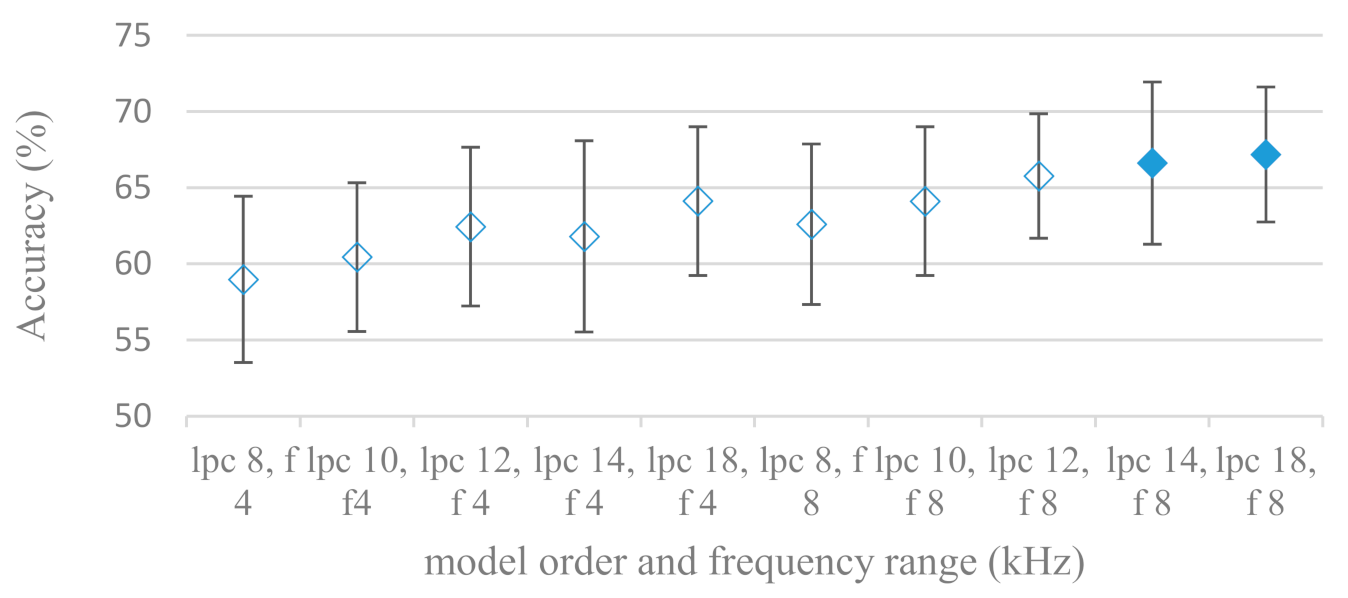
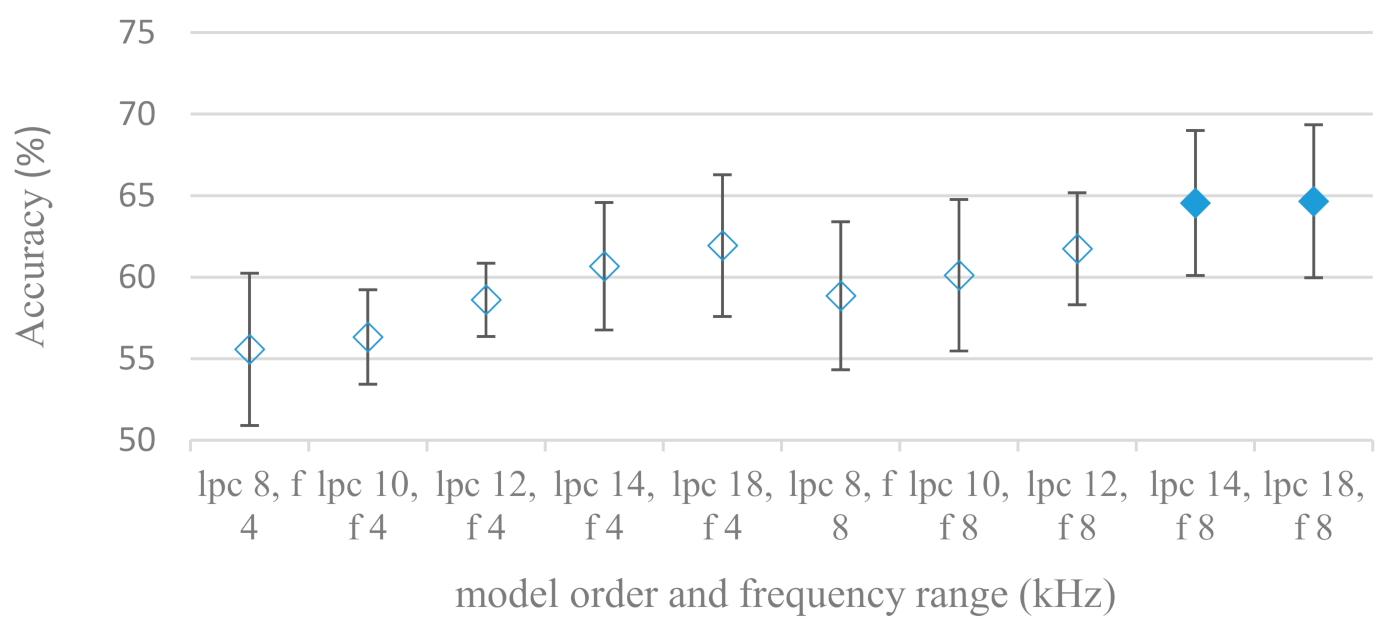
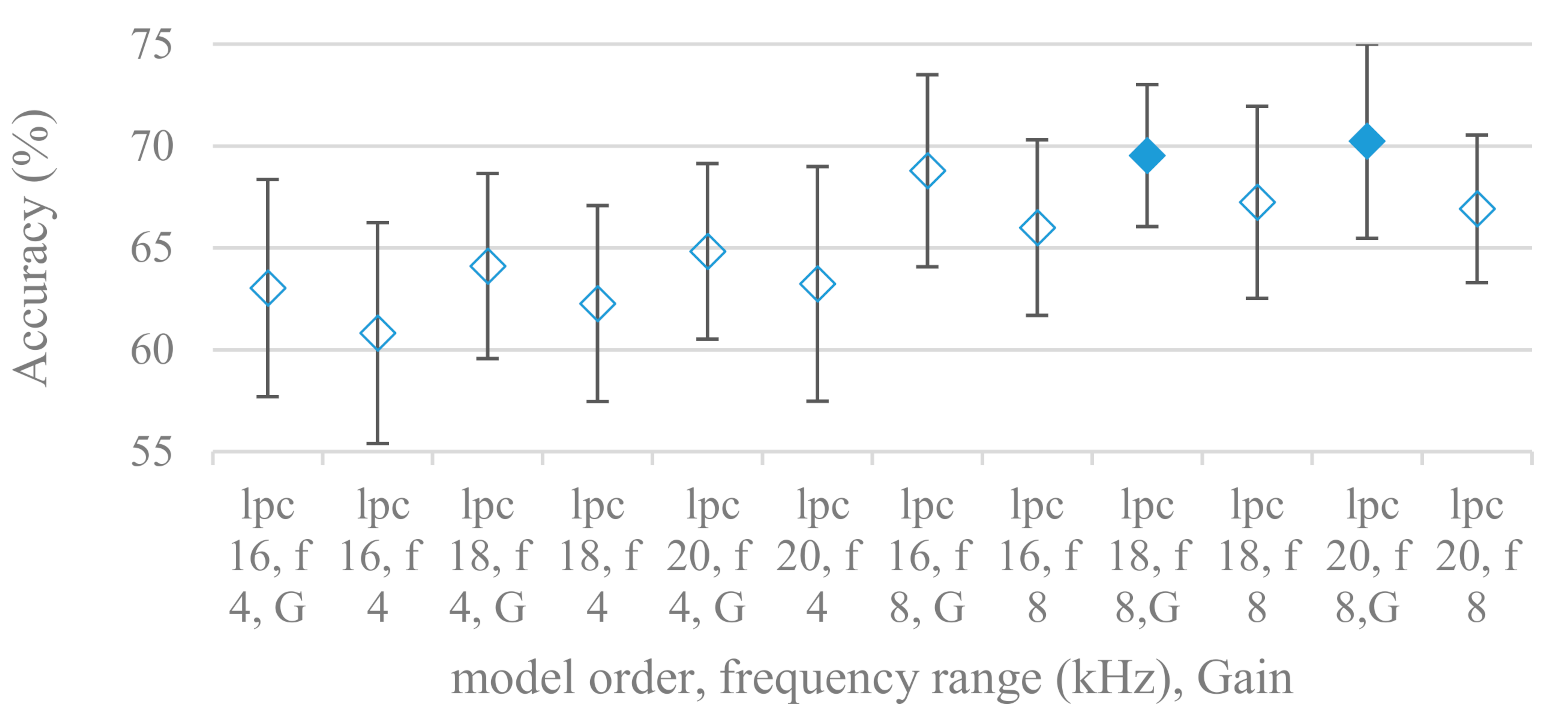
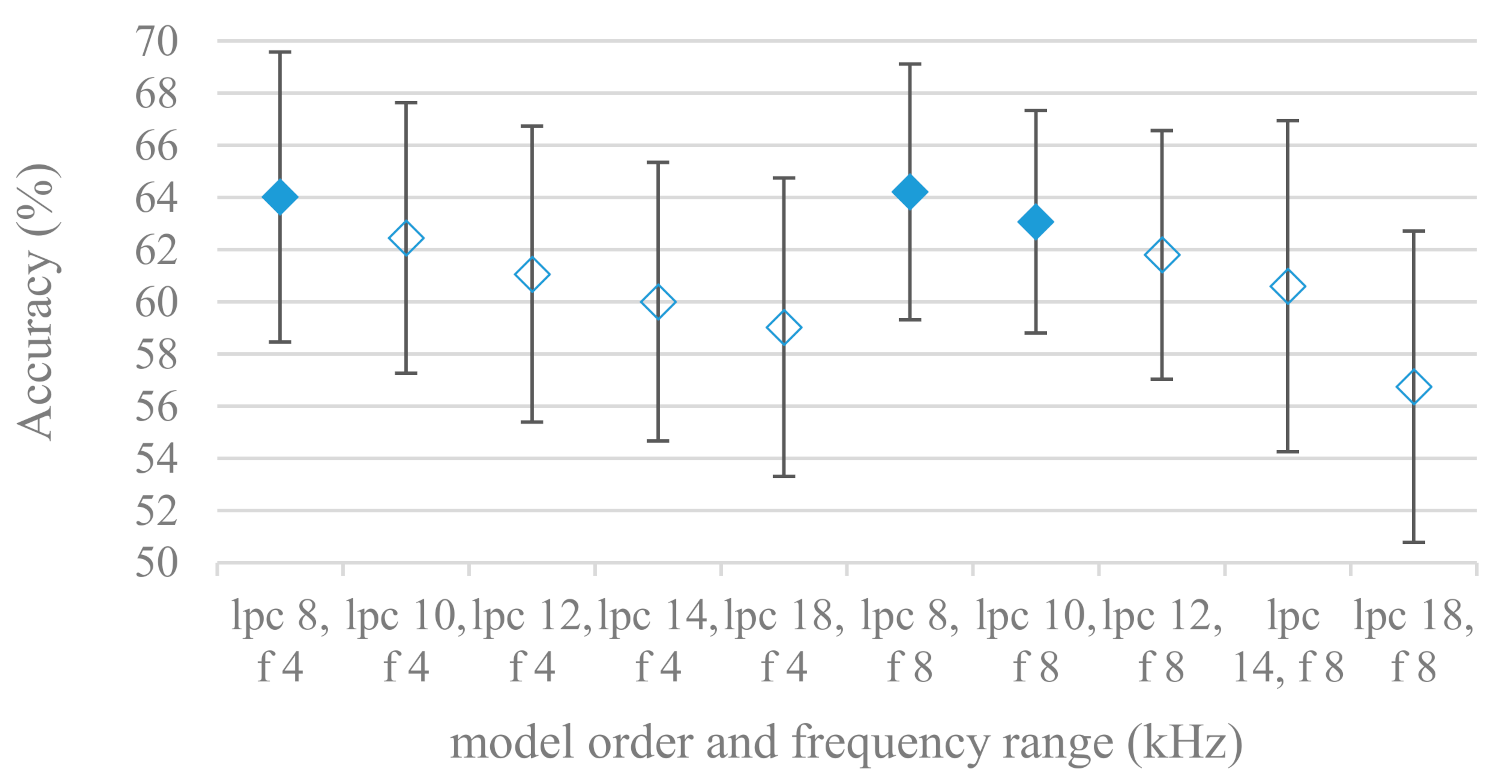
- The importance of vocal tract characteristics extracted by the LPC model is presented in Figure 13, Figure 14 and Figure 15. It was clearly shown that the best performance was achieved by high model orders (18, 20) without a pre-emphasis. This focuses the model to low frequencies and a finer description of speech spectra. Nevertheless, the main contributing factor was the incorporation of gain that represents the speech dynamic, which is related to prosody and thus to emotions. In comparison to psychoacoustic FBs this method proved to be inferior. This can be due to model limitations, e.g., sort of an excitation signal, the model order, parameter estimation (the mean square error of a prediction signal), numerical problems, etc. A high correlation (0.93) between the databases for LPC and gain modeling was recorded.
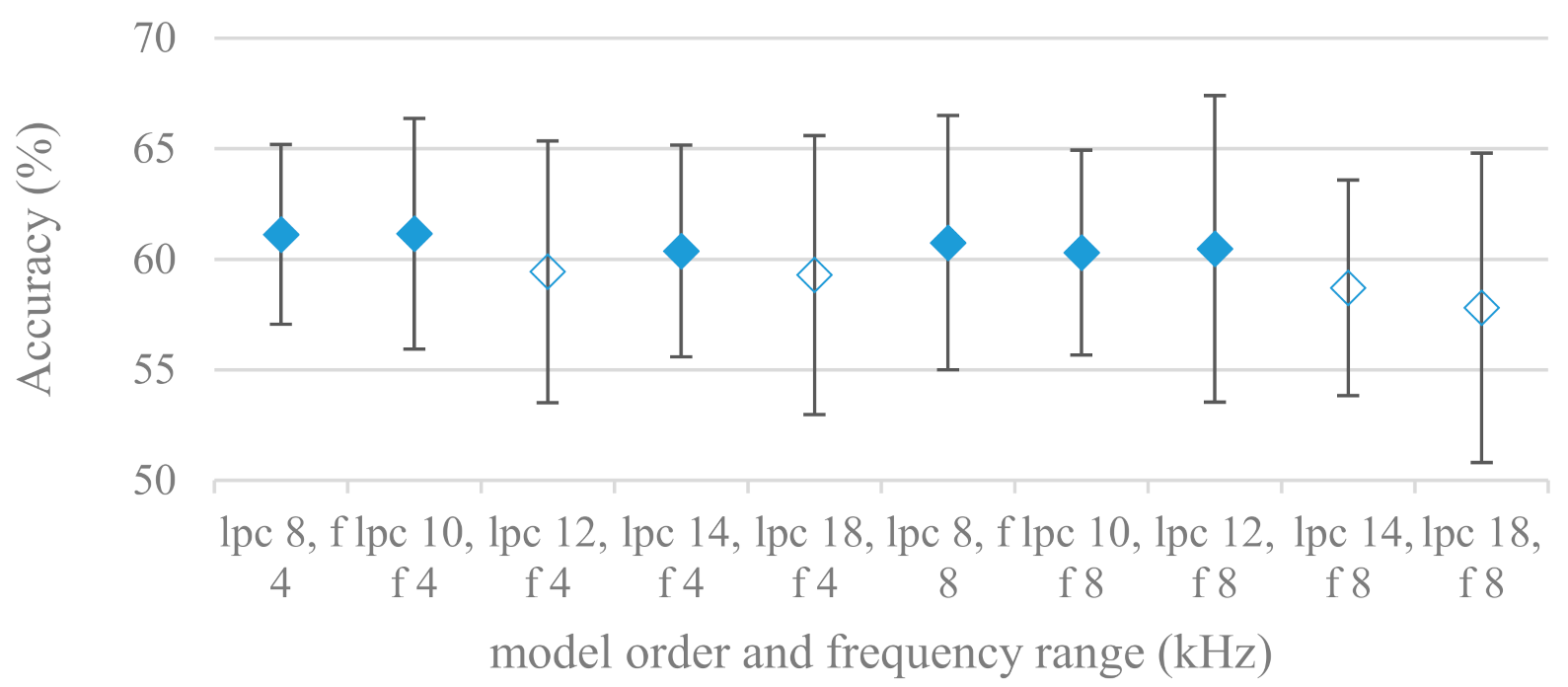
- Excitation signals were also incorporated in our study as they carry relevant information about the speech prosody. They were derived from an inverse LPC filter of different orders. Interesting though explainable behavior was observed, i.e., the less precise the LPC model was the better results were. The best scoring one was with pre-emphasis (did not work for spectral envelopes) having only eight prediction coefficients. Based on the empirics related to LPC, a model order of 8 is not adequate for a precise modeling of speech sampled at 16 kHz. Naturally by having a less precise model more vocal tract information is leaking through an inverse LPC filtering into the excitation signal. This leads us to the conclusion that the improved results (for a less precise model) might have been a consequence of additional information resulting from an improperly removed spectral envelope. These findings are moderately correlated (0.4) to the IEMOCAP database.
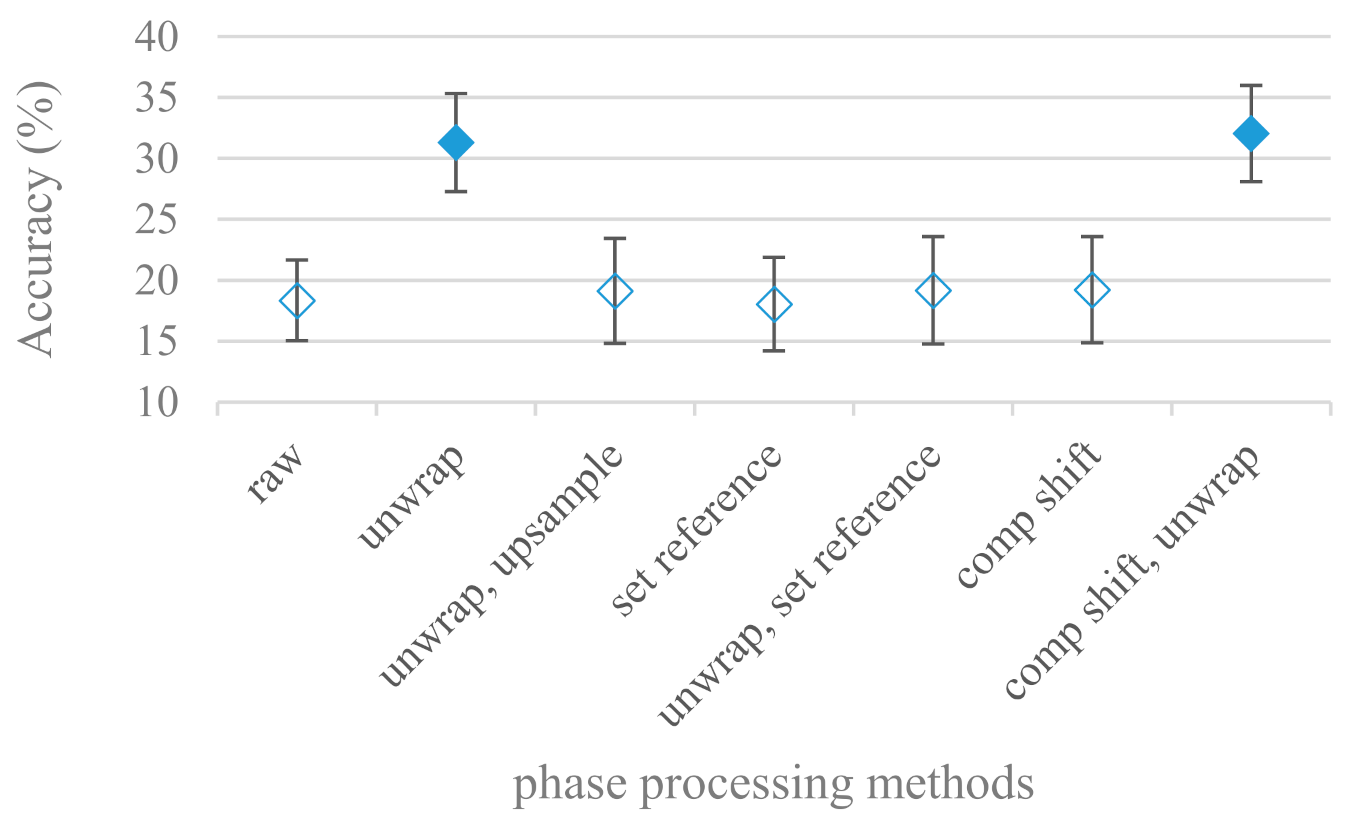
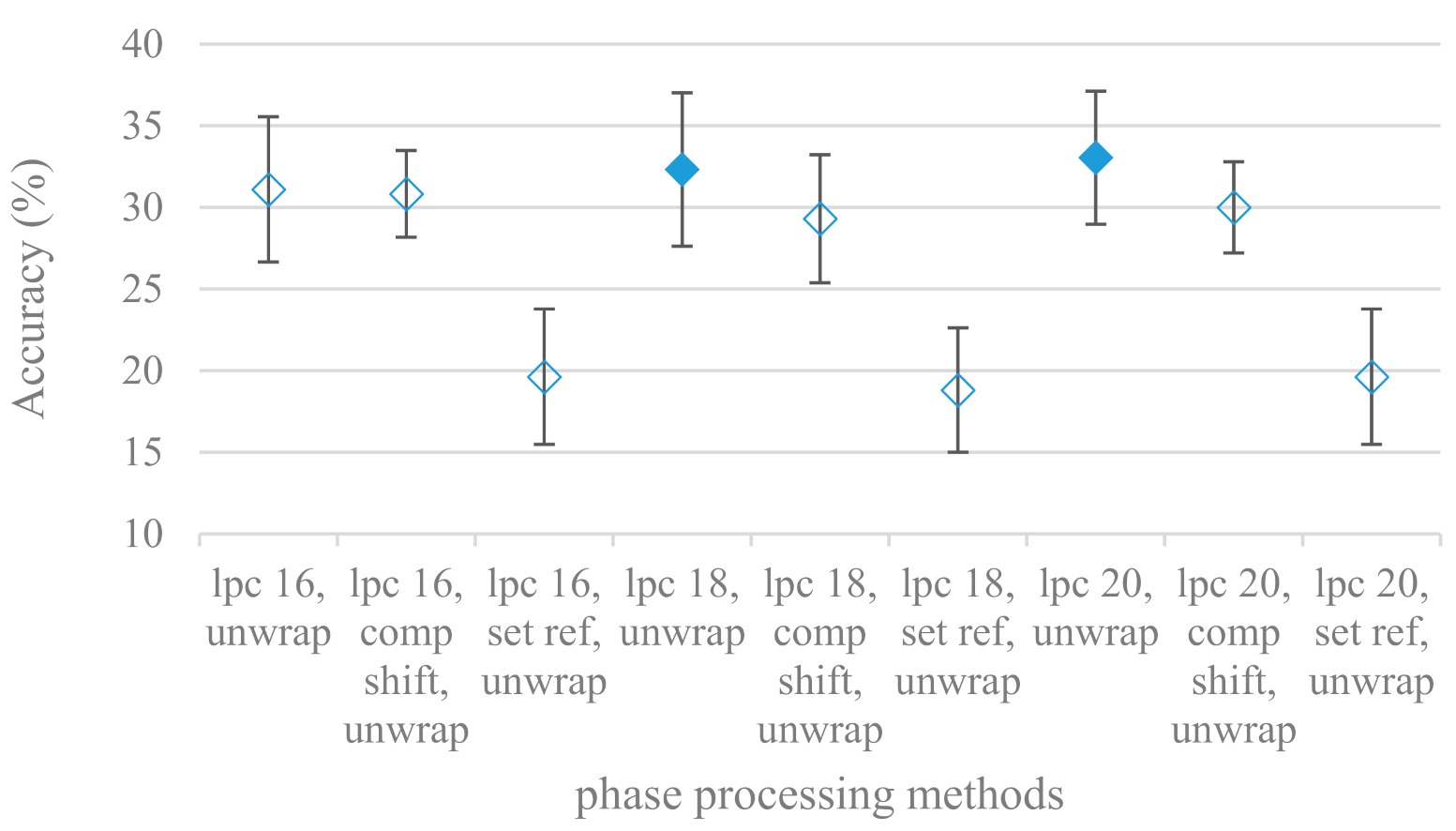
- In a series of phase related experiments (Figure 18 and Figure 19) its modifications, e.g., unwrapping, upsampling, shift compensations, setting reference frequency to a fixed phase, etc., were tested. They were applied to both speech and excitation signals. In all cases the results were much worse (approximately by 50%) than the magnitude based approaches. Nevertheless, the most successful methods for phase extraction were unwrapping and unwrapping combined with time shift compensation.
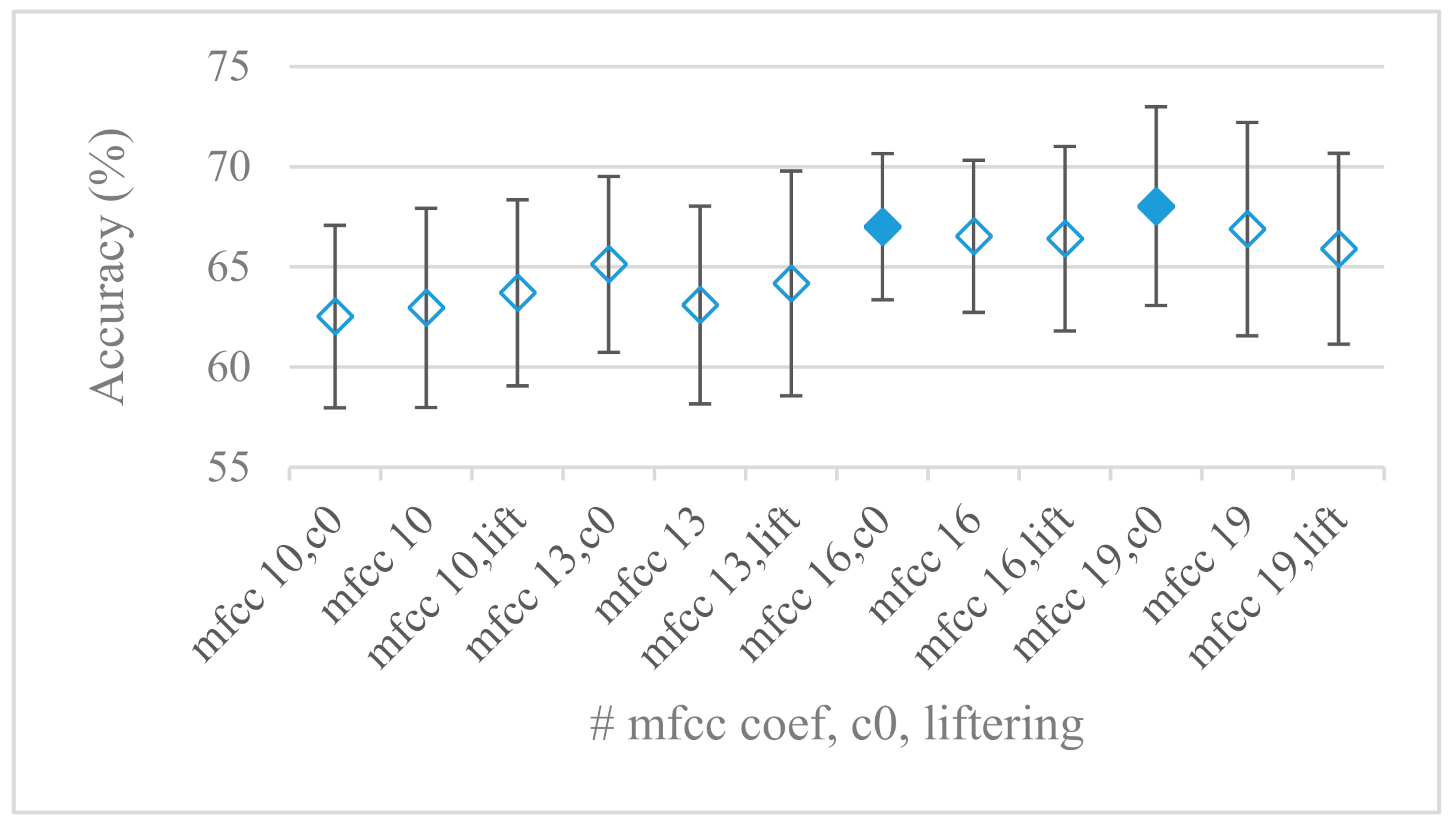
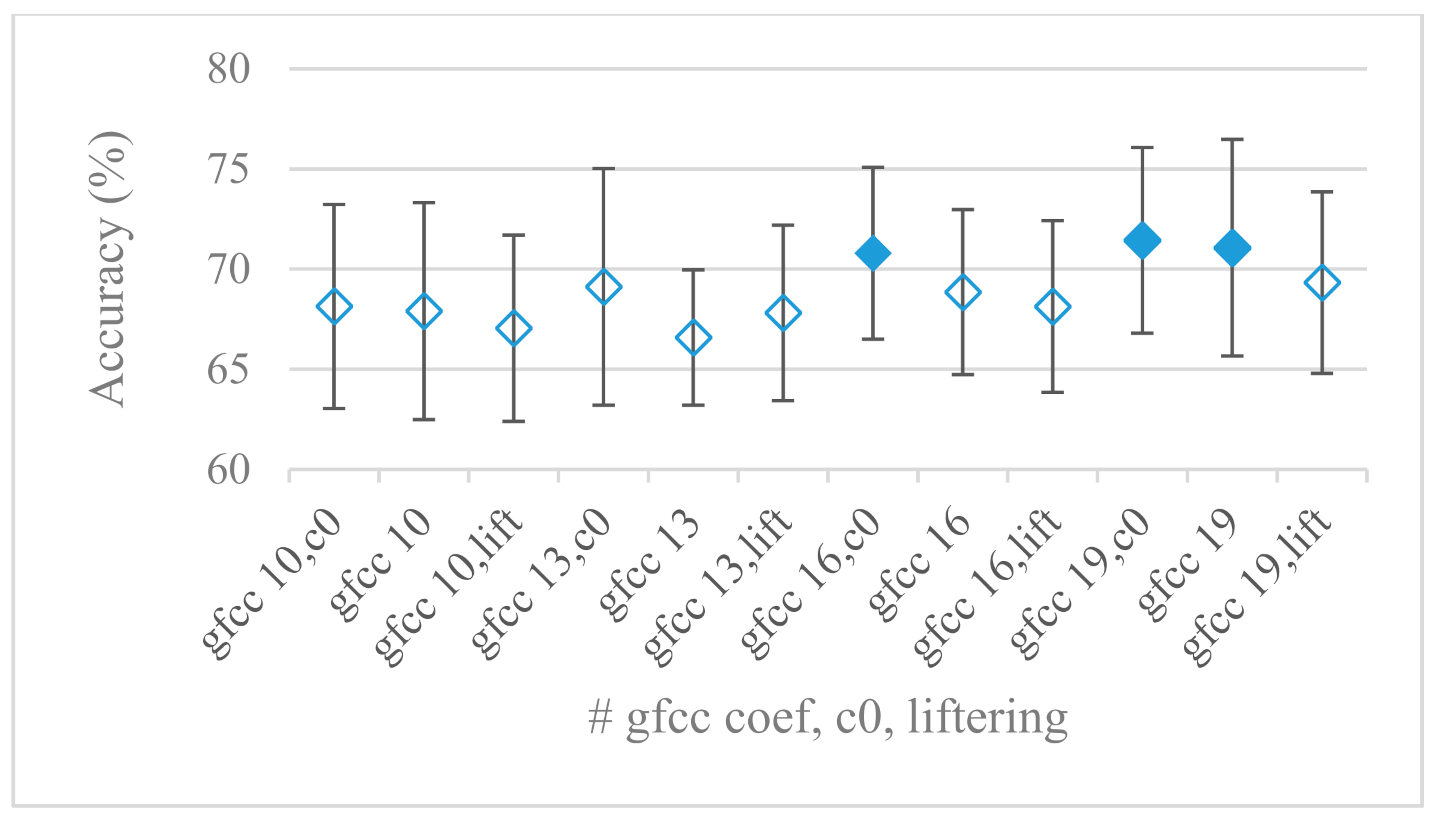
- The most common feature used in many speech applications, i.e., cepstral coefficients in forms of MFCC and GFCC were tested in the concluding experiments. Based on the presented results (Figure 20 and Figure 21) the higher number of coefficients (16–19) led to better accuracies. The Gammatone based design outperformed the Mel one measured both on average and in the best scores. In almost all cases the incorporation of c0 (energy) was clearly beneficial, which is in line with expectations (prosody). However, when it comes to liftering, no obvious merit was observed. It is so because CNNs can easily and more precisely perform such operation if needed using its convolutional layers; moreover, it helps in adverse conditions to increase robustness for the sake of precision, which was not the case. MFCC and GFCC are more complex features involving many underlying settings bound in a nonlinear way. Thus finding optimal settings and making more general conclusions would involve a parallel optimization of all relevant parameters at the same time, e.g., a significantly worse Mel FBs using 35 bands outperformed the best one having 60 FBs (Figure 12) when it was subsequently used for the MFCC calculation. Still such results could not be easily extended to other MFCC/GFCC systems if some settings must be changed not even mentioning different background conditions. MFCC/GFCC experiments proved a solid consistency as they reached high correlations (0.87) between the databases.
- The selected CNN based classification was compared with another common approach—the SVM in the case of the best scoring methods and settings. The original choice proved to be superior for spectrogram- like processing over SVM where more than a 40% improvement was observed for the best features (GFB).
- The most challenging emotions to separate were happiness, which was mostly confused with anger and neutral misclassified with boredom. It is of no surprise as these emotions are very close to each other when considering acoustic and prosodic features. An obvious improvement to separate these cases would be to use high level speech features, e.g., vocabulary, phrases, etc., to get also a context of speech.
- While trying to remove a phase shift (in a frequency domain) between adjacent frames and the up sampled case (by factor M, to get more precise phase unwrapping), we found that the classical formula does not work. By a closer inspection we derived frequency dependent compensation terms that must be applied to the original signal (Equation (2)) prior to the DFT. By doing so the adjacent frames, after the DFT, will have their phases unaffected by the time shift, i.e., the distortion of phase characteristics caused by the time shift of S samples will be suppressed and only the natural (speech related) changes will be preserved.
- In the next work it should be analyzed, which features and settings affect a particular emotion, how successful speech features of different levels work together, and how they are related to other emotional modalities, e.g., facial features.
- The databases consist of only acted emotions by professional actors that might not reflect their true emotions. So, the SER system and its settings only reflect emotions that we believe are correct based on our perception.
- The databases contain only clean speech recorded in the controlled environment. Thus the results do not include session variability, noise, etc., so the presented methods and settings may differ for mismatched conditions. Even though some of the main findings are rather robust as the cross database correlations on different levels were high.
- Even though CNN is a very complex classification method with outstanding results in image/speech processing, we cannot reject that the findings released here can be partly affected by its limitations (structure, training algorithm, numerical precisions, etc.). Nevertheless, when compared to another successful classification method—SVM, still the CNN provided better results.
- The experiments and outcomes are related to single language SER systems (German and English). However, in [42] it was shown that the performance of SER systems and features applied in a cross lingual scenario may drop substantially.
- Even though the knowledge of how each setting, method and preprocessing affects a SER system is important from the theoretical point of view, and may dramatically shorten the design of a particular SER system, in [43] it was documented that using complex classification models and databases it is possible to process even raw speech signals, while achieving challenging results. However, in such a case the extracted features (local or global) are hidden deep in the complex model structure.
- There are many articles presenting particular SER systems focusing on new features, feature fusions, or modeling/classification methods in order to achieve the best performance. In contrary to that, there are few articles testing and analyzing the behavior of specific features and their settings in given conditions, e.g., testing frequency ranges or scales [44], etc. Nevertheless, published results measured even on the same database vary a lot, e.g., from approximately 50% [45] to even 92% [46], mainly due to the experimental set up, evaluation, processing, and classification. This study differs as it provides a unified, complex, and statistically rigorous analysis of great variety of basic speech properties, features and their settings, and calculation methods related to SER, by means of the machine learning. Where it was possible a generalization and explanation of particular findings was provided using signal theory. Some of the results were tested on another database to reveal their robustness. The presented results ranging from approximately 60% to 75% were in line with other similar systems. No obvious contradiction to other comparable results was observed. Nevertheless, differences attributed to the stochastic nature could be spotted, e.g., in [44] the Mel scale performed better (by 1.9%) than a linear frequency, whereas our results showed slightly better scores (by only 0.2%) in favor of a linear frequency, etc. Therefore we introduced and used the concept of equally performing methods throughout the result section.
- When viewing the results in terms of confusion matrices, i.e., ranking of emotions according to their accuracies, very similar outcomes were observed, e.g., in [47,48]. An interesting fact is that there was a perfect match with at least five other articles, where happiness recorded the worst scores and disgust, neutral, and boredom were also low-scorers. The situation with the best performing emotions was not that clear, however, fear and anger were amongst the best. This is also in line with our outcomes.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Amir, N.; Ron, S.; Laor, N. Analysis of an emotional speech corpus in Hebrew based on objective criteria. In Proceedings of the ISCA Workshop (ITRW) on Speech and Emotion, Belfast, Ireland, 5–7 September 2000. [Google Scholar]
- Cen, L.; Wu, F.; Yu, Z.L.; Hu, F. A Real-Time Speech Emotion Recognition System and its Application in Online Learning. In Emotions, Technology, Design, and Learning, 1st ed.; Tettegah, S.Y., Gartmeier, M., Eds.; Academic Press: San Diego, CA, USA, 2016; pp. 27–46. [Google Scholar] [CrossRef]
- Tokuno, S.; Tsumatori, G.; Shono, S.; Takei, E.; Suzuki, G.; Yamamoto, T.; Mitsuyoshi, S.; Shimura, M. Usage of emotion recognition in military health care. In Proceedings of the Defense Science Research Conference and Expo (DSR), Singapore, 3–5 August 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Mitsuyoshi, S.; Nakamura, M.; Omiya, Y.; Shinohara, S.; Hagiwara, N.; Tokuno, S. Mental status assessment of disaster relief personnel by vocal affect display based on voice emotion recognition. Disaster Mil. Med. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- Bosch, E.; Oehl, M.; Jeon, M.; Alvarez, I.; Healey, J.; Ju, W.; Jallais, C. Emotional GaRage: A workshop on in-car emotion recognition and regulation. In Proceedings of the 10th International Conference on Automotive User Interfaces and Interactive Vehicular Applications (AutomotiveUI ‘18), Association for Computing Machinery. New York, NY, USA, 23–25 September 2018; pp. 44–49. [Google Scholar] [CrossRef]
- Katsis, C.D.; Rigas, G.; Goletsis, Y.; Fotiadis, D.I. Emotion recognition in car industry. In Emotion Recognition: A Pattern Analysis Approach; Konar, A., Chakraborty, A., Eds.; Wiley Online Library: Hoboken, NJ, USA, 2015; pp. 515–544. [Google Scholar] [CrossRef]
- Hu, H.; XingXu, M.; Wu, W. GMM Supervector Based SVM With Spectral Features for Speech Emotion Recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ‘07, Honolulu, HI, USA, 15–20 April 2007; pp. IV-413–IV-416. [Google Scholar] [CrossRef]
- El Ayadi, M.H.; Kamel, M.S.; Karray, F. Survey on Speech Emotion Recognition: Features, classification schemes, and databases. Pattern Recognit. 2011, 44, 572–587. [Google Scholar] [CrossRef]
- Sánchez-Gutiérrez, M.E.; Albornoz, E.M.; Martinez-Licona, F.; Rufiner, H.L.; Goddard, J. Deep Learning for Emotional Speech Recognition. In Pattern Recognition; Martínez-Trinidad, J.F., Carrasco-Ochoa, J.A., Olvera-Lopez, J.A., Salas-Rodríguez, J., Suen, C.Y., Eds.; MCPR 2014. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8495. [Google Scholar] [CrossRef]
- Eyben, F.; Scherer, K.R.; Schuller, B.W.; Sundberg, J.; André, E.; Busso, C.; Devillers, L.Y.; Epps, J.; Laukka, P.; Narayanan, S.S.; et al. The Geneva minimalistic acoustic parameter set (GeMAPS) for voice research and affective computing. IEEE Trans. Affect. Comput. 2016, 7, 190–202. [Google Scholar] [CrossRef]
- Posner, J.; Russell, J.A.; Peterson, B.S. The circumplex model of affect: An integrative approach to affective neuroscience, cognitive development, and psychopathology. Dev. Psychopathol. 1980, 17, 715–734. [Google Scholar] [CrossRef] [PubMed]
- Rabiner, L.; Juan, B.H. Fundamentals of Speech Recognition; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Fayek, H.; Lech, M.; Cavedon, L. Evaluating deep learning architectures for speech emotion recognition. Neural Netw. 2017, 92, 60–68. [Google Scholar] [CrossRef] [PubMed]
- Badshah, A.; Ahmad, J.; Rahim, N.; Baik, S. Speech emotion recognition from spectrograms with deep convolutional neural network. Int. Conf. Platf. Technol. Serv. 2017, 1–5. [Google Scholar] [CrossRef]
- Badshah, A.M.; Rahim, N.; Ullah, N.; Ahmad, J.; Muhammad, K.; Lee, M.Y.; Kwon, S.; Baik, S.W. Deep features-based speech emotion recognition for smart affective services. Multimed. Tools Appl. 2019, 78, 5571–5589. [Google Scholar] [CrossRef]
- Zheng, L.; Li, Q.; Ban, H.; Liu, S. Speech emotion recognition based on convolution neural network combined with random forest. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4143–4147. [Google Scholar] [CrossRef]
- Deng, J.; Xu, X.; Zhang, Z.; Frühholz, S.; Grandjean, D.; Schuller, B. Fisher Kernels on Control and Decisi Phase-Based Features for Speech Emotion Recognition. In Dialogues with Social Robots; Jokinen, K., Wilcock, G., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2017; Volume 427. [Google Scholar] [CrossRef]
- Jalili, A.; Sahami, S.; Chi, C.; Amirfattahi, R.R. Speech emotion recognition using cyclostationary spectral analysis. In Proceedings of the 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP), Aalborg, Denmark, 17–20 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kvedalen, E. Signal Processing Using the Teager Energy Operator and Other Nonlinear Operators. Master thesis, University of Oslo, Oslo, Norway, 2003. [Google Scholar]
- Wu, C.; Huang, C.; Chen, H. Text-independent speech emotion recognition using frequency adaptive features. Multimed. Tools Appl. 2018, 77, 24353–24363. [Google Scholar] [CrossRef]
- Puterka, B.; Kacur, J.; Pavlovicova, J. Windowing for Speech Emotion Recognition. In Proceedings of the 2019 International Symposium ELMAR, Zadar, Croatia, 23–25 September 2019; pp. 147–150. [Google Scholar] [CrossRef]
- Puterka, B.; Kacur, J. Time Window Analysis for Automatic Speech Emotion Recognition. In Proceedings of the International Symposium ELMAR, Zadar, Croatia, 16–19 September 2018; ELMAR. 2018; pp. 143–146. [Google Scholar] [CrossRef]
- Daneshfar, F.; Kabudian, S.J. Speech emotion recognition using discriminative dimension reduction by employing a modified quantum-behaved particle swarm optimization algorithm. Multimed. Tools Appl. 2020, 79, 1261–1289. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, Z.; Jin, J.S.; Han, X.; Li, C. Speech emotion recognition with heterogeneous feature unification of deep neural network. Sensors 2019, 19, 2730. [Google Scholar] [CrossRef]
- Özseven, T. Investigation of the effect of spectrogram images and different texture analysis methods on speech emotion recognition. Appl. Acoust. 2018, 142, 70–77. [Google Scholar] [CrossRef]
- Mansour, A.; Chenchah, F.; Lachiri, Z. Emotional speaker recognition in real life conditions using multiple descriptors and i-vector speaker modeling technique. Multimed. Tools Appl. 2019, 78, 6441–6458. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Chui, Ch.; Lemm, J.M.; Sedigh, S. An Introduction to Wavelets; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Sahley, T.; Musiek, F. Basic Fundamentals in Hearing Science; Plural Publishing: San Diego, CA, USA, 2015. [Google Scholar]
- Markel, J.D.; Gray, A.H., Jr. Linear Prediction of Speech; Springer: New York, NY, USA, 1976. [Google Scholar]
- Nakagawa, S.; Wang, L.; Ohtsuka, S. Speaker Identification and Verification by Combining MFCC and Phase Information. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1085–1095. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Li, H.; Lin, Z.; Shen, X.; Brandt, J.; Hua, G. A Convolutional Neural Network Cascade for Face Detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 12 June 2015; pp. 5325–5334. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Rice, J.A. Mathematical Statistics and Data Analysis, 3rd ed.; Duxbury Press: Belmont, CA, USA, 2006. [Google Scholar]
- Daniel, W.W. Applied Nonparametric Statistics, 2nd ed.; PWS-Kent: Boston, MA, USA, 1990. [Google Scholar]
- Burkhardt, F.; Paeschke, A.; Rolfes, M.; Sendlmeier, W.; Weiss, B. A database of German emotional speech. In Proceedings of the Interspeech 2005, Lisbon, Portugal, 4–8 September 2005. [Google Scholar]
- Busso, C.; Bulut, M.; Lee, C.C.; Kazemzadeh, A.; Mower, E.; Kim, S.; Chang, J.N.; Lee, S.; Narayanan, S.S. IEMOCAP: Interactive emotional dyadic motion capture database. J. Lang. Resour. Eval. 2008, 42, 335–359. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning, Series: Information Science and Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kacur, J.; Varga, M.; Rozinaj, G. Speaker Identification in a Multimodal Interface. In Proceedings of the ELMAR-2013, Zadar, Croatia, 25–27 September 2013; pp. 191–194. [Google Scholar]
- Mustaqeem; Kwon, S. CLSTM: Deep Feature-Based Speech Emotion Recognition Using the Hierarchical ConvLSTM Network. Mathematics 2020, 8, 2133. [Google Scholar] [CrossRef]
- Albu, C.; Lupu, E.; Arsinte, R. Emotion Recognition from Speech Signal in Multilingual Experiments. In Proceedings of the 6th International Conference on Advancements of Medicine and Health Care through Technology, Cluj-Napoca, Romania, 17–20 October 2018; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Lech, M.; Stolar, M.; Bolia, R.; Skinner, M. Amplitude-Frequency Analysis of Emotional Speech Using Transfer Learning and Classification of Spectrogram Images. Adv. Sci. Technol. Eng. Syst. J. 2018, 3, 363–371. [Google Scholar] [CrossRef]
- Ren, M.; Nie, W.; Liu, A.; Su, Y. Multi-modal Correlated Network for emotion recognition in speech. Vis. Inform. 2019, 3, 150–155. [Google Scholar] [CrossRef]
- Anvarjon, T.; Mustaqeem; Kwon, S. Deep-Net: A Lightweight CNN-Based Speech Emotion Recognition System Using Deep Frequency Features. Sensors 2020, 20, 5212. [Google Scholar] [CrossRef]
- Mustaqeem; Sajjad, M.; Kwon, S. Clustering-Based Speech Emotion Recognition by Incorporating Learned Features and Deep BiLSTM. IEEE Access 2020, 8, 79861–79875. [Google Scholar] [CrossRef]
- Basu, S.; Chakraborty, J.; Aftabuddin, M. Emotion recognition from speech using convolutional neural network with recurrent neural network architecture. In Proceedings of the 2017 2nd International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 19–20 October 2017; pp. 333–336. [Google Scholar] [CrossRef]
| Tests | Accuracy Correlation | H0-Accuracies Uncorrelated | Methods’ Rank Correlation | H0-Rank Uncorrelated | Match of Equally Performing Methods | Averaged Accuracy Berlin Database | Averaged Accuracy IEMOCAP Database |
|---|---|---|---|---|---|---|---|
| LPC modelling | 0.93 | F | 1 | F | 1 | 0.7 | 0.35 |
| Mell scales ranges | 0.92 | F | 0.89 | F | 0.6 | 0.63 | 0.38 |
| MFCC and GFCC | 0.82 | F | 0.87 | F | 0.67 | 0.67 | 0.39 |
| Classification block/spectrogram lengths | 0.65 | F | 0.70 | F | 0.33 | 0.59 | 0.37 |
| Linear frequency ranges | 0.43 | T | 0.30 | T | 0.25 | 0.62 | 0.39 |
| Filter banks | 0.35 | T | 0.38 | T | 0.33 | 0.67 | 0.41 |
| Excitation signals | 0.4 | T | 0.3 | T | 0.6 | 0.6 | 0.39 |
| Frame lengths/types | 0.11 | T | 0.03 | T | 0.06 | 0.64 | 0.39 |
| Magnitude modifications | 0.07 | T | 0.09 | T | 0 | 0.66 | 0.33 |
| Features | Fmin (kHz) | Fmax (kHz) | Magnitude Modification | Frequency Scale | Feature Vector Length | Signal Type: Excitation/Envelop | Accuracy (%) |
|---|---|---|---|---|---|---|---|
| Methods and settings in over 75% accuracy range | |||||||
| GFB | 0 | 8 | mag | RBF | 60 | enve | 75.38 |
| GFB | 0 | 8 | mag | RBF | 45 | enve | 75.21 |
| MFB | 0 | 8 | mag | MEL | 60 | enve | 74.63 |
| GFB | 0 | 8 | mag | RBF | 30 | enve | 73.51 |
| 10 best methods and settings in over 70% accuracy range | |||||||
| MFB | 0 | 8 | mag | MEL | 45 | enve | 73.48 |
| BFB | 0 | 8 | mag | BAR | 30 | enve | 73.3 |
| BFB | 0 | 8 | mag | BAR | 60 | enve | 73.2 |
| BFB | 0 | 8 | mag | BAR | 45 | enve | 72.68 |
| Spect | 0 | 8 | Log mag | Hz | 160 | both | 72.45 |
| MFB | 0 | 8 | mag | MEL | 30 | enve | 72 |
| Spect | 0 | 8 | mag | Hz | 160 | both | 71.88 |
| GFCC, c0 | 0 | 8 | Log pow | RBF | 19 | enve | 71.4 |
| Spect | 0.3 | 8 | mag | Mel | 155 | both | 71.17 |
| Spect | 0 | 4 | mag | Hz | 80 | both | 71.12 |
| Features | Fmin (kHz) | Fmax (kHz) | Magnitude Modification | Frequency Scale | Feature Vector Length | Signal Type: Excitation/Envelop | Accuracy (%) |
|---|---|---|---|---|---|---|---|
| GFB | 0 | 8 | mag | RBF | 60 | enve | 44.35 |
| GFB | 0 | 4 | mag | RBF | 45 | enve | 44.24 |
| GFCC | 0 | 8 | Log pow | RBF | 19 | enve | 43.67 |
| GFCC, c0 | 0 | 8 | Log pow | RBF | 19 | enve | 43.24 |
| MFB | 0 | 8 | mag | BAR | 60 | enve | 43.02 |
| Emotions | Fear | Disgust | Happy | Angry | Sad | Bored | Neutral |
|---|---|---|---|---|---|---|---|
| Fear | 90.3 | 4.3 | 2.2 | 2.2 | 1.1 | 0 | 0 |
| Disgust | 10.6 | 75.2 | 1.2 | 0 | 0 | 10.6 | 2.5 |
| Happy | 16.7 | 1.9 | 44.4 | 36.1 | 0 | 0 | 0.9 |
| Angry | 1.4 | 0 | 3.5 | 95.1 | 0 | 0 | 0 |
| Sad | 2 | 6.9 | 0 | 0 | 79.3 | 10.3 | 1.5 |
| Bored | 0.6 | 2.9 | 0 | 0.6 | 4 | 85.5 | 6.4 |
| Neutral | 3.2 | 3.2 | 4.8 | 0 | 0 | 24.8 | 64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kacur, J.; Puterka, B.; Pavlovicova, J.; Oravec, M. On the Speech Properties and Feature Extraction Methods in Speech Emotion Recognition. Sensors 2021, 21, 1888. https://doi.org/10.3390/s21051888
Kacur J, Puterka B, Pavlovicova J, Oravec M. On the Speech Properties and Feature Extraction Methods in Speech Emotion Recognition. Sensors. 2021; 21(5):1888. https://doi.org/10.3390/s21051888
Chicago/Turabian StyleKacur, Juraj, Boris Puterka, Jarmila Pavlovicova, and Milos Oravec. 2021. "On the Speech Properties and Feature Extraction Methods in Speech Emotion Recognition" Sensors 21, no. 5: 1888. https://doi.org/10.3390/s21051888
APA StyleKacur, J., Puterka, B., Pavlovicova, J., & Oravec, M. (2021). On the Speech Properties and Feature Extraction Methods in Speech Emotion Recognition. Sensors, 21(5), 1888. https://doi.org/10.3390/s21051888






