1. Introduction
Cyber-Physical Systems (CPSs) are characterized by the strong coupling of the physical and the cyber worlds. The inevitable dependence on highly automated procedures and the increasing integration of
physical parts to highly interconnected
cyber parts render CPSs vulnerable to cyber attacks. On the other hand, the wide use of such systems in various critical domains [
1] (e.g., Smart Grid, Intelligent Transportation Systems, Medical devices, Industrial Control Systems, etc.) increases the impact of such cyber attacks. Furthermore, the
System of Systems (SoS) nature of interconnected, complex CPSs [
2] introduces challenges in addressing security risks. In this context, a complex CPS comprises other CPSs that are interconnected, and control and information flows exist among them. These flows constitute pathways that a cyber attack may leverage to propagate from component to component. More specifically, both or either of the likelihood of the attack and its impact, if successful, may propagate. Because likelihood and impact are the constituents of risk, the cyber risk of the overall system is related to the individual cyber risk of each interconnected component. This in principle means that knowledge of the cyber risk of the individual components of a complex CPS may be leveraged to assess the cyber risk of the overall system, thus also facilitating the analysis of large scale, complex CPSs through a divide-and-conquer-like approach to cyber risk assessment.
The assessment of risk is one of the steps in the risk management process [
3] that concludes with treating the risk by means of controls that aim at achieving retention, reduction, transfer, or avoidance of the risk [
4]. In the general case, each risk can be treated by a number of possible cybersecurity controls, each of which with varying effectiveness and efficiency characteristics. Note that the same control may be effective and efficient in treating more than one risk. Therefore, an important task in formulating the risk treatment plan is the selection of the optimal set of cybersecurity controls, the criterion of optimality in this context being effectiveness and efficiency. Because of the complexity of formulating this as a formal optimization problem, particularly when there are more than one criteria of optimality, the selection of the cybersecurity controls is largely performed empirically, at best with some automated decision support.
In this paper, we propose a novel method for identifying a set of effective and efficient cybersecurity controls for large scale, complex CPSs comprising other CPSs as components. We also propose a method for assessing the aggregated risk that results by taking into account the risk of the individual components and the information and control flows among these components. Specifically, we leverage evolutionary computing to develop a cybersecurity control selection algorithm that uses the aggregated cyber risk of a complex CPS to generate a set of effective and efficient cybersecurity controls to reduce this risk. The algorithm selects the cybersecurity controls among the list of such controls in the NIST Guidelines for Industrial Control Systems Security [
5]. We illustrate the workings of the proposed method by applying it to the navigational systems of two instances of the Cyber-Enabled Ship (C-ES), i.e., vessels with enhanced monitoring, communication, and connection capabilities that include remotely controlled and fully autonomous ships [
6]. The C-ES comprises a variety of interconnected and interdependent CPSs [
7], and, as such, it constitutes a complex CPS. Specifically, we derive the set of cybersecurity controls for both the autonomous and the remotely controlled vessel.
Thus, the contribution of this work is as follows:
A novel method for assessing the aggregate cybersecurity risk of a large scale, complex CPS comprising components connected via links that implement both information and control flows, by using risk measures of its individual components and the information and control flows among these components.
A novel method for selecting a set of effective and efficient cybersecurity controls among those in an established knowledge base, that reduce the residual risk, while at the same time minimizing the cost.
Sets of cybersecurity controls for the navigational systems of two instances of the C-ES, namely the remotely controlled ship and the autonomous ship, derived by employing the two methods.
The remainder of this paper is structured as follows:
Section 2 reviews the related work in the areas of cyber risk propagation and aggregation; optimal selection of cybersecurity controls; and C-ES risk management.
Section 3 provides the background knowledge on genetic algorithms, and on the STRIDE (
Spoofing,
Tampering,
Repudiation,
Information disclosure,
Denial of Service, and
Elevation) and DREAD (
Damage,
Reproducibility,
Exploitability,
Affected, and
Discoverability) risk assessment methods that is necessary to make the paper self-sustained.
Section 4 and
Section 5 present the proposed method for risk aggregation in complex CPSs and the proposed method for optimal cybersecurity control selection, respectively. In
Section 6, we apply the proposed methods to the remotely controlled and the autonomous ship cases and discuss the results. Finally,
Section 7 summarizes our conclusions and outlines topics for future research work.
2. Related Work
Cyber risk is evaluated as a function of the likelihood of an adverse event, such as an attack, occurring; and of the impact that will result when the event occurs. In order for an adverse event to occur, a threat has to successfully exploit one or more vulnerabilities; this can be done by launching one of a number of possible attacks. Hence, the likelihood of the event occurring is, in turn, determined by the likelihood of the threat successfully exploiting at least one vulnerability. Accordingly, in order to analyze how the cyber risk propagates in a complex system made up by interconnected components that are systems by themselves requires analyzing how both the likelihood of the event and its impact propagates. Once this analysis is accomplished, the aggregate cyber risk of the complex system can be assessed.
Several security risk assessment methods applicable to general purpose IT systems have appeared in the literature (see Reference [
8] for a comprehensive survey). Even though several of these methods can be and have been applied to CPSs, they cannot accurately assess cyber risks related to CPSs according to Reference [
9], where a number of approaches for risk assessment for CPSs are listed. A review of risk assessment methods for CPSs, from the perspective of safety, security, and their integration, including a proposal for some classification criteria was made in Reference [
10]. A survey of IoT-enabled cyberattacks that includes a part focused on CPS-based environments can be found in Reference [
11]. Cyber risk assessment methods for CPSs more often than not are domain specific, as they need to take into account safety as an impact factor additional to the “traditional” impact factors of confidentiality, integrity, and availability. For example, an overview of such methods specific to the smart grid case is provided in Reference [
12]. A review of the traditional cybersecurity risk assessment methods that have been used in the maritime domain, is provided in Reference [
13]. Additionally, various risk assessment methods have been proposed to analyze cyber risk in autonomous vessels [
14,
15,
16].
Several works in the literature have studied how individual elements of cyber risk propagate in a network of interconnected systems; both deterministic and stochastic approaches have been used to this end. A threat likelihood propagation model for information systems based on the Markov process was proposed in Reference [
17]. An approach for determining the propagation of the design faults of an information system by means of a probabilistic method was proposed in Reference [
18]. A security risk analysis model (SRAM) that allows the analysis of the propagation of vulnerabilities in information systems, based on a Bayesian network, was proposed in Reference [
19]. Methods for evaluating the propagation of the impact of cyber attacks in CPSs have been proposed in References [
20,
21,
22], among others. Epidemic models were initially used to study malware propagation in information systems [
17]. The propagation of cybersecurity incidents in a CPS is viewed as an epidemic outbreak in Reference [
23] and is analyzed using percolation theory. The method was shown to be applicable for studying malware infection incidents, but it is questionable whether the epidemic outbreak model fits other types of incidents. Percolation theory was also used in Reference [
24] to analyze the propagation of node failures in a network of CPSs comprising cyber and physical nodes organized in two distinct layers, such as in the case of the power grid. The Susceptible–Exposed–Infected–Recovered (SEIR) infectious disease model was used in Reference [
25] to study malware infection propagation in the smart grid. A quantitative risk assessment model that provides asset-wise and overall risks for a given CPS and also considers risk propagation among dependent nodes was proposed in Reference [
26].
A method for assessing the aggregate risk of a set of interdependent critical infrastructures was proposed in References [
27,
28]. The method provides an aggregate cyber risk value at the infrastructure level, rather than a detailed cyber risk assessment at the system/component level. Thus, it is suitable for evaluating the criticality of infrastructure sectors, but not for designing cybersecurity architectures or for selecting appropriate cybersecurity controls. A similar approach for the Energy Internet [
29] was followed to develop an information security risk algorithm based on dynamic risk propagation in Reference [
30]. A framework for modeling and evaluating the aggregate risk of user activity patterns in social networks was proposed in Reference [
31]. A two-level hierarchical model was used in Reference [
32] to represent the structure of essential services in the national cyberspace, and to evaluate the national level (aggregate) risk assessment by taking into account cyber threats and vulnerabilities identified at the lower level.
Based on the above discussion, it is evident that the problem of risk propagation and risk aggregation for complex systems, on one hand, and the problem of optimal selection of cybersecurity controls, on the other, have been individually studied. The conjunct problem of identifying the optimal set of cybersecurity controls that reduces the aggregate risk in a complex CPS cannot be approached by sequential application of methods each of which addresses the problem’s components, due to the inherent nonlinearity of the risk propagation, risk aggregation, and control selection processes on one hand, and the intertwining of these processes. To the best of our knowledge, no method that solves this conjunct problem is currently available.
On the other hand, the systematic selection of cybersecurity controls has been mostly examined in the literature in attempting to identify the optimal set of controls for IT systems within a specified budget; examples of such approaches are those in References [
33,
34,
35]. The outline of a programming tool that supports the selection of countermeasures to secure an infrastructure represented as a hierarchy of components was provided in Reference [
36]. A methodology based on an attack surface model to identify the countermeasures against multiple cyberattacks that optimize the Return On Response Investment (RORI) measure is proposed in Reference [
37]. However, to the best of our knowledge, a method that selects a set of cybersecurity controls that simultaneously optimizes both effectiveness and efficiency, by minimizing the residual risk and the cost of implementation, is still to be proposed.
The work described in this paper addresses these research gaps.
5. Optimal Cybersecurity Control Selection
5.1. Cybersecurity Controls
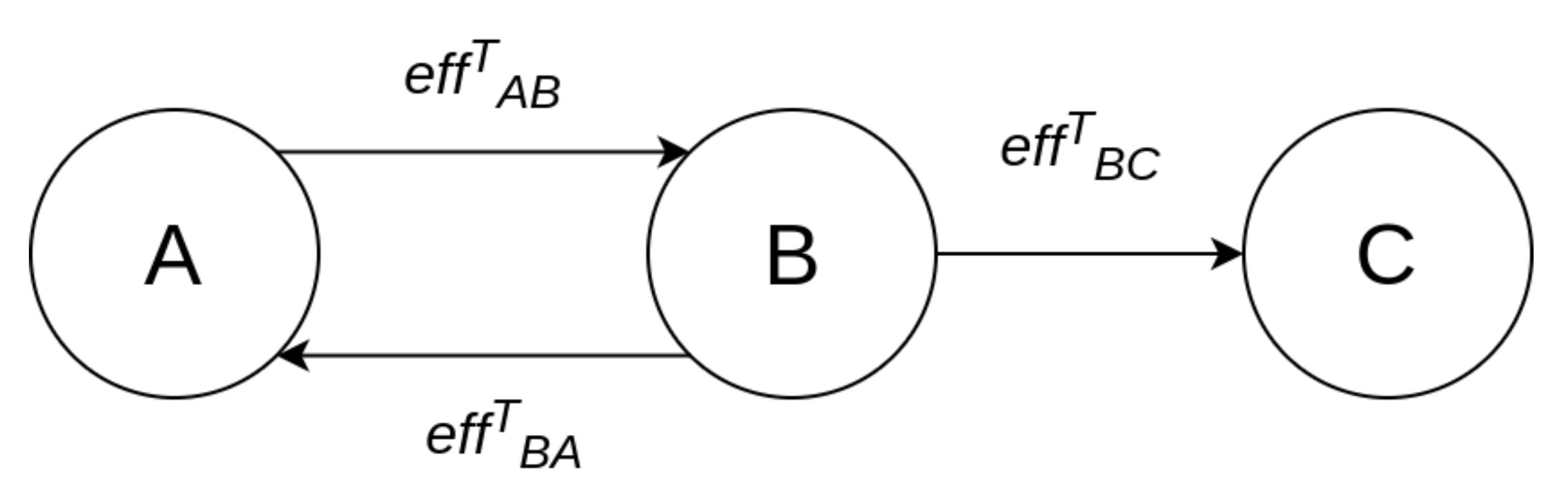
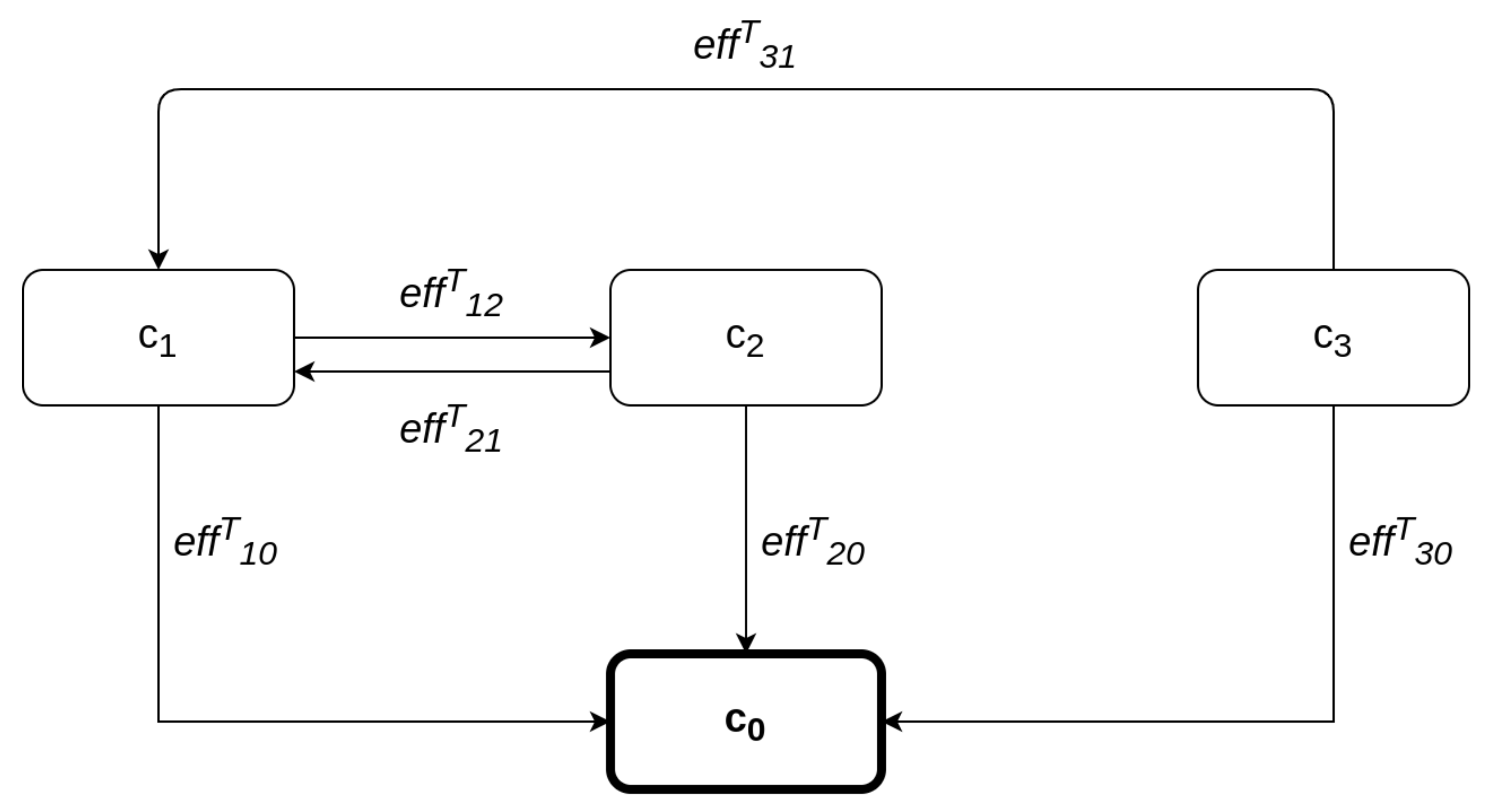
We assume that there exists a list of controls available to apply to the components of the system. Each control m, when applied to component , has a potential effect on the values of and that are used in the calculation of the cyber risk, such effect depending on the effectiveness and the nature of the control. We denote the new Likelihood and Impact values of threat t that result after the application of control m to by and , respectively. These values can be calculated by re-applying DREAD to the system, which is now protected by m.
Additionally, for each control m, a cost metric is defined. This metric is expressed on a 1–5 scale, corresponding to the qualitative classifications very low cost, low cost, medium cost, high cost, and very high cost. Note that the use of this scale was dictated by the fact that it is difficult to measure the cost of implementing a control. However, if such a measure is available, the replacement of the value in the 1–5 scale with the actual cost of the control is straightforward.
For a system with
N components and a list with
M controls with the cost metrics vector
, the following binary matrix
compactly depicts the applied controls throughout the system:
where
Then, the total cost of the applied controls solution is given by .
5.2. Optimization Method
The optimization problem to be solved is to select the optimal (effective and efficient) set of controls among a list of possible ones. This amounts to selecting the set of controls
that minimizes the system
residual risk
, at the lowest total cost
. A closed formula that would allow the application of an exact optimization method, and thus the calculation of the globally optimum solution to the problem, is not possible to construct, unless many, not necessarily realistic, assumptions are made. On the other hand, the large size of the search space (all candidate solutions) prohibits the exhaustive search approach. Hence, a heuristic optimization method has to be employed [
46]; we have selected to use a genetic algorithm, even though any other heuristic optimization method would, in principle, be applicable.
The design parameters of the genetic algorithm are as follows:
The search space comprises all possible combinations of controls applied to components.
Each individual solution is represented by the matrix , which is transformed into a binary vector of size . The value of each element of the vector represents the decision to apply a specific control to a specific component or not. For example, for a system with three components and two controls, the solution would be denoted by the vector , assuming that all controls are applicable to all components.
The fitness function is defined as , where , with being the largest possible cost, that results when applying all available controls to all system components.
The initial population size is 100.
The mutation probability is 0.1.
The next generation is determined by uniform crossover, with crossover probability equal to 0.5, an elite ratio of 0.01, and 0.3 of the population consisting of the fittest members of the previous generation (aka parents).
The algorithm terminates when the maximum number of allowed iterations is used. This number is calculated as .
The algorithm for selecting the optimal set of security controls is depicted in Algorithm 2.
Note that the fitness function consists of two elements, namely the residual risk (which takes values in [0, 3]) and the normalized cost (which takes values in [0, 1]). This non-symmetric approach has been selected to put emphasis on the importance of reducing the residual risk, even by bearing larger cost. This approach results in initial iterations of the algorithm tending to generate solutions that minimize the residual risk. In later iterations of the algorithm, the less costly combinations of controls prevail, among those that lead to the maximum possible risk reduction.
| Algorithm 2: Algorithm for selecting the optimal set of security controls |
![Sensors 21 01691 i002 Sensors 21 01691 i002]() |
![Sensors 21 01691 i003 Sensors 21 01691 i003]() |
6. Application to the C-ES
Autonomous and remotely controlled ships—both variants of the Cyber-Enabled Ship (C-ES)—are being increasingly developed. At the same time, the maritime transportation sector contributes significantly to the gross domestic product of many countries around the world. It is not surprising, then, that the cybersecurity of the sector has been designated a very high priority by international organizations [
47] and national governments [
48] alike. The CPSs comprising the C-ES were identified, and the overall ICT architecture of the C-ES in the form of a tree structure was proposed in Reference [
6]. An extended Maritime Architectural Framework (e-MAF) was proposed, and the interconnections, dependencies, and interdependencies among the CPSs of the C-ES were described in Reference [
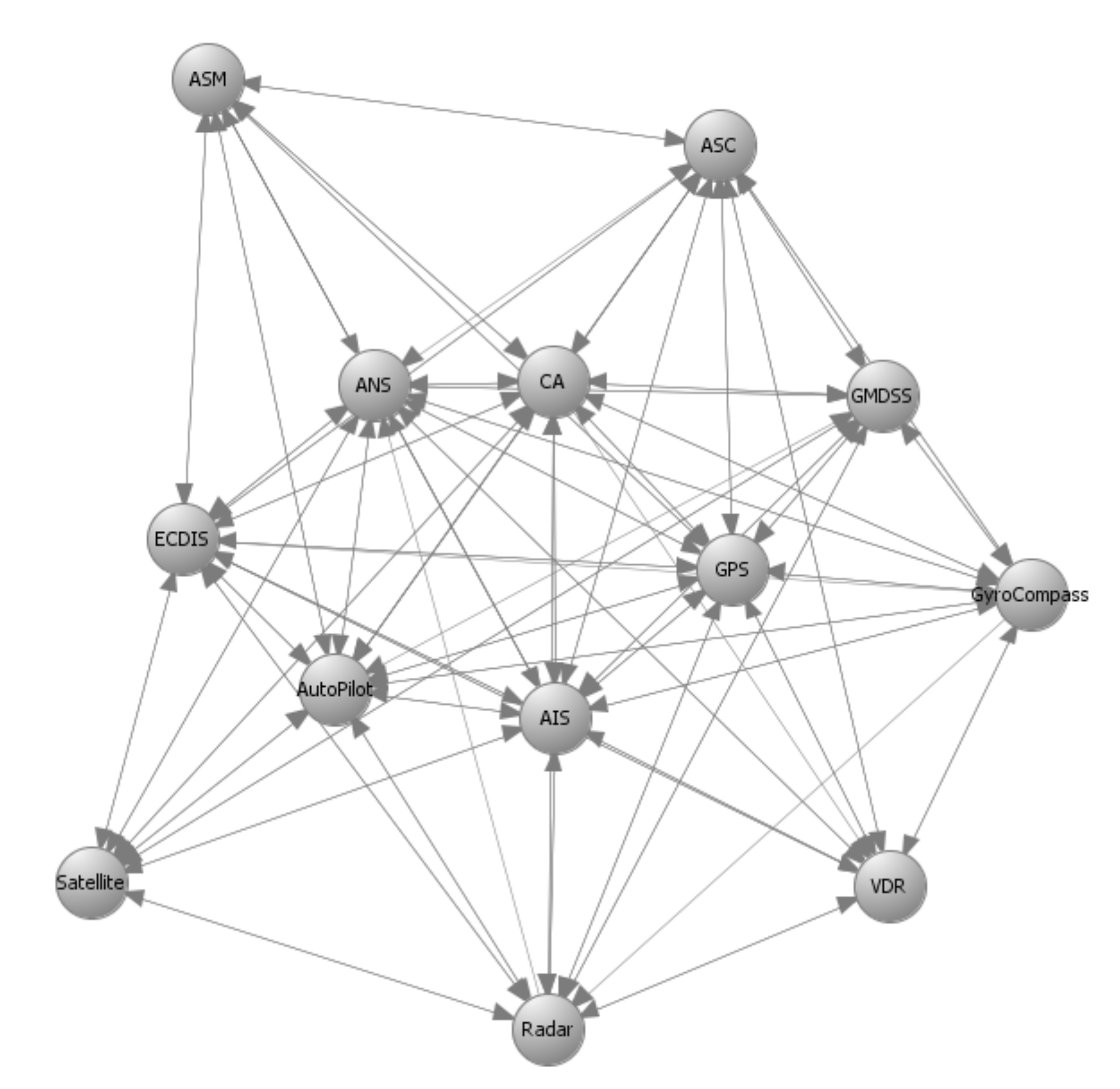
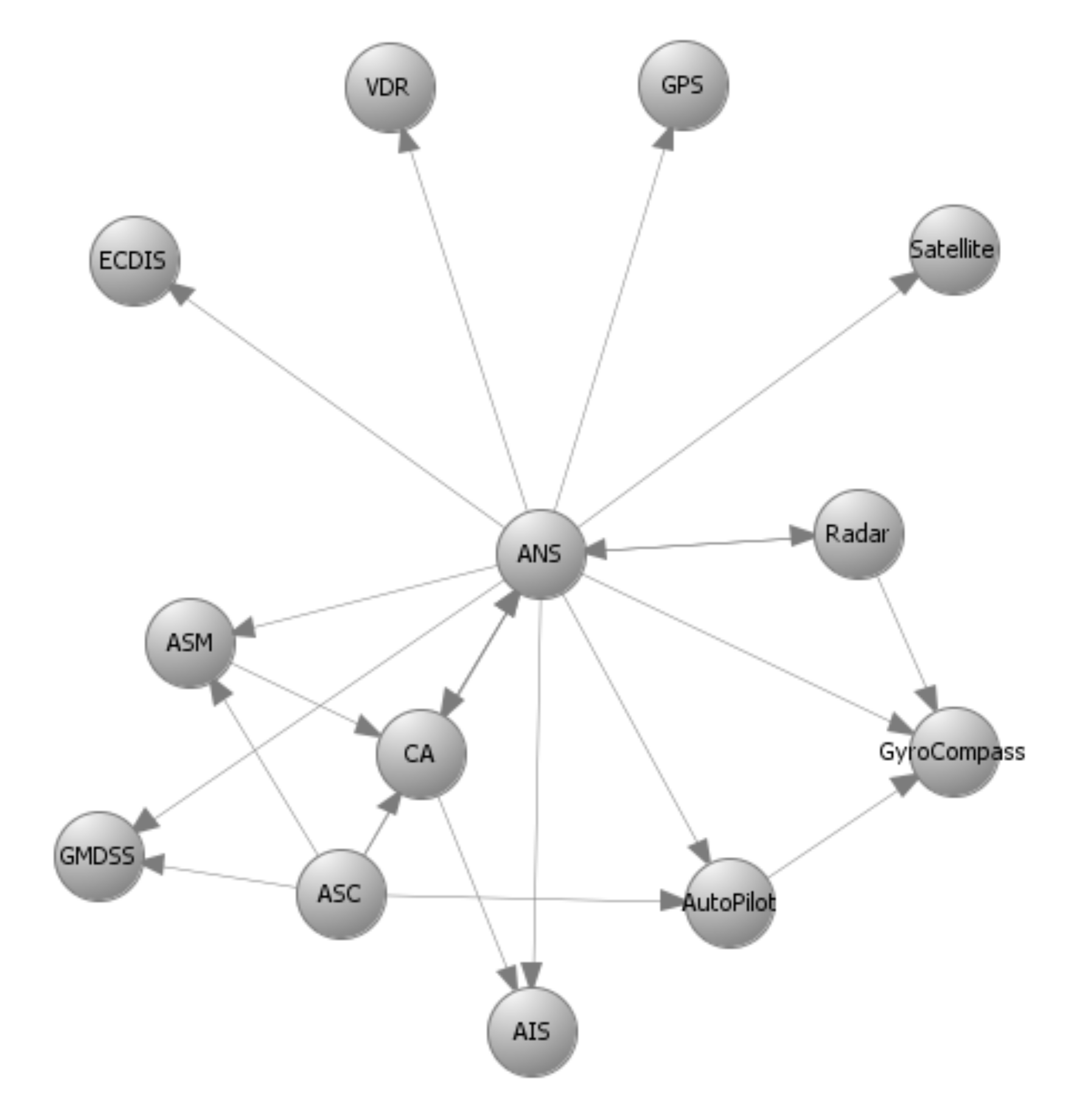
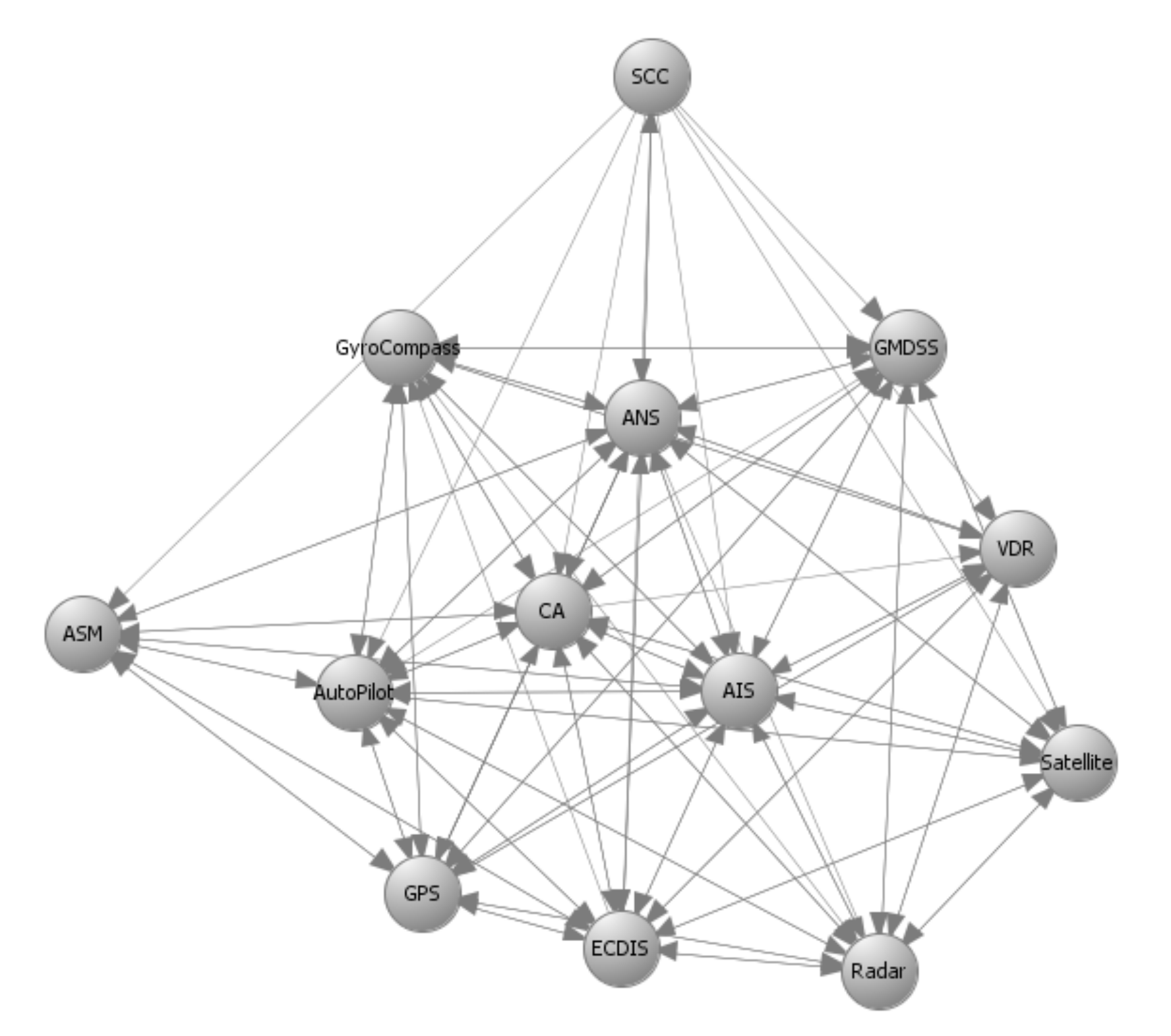
7]. These results are depicted in the form of directed graphs in
Figure 3,
Figure 4,
Figure 5 and
Figure 6 for the two variants of the C-ES. Furthermore, an initial threat analysis of the generic ICT architecture of the C-ES identified the three most vulnerable onboard systems, namely the Automatic Identification System (AIS), the Electronic Chart Display Information System (ECDIS), and the Global Maritime Distress and Safety System (GMDSS) [
6]. These results were verified by means of the comprehensive threat and risk analysis that was presented in Reference [
44]. The most critical attack paths within the navigational CPSs of the C-ES were identified in Reference [
22]. The cybersecurity and safety requirements for the CPSs of the C-ES were identified in References [
49,
50], and an initial set of cybersecurity controls that satisfy these requirements was proposed in Reference [
44].
Building upon earlier work, and as a step towards defining the cybersecurity architecture of such vessels, we selected the CPSs of the C-ES to illustrate the applicability of the methods proposed in this paper. The results are presented in the sequel for the autonomous and the remotely controlled vessel.
6.1. The Cyber-Enabled Ship
The CPSs of the C-ES were identified and described in Reference [
6], where a threat analysis and a qualitative risk analysis were carried out, and the most vulnerable onboard systems were identified. Three distinct sub-groups of onboard CPSs were identified, namely the bridge CPSs; the engine CPSs; and the Shore Control Center (SCC) CPSs. The SCC is a sub-component of the remotely controlled vessel, that aims to control and navigate one or more ships from the shore. The interconnections, dependencies, and interdependencies of these CPSs were identified in Reference [
7] and were later used to define the cybersecurity requirements of the C-ES in Reference [
49]. The CPSs considered herein are:
The Autonomous Navigation System (ANS) is responsible for the navigational functions of the vessel. ANS controls all the navigational sub-systems and communicates with the SCC by transmitting dynamic, voyage, static, and safety data to ensure the vessel’s safe navigation.
The Autonomous Ship Control (ASC) acts as an additional control for the C-ES and aims to assess the data derived from the sensors and from the SCC.
The Advanced Sensor Module (ASM) automatically analyzes sensor data to enhance the environmental observations, such as ships in the vicinity. By leveraging sensor fusion techniques, this module analyzes data derived from navigational sensors, such as the Automatic Identification System (AIS) and the Radar.
The Automatic Identification System (AIS) facilitates the identification, monitoring, and locating of the vessel by analyzing voyage, dynamic, and static data. Further, the AIS contributes to the vessel’s collision avoidance system by providing real time data.
The Collision Avoidance (CA) system ensures the safe passage of the vessel by avoiding potential obstacles. The system analyzes the voyage path by leveraging anti-collision algorithms conforming to the accordant COLREGs regulations [
51].
The Electronic Chart Display Information System (ECDIS) supports the vessel’s navigation by providing the necessary nautical charts, along with vessel’s attributes, such as position and speed.
The marine RADAR provides the bearing and distance of objects in the vicinity of the vessel, for collision avoidance and navigation at sea.
The Voyage Data Recorder (VDR) gathers and stores all the navigational data of the vessel specifically related to vessel’s condition, position, movements, and communication recordings.
The Auto Pilot (AP) controls the trajectory of the vessel without requiring continuous manual control by a human operator.
The methods proposed in
Section 4 and
Section 5 used as input prior results, namely the system components and their interconnections that make up the system graph representation; the impact and likelihood values associated with the STRIDE threats and computed by means of DREAD for each individual component; and the list of available cybersecurity controls, along with information on their cost and effectiveness.
Figure 3,
Figure 4,
Figure 5 and
Figure 6 depict the graph representations of the onboard navigational CPSs of the autonomous and of the remotely controlled ship, respectively, along with their interconnections and interdependencies [
6,
22,
44]. Impact and likelihood values associated with the STRIDE threats and computed by means of DREAD are depicted in
Table 2 and
Table 3 [
44]. Each line of
Table 2 and
Table 3 represents one of the STRIDE threats, indicated by the corresponding initial. Each column of the Table represents individual CPSs, indicated by their corresponding initials, as defined in
Section 6.1. The values inside the cells are the corresponding impact (left table) and likelihood (right table) values per STRIDE threat and per individual component; these have been calculated by means of Equations (
1) and (
2), respectively. These values are subsequently used as input to Algorithm 1, to calculate the aggregate risk of each CPS.
The list of available cybersecurity controls has been defined based on the NIST guidelines for Industrial Control Systems security [
5] by following a systematic process proposed in Reference [
44]. The effectiveness and the cost of each security control are estimated considering their applicability, the extent to which each control reduces the impact or/and the likelihood, and the resources needed to implement it.
6.2. Optimal Controls for the Autonomous Ship
Autonomous ships are equipped with advanced interconnected CPSs able to navigate and sail the vessels without human intervention. The onboard navigational CPSs of the autonomous ship are described by the directed graphs
and
depicted in
Figure 3 and
Figure 4, respectively, as discussed in detail in References [
6,
44].
represents information flow connections and
control flow connections.
Table 4 depicts the effect coefficients between all the considered systems. Each line and each column of
Table 4 represents a CPS of the C-ES, indicated by their corresponding initials, as defined in
Section 6.1 above. The values inside the cells are the effect coefficients between each pair of these systems; specifically, the value in the cell at row
i and column
j is the value of
. These have been calculated by means of Equation (
13), which derives from Equation (
4) when the function
f is the average of the information and control effect coefficients. These values are also subsequently used as input to Algorithm 1, to calculate the aggregate risk of each CPS.
It is worth noticing that CPSs with high information and control flows, such as the ANS and the ASC, are characterized by high values of the effect coefficient.
The security controls in the optimal set are selected from the initial list of available controls by applying the method described in
Section 5.
Table 5 depicts the optimal set of security controls per STRIDE threat and per CPS component. It also depicts the associated initial global risk (without controls) and the residual global risk (with the optimal controls applied). These values have been calculated by employing Algorithm 1.
Each line of
Table 5 represents one of the STRIDE threats. The first column represents the global initial risk (i.e., without any security controls in place) of the C-ES, as assessed by means of Algorithm 1. The second column represents each constituent CPS, and the third column the optimal set of security controls identified by means of Algorithm 2. Finally, the fourth column represents the residual risk (i.e., with the optimal set of security controls in place) of the C-ES, as assessed by applying again Algorithm 1 with the risks of each individual CPS updated according to the effectiveness of the applied controls.
6.3. Optimal Controls for the Remotely Controlled Ship
Remotely controlled vessels are equipped with CPSs that allow the control and operation of the vessel from the shore. Similarly with the autonomous vessel variant, the navigational CPSs of the remotely controlled ship are described by the directed graphs
and
in
Figure 5 and
Figure 6. The SCC is a critical component in this variant of the C-ES, since the control and monitoring of the vessel critically depends on the SCC’s normal operation. This is why the effect coefficients attain high values between systems that support the remote operations, such as the SCC, ANS, and ECDIS. All effect coefficients between the CPSs of the remotely controlled vessel are depicted in
Table 6. Similarly to the case of the autonomous ship, the total effect coefficients have been calculated by means of Equation (
13).
The security controls in the optimal set are selected from the initial list of available controls by applying the method described in
Section 5.
Table 7 depicts the optimal set of security controls per STRIDE threat and per CPS component. It also depicts the associated initial global risk (without controls) and the residual global risk (with the optimal controls applied). These values have been calculated in the same manner as the corresponding ones of the first C-ES variant.
6.4. Discussion
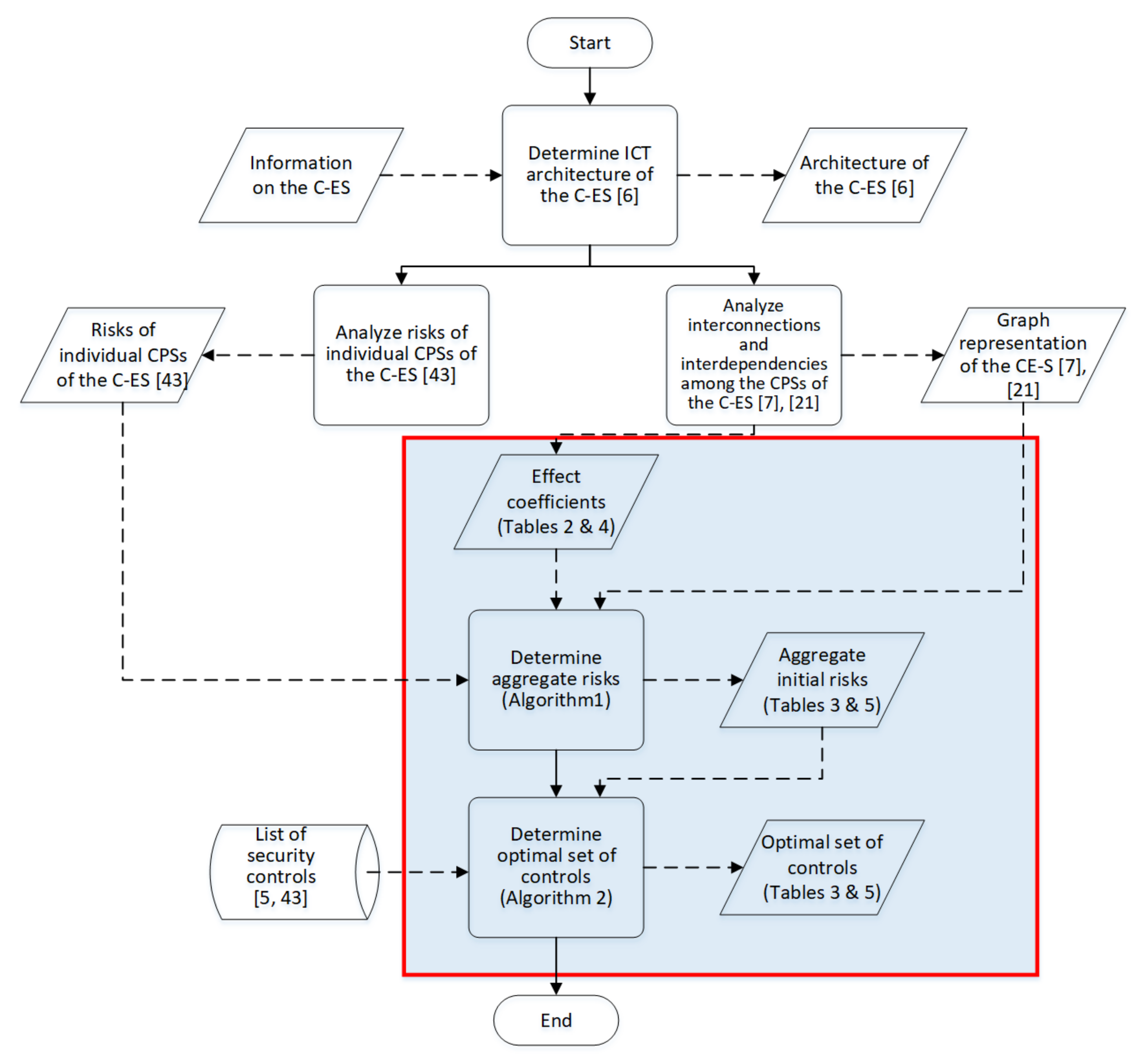
The overall process followed to carry out the case studies is depicted graphically in
Figure 7. In this figure, rectangles represent processing steps, and skewed rectangles represent input/output; solid lines link processing steps, whilst dashed ones link input/output to processing steps. The shaded area delineates the content of this paper.
As can be seen in
Table 5, in the case of the autonomous ship, twenty different security controls are recommended for application to seven of the ten navigational CPSs. The fact that these CPSs have been found in previous works [
6,
44] to be the most vulnerable onboard navigational systems, verifies the consistency of the proposed methods. Similarly, as can be seen in
Table 7, twenty different security controls are recommended for application to six out of the ten navigational CPSs; again, these CPSs are the most vulnerable.
The optimal controls sets are different in the two variants of the C-ES. This reflects the difference in the level of autonomy of each variant: According to the IMO classification, the remotely controlled vessel lies at the second or third autonomy level, while the autonomous ship lies at the fourth level [
52]. Different levels of autonomy mean different levels of interaction with humans and different levels of importance of the SCC in the ship’s operation, which, in turn, mean different levels of risk for the same threat.
The security controls that are recommended by any automated decision support method, including the methods proposed herein, need to be re-considered, consolidated, and checked for applicability by domain experts and stakeholders together. The proposed methods enable the execution of what-if scenarios, including by modifying the initial list of the available security controls, and/or by modifying parameters of the genetic algorithm.
7. Conclusions
The growing utilization of highly interconnected CPSs in critical domains increases the attack surface, making the infrastructure more vulnerable to cyber attacks. In this paper, we model a complex CPS as a digraph in which nodes represent sub-CPSs and in which edges represent information and control flows among these subsystems. By leveraging this model, we proposed a novel method for assessing the aggregate cybersecurity risk of large scale, complex CPSs comprising interconnected and interdependent components, by using risk measures of its individual components and the information and control flows among these components. Building upon this method, we proposed a novel method, based on evolutionary programming, for selecting a set of effective and efficient cybersecurity controls among those in an established knowledge base, that reduces the aggregate residual risk, while at the same time minimizing the cost. We then used both methods to select optimal sets of cybersecurity controls for the navigational systems of two instances of the C-ES, namely the remotely controlled ship and the autonomous ship. These sets lead to the definition of the cybersecurity architecture of such vessels. They have been found to be in line with previous results that identified the most vulnerable navigational CPSs of the C-ES, and to minimize the global residual risk. In the future, we intend to develop a software tool that will implement the proposed methods, and to use it to experientially examine the usability of the proposed approach with domain experts and stakeholders, in the C-ES and other critical application domains.