RcdMathLib: An Open Source Software Library for Computing on Resource-Limited Devices
Abstract
1. Introduction
- An open source library for numerical computations on resource-limited devices and embedded systems. The software permits a user or a mobile device to solve multivariant linear equation systems based on efficient algorithms such as the Householder or the Moore–Penrose inverse. The Moore–Penrose inverse is implemented by using the SVD method.
- A module for solving multivariant nonlinear equation systems as well as optimization and curve fitting problems on a resource-contained device on the basis of the SVD algorithm.
- A utilities-module provides various algorithms such as the Shell sort algorithm or the Box–Muller method to generate normally distributed random variables.
- A localization module for positioning systems that use distance measurements or DC-pulsed, magnetic signals. This module enables an adaptive, optimized localization of mobile devices.
- A software routine to locally reduce multipath errors on mobile devices.
2. Related Work
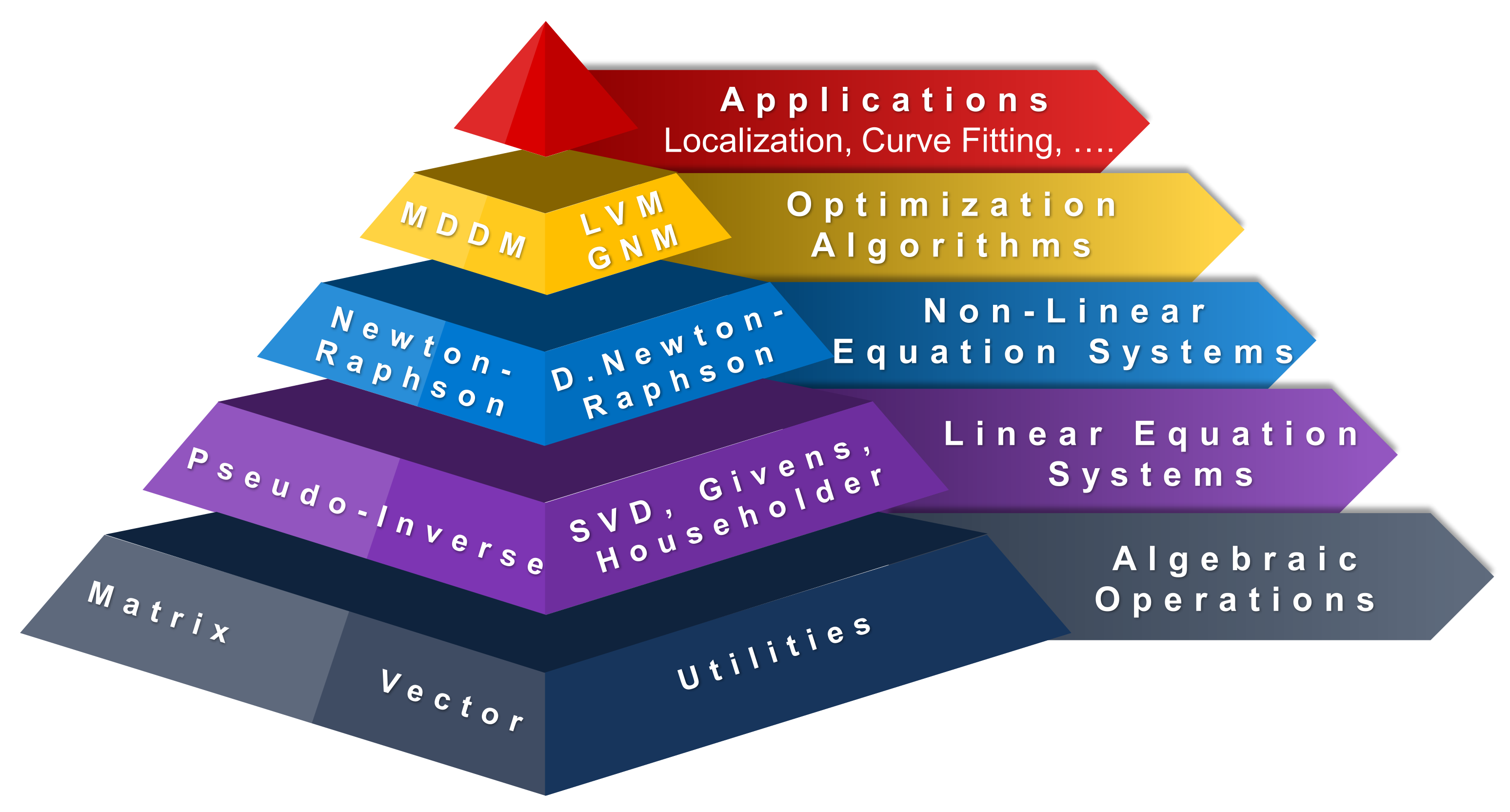
3. Library Architecture and Description
3.1. Linear Algebra Module Layer
- Basic operations submodule: provides algebraic operations such as addition or multiplication of vectors or matrices. This submodule distinguishes between vector and matrix operations.
- Pseudo-inverse submodule: enables the computation of the inverse of quadratic as well as of rectangular matrices. The matrix inverse can be calculated by using the Moore–Penrose, Givens, or Householder algorithms [29].
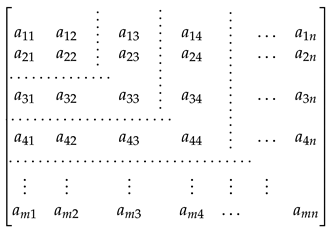
- Linear solve submodule: permits the solution of under-determined and over-determined linear equation systems. We solve the linear equation systems using two matrix decompositions: the SVD and QR factorizations. The first method uses the Moore–Penrose inverse, while the second approach applies the Householder or the Givens algorithms with the combination of the back substitution method. We also provide the Gaussian Elimination (GE) with a pivoting algorithm, which is based on the LU decomposition. We use the GE-based method only for testing purposes or for devices with very limited stack memory. We suggest using the SVD- or the QR-based methods due to the numerical stability and the support of non-quadratic matrices [30].
3.2. Non-Linear Algebra Module Layer
- Optimization submodule: enables the optimization of an approximate solution by using Nonlinear Least Squares (NLS) methods such as modified Gauss–Newton (GN) or the LVM algorithms. These methods are iterative and need a start value as an approximate solution. Moreover, the user should give a pointer to an error function and to a Jacobian matrix. The modified GN and the LVM algorithms will be briefly described in Section 3.2.1 and Section 3.2.2.
- Nonlinear equations submodule: allows for the solution of multivariate nonlinear equation systems by using Newton–Raphson and damped Newton–Raphson methods [33]. The user must deliver a start value as well as a pointer to nonlinear equation systems to solve, and a pointer to the appropriate Jacobian matrix.
3.2.1. Gauss–Newton Algorithm
3.2.2. Levenberg–Marquardt Algorithm
| Algorithm 1 LVM algorithm |
|
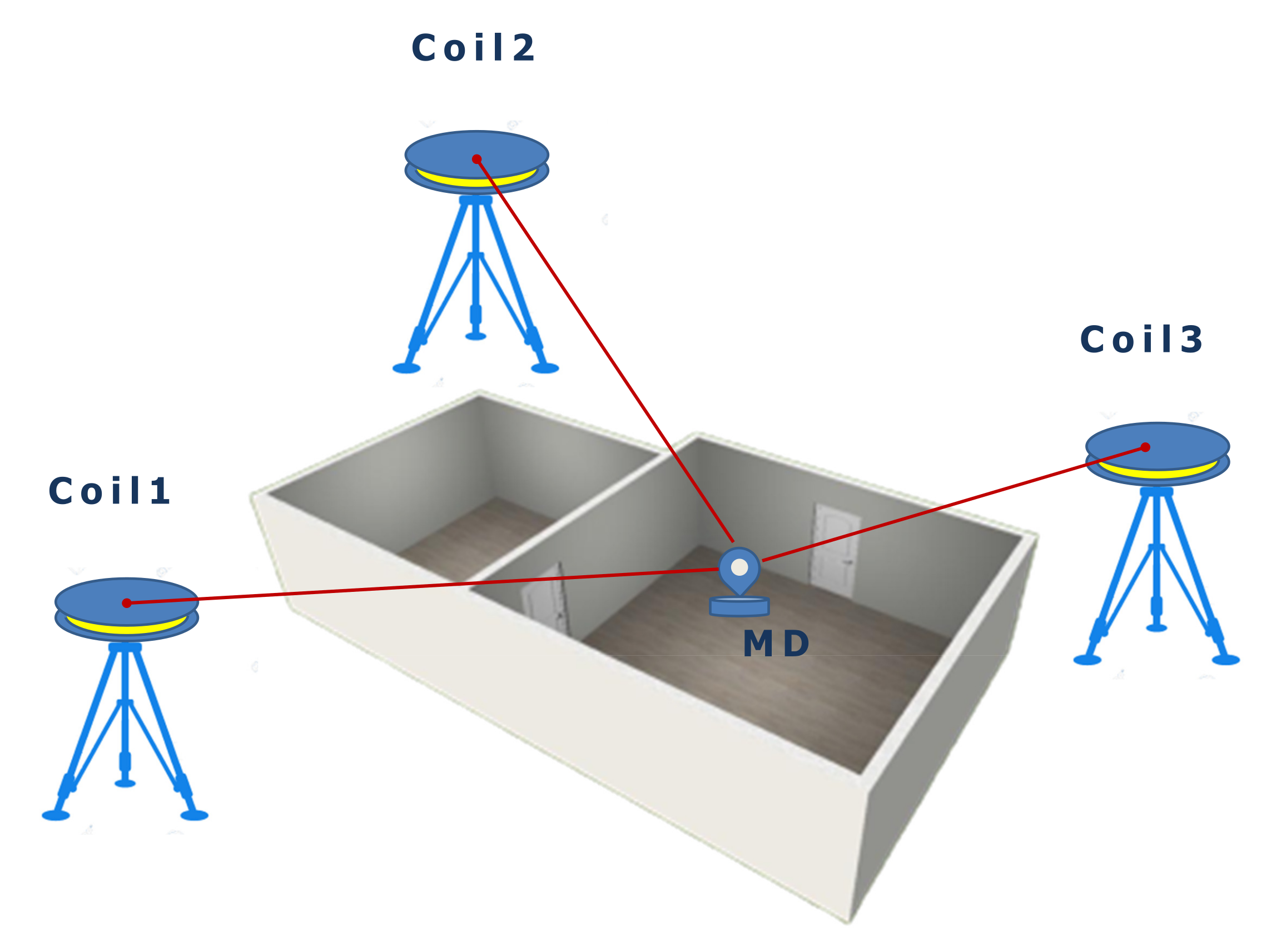
3.3. Localization Module Layer
3.3.1. Introduction and Layer Description
3.3.2. Multipath Distance Detection and Mitigation and Position Optimization Algorithm
| Algorithm 2 MDDM algorithm | |
| 1: function recog_mitigate_multipath_alg() | |
| 2: ; ; | |
| 3: distances , ; | ▹ distance measures to n RSs |
| 4: while do | |
| 5: ; | ▹ choose k RSs |
| 6: | ▹ Compute a position related to k RSs |
| 7: ; | ▹ residuals |
| 8: ; | |
| 9: ; | |
| 10: ; | |
| 11: end while | |
| 12: | ▹ the solution |
| 13: | ▹ calculate PDOP-value of |
| 14: if then | |
| 15: LVM_ALG() | ▹ optimize the position |
| 16: end if | |
| 17: end function |
3.4. Documentation and Examples’ Modules
4. Implementation Issues
| Algorithm 3 Inverse of an upper triangular matrix |
|
4.1. Singular Value Decomposition
- First phase (bidiagonalization)A () matrix A is transformed to an upper bidiagonal matrix by using the Householder bidiagonalization, where . The matrix A is transformed as follows:where B is an bidiagonal matrix equal to
- Second phase (reduction to the diagonal form)The bidiagonal matrix B is further reduced to a diagonal matrix by using orthogonal equivalence transformations as follows:where is the matrix of the singular values and the matrices and are orthogonal. The singular vector matrices can be computed as follows:We implemented the first and second phases by the Golub–Kahan bidiagonal procedure and the Golub–Reinsch algorithm. Both algorithms will be described in detail in Section 4.1.1 and Section 4.1.2. In this description, we will mention some implementation issues.
4.1.1. Golub–Kahan Bi-Diagonal Procedure
4.1.2. Golub–Reinsch Algorithm
- Splitting:
- If the matrix entry is equal to zero, we split the matrix into two block diagonal-matrices whose singular values can be computed independently:where is the singular value decomposition of the matrix ; in this case, we compute the matrix first. If the split occurs at i equal to n, then the matrix is equal to and is a singular value.
- Cancellation:
- If the matrix entry is equal to zero, we split the matrix by using Givens rotations from the left to zero out row i as follows:whereas the budge b is removed by using the Givens rotations for . Since the matrix element is equal to zero, the matrix splits again into two block diagonal sub-matrices (see the splitting step).
- Negligibility:
- The values of the matrix elements or will be small but not exactly zero due to the finite precision arithmetic used by digital processors. Therefore, we require a threshold to decide when the elements or can be considered zero. Golub and Reinsch [58] recommend the following threshold rule:where is the machine precision. Björck [27] suggests the following approach:
5. Usage of the RcdMathLib
Simple Example


6. Evaluation of the Algorithms
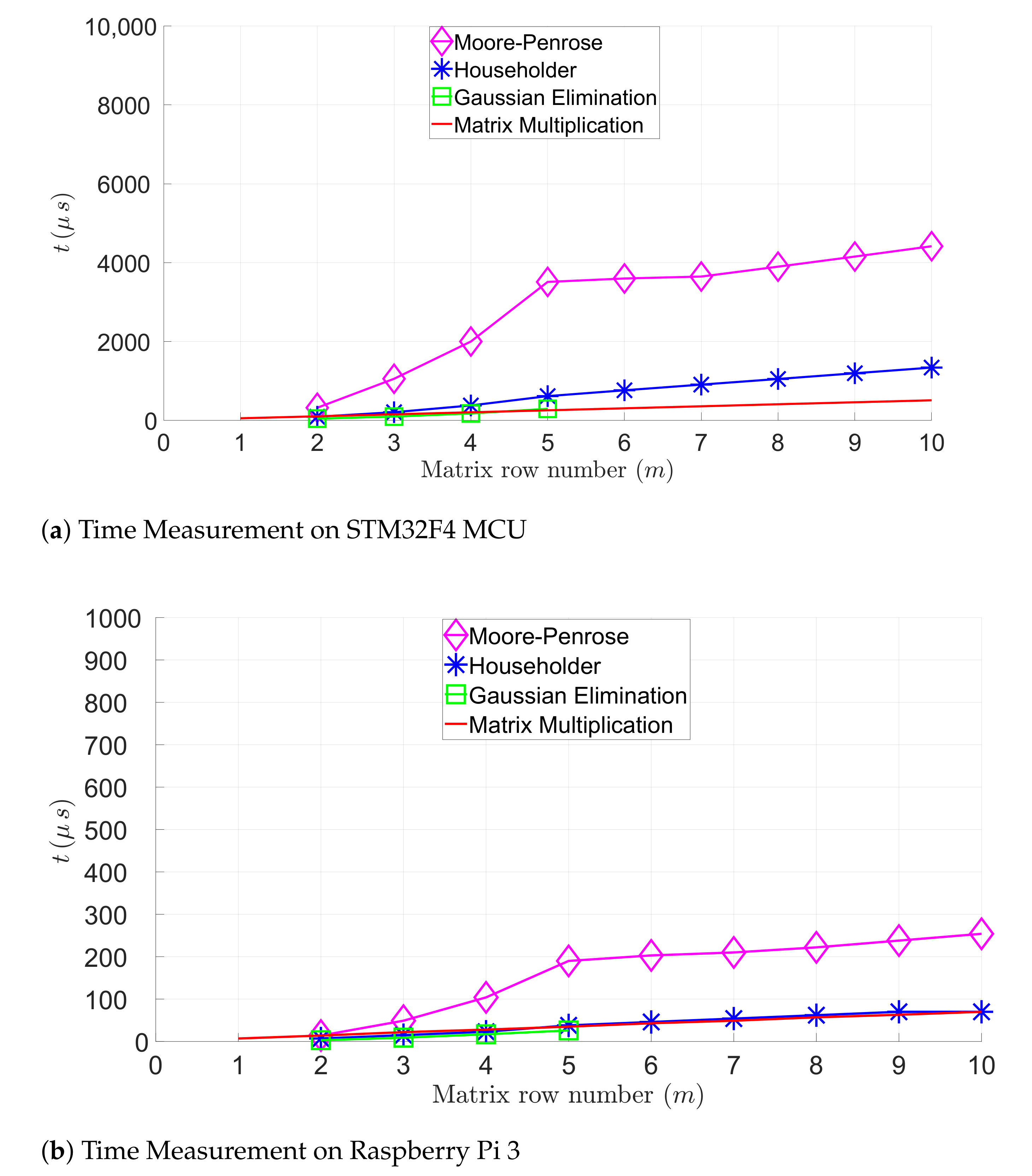
6.1. Evaluation of the Linear Algebra Module

6.2. Evaluation of the Non-Linear Algebra Module
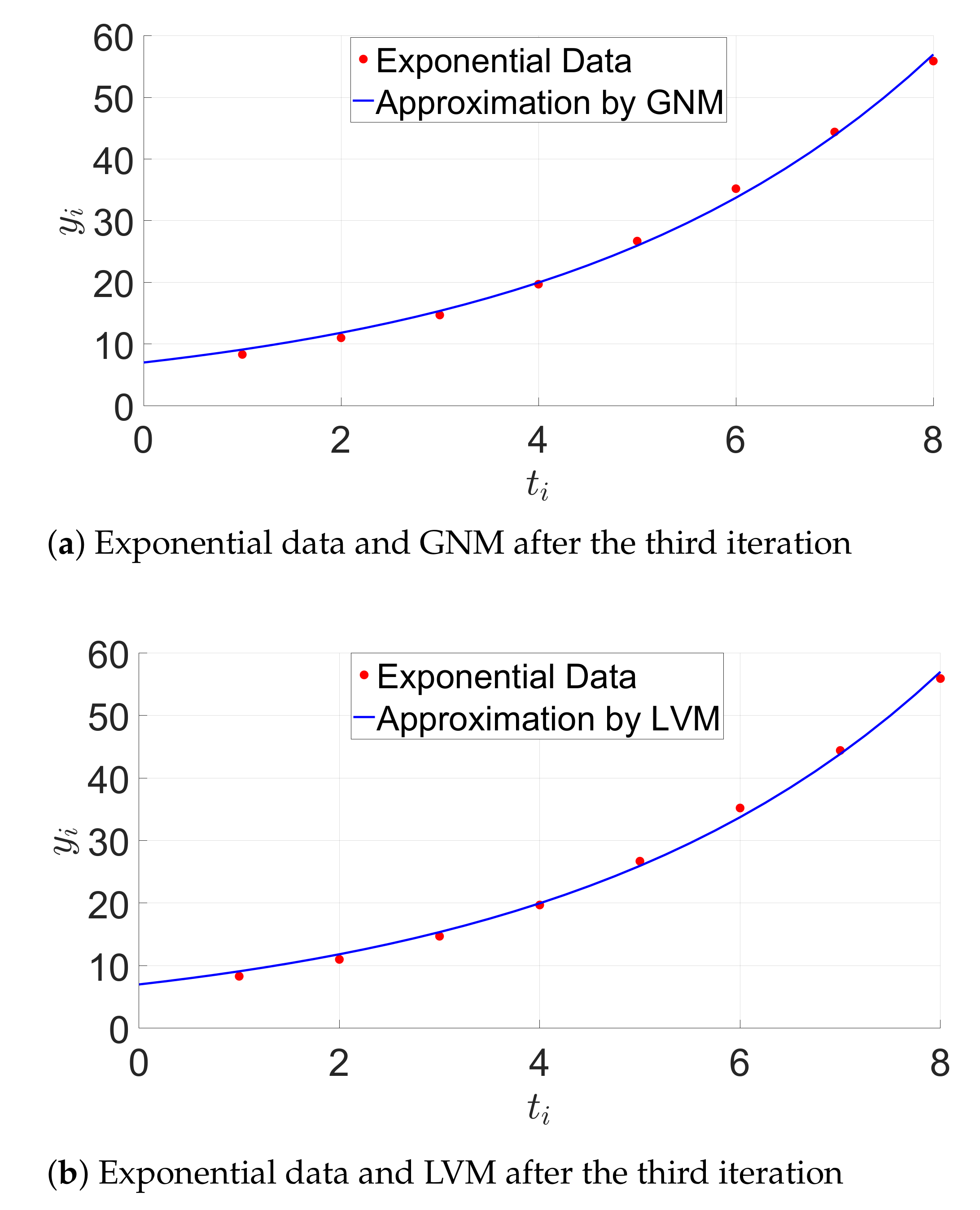
6.2.1. Evaluation with Exponential Data
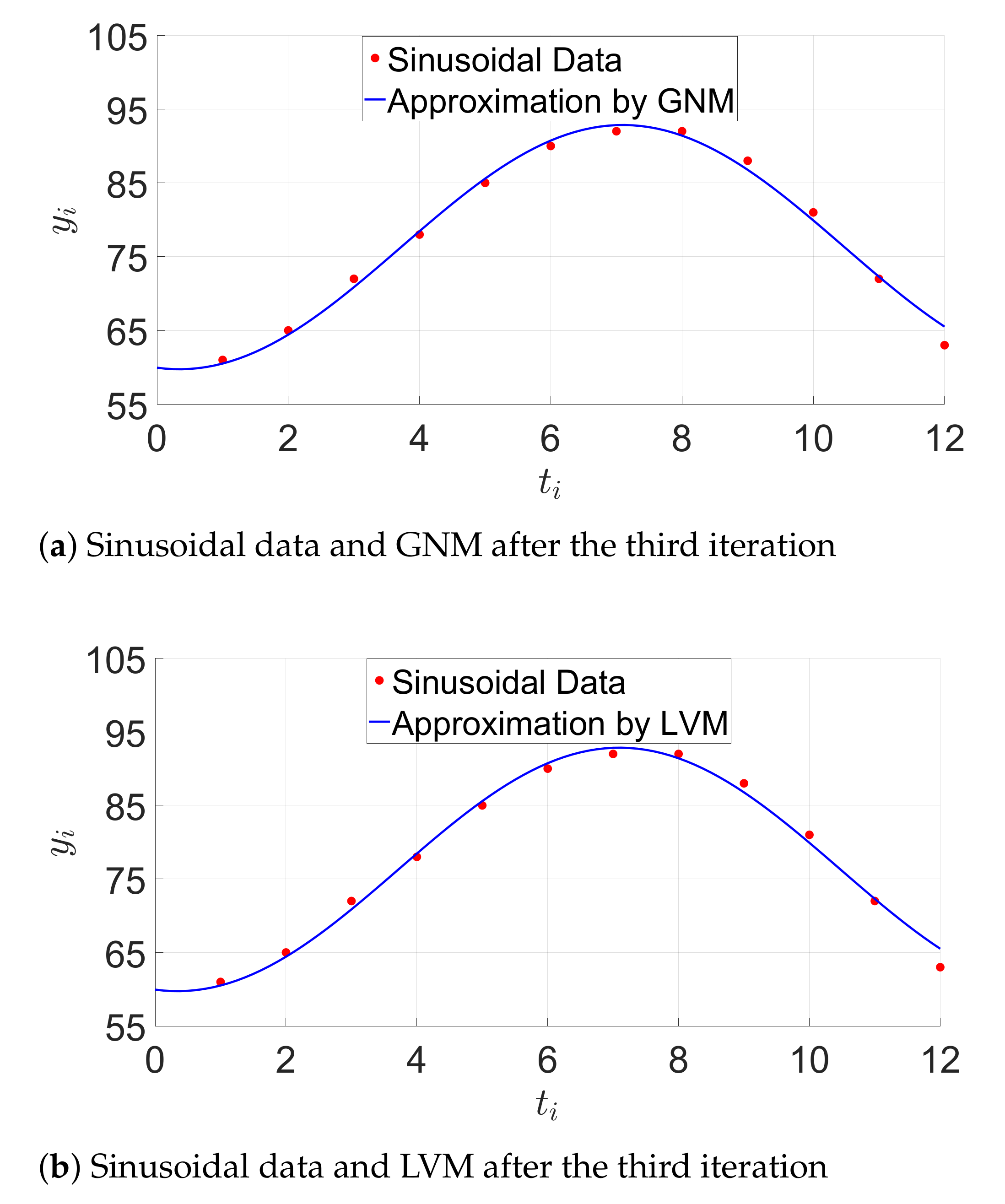
6.2.2. Evaluation with Sinusoidal Data
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ceruzzi, P.E. The Early Computers of Konrad Zuse, 1935 to 1945. Ann. Hist. Comput. 1981, 3, 241–262. [Google Scholar] [CrossRef]
- Ceruzzi, P.E. A History of Modern Computing, 2nd ed.; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Lee, J.A.N. Computer Pioneers; IEEE Computer Society Press: Los Alamitos, CA, USA, 1995. [Google Scholar]
- Partlett, B. Handbook for Automatic Computation, Vol. II, Linear Algebra (J. H. Wilkinson and C. Reinsch). SIAM Rev. 1972, 14, 658–661. [Google Scholar] [CrossRef]
- Dongarra, J.J.; Moler, C.B.; Bunch, J.R.; Stewart, G.W. LINPACK Users’ Guide; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1979. [Google Scholar] [CrossRef]
- Garbow, B.S.; Boyle, J.M.; Dongarra, J.J.; Moler, C.B. Matrix Eigensystem Routines—EISPACK Guide Extension; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar] [CrossRef]
- Cleve Moler. A Brief History of MATLAB. In Technical Articles and Newsletters; MathWorks: Natick, MA, USA, 2019. [Google Scholar]
- Naveen, S.; Kounte, M.R. Key Technologies and challenges in IoT Edge Computing. In Proceedings of the 2019 Third International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Palladam, India, 12–14 December 2019; pp. 61–65. [Google Scholar] [CrossRef]
- Kasmi, Z. Home of the RcdMathLib (Mathematical Library for Resource-Constrained Devices). 2021. Available online: https://git.imp.fu-berlin.de/zkasmi/RcdMathLib/-/wikis/Home (accessed on 25 February 2021).
- Strang, G. Linear Algebra and Its Applications, 4th ed.; Thomson, Brooks/Cole: Belmont, CA, USA, 2006. [Google Scholar]
- Schanze, T. Compression and Noise Reduction of Biomedical Signals by Singular Value Decomposition. IFAC-PapersOnLine 2018, 51, 361–366. [Google Scholar] [CrossRef]
- Kasmi, Z. Open Platform Architecture for Decentralized Localization Systems Based on Resource-Constrained Devices. Ph.D. Thesis, Freie Universität Berlin, Department of Mathematics and Computer Science, Berlin, Germany, 2019. [Google Scholar]
- Madsen, K.; Nielsen, H.B.; Tingleff, O. Methods for Non-Linear Least Squares Problems, 2nd ed.; Technical University of Denmark: Lyngbyn, Denmark, 2004. [Google Scholar]
- Rose, J.A.; Tong, J.R.; Allain, D.J.; Mitchell, C.N. The Use of Ionospheric Tomography and Elevation Masks to Reduce the Overall Error in Single-Frequency GPS Timing Applications. Adv. Space Res. 2011, 47, 276–288. [Google Scholar] [CrossRef]
- Guckenheimer, J. Numerical Computation in the Information Age. In SIAM NEWS; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1988. [Google Scholar]
- Arm Limited. Arm Performance Libraries. 2019. Available online: https://developer.arm.com/tools-and-software/server-and-hpc/arm-architecture-tools/arm-performance-libraries (accessed on 25 February 2021).
- Sanchez, J.; Canton, M.P. Microcontrollers: High-Performance Systems and Programming; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Texas Instruments Incorporated. MSP430 IQmathLib User’s Guide; Texas Instruments Incorporated: Dallas, TX, USA, 2015. [Google Scholar]
- Aimonen, P. Cross Platform Fixed Point Maths Library 2012–2019. Available online: https://github.com/PetteriAimonen/libfixmath (accessed on 25 February 2021).
- Nicolosi, A. A Simple, Tiny and Efficient BLAS Library, Designed for PC and Microcontrollers. 2018. Available online: https://github.com/alenic/microBLAS (accessed on 25 February 2021).
- Matlack, C. Minimal Linear Algebra Library. 2018. Available online: https://github.com/eecharlie/MatrixMath (accessed on 25 February 2021).
- Stewart, T. A Library for Representing Matrices and Doing Matrix Math on Arduino. 2018. Available online: https://github.com/tomstewart89/BasicLinearAlgebra (accessed on 25 February 2021).
- Oliphant, T.E. Guide to NumPy, 2nd ed.; CreateSpace Independent Publishing Platform: North Charleston, SC, USA, 2015. [Google Scholar]
- Nunez-Iglesias, J.; van der Walt, S.; Dashnow, H. Elegant SciPy: The Art of Scientific Python, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2017. [Google Scholar]
- Bell, C. MicroPython for the Internet of Things: A Beginner’s Guide to Programming with Python on Microcontrollers; Apress: Berkeley, CA, USA, 2017. [Google Scholar] [CrossRef]
- Kurniawan, A. CircuitPython Development Workshop; PE Press: Berlin, Germany, 2018. [Google Scholar]
- Björck, A. Numerical Methods for Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Barata, J.; Hussein, M. The Moore-Penrose Pseudoinverse. A Tutorial Review of the Theory. Braz. J. Phys. 2011, 42, 146–165. [Google Scholar] [CrossRef]
- Kaw, A. Introduction to Matrix Algebra; University of South Florida: Tampa, FL, USA, 2008. [Google Scholar]
- Sengupta, S.; Korobkin, C.P. C++: Object-Oriented Data Structures; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Bailey, R. The Box-Muller Method and the T-distribution; Department of Economics Discussion Paper; University of Birmingham, Department of Economics: Birmingham, UK, 1992. [Google Scholar]
- Allgower, E.; Georg, K.; Research, U.; Foundation, N. Computational Solution of Nonlinear Systems of Equations; Lectures in Applied Mathematics; American Mathematical Society: Providence, RI, USA, 1990. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Gao, Y. Two New Levenberg-Marquardt Methods for Non-smooth Nonlinear Complementarity Problems. Sci. Asia 2014, 40, 89. [Google Scholar] [CrossRef][Green Version]
- Song, L.; Gao, Y. On The Local Convergence of a Levenberg-Marquardt Method for Non-smooth Nonlinear Complementarity Problems. Sci. Asia 2017, 43, 377. [Google Scholar] [CrossRef]
- Du, S.Q. Some Global Convergence Properties of the Levenberg-Marquardt Methods with Line Search. J. Appl. Math. Inform. 2013, 31, 373–378. [Google Scholar] [CrossRef][Green Version]
- Dahmen, W.; Reusken, A. Numerik für Ingenieure und Naturwissenschaftler; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Guerchali, N. Untersuchung des Levenberg-Marquardt-Algorithmus zur Indoor-Lokalisierung für den STMF407-Mikrocontroller. Bachelor’s Thesis, Fachhochschule Aachen, Aachen, Germany, 2017. [Google Scholar]
- Ramnath, S.; Javali, A.; Narang, B.; Mishra, P.; Routray, S.K. IoT-Based Localization and Tracking. In Proceedings of the 2017 International Conference on IoT and Application (ICIOT), Nagapattinam, India, 19–20 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Reed, J.H. An Introduction to Ultra Wideband Communication Systems, 1st ed.; Prentice Hall Press: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- AeroScout Corporation. Available online: http://www.aeroscout.com (accessed on 25 February 2021).
- Holm, S. Ultrasound Positioning Based on Time-of-Flight and Signal Strength. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, Australia, 13–15 November 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Pasku, V.; De Angelis, A.; De Angelis, G.; Arumugam, D.D.; Dionigi, M.; Carbone, P.; Moschitta, A.; Ricketts, D.S. Magnetic Field-Based Positioning Systems. IEEE Commun. Surv. Tutor. 2017, 19, 2003–2017. [Google Scholar] [CrossRef]
- Chawathe, S.S. Low-Latency Indoor Localization Using Bluetooth Beacons. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Norrdine, A. An Algebraic Solution to the Multilateration Problem. In Proceedings of the Third International Conference on Indoor Positioning and Indoor Navigation (IPIN2012), Sydney, Australia, 13–15 November 2012; pp. 1–5. [Google Scholar]
- Kasmi, Z.; Norrdine, A.; Blankenbach, J. Platform Architecture for Decentralized Positioning Systems. Sensors 2017, 17, 957. [Google Scholar] [CrossRef] [PubMed]
- Kasmi, Z.; Guerchali, N.; Norrdine, A.; Schiller, J.H. Algorithms and Position Optimization for a Decentralized Localization Platform Based on Resource-Constrained Devices. IEEE Trans. Mob. Comput. 2019, 18, 1731–1744. [Google Scholar] [CrossRef]
- Prigge, E.A.; How, J.P. Signal architecture for a distributed magnetic local positioning system. IEEE Sens. J. 2004, 4, 864–873. [Google Scholar] [CrossRef]
- Prieto, J.C.; Croux, C.; Jiménez, A.R. RoPEUS: A New Robust Algorithm for Static Positioning in Ultrasonic Systems. Sensors 2009, 9, 4211. [Google Scholar] [CrossRef] [PubMed]
- Van Heesch, D. Doxygen: Generate Documentation from Source Code. Available online: https://www.doxygen.nl/index.html (accessed on 25 February 2021).
- Datta, B.N. Numerical Linear Algebra and Applications, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Trefethen, L.; Schreiber, R. Average-Case Stability of Gaussian Elimination. SIAM J. Matrix Anal. Appl. 1990, 11. [Google Scholar] [CrossRef]
- Trefethen, L.; Bau, D. Numerical Linear Algebra; Other Titles in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Stewart, G.W. Matrix Algorithms: Volume 1, Basic Decompositions; Matrix Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998. [Google Scholar]
- Thisted, R.A. Elements of Statistical Computing: Numerical Computation; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 1988. [Google Scholar]
- Gander, W.; Gander, M.J.; Kwok, F. Scientific Computing—An Introduction Using Maple and MATLAB; Springer Publishing Company, Incorporated: New York, NY, USA, 2014. [Google Scholar]
- Golub, G.H.; Reinsch, C. Singular Value Decomposition and Least Squares Solutions. Numer. Math. 1970, 14, 403–420. [Google Scholar] [CrossRef]
- Free Software Foundation, Inc. GNU Lesser General Public License, Version 2.1. 2021. Available online: https://www.gnu.org/licenses/old-licenses/lgpl-2.1.en.html (accessed on 25 February 2021).
- Baccelli, E.; Hahm, O.; Günes, M.; Wählisch, M.; Schmidt, T.C. RIOT OS: Towards an OS for the Internet of Things. In Proceedings of the 2013 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Turin, Italy, 14–19 April 2013; pp. 79–80. [Google Scholar] [CrossRef]
- Hope, M. Linaro Toolchain Binaries. 2020. Available online: https://launchpad.net/linaro-toolchain-binaries (accessed on 25 February 2021).
- Team, O. OpenOCD—Open On-Chip Debugger Reference Manual; Samurai Media Limited: London, UK, 2015. [Google Scholar]
- Kasmi, Z. GitLab of the RcdMathLib (Mathematical Library for Resource-Constrained Devices). 2021. Available online: https://git.imp.fu-berlin.de/zkasmi/RcdMathLib (accessed on 25 February 2021).
- Croeze, A.; Pittman, L.; Reynolds, W. Solving Nonlinear Least-Squares Problems with the Gauss–Newton and Levenberg–Marquardt Methods; Technical Report; Department of Mathematics, Louisiana State University: Baton Rouge, LA, USA, 2012. [Google Scholar]
- Zhao, X.L.; Huang, T.Z.; Gu, X.M.; Deng, L.J. Vector Extrapolation based Landweber Method for Discrete ill-posed Problems. Math. Probl. Eng. 2017, 2017, 1375716. [Google Scholar] [CrossRef]

| Library | Capabilities | Platform |
|---|---|---|
| GNU Scientific Library (GSL) | Basic linear algebra, FFT, basic mathematical routines | No support for resource-limited devices |
| C standard mathematical library <math.h> | Basic mathematical functions | Support for resource-limited devices |
| IQmath and Qmath | Basic mathematical functions | MSP430 and MSP432 microcontrollers |
| Libfixmatrix | Basic mathematical functions and matrix inversion | ARM Cortex-M3 processors |
| MicroBLAS | Basic linear algebra | PC and microcontrollers |
| MatrixMath and BasicLinearAlgebra | Basic matrix operations | Restricted to the Arduino platform |
| NumPy, SciPy | Linear algebra computational mathematics | No support for resource-limited devices |
| math and cmath (MicroPython) | Basic mathematical functions | ARM Cortex-M processors or CircuitPython- powered boards |
| RcdMathLab | mathematical functions for nonlinear, linear algebra optimization, and localization. Utilities | PCs and microcontrollers: Platforms using C compiler |
| Algorithm | Complexity [Flops] |
|---|---|
| Matrix multiplication: | |
| QR-Householder | |
| Golub–Kahan–Reinsch |
| Algorithm | Mean Execution Time (s) | |
|---|---|---|
| STM32F4 | Raspberry Pi 3 | |
| Matrix multiplication: | 356 | 49 |
| Householder-based solution | 906 | 54 |
| Golub–Kahan–Reinsch-based solution | 3647 | 204 |
| Algorithm | Mean Execution Time (s) | |
|---|---|---|
| STM32F4 | Raspberry Pi 3 | |
| Gauss–Newton | 1065 | 35 |
| Levenberg–Marquardt | 1194 | 42 |
| Algorithm | Mean Execution Time (s) | |
|---|---|---|
| STM32F4 | Raspberry Pi 3 | |
| Gauss–Newton | 3165 | 157 |
| Levenberg–Marquardt | 2825 | 141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasmi, Z.; Norrdine, A.; Schiller, J.; Güneş, M.; Motzko, C. RcdMathLib: An Open Source Software Library for Computing on Resource-Limited Devices. Sensors 2021, 21, 1689. https://doi.org/10.3390/s21051689
Kasmi Z, Norrdine A, Schiller J, Güneş M, Motzko C. RcdMathLib: An Open Source Software Library for Computing on Resource-Limited Devices. Sensors. 2021; 21(5):1689. https://doi.org/10.3390/s21051689
Chicago/Turabian StyleKasmi, Zakaria, Abdelmoumen Norrdine, Jochen Schiller, Mesut Güneş, and Christoph Motzko. 2021. "RcdMathLib: An Open Source Software Library for Computing on Resource-Limited Devices" Sensors 21, no. 5: 1689. https://doi.org/10.3390/s21051689
APA StyleKasmi, Z., Norrdine, A., Schiller, J., Güneş, M., & Motzko, C. (2021). RcdMathLib: An Open Source Software Library for Computing on Resource-Limited Devices. Sensors, 21(5), 1689. https://doi.org/10.3390/s21051689






