An Indoor Visible Light Positioning System Using Tilted LEDs with High Accuracy
Abstract
1. Introduction
2. Proposed Visible Light Positioning (VLP) System Model
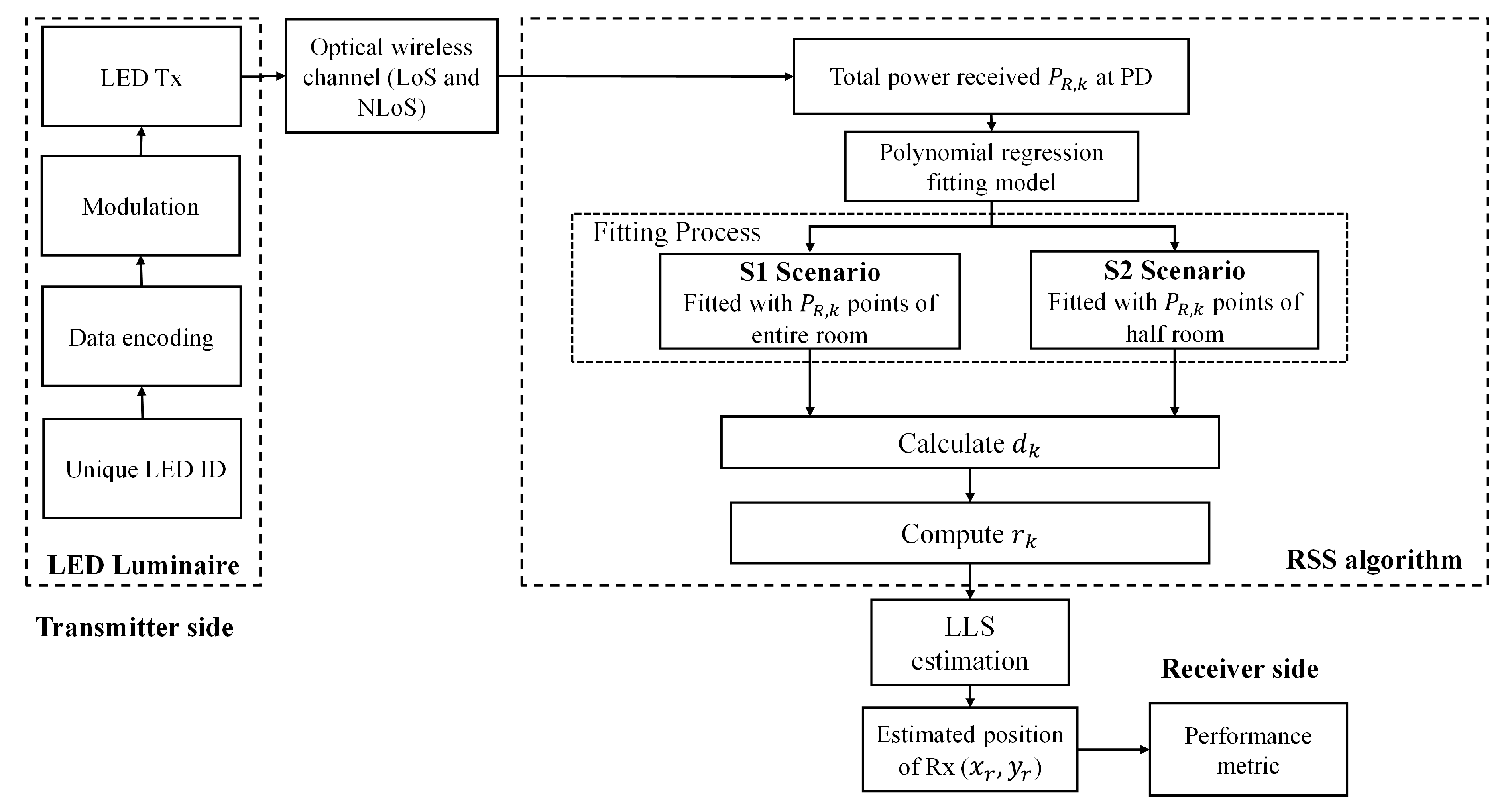
3. Positioning Algorithm
3.1. Distance Estimation Using Polynomial Regression
3.2. Linear Least Square (LLS) Estimation
4. Results and Discussion
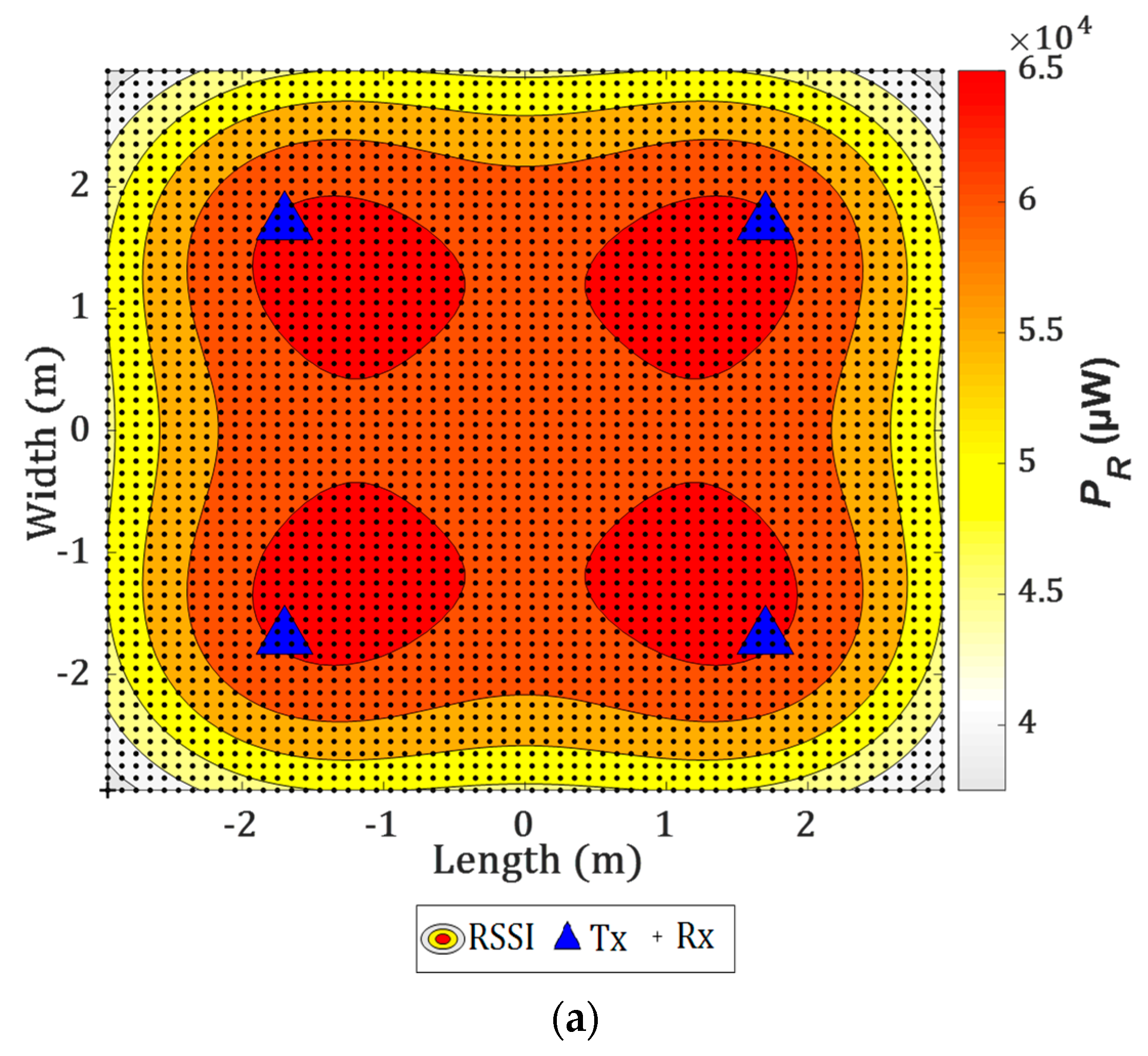
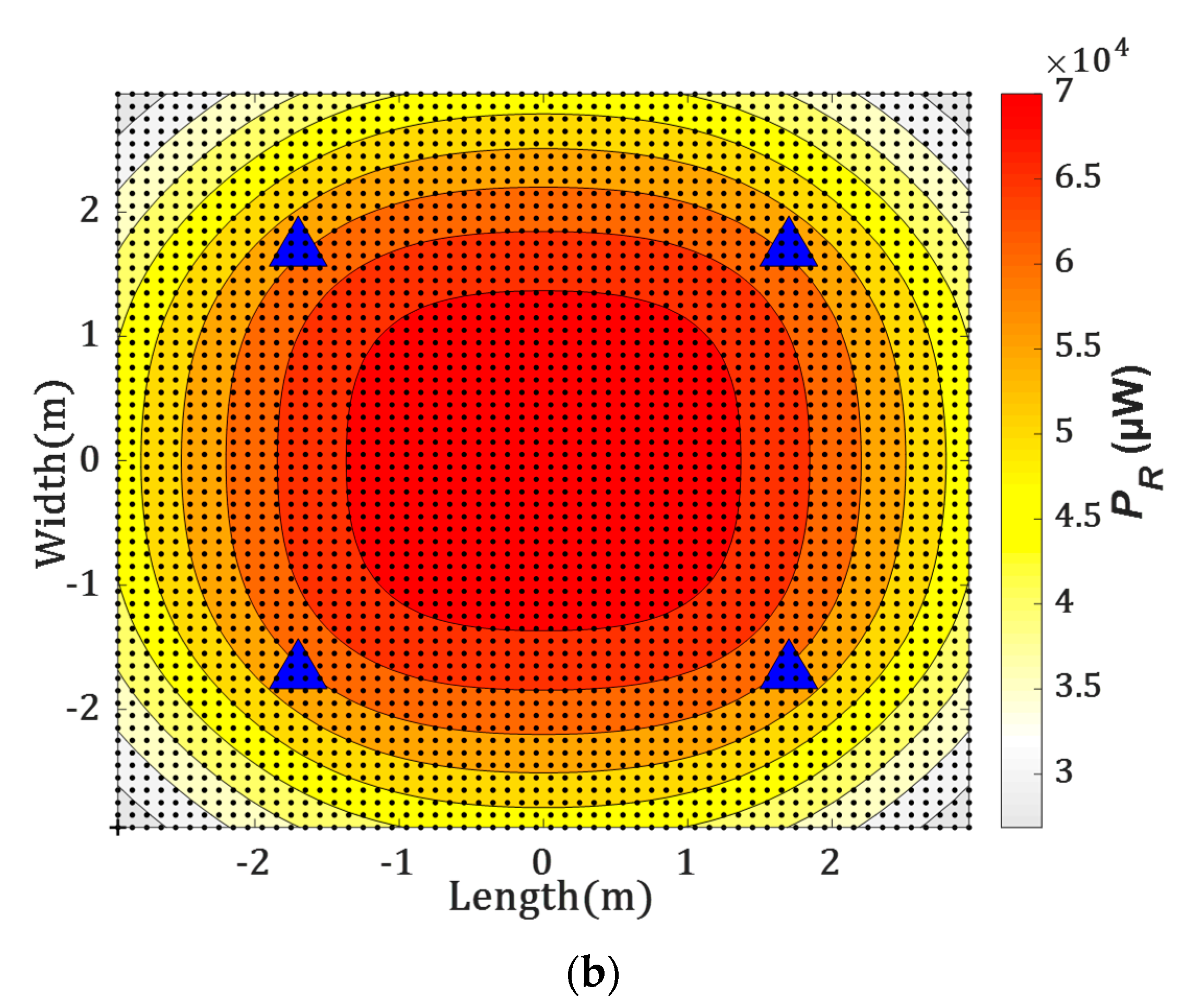
4.1. Impact of the Transmitter (Tx) Tilting on the Radiation Pattern
4.2. Polynomial Fitting
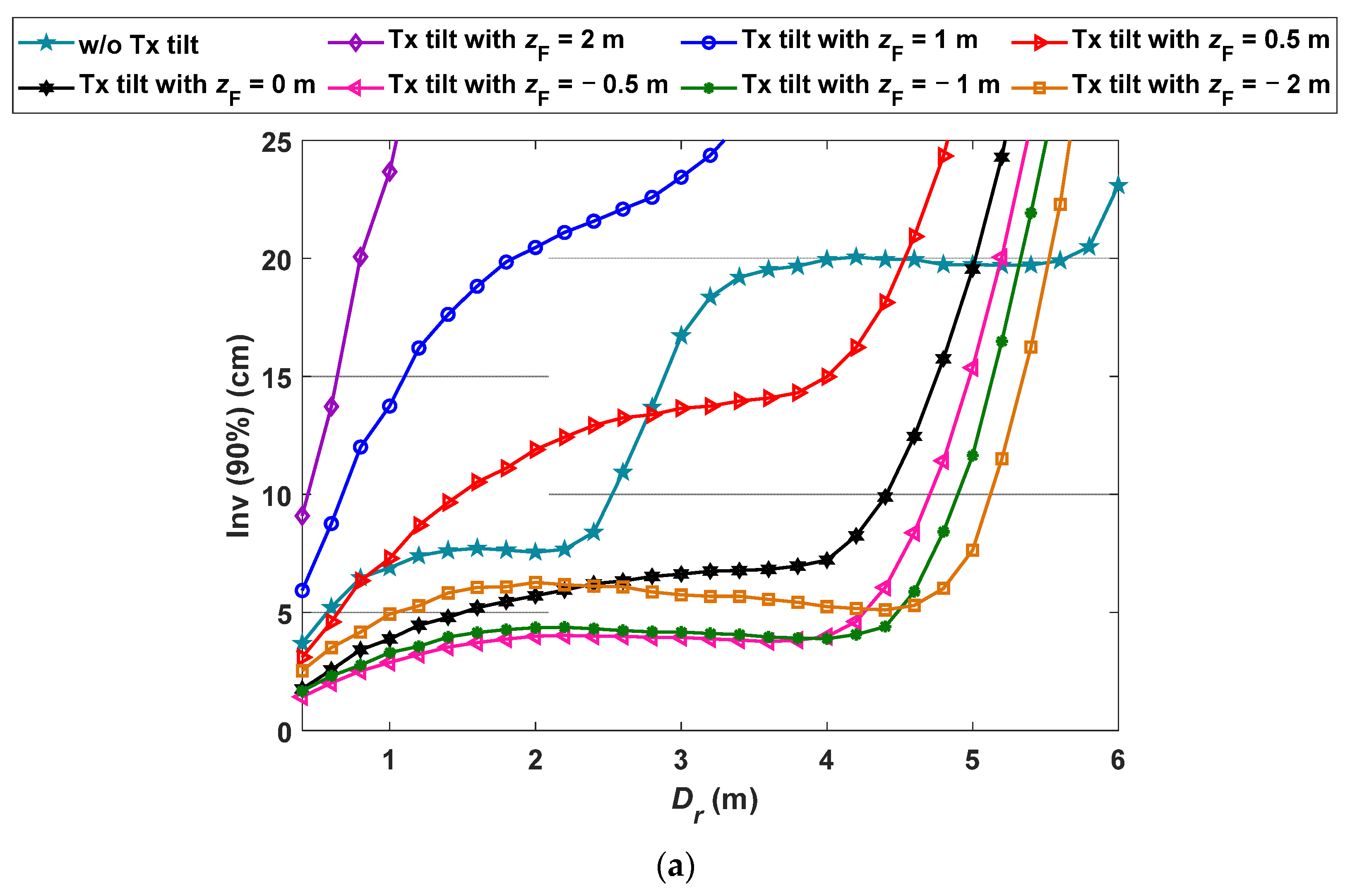
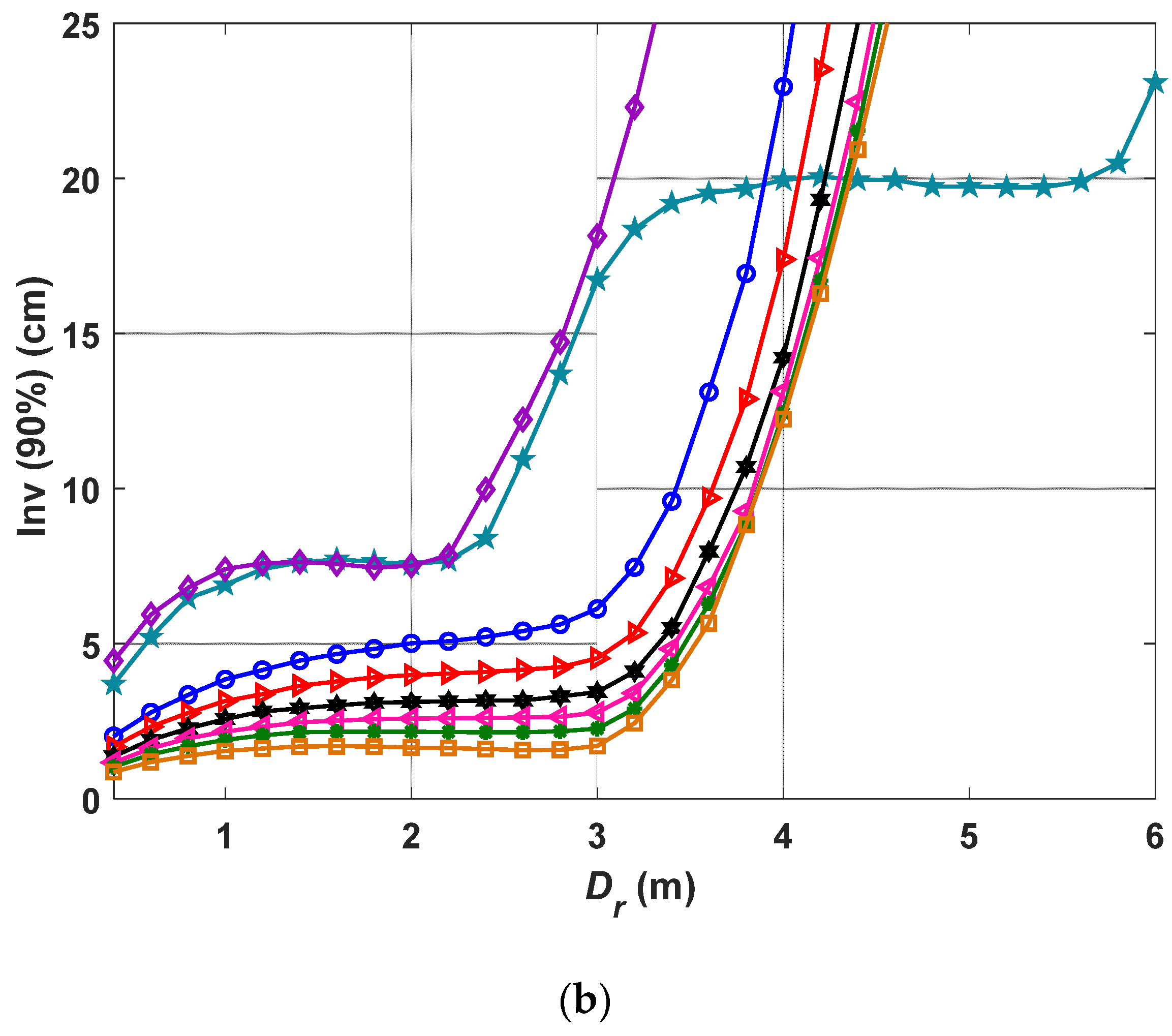
4.3. Impact of the Tx Tilting and the Altitude of F on VLP
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Short Form | Description |
| ADT | Angle diversity transmitter |
| ANN | Artificial neural network |
| CDF | Cumulative distribution function |
| IS | Image sensor |
| LEDs | Light-emitting diodes |
| LLS | Linear least square |
| LoS | Line of sight |
| NLLS | Nonlinear least square |
| NLoS | Non-line of sight |
| OOK | On-off keying |
| PA | Positioning accuracy |
| PDs | Photodiodes |
| PR | Polynomial regression |
| RF | Radio frequency |
| RMS | Root mean square |
| RSS | Received signal strength |
| RSSI | Received signal strength indicator |
| Rx | Receiver |
| TOF | Time of flight |
| Tx | Transmitter |
| VLC | Visible light communication |
| VLP | Visible light positioning |
| WCS | World coordinate system |
References
- Nguyen, C.T.; Saputra, Y.M.; Huynh, N.V.; Nguyen, N.-T.; Khoa, T.V.; Tuan, B.M.; Nguyen, D.N.; Hoang, D.T.; Vu, T.X.; Dutkiewicz, E.; et al. A Comprehensive Survey of Enabling and Emerging Technologies for Social Distancing—Part I: Fundamentals and Enabling Technologies. IEEE Access 2020, 8, 153479–153507. [Google Scholar] [CrossRef]
- Luo, J.; Fan, L.; Li, H. Indoor Positioning Systems Based on Visible Light Communication: State of the Art. IEEE Commun. Surv. Tutor. 2017, 19, 2871–2893. [Google Scholar] [CrossRef]
- Armstrong, J.; Sekercioglu, Y.A.; Neild, A. Visible Light Positioning: A Roadmap for International Standardization. IEEE Commun. Mag. 2013, 51, 68–73. [Google Scholar] [CrossRef]
- Chung, J.; Donahoe, M.; Schmandt, C.; Kim, I.-J.; Razavai, P.; Wiseman, M. Indoor location sensing using geo-magnetism. In Proceedings of the 9th International Conference on Mobile Systems, Applications, and Services, Washington, DC, USA, 29 June–1 July 2011; pp. 141–154. [Google Scholar]
- Youssef, M.; Agrawala, A. The Horus WLAN location determination system. In Proceedings of the 3rd International Conference on Mobile Systems, Applications, and Services, Washington, DC, USA, 6–8 June 2005; pp. 205–218. [Google Scholar]
- Chen, Y.; Lymberopoulos, D.; Liu, J.; Priyantha, B. FM-based indoor localization. In Proceedings of the 10th International Conference on Mobile Systems, Applications, and Services, Low Wood Bay, Lake District, UK, 26–28 June 2012; pp. 169–182. [Google Scholar]
- Elgala, H.; Mesleh, R.; Haas, H. Indoor optical wireless communication: Potential and state-of-the-art. IEEE Commun. Mag. 2011, 49, 56–62. [Google Scholar] [CrossRef]
- Maheepala, M.; Kouzani, A.Z.; Joordens, M.A. Light-Based Indoor Positioning Systems: A Review. IEEE Sens. J. 2020, 20, 3971–3995. [Google Scholar] [CrossRef]
- Do, T.H.; Yoo, M. An in-Depth Survey of Visible Light Communication Based Positioning Systems. (in eng). Sensors 2016, 16, 678. [Google Scholar] [CrossRef]
- Chaudhary, N.; Alves, L.N.; Ghassemlooy, Z. Current Trends on Visible Light Positioning Techniques. In Proceedings of the 2019 2nd West Asian Colloquium on Optical Wireless Communications (WACOWC), Teheran, Iran, 27–28 April 2019; pp. 100–105. [Google Scholar]
- Lee, J.; Kim, S.; Han, S. 3D Visible Light Indoor Positioning by Bokeh Based Optical Intensity Measurement in Smartphone Camera. IEEE Access 2019, 7, 91399–91406. [Google Scholar] [CrossRef]
- Cheng, H.; Xiao, C.; Ji, Y.; Ni, J.; Wang, T. A Single LED Visible Light Positioning System Based on Geometric Features and CMOS Camera. IEEE Photonics Technol. Lett. 2020, 32, 1097–1100. [Google Scholar] [CrossRef]
- Younus, O.I.; Hassan, N.B.; Ghassemlooy, Z.; Haigh, P.A.; Zvanovec, S.; Alves, L.N.; Minh, H.L. Data Rate Enhancement in Optical Camera Communications Using an Artificial Neural Network Equaliser. IEEE Access 2020, 8, 42656–42665. [Google Scholar] [CrossRef]
- Rabadan, J.; Guerra, V.; Guerra, C.; Rufo, J.; Perez-Jimenez, R. A Novel Ranging Technique Based on Optical Camera Communications and Time Difference of Arrival. Appl. Sci. 2019, 9, 2382. [Google Scholar] [CrossRef]
- Zhuang, Y.; Hua, L.; Qi, L.; Yang, J.; Cao, P.; Cao, Y.; Wu, Y.; Thompson, J.; Haas, H. A Survey of Positioning Systems Using Visible LED Lights. IEEE Commun. Surv. Tutor. 2018, 20, 1963–1988. [Google Scholar] [CrossRef]
- Chaudhary, N.; Alves, L.N.; Ghassemlooy, Z. Impact of Transmitter Positioning Uncertainty on RSS-based Visible Light Positioning Accuracy. In Proceedings of the 12th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020. [Google Scholar]
- Plets, D.; Almadani, Y.; Bastiaens, S.; Ijaz, M.; Martens, L.; Joseph, W. Efficient 3D trilateration algorithm for visible light positioning. J. Opt. 2019, 21, 05LT01. [Google Scholar] [CrossRef]
- Chvojka, P.; Zvanovec, S.; Haigh, P.A.; Ghassemlooy, Z. Channel Characteristics of Visible Light Communications within Dynamic Indoor Environment. J. Lightwave Technol. 2015, 33, 1719–1725. [Google Scholar] [CrossRef]
- Naz, A.; Asif, H.M.; Umer, T.; Ayub, S.; Al-Turjman, F. Trilateration-based indoor localization engineering technique for visible light communication system. Softw. Pract. Exp. 2020, 1–14. [Google Scholar]
- Gu, W.; Aminikashani, M.; Deng, P.; Kavehrad, M. Impact of Multipath Reflections on the Performance of Indoor Visible Light Positioning Systems. J. Lightwave Technol. 2016, 34, 2578–2587. [Google Scholar] [CrossRef]
- Plets, D.; Eryildirim, A.; Bastiaens, S.; Stevens, N.; Martens, L.; Joseph, W. A Performance Comparison of Different Cost Functions for RSS-Based Visible Light Positioning Under the Presence of Reflections. In Proceedings of the 4th ACM Workshop on Visible Light Communication Systems, Snowbird, UT, USA, 16 October 2017. [Google Scholar]
- Liu, Y.; Zhang, J.; Liu, Y.; Chen, B.; Liu, S.; Zuo, Y. A new indoor visible light positioning scheme to reduce the influence of reflections. In Proceedings of the 17th International Conference on Optical Communications and Networks (ICOCN2018), Zhuhai, China, 16–19 November 2018. [Google Scholar]
- Wang, J.-Y.; Li, Q.-L.; Zhu, J.-X.; Wang, Y. Impact of receiver’s tilted angle on channel capacity in VLCs. Electron. Lett. 2017, 53, 421–423. [Google Scholar] [CrossRef]
- Plets, D.; Bastiaens, S.; Martens, L.; Joseph, W. An Analysis of the Impact of LED Tilt on Visible Light Positioning Accuracy. Electronics 2019, 8, 389. [Google Scholar] [CrossRef]
- Raes, W.; Stevens, N. Performance Assessment of Artificial Neural Networks on the RSS-Based Visible Light Positioning Accuracy with Random Transmitter Tilt. In Proceedings of the International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020. [Google Scholar]
- Lixuan, W.; Caili, G.; Luo, P.; Li, Q. Indoor visible light localization algorithm based on received signal strength ratio with multi-directional LED array. In Proceedings of the 2017 IEEE International Conference on Communications Workshops (ICC Workshops), Paris, France, 21–25 May 2017; pp. 138–143. [Google Scholar]
- Yin, L.; Wu, X.; Haas, H. Indoor Visible Light Positioning with Angle Diversity Transmitter. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar]
- Zhou, B.; Liu, A.; Lau, V. Performance Limits of Visible Light-Based User Position and Orientation Estimation Using Received Signal Strength Under NLOS Propagation. IEEE Trans. Wirel. Commun. 2019, 18, 5227–5241. [Google Scholar] [CrossRef]
- Miramirkhani, F.; Uysal, M. Channel Modeling and Characterization for Visible Light Communications. IEEE Photonics. J. 2015, 7, 1–16. [Google Scholar] [CrossRef]
- Uysal, M.; Miramirkhani, F.; Narmanlioglu, O.; Baykas, T.; Panayirci, E. IEEE 802.15.7r1 Reference Channel Models for Visible Light Communications. IEEE Commun. Mag. 2017, 55, 212–217. [Google Scholar] [CrossRef]
- Chaleshtori, Z.N.; Ghassemlooy, Z.; Eldeeb, H.B.; Uysal, M.; Zvanovec, S. Utilization of an OLED-Based VLC System in Office, Corridor, and Semi-Open Corridor Environments. Sensors 2020, 20, 6869. [Google Scholar] [CrossRef] [PubMed]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab®, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Chaudhary, N.; Alves, L.N.; Ghassemblooy, Z. Feasibility Study of Reverse Trilateration Strategy with a Single Tx for VLP. In Proceedings of the 2019 2nd West Asian Colloquium on Optical Wireless Communications (WACOWC), Teheran, Iran, 27–28 April 2019; pp. 121–126. [Google Scholar]
- Younus, O.I.; Minh, H.L.; Dat, P.T.; Yamamoto, N.; Pham, A.T.; Ghassemlooy, Z. Dynamic Physical-Layer Secured Link in a Mobile MIMO VLC System. IEEE Photonics J. 2020, 12, 1–14. [Google Scholar] [CrossRef]
- Shawky, S.; El-Shimy, M.A.; El-Sahn, Z.A.; Rizk, M.R.M.; Aly, M.H. Improved VLC-based indoor positioning system using a regression approach with conventional RSS techniques. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), Valencia, Spain, 26–30 June 2017; pp. 904–909. [Google Scholar]
- Sun, X.; Duan, J.; Zou, Y.; Shi, A. Impact of multipath effects on theoretical accuracy of TOA-based indoor VLC positioning system. Photonics Res. 2015, 3, 296–299. [Google Scholar] [CrossRef]
- De Normalisation, C.E. EN 12464-1: Light and Lighting-Lighting of Work Places, Part 1: Indoor Work Places; BSI: London, UK, 2002. [Google Scholar]
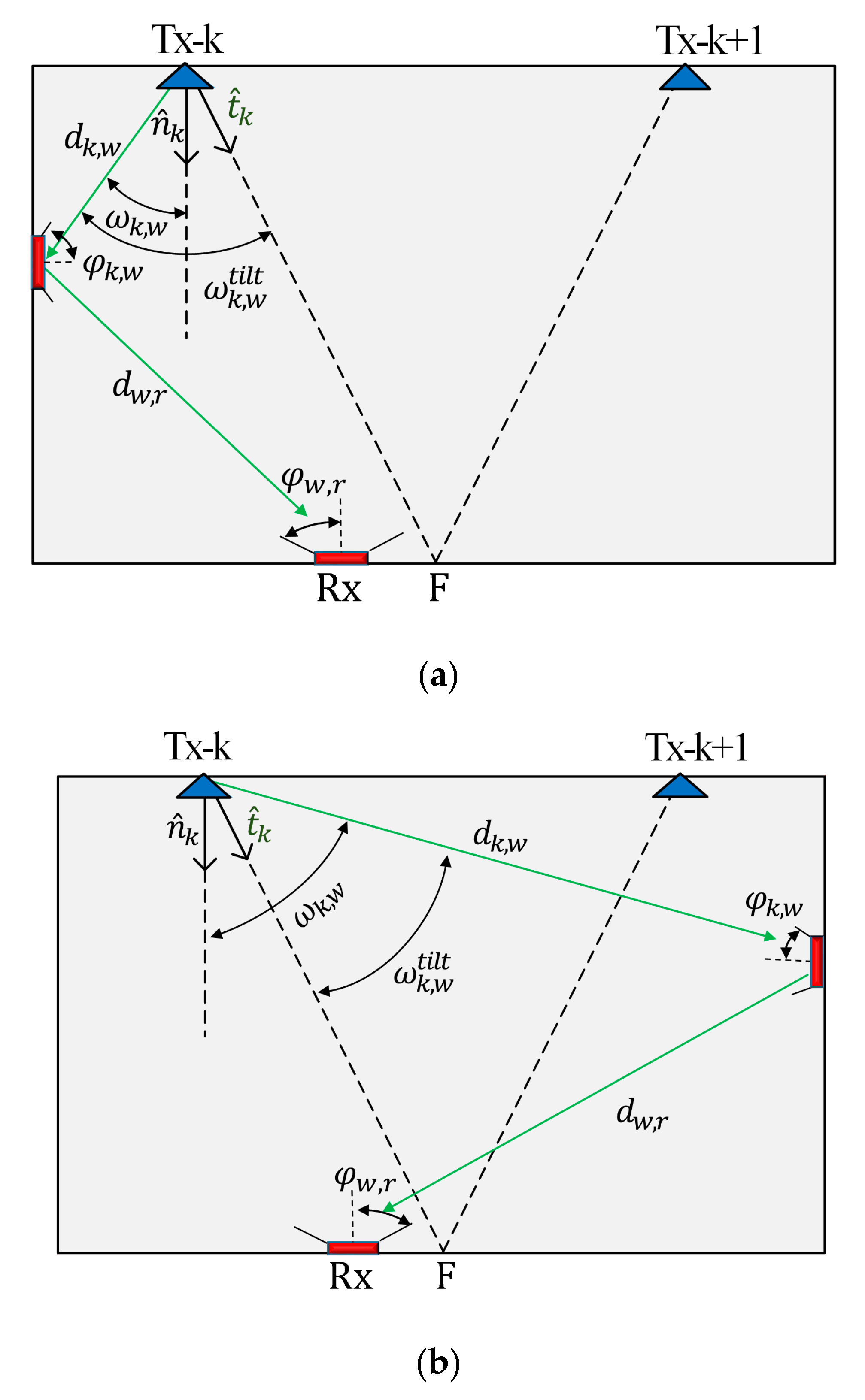
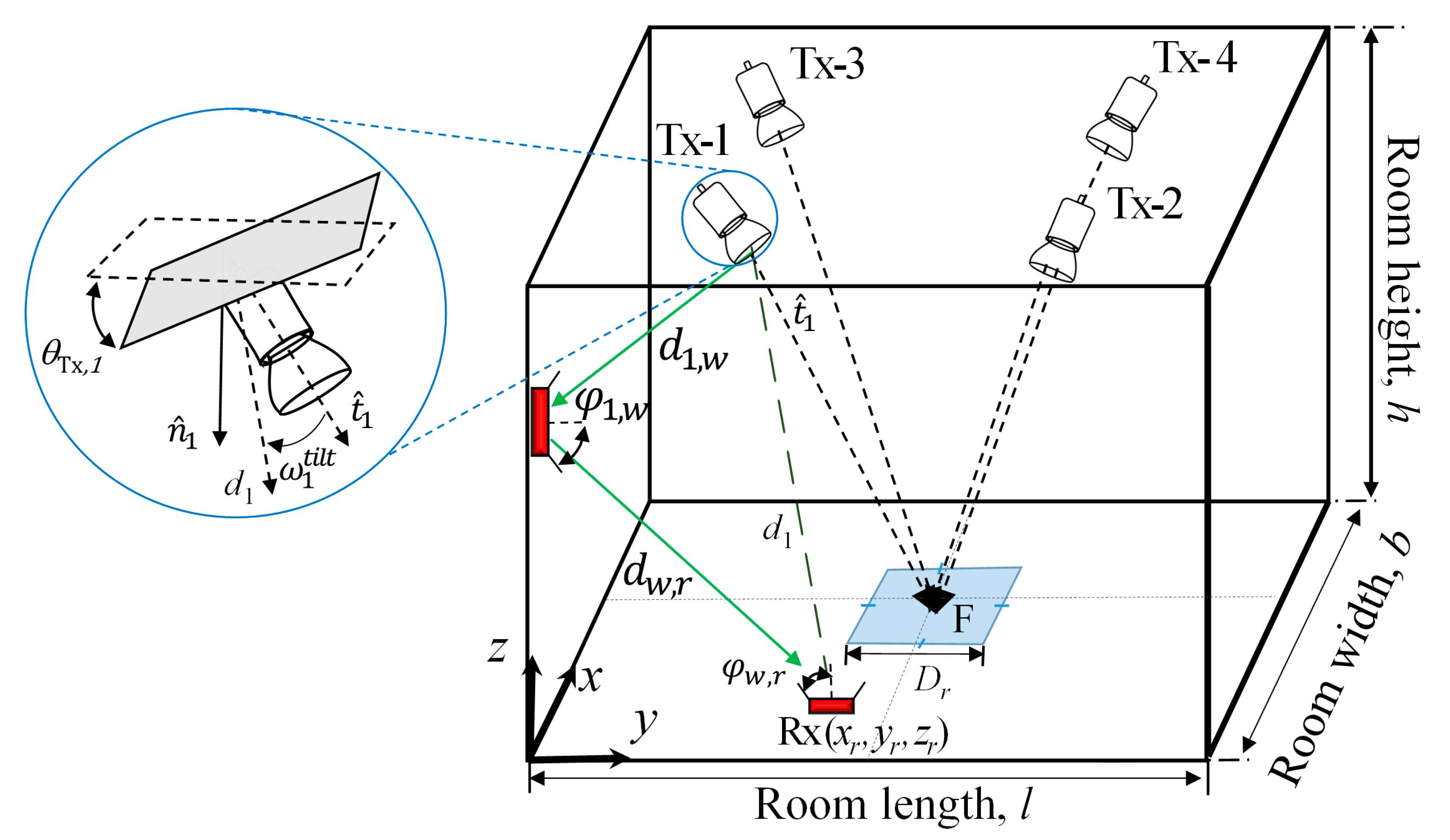



| Parameter | Symbol | Value |
|---|---|---|
| Room size | (l, b, h) | 6 × 6 × 3 m3 |
| The coordinates of | ||
| Tx-1 | (x1, y1, z1) | (−1.7 m, −1.7 m, 3 m) |
| Tx-2 | (x2, y2, z2) | (1.7 m, −1.7 m, 3 m) |
| Tx-3 | (x3, y3, z3) | (−1.7 m, 1.7 m, 3 m) |
| Tx-4 | (x4, y4, z4) | (1.7 m, 1.7 m, 3 m) |
| Transmit power of each Tx | 1 W | |
| Receiver’s field of view | FoV | 75° |
| Reflection coefficient | 0.7 | |
| Half power angle | HPA | 60° |
| Photodiode area | 10−4 m2 | |
| Responsivity | 1 A/W | |
| Reflection coefficient | 0.7 |
| Tx Number | |
|---|---|
| Tx-1 | [0.4, 0.4, −0.8] |
| Tx-2 | [−0.4, 0.4, −0.8] |
| Tx-3 | [0.4, −0.4, −0.8] |
| Tx-4 | [−0.4, −0.4, −0.8] |
| Cases | Estimated Polynomial Coefficients (No Units) | R2 | ||||
|---|---|---|---|---|---|---|
| With tilted Tx | 7.38 × 104 | −3.60 × 105 | 2.37 × 104 | −6.26 × 102 | 8.10 | 0.98 |
| Without tilted Tx | 8.86 × 106 | 9.93 × 105 | 3.96 × 104 | 7.35 × 102 | 7.44 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaudhary, N.; Younus, O.I.; Alves, L.N.; Ghassemlooy, Z.; Zvanovec, S.; Le-Minh, H. An Indoor Visible Light Positioning System Using Tilted LEDs with High Accuracy. Sensors 2021, 21, 920. https://doi.org/10.3390/s21030920
Chaudhary N, Younus OI, Alves LN, Ghassemlooy Z, Zvanovec S, Le-Minh H. An Indoor Visible Light Positioning System Using Tilted LEDs with High Accuracy. Sensors. 2021; 21(3):920. https://doi.org/10.3390/s21030920
Chicago/Turabian StyleChaudhary, Neha, Othman Isam Younus, Luis Nero Alves, Zabih Ghassemlooy, Stanislav Zvanovec, and Hoa Le-Minh. 2021. "An Indoor Visible Light Positioning System Using Tilted LEDs with High Accuracy" Sensors 21, no. 3: 920. https://doi.org/10.3390/s21030920
APA StyleChaudhary, N., Younus, O. I., Alves, L. N., Ghassemlooy, Z., Zvanovec, S., & Le-Minh, H. (2021). An Indoor Visible Light Positioning System Using Tilted LEDs with High Accuracy. Sensors, 21(3), 920. https://doi.org/10.3390/s21030920









