Controlling the Connected Vehicle with Bi-Directional Information: Improved Car-Following Models and Stability Analysis
Abstract
:1. Introduction
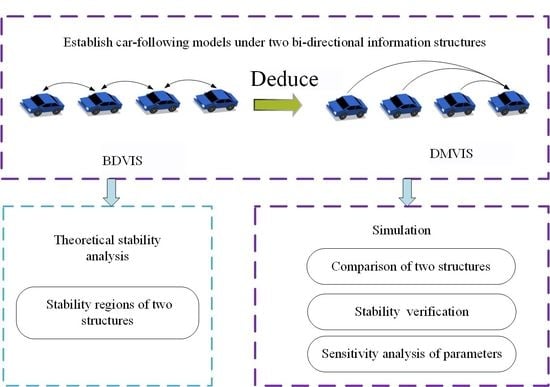
2. Methodology
2.1. Bidirectional Information Structure for Car-Following Model
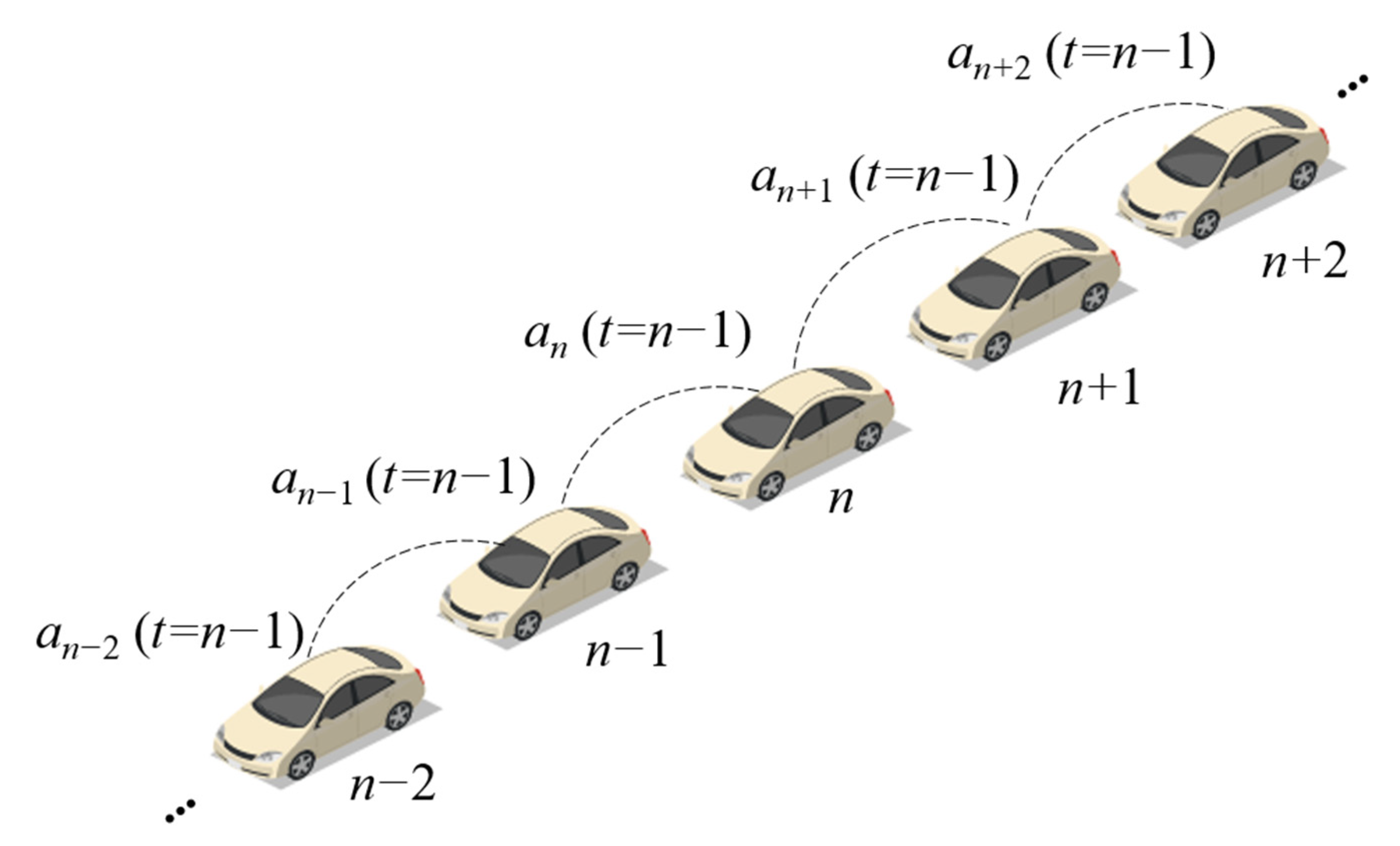
2.1.1. The BDVIS Based on Acceleration
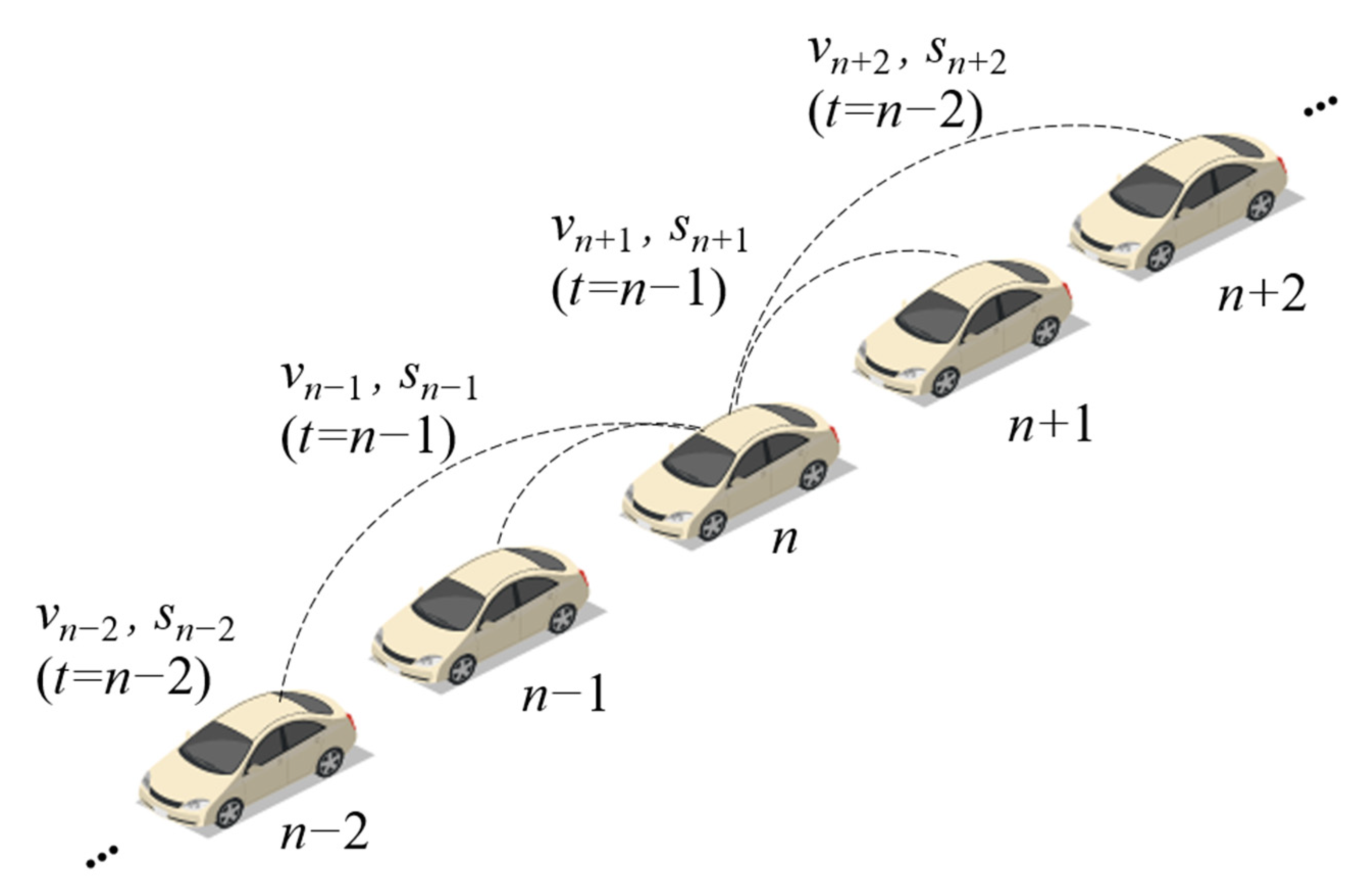
2.1.2. The DMVIS Deduced from the BDVIS
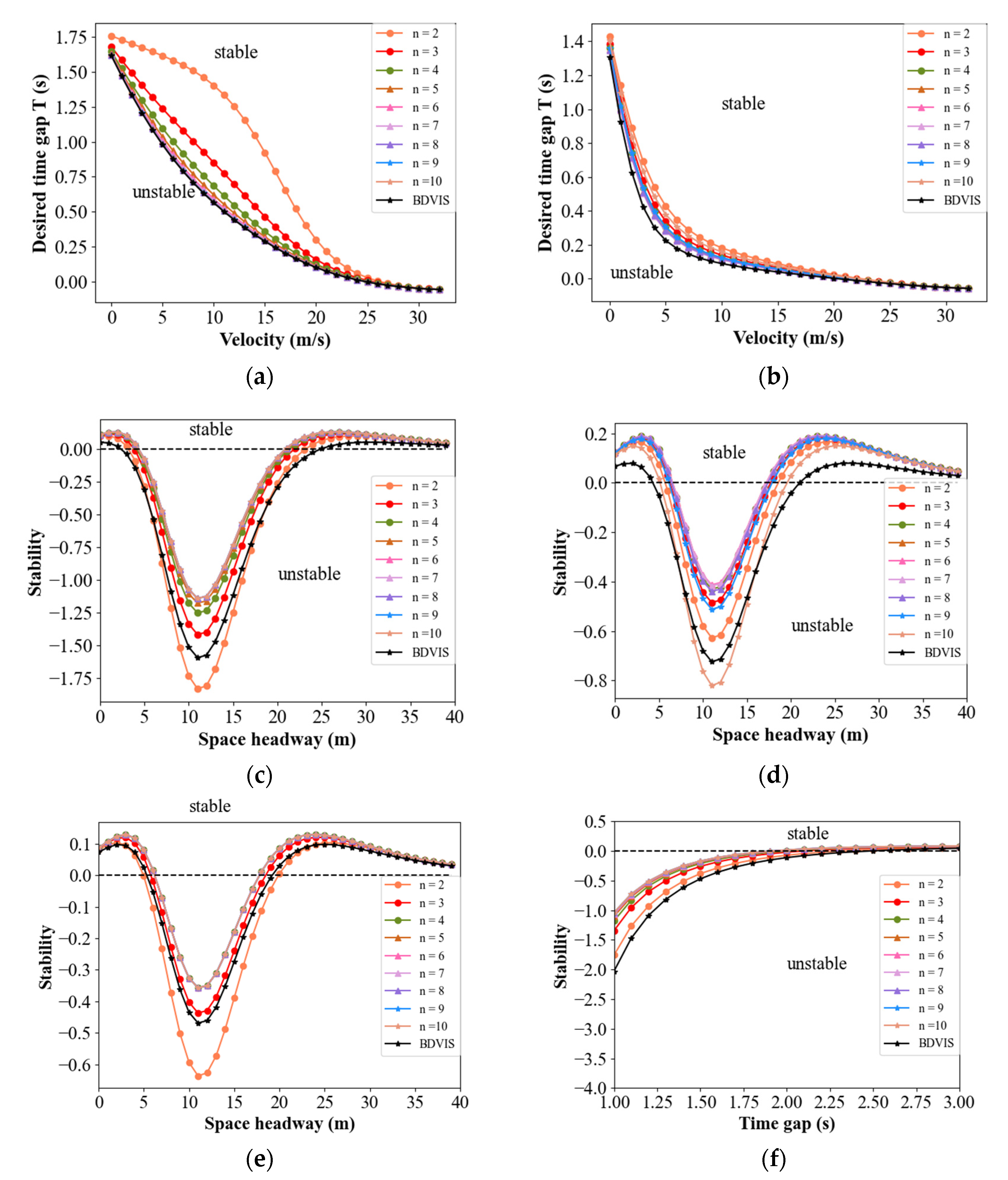
2.2. Linear Stability Analysis for Car-Following Models
2.2.1. Stability Analysis for BDVIS
2.2.2. Stability Analysis for DMVIS
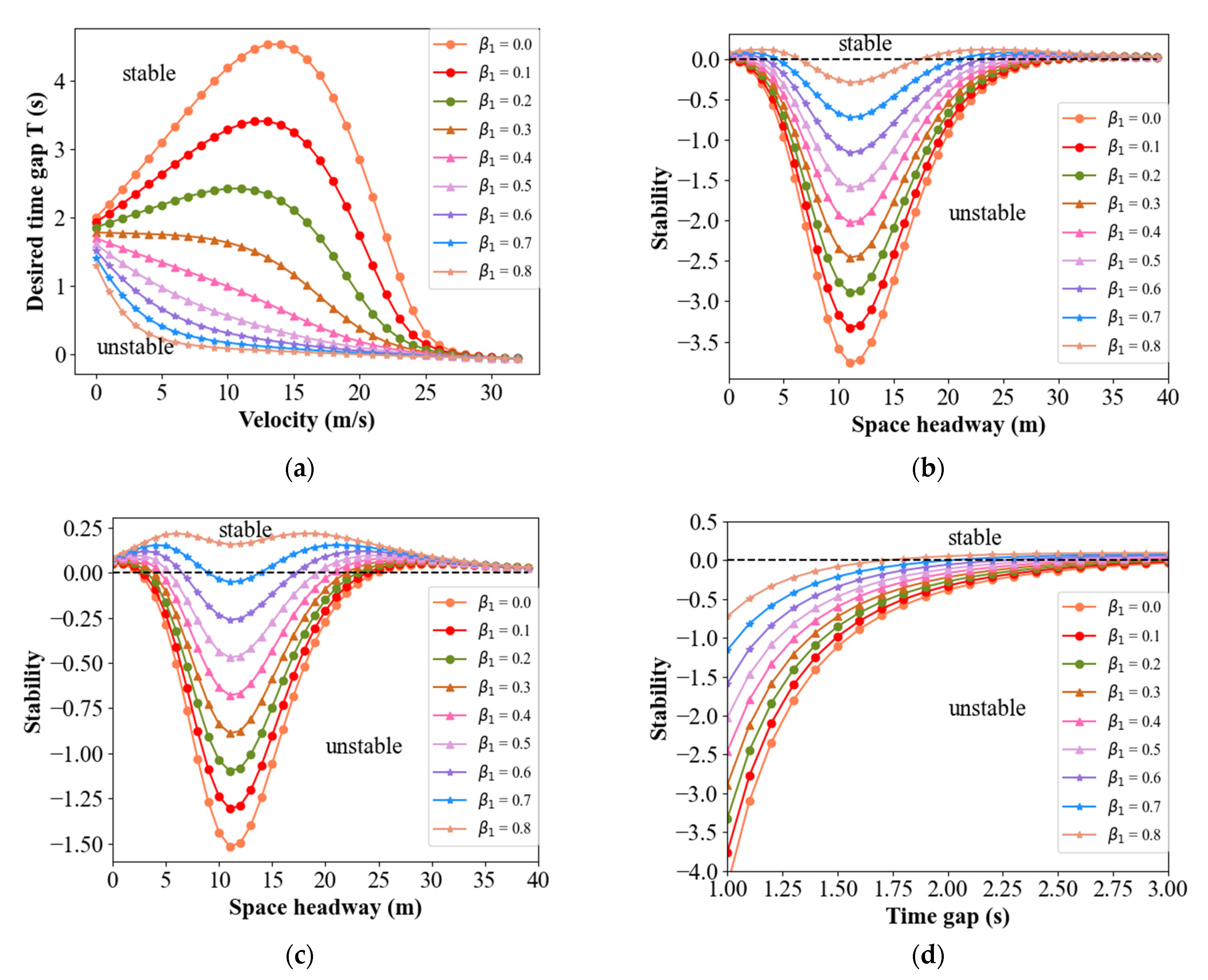
2.2.3. Results of Stability Analysis
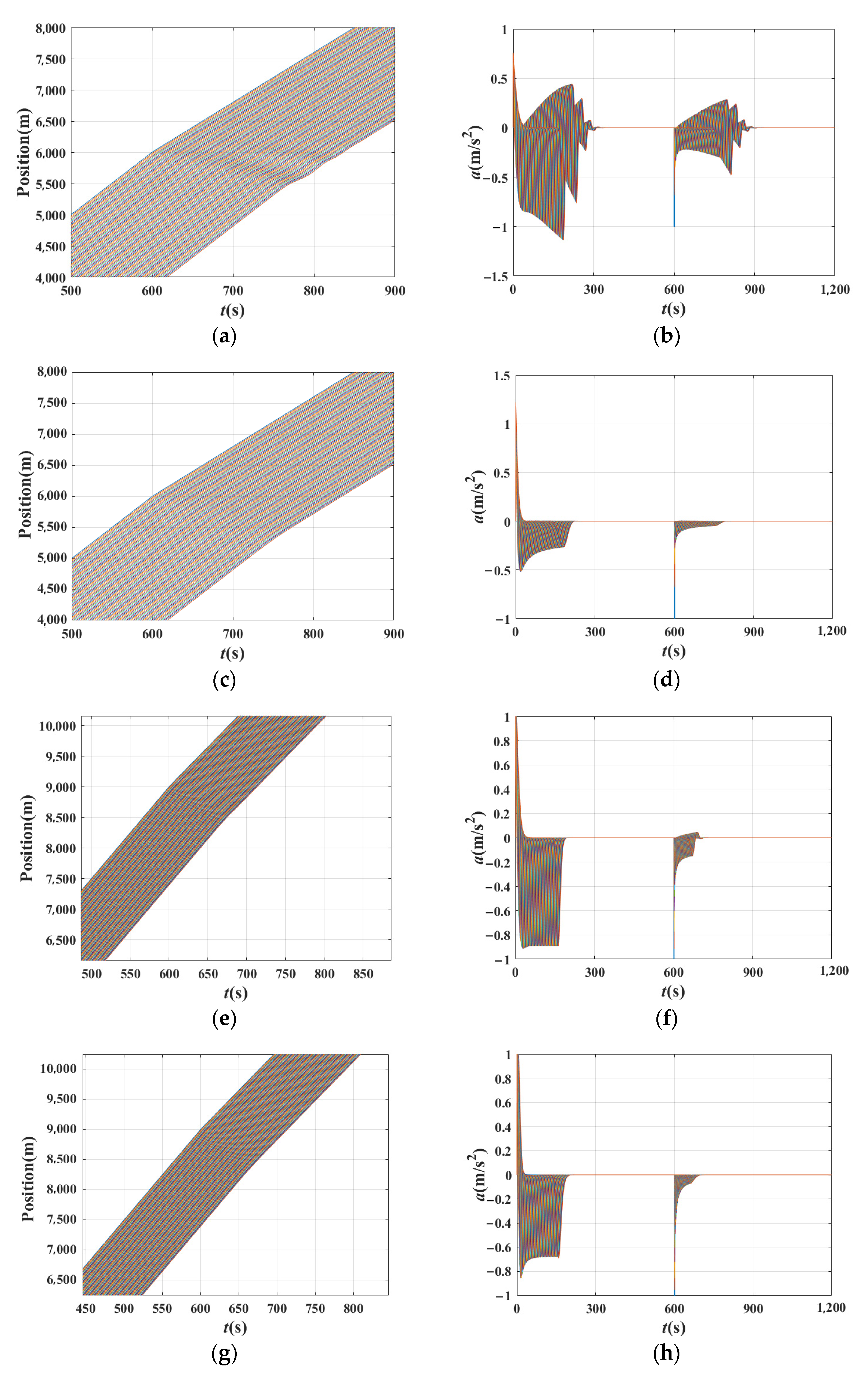
3. Experiment and Simulation
3.1. Description of the Experiments
- (1)
- Verify the theoretical stability results through numerical simulations of a platoon, taking the BDVIS as the representative. (Experiments 1)
- (2)
- Explore traffic response properties with different proportions of forward-looking (β1) or forward-looking terms (β2) based on the BDVIS. (Experiments 2~3)
3.2. Evaluation Index
3.3. Simulation Environment
4. Result and Discussion
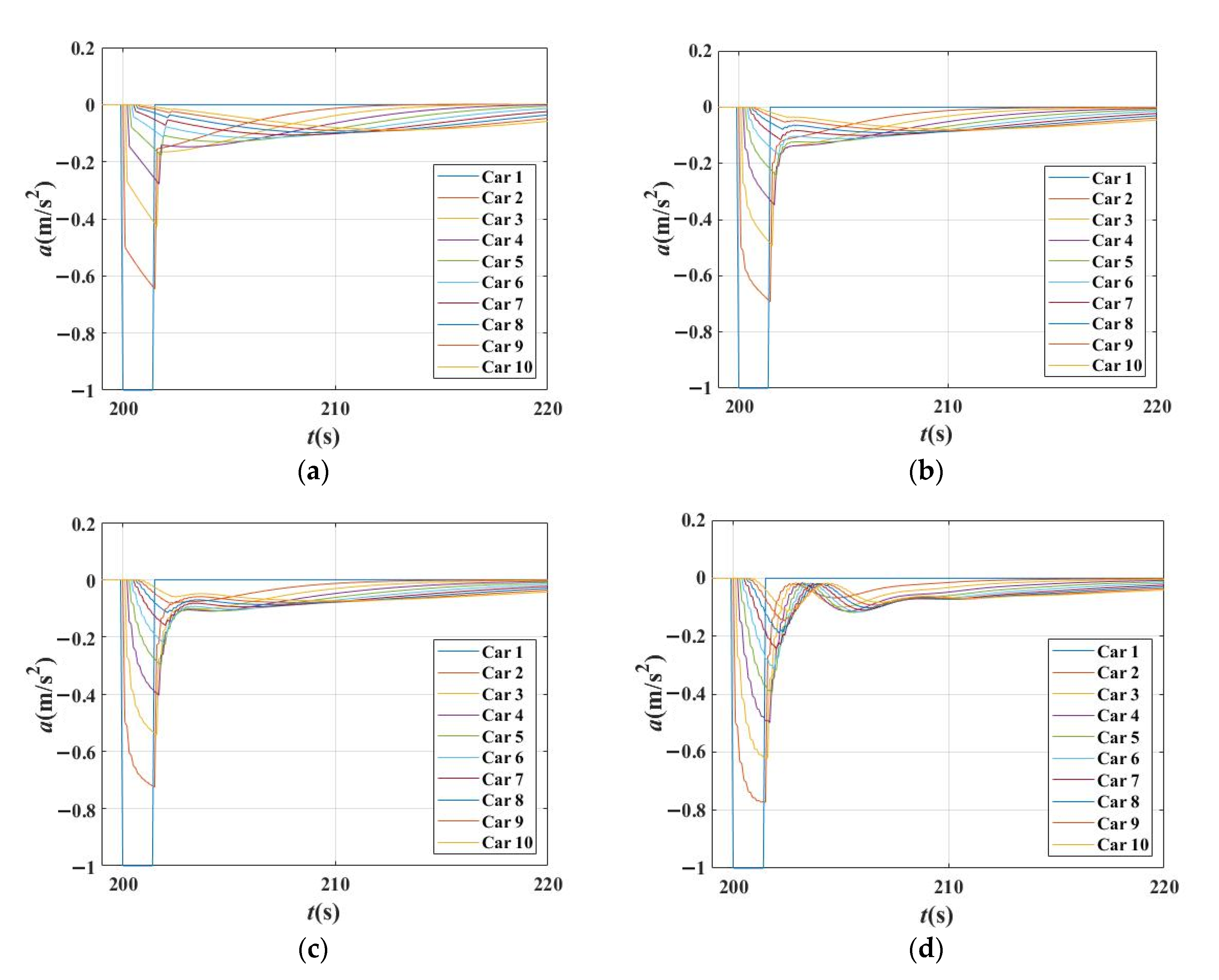
4.1. Verification of Theoretical Stability Results of the BDVIS
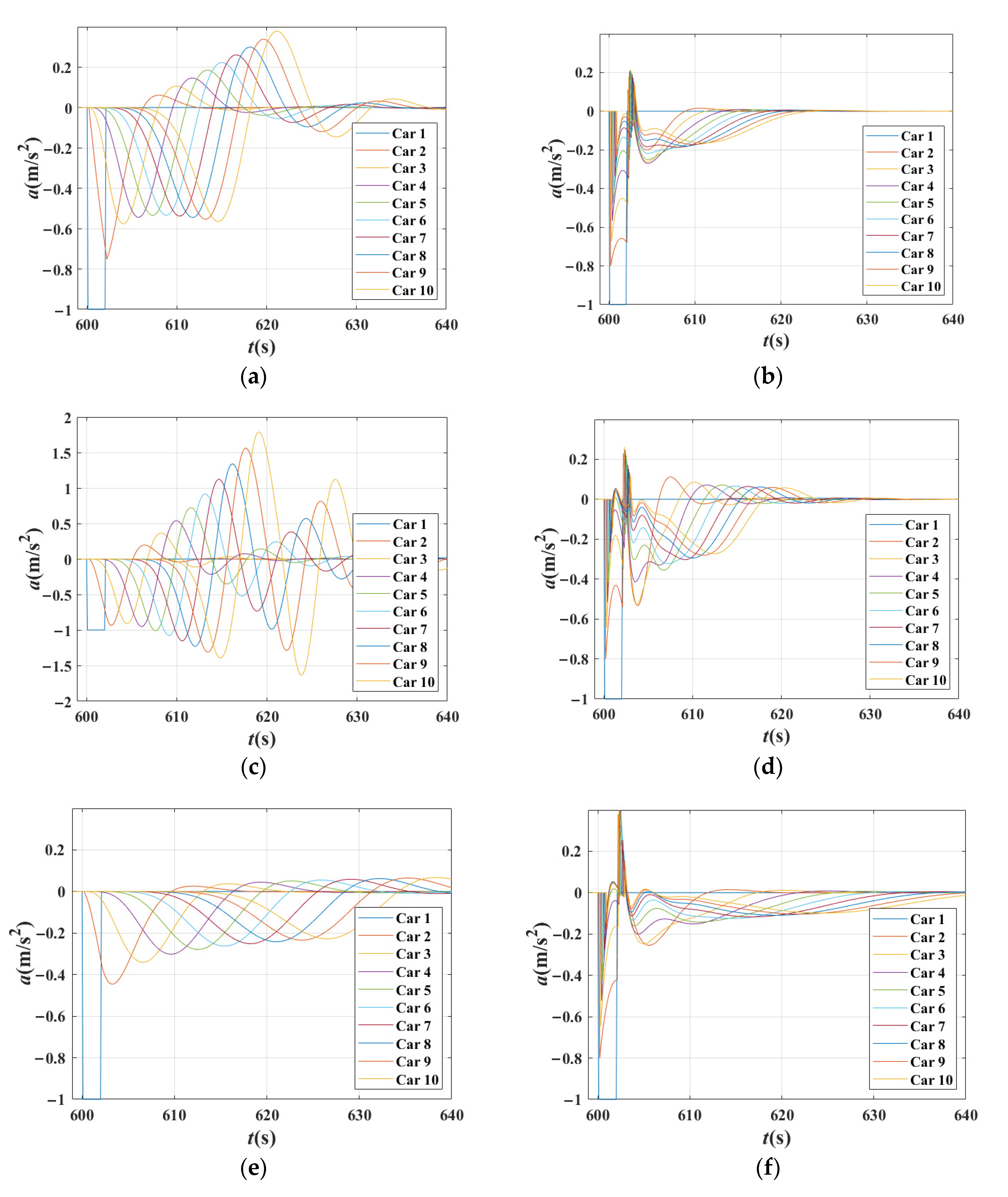
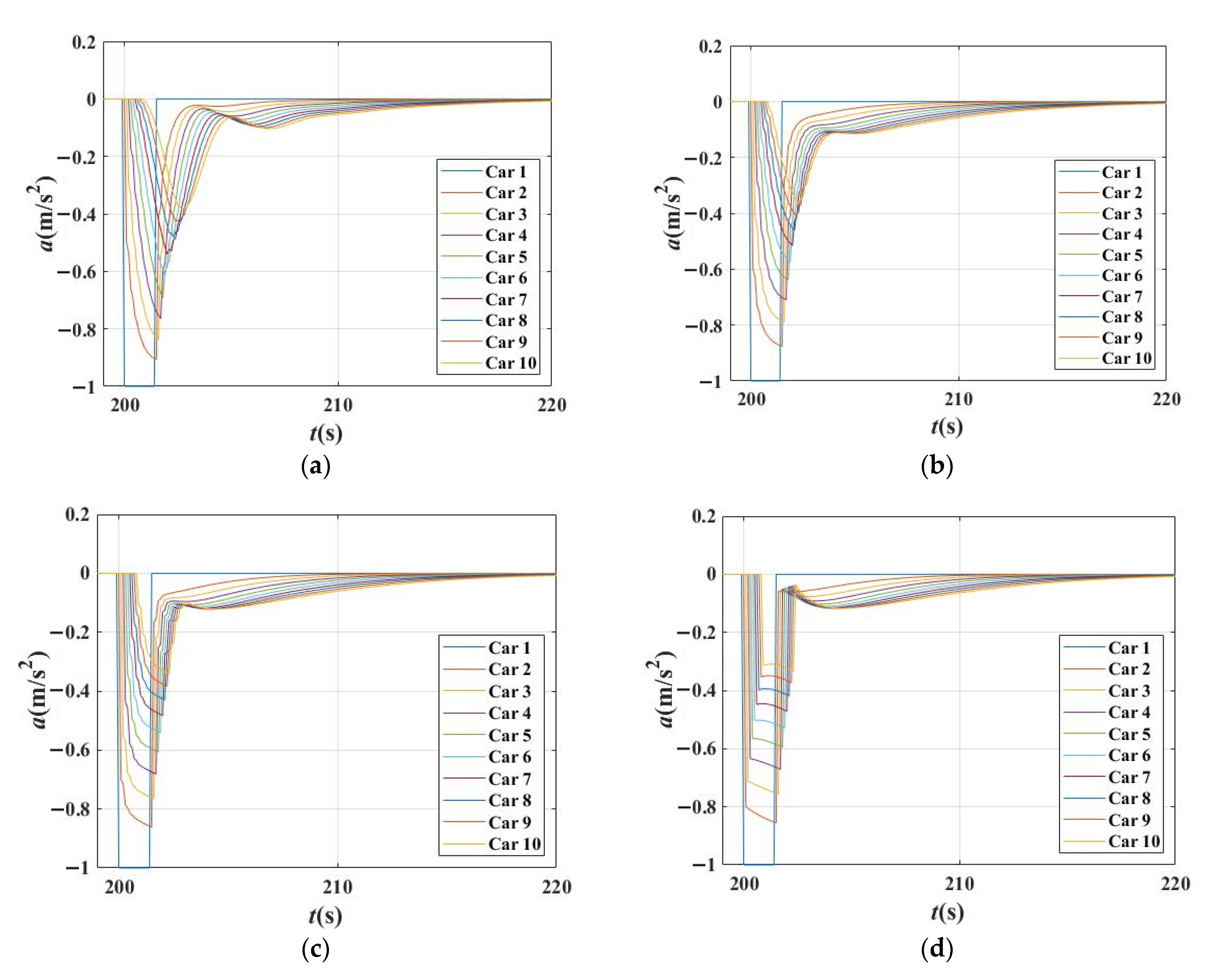
4.2. Sensitivity Analysis of β1 and β2 Based on the BDVIS
4.2.1. The Disturbance Influence Time in Different Combination of β1 and β2
4.2.2. The Characteristics of Acceleration Curves in Different Combinations of β1 and β2
5. Conclusions
- (1)
- The theoretical and simulation results indicated the BDVIS and the DMVIS improve the traffic flow stability. The stability can be further improved by increasing the proportion of the acceleration of the preceding or following vehicles.
- (2)
- If vehicles are on the two sides of the platoon, the BDVIS is better for improving string stability. If vehicles are in the middle section of the platoon and are able to obtain the multiple steps of historical information, DMVIS is a better option.
- (3)
- The preceding and following proportions β1 and β2 have different influences on traffic response properties. The β2 has the benefit of reducing DIT, but the β1 extends DIT.
- (4)
- If traffic is stable, any of the parameters extends the influence time. This reveals that neither β1 or β2 is the biggest and the best for the traffic.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, L.; Jin, P.J.; Huang, H. An anisotropic continuum model considering bi-directional information impact. Transp. Res. Part B Methodol. 2015, 75, 36–57. [Google Scholar] [CrossRef]
- Ghiasi, A.; Li, X.; Ma, J. A mixed traffic speed harmonization model with connected autonomous vehicles. Transp. Res. Part C Emerg. Technol. 2019, 104, 210–233. [Google Scholar] [CrossRef]
- Wang, C.; Gong, S.; Zhou, A.; Li, T.; Peeta, S. Cooperative adaptive cruise control for connected autonomous vehicles by factoring communication-related constraints. Transp. Res. Part C Emerg. Technol. 2019, 38, 242–262. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W. Lattice hydrodynamic modeling with continuous self-delayed traffic flux integral and vehicle overtaking effect. Mod. Phys. Lett. B 2020, 34, 2050071. [Google Scholar] [CrossRef]
- Qi, X.; Cheng, R.; Ge, H. Nonlinear analysis of a new two-lane lattice hydrodynamic model accounting for “backward looking” effect and relative flow information. Mod. Phys. Lett. B 2019, 33, 1950223. [Google Scholar] [CrossRef]
- Jiao, Y.; Ge, H.; Cheng, R. Nonlinear analysis for a modified continuum model considering electronic throttle (ET) and backward looking effect. Phys. A Stat. Mech. Its Appl. 2019, 535, 122362. [Google Scholar] [CrossRef]
- Wang, Z.; Ge, H.; Cheng, R. An extended macro model accounting for the driver’s timid and aggressive attributions and bounded rationality. Phys. A Stat. Mech. Its Appl. 2020, 540, 122988. [Google Scholar] [CrossRef]
- Ngoduy, D.; Jia, D. Multi anticipative bidirectional macroscopic traffic model considering cooperative driving strategy. Transp. B 2017, 5, 100–114. [Google Scholar] [CrossRef]
- Jiang, C.; Cheng, R.; Ge, H. An improved lattice hydrodynamic model considering the “backward looking” effect and the traffic interruption probability. Nonlinear Dyn. 2018, 91, 777–784. [Google Scholar] [CrossRef]
- Tang, T.; Shi, W.; Shang, H.; Wang, Y. A new car-following model with consideration of inter-vehicle communication. Nonlinear Dyn. 2014, 76, 2017–2023. [Google Scholar] [CrossRef]
- Yu, S.; Shi, Z. An improved car-following model considering relative velocity fluctuation. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 319–326. [Google Scholar] [CrossRef]
- Wen-Xing, Z.; Li-Dong, Z. A new car-following model for autonomous vehicles flow with mean expected velocity field. Phys. A Stat. Mech. Its Appl. 2018, 492, 2154–2165. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, X.; Yu, S.; Li, X.; Shi, Z. An improved car-following model with multiple preceding cars’ velocity fluctuation feedback. Phys. A Stat. Mech. Its Appl. 2017, 471, 436–444. [Google Scholar] [CrossRef]
- Zheng, L.; He, Z. Traffic flow cellular automaton model with bi-directional information in an open boundary condition. Transp. Saf. Environ. 2021, 3, 1–9. [Google Scholar] [CrossRef]
- Herman, R.; Montroll, E.W.; Potts, R.B.; Rothery, R.W. Traffic dynamics: Analysis of stability in car following. Oper. Res. 1959, 7, 86–106. [Google Scholar] [CrossRef]
- Nakayama, A.; Sugiyama, Y.; Hasebe, K. Effect of looking at the car that follows in an optimal velocity model of traffic flow. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2002, 65, 016112. [Google Scholar] [CrossRef]
- Hasebe, K.; Nakayama, A.; Sugiyama, Y. Dynamical model of a cooperative driving system for freeway traffic. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2003, 68, 6. [Google Scholar] [CrossRef]
- Ge, H.X.; Zhu, H.B.; Dai, S.Q. Effect of looking backward on traffic flow in a cooperative driving car following model. Eur. Phys. J. B 2006, 54, 503–507. [Google Scholar] [CrossRef]
- Yang, S.; Liu, W.; Sun, D.; Li, C. A new extended multiple car-following model considering the backward-looking effect on traffic flow. J. Comput. Nonlinear Dyn. 2013, 8, 011016. [Google Scholar] [CrossRef]
- Sun, D.H.; Liao, X.Y.; Peng, G.H. Effect of looking backward on traffic flow in an extended multiple car-following model. Phys. A Stat. Mech. Its Appl. 2011, 390, 631–635. [Google Scholar] [CrossRef]
- Hu, Y.; Ma, T.; Chen, J. Multi-anticipative bi-directional visual field traffic flow models in the connected vehicle environment. Phys. A Stat. Mech. Its Appl. 2021, 584, 126372. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, K.; Li, G.; Li, S.; Wang, T. Dynamics of traffic flow affected by the future motion of multiple preceding vehicles under vehicle-connected environment: Modeling and stabilization. Phys. A Stat. Mech. Its Appl. 2021, 565, 125538. [Google Scholar] [CrossRef]
- Jiao, S.; Zhang, S.; Zhou, B.; Zhang, Z.; Xue, L. An extended car-following model considering the drivers’ characteristics under a V2V communication environment. Sustainability 2020, 12, 1552. [Google Scholar] [CrossRef] [Green Version]
- Hou, P.; Yu, H.; Yan, C.; Hong, J. An extended car-following model based on visual angle and backward looking effect. Chin. J. Phys. 2017, 55, 2092–2099. [Google Scholar] [CrossRef]
- Chen, C.; Cheng, R.; Ge, H. An extended car-following model considering driver’s sensory memory and the backward looking effect. Phys. A Stat. Mech. Its Appl. 2019, 525, 278–289. [Google Scholar] [CrossRef]
- Ma, G.; Ma, M.; Liang, S.; Wang, Y.; Zhang, Y. An improved car-following model accounting for the time-delayed velocity difference and backward looking effect. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105221. [Google Scholar] [CrossRef]
- Ma, D.; Han, Y.; Qu, F.; Jin, S. Modeling and analysis of car-following behavior considering backward-looking effect. Chin. Phys. B 2021, 30, 034501. [Google Scholar] [CrossRef]
- Yang, D.; Jin, P.; Pu, Y.; Ran, B. Safe distance car-following model including backward-looking and its stability analysis. Eur. Phys. J. B 2013, 86, 92. [Google Scholar] [CrossRef]
- Barrachina, X.; Conejero, J.A.; Murillo-Arcila, M.; Seoane-Sepúlveda, J.B. Distributional chaos for the Forward and Backward Control traffic model. Linear Algebra Appl. 2015, 479, 202–215. [Google Scholar] [CrossRef]
- Montanino, M.; Punzo, V. On string stability of a mixed and heterogeneous traffic flow: A unifying modelling framework. Transp. Res. Part B Methodol. 2021, 144, 133–154. [Google Scholar] [CrossRef]
- Montanino, M.; Monteil, J.; Punzo, V. From homogeneous to heterogeneous traffic flows: Lp String stability under uncertain model parameters. Transp. Res. Part B Methodol. 2021, 146, 136–154. [Google Scholar] [CrossRef]
- Wang, M.; Daamen, W.; Hoogendoorn, S.P.; Van Arem, B. Cooperative Car-Following Control: Distributed Algorithm and Impact on Moving Jam Features. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1459–1471. [Google Scholar] [CrossRef]
- Yi, Z.; Lu, W.; Xu, L.; Qu, X.; Ran, B. An Intelligent Back-Looking Distance Driver Model and Stability Analysis for Connected and Automated Vehicles. J. Cent. South Univ. 2020, 27, 3499–3512. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Peeta, S.; He, X.; Zheng, T.; Feng, H. An extended microscopic traffic flow model based on the spring-mass system theory. Mod. Phys. Lett. B 2017, 31, 1750090. [Google Scholar] [CrossRef]
- Jin, P.; Yang, D.; Ran, B.; Cebelak, M.; Walton, C. Bidirectional control characteristics of general motors and optimal velocity car-following models. Transp. Res. Rec. 2013, 110–119. [Google Scholar] [CrossRef] [Green Version]
- Du, W.; Li, Y.; Zhang, J. Stability Analysis and Control of an Extended Car-Following Model under Honk Environment. Int. J. Intell. Transp. Syst. Res. 2021, 1–10. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Xu, S.; Qian, Y. Stability analysis of an extended intelligent driver model and its simulations under open boundary condition. Phys. A Stat. Mech. Its Appl. 2015, 419, 526–536. [Google Scholar] [CrossRef]
- Sun, J.; Zheng, Z.; Sun, J. Stability analysis methods and their applicability to car-following models in conventional and connected environments. Transp. Res. Part B Methodol. 2018, 109, 212–237. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kesting, A.; Treiber, M.; Schönhof, M.; Kranke, F.; Helbing, D. Jam-Avoiding Adaptive Cruise Control (ACC) and its Impact on Traffic Dynamics. In Traffic Granul. Flow’05; Springer: Berlin/Heidelberg, Germany, 2007; pp. 633–643. [Google Scholar] [CrossRef] [Green Version]
- Kesting, A.; Treiber, M.; Schönhof, M.; Helbing, D. Adaptive cruise control design for active congestion avoidance. Transp. Res. Part C Emerg. Technol. 2008, 16, 668–683. [Google Scholar] [CrossRef]
- Jiang, R.; Wu, Q.; Zhu, Z. Full velocity difference model for a car-following theory. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2001, 64, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, S.; Liu, Q.; Li, X. Full velocity difference and acceleration model for a car-following theory. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1229–1234. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef] [Green Version]




| Model | Formulation | fs, fv, f∆v | Parameters |
|---|---|---|---|
| IDM [39,40,41] | |||
| FVD [42,43] | |||
| OV [42] | |||
| ACC [44] |
| Experiment | Basic Model | Parameter Settings | Characteristics | ||
|---|---|---|---|---|---|
| T/S/thw | β1 | β2 | |||
| 1 | IDM | T = 1.5 | 0 | 0 | unstable |
| 0.4 | 0 | stable | |||
| T = 0.6 | 0.3 | 0 | unstable | ||
| 0.3 | 0.2 | stable | |||
| FVD | S = 20 | 0.0 | 0 | unstable | |
| 0.8 | 0 | stable | |||
| OV | S = 20 | 0.0 | 0 | unstable | |
| 0.8 | 0 | stable | |||
| ACC | thw = 2.5 | 0.0 | 0 | unstable | |
| 0.8 | 0 | stable | |||
| 2 | IDM | T = 1.5 | 0~0.4 | 0~0.9 | β1 + β2 < 1, β1 > β2 |
| 3 | IDM | T = 1.5 | 0.5 | 0.3 | β1 + β2 = 0.8 |
| 0.6 | 0.2 | ||||
| 0.7 | 0.1 | ||||
| 0.8 | 0 | ||||
| IDM | T = 1.5 | 0.0 | 0 | β2 fixed | |
| 0.3 | 0 | ||||
| 0.6 | 0 | ||||
| 0.9 | 0 | ||||
| IDM | T = 1.5 | 0.5 | 0 | β1 fixed | |
| 0.5 | 0.2 | ||||
| 0.5 | 0.3 | ||||
| 0.5 | 0.4 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, Z.; Lu, W.; Qu, X.; Li, L.; Mao, P.; Ran, B. Controlling the Connected Vehicle with Bi-Directional Information: Improved Car-Following Models and Stability Analysis. Sensors 2021, 21, 8322. https://doi.org/10.3390/s21248322
Yi Z, Lu W, Qu X, Li L, Mao P, Ran B. Controlling the Connected Vehicle with Bi-Directional Information: Improved Car-Following Models and Stability Analysis. Sensors. 2021; 21(24):8322. https://doi.org/10.3390/s21248322
Chicago/Turabian StyleYi, Ziwei, Wenqi Lu, Xu Qu, Linheng Li, Peipei Mao, and Bin Ran. 2021. "Controlling the Connected Vehicle with Bi-Directional Information: Improved Car-Following Models and Stability Analysis" Sensors 21, no. 24: 8322. https://doi.org/10.3390/s21248322
APA StyleYi, Z., Lu, W., Qu, X., Li, L., Mao, P., & Ran, B. (2021). Controlling the Connected Vehicle with Bi-Directional Information: Improved Car-Following Models and Stability Analysis. Sensors, 21(24), 8322. https://doi.org/10.3390/s21248322