Simultaneous Determination of Droplet Size, pH Value and Concentration to Evaluate the Aging Behavior of Metalworking Fluids
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
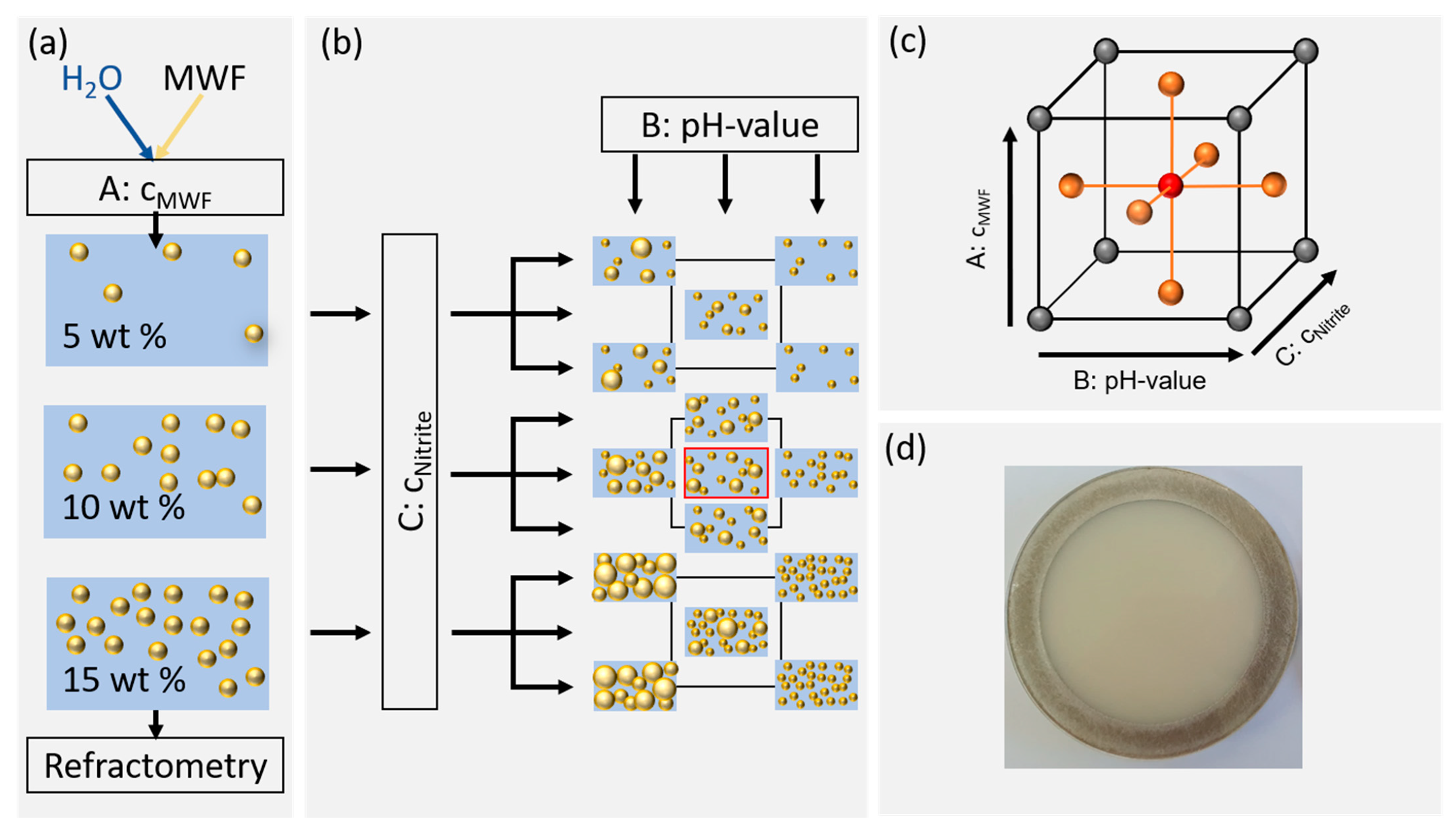
2.2. Sample Preparation
2.3. Response Surface Model
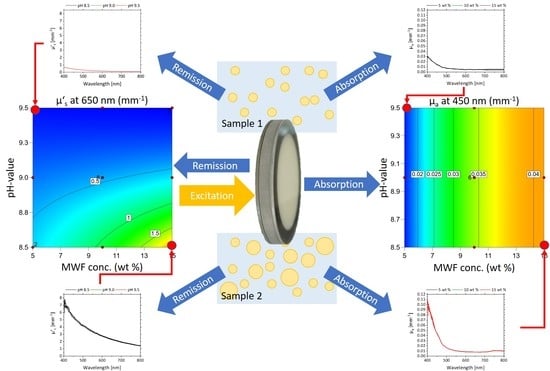
2.4. Determination of the Effective Scattering Coefficient μ’s and the Absorption Coefficient μa
2.5. Dynamic Light Scattering for Hydrodynamic Radius Determination
2.6. Multivariate Data Analysis
3. Results and Discussion
3.1. Response Surface Model
3.2. Multivariate Data Analysis
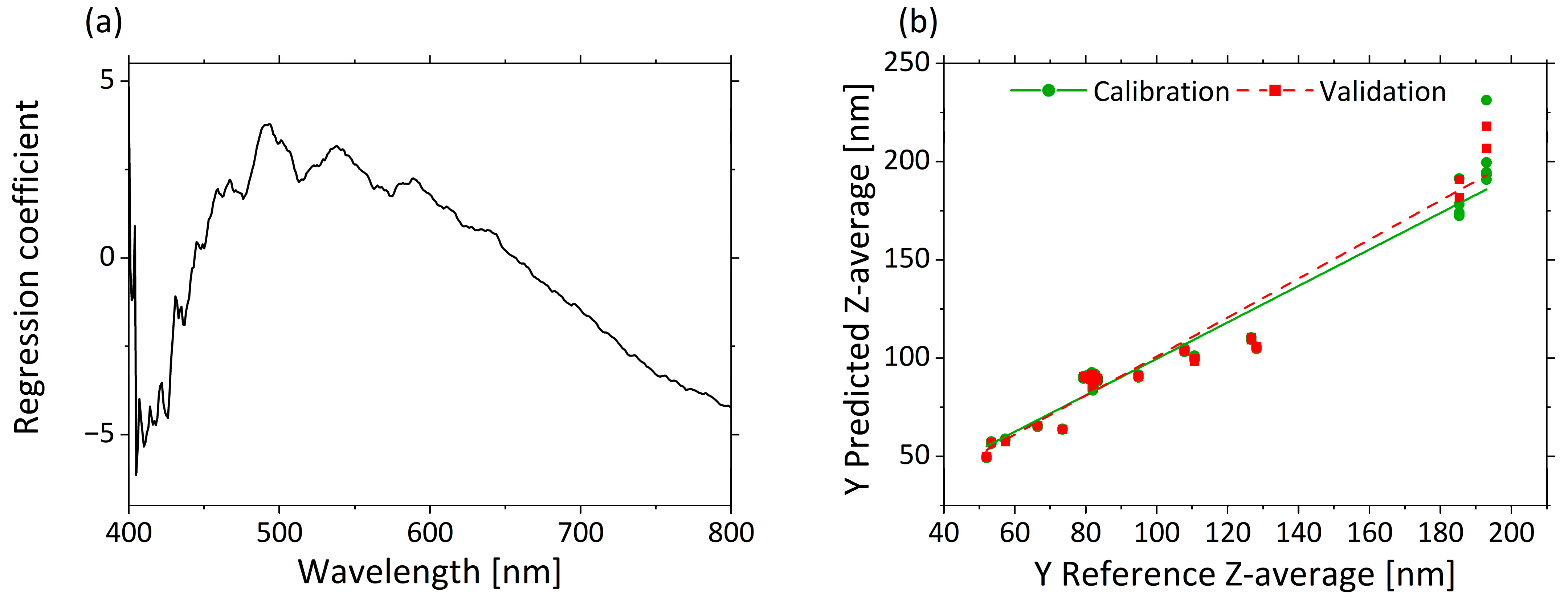
3.2.1. Correlation of µ’s and Z-Average by PLS-R
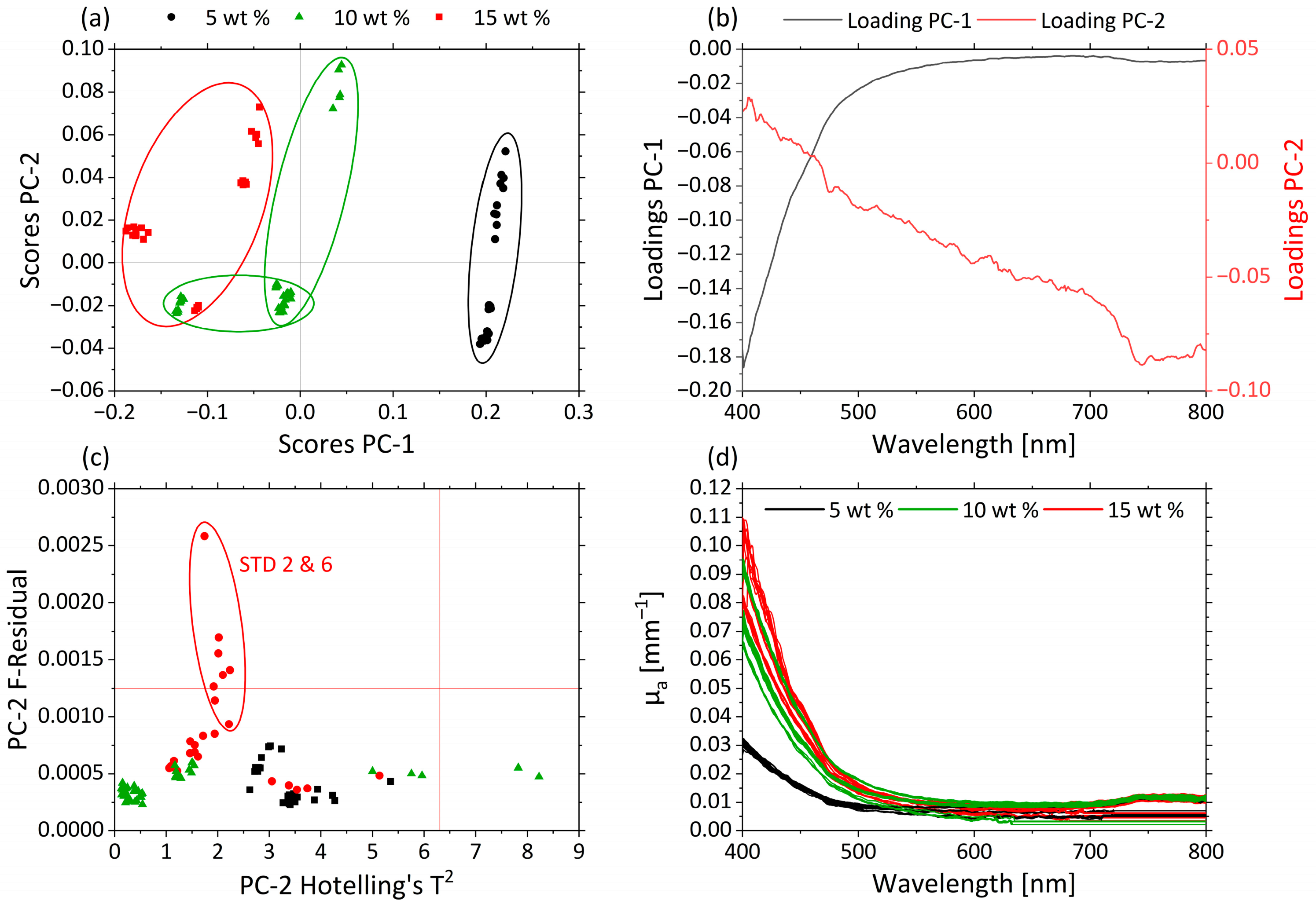
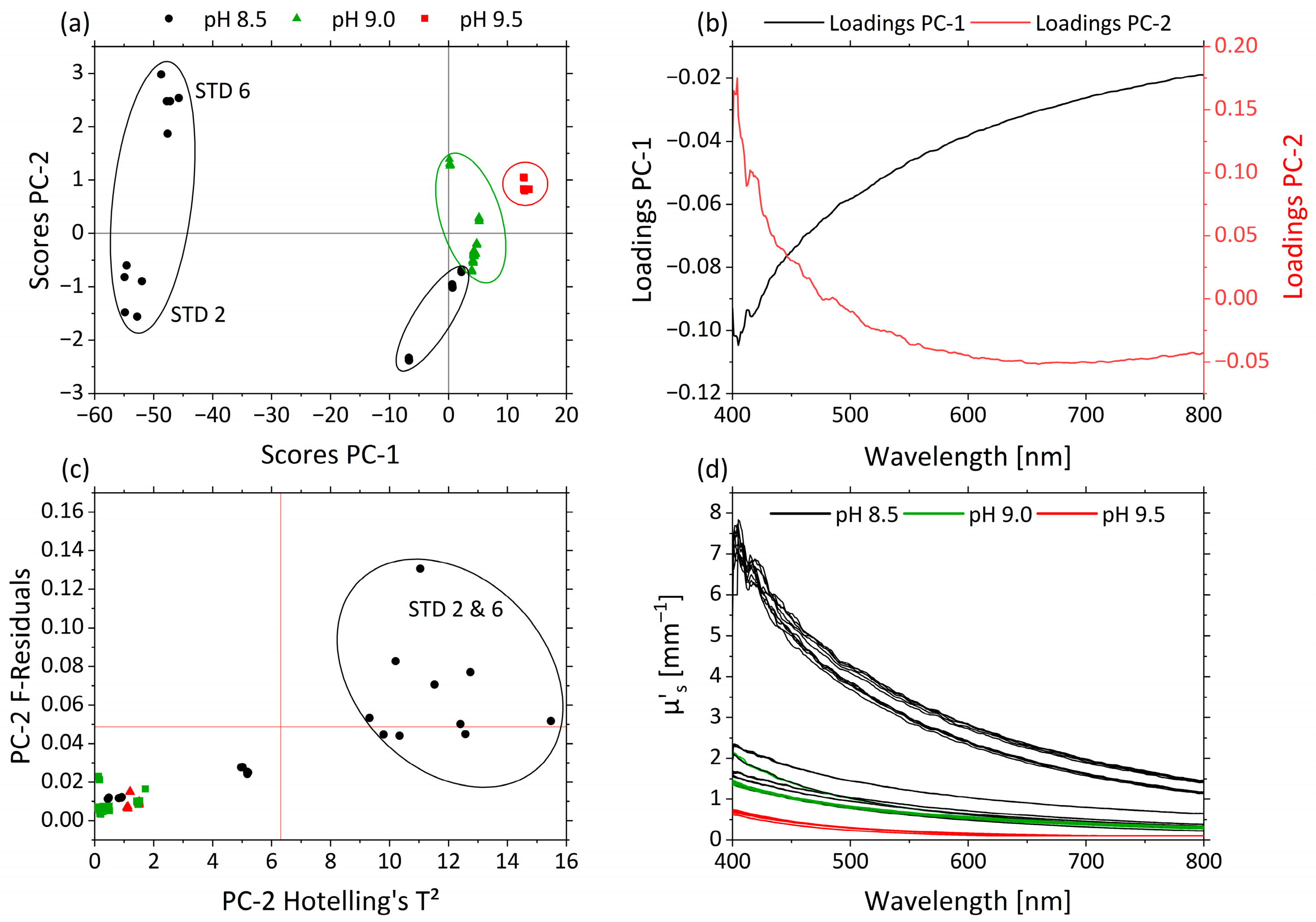
3.2.2. Effects of pH and MWF Concentration on µa- and µ’s-Spectra as Revealed by PCA
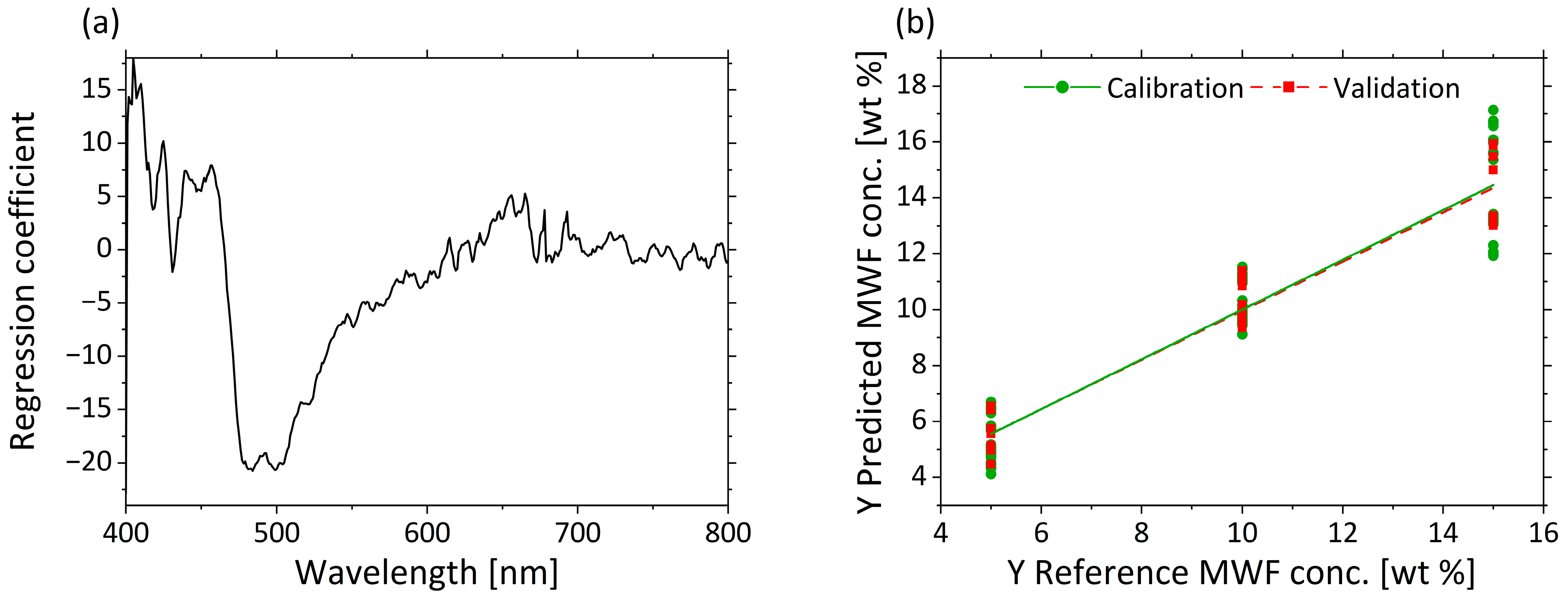
3.2.3. Determination of MWF Concentration Based on µa
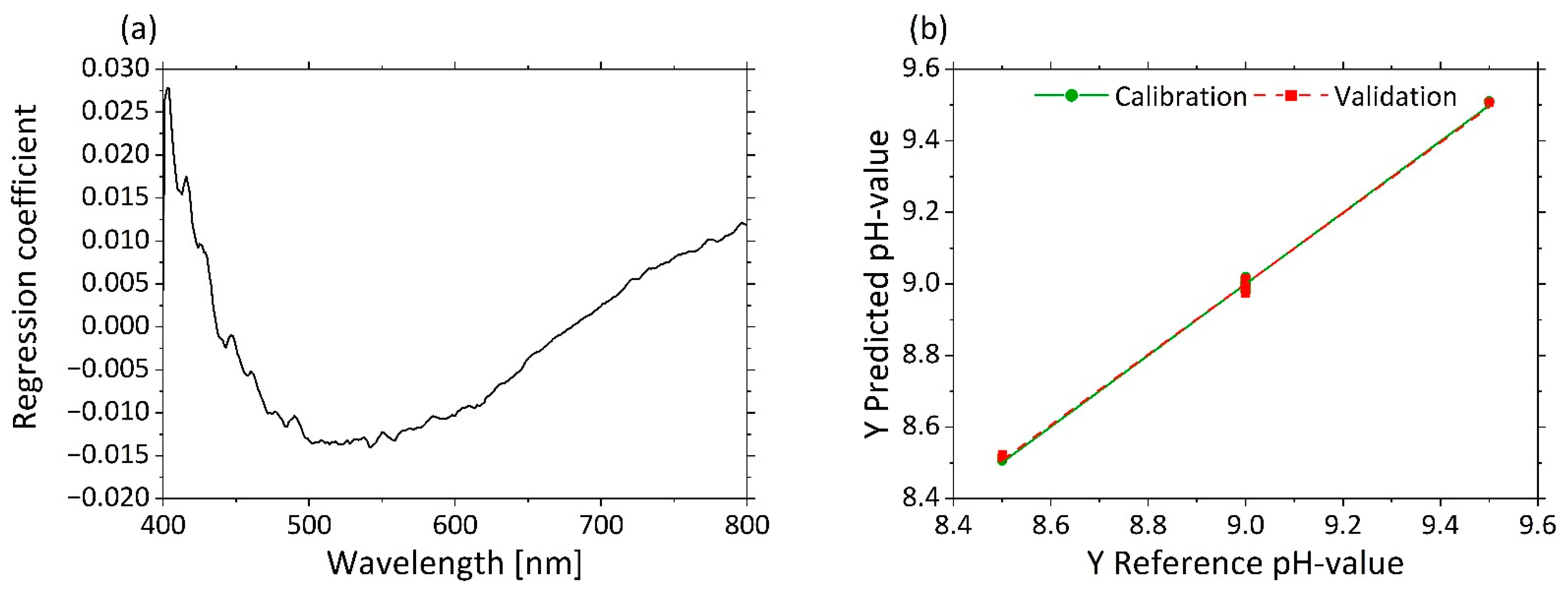
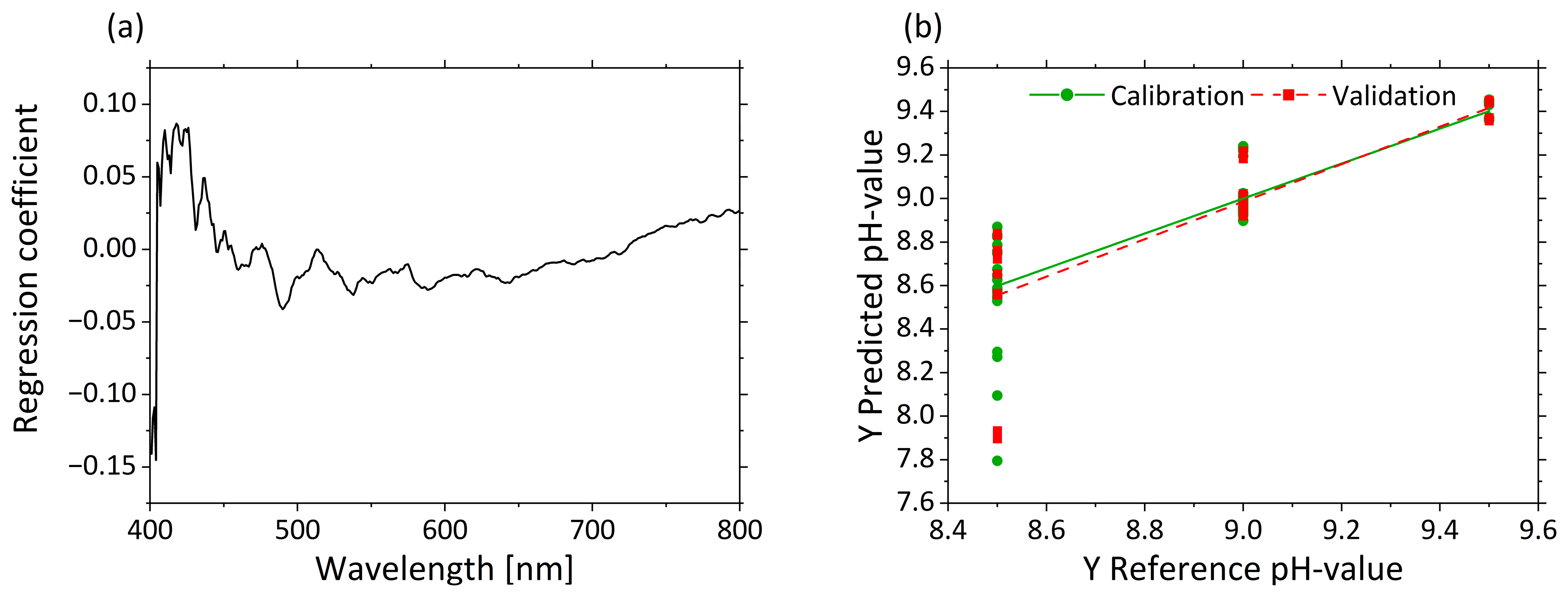
3.2.4. Determination of pH Based on µ’s
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| µ’s | effective scattering coefficient |
| µa | absorption coefficient |
| λ | wavelength |
| ANOVA | analysis of variance |
| CMWF | metalworking fluid concentration |
| CNitrite | nitrite concentration |
| d | diameter |
| DLS | dynamic light scattering |
| FCD | face-centered central composite design |
| i. e. | id est |
| InGaAs | indium gallium arsenide |
| mm | millimeter |
| MWF | metallworking fluids |
| nm | nanometer |
| nMWFconcentrate | refractive index of metalworking fluid concentrate |
| nwater | refractive index of water |
| PC | principal component |
| PCA | principal component analysis |
| PI | prediction interval |
| PLS-R | partial least squares regression |
| QDA | quadratic discriminant analysis |
| R2 | coefficient of determination |
| R²c | coefficient of determination for calibration |
| R²p | coefficient of determination for prediction |
| RMSEC | root mean square error of calibration |
| RMSEP | root mean square error of prediction |
| RSM | response surface model |
| s | second |
| Si | silicium |
| STD | standard order |
| SVD | singular value decomposition |
| Val | validation point |
| wt% | weight percent |
Appendix A. Determination of pH Based on µ’s −10 wt%
References
- Spasiano, D.; Petrella, A.; Lacedra, V. Chemical Destabilization of Fresh and Spent Cutting Oil Emulsions: Differences between an Ecofriendly and Two Commercial Synthetic Lubricants. Sustainability 2020, 12, 5697. [Google Scholar] [CrossRef]
- Sułek, M.W.; Bąk-Sowińska, A.; Przepiórka, J. Ecological Cutting Fluids. Materials 2020, 13, 5812. [Google Scholar] [CrossRef]
- Benedicto, E.; Rubio, E.M.; Carou, D.; Santacruz, C. The Role of Surfactant Structure on the Development of a Sustainable and Effective Cutting Fluid for Machining Titanium Alloys. Metals 2020, 10, 1388. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung e.V. Schmierstoffe Bearbeitungsmedien für die Umformung und Zerspanung von Werkstoffen: Begriffe; Beuth Verlag: Berlin, Germany, 2013. [Google Scholar]
- Herrmann, C.; Madanchi, N.; Winter, M.; Ohlschlager, G.; Greßmann, A.; Zettl, E.; Schwengers, K.; Lange, U. Ökologische und Ökonomische Bewertung des Ressourcenaufwands: Wassermischbare Kühlschmierstoffe. 2017. Available online: https://www.ressource-deutschland.de/fileadmin/user_upload/downloads/studien/Studie_Kuehlschmierstoffe_barrierefrei.pdf (accessed on 21 November 2021).
- Brinksmeier, E.; Meyer, D.; Huesmann-Cordes, A.G.; Herrmann, C. Metalworking fluids—Mechanisms and performance. CIRP Ann. 2015, 64, 605–628. [Google Scholar] [CrossRef] [Green Version]
- Verein Deutscher Ingenieure e.V. Pflege von Kühlschmierstoffen für Spanende und Umformende Fertigungsverfahren: Maßnahmen zur Qualitätserhaltung, Prozessverbesserung, Abfall- und Abwasserverminderung; Beuth Verlag: Berlin, Germany, 2014. [Google Scholar]
- Grossi, M.; Riccò, B. An automatic titration system for oil concentration measurement in metalworking fluids. Measurement 2017, 97, 8–14. [Google Scholar] [CrossRef]
- Kiefer, J.; Seidel, B.; Meyer, D. Optical Spectroscopy for Analysis and Monitoring of Metalworking Fluids. Appl. Spectrosc. 2018, 72, 1790–1797. [Google Scholar] [CrossRef] [PubMed]
- Seidel, B.; Meyer, D. Investigation of the Influence of Aging on the Lubricity of Metalworking Fluids by Means of Design of Experiment. Lubricants 2019, 7, 94. [Google Scholar] [CrossRef] [Green Version]
- Assenhaimer, C.; Domingos, A.S.; Glasse, B.; Fritsching, U.; Guardani, R. Long-term monitoring of metalworking fluid emulsion aging using a spectroscopic sensor. Can. J. Chem. Eng. 2017, 95, 2341–2349. [Google Scholar] [CrossRef]
- Assenhaimer, C.; Machado, L.J.; Glasse, B.; Fritsching, U.; Guardani, R. Use of a spectroscopic sensor to monitor droplet size distribution in emulsions using neural networks. Can. J. Chem. Eng. 2014, 92, 318–323. [Google Scholar] [CrossRef]
- Glasse, B.; Assenhaimer, C.; Guardani, R.; Fritsching, U. Turbidimetry for the stability evaluation of emulsions used in machining industry. Can. J. Chem. Eng. 2014, 92, 324–329. [Google Scholar] [CrossRef]
- Glasse, B.; Fritsching, U.; Koch, T.; de Paiva, J.L.; Guardani, R. Turbidimetric Spectroscopy for the Evaluation of Metalworking Fluids Stability. Tribol. Trans. 2012, 55, 237–244. [Google Scholar] [CrossRef]
- Menniti, A.; Rajagopalan, K.; Kramer, T.A.; Clark, M.M. An evaluation of the colloidal stability of metal working fluid. J. Colloid Interface Sci. 2005, 284, 477–488. [Google Scholar] [CrossRef] [PubMed]
- Deluhery, J.; Rajagopalan, N. A turbidimetric method for the rapid evaluation of MWF emulsion stability. Colloids Surf. A Physicochem. Eng. Asp. 2005, 256, 145–149. [Google Scholar] [CrossRef]
- Matos, M.; Lobo, A.; Benito, J.M.; Coca, J.; Pazos, C. Extending the Useful Life of Metalworking Fluids in a Copper Wire Drawing Industry by Monitoring Their Functional Properties. Tribol. Trans. 2012, 55, 685–692. [Google Scholar] [CrossRef]
- Assenhaimer, C. Evaluation of Emulsion Destabilization by Light Scattering Applied to Metalworking Fluids. Ph.D. Thesis, Universidade de São Paulo, São Paulo, Brazil, 2015. [Google Scholar]
- Ulrich, C.; Dan, L.; Mårtensson, P.; Kluftinger, A.; Gawronski, M.; Björefors, F. Evaluation of industrial cutting fluids using electrochemical impedance spectroscopy and multivariate data analysis. Talanta 2012, 97, 468–472. [Google Scholar] [CrossRef]
- Seidl, R.; Weiss, S.; Kessler, R.W.; Kessler, W.; Zikulnig-Rusch, E.M.; Kandelbauer, A. Prediction of Residual Curing Capacity of Melamine-Formaldehyde Resins at an Early Stage of Synthesis by In-Line FTIR Spectroscopy. Polymers 2021, 13, 2541. [Google Scholar] [CrossRef] [PubMed]
- Englert, T.; Stiedl, J.; Green, S.; Jacob, T.; Chassé, T.; Rebner, K. Quantifying flux residues after soldering on technical copper using ultraviolet visible (UV–Vis) spectroscopy and multivariate analysis. Microelectron. Reliab. 2021, 125, 114367. [Google Scholar] [CrossRef]
- Steinbach, J.C.; Schneider, M.; Hauler, O.; Lorenz, G.; Rebner, K.; Kandelbauer, A. A Process Analytical Concept for In-Line FTIR Monitoring of Polysiloxane Formation. Polymers 2020, 12, 2473. [Google Scholar] [CrossRef] [PubMed]
- Ulitzsch, S.; Bäuerle, T.; Stefanakis, M.; Brecht, M.; Chassé, T.; Lorenz, G.; Kandelbauer, A. Synthesis of an Addition-Crosslinkable, Silicon-Modified Polyolefin via Reactive Extrusion Monitored by In-Line Raman Spectroscopy. Polymers 2021, 13, 1246. [Google Scholar] [CrossRef] [PubMed]
- Foschum, F.; Bergmann, F.; Kienle, A. Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. Part 1: Theory. Appl. Opt. 2020, 59, 3203–3215. [Google Scholar] [CrossRef] [PubMed]
- Grossi, M.; Riccò, B. Oil Concentration Measurement in Metalworking Fluids by Optical Spectroscopy. In Proceedings of the 18th International Trade Dair of Material & Energy Recovery and Sustainable Development, Rimini, Italy, 5–8 November 2014. [Google Scholar]
- Glasse, B.; Assenhaimer, C.; Guardani, R.; Fritsching, U. Analysis of the Stability of Metal Working Fluid Emulsions by Turbidity Spectra. Chem. Eng. Technol. 2013, 36, 1202–1208. [Google Scholar] [CrossRef]
- Bergmann, F.; Foschum, F.; Zuber, R.; Kienle, A. Precise determination of the optical properties of turbid media using an optimized integrating sphere and advanced Monte Carlo simulations. Part 2: Experiments. Appl. Opt. 2020, 59, 3216–3226. [Google Scholar] [CrossRef] [PubMed]
- Benito, J.M.; Cambiella, A.; Lobo, A.; Gutiérrez, G.; Coca, J.; Pazos, C. Formulation, characterization and treatment of metalworking oil-in-water emulsions. Clean Technol. Environ. Policy 2010, 12, 31–41. [Google Scholar] [CrossRef]
- Bundesanstalt für Arbeitsschutz und Arbeitsmedizin. Verwendungsbeschränkungen für Wassermischbare bzw. Wassergemischte Kühlschmierstoffe, bei deren Einsatz N-Nitrosamine Auftreten Können; Beuth Verlag: Berlin, Germany, 2007. [Google Scholar]
- Deutsche Gesetzliche Unfallversicherung. Inhibitoren der Nitrosaminbildung: Wirksamkeitsnachweis, Praktikables Maßnahmenkonzept nach TRGS 611, 2016 (FB HM-045). Available online: https://www.dguv.de/medien/fb-holzundmetall/publikationen-dokumente/infoblaetter/infobl_deutsch/045_inhibitoren_trgs611.pdf (accessed on 3 December 2021).
- Daimon, M.; Masumura, A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. [Google Scholar] [CrossRef]
- Berghof Gigahertz-Optik. Material Determination with Spherespectro 150H: For Scattering Samples. Available online: https://www.gigahertz-optik.com/assets/Uploads/SphereSpectro150H_DINA4_EN_Brochure.pdf (accessed on 21 November 2021).
- Stefanakis, M.; Lorenz, A.; Bartsch, J.W.; Bassler, M.C.; Wagner, A.; Brecht, M.; Pagenstecher, A.; Schittenhelm, J.; Boldrini, B.; Hakelberg, S.; et al. Formalin Fixation as Tissue Preprocessing for Multimodal Optical Spectroscopy Using the Example of Human Brain Tumour Cross Sections: Supplementary Material. J. Spectrosc. 2021, 2021, 5598309. [Google Scholar] [CrossRef]
- Bassler, M.C.; Stefanakis, M.; Sequeira, I.; Ostertag, E.; Wagner, A.; Bartsch, J.W.; Roeßler, M.; Mandic, R.; Reddmann, E.F.; Lorenz, A.; et al. Comparison of Whiskbroom and Pushbroom darkfield elastic light scattering spectroscopic imaging for head and neck cancer identification in a mouse model. Anal. Bioanal. Chem. 2021, 2021, 7363–7383. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; ISBN 978-1118-14692-7. [Google Scholar]
- Ulitzsch, S.; Bäuerle, T.; Chassé, T.; Lorenz, G.; Kandelbauer, A. Optimizing the Process Efficiency of Reactive Extrusion in the Synthesis of Vinyltrimethoxysilane-Grafted Ethylene-Octene-Copolymer (EOC-g-VTMS) by Response Surface Methodology. Polymers 2020, 12, 2798. [Google Scholar] [CrossRef] [PubMed]
- Rabenstein, A.; Koch, T.; Remesch, M.; Brinksmeier, E.; Kuever, J. Microbial degradation of water miscible metal working fluids. Int. Biodeterior. Biodegrad. 2009, 63, 1023–1029. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung e.V. Prüfung von Metallbearbeitungsflüssigkeiten—Bestimmung des pH-Wertes von Wassergemischten Metallbearbeitungsflüssigkeiten; Beuth Verlag: Berlin, Germany, 2013. [Google Scholar]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley: New York, NY, USA, 1998; ISBN 0-471-29340-7. [Google Scholar]
- Petty, G.W. A First Course in Atmospheric Radiation, 2nd ed.; Sundog Publications: Madison, WI, USA, 2006; ISBN 978-0-9729033-1-8. [Google Scholar]


| Factor | Name | Unit | −1 | 0 | +1 |
|---|---|---|---|---|---|
| A | MWF concentration | % | 5 | 10 | 15 |
| B | pH | pH | 8.5 | 9.0 | 9.5 |
| C | Nitrite concentration | mg∙L−1 | 0 | 50 | 100 |
| Factor Level Settings | Response Values | |||||
|---|---|---|---|---|---|---|
| STD | Run | A | B | C | ||
| CMWF | pH Value | CNitrite | µ’s | Z-Average | ||
| /wt% | /mg∙L−1 | /mm−1 | /nm | |||
| 1 | 14 | 5 | 8.5 | 0 | 0.538 | 128.1 |
| 2 | 15 | 15 | 8.5 | 0 | 2.303 | 193.0 |
| 3 | 20 | 5 | 9.5 | 0 | 0.129 | 66.4 |
| 4 | 10 | 15 | 9.5 | 0 | 0.112 | 53.3 |
| 5 | 9 | 5 | 8.5 | 100 | 0.606 | 126.6 |
| 6 | 13 | 15 | 8.5 | 100 | 1.932 | 185.3 |
| 7 | 8 | 5 | 9.5 | 100 | 0.124 | 73.5 |
| 8 | 3 | 15 | 9.5 | 100 | 0.116 | 57.3 |
| 9 | 1 | 5 | 9 | 50 | 0.393 | 107.8 |
| 10 | 17 | 15 | 9 | 50 | 0.504 | 82.0 |
| 11 | 7 | 10 | 8.5 | 50 | 0.910 | 110.7 |
| 12 | 2 | 10 | 9.5 | 50 | 0.100 | 52.0 |
| 13 | 11 | 10 | 9 | 0 | 0.451 | 79.3 |
| 14 | 6 | 10 | 9 | 100 | 0.434 | 81.8 |
| 15 | 16 | 10 | 9 | 50 | 0.472 | 83.3 |
| 16 | 19 | 10 | 9 | 50 | 0.458 | 82.7 |
| 17 | 4 | 10 | 9 | 50 | 0.489 | 81.9 |
| 18 | 5 | 10 | 9 | 50 | 0.460 | 80.6 |
| 19 | 18 | 10 | 9 | 50 | 0.462 | 81.4 |
| 20 | 12 | 10 | 9 | 50 | 0.472 | 94.9 |
| Val1 | 21 | 11.2 | 8.8 | 0 | 0.757 | 85.2 |
| Val2 | 22 | 13.8 | 8.7 | 0 | 1.040 | 118.4 |
| µ‘s | Z-Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
| Model | 2.70 | 4 | 0.6749 | 390.28 | <0.0001 | Model | 0.43 | 4 | 0.1087 | 80.84 | <0.0001 |
| A-cMWF | 0.13 | 1 | 0.13 | 76.54 | <0.0001 | A-cMWF | 0.00 | 1 | 0.00 | 0.03 | 0.8578 |
| B-pH | 2.31 | 1 | 2.31 | 1335.02 | <0.0001 | B-pH | 0.37 | 1 | 0.37 | 273.73 | <0.0001 |
| AB | 0.19 | 1 | 0.19 | 109.32 | <0.0001 | AB | 0.04 | 1 | 0.04 | 27.76 | <0.0001 |
| B² | 0.07 | 1 | 0.07 | 40.24 | <0.0001 | A² | 0.03 | 1 | 0.03 | 21.84 | 0.0003 |
| Residual | 0.03 | 15 | 0.0017 | - | - | Residual | 0.02 | 15 | 0.0013 | - | - |
| Lack of fit | 0.02 | 4 | 0.0050 | 8.93 | 0.002 | Lack of fit | 0.01 | 4 | 0.0036 | 7.03 | 0.005 |
| Pure error | 0.01 | 11 | 0.0006 | - | - | Pure error | 0.01 | 11 | 0.0005 | - | - |
| Cor total | 2.73 | 19 | - | - | - | Cor total | 0.4549 | 19 | - | - | - |
| STD | µ’s | Z-Average | |
|---|---|---|---|
| Val1 | Predicted Value (±95%PI) | 0.762 (0.601–0.995) | 100.3 (82.7–120.9) |
| Actual Value | 0.757 | 85.2 | |
| Residual | −0.005 | −15.1 | |
| Val2 | Predicted Value (±95%PI) | 1.176 (0.919–1.491) | 134.8 (110.4–163.5) |
| Actual Value | 1.040 | 118.4 | |
| Residual | −0.136 | −16.4 |
| Actual | 8.5 | 9.0 | 9.5 | |
|---|---|---|---|---|
| Predicted | ||||
| 8.5 | 24 | 0 | 0 | |
| 9.0 | 1 | 50 | 0 | |
| 9.5 | 0 | 0 | 25 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wahrendorff, P.; Stefanakis, M.; Steinbach, J.C.; Allnoch, D.; Zuber, R.; Kapfhammer, R.; Brecht, M.; Kandelbauer, A.; Rebner, K. Simultaneous Determination of Droplet Size, pH Value and Concentration to Evaluate the Aging Behavior of Metalworking Fluids. Sensors 2021, 21, 8299. https://doi.org/10.3390/s21248299
Wahrendorff P, Stefanakis M, Steinbach JC, Allnoch D, Zuber R, Kapfhammer R, Brecht M, Kandelbauer A, Rebner K. Simultaneous Determination of Droplet Size, pH Value and Concentration to Evaluate the Aging Behavior of Metalworking Fluids. Sensors. 2021; 21(24):8299. https://doi.org/10.3390/s21248299
Chicago/Turabian StyleWahrendorff, Patrick, Mona Stefanakis, Julia C. Steinbach, Dominik Allnoch, Ralf Zuber, Ralf Kapfhammer, Marc Brecht, Andreas Kandelbauer, and Karsten Rebner. 2021. "Simultaneous Determination of Droplet Size, pH Value and Concentration to Evaluate the Aging Behavior of Metalworking Fluids" Sensors 21, no. 24: 8299. https://doi.org/10.3390/s21248299
APA StyleWahrendorff, P., Stefanakis, M., Steinbach, J. C., Allnoch, D., Zuber, R., Kapfhammer, R., Brecht, M., Kandelbauer, A., & Rebner, K. (2021). Simultaneous Determination of Droplet Size, pH Value and Concentration to Evaluate the Aging Behavior of Metalworking Fluids. Sensors, 21(24), 8299. https://doi.org/10.3390/s21248299