1. Introduction
The development of underwater robotics and environmental monitoring systems has created the need to provide wireless communication in the water. In addition, there are the needs of the military and state services, e.g., in the field of minefield control or surveillance systems in strategic areas, such as ports [
1]. Despite significant progress in the development of telecommunications systems, wireless communication in the aquatic environment still causes many problems. In such an environment, acoustic waves propagate the best, so it is primarily used as a transmission medium. Unfortunately, the propagation of a sound wave in water is accompanied by many unfavorable phenomena that affect the overall quality of transmission expressed by the range of data transmission, bit error rate or bit rate. Among these phenomena, the most important are the multipath propagation leading to intersymbol interference and the Doppler effect which, due to the relatively low speed of sound propagation in the water environment, is hundreds of thousands of times stronger than that it is in the case of radio communication [
2]. Besides, serious difficulties exist in obtaining relatively fast (about kilobits) and reliable (BER about 10
−3) transmission are caused by waters with intensive hydrotechnical infrastructure, such as ports [
3]. Communication under NLOS conditions is a special case. Ensuring such communication is necessary, for example, when exploring wrecks. Often, such exploration is performed by a diver or with the use of an underwater vehicle does not allow the use of cables due to the need to enter into the wreckage and the high risk of entanglement or deadlock of the transmitting cables. In this case, the complex layout of the corridors in the wreckage requires wireless communication. Such communication must be ensured with a relatively low bit error rate of 10
−2–10
−3 and a relatively high bit rate, in the range of kilobits, which would allow, for example, with the use of appropriate vocoders, for voice communication with the diver. Unfortunately, currently proposed commercial solutions do not allow communication under NLOS conditions with such parameters. Therefore, this work is aimed at developing a method of wireless underwater communication under NLOS conditions.
Generally, there are three methods of wireless transmission in water, described in the literature. Radio frequency (RF) transmission is possible at very short distances in sensor networks [
4]. Optical communication, of great interest in recent years [
5,
6], is also feasible as a technique that promises high throughputs over long distances. However, at present most research is still carried out under line-of-sight (LOS) laboratory conditions. The authors of this publication found one article discussing wireless optical communication in water under NLOS conditions [
7]. However, the tests in [
7] were carried out only in laboratory conditions, in which the distance between the receiver and the transmitter was only 90 cm. The third method is acoustic underwater communication, which has a long history [
8]. The physical phenomena associated with it are well known, what allows for the creation of simulators of hydroacoustic channels based on measurements carried out in various reservoirs and with various measurement methods [
9]. Despite the extensive knowledge about the phenomena occurring during the propagation of acoustic waves in water [
2,
10,
11,
12], this environment is still a challenge in the field of designing underwater wireless communication systems. This is mainly due to the high variability of the propagation environment over time, especially in shallow waters [
13], hence the great interest of reliable and efficient methods of wireless acoustic communication underwater. In the literature, the wireless underwater acoustic communication systems using linear frequency modulation [
14], BPSK, QPSK and 4-QAM modulations [
15,
16,
17], as well as proposals for the use of the OFDM technique [
18,
19] can be found. However, the authors of those system worked under LOS conditions and did not checked the performance of their systems under NLOS conditions.
The further structure of this paper is as follows: the second chapter presents the method of data transmission developed by us, the third chapter describes the channel model, chapter four describes the test stand and presents the results of tests carried out in simulations and laboratory conditions, and chapter five contains conclusions from the research and proposes further research towards the development of the underwater acoustic communication system.
2. Proposed Method of Data Transmission
The data transmission set used in this work consists of two parts, transmitting and receiving. It operates in the single input multiple output (SIMO) mode, i.e., the transmitter uses a single transmitting hydrophone as a projector, and the receiver has a set of three receiving hydrophones in fixed spatial configuration. The basic parameters of the data transmission system are as follows:
—the number of symbol in a frame.
—the number of bits in one symbol.
—the lower frequency of the bandwidth (in Hz).
—the frequency resolution of the spectrum in the transmitter (in Hz).
—the frequency interval between bits (in Hz).
—the desired frequency resolution at the receiver (in Hz).
—the guard interval (in sec).
—the preamble carrier frequency.
—the preamble sequence length.
—the preamble modulation rate.
These parameters defining the communication conditions, are set prior to transmission. They are available to both the transmitter and the receiver. In addition, their change allows the system to be adapted to the need of the use and the conditions of the sound wave propagation in water.
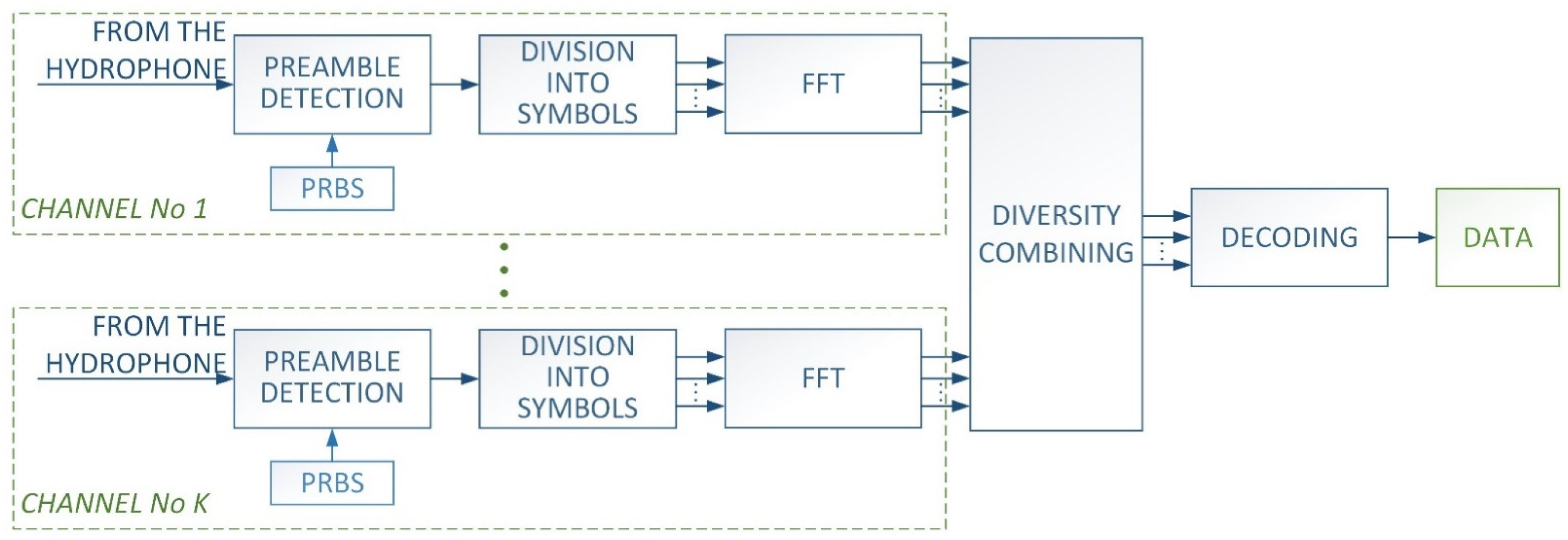
The transmitter works in accordance with the block diagram shown in
Figure 1.
The binary data is divided into individual symbols depending on the number of symbols in the frame and the number of bits transmitted in one symbol. After being divided into symbols, each symbol is mapped to the frequencies. Before the mapping begins, a frequency grid is generated based on the configuration data, i.e., the lower frequency of the bandwidth, the frequency resolution of the spectrum at the transmitter, the number of bits transmitted in the symbol, and the frequency interval between bits. In this work, the MFSK modulation in which each bit is mapped to two frequencies was used. In the used MFSK modulation technique a detection threshold at the receiver is not required, moreover the transmitted signal power does not depend on the symbol form. For a pair of frequencies assigned to a bit, the signal is emitted on one of them, depending on the value of the bit. Forcing the emission is carried out by entering the value 1 or 0 on the appropriate spectrum component occupied by a given bit. This produces a vector that maps data to frequencies. In the next step, an inverse fast Fourier transform (IFFT) is performed on the vectors previously formed for each symbol, with a random phase assumed for each spectral component. The phase randomization aims to evenly distribute the instantaneous values of signal in the time domain and simultaneous reducing the probability of periodic signal amplification. The next step is forming the output signal, which consists in the appropriate time setting of the individual symbols in relation to each other, as well as adding the so-called preamble. The preamble is generated based on a known pseudo-random binary sequence (PRBS) of a predetermined length that modulates the phase of a sinusoidal signal with the predetermined carrier frequency. The final form of the signal is shown in
Figure 2.
After the preamble, and between the individual symbols, a defined waiting time is used to enable the just-transmitted signal to fade out in the propagation environment. This is to prevent any interference between the individual symbols. The presence of the previous signal in the propagation environment during the transmission of the next one may lead to inter-symbol interference and ultimately errors in reception. In the presented case it was assumed that the guard interval is longer than the channel memory time.
In the receiver, the process is opposite of that in the transmitter.
Figure 3 shows the block diagram of the receiver. After recording the signal, an attempt is made to detect the preamble.
It consists in correlating the signal transferred to the baseband with the known PRBS, what can be written in the form [
3]:
where:
where:
—received signal,
—represents a pseudo-random sequence,
—carrier frequency,
—discreet time (sample).
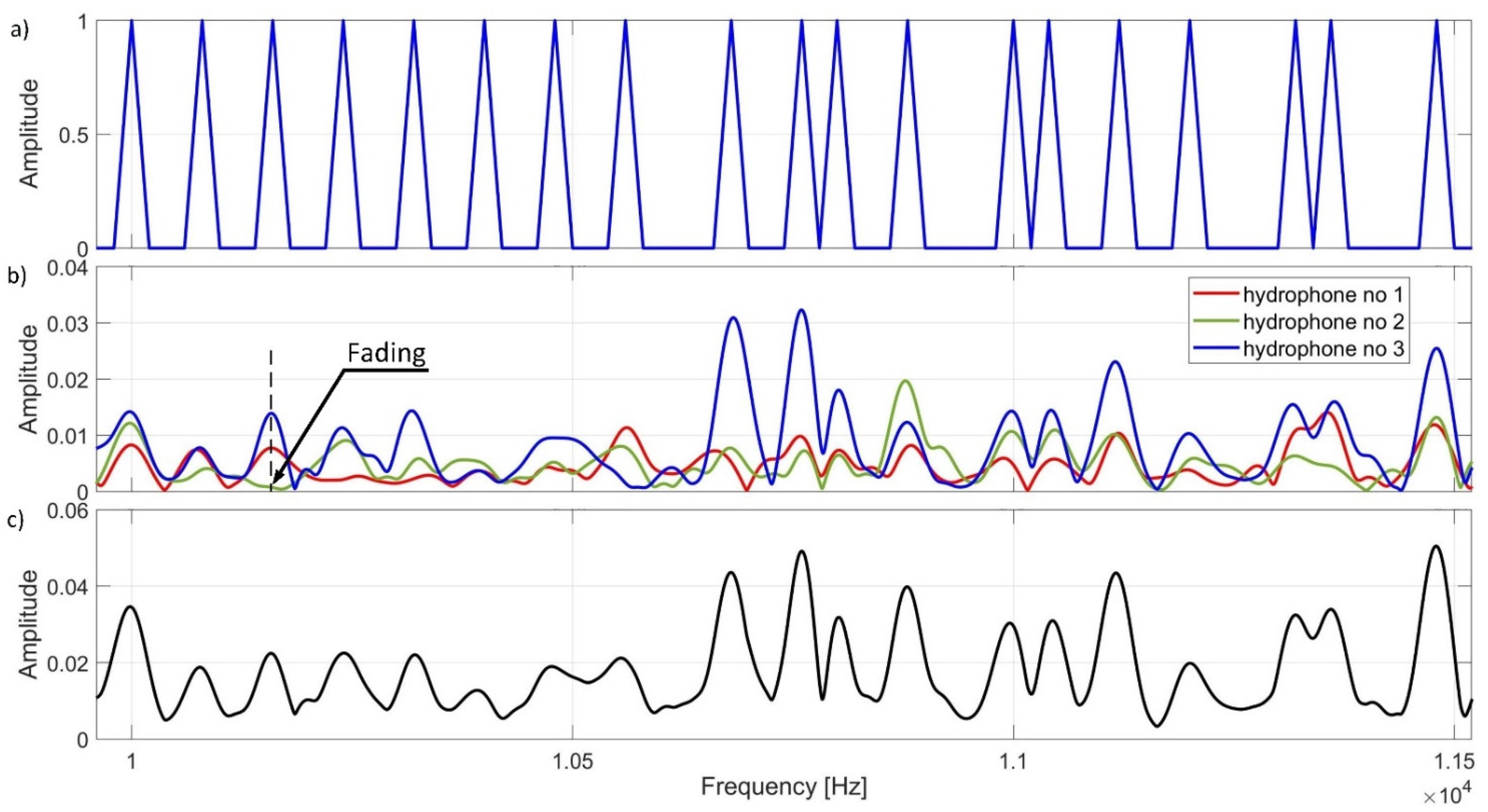
Next, a decision is made as to whether or not there is a preamble, based on the maximum value of the correlation and the mean values in its surroundings. If this process fails, the recorded fragment is discarded, the next fragment is registered, and the preamble detection procedure is repeated. After detecting the preamble, the reception is carried out. Based on the information about the preamble time position in the recorded signal, the signal is split into time slices according to the configuration data. Each of the time fragments is transformed into the frequency domain. Prior to performing the Fourier transform, the time signal is zero-padded to obtain the desired frequency resolution at the receiver, and additionally it is windowed using a Hann’s window to minimize leakage. In the next step, diversity combining takes place. It consists of summing the spectra corresponding to the individual symbols obtained from the receiving paths. The summing is performed with the same weights after normalizing the spectra to the value 1 in the band in which the data transmission takes place. This is to prevent one of the receivers from unduly influencing the final result, which may be caused by, e.g., higher receiver sensitivity or higher gain in the receiving path. The use of the diversity combining technique is primarily to counteract the occurrence of selective fading. The fading, caused by multipath propagation, may lead to a situation in which it will not be possible to receive data on a given frequency. This would cause an increase in the bit error rate (BER). Depending on the phase difference of the incoming signals, the met signal may be amplified, completely suppressed or an intermediate situation may occur. When the path distance difference
is equal to an odd multiple of the wavelength
, there is complete suppression, which can be written as [
20]:
Knowing that:
where:
—speed of the wave in propagation environment,
—frequency of the wave, can be written as:
The frequency at which the fading occurs repeats with a period equal to .
As described in [
21], the second advantage of using diversity combining in the presented method, consisting of summing the spectra from individual reception paths, is the reduction of the variance of the components of the resultant amplitude spectrum derived from noise. After the diversity combining, the spectra obtained for individual symbols are decoded. The decoding consists of making a decision about the value of the transmitted bit on the basis of examining the dependence of the amplitude values between the spectrum components on which the bit is emitted, to investigate whether, for a given pair of frequencies at which a single bit is transmitted, which frequency component (lower or higher) has the greater amplitude. Depending on that, the value of 0 or 1 is assumed as the transmitted data. No single components are examined, but those components coming from the surrounding frequency at which transmission of a given bit are expected.
3. Model of the Multipath Channel
Let the discrete hydroacoustic signal
and the channel impulse response (CIR)
of the multipath channel in the SISO (single input single output) system be given. Assuming that the channel is stationary in the considered time interval, the received signal can be expressed as a sum of
multipath components of a certain amplitude
reaching the receiver with a certain delay
in the presence of noise
, i.e., in the form:
where:
—a discrete time (sample).
The impulse response characterizes the propagation conditions of the acoustic wave along the path between the transmitter and receiver, including multipath conditions. The form of this response will depend on the mutual spatial position of the transmitter and receiver in the water area. Accordingly, the received signal may be represented as a convolution of the transmitted signal, with the impulse response of the channel in the presence of noise
[
22]:
In the case of a SIMO (single input multiply output) system, i.e., with one transmitter and
receivers, the relationship between the output and input signals can be expressed as a matrix equation [
20]:
where: vector
having a dimension of (
) contains instantaneous values of signals received at time
by individual hydrophones, vector
having a dimension of (
) represents instantaneous noise values at time
in each receiving channel, vector
having a dimension of (
) describes the propagation conditions of the hydroacoustic channel, where the elements
of this vector represent the impulse response of the hydroacoustic channel between the transmitting hydrophone and the
-th receiving hydrophone.
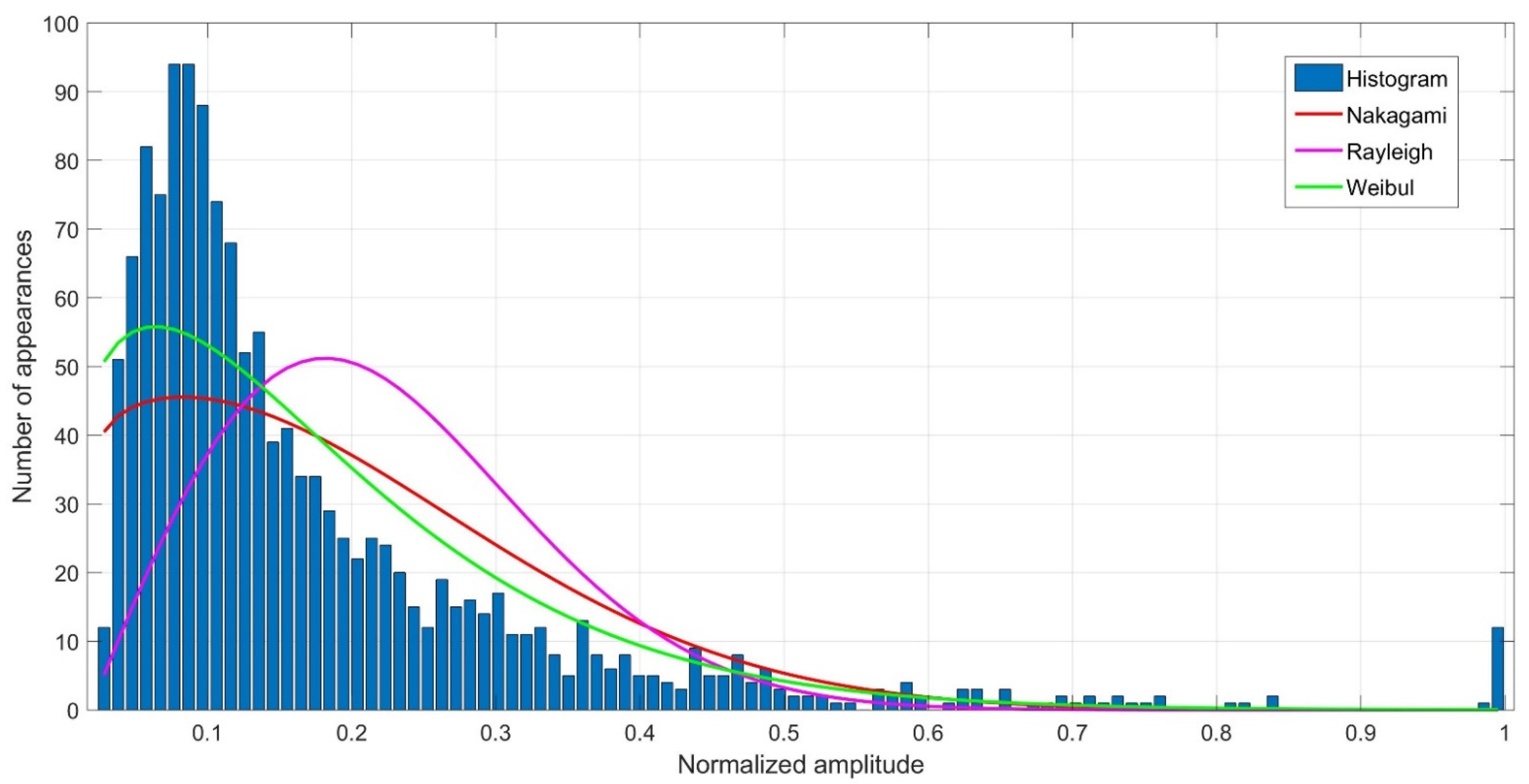
In wireless communication systems distributions such as Rayleigh, Weibull, Nakagami are commonly used to model propagation conditions.
In the matrix model given by (8), a vector
was introduced, representing the noise recorded in each receiver. Most often it is assumed that the noise has a Gaussian distribution, where the real part and the imaginary part of the noise
are independent random variables with zero mean value and variance
[
20]:
The power of such defined noise in each receiver will be the same, i.e., .
The above analysis concerned the time domain. In the proposed method of diversity combining, the signal spectra from individual hydrophones are summed up. Then the variance
of the noise observed in the spectrum of the diversity combined signal decreases according to the equation [
21]:
where:
—the number of spectrum components,
—the number of spectra used to derive the mean value of the spectrum.
4. Description of the Laboratory Stand
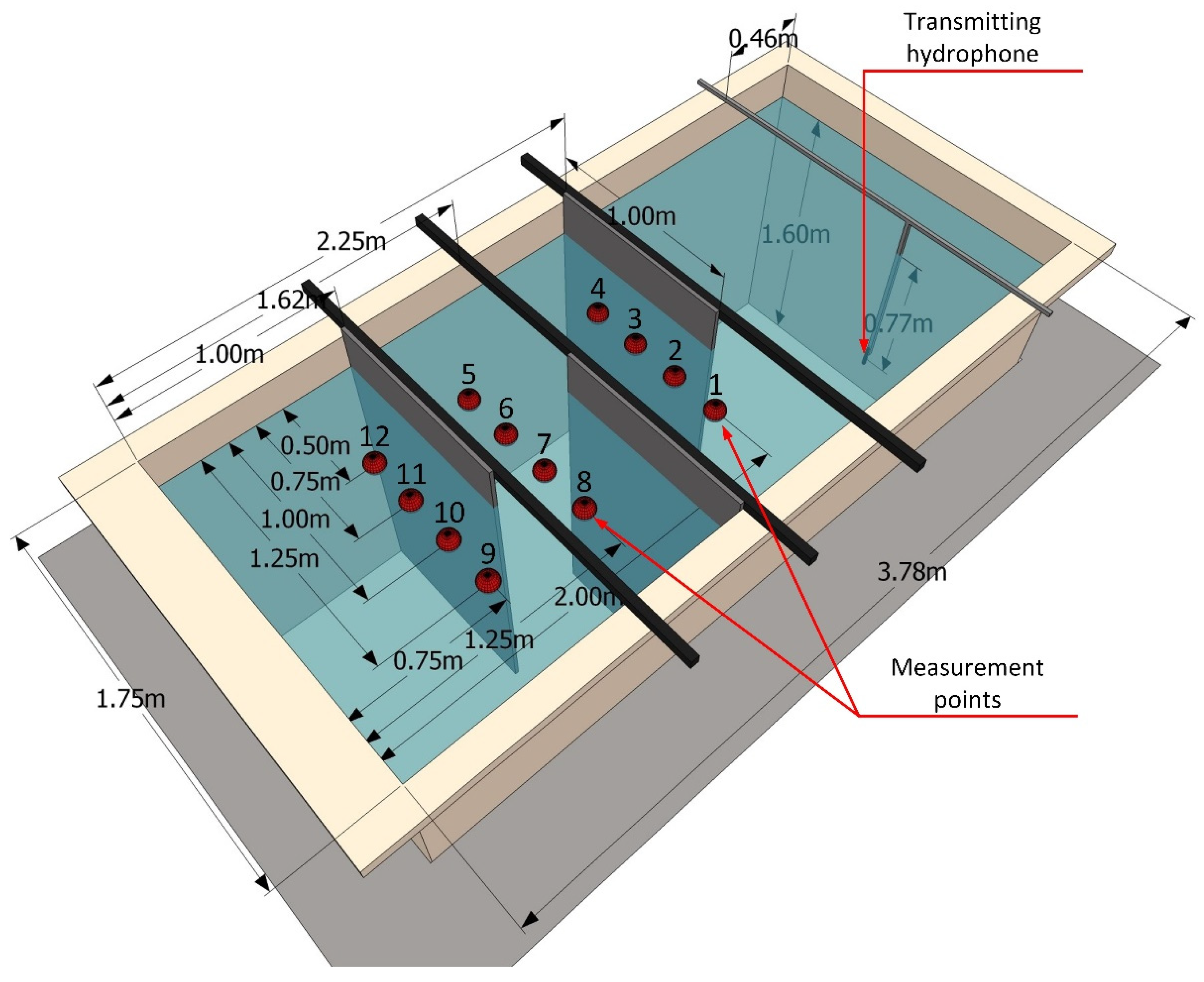
The tests were carried out in a laboratory tank shown in
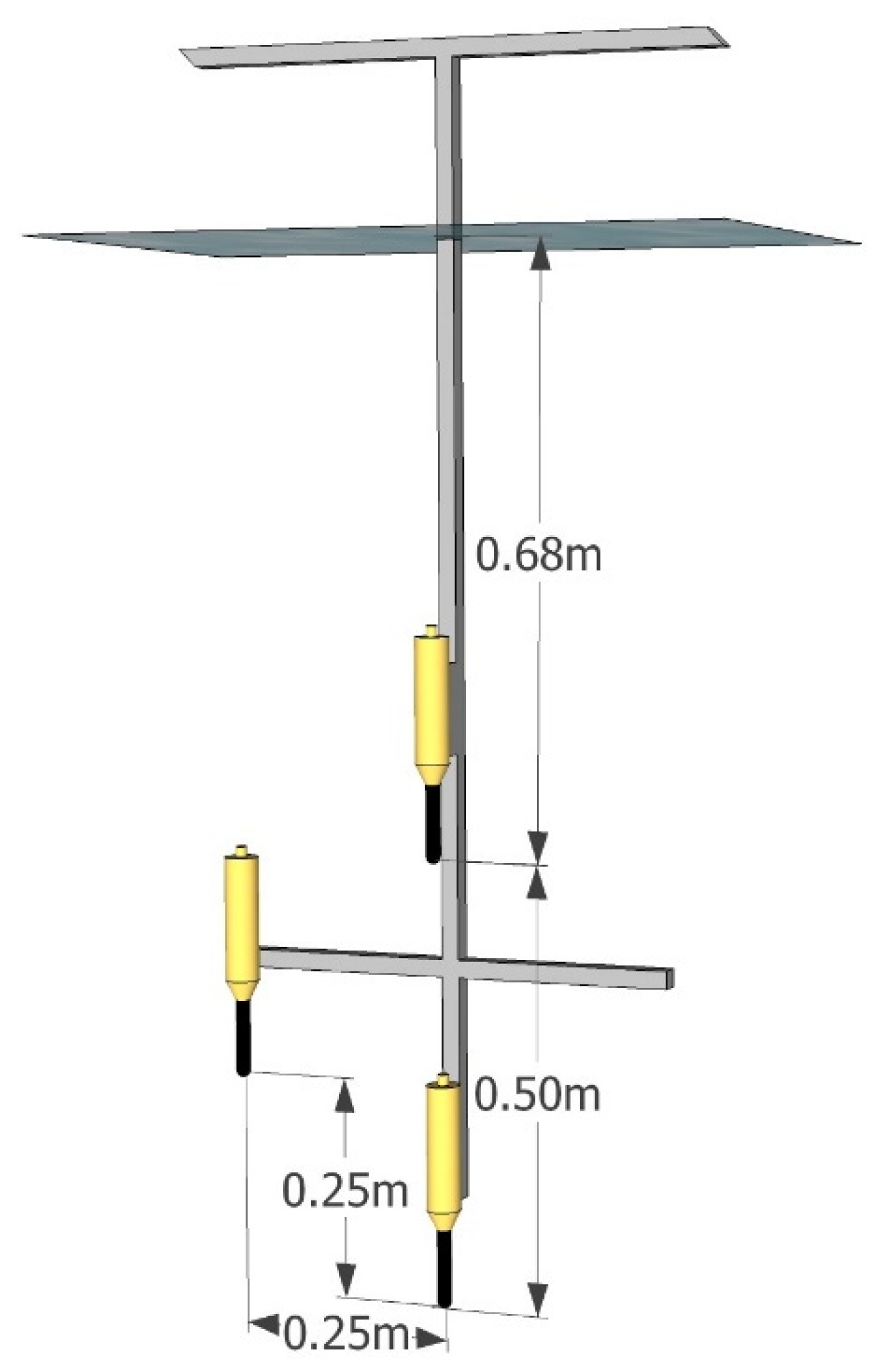
Figure 4. The walls of the tank were smooth, made of polypropylene (PP) with a thickness of 10 mm. The internal dimensions of the tank were: 3.78 m × 1.75 m × 1.8 m. The water column was 1.6 m high. The tank was divided into four compartments to achieve NLOS conditions. Acoustic panels AKU-PRO 140 made of material with a density of 140 kg/m³ and a thickness of 20 mm were used as partitions. The edge of the panels adjoined one of the tank walls and the bottom. The upper edge protruded above the water level. In this way, an artificial corridor was created, reflecting, for example, the interior of the wreck. On one side of the tank, in front of the compartments, a Reson TC4013 transmitting hydrophone was placed. The signal to this hydrophone was fed from a PC via a digital-to-analog NI USB6366 card and an Etec PA1001 power amplifier. Three Reson TC4014 hydrophones were placed on the receiving path. Their spatial configuration is shown in
Figure 5. The hydrophones were powered by 12 V, and the signals were fed through the NI USB6366 analog-to-digital converter card to a PC, where they were recorded and processed. The software of both the transmitter and the receiver was implemented in the Matlab environment.
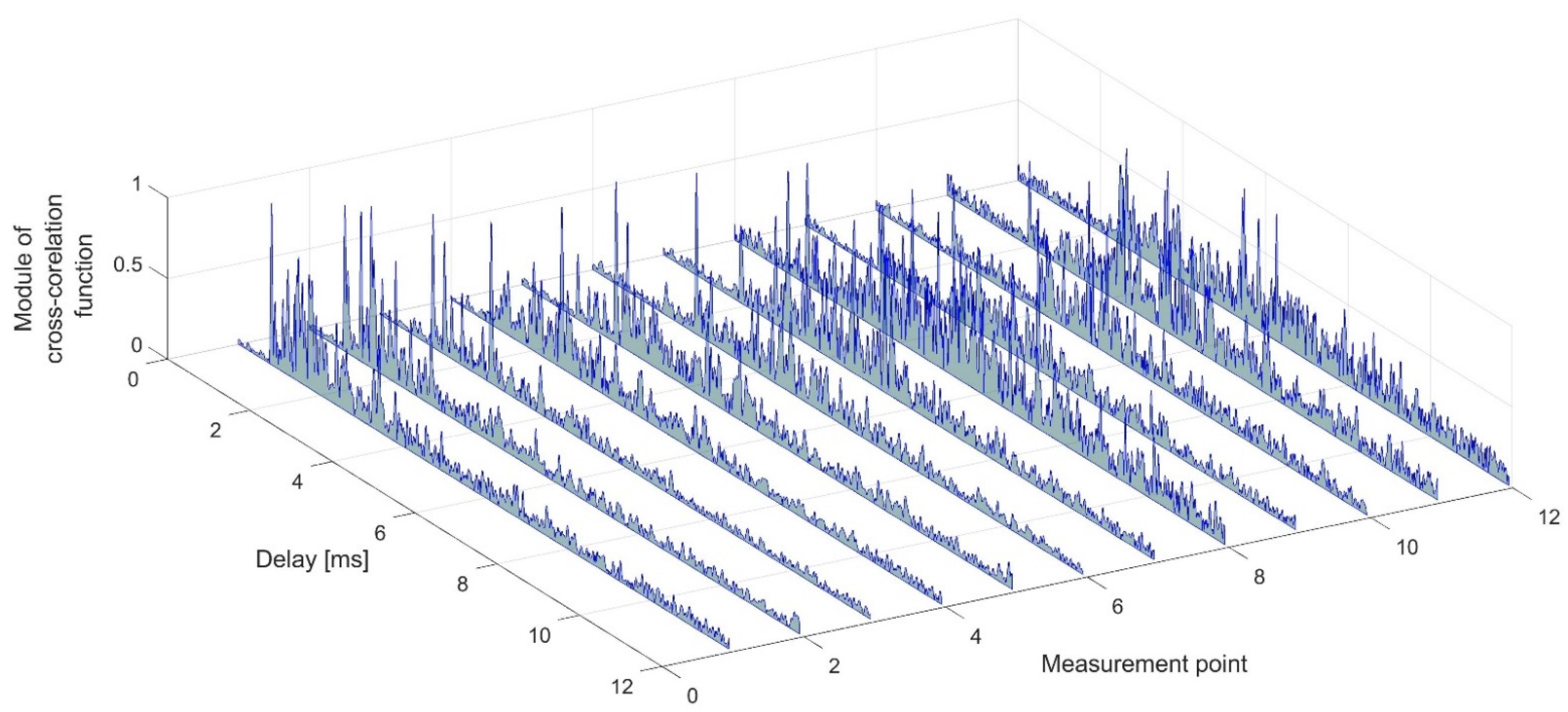
The measurements were performed by locating the receiving hydrophones at 12 selected points, which are marked in
Figure 4. At each point, 10 transmissions were made. In each transmission 10,000 bits were sent.
6. Conclusions
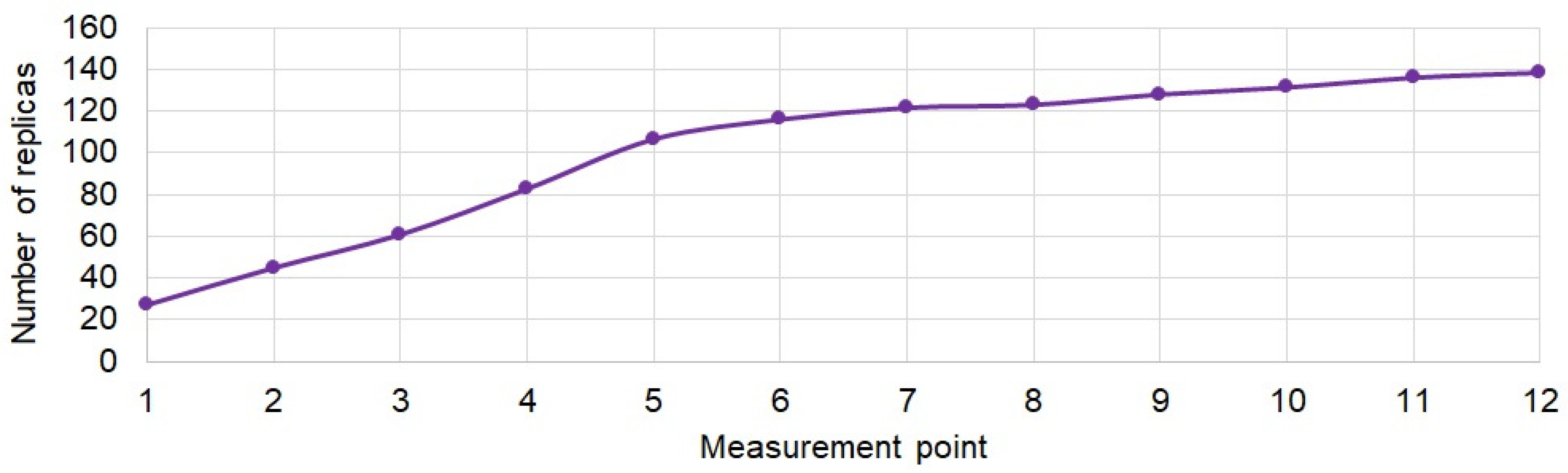
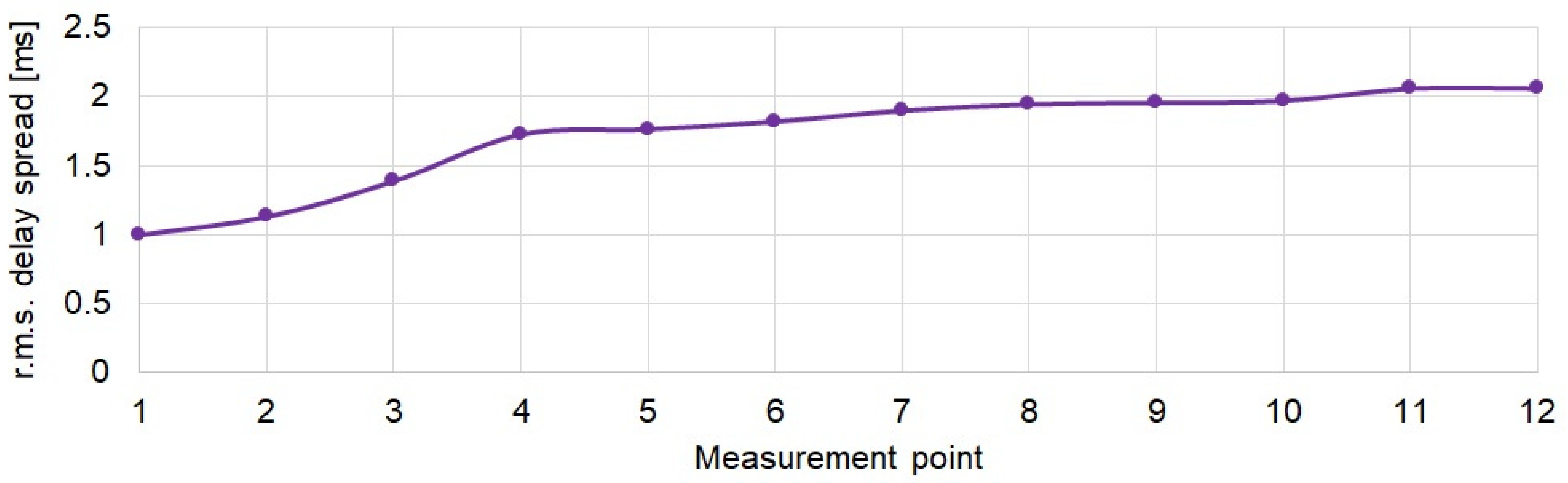
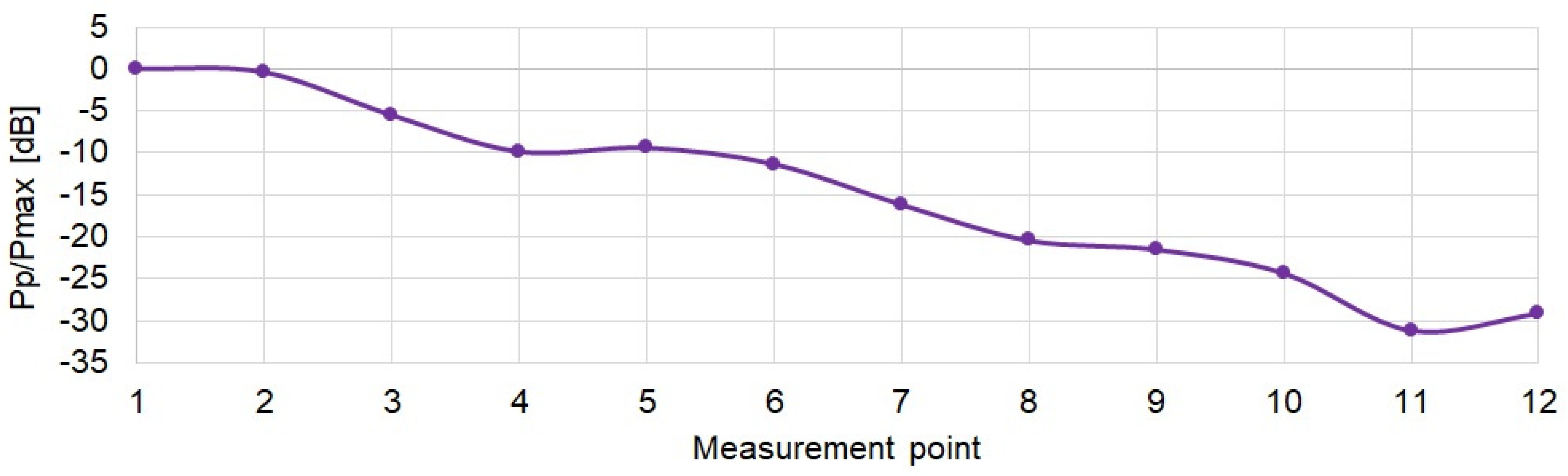
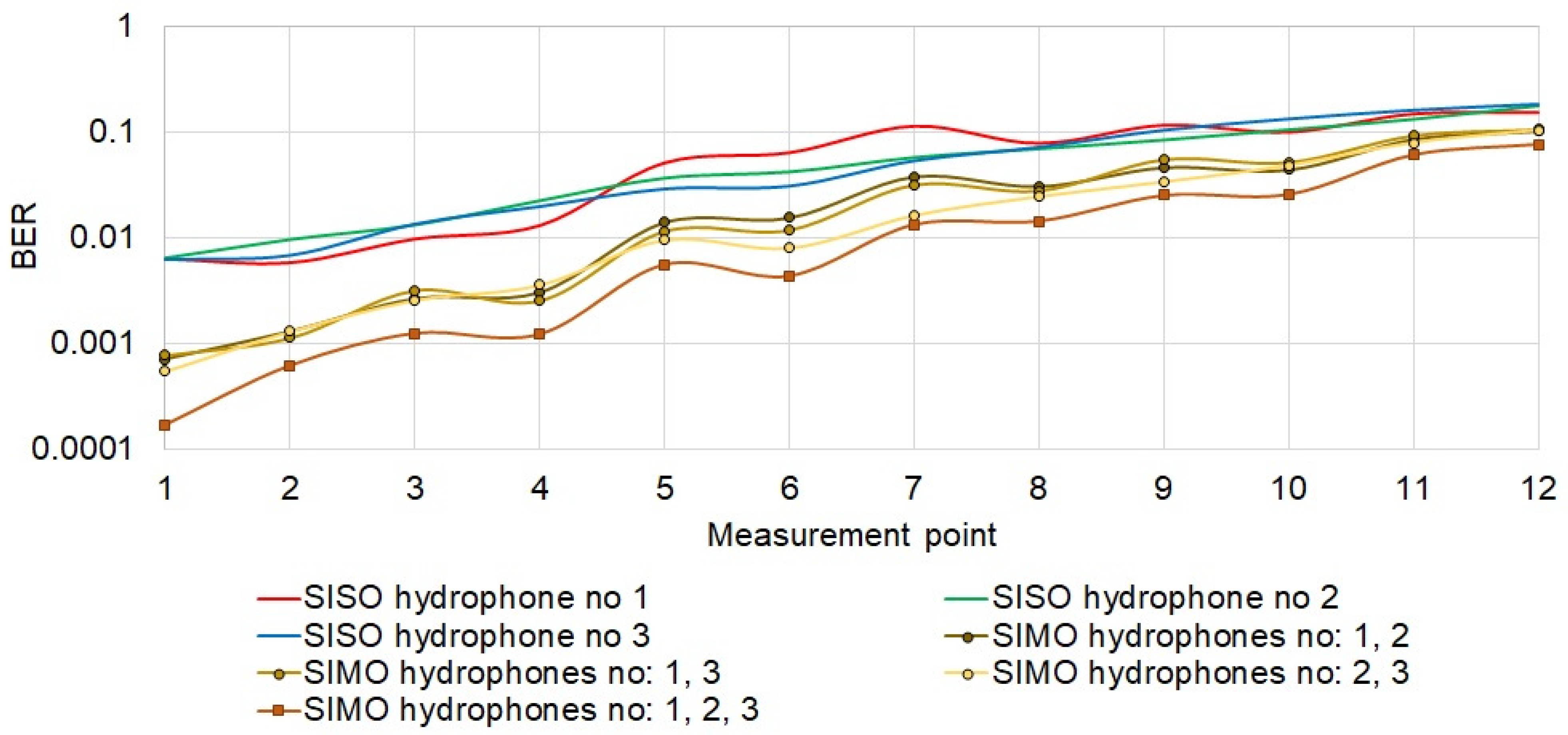
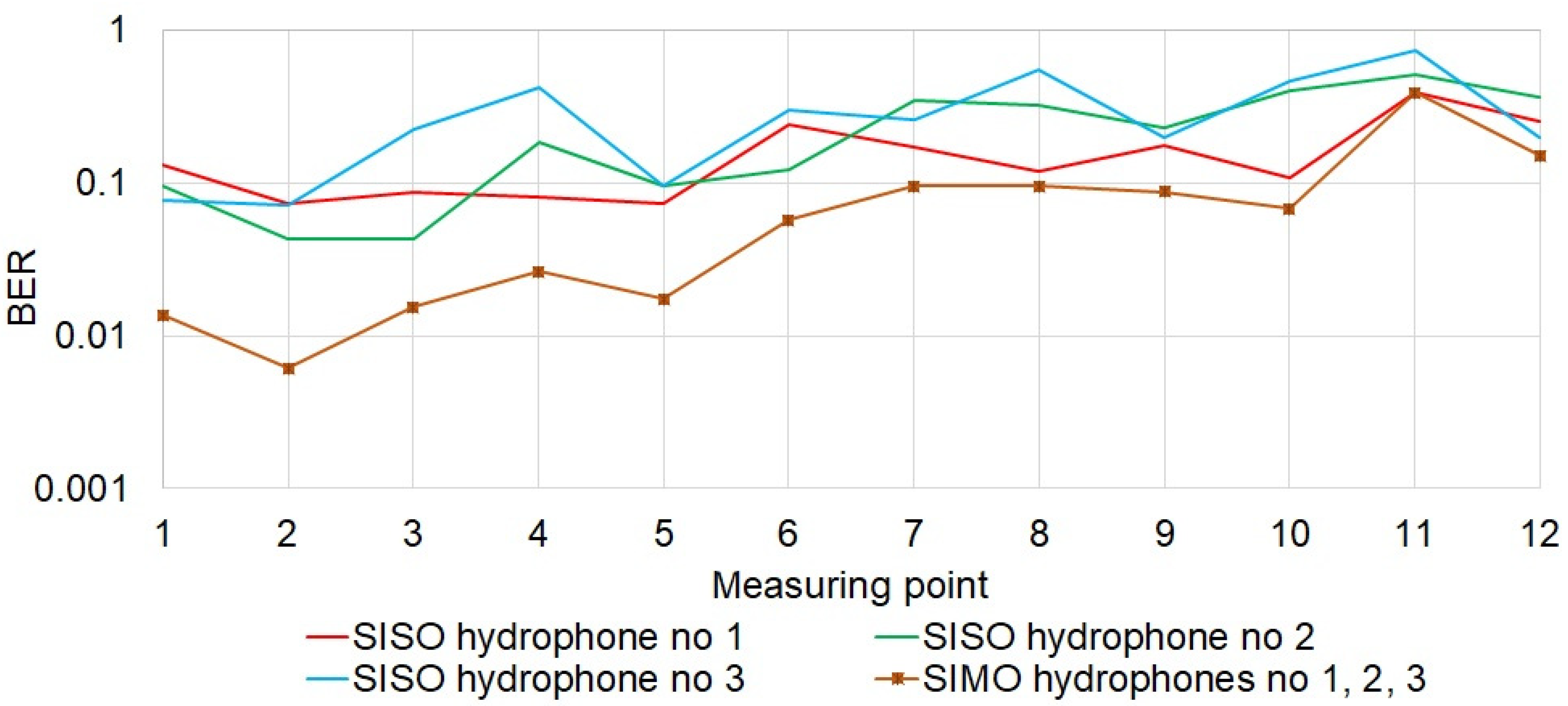
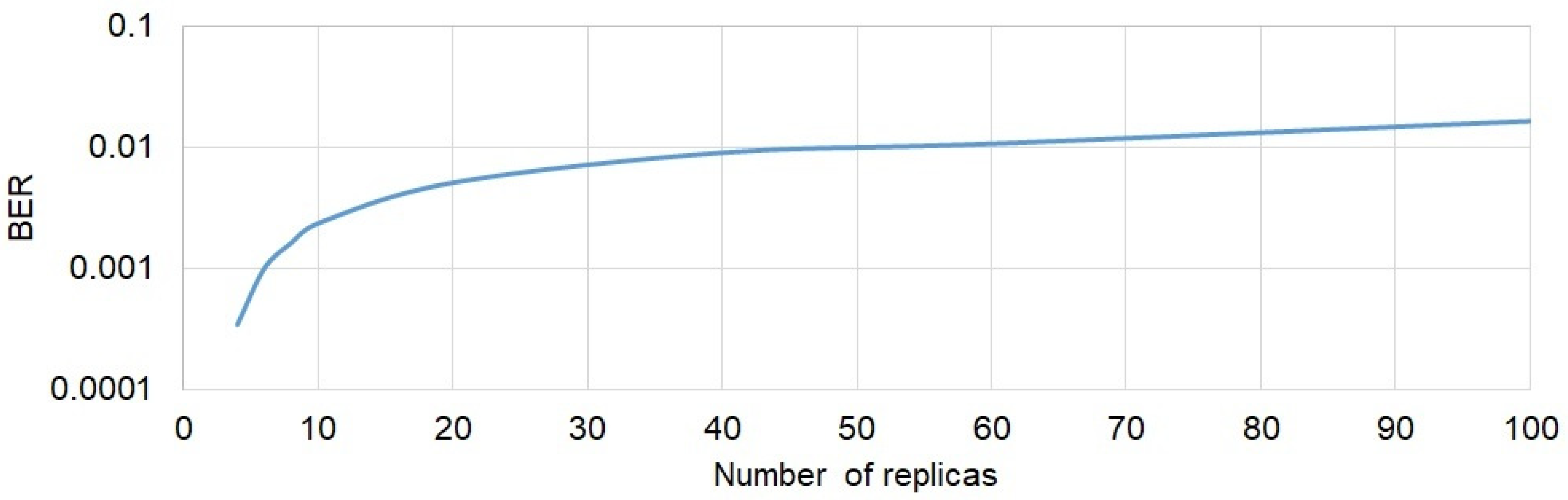
Wireless data transmission in water environment is a non-trivial problem. Additionally, complications arise when NLOS conditions occur. Considering the demand for communication systems operating in such conditions, the possibilities of wireless underwater communication in the absence of direct visibility of the hydrophones were tested in this work. The tests were carried out in laboratory conditions simulating the situation which, for example, could be met in a wreck. By examining the impulse responses, it was found that NLOS conditions were indeed achieved in the experimental tank. The determined spectrum of received signals confirmed the presence of frequency-selective fading in the prepared artificial corridor in the laboratory tank. In the adopted measurement scenario, it was shown that the number of replicas increases with movement down the corridor, while the root mean square delay spread does not increase significantly. We found that the proposed technique of signal formation and diversity combining presented in this paper ensured a high quality of transmission compared to the DSSS technique. As expected, diversity combining greatly improves the transmission quality.
The original qualities of this paper include: the impulse response studies in NLOS conditions, the evaluation of the quality of diversity combining in conditions of strong multipath propagation using the MFSK technique of forming the transmitted signal.
The presented research results provide the basis for undertaking work leading to a communication system with autonomous underwater vehicles which operate in difficult propagation conditions, such as wrecks and ports.