Image-Based Automated Width Measurement of Surface Cracking
Abstract
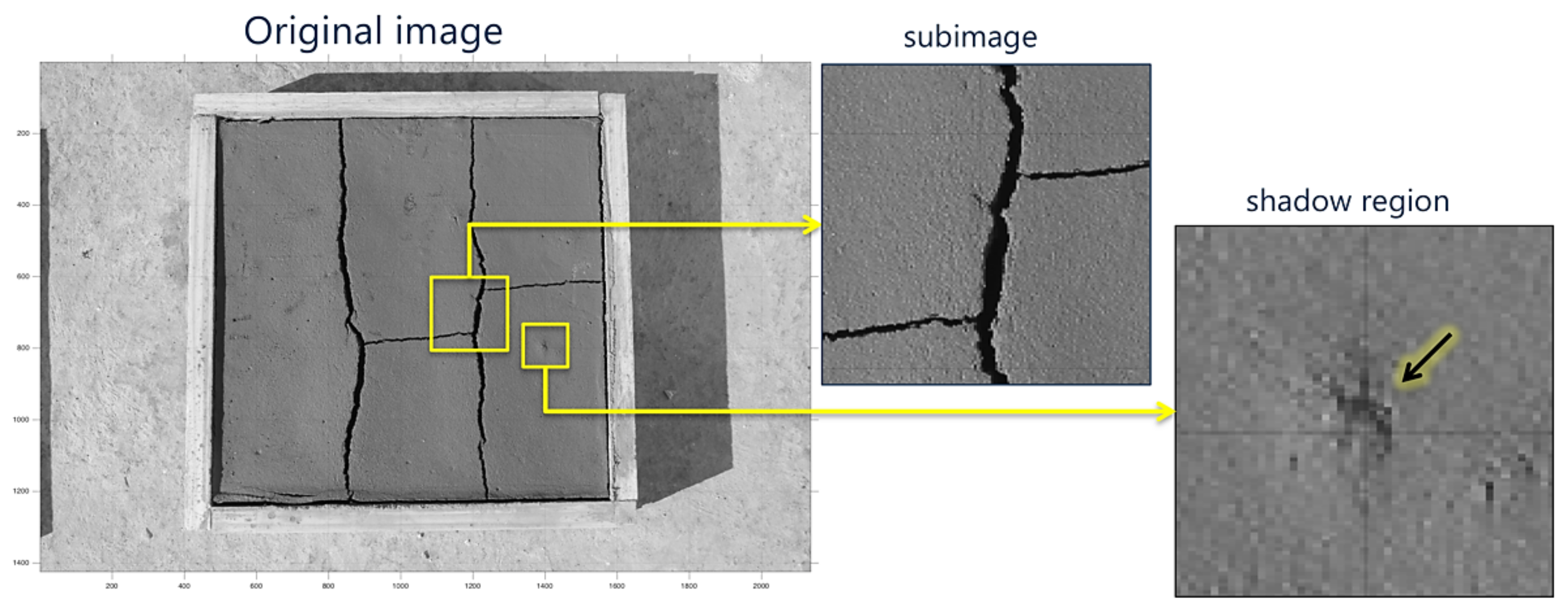
1. Introduction
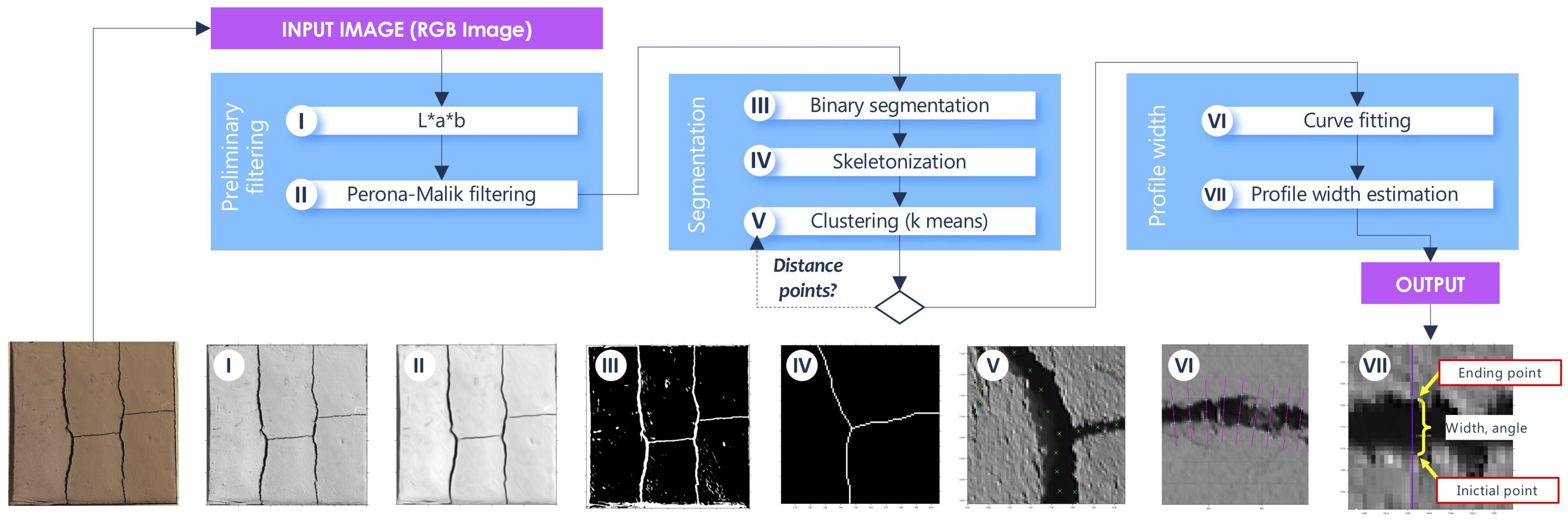
2. Method
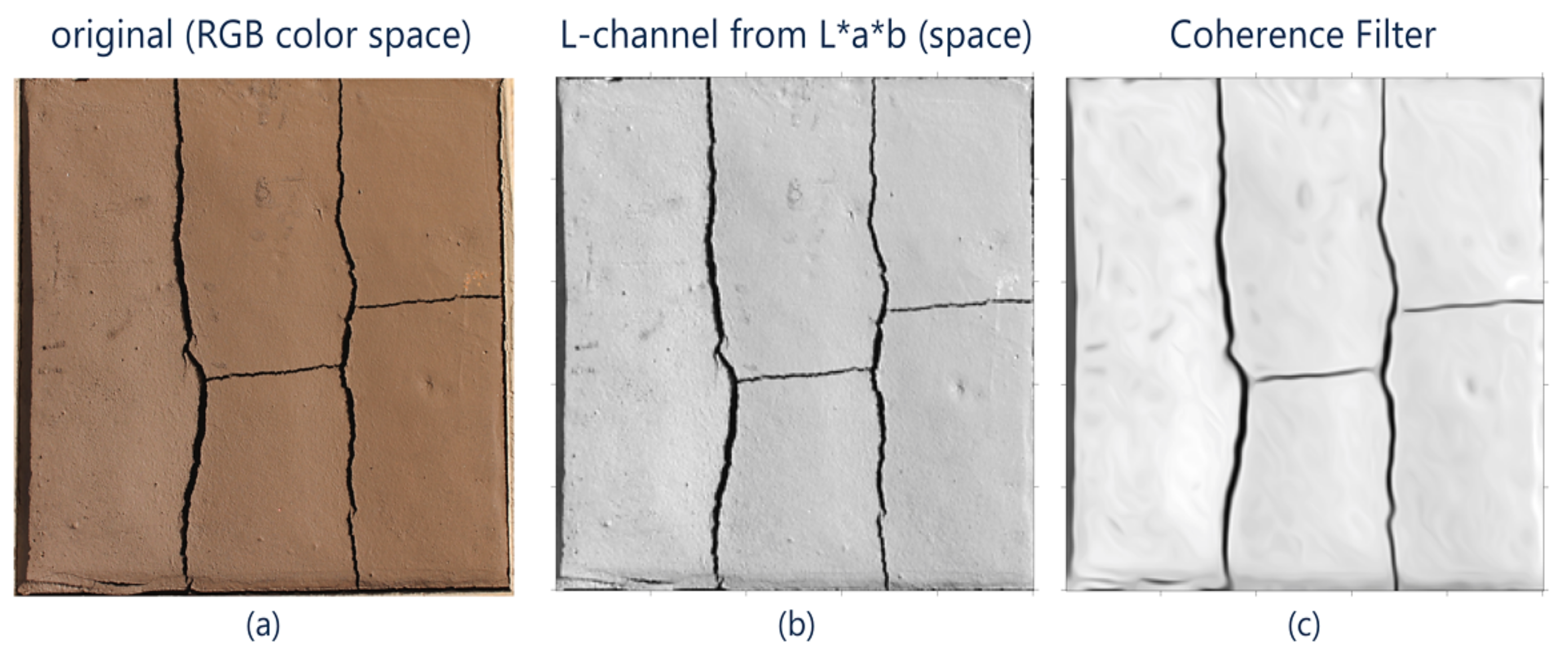
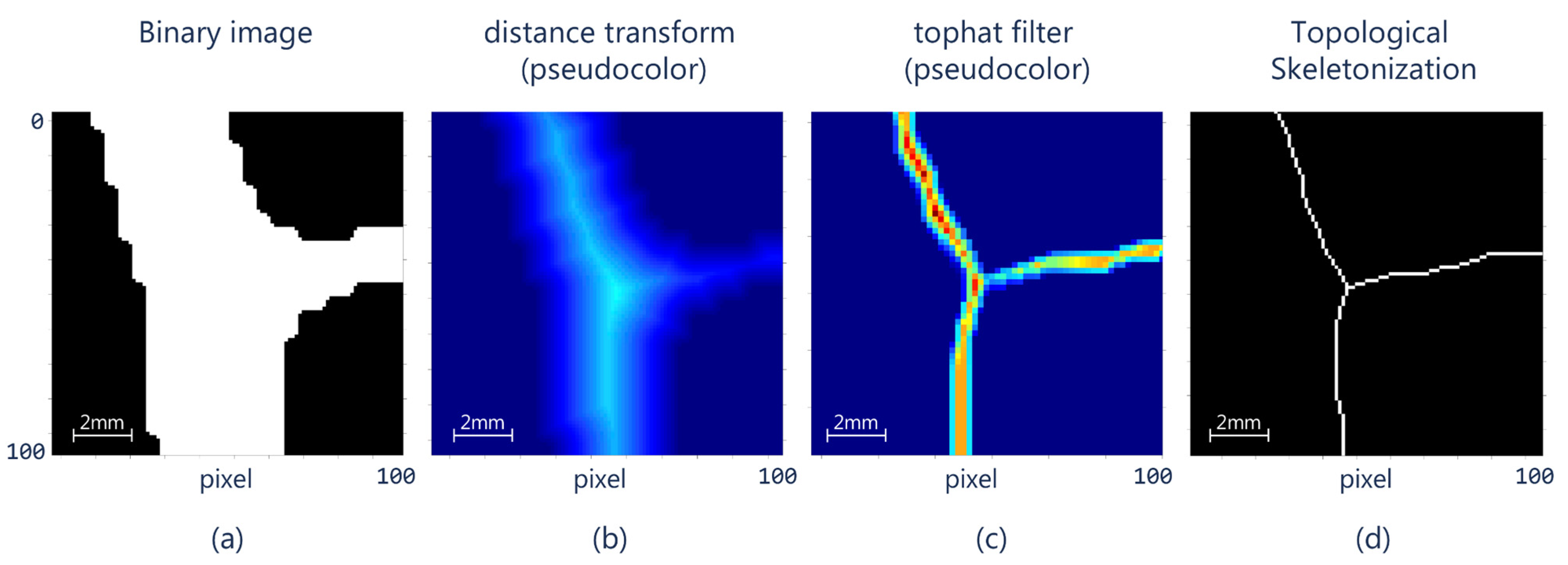
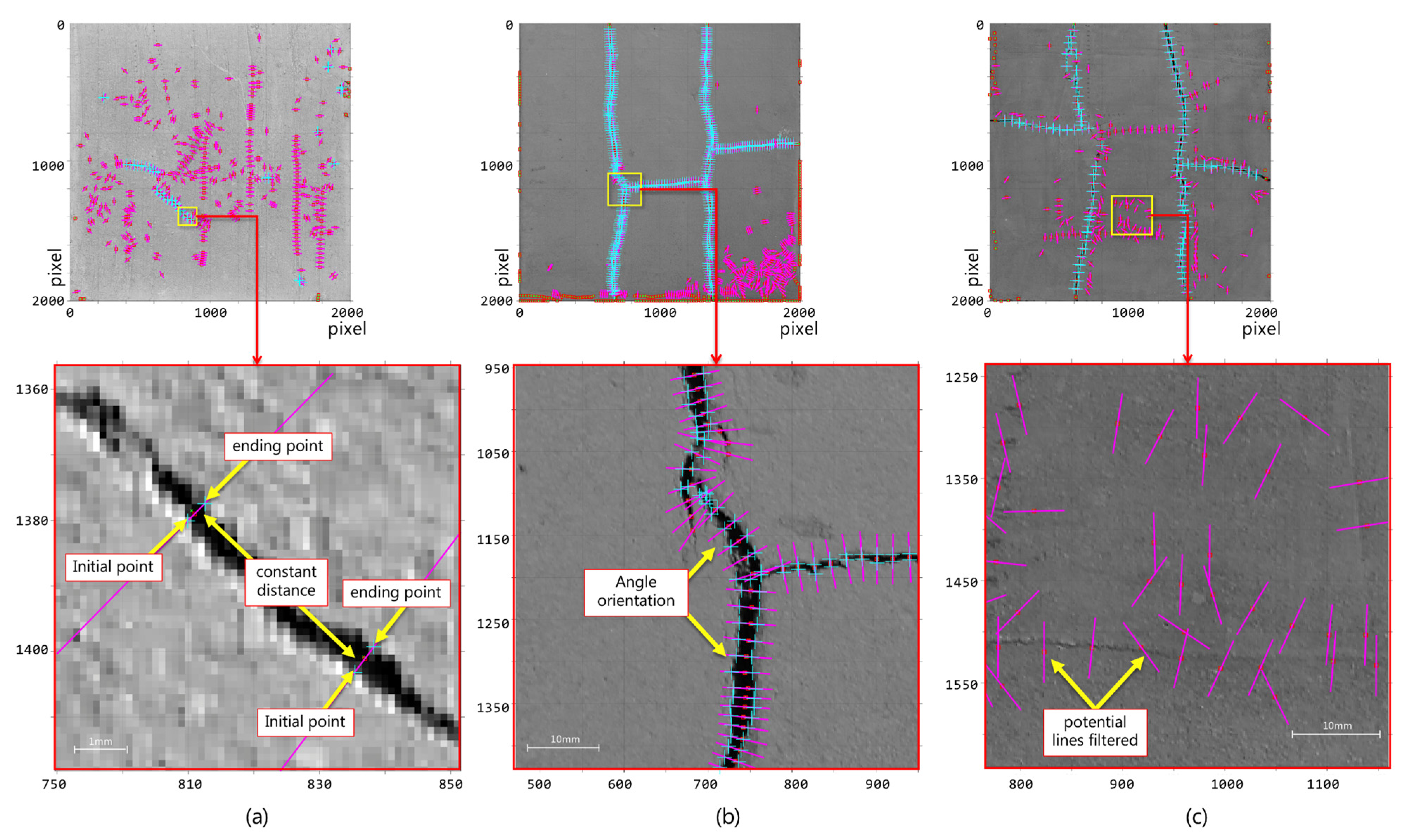
2.1. Step I: Preliminary Filtering
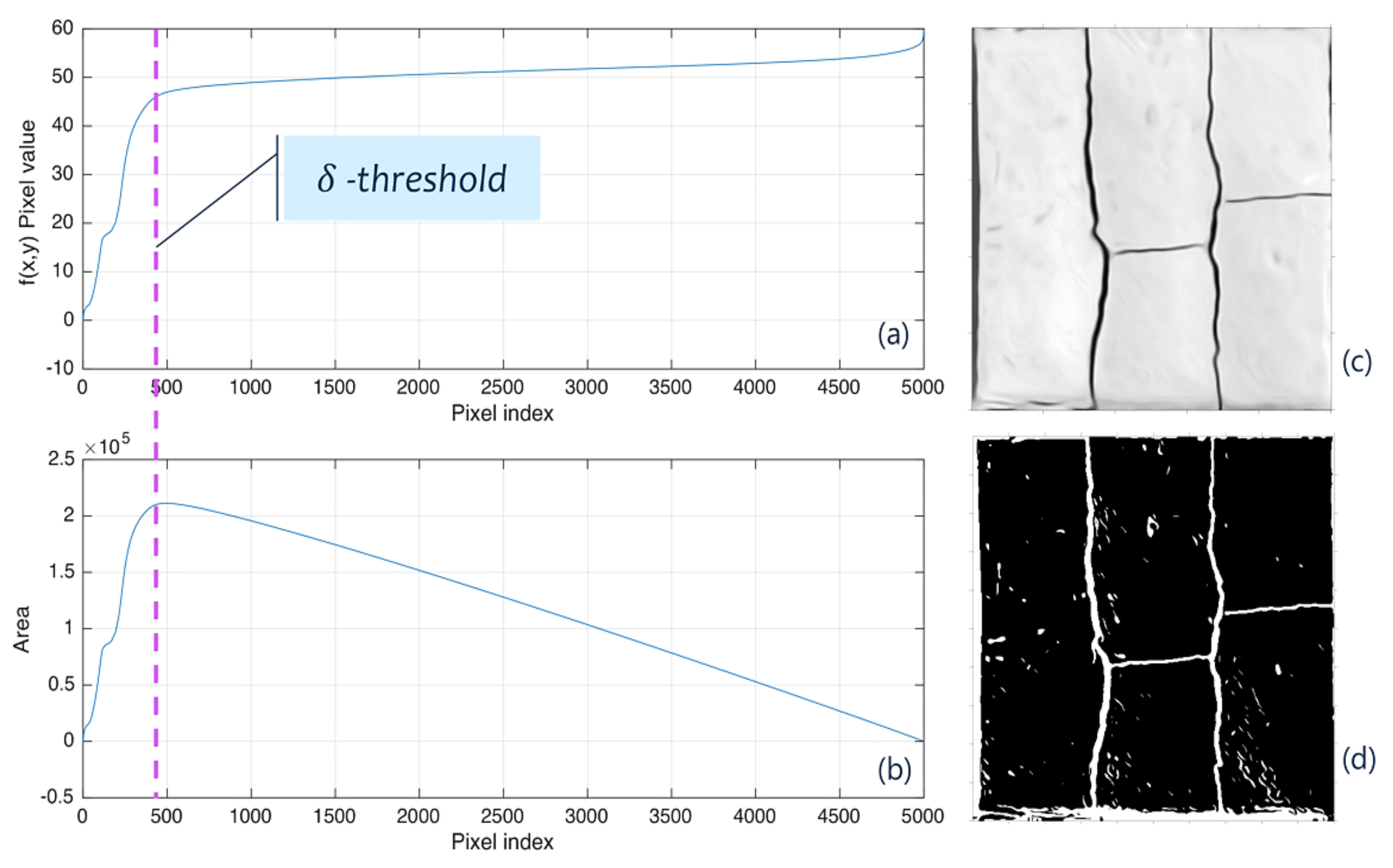
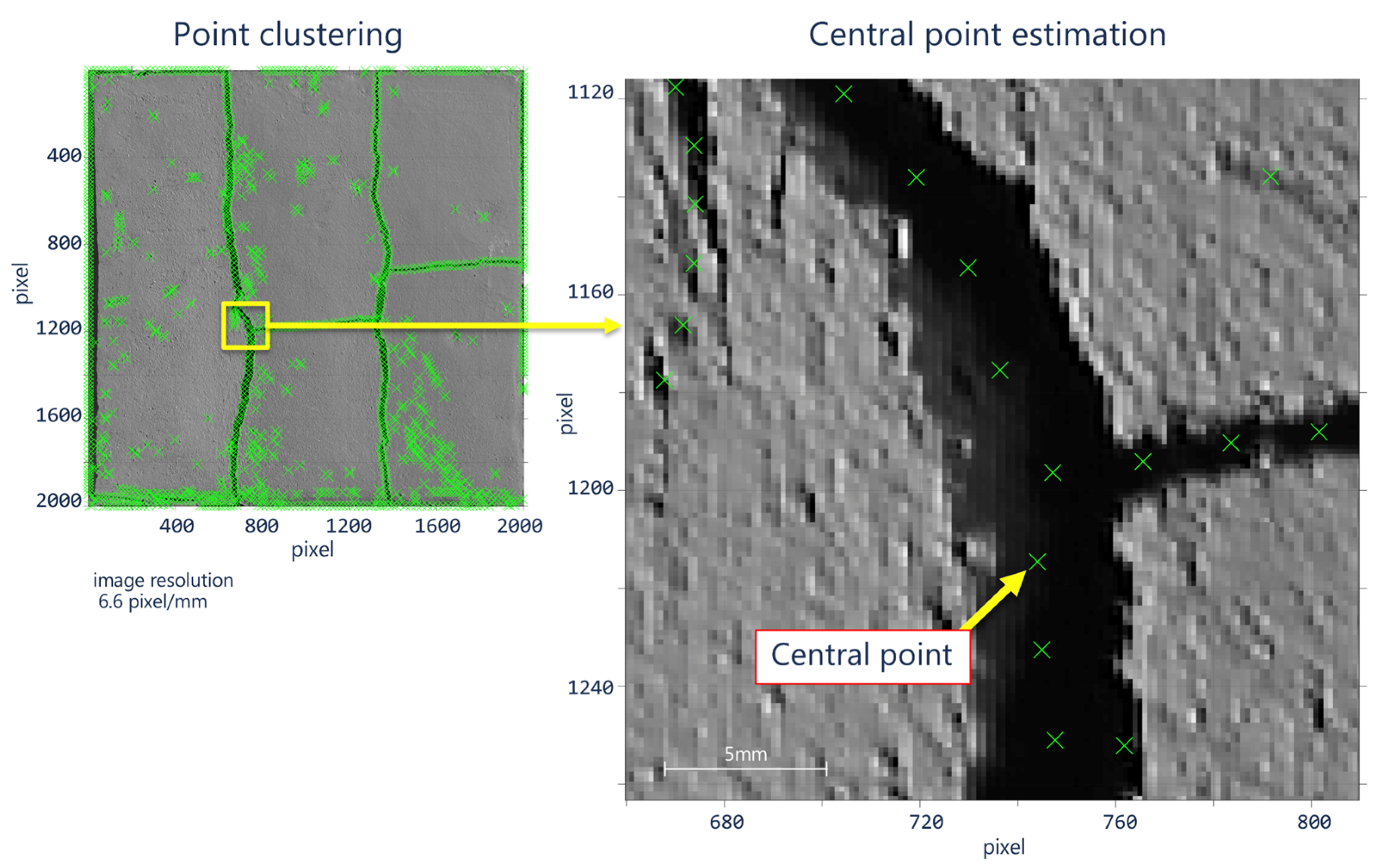
2.2. Step II: Binary Segmentation
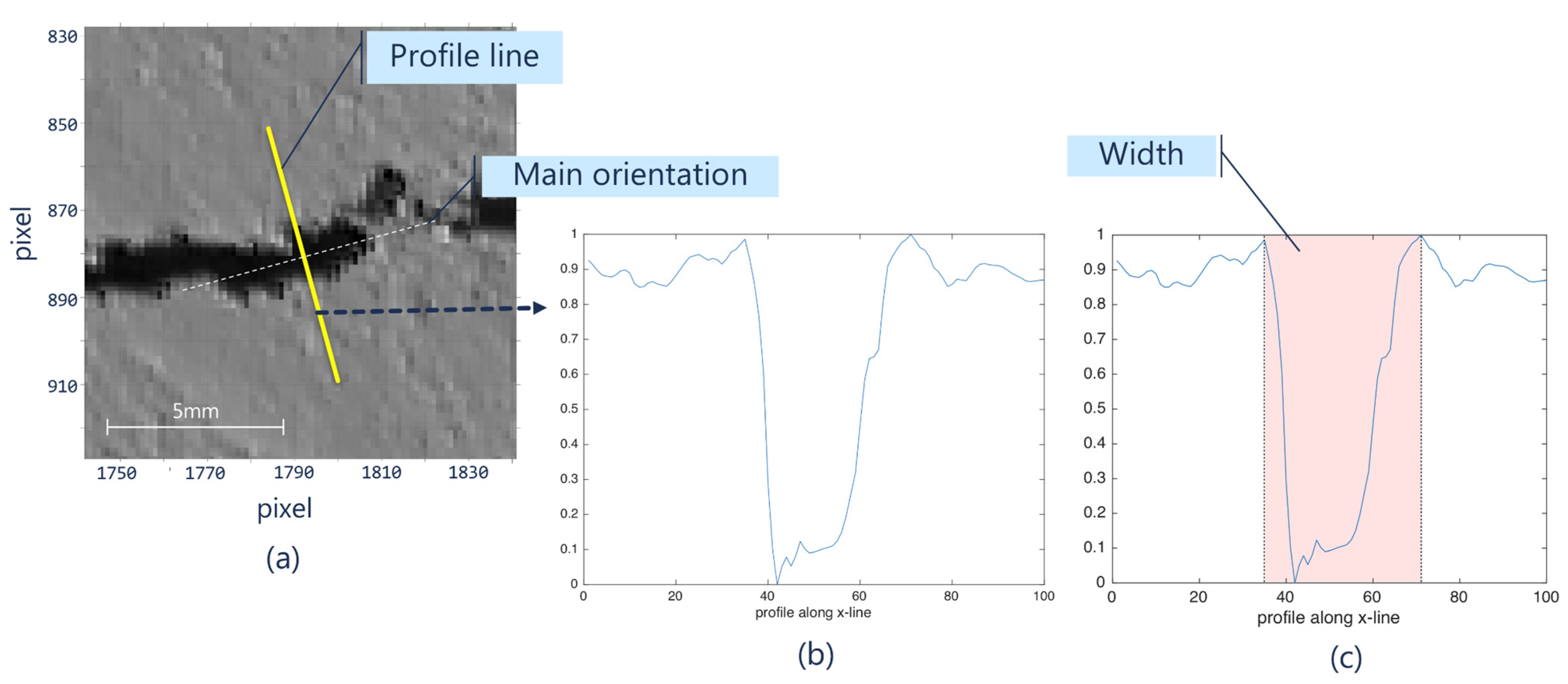
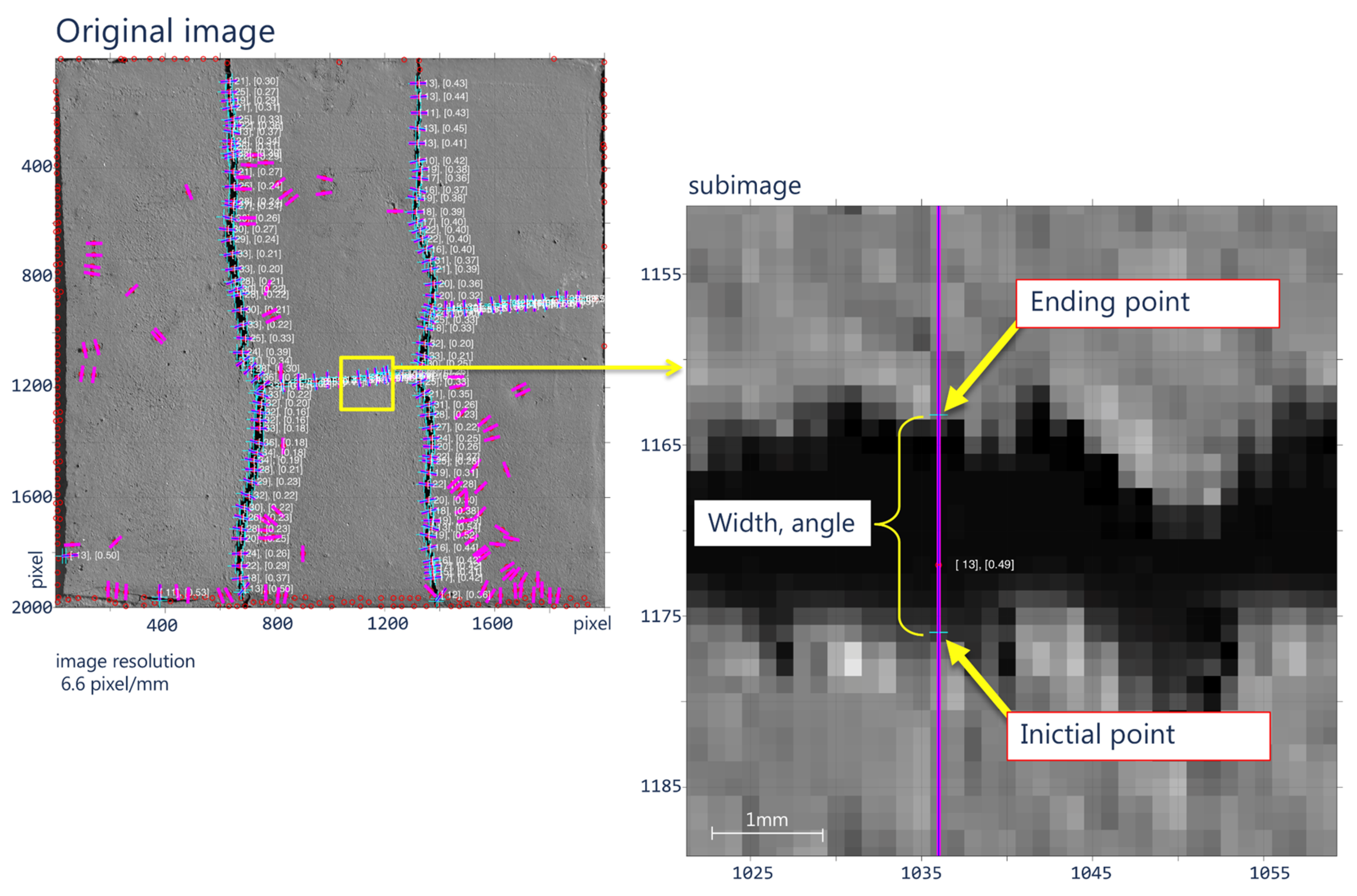
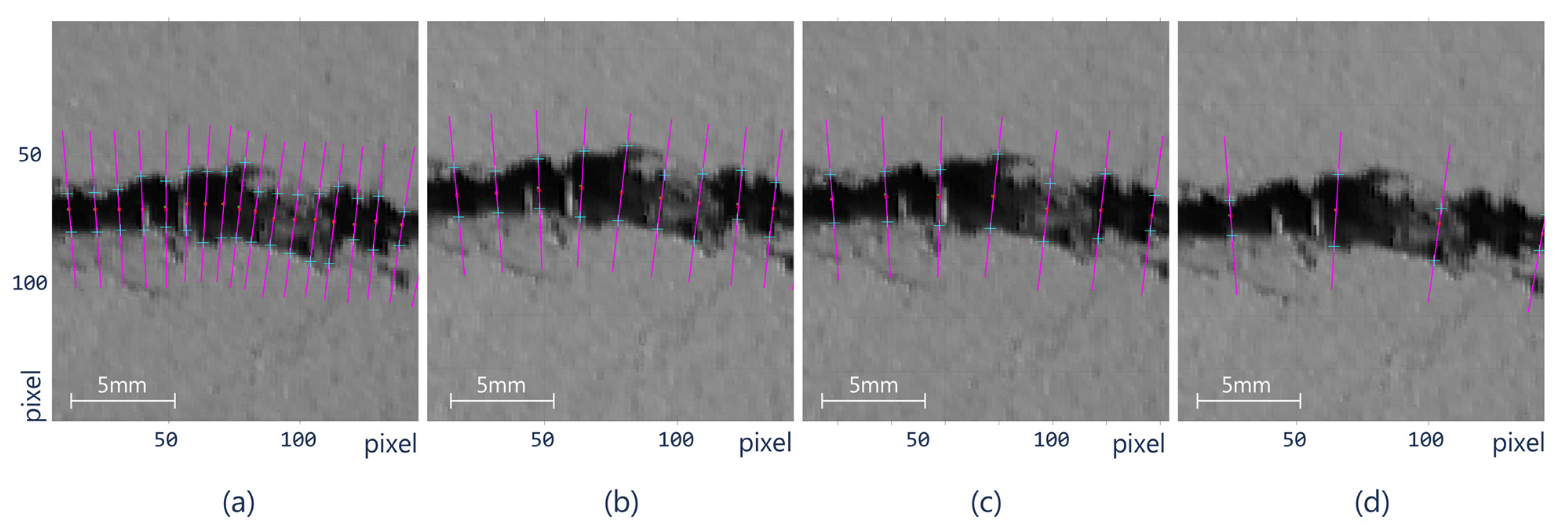
2.3. Step III. Profile Width
3. Results
- (1)
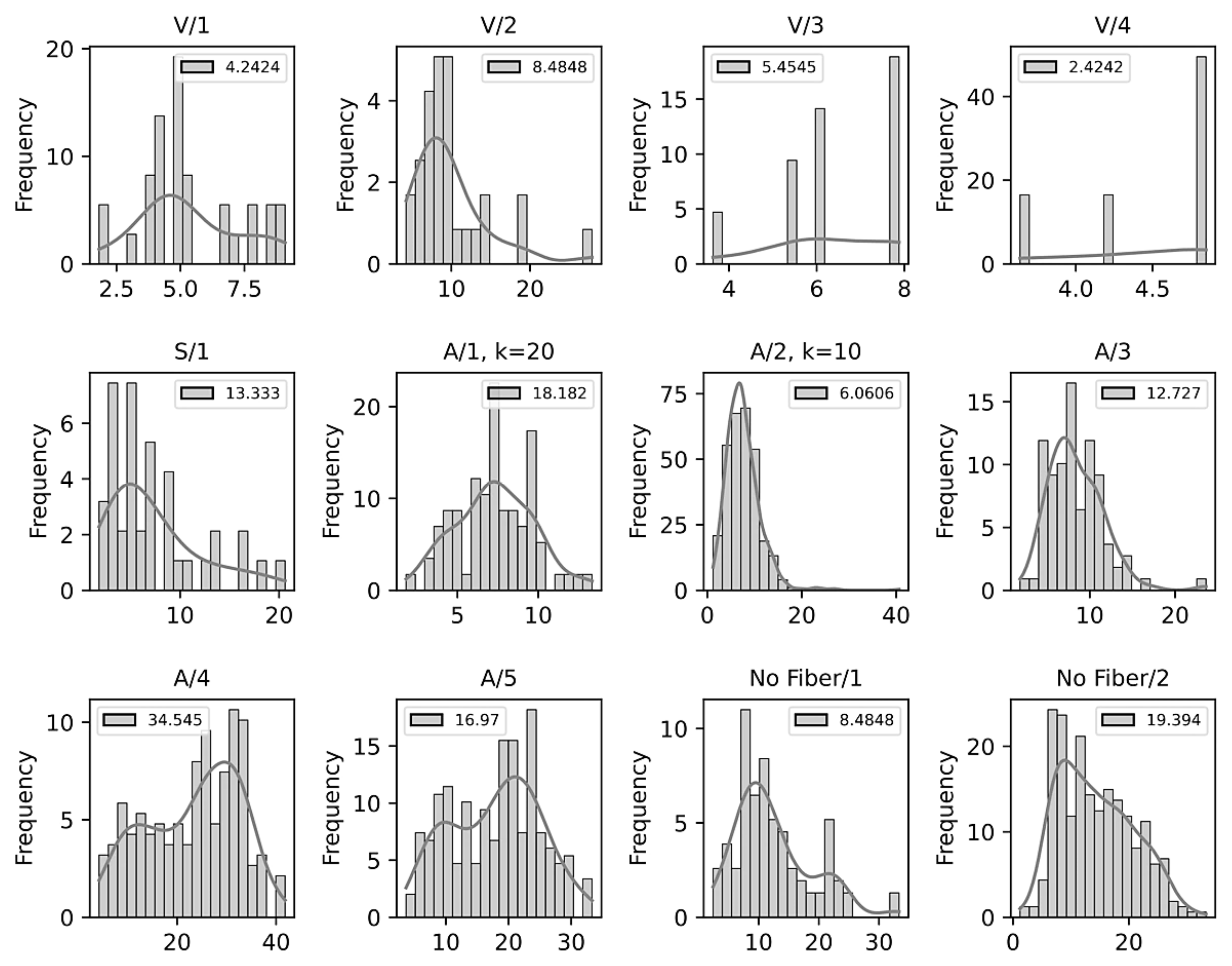
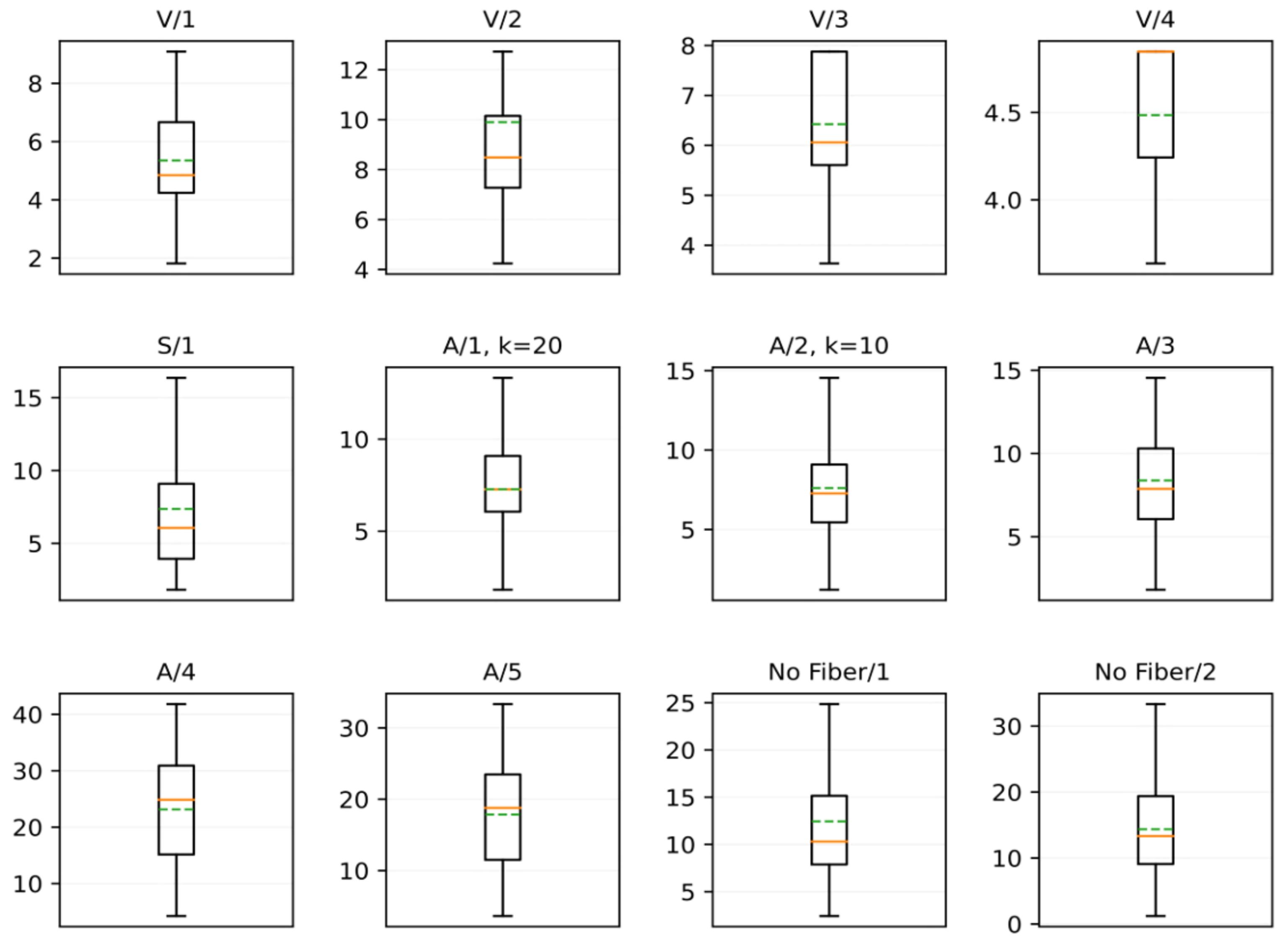
- No clear distribution: Samples V/3 and V/4 show this case. In these samples, it was possible to extract only a limited number of measurement points due to the small number of cracks present in the sample. Thus, it is not possible to associate the data with a specific distribution. This limitation of the method is a particular point for future improvement.
- (2)
- Normal distribution: This phenomenon is present in samples with a regular cracking pattern. It is clearly observed in samples A/1, A/2, and A/3. Additionally, in sample A/2, the number of measurements was increased from 75 to 606 through parameter k (Figure 10). By increasing the number of measurements, it is possible to observe a normal behavior and a lower error in relation to the manual process (p-value 0.906 versus p-value 0.308).
- (3)
- Bimodal distribution: This phenomenon can be clearly observed in samples No Fiber/1, A/4, and A/5 (Figure 13). These samples exhibit two types of cracks (coarse and fine), which have a vertical and/or horizontal cracking behavior. In some cases, a greater width was found in the horizontal cracks. However, it is worth mentioning that all the cracks have internal angles that can only be appreciated in images with a higher magnification (Figure 13a).
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhao, P.; Zsaki, A.M.; Nokken, M.R. Using digital image correlation to evaluate plastic shrinkage cracking in cement-based materials. Constr. Build. Mater. 2018, 182, 108–117. [Google Scholar] [CrossRef]
- Bertelsen, I.M.G.; Kragh, C.; Cardinaud, G.; Ottosen, L.M.; Fischer, G. Quantification of plastic shrinkage cracking in mortars using digital image correlation. Cem. Concr. Res. 2019, 123, 105761. [Google Scholar] [CrossRef]
- Davoudi, R.; Miller, G.R.; Kutz, J.N. structural load estimation using machine vision and surface crack patterns for shear-critical RC beams and slabs. J. Comput. Civ. Eng. 2018, 32, 04018024. [Google Scholar] [CrossRef]
- Hoang, N.-D. Image processing-based recognition of wall defects using machine learning approaches and steerable filters. Comput. Intel. Neurosci. 2018, 2018, 7913952. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Deng, H.; Dong, Q.; Gu, X.; Zhang, T.; Wang, Y. An advanced Otsu method integrated with edge detection and decision tree for crack detection in highway transportation infrastructure. Adv. Mater. Sci. Eng. 2021, 2021, 9205509. [Google Scholar] [CrossRef]
- Araya-Letelier, G.; Maturana, P.; Carrasco, M.; Antico, F.C.; Gómez, M.S. Mechanical-damage behavior of mortars reinforced with recycled polypropylene fibers. Sustainability 2019, 11, 2200. [Google Scholar] [CrossRef]
- Concha-Riedel, J.; Araya-Letelier, G.; Antico, F.C.; Reidel, U.; Glade, A. Influence of jute fibers to improve flexural toughness, impact resistance and drying shrinkage cracking in adobe mixes. In Earthen Dwellings and Structures; Reddy, B.V.V., Mani, M., Walker, P., Eds.; Springer: Singapore, 2019; ISBN 978-981-13-5883-8. [Google Scholar]
- Araya-Letelier, G.; Gonzalez-Calderon, H.; Kunze, S.; Burbano-Garcia, C.; Reidel, U.; Sandoval, C.; Bas, F. Waste-based natural fiber reinforcement of adobe mixtures: Physical, mechanical, damage and durability performance assessment. J. Clean. Prod. 2020, 273, 122806. [Google Scholar] [CrossRef]
- Bertelsen, I.M.G.; Ottosen, L.M.; Fischer, G. Quantitative analysis of the influence of synthetic fibres on plastic shrinkage cracking using digital image correlation. Constr. Build. Mater. 2019, 199, 124–137. [Google Scholar] [CrossRef]
- Löfgren, I. Calculation of crack width and crack spacing. In Proceedings of the Nordic Mini-Seminar: “Fibre Reinforced Concrete”, Trondheim, Norway, 15 November 2007. [Google Scholar]
- Tang, P.; Huber, D.; Akinci, B. Characterization of laser scanners and algorithms for detecting flatness defects on concrete surfaces. J. Comput. Civ. Eng. 2011, 25, 31–42. [Google Scholar] [CrossRef]
- Pragalath, H.; Seshathiri, S.; Rathod, H.; Esakki, B.; Gupta, R. Deterioration assessment of infrastructure using fuzzy logic and image processing algorithm. J. Perform. Constr. Facil. 2018, 32, 04018009. [Google Scholar] [CrossRef]
- Nishikawa, T.; Yoshida, J.; Sugiyama, T.; Fujino, Y. Concrete crack detection by multiple sequential image filtering: Concrete crack detection by image processing. Comput. Aided Civil Infrastruct. Eng. 2012, 27, 29–47. [Google Scholar] [CrossRef]
- Hsieh, Y.-A.; Tsai, Y.J. Machine learning for crack detection: Review and model performance comparison. J. Comput. Civ. Eng. 2020, 34, 04020038. [Google Scholar] [CrossRef]
- Christen, R.; Bergamini, A.; Motavalli, M. High precision measurement of surface cracks using an optical system. Meas. Sci. Technol. 2009, 20, 20–077001. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Nakamura, S.; Saegusa, R.; Hashimoto, S. Image-based crack detection for real concrete surfaces. IEEJ Trans. Electron. Eng. 2008, 3, 128–135. [Google Scholar] [CrossRef]
- Dare, P.; Hanley, H.; Fraser, C.; Riedel, B.; Niemeier, W. An operational application of automatic feature extraction: The measurement of cracks in concrete structures. Photogramm. Rec. 2002, 17, 453–464. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: New York, NY, USA, 2003. [Google Scholar]
- Detchev, I.; Habib, A.; El-Badry, M.; Bahreh, V.M. Detection of cracks in a concrete beam-column joint using target gridding. In Proceedings of the American Society of Photogrammetry and Remote Sensing Annual Conference, Baltimore, MD, USA, 24–28 March 2013; p. 9. [Google Scholar]
- Sohn, H.-G.; Lim, Y.-M.; Yun, K.-H.; Kim, G.-H. Monitoring crack changes in concrete structures. Comput. Aided Civil Eng. 2005, 20, 52–61. [Google Scholar] [CrossRef]
- Habib, A.; Lichti, D.; El-Badry, M.; Detchev, I. Optical remote sensing systems for structural deflection measurement and crack characterization. In Proceedings of the 9th International Conference on Short and Medium Span Bridges, Calgary, AB, Canada, 15–18 July 2014. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Hashimoto, S. Fast crack detection method for large-size concrete surface images using percolation-based image processing. Mach. Vis. Appl. 2010, 21, 797–809. [Google Scholar] [CrossRef]
- Chen, L.-C.; Shao, Y.-C.; Jan, H.-H.; Huang, C.-W.; Tien, Y.-M. measuring system for cracks in concrete using multitemporal images. J. Surv. Eng. 2006, 132, 77–82. [Google Scholar] [CrossRef]
- Berrocal, C.G.; Löfgren, I.; Lundgren, K.; Görander, N.; Halldén, C. Characterisation of bending cracks in R/FRC using image analysis. Cem. Concr. Res. 2016, 90, 104–116. [Google Scholar] [CrossRef]
- Hoang, N.-D. Detection of surface crack in building structures using image processing technique with an improved otsu method for image thresholding. Adv. Civil Eng. 2018, 2018, 3924120. [Google Scholar] [CrossRef]
- Cho, H.; Yoon, H.-J.; Jung, J.-Y. Image-based crack detection using crack width transform (CWT) algorithm. IEEE Access 2018, 6, 60100–60114. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, Y.; Sun, H.; Huang, W. Pavement crack detection using hessian structure propagation. Adv. Eng. Inf. 2021, 49, 101303. [Google Scholar] [CrossRef]
- Alipour, M.; Harris, D.K. Increasing the robustness of material-specific deep learning models for crack detection across different materials. Eng. Struct. 2020, 206, 110157. [Google Scholar] [CrossRef]
- Kang, D.; Benipal, S.S.; Gopal, D.L.; Cha, Y.-J. Hybrid pixel-level concrete crack segmentation and quantification across complex backgrounds using deep learning. Autom. Constr. 2020, 118, 103291. [Google Scholar] [CrossRef]
- Rao, A.S.; Nguyen, T.; Palaniswami, M.; Ngo, T. Vision-Based Automated Crack Detection Using Convolutional Neural Networks for Condition Assessment of Infrastructure. Struct. Health Monit. 2021, 20, 2124–2142. [Google Scholar] [CrossRef]
- Munawar, H.S.; Hammad, A.W.A.; Haddad, A.; Soares, C.A.P.; Waller, S.T. Image-based crack detection methods: A review. Infrastructures 2021, 6, 115. [Google Scholar] [CrossRef]
- Yamane, T.; Chun, P. Crack detection from a concrete surface image based on semantic segmentation using deep learning. ACT 2020, 18, 493–504. [Google Scholar] [CrossRef]
- Park, S.E.; Eem, S.-H.; Jeon, H. Concrete crack detection and quantification using deep learning and structured light. Constr. Build. Mater. 2020, 252, 119096. [Google Scholar] [CrossRef]
- Liu, J.; Yang, X.; Lau, S.; Wang, X.; Luo, S.; Lee, V.C.; Ding, L. Automated pavement crack detection and segmentation based on two-step convolutional neural network. Comput. Aided Civil Infrastr. Eng. 2020, 35, 1291–1305. [Google Scholar] [CrossRef]
- Abdellatif, M.; Peel, H.; Cohn, A.G.; Fuentes, R. Combining block-based and pixel-based approaches to improve crack detection and localisation. Autom. Constr. 2021, 122, 103492. [Google Scholar] [CrossRef]
- Mohan, A.; Poobal, S. Crack detection using image processing: A critical review and analysis. Alex. Eng. J. 2018, 57, 787–798. [Google Scholar] [CrossRef]
- Alexander, M.G.; Bentur, A.; Mindess, S. Durability of Concrete: Design and Construction; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4822-3725-2. [Google Scholar]
- ACI Committee 224 American Concrete Institute. Control of Cracking in Concrete Structures ACI 224 R-01; American Concrete Institute: Farmington Hills, OK, USA, 2001; ISBN 978-0-87031-056-0. [Google Scholar]
- Newman, T.S.; Jain, A.K. A survey of automated visual inspection. Comput. Vis. Image Underst. 1995, 61, 231–262. [Google Scholar] [CrossRef]
- Chen, H.-C.; Chien, W.-J.; Wang, S.-J. Contrast-based color image segmentation. IEEE Signal Process. Lett. 2004, 11, 641–644. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intel. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Kamalaveni, V.; Rajalakshmi, R.A.; Narayanankutty, K.A. Image denoising using variations of perona-malik model with different edge stopping functions. Procedia Comput. Sci. 2015, 58, 673–682. [Google Scholar] [CrossRef]
- Liu, K.; Tan, J.; Ai, L. Hybrid regularizers-based adaptive anisotropic diffusion for image denoising. SpringerPlus 2016, 5, 404. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Weickert, J. Anisotropic Diffusion in Image Processing; B.G. Teubner: Stuttgart, Germany, 1998. [Google Scholar]
- Barbu, T. Robust anisotropic diffusion scheme for image noise removal. Procedia Comput. Sci. 2014, 35, 522–530. [Google Scholar] [CrossRef]
- Telea, A.; van Wijk, J.J. An Augmented Fast Marching Method for Computing Skeletons and Centerlines. In Proceedings of the IEEE TCVG Symposium on Visualization, Barcelona, Spain, 27–29 May 2002. [Google Scholar]
- Gonzalez, R.; Woods, R.E. Digital Image Processing; Addision Wesley: San Francisco, CA, USA, 1992. [Google Scholar]
- Dhanachandra, N.; Manglem, K.; Chanu, Y.J. Image Segmentation using K-means clustering algorithm and subtractive clustering algorithm. Procedia Comput. Sci. 2015, 54, 764–771. [Google Scholar] [CrossRef]
- Fitzgibbon, A.W.; Pilu, M.; Fisher, R.B. Direct least squares fitting of ellipses. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 1, pp. 253–257. [Google Scholar]
- Araya-Letelier, G.; Antico, F.C.; Concha-Riedel, J.; Glade, A.; Wiener, M.J. Effectiveness of polypropylene fibers on impact and shrinkage cracking behavior of adobe mixes. In Earthen Dwellings and Structures Effectiveness; Reddy, B.V.V., Mani, M., Walker, P., Eds.; Springer: Singapore, 2019; ISBN 978-981-13-5883-8. [Google Scholar]
- Araya-Letelier, G.; Concha-Riedel, J.; Antico, F.C.; Valdés, C.; Cáceres, G. Influence of natural fiber dosage and length on adobe mixes damage-mechanical behavior. Constr. Build. Mater. 2018, 174, 645–655. [Google Scholar] [CrossRef]
- Araya-Letelier, G.; Antico, F.C.; Burbano-Garcia, C.; Concha-Riedel, J.; Norambuena-Contreras, J.; Concha, J.; Saavedra Flores, E.I. Experimental evaluation of adobe mixtures reinforced with jute fibers. Constr. Build. Mater. 2021, 276, 122127. [Google Scholar] [CrossRef]
- Ruxton, G.D. The unequal variance T-test is an underused alternative to student’s t-test and the Mann–Whitney U test. Behav. Ecol. 2006, 17, 688–690. [Google Scholar] [CrossRef]


| Automatic Measurement | Manual Measurement (30 Points) | t-Test Comparison | Image Features | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Image Code | Count | Mean (Pixel) | std (Pixels) | Mean (Pixels) | std (Pixels) | Z-Score | p-Value | Light Type | k | Fiber Type |
| V/1 | 30 | 5.35 | 1.99 | 5.26 | 1.44 | −0.25 | 0.801 | Midday sun | 20 | Vegetal |
| V/2 | 30 | 9.90 | 4.95 | 9.55 | 2.04 | −0.43 | 0.671 | Midday sun | 20 | Vegetal |
| V/3 | 10 | 6.42 | 1.43 | 6.56 | 2.08 | 0.20 | 0.842 | Light (3000 K) | 10 | Vegetal |
| V/4 | 5 | 4.48 | 0.54 | 4.32 | 1.11 | −0.50 | 0.624 | Light (3000 K) | 20 | Vegetal |
| S/1 | 39 | 7.37 | 4.72 | 6.21 | 4.65 | −1.03 | 0.308 | Afternoon Sun | 20 | Industrial |
| A/1 | 75 | 7.28 | 2.40 | 7.80 | 1.87 | 0.88 | 0.386 | Afternoon Sun | 20 | Animal |
| A/2 | 606 | 7.61 | 3.72 | 7.80 | 1.87 | 0.11 | 0.906 | Afternoon Sun | 10 | Animal |
| A/3 | 95 | 8.38 | 3.26 | 8.83 | 3.06 | 0.49 | 0.622 | Light (3000 K) | 20 | Animal |
| A/4 | 192 | 23.15 | 9.39 | 22.71 | 8.22 | −0.31 | 0.761 | Midday sun | 10 | Animal |
| A/5 | 234 | 17.86 | 7.15 | 17.67 | 7.79 | −0.38 | 0.699 | Light (3000 K) | 10 | Animal |
| NoFiber/1 | 95 | 12.43 | 6.36 | 12.47 | 7.39 | −0.39 | 0.694 | Afternoon Sun | 20 | No Fiber |
| NoFiber/2 | 308 | 14.37 | 6.42 | 14.83 | 8.14 | 0.22 | 0.827 | Light (3000 K) | 20 | No Fiber |
| TOTAL | 1719 regions | |||||||||
| Technique | Noise Removal | Length Estimation | Route Tracing (Tortuosity) | Light Source Setup | Spatial Width Distribution | Ref |
|---|---|---|---|---|---|---|
| Edge distance + Linear fit | None (automatic threshold) | No | No | Yes | No | [15] |
| Percolation + Binarization | Percolation processing | No | No | No | No | [16] |
| Percolation + Neighbor boundary | Percolation processing | No | No | No | No | [22] |
| Skeletonization between two points | None (clumping process) | No | Yes | No | No | [23] |
| Digital image correlation (DIC) | None (automatic threshold) | Yes | No | Yes | No | [2] |
| Top-Hat + Otsu Binarization | Gaussian function-based spatial filter | No | No | No | No | [5] |
| Feature extraction and SVM algorithm | Steerable Filter | Yes | No | No | No | [4] |
| Genetic Algorithm | Multi-sequential image filter | Yes | Yes | No | No | [13] |
| Deep Learning | Fast-RCNN + TuFF | No | No | No | No | [29] |
| Hessian structure propagation | None | No | Yes | No | No | [27] |
| Deep Learning | YOLO | Yes | No | Yes | No | [33] |
| filtering + edge searching. | Frangi filtering | Yes | No | No | No | [26] |
| Bwdist transform + Arc Length | Morphological operations (Aperture) | Yes | Yes | Yes | No | [24] |
| M2GLD | Min-Max Gray Level Discrimination | No | No | No | No | [25] |
| Proposed technique | L*a*b + Coherence Filter | Yes | Yes | No | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco, M.; Araya-Letelier, G.; Velázquez, R.; Visconti, P. Image-Based Automated Width Measurement of Surface Cracking. Sensors 2021, 21, 7534. https://doi.org/10.3390/s21227534
Carrasco M, Araya-Letelier G, Velázquez R, Visconti P. Image-Based Automated Width Measurement of Surface Cracking. Sensors. 2021; 21(22):7534. https://doi.org/10.3390/s21227534
Chicago/Turabian StyleCarrasco, Miguel, Gerardo Araya-Letelier, Ramiro Velázquez, and Paolo Visconti. 2021. "Image-Based Automated Width Measurement of Surface Cracking" Sensors 21, no. 22: 7534. https://doi.org/10.3390/s21227534
APA StyleCarrasco, M., Araya-Letelier, G., Velázquez, R., & Visconti, P. (2021). Image-Based Automated Width Measurement of Surface Cracking. Sensors, 21(22), 7534. https://doi.org/10.3390/s21227534









