An Alternative Statistical Characterization of TWDP Fading Model
Abstract
1. Introduction
- 1
- Existing TWDP parameterization is not in accordance with the model’s underlying physical mechanisms,
- 2
- Analytical forms of the existing expressions for PDF and MGF disallow accurate evaluation of the effects of TWDP fading on system performance.
- 1
- We proposed alternative TWDP parameterization, which is in accordance with the model’s underlying physical mechanisms.
- 2
- 3
- We derived the alternative exact form of SNR MGF based on the adopted CDF expression and proposed parameterization, which is shown to be suitable for mathematical manipulations.
- 4
- Based on the obtained MGF, we derived M-ary PSK ASEP in exact infinite-series form, which is, to the best of our knowledge, the first such expression proposed to date.
- 5
- We also derived asymptotic M-ary PSK ASEP as a simple closed-form expression, which tightly follows the exact one for the practical range of SNR values, i.e., for SNR > 20 dB.
2. TWDP Fading Model
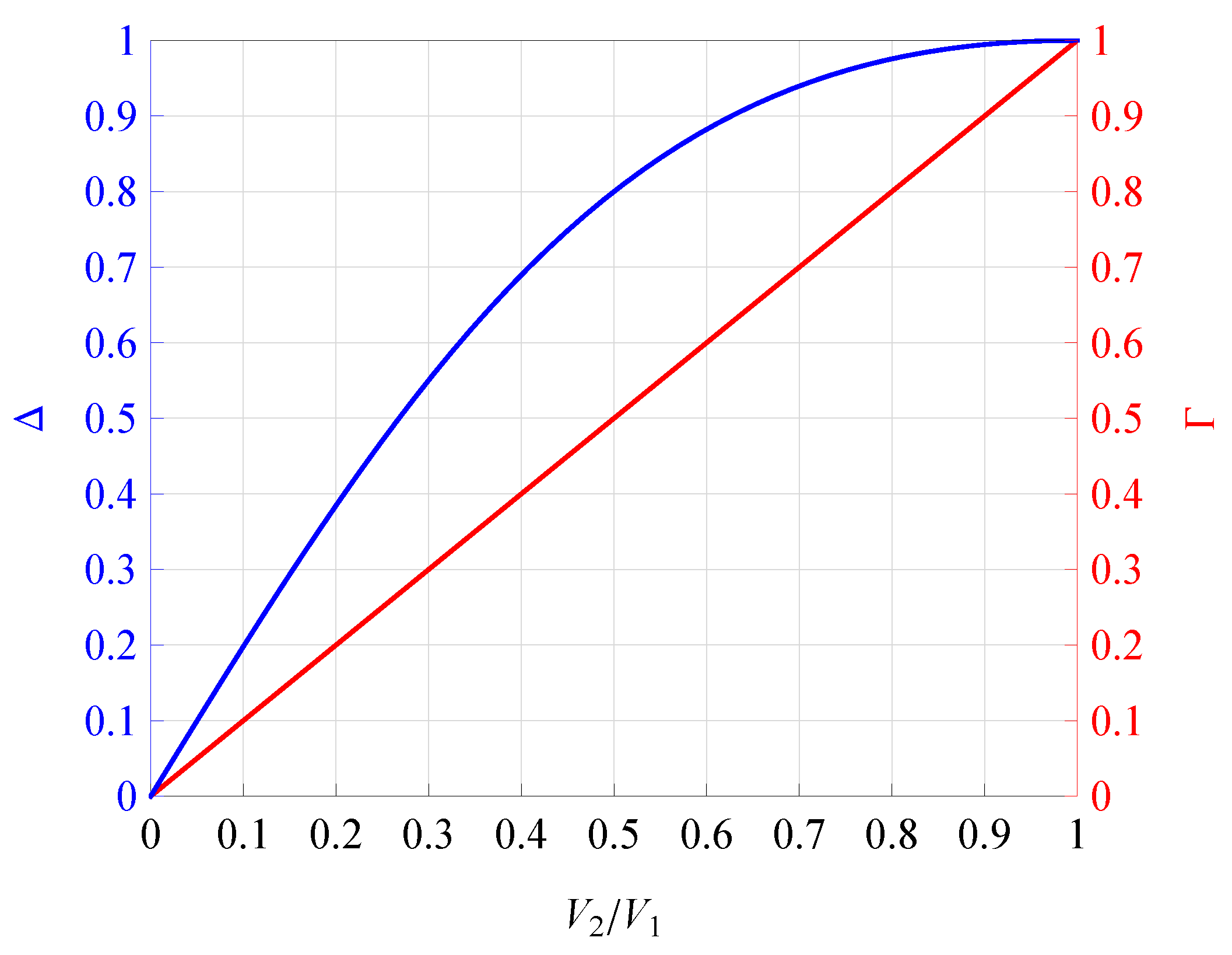
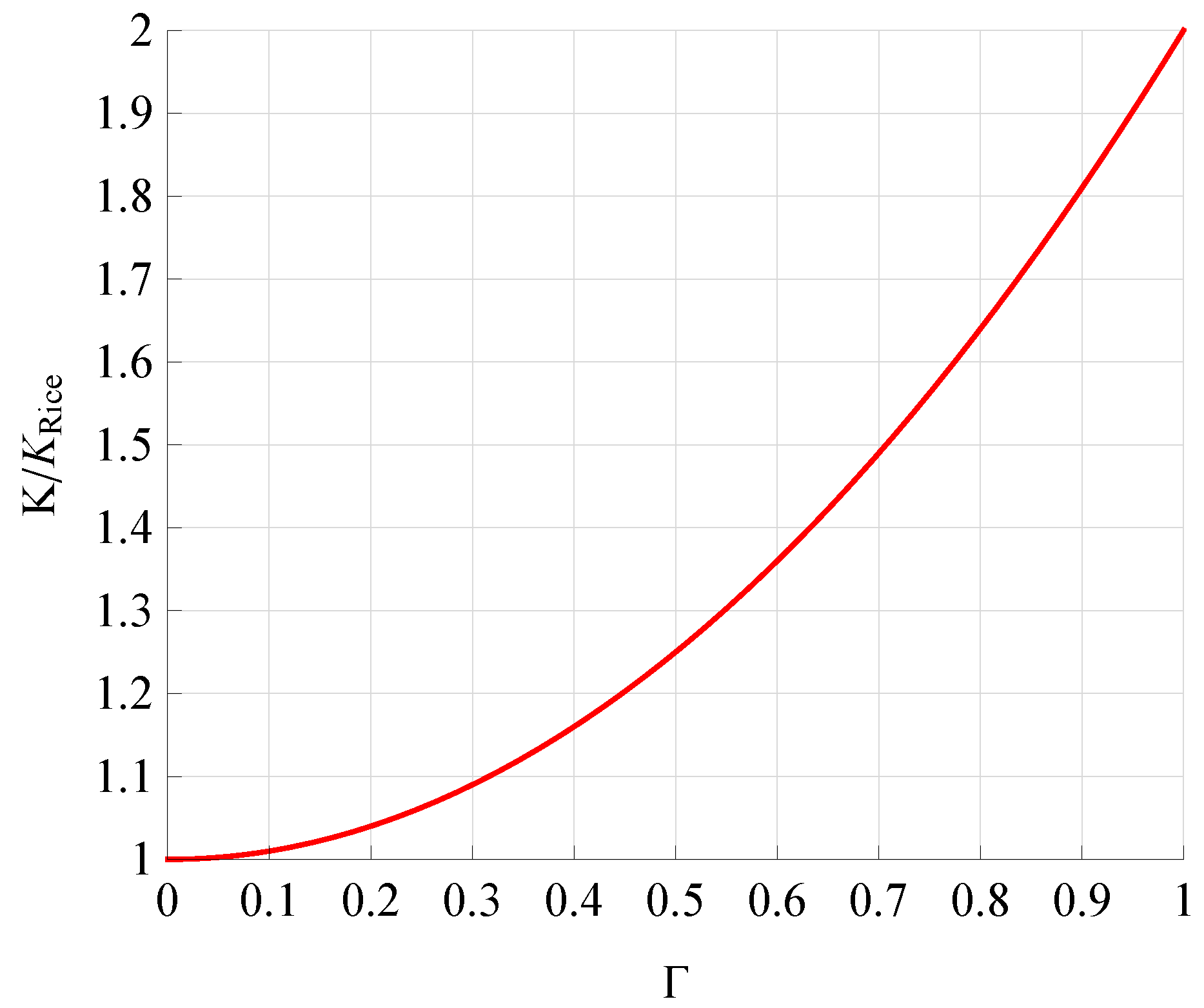
2.1. The Revision of Parameter
2.2. Envelope PDF and CDF Expressions
2.2.1. Special Cases of a TWDP Model
2.2.2. Convergence Analysis
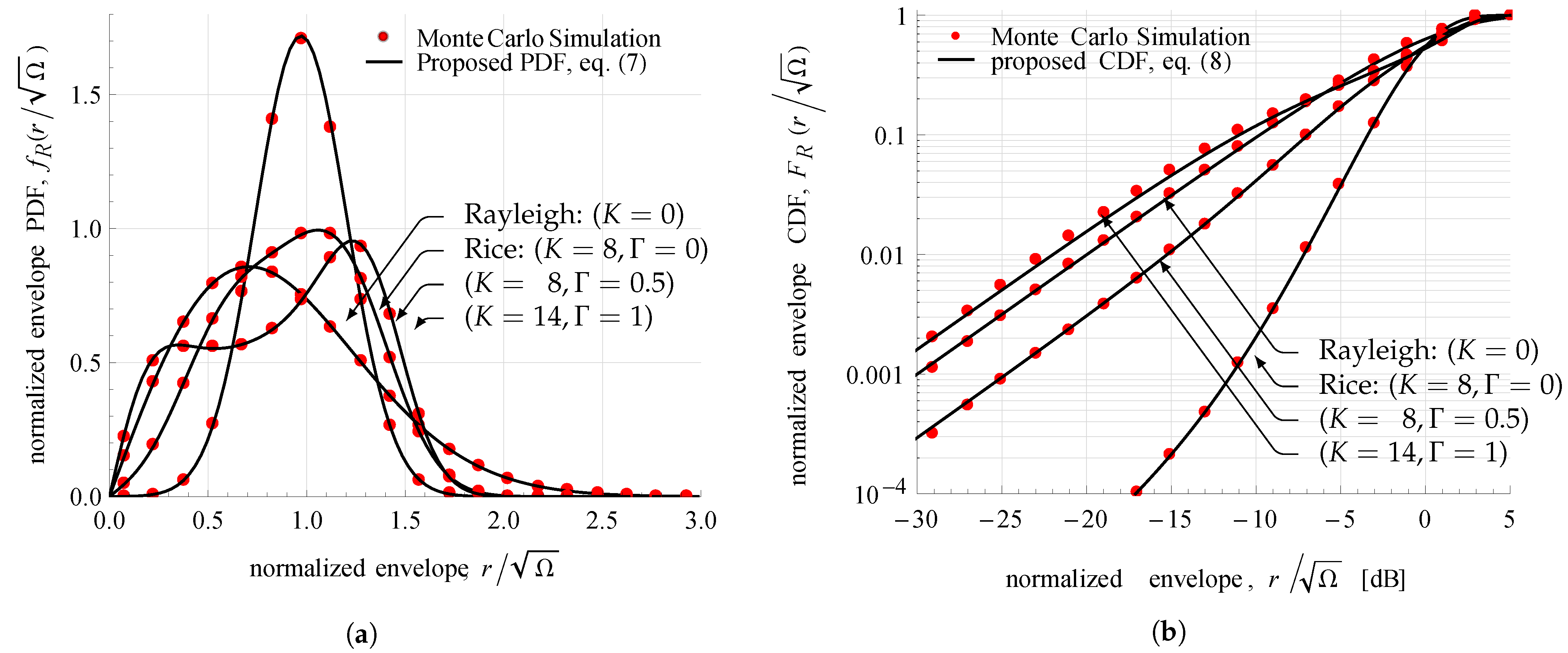
2.2.3. Graphical Results
3. Alternative form of TWDP SNR MGF Expression
4. Error Probability of M-ary PSK Receiver in TWDP Fading Channel
4.1. The Exact M-ary PSK ASEP Expression
4.2. Asymptotic Expression of M-ary PSK ASEP
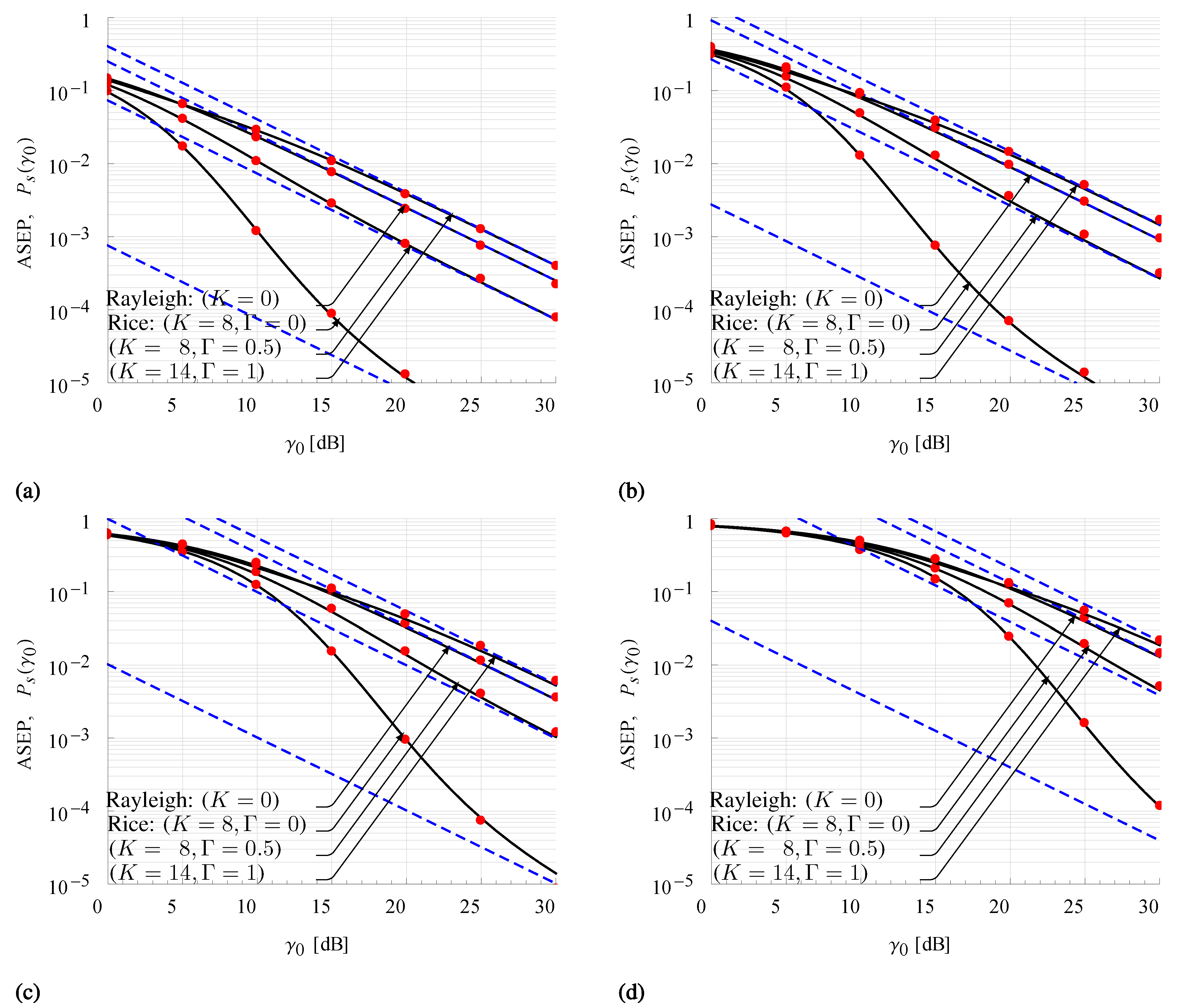
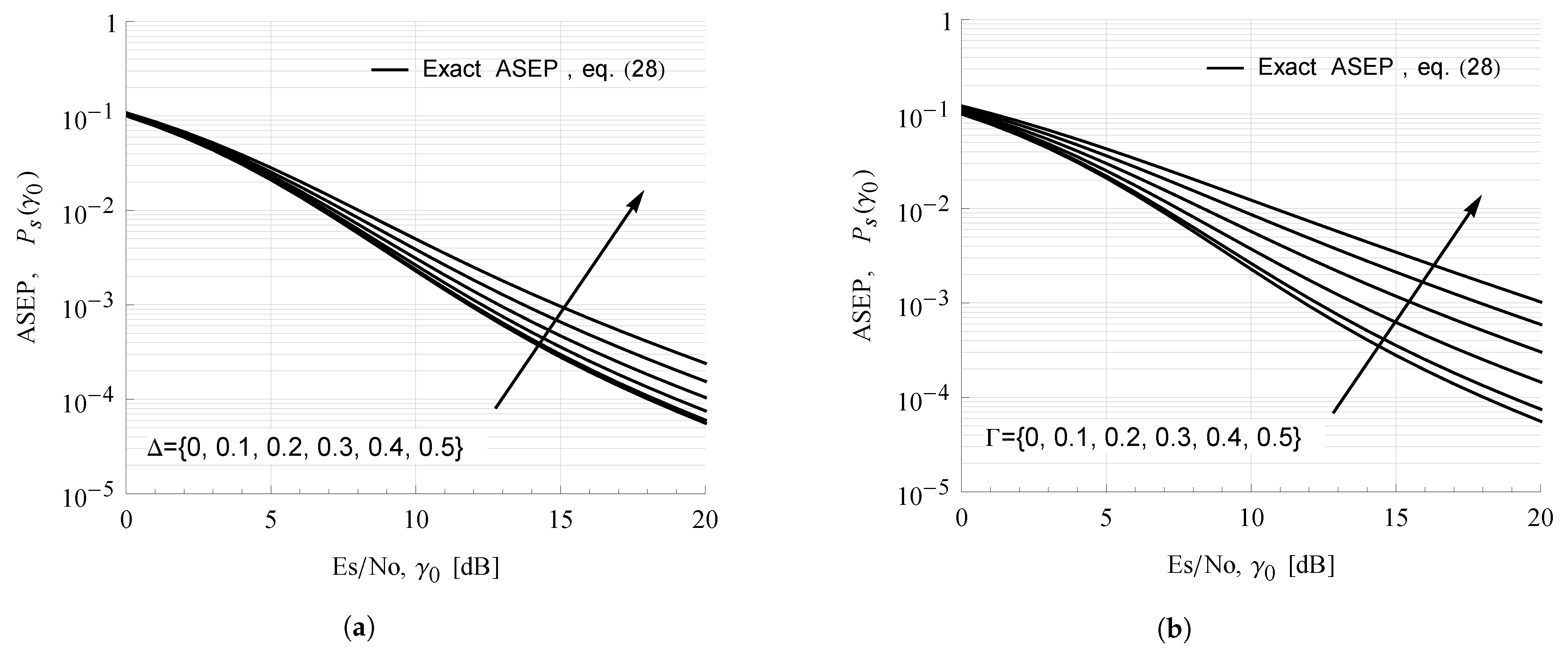
4.3. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Durgin, G.D.; Rappaport, T.S.; de Wolf, D.A. New analytical models and probability density functions for fading in wireless communications. IEEE Trans. Commun. 2002, 50, 1005–1015. [Google Scholar] [CrossRef]
- Rao, M.; Lopez-Martinez, F.J.; Goldsmith, A. Statistics and system performance metrics for the two wave with diffuse power fading model. In Proceedings of the 2014 48th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 19–21 March 2014. [Google Scholar]
- Oh, S.H.; Li, K.H. BER performance of BPSK receivers over two-wave with diffuse power fading channels. IEEE Trans. Wirel. Commun. 2005, 4, 1448–1454. [Google Scholar] [CrossRef]
- Suraweera, H.A.; Lee, W.S.; Oh, S.H. Performance analysis of QAM in a two-wave with diffuse power fading environment. IEEE Commun. Lett. 2008, 12, 109–111. [Google Scholar] [CrossRef]
- Dixit, D.; Sahu, P.R. Performance of QAM signaling over TWDP fading channels. IEEE Trans. Wirel. Commun. 2013, 12, 1794–1799. [Google Scholar] [CrossRef]
- Singh, S.; Kansal, V. Performance of M-ary PSK over TWDP fading channels. Int. J. Electron. Lett. 2016, 4, 433–437. [Google Scholar] [CrossRef]
- Tan, B.S.; Li, K.H.; Teh, K.C. Symbol-error rate of selection combining over two-wave with diffuse power fading. In Proceedings of the 2011 5th International Conference on Signal Processing and Communication Systems (ICSPCS), Honolulu, HI, USA, 12–14 December 2011. [Google Scholar]
- Haghani, S. Average BER of BFSK with postdetection switch-and-stay combining in TWDP fading. In Proceedings of the 2011 IEEE Vehicular Technology Conference (VTC Fall), San Francisco, CA, USA, 5–8 September 2011. [Google Scholar]
- Lee, W.S.; Oh, S.H. Performance of dual switch-and-stay diversity NCFSK systems over two-Wave with diffuse power fading channels. In Proceedings of the 2007 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007. [Google Scholar]
- Haghani, S.; Dashtestani, H. BER of noncoherent MFSK with postdetection switch-and-stay combining in TWDP fading. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2011. [Google Scholar]
- Oh, S.H.; Li, K.H.; Lee, W.S. Performance of BPSK pre-detection MRC systems over two-wave with diffuse power fading channels. IEEE Trans. Wirel. Commun. 2007, 6, 2772–2775. [Google Scholar] [CrossRef]
- Subadara, R.; Singh, A.D. Performance of M-MRC receivers over TWDP fading channels. Int. J. Electron. Commun. 2014, 68, 569–572. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, N. Symbol error probability of QAM with MRC diversity in two-wave with diffuse power fading channels. IEEE Commun. Lett. 2011, 15, 10–12. [Google Scholar] [CrossRef]
- Lee, W.S. Performance of postdetection EGC NCFSK and DPSK systems over two-wave with diffuse power fading channels. In Proceedings of the 2007 International Symposium on Communications and Information Technologies, Sydney, NSW, Australia, 17–19 October 2007. [Google Scholar]
- Kim, D.; Lee, H.; Kang, J. Comprehensive analysis of the impact of TWDP fading on the achievable error rate performance of BPSK signaling. IEICE Trans. Commun. 2018, E101.B, 500–507. [Google Scholar] [CrossRef]
- Rao, M.; Lopez-Martinez, F.J.; Alouini, M.; Goldsmith, A. MGF approach to the analysis of generalized two-ray fading models. IEEE Trans. Wirel. Commun. 2015, 14, 2548–2561. [Google Scholar]
- Ermolova, N.Y. Capacity analysis of Two-Wave with Diffuse Power Fading channels using a mixture of Gamma distributions. IEEE Commun. Lett. 2016, 20, 2245–2248. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, W.; Li, X.; Sun, Q.; Peppas, K.P. New results on the Fluctuating Two-Ray model with arbitrary fading parameters and its applications. IEEE Trans. Veh. Technol. 2018, 67, 2766–2770. [Google Scholar] [CrossRef]
- Hashemi, H.; Haghighat, J.; Eslami, M.; Hamouda, W.A. Analysis of equal gain combining over Fluctuating Two-Ray channels with applications to millimeter-wave communications. IEEE Trans. Veh. Technol. 2020, 69, 1751–1765. [Google Scholar] [CrossRef]
- Bilim, M.; Kapucu, N. Average symbol error rate analysis of QAM schemes over millimeter wave Fluctuating Two-Ray fading channels. IEEE Access 2019, 7, 105746–105754. [Google Scholar] [CrossRef]
- Rappaport, T.; Heath, R.; Daniels, R.; Murdock, J. Millimeter Wave Wireless Communications; Prentice Hall: Upper Saddle River, NJ, USA, 2015. [Google Scholar]
- Frolik, J. A case for considering hyper-Rayleigh fading channels. IEEE Trans. Wirel. Commun. 2007, 6, 1235–1239. [Google Scholar] [CrossRef]
- Zöchmann, E.; Blumenstein, J.; Marsalek, R.; Rupp, M.; Guan, K. Parsimonious channel models for millimeter wave railway communications. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar]
- Zöchmann, E.; Hofer, M.; Lerch, M.; Pratschner, S.; Bernadó, L.; Blumenstein, J.; Caban, S.; Sangodoyin, S.; Groll, H.; Zemen, T.; et al. Position-specific statistics of 60 GHz vehicular channels during overtaking. IEEE Access 2019, 7, 14216–14232. [Google Scholar] [CrossRef]
- Zöchmann, E.; Caban, S.; Mecklenbräuker, C.F.; Pratschner, S.; Lerch, M.; Schwarz, S.; Rupp, M. Better than Rician: Modelling millimetre wave channels as two-wave with diffuse power. EURASIP J. Wirel. Commun. Netw. 2019, 2019. [Google Scholar] [CrossRef]
- Mavridis, T.; Petrillo, L.; Sarrazin, J.; Benlarbi-Delaï, A.; De Doncker, P. Near-body shadowing analysis at 60 GHz. IEEE Trans. Antennas Propag. 2015, 63, 4505–4511. [Google Scholar] [CrossRef]
- Frolik, J. On appropriate models for characterizing hyper-Rayleigh fading. IEEE Trans. Wirel. Commun. 2008, 7, 5202–5207. [Google Scholar] [CrossRef]
- Laishram, M.D.; Aheibam, D.S. Performance of dual-branch selection combining receiver over Fluctuating Two-Ray (FTR) fading channels for 5G mmWave communications. AEU-Int. J. Electron. Commun. 2020, 117, 153093. [Google Scholar] [CrossRef]
- Al-Hmood, H.; Al-Raweshidy, H.S. Performance analysis of mmWave communications with selection combining over Fluctuating-Two Ray fading model. IEEE Commun. Lett. 2021, 25, 2531–2535. [Google Scholar] [CrossRef]
- Kostic, I.M. Envelope probability density function of the sum of signal, noise and interference. Electron. Lett. 1978, 14, 490–491. [Google Scholar] [CrossRef]
- Kostic, I.M. Envelope probability distribution of the sum of signal, noise and interference. In Proceedings of the TELFOR 96 Conference, Beograd, Serbia, 26–28 November 1996; pp. 301–303. [Google Scholar]
- Kostic, I.M. Private Communication, 2020.
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- András, S.; Baricz, A.; Sun, Y. The generalized Marcum Q-function: An orthogonal polynomial approach. Acta Univ. Sapientiae Mathematica 2011, 3, 60–76. [Google Scholar]
- Joshi, C.M.; Bissu, S.K. Some inequalities of Bessel and modified Bessel functions. J. Aust. Math. Soc. 1991, 50, 490–491. [Google Scholar] [CrossRef]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2005. [Google Scholar]
- Wolfram Mathematica. Available online: https://functions.wolfram.com/07.23.03.0080.01 (accessed on 14 October 2020).
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series: Direct Laplace Transforms; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1992; Volume 4. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, 10th ed.; US Government Printing Office: Washington, DC, USA, 1972. [Google Scholar]
- Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Hypergeometric Summation and Special Function Identities; Advanced Lectures in Mathematics; Springer Fachmedien Wiesbaden: Braunschweig/Wiesbaden, Germany, 1998. [Google Scholar]
- Steidley, K.D. Table of 2F1(a, b; c; z) for a = 0(1/2)7, b = 0(1/2)7 and c = 0(1/2)5/2 with Comments on Closed Forms of 2F1(a, b; c; z); National Aeronautics and Space Administration: Washington, DC, USA, 1963. [Google Scholar]
- Shayesteh, M.; Aghamohammadi, A. On the error probability of linearly modulated signals on frequency-flat Ricean, Rayleigh, and AWGN channels. IEEE Trans. Commun. 1995, 43, 1454–1466. [Google Scholar] [CrossRef]
- Pauw, C.; Schilling, D. Probability of error of M-ary PSK and DPSK on a Rayleigh fading channel. IEEE Trans. Commun. 1988, 36, 755–756. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maric, A.; Kaljic, E.; Njemcevic, P. An Alternative Statistical Characterization of TWDP Fading Model. Sensors 2021, 21, 7513. https://doi.org/10.3390/s21227513
Maric A, Kaljic E, Njemcevic P. An Alternative Statistical Characterization of TWDP Fading Model. Sensors. 2021; 21(22):7513. https://doi.org/10.3390/s21227513
Chicago/Turabian StyleMaric, Almir, Enio Kaljic, and Pamela Njemcevic. 2021. "An Alternative Statistical Characterization of TWDP Fading Model" Sensors 21, no. 22: 7513. https://doi.org/10.3390/s21227513
APA StyleMaric, A., Kaljic, E., & Njemcevic, P. (2021). An Alternative Statistical Characterization of TWDP Fading Model. Sensors, 21(22), 7513. https://doi.org/10.3390/s21227513





