A Self-Calibration Stitching Method for Pitch Deviation Evaluation of a Long-Range Linear Scale by Using a Fizeau Interferometer
Abstract
:1. Introduction
2. Principle
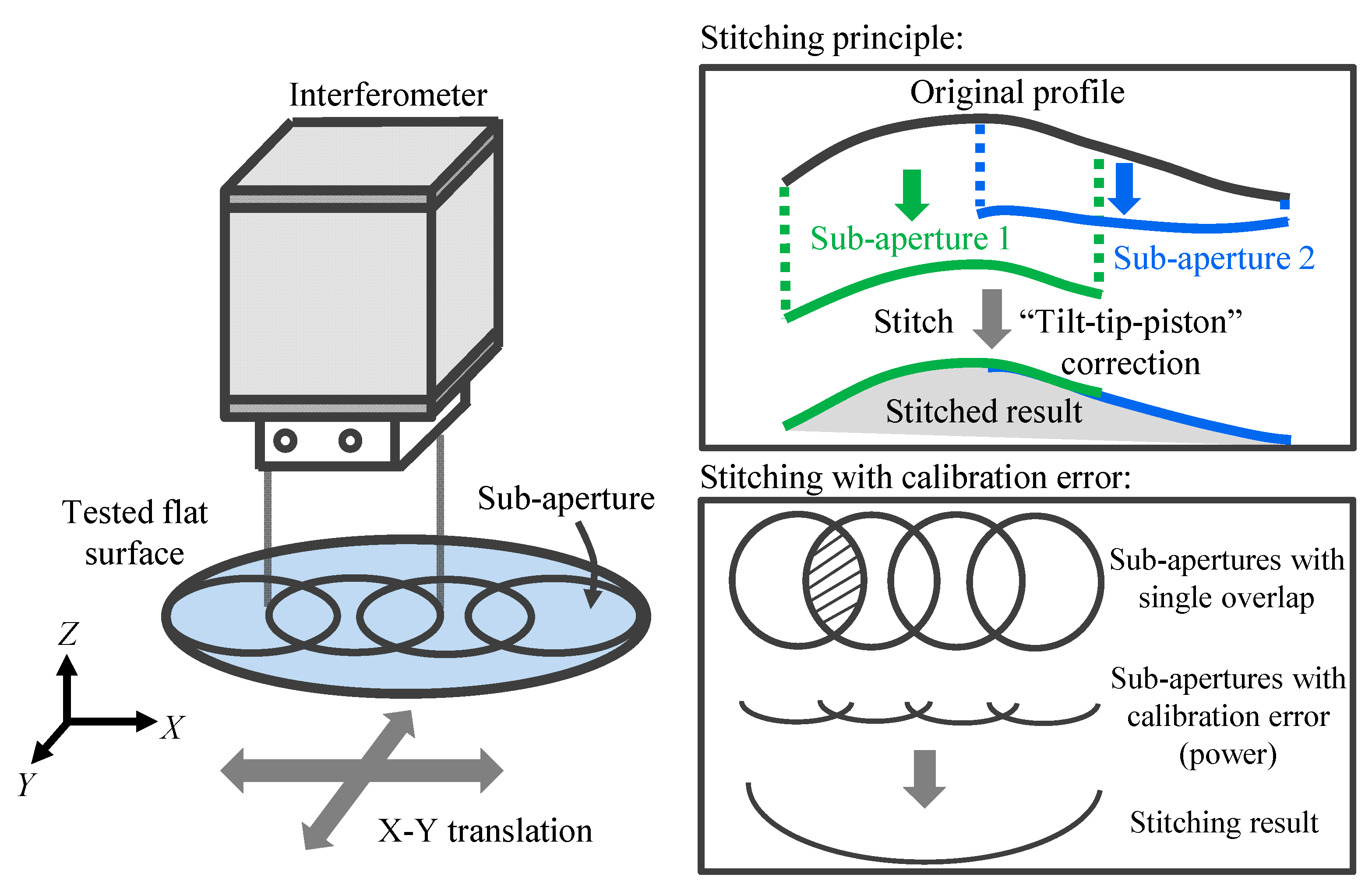
2.1. Basic Principle of Z-Directional Surface Form Stitching Interferometry
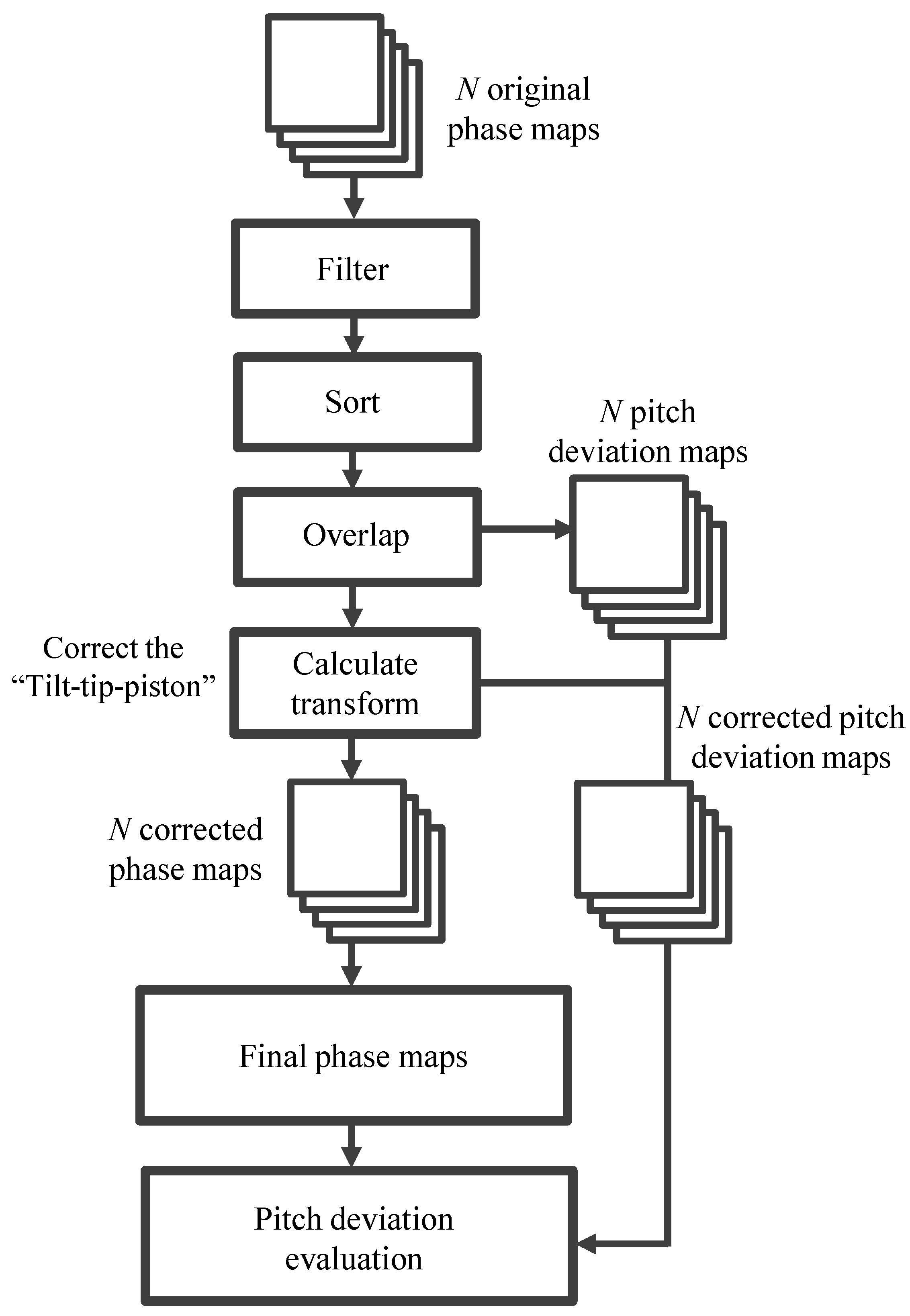
2.2. Self-Calibrated Stitching of X-Directional Pitch Deviation of the Long-Range Linear Scale
3. Simulations
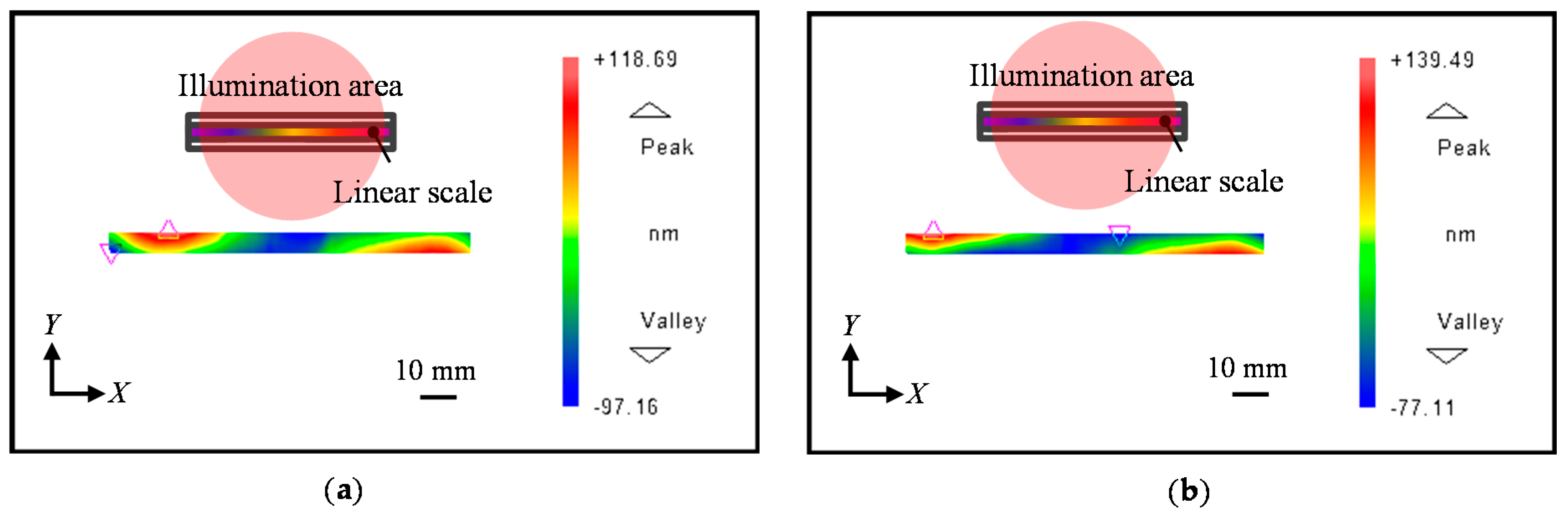
4. Experiments
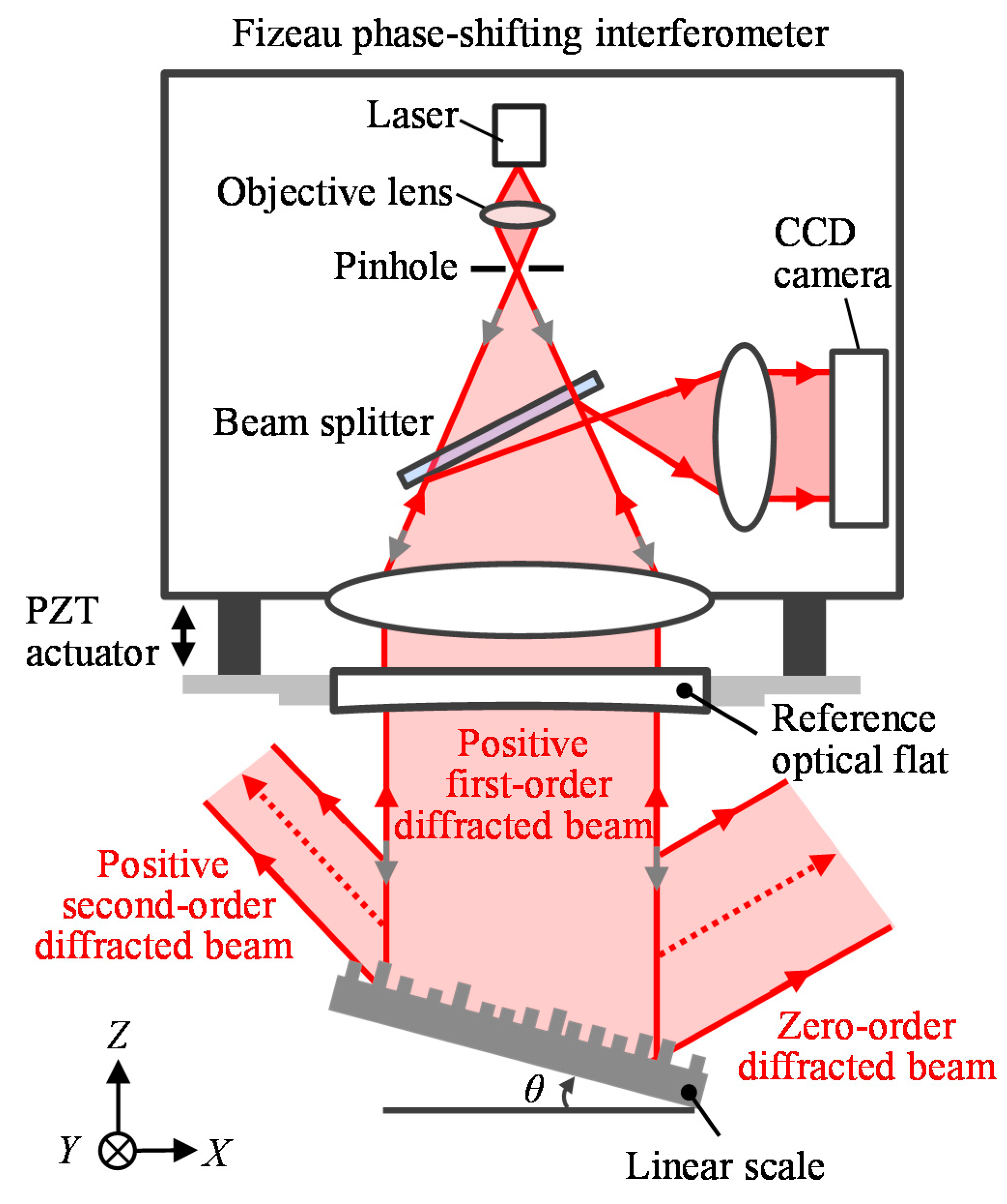
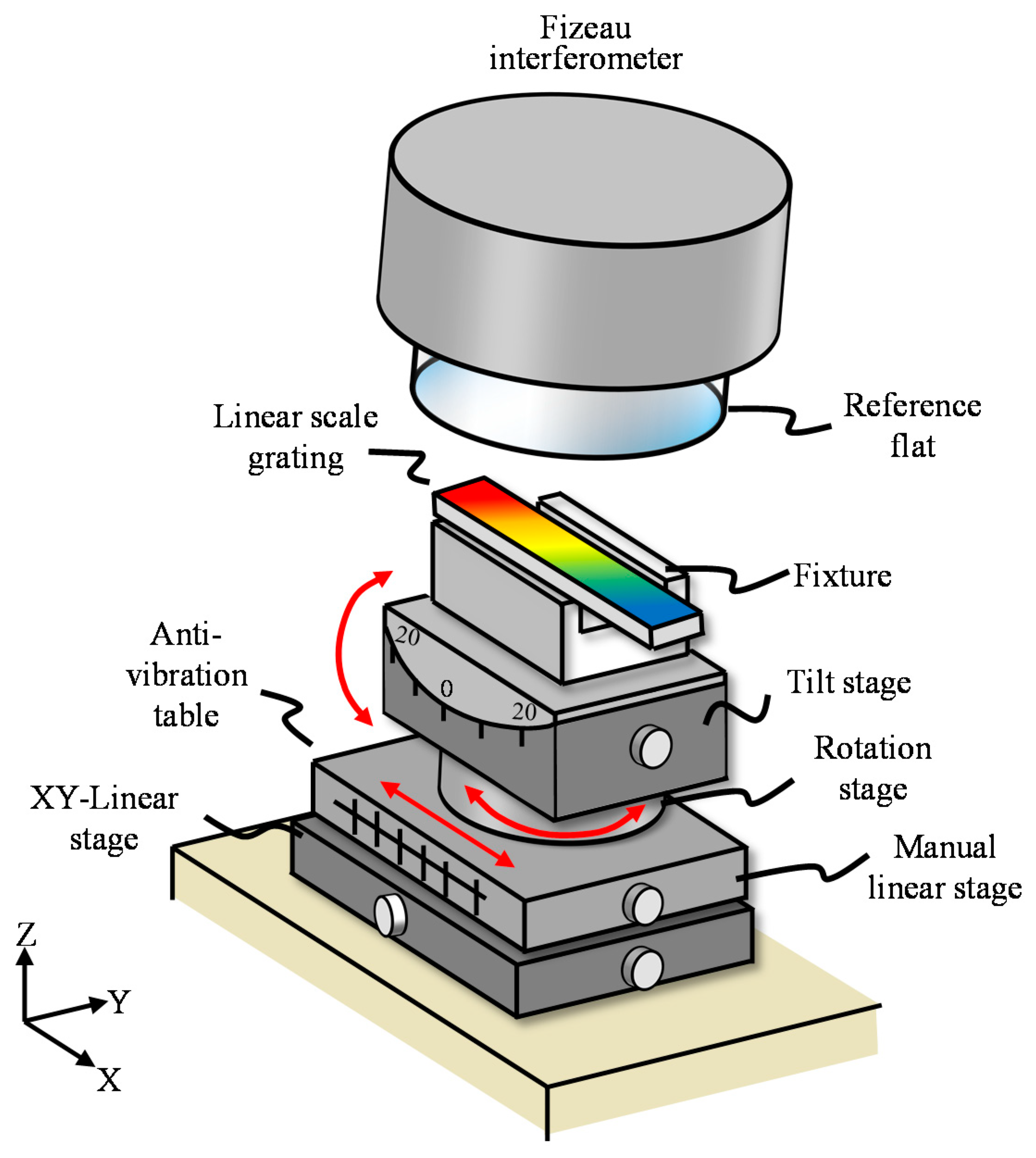
4.1. Experimental Setup
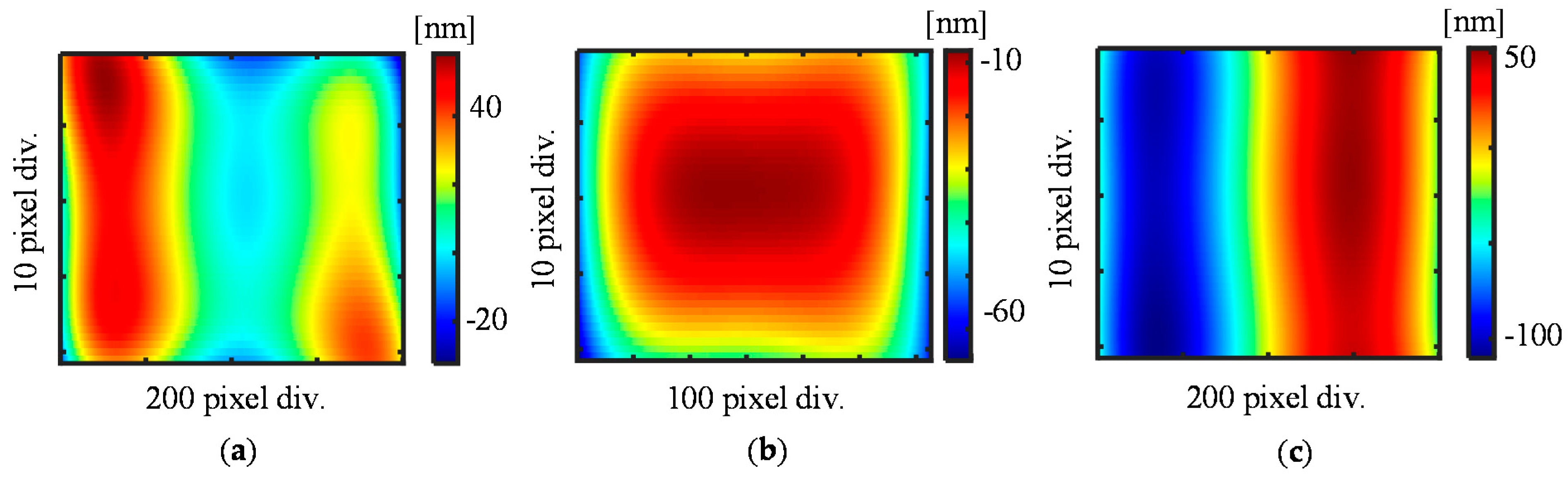
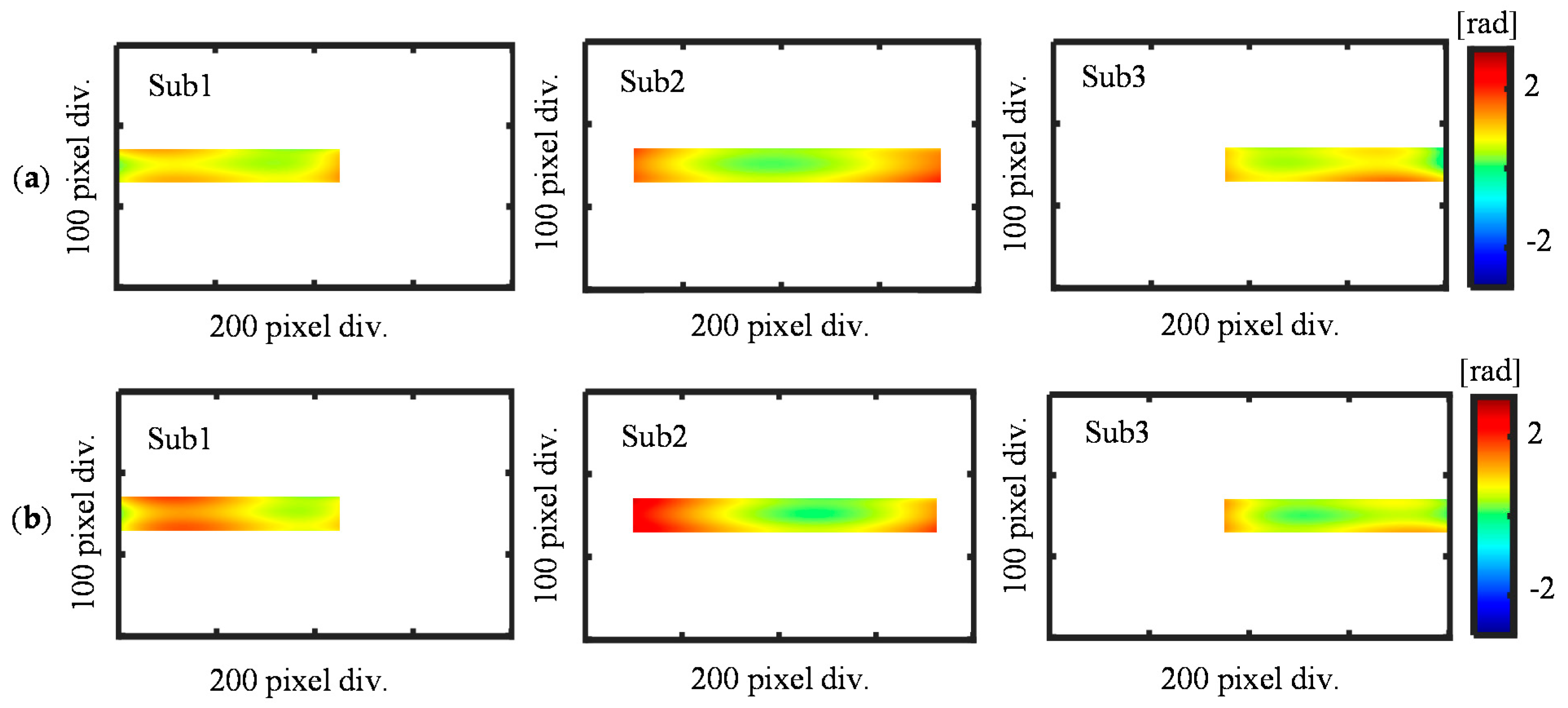
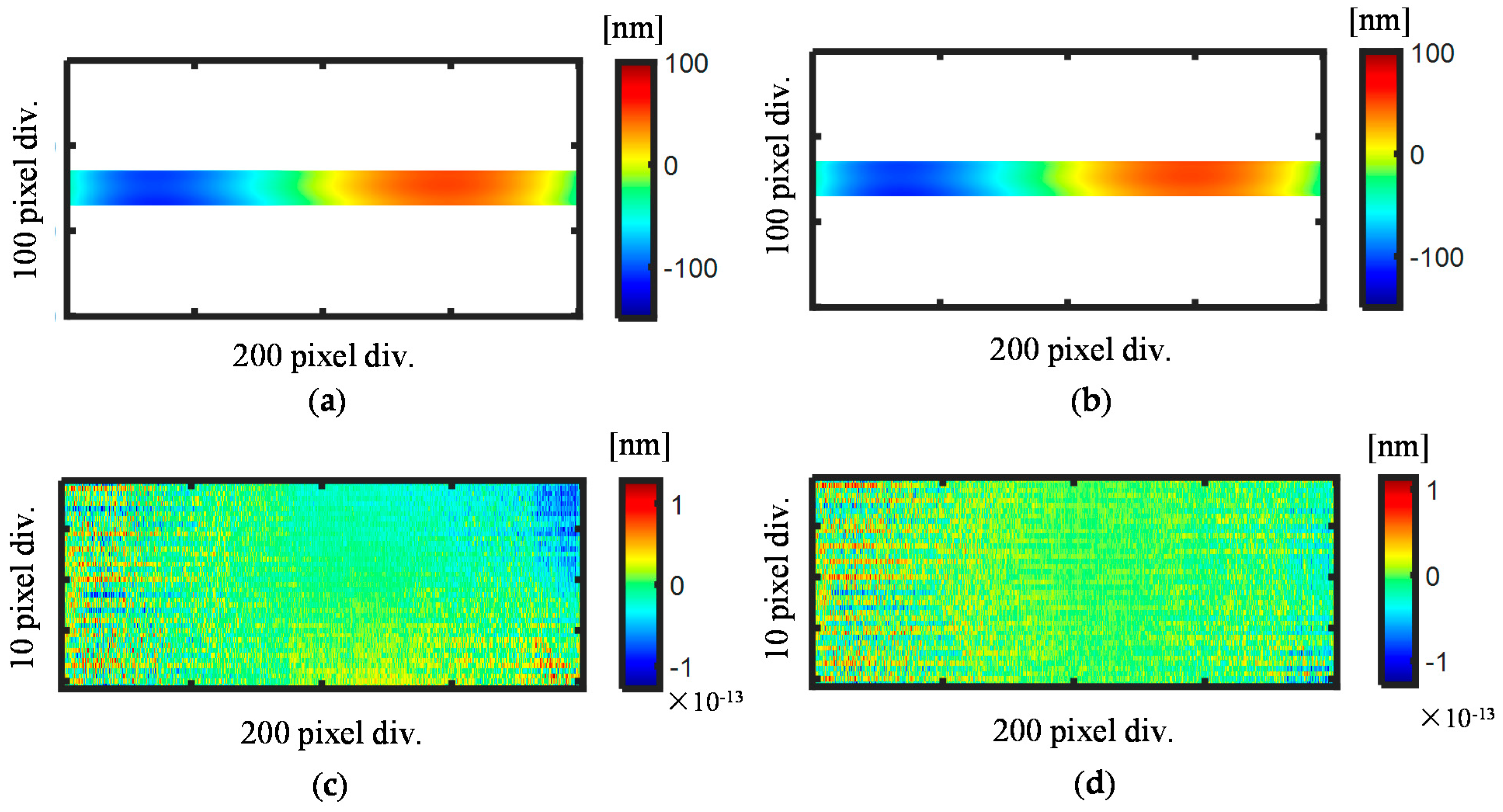
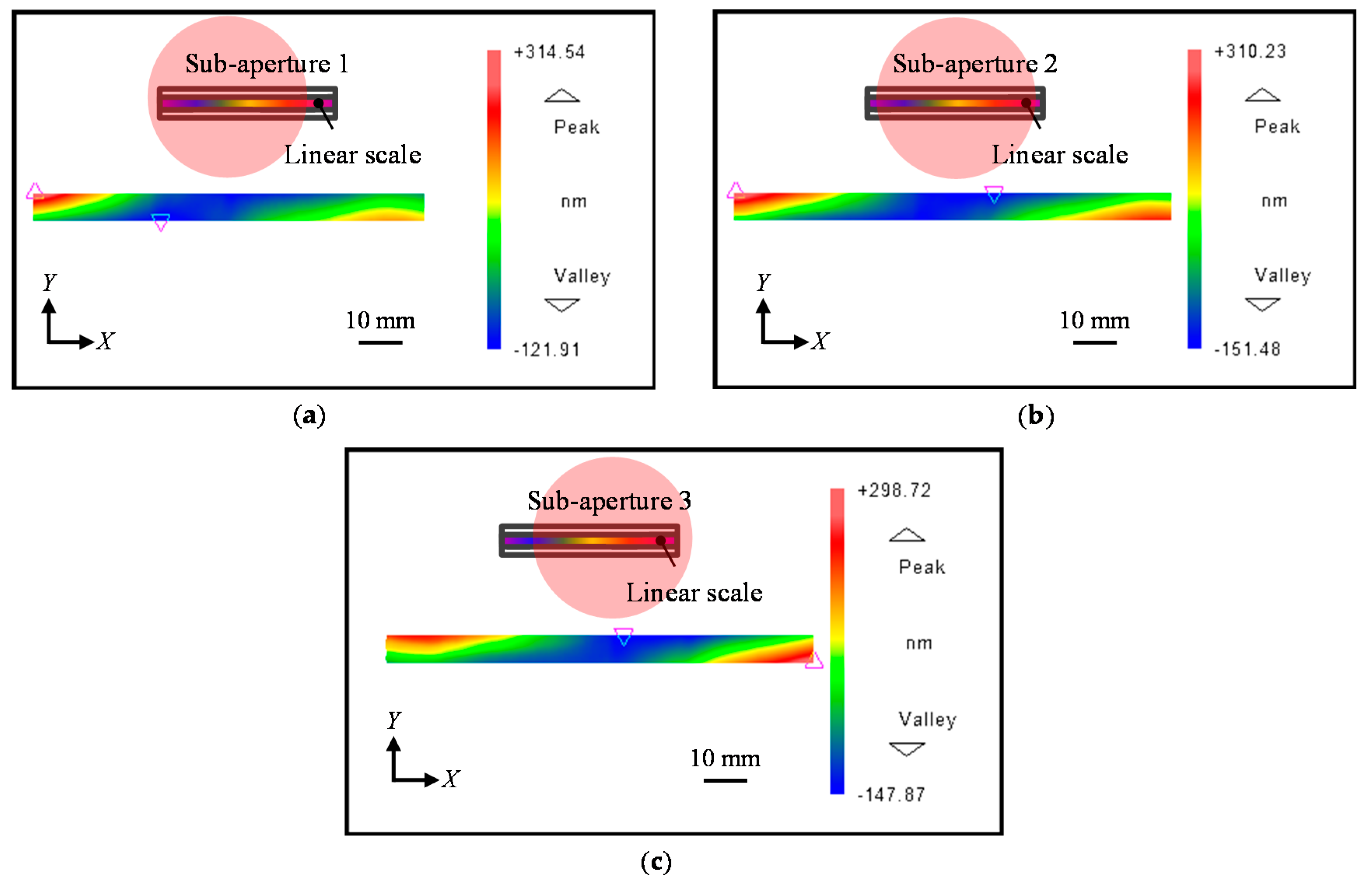
4.2. Experiment Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Gao, W.; Kim, S.-W.; Bosse, H.; Haitjema, H.; Chen, Y.; Lu, X.; Knapp, W.; Weckenmann, A.; Estler, W.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.; Leach, R.; Cheung, C.; Savio, E.; Linares, J. On-machine and in-process surface metrology for precision manufacturing. CIRP Ann. 2019, 68, 843–866. [Google Scholar] [CrossRef] [Green Version]
- Schwenke, H.; Schmitt, R.; Jatzkowski, P.; Warmann, C. On-the-fly calibration of linear and rotary axes of machine tools and CMMs using a tracking interferometer. CIRP Ann. 2009, 58, 477–480. [Google Scholar] [CrossRef]
- Fan, K.-C.; Li, R.-J.; Xu, P. Design and Verification of Micro/Nano-Probes for Coordinate Measuring Machines. Nanomanufacturing Metrol. 2018, 2, 1–15. [Google Scholar] [CrossRef]
- Linear Encoder Products—Sealed and Enclosed—HEIDENHAIN. Available online: https://www.heidenhain.us/product/linear-encoders-for-length-measurement/ (accessed on 10 July 2021).
- Gao, W.; Araki, T.; Kiyono, S.; Okazaki, Y.; Yamanaka, M. Precision nano-fabrication and evaluation of a large area sinusoidal grid surface for a surface encoder. Precis. Eng. 2003, 27, 289–298. [Google Scholar] [CrossRef]
- Kunzmann, H.; Pfeifer, T.; Flügge, J. Scales vs. Laser Interferometers Performance and Comparison of Two Measuring Systems. CIRP Ann. 1993, 42, 753–767. [Google Scholar] [CrossRef]
- Teimel, A. Technology and applications of grating interferometers in high-precision measurement. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Fleming, A. A review of nanometer resolution position sensors: Operation and performance. Sens. Actuators A Phys. 2013, 190, 106–126. [Google Scholar] [CrossRef]
- Bosse, H.; Häßler-Grohne, W.; Flügge, J.; Köning, R. Final report on CCL-S3 supplementary line scale comparison Nano3. Metrologia 2003, 40, 04002. [Google Scholar] [CrossRef]
- Sawabe, M.; Maeda, F.; Yamaryo, Y.; Simomura, T.; Saruki, Y.; Kubo, T.; Sakai, H.; Aoyagi, S. A new vacuum interferometric comparator for calibrating the fine linear encoders and scales. Precis. Eng. 2004, 28, 320–328. [Google Scholar] [CrossRef]
- Coveney, T. A review of state-of-the-art 1D length scale calibration instruments. Meas. Sci. Technol. 2019, 31, 042002. [Google Scholar] [CrossRef]
- Chen, X.; Koenders, L. A novel pitch evaluation of one-dimensional gratings based on a cross-correlation filter. Meas. Sci. Technol. 2014, 25, 044007. [Google Scholar] [CrossRef] [Green Version]
- Dai, G.; Koenders, L.; Fluegge, J.; Hemmleb, M. Fast and accurate: High-speed metrological large-range AFM for surface and nanometrology. Meas. Sci. Technol. 2018, 29, 054012. [Google Scholar] [CrossRef] [Green Version]
- Klapetek, P.; Valtr, M.; Picco, L.; Payton, O.; Martinek, J.; Yacoot, A.; Miles, M. Large area high-speed metrology SPM system. Nanotechnology 2015, 26, 065501. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Kimura, A. A fast evaluation method for pitch deviation and out-of-flatness of a planar scale grating. CIRP Ann. 2010, 59, 505–508. [Google Scholar] [CrossRef]
- Chen, X.; Shimizu, Y.; Xiong, X.; Chen, Y.-L.; Gao, W. Self-calibration of Fizeau interferometer and planar scale gratings in Littrow setup. Opt. Express 2017, 25, 21567–21582. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Matsukuma, H.; Shimizu, Y.; Gao, W. Evaluation of the pitch deviation of a linear scale based on a self-calibration method with a Fizeau interferometer. Meas. Sci. Technol. 2020, 31, 094002. [Google Scholar] [CrossRef]
- Xiong, X.; Shimizu, Y.; Chen, X.; Matsukuma, H.; Gao, W. Uncertainty Evaluation for Measurements of Pitch Deviation and Out-of-Flatness of Planar Scale Gratings by a Fizeau Interferometer in Littrow Configuration. Appl. Sci. 2018, 8, 2539. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Zhang, G. A review of interferometry for geometric measurement. Meas. Sci. Technol. 2018, 29, 102001. [Google Scholar] [CrossRef]
- Vannoni, M.; Martín, I.F. Large aperture Fizeau interferometer commissioning and preliminary measurements of a long x-ray mirror at European X-ray Free Electron Laser. Rev. Sci. Instrum. 2016, 87, 51901. [Google Scholar] [CrossRef] [Green Version]
- Bray, M. Stitching interferometry and absolute surface shape metrology: Similarities. Int. Symp. Opt. Sci. Technol. 2001, 4451, 375–383. [Google Scholar] [CrossRef]
- Huang, L.; Idir, M.; Zuo, C.; Wang, T.; Tayabaly, K.; Lippmann, E. Two-dimensional stitching interferometry based on tilt measurement. Opt. Express 2018, 26, 23278–23286. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Xu, H.; Yu, Y.; Chen, M. Stitching interferometry for cylindrical optics with large angular aperture. Meas. Sci. Technol. 2015, 26, 025204. [Google Scholar] [CrossRef]
- Huang, L.; Wang, T.; Tayabaly, K.; Kuhne, D.; Xu, W.; Xu, W.; Vescovi, M.; Idir, M. Stitching interferometry for synchrotron mirror metrology at National Synchrotron Light Source II (NSLS-II). Opt. Lasers Eng. 2020, 124, 105795. [Google Scholar] [CrossRef]
- Yumoto, H.; Koyama, T.; Matsuyama, S.; Yamauchi, K.; Ohashi, H. Stitching interferometry for ellipsoidal x-ray mirrors. Rev. Sci. Instrum. 2016, 87, 051905. [Google Scholar] [CrossRef]
- Chen, S.; Dai, Y.; Li, S.; Peng, X.; Wang, J. Error reductions for stitching test of large optical flats. Opt. Laser Technol. 2012, 44, 1543–1550. [Google Scholar] [CrossRef]
- Bray, M. Stitching interferometry: The practical side of things. Opt. Eng. Appl. 2009, 7426, 74260Q. [Google Scholar] [CrossRef]
- Bray, M. Stitching interferometry: How and why it works. Opt. Syst. Des. Prod. 1999, 3739, 259–273. [Google Scholar] [CrossRef]
- Murphy, P.; Forbes, G.; Fleig, J.; Dumas, P.; Tricard, M. Stitching Interferometry: A Flexible Solution for Surface Metrology. Opt. Photon-News 2003, 14, 38–43. [Google Scholar] [CrossRef]
- Chen, S.; Wu, C.; Tie, G.; Zhai, D. Stitching test of large flats by using two orthogonally arranged wavefront interferometers. Appl. Opt. 2017, 56, 9193. [Google Scholar] [CrossRef]
- Zhao, C.; Burge, J.H. Stitching of off-axis sub-aperture null measurements of an aspheric surface. Opt. Eng. Appl. 2008, 7063, 706316. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Q.; Peng, X.; Yu, Y. Stitching interferometry of high numerical aperture cylindrical optics without using a fringe-nulling routine. J. Opt. Soc. Am. A 2015, 32, 1964–1972. [Google Scholar] [CrossRef] [PubMed]
- Okada, K.; Otsubo, M.; Tsujiuchi, J. Measurement of large plane surface shapes by connecting small-aperture interferograms. Opt. Eng. 1994, 33, 608–613. [Google Scholar] [CrossRef]
- Wiegmann, A.; Stavridis, M.; Walzel, M.; Siewert, F.; Zeschke, T.; Schulz, M.; Elster, C. Accuracy evaluation for sub-aperture interferometry measurements of a synchrotron mirror using virtual experiments. Precis. Eng. 2011, 35, 183–190. [Google Scholar] [CrossRef]
- Xue, J.; Huang, L.; Gao, B.; Kaznatcheev, K.; Idir, M. One-dimensional stitching interferometry assisted by a triple-beam interferometer. Opt. Express 2017, 25, 9393–9405. [Google Scholar] [CrossRef]
- De Groot, P.J. Correlated errors in phase-shifting laser Fizeau interferometry. Appl. Opt. 2014, 53, 4334. [Google Scholar] [CrossRef] [PubMed]
- Crimmins, T.R. Geometric filter for speckle reduction. Appl. Opt. 1985, 24, 1438–1443. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Quan, L.; Shimizu, Y.; Matsukuma, H.; Gao, W. Self-calibration of a variable-line-spacing grating for an absolute optical encoder with a Fizeau interferometer. Meas. Sci. Technol. 2021, 32, 064005. [Google Scholar] [CrossRef]






| a | b | c | |
|---|---|---|---|
| IX+1,1 | −2.06 | −8.24 | −0.59 |
| IX+1,3 | 1.95 | 8.37 | −0.39 |
| IX−1,1 | −2.29 | −10.44 | −0.66 |
| IX−1,3 | 2.25 | 9.98 | −0.33 |
| eX,1 | 28.80 | 280.04 | 8.47 |
| eX,3 | −38.62 | −204.10 | −7.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, X.; Shimizu, Y.; Matsukuma, H.; Gao, W. A Self-Calibration Stitching Method for Pitch Deviation Evaluation of a Long-Range Linear Scale by Using a Fizeau Interferometer. Sensors 2021, 21, 7412. https://doi.org/10.3390/s21217412
Xiong X, Shimizu Y, Matsukuma H, Gao W. A Self-Calibration Stitching Method for Pitch Deviation Evaluation of a Long-Range Linear Scale by Using a Fizeau Interferometer. Sensors. 2021; 21(21):7412. https://doi.org/10.3390/s21217412
Chicago/Turabian StyleXiong, Xin, Yuki Shimizu, Hiraku Matsukuma, and Wei Gao. 2021. "A Self-Calibration Stitching Method for Pitch Deviation Evaluation of a Long-Range Linear Scale by Using a Fizeau Interferometer" Sensors 21, no. 21: 7412. https://doi.org/10.3390/s21217412
APA StyleXiong, X., Shimizu, Y., Matsukuma, H., & Gao, W. (2021). A Self-Calibration Stitching Method for Pitch Deviation Evaluation of a Long-Range Linear Scale by Using a Fizeau Interferometer. Sensors, 21(21), 7412. https://doi.org/10.3390/s21217412








