Optimized Classification of Suspended Particles in Seawater by Dense Sampling of Polarized Light Pulses
Abstract
:1. Introduction
2. Methods and Materials
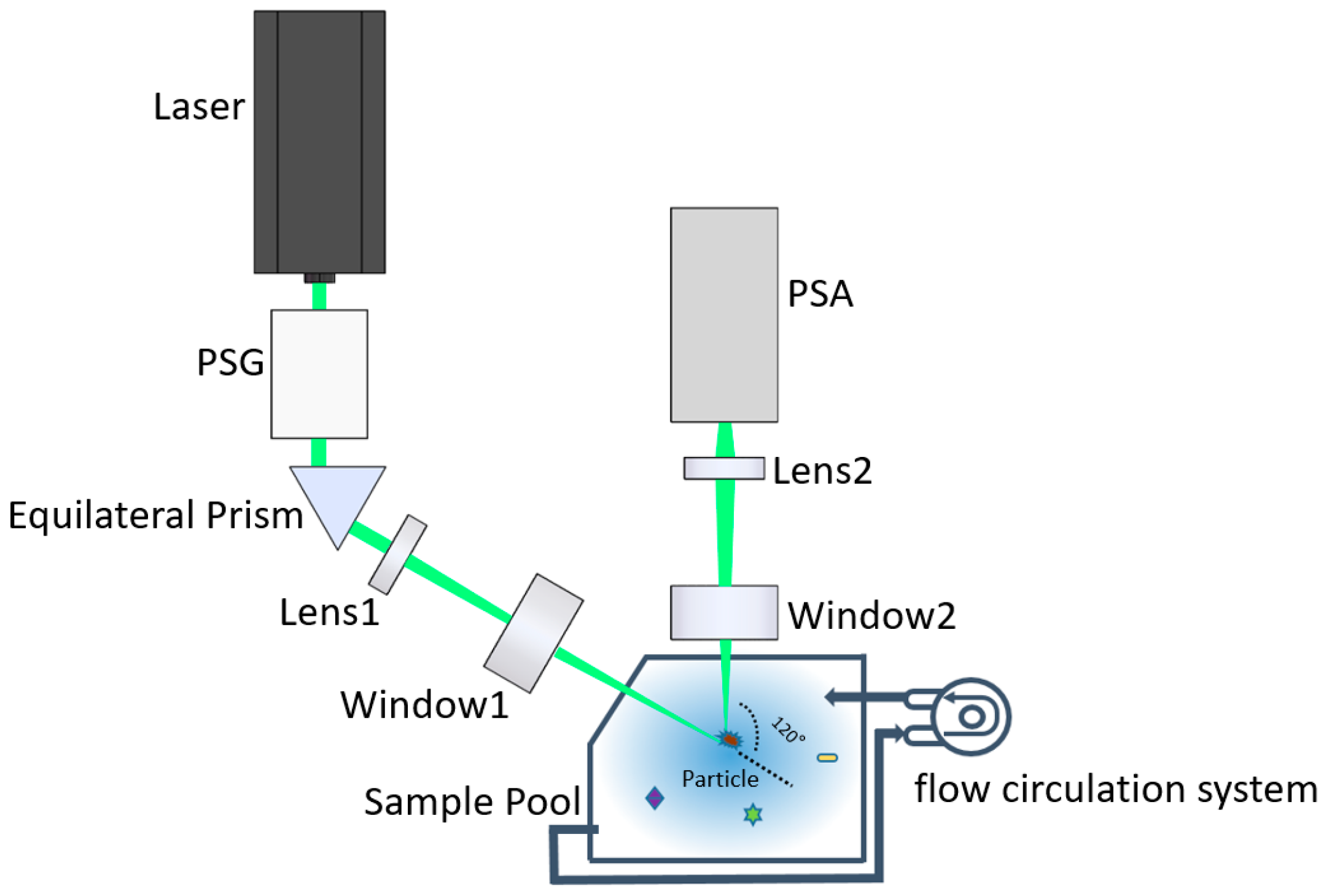
2.1. Principle of the Experimental Setup
2.2. Samples
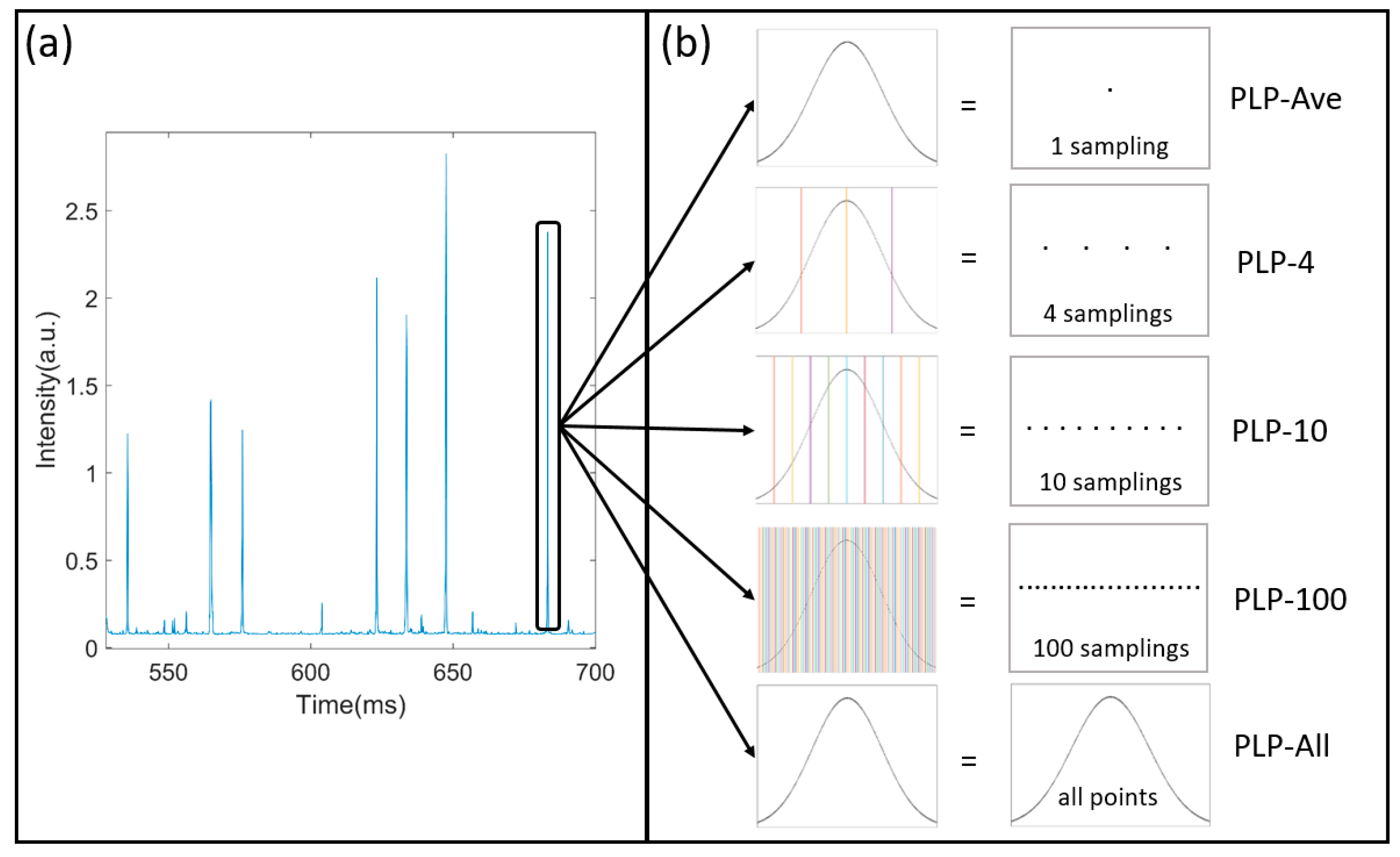
2.3. Polarized Light Pulse Processing Algorithm
2.4. Analytical Methods
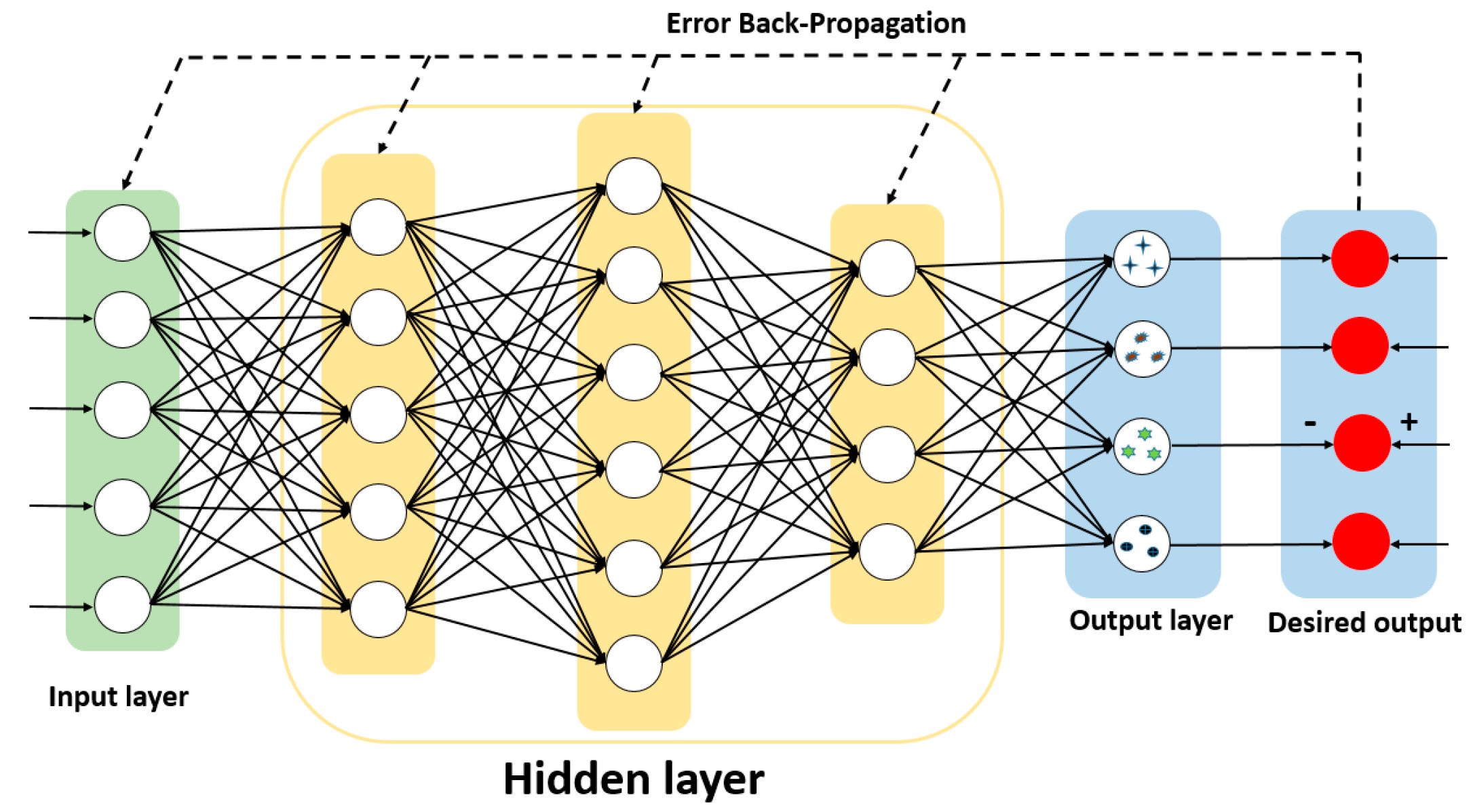
2.5. Algorithm Theory
3. Results
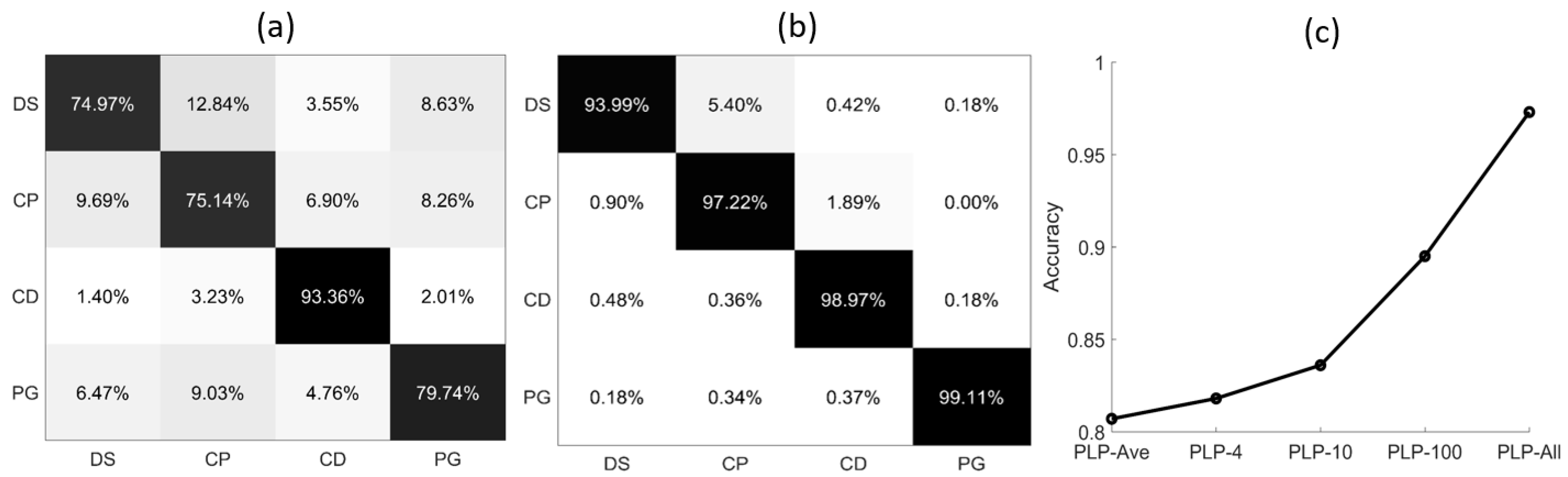
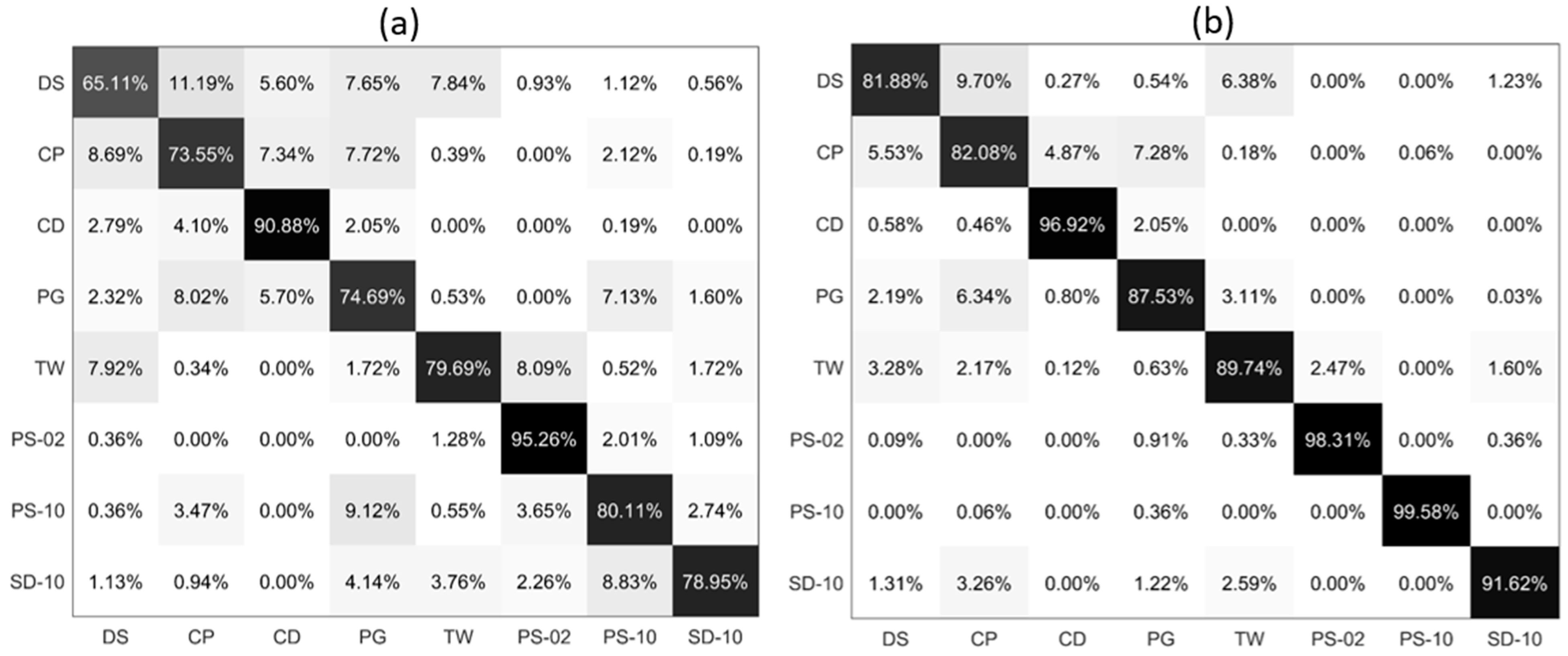
3.1. Classification of the Four Types of Microalgae
3.2. The Mixed Experiment Prediction
3.3. Comparative Analysis
4. Discussion
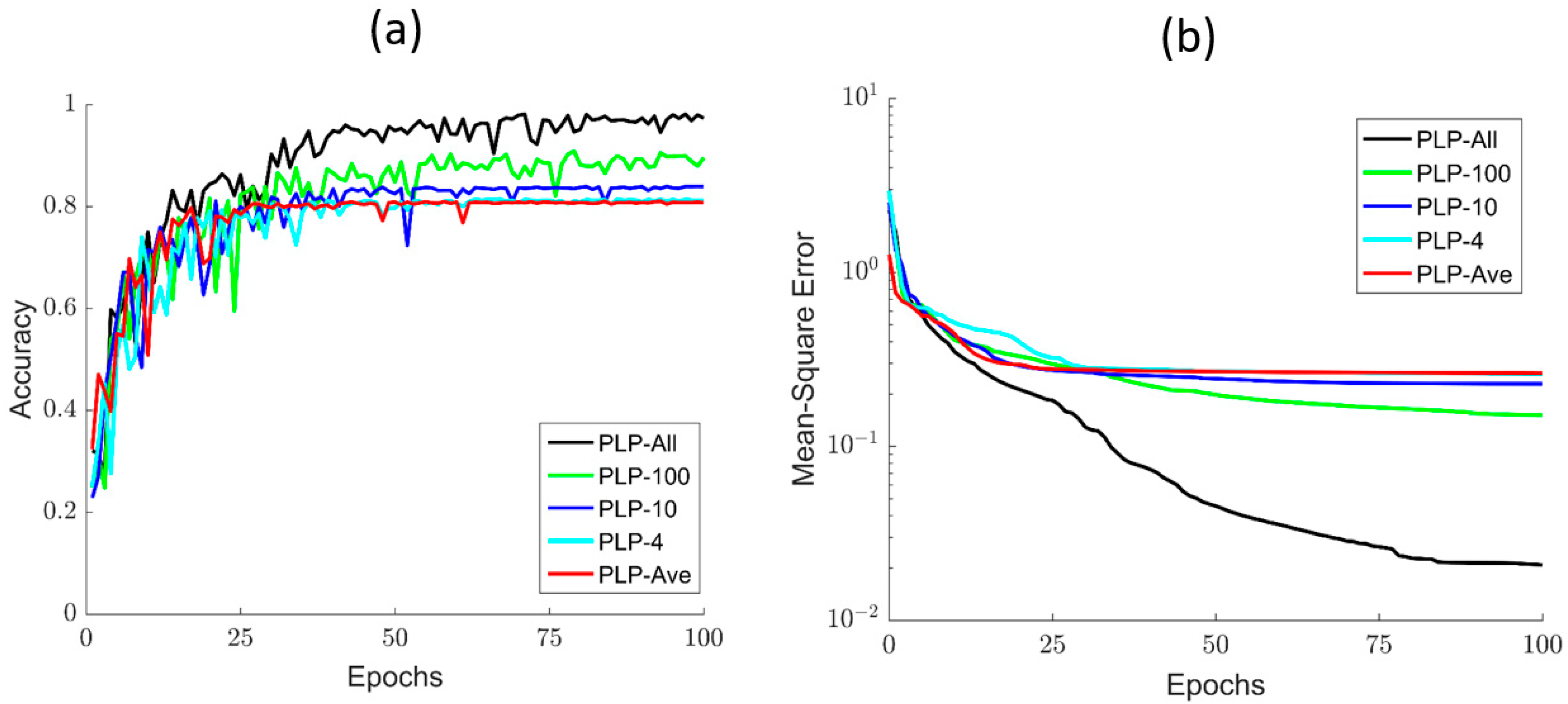
4.1. Training Details of Different Models
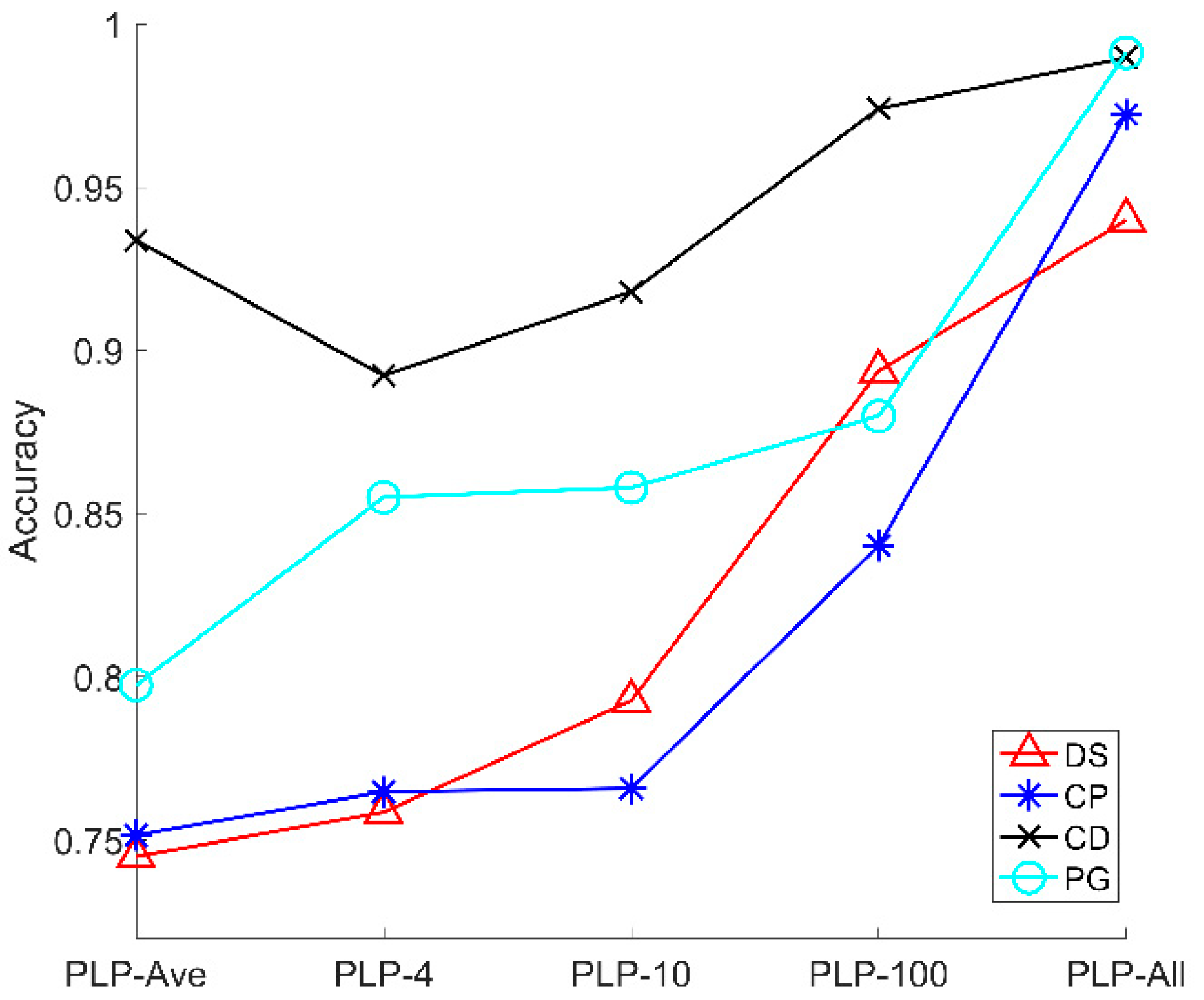
4.2. Accuracy of Four Microalgal Samples
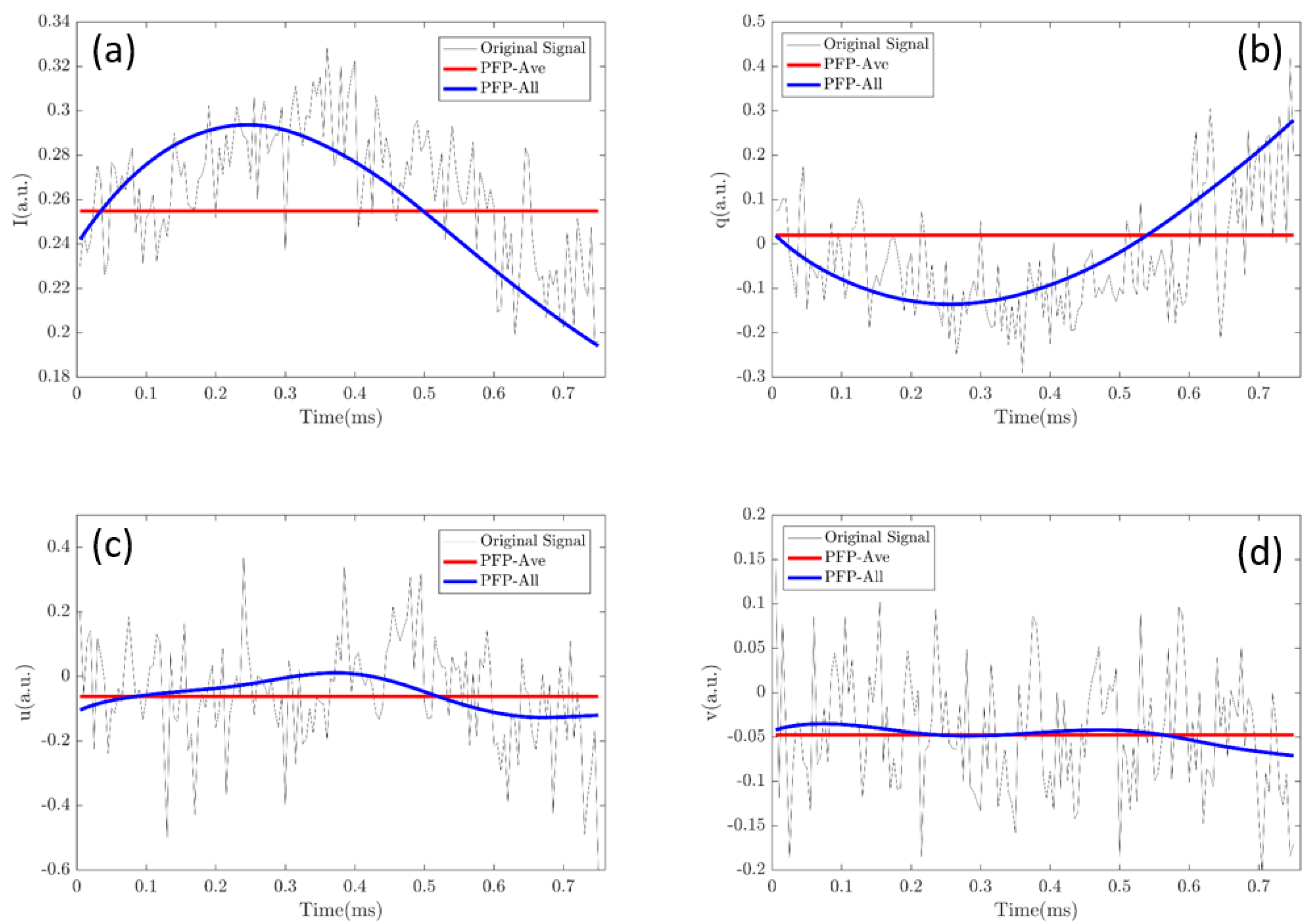
4.3. Origin of the Performance of PLP-All Method
4.4. Comparative Different Machine Learning Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, J. Coordination degree of marine biological ecological resources based on multi-source monitoring data. Arab. J. Geosci. 2021, 14, 654. [Google Scholar] [CrossRef]
- Ledoux, L.; Turner, R.K. Valuing ocean and coastal resources: A review of practical examples and issues for further action. Ocean Coast. Manag. 2002, 45, 583–616. [Google Scholar] [CrossRef]
- Borja, A.; Ranasinghe, A.; Weisberg, S.B. Assessing ecological integrity in marine waters, using multiple indices and ecosystem components: Challenges for the future. Mar. Pollut. Bull. 2009, 59, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Haward, M. Plastic pollution of the world’s seas and oceans as a contemporary challenge in ocean governance. Nat. Commun. 2018, 9, 667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, C.; Chen, J.; Yuan, X.; Yang, Z.; Balsam, W.; Ji, J. Seasonal variation in the mineralogy of the suspended particulate matter of the lower Changjiang River at Nanjing, China. Clay Clay Miner. 2010, 58, 691–706. [Google Scholar] [CrossRef]
- Shang, D.; Qin, R.; Xu, H.; Xu, C.; Sun, K.; Zhou, Y. Variation of Suspended Particles in the Bottom Layer of the East China Sea with Data from Seafloor Observatory. Sensors 2019, 19, 5156. [Google Scholar] [CrossRef] [Green Version]
- Hallegraeff, G.M. Ocean climate change, phytoplankton community responses, and harmful algal blooms: A formidable predictive challenge. J. Phycol. 2010, 46, 220–235. [Google Scholar] [CrossRef]
- Griffith, A.W.; Gobler, C.J. Harmful algal blooms: A climate change co-stressor in marine and freshwater ecosystems. Harmful Algae 2020, 91, 101590. [Google Scholar] [CrossRef] [PubMed]
- Hoagland, P.; Kirkpatrick, B.; Jin, D.; Kirkpatrick, G.; Fleming, L.E.; Ullmann, S.G.; Beet, A.; Hitchcock, G.; Harrison, K.K.; Li, Z.C.; et al. Lessening the Hazards of Florida Red Tides: A Common Sense Approach. Front. Mar. Sci. 2020, 7, 538. [Google Scholar] [CrossRef]
- Lebreton, L.; Joost, V.; Damsteeg, J.W.; Slat, B.; Andrady, A.; Reisser, J. River plastic emissions to the world’s oceans. Nat. Commun. 2017, 8, 15611. [Google Scholar] [CrossRef] [PubMed]
- Wright, S.L.; Thompson, R.C.; Galloway, T.S. The physical impacts of microplastics on marine organisms: A review. Environ. Pollut. 2013, 178, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Sul, J.; Costa, M.F. The present and future of microplastic pollution in the marine environment. Environ. Pollut. 2014, 185, 352–364. [Google Scholar]
- Pang, C.; Wei, Y.U.; Yang, Y.; Han, D. An improved method for evaluating the seasonal variability of total suspended sediment flux field in the Yellow and East China Seas. Int. J. Sediment Res. 2011, 26, 1–14. [Google Scholar] [CrossRef]
- Bi, N.; Yang, Z.; Wang, H.; Hu, B.; Ji, Y. Sediment dispersion pattern off the present Huanghe (Yellow River) subdelta and its dynamic mechanism during normal river discharge period. Estuar. Coast. Shelf Sci. 2010, 86, 352–362. [Google Scholar] [CrossRef]
- Zhang, T.; Qin, M.; Wei, C.; Li, D.; Lu, X.; Zhang, L. Suspended particles phoD alkaline phosphatase gene diversity in large shallow eutrophic Lake Taihu. Sci. Total. Environ. 2020, 728, 138615. [Google Scholar] [CrossRef] [PubMed]
- Greenstein, K.E.; Wert, E.C. Using rapid quantification of adenosine triphosphate (ATP) as an indicator for early detection and treatment of cyanobacterial blooms. Water Res. 2019, 154, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Gilerson, A.; Zhou, J.; Hlaing, S.; Ioannou, I.; Schalles, J.; Gross, B.; Moshary, F.; Ahmed1, S. Fluorescence component in the reflectance spectra from coastal waters. Dependence on water composition. Opt. Express 2007, 15, 15702–15721. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Zhang, Y.; Ma, R. Influence of Particle Composition on Remote Sensing Reflectance and MERIS Maximum Chlorophyll Index Algorithm: Examples from Taihu Lake and Chaohu Lake. IEEE Geosci. Remote. Sens. Lett. 2017, 12, 1170–1174. [Google Scholar]
- Zhang, F.; Su, R.; Wang, X.; Wang, L.; He, J.; Cai, M.; Luo, W.; Zheng, Z. A fluorometric method for the discrimination of harmful algal bloom species developed by wavelet analysis. J. Exp. Mar. Biol. Ecol. 2009, 368, 37–43. [Google Scholar] [CrossRef]
- Li, J.; Liao, R.; Tao, Y.; Zhuo, Z.; Liu, Z.; Deng, H.; Ma, H. Probing the Cyanobacterial Microcystis Gas Vesicles after Static Pressure Treatment: A Potential In Situ Rapid Method. Sensors 2020, 20, 4170. [Google Scholar] [CrossRef]
- Polle, J.E.W.; Benemann, J.R.; Tanaka, A.; Melis, A. Photosynthetic apparatus organization and function in the wild type and a chlorophyll b-less mutant of Chlamydomonas reinhardtii. Dependence on carbon source. Planta 2000, 211, 335–344. [Google Scholar] [CrossRef] [PubMed]
- Khanal, R.; Uk, S.; Kodikara, D.; Siev, S.; Yoshimura, C. Impact of water level fluctuation on sediment and phosphorous dynamics in tonle sap lake, cambodia. Water Air Soil Poll. 2021, 232, 139. [Google Scholar] [CrossRef]
- Okullo, W.; Ssenyonga, T.; Hamre, B.; Frette, O.; Sorensen, K.; Stamnes, J.J.; Steigen, A.; Stamnes, K. Parameterization of the inherent optical properties of Murchison Bay, Lake Victoria. Appl. Opt. 2007, 46, 8553–8561. [Google Scholar] [CrossRef]
- Zhou, J.; Gilerson, A.; Ioannou, I.; Schalles, J.; Gross, B.; Moshary, F.; Ahmed, S.A. Retrieving quantum yield of sun-induced chlorophyll fluorescence near surface from hyperspectral in-situ measurement in productive water. Opt. Express 2008, 16, 17468–17483. [Google Scholar] [CrossRef] [PubMed]
- Sandven, H.; Kristoffersen, A.S.; Chen, Y.C.; Hamre, B. In situ measurements of the volume scattering function with LISST-VSF and LISST-200X in extreme environments: Evaluation of instrument calibration and validity. Opt. Express 2020, 28, 37373–37396. [Google Scholar] [CrossRef]
- Olson, R.J.; Sosik, H.M. A submersible imaging-in-flow instrument to analyze nano-and microplankton: Imaging FlowCytobot. Limnol. Oceanogr. Meth. 2007, 5, 195–203. [Google Scholar] [CrossRef] [Green Version]
- Olson, R.J.; Shalapyonok, A.; Kalb, D.J.; Graves, S.W.; Sosik, H. Imaging FlowCytobot modified for high throughput by in-line acoustic focusing of sample particles. Limnol. Oceanogr. Meth. 2017, 15, 867–874. [Google Scholar] [CrossRef] [Green Version]
- He, H.; He, C.; Chang, J.; Lv, D.; Wu, J.; Duan, C.; Zhou, Q.; Zeng, N.; He, Y.; Ma, H. Monitoring microstructural variations of fresh skeletal muscle tissues by Mueller matrix imaging. J. Biophotonics 2017, 10, 664–673. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Chen, R.; Lin, J.; Pan, J.; Wu, Y.; Li, Y.; Chen, J.; Zeng, H. Gastric cancer detection based on blood plasma surface-enhanced Raman spectroscopy excited by polarized laser light. Biosens. Bioelectron. 2011, 26, 3167–3174. [Google Scholar] [CrossRef]
- Shen, Y.; Huang, R.; He, H.; Liu, S.; Dong, Y.; Wu, J.; Ma, H. Comparative study of the influence of imaging resolution on linear retardance parameters derived from the Mueller matrix. Biomed. Opt. Express 2020, 12, 211–225. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, N.; Chen, S.; Zhan, D.; He, Y.; Ma, H. Study on morphological analysis of suspended particles using single angle polarization scattering measurements. J. Quant. Spectrosc. Radiat. Transf. 2019, 224, 556–565. [Google Scholar] [CrossRef]
- Sun, M.; He, H.; Zeng, N.; Du, E.; Guo, Y.; Liu, S.; Wu, J.; He, Y.; Ma, H. Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters. Biomed. Opt. Express 2014, 5, 4223–4234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Liao, R.; Dai, J.; Liu, Z.; Xiong, Z.; Zhang, T.; Chen, H.; Ma, H. Differentiation of suspended particles by polarized light scattering at 120°. Opt. Express 2018, 26, 22419–22431. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.; Li, Q.; Mao, X. A prototype for detection of particles in sea water by using polarize-light scattering. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019. [Google Scholar]
- Wang, Y.; Dai, J.; Liao, R.; Zhou, J.; Meng, F.; Yao, Y.; Chen, H.; Ma, H. Characterization of physiological states of thesuspended marine microalgae using polarized light scattering. Appl. Opt. 2020, 59, 1307–1312. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wang, G.; Li, C.; Xu, Z.; Gao, W.; Shen, F. Retrieval of phytoplankton cell size from chlorophyll a specific absorption and scattering spectra of phytoplankton. Appl. Opt. 2017, 56, 8362. [Google Scholar] [CrossRef] [PubMed]
- Coesel, S.N.; Baumgartner, A.C.; Teles, L.M.; Ramos, A.A.; Henriques, N.M.; Cancela, L. Nutrient limitation is the main regulatory factor for carotenoid accumulation and for psy and pds steady state transcript levels in Dunaliella salina (chlorophyta) exposed to high light and salt stress. Mar. Biotechnol. 2008, 10, 602–611. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.J.; Lundholm, N.; Li, Y. A study of Chaetoceros debilis sensu lato species (bacillariophyceae), with ememdation of C. debilis and description of C. galeatus sp. nov. 1. J. Phycol. 2020, 56, 784–797. [Google Scholar] [CrossRef]
- Song, H.; Chen, Y.; Kg, E.; Liu, S.; Yu, Z.; Chen, N. High genetic diversity of the harmful algal bloom species Phaeocystis globosa revealed using the molecular marker cox1. Harmful Algae 2021, 107, 102065. [Google Scholar] [CrossRef]
- Weng, H.X.; Qin, Y.C.; Sun, X.W.; Dong, H.; Chen, X.H. Iron and phosphorus effects on the growth of Cryptomonas sp. (cryptophyceae) and their availability in sediments from the pearl river estuary, china. Estuar. Coast. Shelf Sci. 2007, 73, 501–509. [Google Scholar] [CrossRef]
- Li, W.; Yang, Y.; Li, Z.; Xu, J.; Gao, K. Effects of seawater acidification on the growth rates of the diatom Thalassiosira (conticribra) weissflogii under different nutrient, light, and UV radiation regimes. J. Appl. Phycol. 2017, 29, 133–142. [Google Scholar] [CrossRef]
- He, C.; He, H.; Chang, J.; Chen, B.; Ma, H.; Booth, M.J. Polarisation optics for biomedical and clinical applications: A review. Light-Sci. Appl. 2021, 10, 194. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.Y.; Chipman, R.A. Mueller matrices and the degree of polarization. Opt. Commun. 1998, 146, 11–14. [Google Scholar] [CrossRef]
- Parker, J.R. Rank and response combination from confusion matrix data. Inform. Fusion 2000, 2, 113–120. [Google Scholar] [CrossRef]
| Dataset | Training Set | Test Set |
|---|---|---|
| PLP-Ave model | 80.87% | 80.77% |
| PLP-All model | 97.80% | 97.32% |
| Preset Pulse Number | PLP-Ave Model Prediction | PLP-All Model Prediction | |
|---|---|---|---|
| Group 1 | 100, 100, 100, 100 | 115, 104, 133, 40 | 115, 103, 99, 75 |
| Group 2 | 200, 300, 100, 200 | 292, 258, 80, 194 | 214, 308, 108, 194 |
| Group 3 | 200, 400, 100, 300 | 280, 320, 84, 286 | 234, 364, 100, 268 |
| Dataset | Training Set | Test Set |
|---|---|---|
| PLP-Ave model | 79.89% | 80.20% |
| PLP-All model | 90.80% | 90.90% |
| Dataset | Training Set | Test Set |
|---|---|---|
| PLP-Ave model | 74.39% | 74.38% |
| PLP-All model | 94.71% | 94.57% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Deng, H.; Li, J.; Liao, R.; Ma, H. Optimized Classification of Suspended Particles in Seawater by Dense Sampling of Polarized Light Pulses. Sensors 2021, 21, 7344. https://doi.org/10.3390/s21217344
Guo Z, Deng H, Li J, Liao R, Ma H. Optimized Classification of Suspended Particles in Seawater by Dense Sampling of Polarized Light Pulses. Sensors. 2021; 21(21):7344. https://doi.org/10.3390/s21217344
Chicago/Turabian StyleGuo, Zhiming, Hanbo Deng, Jiajin Li, Ran Liao, and Hui Ma. 2021. "Optimized Classification of Suspended Particles in Seawater by Dense Sampling of Polarized Light Pulses" Sensors 21, no. 21: 7344. https://doi.org/10.3390/s21217344
APA StyleGuo, Z., Deng, H., Li, J., Liao, R., & Ma, H. (2021). Optimized Classification of Suspended Particles in Seawater by Dense Sampling of Polarized Light Pulses. Sensors, 21(21), 7344. https://doi.org/10.3390/s21217344







