Determination of Blasting Vibration Safety Criterion for HDPE Pipeline Using Vibration and Strain Data in a Coastal Metro Line
Abstract
:1. Introduction
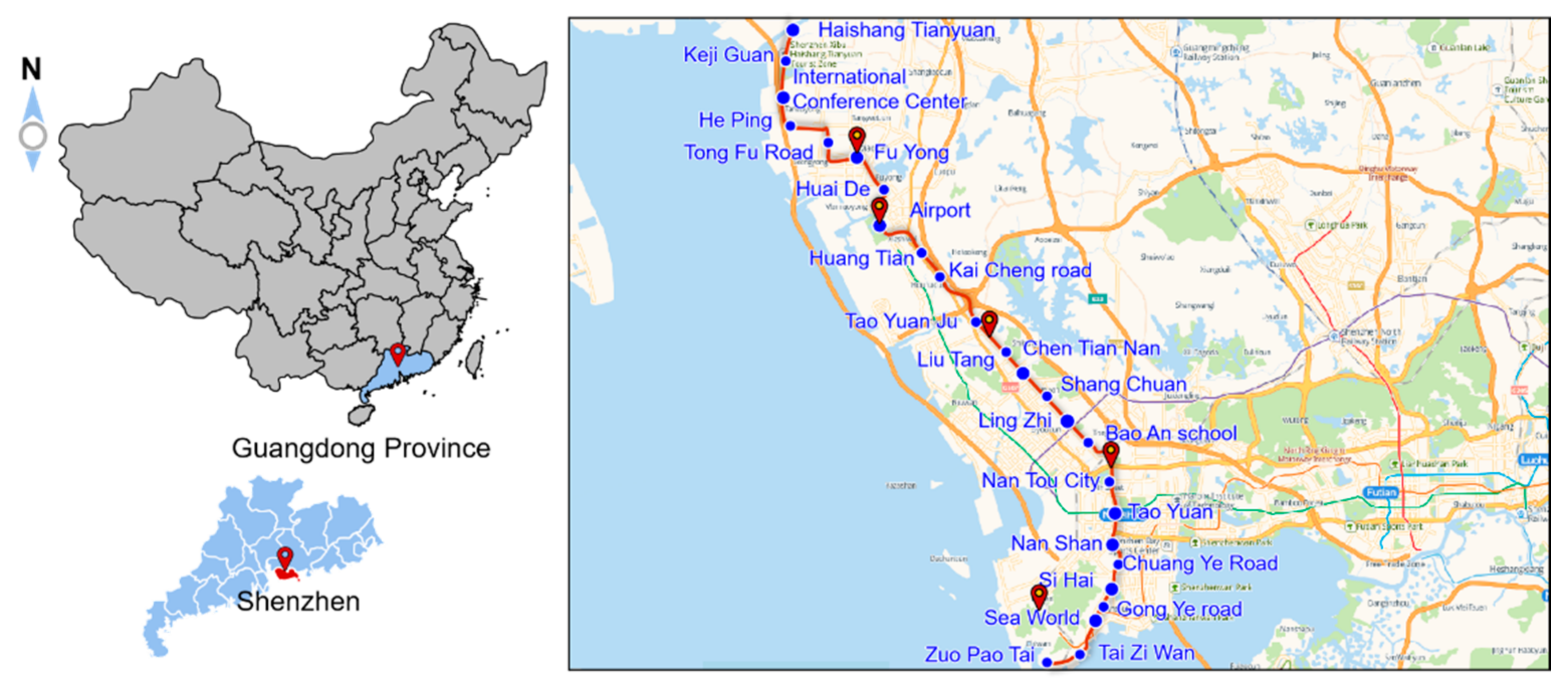
2. Generalization of Coastal Metro Project
2.1. Brief Introduction of Coastal Metro Engineering and Construction Method
2.2. Characteristics of Buried Pipelines near Coastal Metro
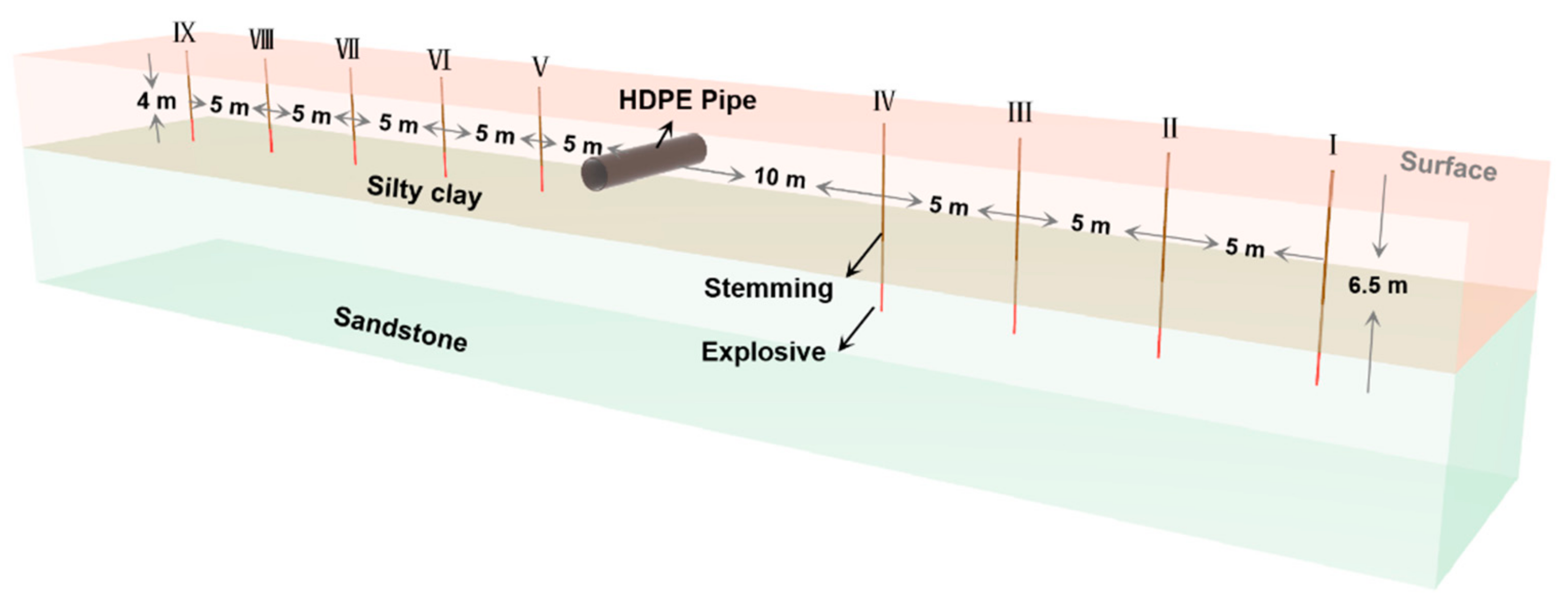
2.3. Full-Scale Blasting Test near the HDPE Pipeline
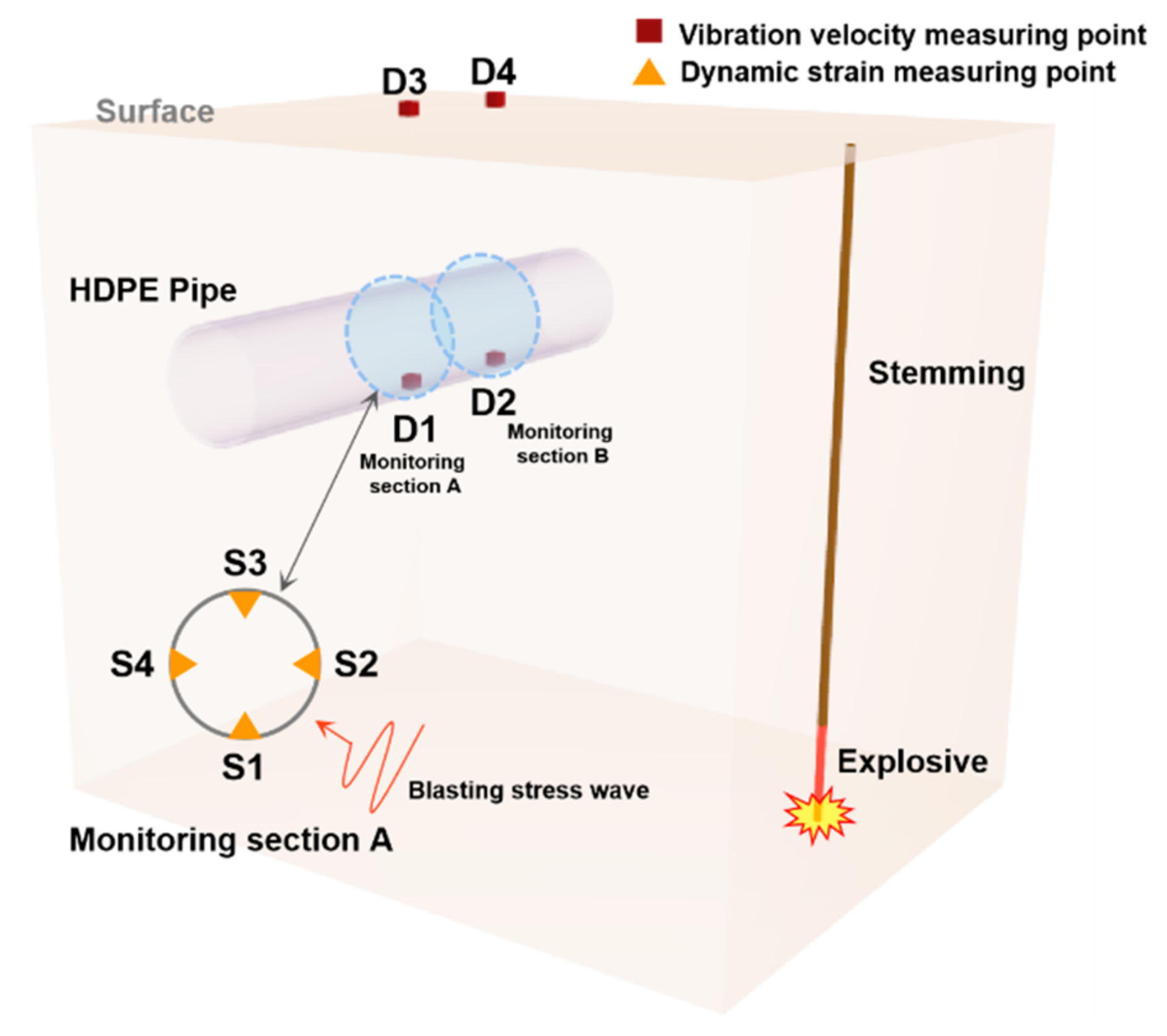
2.4. Monitoring Sensors and Systems
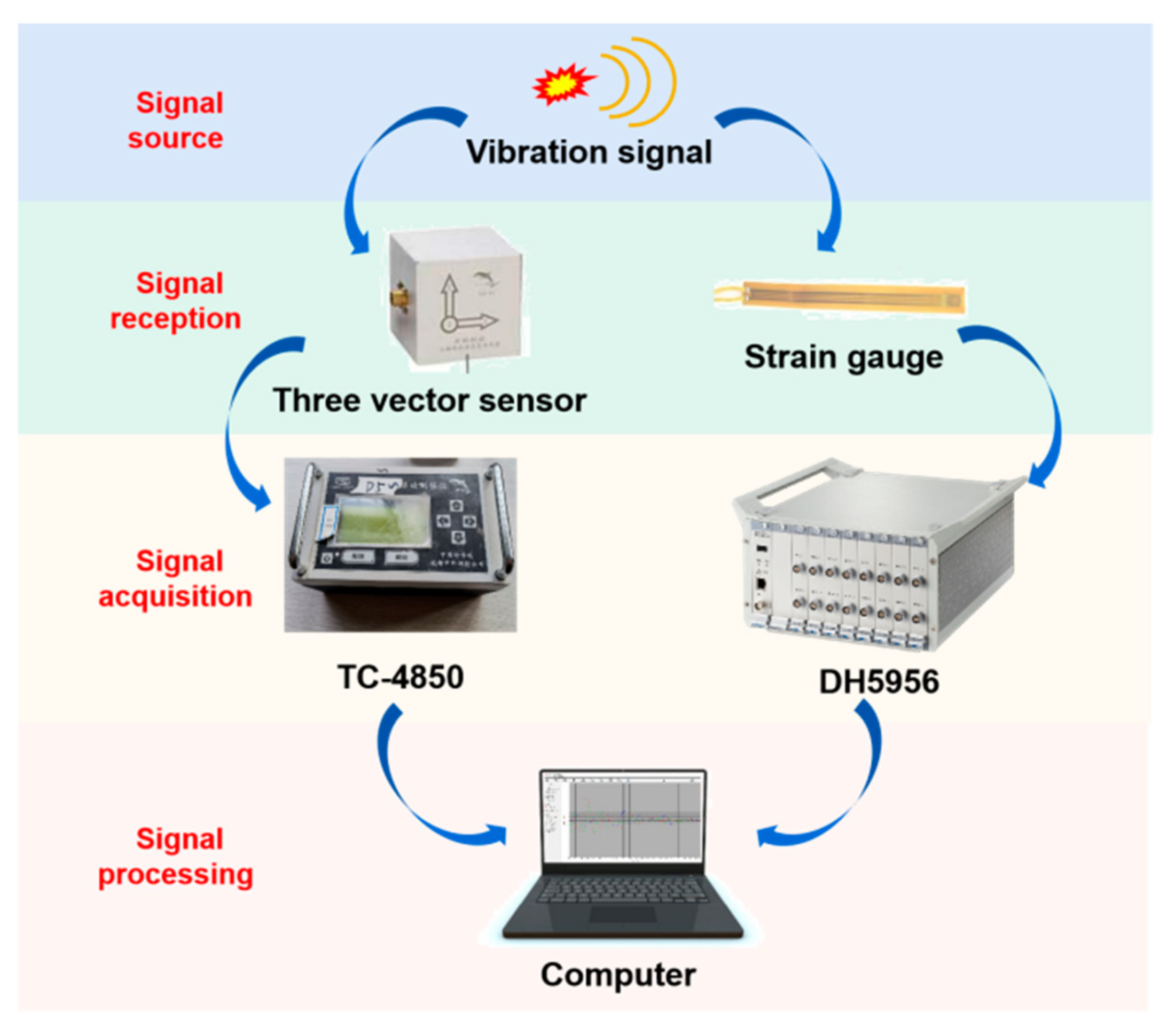
2.4.1. Vibration Test System
2.4.2. Strain Testing System
2.5. Analysis of Test Results
2.5.1. Analysis of Vibration Velocity Test Results
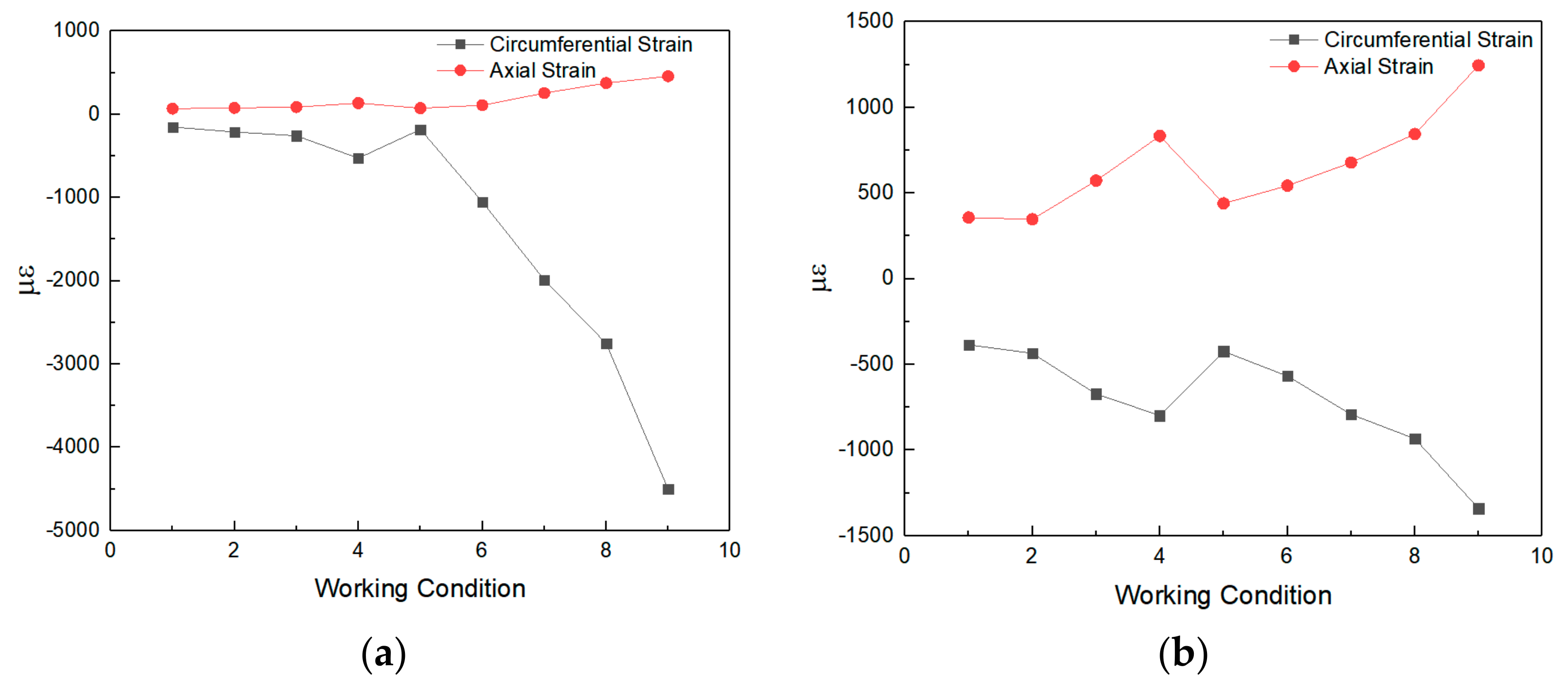
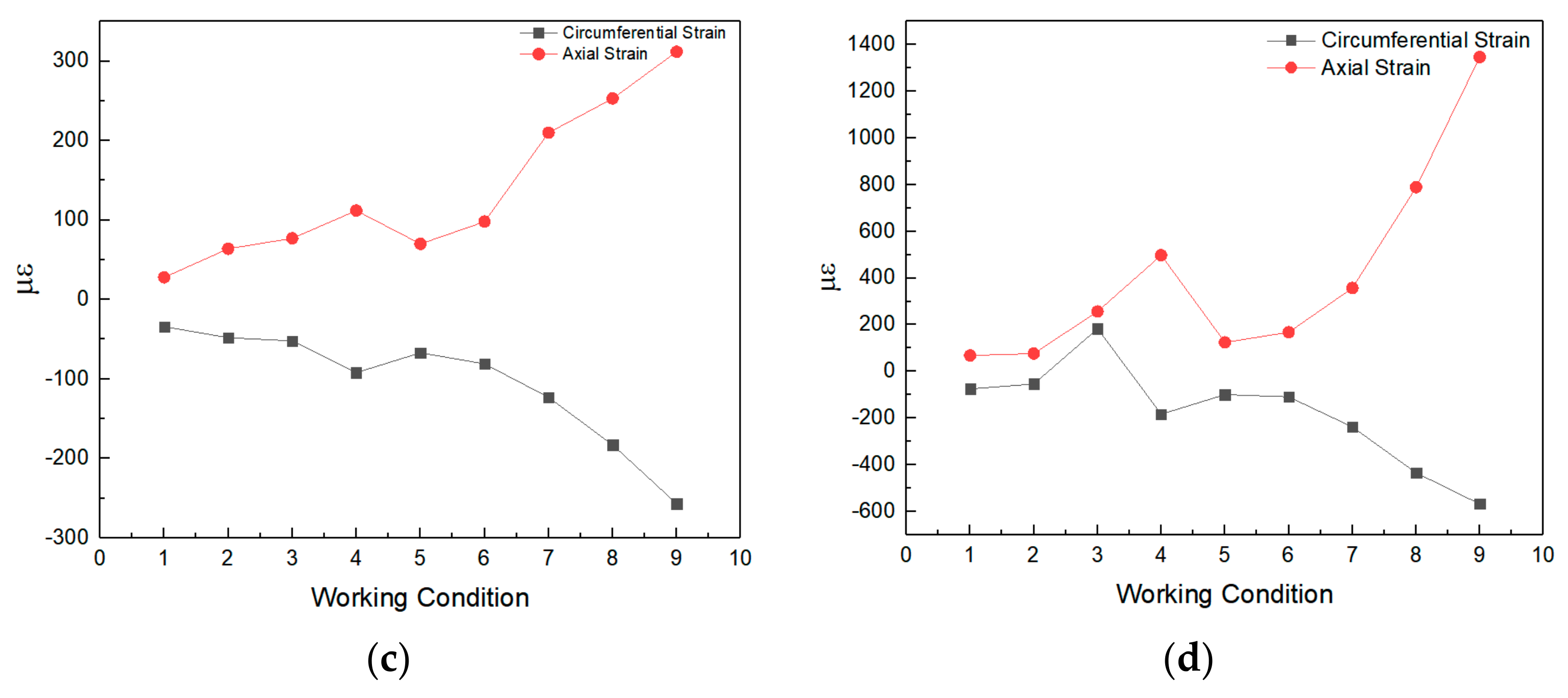
2.5.2. Analysis of Dynamic Strain Test Results
3. Numerical Modeling of Dynamic Calculation and Verification for Buried HDPE Pipeline
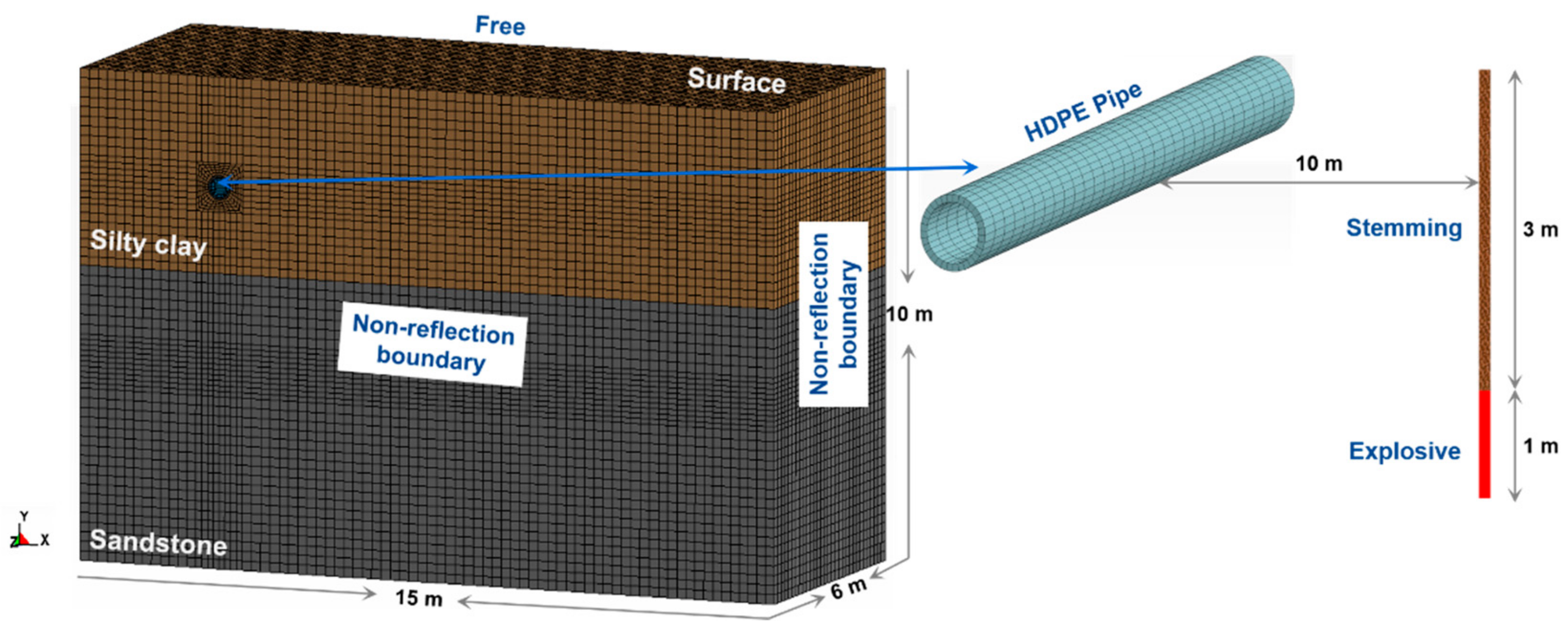
3.1. Numerical Modeling of Dynamic Calculation for Buried Pipeline
3.2. Numerical Model and Parameter Validation Analysis
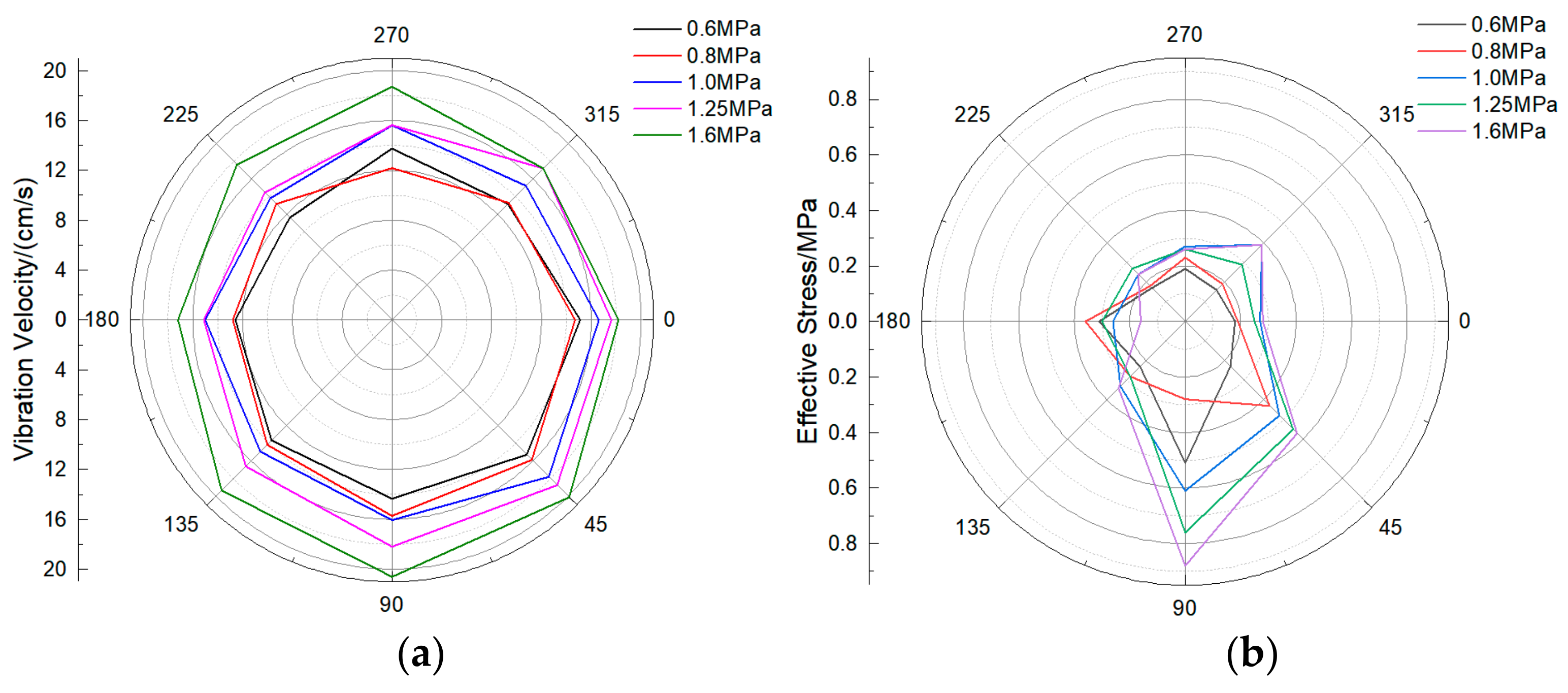
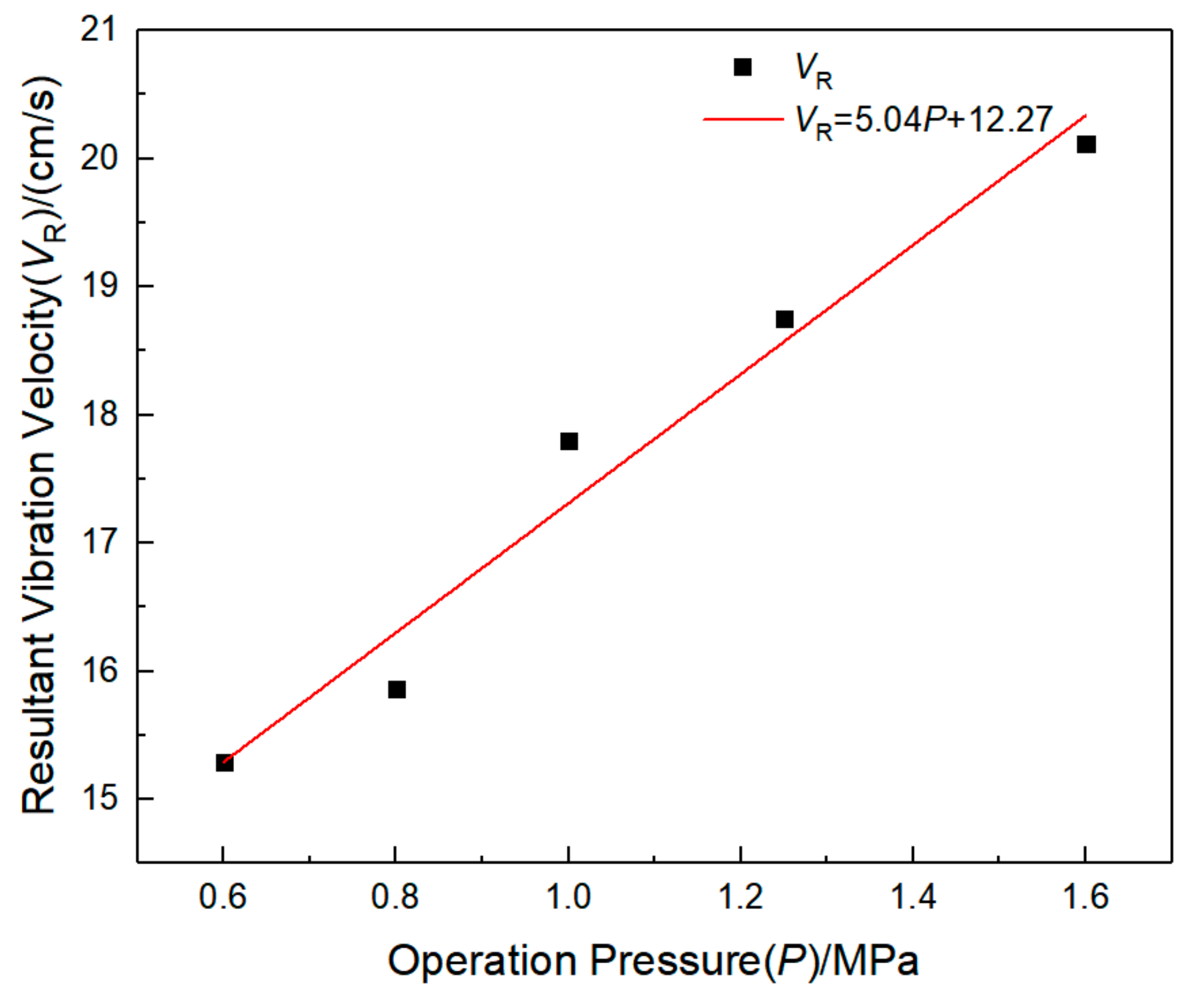
3.3. Dynamic Response Analysis of Water Pipeline under Different Operating Pressures
3.4. Dynamic Response Analysis of Water Pipeline under Different Buried Depths
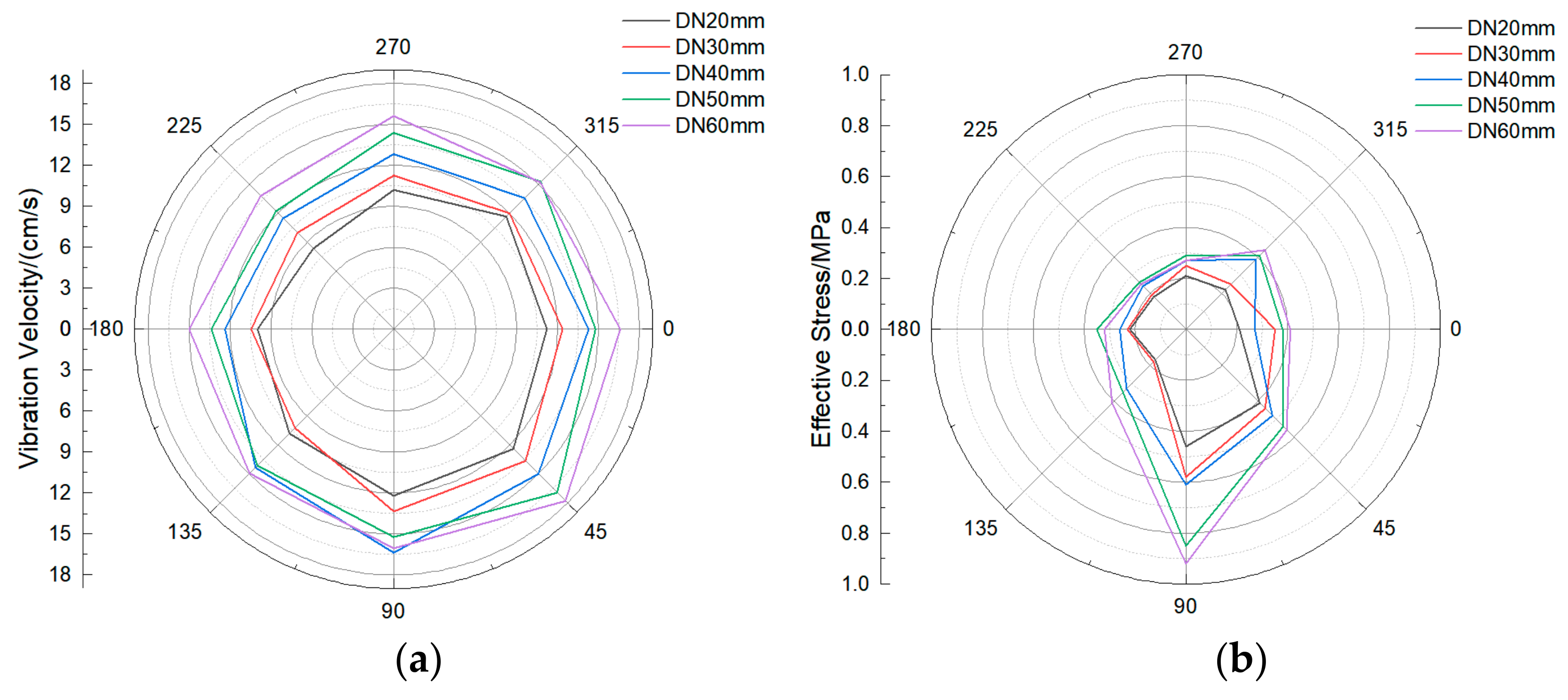
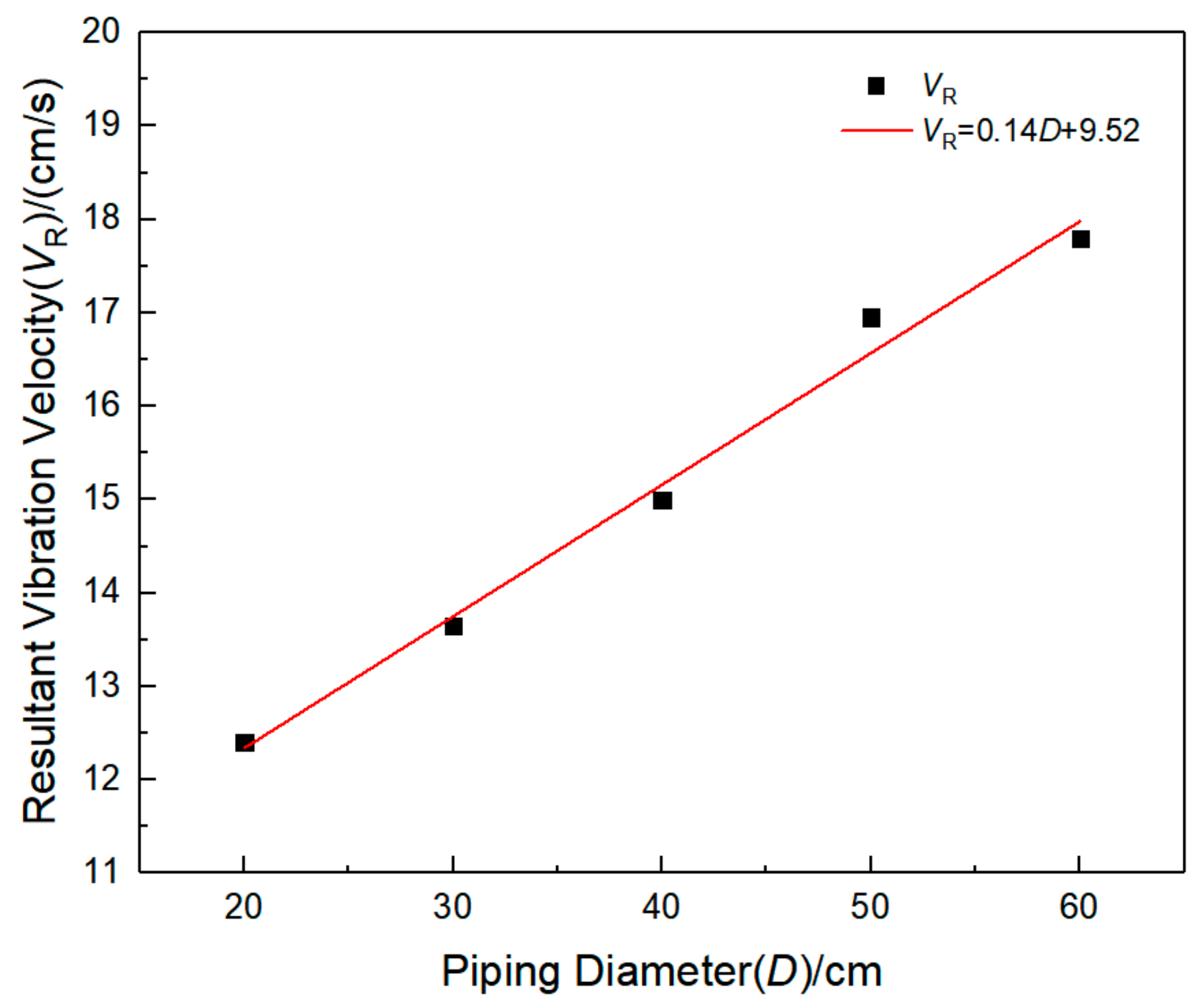
3.5. Dynamic Response Analysis of Water Pipeline under Different Diameters
4. Safety Criterion of Blasting Vibration Velocity of Buried Pipeline
4.1. Dimensionless Analysis Models for Pipeline Safety Assessment
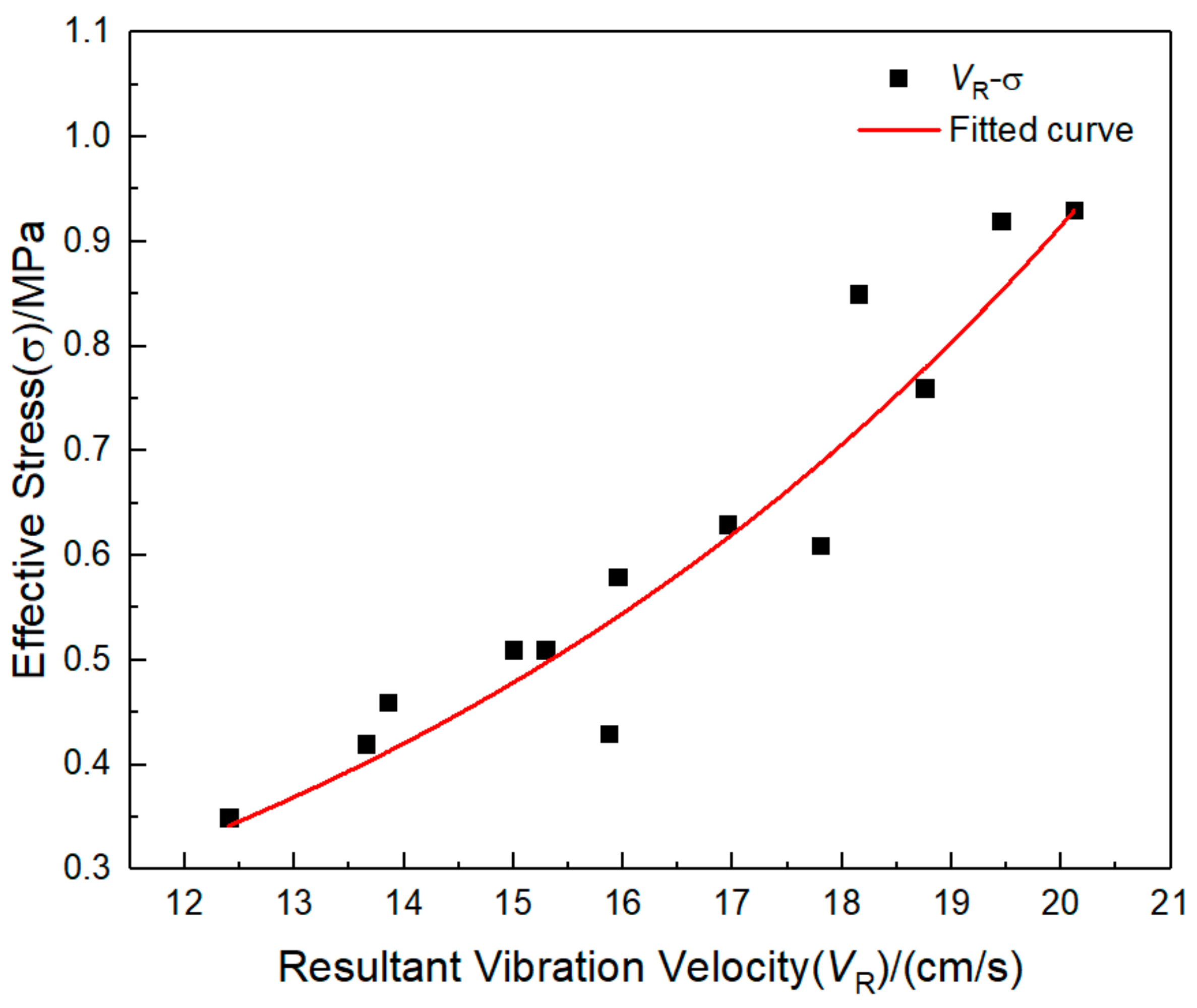
4.2. Safety Criterion of the Pipeline Based on the Prediction Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Giannaros, E.; Kotzakolios, T.; Kostopoulos, V. Blast response of composite pipeline structure using finite element techniques. J. Compos. Mater. 2016, 50, 3459–3476. [Google Scholar] [CrossRef]
- Won, J.H.; Kim, M.K.; Kim, G.; Cho, S.H. Blast-induced dynamic response on the interface of a multilayered pipeline. Struct. Infrastruct. Eng. 2014, 10, 80–92. [Google Scholar] [CrossRef]
- Ha, D.; Abdoun, T.H.; O’Rourke, M.J.; Symans, M.D.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Centrifuge Modeling of Earthquake Effects on Buried High-Density Polyethylene (HDPE) Pipelines Crossing Fault Zones. J. Geotech. Geoenviron. Eng. 2008, 134, 1501–1515. [Google Scholar] [CrossRef]
- Abdoun, T.H.; Ha, D.; O’Rourke, M.J.; Symans, M.D.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Factors influencing the behavior of buried pipelines subjected to earthquake faulting. Soil Dyn. Earthq. Eng. 2009, 29, 415–427. [Google Scholar] [CrossRef]
- Wang, H.T.; Jin, H.; Jia, J.Q. Model test study on the influence of subway tunnel drilling and blasting construction on adjacent buried pipelines. Chin. J. Rock Mech. Eng. 2018, 37 (Suppl. 1), 3332–3339. [Google Scholar]
- Zhu, B.; Jiang, N.; Jia, Y.S.; Zhao, K.; Yao, Y.; Zhou, C. Field experiment on blasting vibration effect of underpass gas pipeline. Chin. J. Rock Mech. Eng. 2019, 38, 2582–2592. [Google Scholar]
- Xia, Y.Q.; Jiang, N.; Yao, Y.K.; Zhou, C.B.; Luo, X.D.; Wu, T.Y. Experiment study on dynamic response of spigot concrete pipe buried in silty clay layer subjected to blasting seismic wave. Explos. Shock Waves 2020, 40, 73–83. [Google Scholar]
- Zhong, D.W.; Lu, Z.; Huang, X.; Chen, C.; Si, J.F. Experimental study on buried PE pipeline under blasting loads. Blasting 2018, 35, 1–5. [Google Scholar]
- Zhang, J.; Zhang, L.; Liang, Z. Buckling failure of a buried pipeline subjected to ground explosions. Process. Saf. Environ. Prot. 2018, 114, 36–47. [Google Scholar] [CrossRef]
- Parviz, M.; Aminnejad, B.; Fiouz, A. Numerical simulation of dynamic response of water in buried pipeline under explosion. KSCE J. Civ. Eng. 2017, 21, 2798–2806. [Google Scholar] [CrossRef]
- Francini, R.B.; Baltz, W.N. Blasting and construction vibrations near existing pipelines: What are the appropriate levels? J. Pipeline Eng. 2009, 8, 253–262. [Google Scholar]
- Jiang, N.; Gao, T.; Zhou, C.; Luo, X. Effect of excavation blasting vibration on adjacent buried gas pipeline in a metro tunnel. Tunn. Undergr. Space Technol. 2018, 81, 590–601. [Google Scholar] [CrossRef]
- Xia, Y.; Jiang, N.; Zhou, C.; Luo, X. Safety assessment of upper water pipeline under the blasting vibration induced by Subway tunnel excavation. Eng. Fail. Anal. 2019, 104, 626–642. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, H.; Liu, X.; Bolati, D.; Liu, G.; Chen, P.; Zhao, Y. Stress and strain analysis of buried PE pipelines subjected to mechanical excavation. Eng. Fail. Anal. 2019, 106, 104171. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, C.B.; Lu, S.W.; Jiang, N.; Wu, C. Dynamic response characteristics of adjacent buried concrete pipelines under blasting vibration. J. Harbin Inst. Technol. 2017, 46, 79–84. [Google Scholar]
- Rigby, S.; Knighton, R.; Clarke, S.; Tyas, A. Reflected Near-field Blast Pressure Measurements Using High Speed Video. Exp. Mech. 2020, 60, 875–888. [Google Scholar] [CrossRef]
- Lee, Y.G.; Kim, S.H.; Park, J.S.; Kang, J.W.; Yoon, S.J. Full-scale field test for buried glass-fiber reinforced plastic pipe with large diameter. Compos. Struct. 2015, 120, 167–173. [Google Scholar] [CrossRef]
- Sandhu, I.S.; Sharma, A.; Thangadurai, M.; Kala, M.B.; Singh, M.; Saroha, D.R.; Alegaonkar, P.S. Comparison of Blast Pressure Mitigation in Rubber Foam in a Blast Wave Generator and Field Test Setups. Combust. Explos. Shock Waves 2020, 56, 116–123. [Google Scholar] [CrossRef]
- Jeon, S.H.; Moon, H.D.; Sim, C.; Ahn, J.-H. Construction stage analysis of a precast concrete buried arch bridge with steel outriggers from full-scale field test. Structures 2021, 29, 1671–1689. [Google Scholar] [CrossRef]
- Lee, S.-H.; Eum, K.-Y.; Le, T.H.M.; Park, D.-W. Evaluation on mechanical behavior of asphalt concrete trackbed with slab panel using full-scale static and dynamic load test. Constr. Build. Mater. 2021, 276, 122207. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, C.; Jiang, N.; Xu, X. Effect of Excavation Blasting in an Under-Cross Tunnel on Airport Runway. Geotech. Geol. Eng. 2015, 33, 973–981. [Google Scholar] [CrossRef]
- Jiang, N.; Zhu, B.; He, X.; Zhou, C.; Luo, X.; Wu, T. Safety assessment of buried pressurized gas pipelines subject to blasting vibrations induced by metro foundation pit excavation. Tunn. Undergr. Space Technol. 2020, 102, 103448. [Google Scholar] [CrossRef]
- Lu, W.; Fan, Y.; Yang, J.; Yan, P.; Chen, M. Development of a model to predict vibrations induced by transient release of in-situ stress. J. Vib. Control 2017, 23, 1828–1843. [Google Scholar] [CrossRef]
- Xia, X.; Li, H.; Liu, Y.; Yu, C. A case study on the cavity effect of a water tunnel on the ground vibrations induced by excavating blasts. Tunn. Undergr. Space Technol. 2018, 71, 292–297. [Google Scholar] [CrossRef]
- Jiang, N.; Zhu, B.; Zhou, C.; Li, H.; Wu, B.; Yao, Y.; Wu, T. Blasting vibration effect on the buried pipeline: A brief overview. Eng. Fail. Anal. 2021, 129, 105709. [Google Scholar] [CrossRef]
- Zhong, D.W.; Gong, X.C.; Tu, S.W.; Huang, X. Dynamic responses of PE pipes directly buried in high saturated clay to blast wave. Combust. Explos. Shock Waves 2019, 39, 51–62. [Google Scholar]
- DBJ52T 039-2017. Technical Specification for Outdoor Buried Polyethylene (PE) Water Supply Pipeline Engineering; Architecture & Building Press: Beijing, China, 2017; pp. 27–35. [Google Scholar]
- Zhang, Z.; Zhou, C.H.; Lu, S.W.; Wu, C.; Wang, C. Characteristics of surface vibration propagation in tunnels of ultra-shallow buried subway stations. J. Cent. South Univ. Sci. Technol. 2017, 48, 2119–2125. [Google Scholar]
- Zhu, B.; Jiang, N.; Zhou, C.; Luo, X.; Yao, Y.; Wu, T. Dynamic failure behavior of buried cast iron gas pipeline with local external corrosion subjected to blasting vibration. J. Nat. Gas Sci. Eng. 2021, 88, 103803. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, Z.; Feng, D.; Zhang, C.; Xia, C.; Tu, Y. Response of the buried steel pipeline caused by perilous rock impact: Parametric study. J. Loss Prev. Process. Ind. 2016, 43, 385–396. [Google Scholar] [CrossRef]
- Jiang, N.; Zhou, C.; Lu, S.; Zhang, Z. Propagation and prediction of blasting vibration on slope in an open pit during underground mining. Tunn. Undergr. Space Technol. 2017, 70, 409–421. [Google Scholar] [CrossRef]
- Tian, F.; Gao, Y.; Sun, C.H. Stress analysis and pipe wall thickness calculation of power pipeline. Pipeline Tech. Equip. 2000, 4, 4–6. [Google Scholar]
- Luo, L.; Ma, Y.; Zhang, Y.J.; Liu, Y.J.; L, X. Numerical simulation of strength failure of buried polyethylene pipes under ground settlement. J. Build. Mater. 2020, 23, 473–478. [Google Scholar]





| Stratum | Natural Weight-Specific Density (ρ)/(kN·m3) | Friction Angle (φ)/(°) | Cohesion (c)/(kPa) | Bearing Capacity (fk)/(kPa) |
|---|---|---|---|---|
| Landfill | 19.2 | 18 | 8 | 120–160 |
| Silty clay | 19.3 | 12 | 25 | 160–180 |
| Weathered granite | 26.8 | 5.5 | 43 | 2000–4000 |
| Tubing | Elastic Modulus (E)/(MPa) | Density (ρ)/(g/cm3) | Ring Stiffness (SN)/(kN/m2) | Ultimate Strength (σu)/(MPa) | Poisson Ratio (μ) |
|---|---|---|---|---|---|
| HDPE | 834.9 | 0.936 | 8 | 31.6 | 0.46 |
| Working Condition | Burial Depth/m | Explosive Quantity/kg | Horizontal Distance/m |
|---|---|---|---|
| 1 | 6.5 | 8 | 25 |
| 2 | 6.5 | 8 | 20 |
| 3 | 6.5 | 8 | 15 |
| 4 | 6.5 | 8 | 10 |
| 5 | 4 | 8 | 25 |
| 6 | 4 | 8 | 20 |
| 7 | 4 | 8 | 15 |
| 8 | 4 | 8 | 10 |
| 9 | 4 | 9.6 | 5 |
| Working Condition | D1 | D2 | D3 | D4 | ||||
|---|---|---|---|---|---|---|---|---|
| VR/(cm/s) | f/Hz | VR/(cm/s) | f/Hz | VR/(cm/s) | f/Hz | VR/(cm/s) | f/Hz | |
| 1 | 8.32 | 25 | 8.60 | 43 | 7.92 | 41 | 6.97 | 37 |
| 2 | 9.47 | 31 | 8.28 | 33 | 8.31 | 61 | 7.87 | 57 |
| 3 | 12.24 | 35 | 12.31 | 43 | 11.58 | 50 | 11.61 | 42 |
| 4 | 16.37 | 52 | 14.54 | 40 | 14.89 | 43 | 13.29 | 36 |
| 5 | 9.23 | 48 | 8.75 | 56 | 9.02 | 23 | 8.38 | 45 |
| 6 | 11.87 | 53 | 12.67 | 54 | 11.88 | 47 | 12.21 | 67 |
| 7 | 13.35 | 18 | 14.38 | 49 | 10.34 | 124 | 11.38 | 88 |
| 8 | 17.20 | 62 | 16.54 | 43 | 18.61 | 42 | 16.61 | 37 |
| 9 | 22.25 | 44 | 20.35 | 38 | 20.31 | 37 | 18.27 | 77 |
| Working Condition Group | Internal Pressure (A)/MPa | Dimension (B) | Buried Depth (C)/m | |
|---|---|---|---|---|
| Diameter/mm | Wall Thickness/mm | |||
| I | 0.6 | 200 | 18 | 1 |
| II | 0.8 | 300 | 28 | 1.5 |
| III | 1.0 | 400 | 36 | 2 |
| IV | 1.25 | 500 | 45 | 2.5 |
| V | 1.6 | 600 | 55 | 3 |
| Material | ρ/(g/cm3) | E/GPa | G/GPa | μ | c/MPa | φ/(°) | σt/MPa |
|---|---|---|---|---|---|---|---|
| Pipeline | 0.936 | 0.8349 | - | 0.46 | - | - | 31.600 |
| Soft layer | 1.980 | 0.0390 | 0.027 | 0.35 | 0.035 | 15 | 0.028 |
| Rock stratum | 2.680 | 52.0000 | 11.26 | 0.25 | 5.500 | 43 | 2.580 |
| Parameter | Density/(g/cm3) | Sound Velocity/(m/s) | S1 | S2 | S3 |
|---|---|---|---|---|---|
| Value | 1.0 | 1 500 | 2.56 | 1.986 | 1.2268 |
| Parameter | ρ/(g/cm3) | A/GPa | B/GPa | R1 | R2 | ω | E0/GPa | V/cm3 |
|---|---|---|---|---|---|---|---|---|
| Value | 1.25 | 214 | 18.2 | 4.2 | 0.9 | 0.15 | 4.19 | 1 |
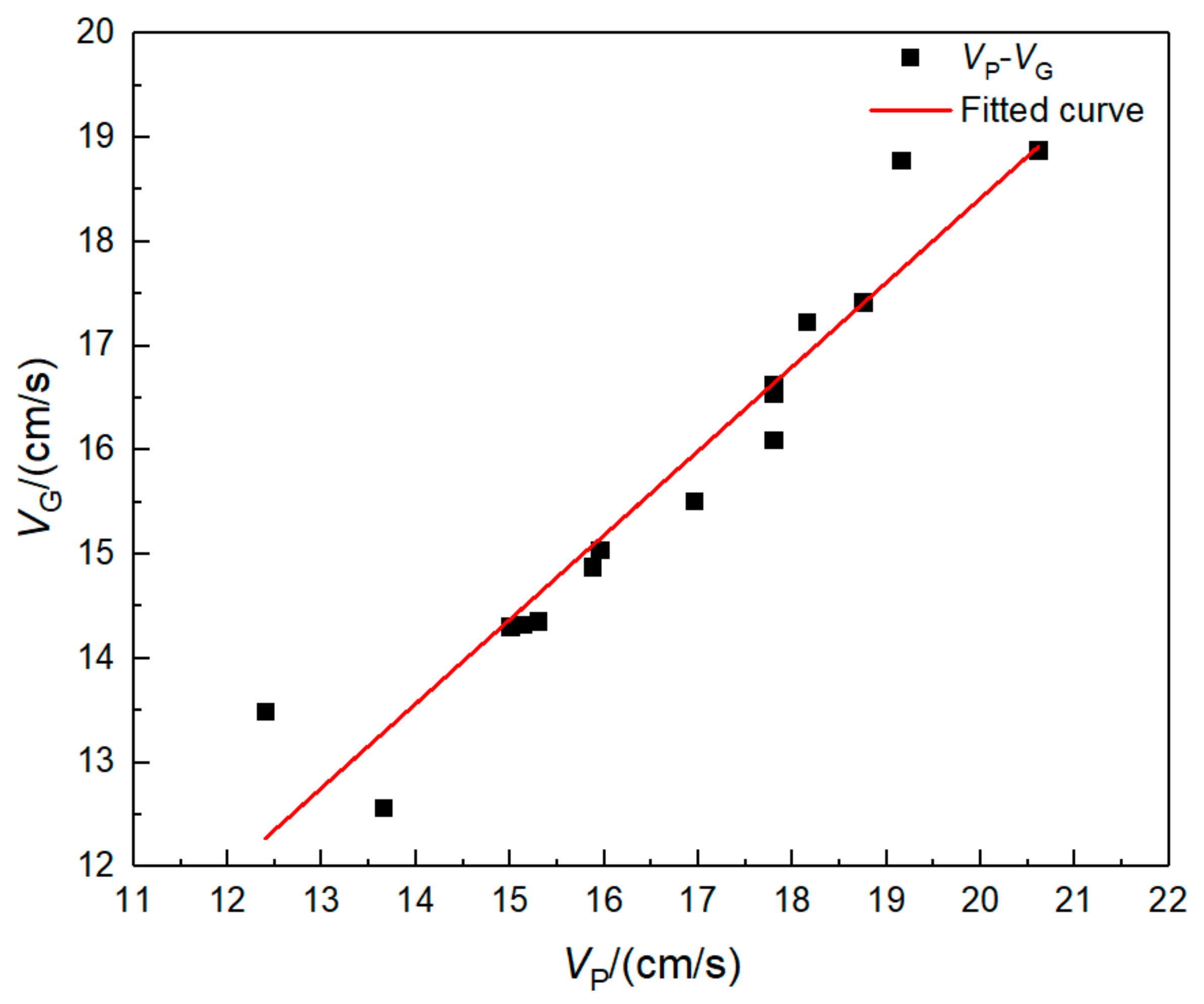
| Measuring Point | VRF (cm/s) | VRN (cm/s) | EVR |
|---|---|---|---|
| D1 | 16.37 | 17.41 | 6.35% |
| D2 | 14.54 | 15.98 | 9.90% |
| D3 | 14.89 | 15.66 | 5.17% |
| D4 | 13.29 | 14.57 | 9.63% |
| Work Condition (A) | I | II | III | IV | V | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pipe | Ground | Pipe | Ground | Pipe | Ground | Pipe | Ground | Pipe | Ground | ||
| VR/(cm/s) | 15.29 | 14.36 | 15.8 | 14.88 | 17.80 | 16.13 | 18.75 | 17.42 | 20.61 | 18.88 | |
| f/Hz | X | 37 | 57 | 78 | 62 | 65 | 67 | 52 | 78 | 53 | 83 |
| Y | 55 | 43 | 43 | 34 | 44 | 53 | 46 | 52 | 27 | 50 | |
| Z | 33 | 22 | 31 | 26 | 34 | 29 | 35 | 41 | 36 | 43 | |
| Work Condition (B) | I | II | III | IV | V | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pipe | Ground | Pipe | Ground | Pipe | Ground | Pipe | Ground | Pipe | Ground | ||
| VR/(cm/s) | 15.1S | 14.33 | 15.95 | 15.04 | 17.80 | 16.55 | 18.15 | 17.23 | 19.15 | 18.78 | |
| f/Hz | X | 57 | 45 | 48 | 76 | 54 | 79 | 50 | 83 | 62 | 67 |
| Y | 43 | 51 | 56 | 64 | 31 | 66 | 33 | 72 | 47 | 71 | |
| Z | 24 | 32 | 43 | 36 | 45 | 52 | 25 | 60 | 65 | 55 | |
| Work Condition (C) | I | II | III | IV | V | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pipe | Ground | Pipe | Ground | Pipe | Ground | Pipe | Ground | Pipe | Ground | ||
| VR/(cm/s) | 12.4 | 13.5 | 13.65 | 12.57 | 15.0 | 14.31 | 16.95 | 15.51 | 17.80 | 16.63 | |
| f/Hz | X | 49 | 55 | 53 | 81 | 61 | 81 | 55 | 73 | 41 | 72 |
| Y | 56 | 45 | 46 | 54 | 41 | 54 | 55 | 62 | 35 | 43 | |
| Z | 31 | 43 | 29 | 31 | 39 | 42 | 43 | 46 | 44 | 64 | |
| Variable | Dimension | |
|---|---|---|
| Dependent variable | Peak vibration velocity of pipeline particle/v | LT−1 |
| Independent variable | Explosive quality/Q | M |
| Distance from measuring point to explosion source/r | L | |
| Buried depth of pipeline/H | L | |
| Diameter of pipeline/D | L | |
| Pipeline operating pressure/P | ML−1T−2 | |
| Density of rock and soil mass/ρ | ML−3 |
| Working Condition | D/(cm) | H/(m) | P/(MPa) | r/(m) | Q/(kg) | VP/(cm/s) |
|---|---|---|---|---|---|---|
| 1 | 20.0 | 1.0 | 0.6 | 11.14 | 8 | 10.25 |
| 2 | 20.0 | 2.0 | 1.0 | 10.73 | - | 12.25 |
| 3 | 40.0 | 3.0 | 1.0 | 10.38 | - | 19.30 |
| 4 | 20.0 | 3.0 | 1.6 | 10.41 | - | 17.65 |
| 5 | 40.0 | 1.0 | 1.6 | 11.09 | - | 12.85 |
| 6 | 20.0 | 2.0 | 1.6 | 10.73 | - | 15.60 |
| 7 | 60.0 | 2.0 | 0.6 | 10.66 | - | 15.29 |
| 8 | 60.0 | 2.0 | 0.8 | 10.66 | - | 15.86 |
| 9 | 60.0 | 2.0 | 1.0 | 10.66 | - | 17.80 |
| 10 | 60.0 | 2.0 | 1.25 | 10.66 | - | 18.75 |
| 11 | 60.0 | 2.0 | 1.6 | 10.66 | - | 20.12 |
| 12 | 20.0 | 2.0 | 1.0 | 10.73 | - | 12.40 |
| 13 | 30.0 | 2.0 | 1.0 | 10.72 | - | 13.65 |
| 14 | 40.0 | 2.0 | 1.0 | 10.70 | - | 15.00 |
| 15 | 50.0 | 2.0 | 1.0 | 10.68 | - | 16.95 |
| 16 | 60.0 | 2.0 | 1.0 | 10.66 | - | 17.80 |
| 17 | 60.0 | 1.0 | 1.0 | 11.05 | - | 13.85 |
| 18 | 60.0 | 1.5 | 1.0 | 10.85 | - | 14.95 |
| 19 | 60.0 | 2.0 | 1.0 | 10.66 | - | 17.80 |
| 20 | 60.0 | 2.5 | 1.0 | 10.50 | - | 18.15 |
| 21 | 60.0 | 3.0 | 1 | 10.36 | - | 19.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, N.; Zhang, Y.; Wu, T.; Yao, Y.; Luo, X. Determination of Blasting Vibration Safety Criterion for HDPE Pipeline Using Vibration and Strain Data in a Coastal Metro Line. Sensors 2021, 21, 7252. https://doi.org/10.3390/s21217252
Jiang N, Zhang Y, Wu T, Yao Y, Luo X. Determination of Blasting Vibration Safety Criterion for HDPE Pipeline Using Vibration and Strain Data in a Coastal Metro Line. Sensors. 2021; 21(21):7252. https://doi.org/10.3390/s21217252
Chicago/Turabian StyleJiang, Nan, Yuqi Zhang, Tingyao Wu, Yingkang Yao, and Xuedong Luo. 2021. "Determination of Blasting Vibration Safety Criterion for HDPE Pipeline Using Vibration and Strain Data in a Coastal Metro Line" Sensors 21, no. 21: 7252. https://doi.org/10.3390/s21217252
APA StyleJiang, N., Zhang, Y., Wu, T., Yao, Y., & Luo, X. (2021). Determination of Blasting Vibration Safety Criterion for HDPE Pipeline Using Vibration and Strain Data in a Coastal Metro Line. Sensors, 21(21), 7252. https://doi.org/10.3390/s21217252






