Abstract
This paper is focused on the analysis of unfairness of random media access in Local Operating Networks (LON), which is one of the commercial platforms of the Industrial Internet of Things (IIoT). The unfairness in accessing the LON channel is introduced by a collision avoidance mechanism in the predictive p-persistent CSMA protocol adopted at the media access control layer. The study on the bandwidth share in predictive p-persistent CSMA calls for the analysis of multiple memoryless backoff. In this paper, it is shown that the channel access in LON systems is unfair in the short term for medium traffic load conditions, and in the long term for heavy loaded networks. Furthermore, it is explained that the average bandwidth allocated to a particular node is determined implicitly by the load scenario, while an actual node bandwidth fluctuates in time according to stochastic dynamics of the predictive p-persistent CSMA. Next, it is formally proven that the average bandwidth available to a node is a linear function of its backoff state and does not depend on backoff states of the other stations. Finally, it is demonstrated that possibly unfair bandwidth share in LON networks determined implicitly by load scenario is stable because, with lowering a fraction of actual network bandwidth accessible by a given station, the probability to decrease it in the future also drops.
1. Introduction
Fairness is a concept generally attributed to allocation of limited resources among a set of agents or individuals [1]. The importance of fairness issues in resource allocation has been recognized and well studied in a variety of research problems [1,2,3,4], along with applications in network engineering [5,6,7,8,9]. For communication services, a problem of fair sharing concerns all scarce resources, including link and flow scheduling, channel assignment, rate allocation, congestion control and routing protocols [5]. In an egalitarian vision, fairness simply means allocating the same share to all users, while any scheme resulting in uneven allocation of resources is recognized unfair.
Guaranteeing fairness in accessing the communication channel is a significant issue in distributed computing systems aimed to allocate network resources equitably. Sharing the network bandwidth in random access networks is fair only if the contending nodes have equal chances to possess the channel. Nevertheless, in many random access protocols the contention is, or in some scenarios could be, unfair. Inequitable sharing network resources causes a discrimination of some users implying a decrease of a fraction of bandwidth available to them, and a corresponding increase of their access delays. Due to usual demand on real-time operation, possible unfairness in network access is a more severe issue in networked control systems and Industrial Internet of Things than in conventional data computer networks. In general, a guarantee of fair access concerns the network with medium or heavy traffic load since inequality in sharing the bandwidth is not a problem when the channel is mostly idle, simply because the bandwidth is then not a scarce resource [6,7].
1.1. Unfairness of Network Access
A fair network access has to be guaranteed on various levels of the network protocol stack. Unequal chances to win the contention among the nodes might be introduced by the Physical Layer since different distances of devices from the transmitting station in the spatially distributed network yield distinct propagation delays of a signal in a communication medium. As a result, at the end of the transmission, some nodes sense the channel to be idle, and the others may detect the channel still to be busy. To resolve this problem, in the slotted random access protocols, the contention slot width and the minimum interpacket time are adjusted to the maximum end-to-end propagation delay [10].
Unfair access may appear in underwater acoustic sensor networks (UASN) due to slow propagation of sound speed in water (1500 m/s). The requests sent by the nodes that are far from the receiver may be processed later than the requests transmitted by the nodes that are close to the receiving node. This implies unfair channel access and calls for development of specialized protocols for UASN resolving spatial-temporal uncertainty [11].
A fair sharing network bandwidth belongs essentially to the tasks of Media Access Control (MAC) protocols designed to allocate network resources among the nodes equitably. Some communication standards in Industrial Internet of Things use priority systems that introduce the intended inequality in dividing the limited network resources among the stations to favor transmission of messages produced by distinct nodes, or of urgent messages in general.
Unfairness might be an unavoidable effect of the media access control mechanism used. An example is the dominance protocol adopted to resolve the collisions in Carrier Sense Multiple Access (CSMA) schemes (e.g., in Controller Area Networks (CAN) or Inter-Integrated Circuit (I2C) serial communication bus). This protocol has a good total throughput (no waste of bandwidth due to collisions), high efficiency and offers global prioritization at the cost of unfairness in sharing communication resources. In particular, if the usage of shared channel is not limited, the node with high priority can monopolize the network resources.
Furthermore, unfairness may appear in heterogeneous sensor networks (HSNs) if the applications generate data packets of a different size (e.g., temperature, humidity, or images) implying unequal bandwidth share [8,12]. Fairness can be also strongly disturbed under network attacks [12,13]. For example, under multiple access attacks (e.g., backoff attack) misbehaving stations would achieve a larger portion of the network bandwidth at the expense of the stations that respect the regular MAC mechanism [13].
Conversely, unfairness may result from mechanisms aimed to maximize the network throughput. In particular, in random access protocols, unfair sharing channel bandwidth is often introduced by collision avoidance schemes based on feedback from the network. A representative example is the IEEE 802.11 protocol for WLANs. Resetting the contention window size CW to its minimum value CWmin after each successful transmission leads to a short-term unfairness since a winning station will be privileged to win the contention on its next attempt. If the network is heavily loaded, the other stations will suffer severe throughput degradation resulting in unfair share of wireless channel bandwidth. Thus, binary exponential backoff in the IEEE 802.11 favors the winning stations to continue winning the contention in the near future [6,7].
Fairness and system efficiency are usually contradictory objectives [1,2]. A scheme that maximizes throughput without regard to treating individual flows equitably is regarded as fully “efficient”. If fairness considerations are incorporated, the efficiency of the system is likely to decrease. The tradeoff between fairness and system efficiency is a common issue and concerns not only communication systems [2,9,12,14]. The efficiency loss (i.e., the difference between the maximum system efficiency and the efficiency under the fair scheme) relative to the maximum system efficiency can represent the “price of fairness” [3]. Some approaches are aimed to maximize both the system efficiency (e.g., throughput) and fairness [14]. A variety of mechanisms to increase fairness in Internet-of-Things-based networks has been proposed and examined in recently published works [12,13,15,16].
1.2. Paper Contribution
The present study addresses a problem of the unfairness in accessing the channel introduced by a random access scheme adopted in Local Operating Networks (LON), one of communication platforms that belong to Industrial Internet of Things (IIoT). LON has become a classical solution in building automation, home networking, street lighting control, and smart cities [10].
The media access control mechanism adopted in LON in its non-priority phase, called the predictive p-persistent CSMA, belongs to the class of MAC protocols aimed essentially to share average bandwidth equitably to all the nodes in the network. The predictive p-persistent CSMA scheme uses the collision avoidance mechanism similar to the IEEE 802.11 protocol. The collision avoidance allows to keep high total network throughput even under overload conditions by scaling the backoff to the expected traffic load [17]. However, as it will be shown in this paper, the collision avoidance causes sharing network bandwidth among the stations inequitably as a side effect of maximizing the total throughput. The predictive p-persistent CSMA is thus the example of a MAC protocol that sacrifices fairness for better efficiency beside the IEEE 802.11 [6,7], or Dynamic Channel Negotiation MAC (DCN-MAC) for Underwater Acoustic Sensor Networks [11].
Unlike IEEE 802.11 protocol, unfairness of the predictive p-persistent CSMA except preliminary study in [18], has not been yet indicated and analyzed neither in the technical documentation, nor in engineering literature. Meanwhile, the problem of unequal access is significant since, as follows from the forthcoming discussion, the unfairness is an inherent part of the predictive p-persistent CSMA operation in most network traffic scenarios. Thus, the present work contributes to rapidly growing research on fairness of various network services including Internet-of-Things-based networks.
The study on the predictive p-persistent CSMA protocol fairness calls for the analysis of multiple memoryless backoff. In the literature, there are many works that deal with the multiple non-memoryless backoff since it models the operation of Distributed Coordination Function (DCF) mechanism in the IEEE 802.11 (e.g., [19]), and for example also in Sensor MAC (SMAC) [20], WiseMAC [21], Timeout MAC (TMAC) [22], and Dynamic Sensor MAC (DSMAC+) [23]. Lower attention has been devoted to the analysis of the multiple memoryless backoff [17,18,24,25,26,27,28]. The latter has been adopted not only in the predictive p-persistent CSMA but also in the IEEE 802.3 (Ethernet) and IEEE 802.15.4 protocols [29,30]. In order to investigate the access unfairness, this paper is focused on the examination of stochastic dynamics of the predictive p-persistent CSMA. The presented research addresses four main aspects:
- specification of reasons that evoke the unfairness of the network access in the predictive p-persistent CSMA;
- analysis of possible unequal bandwidth distribution among the contending nodes;
- impact of unequal bandwidth distribution on the total network utilization that represent system efficiency;
- examination of the bandwidth allocation stability in time aimed to assess if unfairness tends to escalate or is under self-imposed limit.
The original contributions made by this paper to the state of the art are as follows. First, it is shown that the channel access in the predictive p-persistent CSMA is unfair in short term for medium traffic load conditions, and in long term for heavy loaded network. Second, it is explained that the average bandwidth allocated to a particular node is determined implicitly by the load scenario (i.e., rate and specification of input traffic generated to the network by a particular node and other contending nodes), while an actual node bandwidth fluctuates in time according to stochastic dynamics of the predictive p-persistent CSMA. Next, it is formally proven that the average bandwidth available to a node is a linear function of its backoff state and does not depend on backoff states of the other stations. Finally, it is demonstrated that possibly unfair network bandwidth share in LON networks determined implicitly by load scenario is stable in time because, with lowering a fraction of actual network bandwidth accessible by a given station, the probability to decrease this actual bandwidth in the future also drops. The presented analysis is based on qualitative measures of fairness.
2. Fairness in LON Networks
Local Operating Networks (LON) platform is one of leading standards in Industrial Internet of Things addressed to a wide range of applications. Thus far, tens of millions of devices have been installed with LON technology worldwide. In particular, LON has become a classical solution in building automation, home networking, street lighting and smart cities [10].
2.1. Reason of Unfairness
LON networked control systems are built upon event-driven architecture [10] and adopt event-triggered transmission strategy [31,32]. One of efficient services employed in LON platform to improve utilization of the network bandwidth is multicast addressing. This service is rare in industrial networking. A multicast message is received by a group of destination nodes. Thus, multicast transactions save communication bandwidth since a single multicast (one-to-many) message can substitute a set of unicast (one-to-one) messages addressed to each recipient individually [33].
Because the random access protocol of CSMA type used in the LonTalk MAC sublayer does not provide guarantee of message delivery, the classical acknowledged message service is used by default to improve end-to-end communication reliability. As a response to the acknowledged multicast message reception, each receiver generates a positive acknowledgement to the sender. In the LonTalk random access protocol, the acknowledgement packets contend for the channel access together with messages since there is no dedicated collision-free channel for sending acknowledgements as it is in the IEEE 802.11. Thus, soon after a successful transmission of a multicast acknowledged message, a number of nodes equal to the number of multicast message recipients almost at the same time try to access the channel to send the acknowledgement packets additionally to the traffic of the original messages or stale acknowledgements. To avoid excessive collisions due to a burst of acknowledgements, a collision avoidance with a prediction mechanism is used in the LonTalk random access protocol. The prediction is based on accumulating the numbers of expected acknowledgements (or responses) encoded in the header of each message sent or received, and on accumulating the number of expected message retransmissions by detecting collisions if hardware collision detection is provided. Each node predicts the expected traffic autonomously using backlog counters implemented in the protocol. The actual number of contention slots used by each node to randomize the network access is proportional to its current backlog state.
The fundamental problem is that there is no global coordination of states of backlog counters among the nodes. Since the backlog increments encoded in the packet headers and used for traffic prediction is distributed through the network only by successfully transmitted messages, the states of backlog counters are consistent any time provided that the channel is noise-free and collision-free, or at least if unsuccessful transmissions are recognized by all the nodes (not only transmitters of messages involved in collision). Otherwise, the numbers of contention slots used to randomize the channel access may vary among the contending nodes, which favors the node(s) with the lowest backlog state to win the contention. The contending nodes with higher backlog states have lower chance to possess the channel. Thus, the inconsistency of backlog states results in unfairness of channel access in LON networks.
2.2. Protocol Specification
The random access scheme in the LonTalk protocol, registered as the ANSI/CEA-709.1-B standard, is the predictive p-persistent CSMA that belongs to variable-window slotted-CSMA protocols [17,33]. A node contending for a channel selects a random backoff expressed as a random number of slots drawn from the uniform distribution between 1 and W, where W is the size of the contention window. If the channel is still idle when the random delay expires, the node transmits in slot r. Otherwise, the node receives an incoming packet, discards the slot drawn and competes for the channel access again. If more than one node chooses the same slot number, and when that slot has the lowest number selected by any node with a packet to send, then a collision happens. All the packets involved in a collision are corrupted.
In the predictive p-persistent CSMA scheme, the size of the contention window managed by each node autonomously, varies in time and is dynamically adjusted to the expected channel load. The number of slots grows by factor BL, called the estimated backlog since W = 16BL, where BL is the actual state of the backlog counter that cannot be lower than one, and higher than 63.
The predictive p-persistent CSMA scheme belongs to variable-window CSMA protocols with memoryless backoff, which means that the contenders draw a number of a contention slot in every transmission attempt anew and cancel them when the transmission is detected in the channel). For a comparison, in the IEEE 802.11, the non-memoryless backoff is applied where the competing nodes freeze their backoff timers in case of detecting transmission, wait to the end of the current packet transmission, and then resume these timers.
On the top of the predictive p-persistent CSMA, the acknowledged and the unacknowledged message services are provided. As a response to an acknowledged message reception, each receiver generates a positive acknowledgement packet to the sender. The message may be addressed to a single recipient (unicast), or to a group of recipients (multicast). In the unacknowledged service, the acknowledgements are not applicable. In the LonTalk, the acknowledgement packets compete for the channel together with messages according to the same contention algorithm.
2.3. Backlog Counting Algorithm
As stated, the backlog estimation is based on predicting the current number of packets expected in a channel contention. The actual state of the backlog counter BL varies from one to the next transmission attempt and relies on the accumulation of consecutive backlog increments and decrements [17,33].
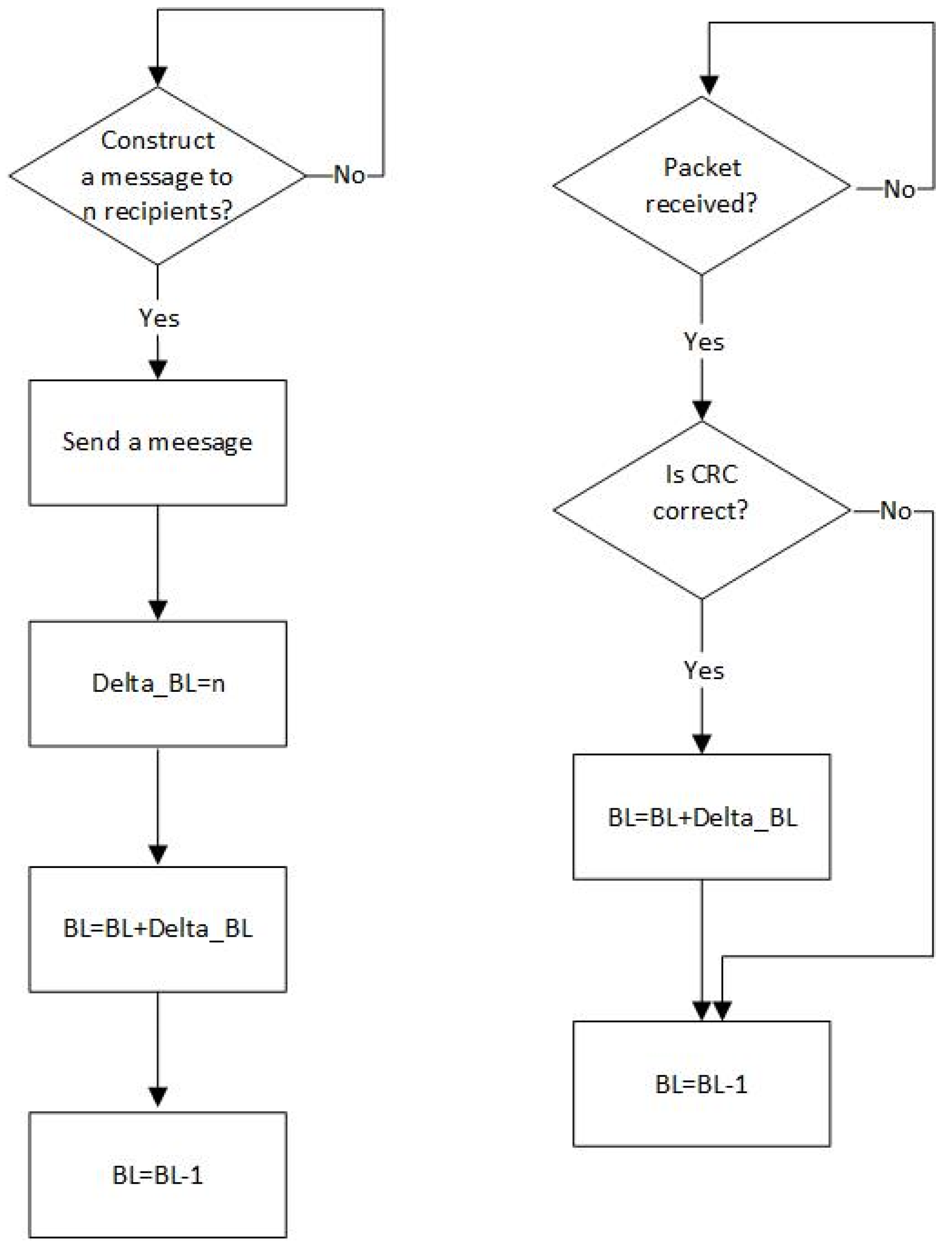
Backlog counting, built into the node firmware, consists in the following principles: (i) successive backlog increments based on the information included in the header of each packet sent or successfully received by a particular node; this information is encoded in the 6-bit long data field Delta_BL; (ii) successive backlog decrements by one at the end of packet transmission provided that the collision is not detected (Figure 1).
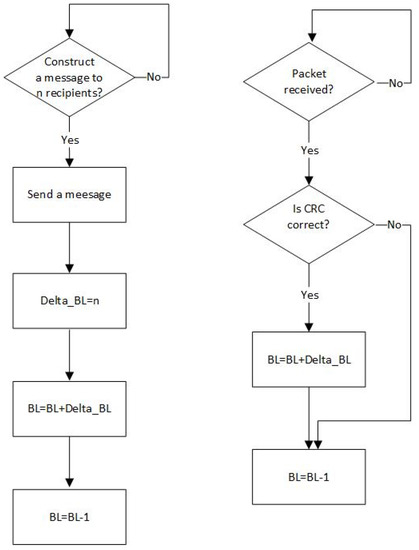
Figure 1.
Backlog counting algorithm for transmitting nodes (left diagram), and for receiving nodes (right diagram) if the nodes are not equipped with collision detection.
Thus, the backlog BL is increased after successful packet transmission or reception by a Delta_BL-1 where Delta_BL represents the number of acknowledgements that will be generated by receiver(s) as a result of a successful packet reception. For unicast messages Delta_BL equals one, and for multicast messages Delta_BL is higher than one but lower than 63 which is the maximum size of a group of receiving nodes addressed by a single multicast message. Consequently, the Delta_BL equals zero either for the unacknowledged messages, or for the acknowledgement packets. The data field Delta_BL is read by each node in the network, where a packet is broadcasted before examination of packet destination address(es).
2.4. Aim of Collision Detection
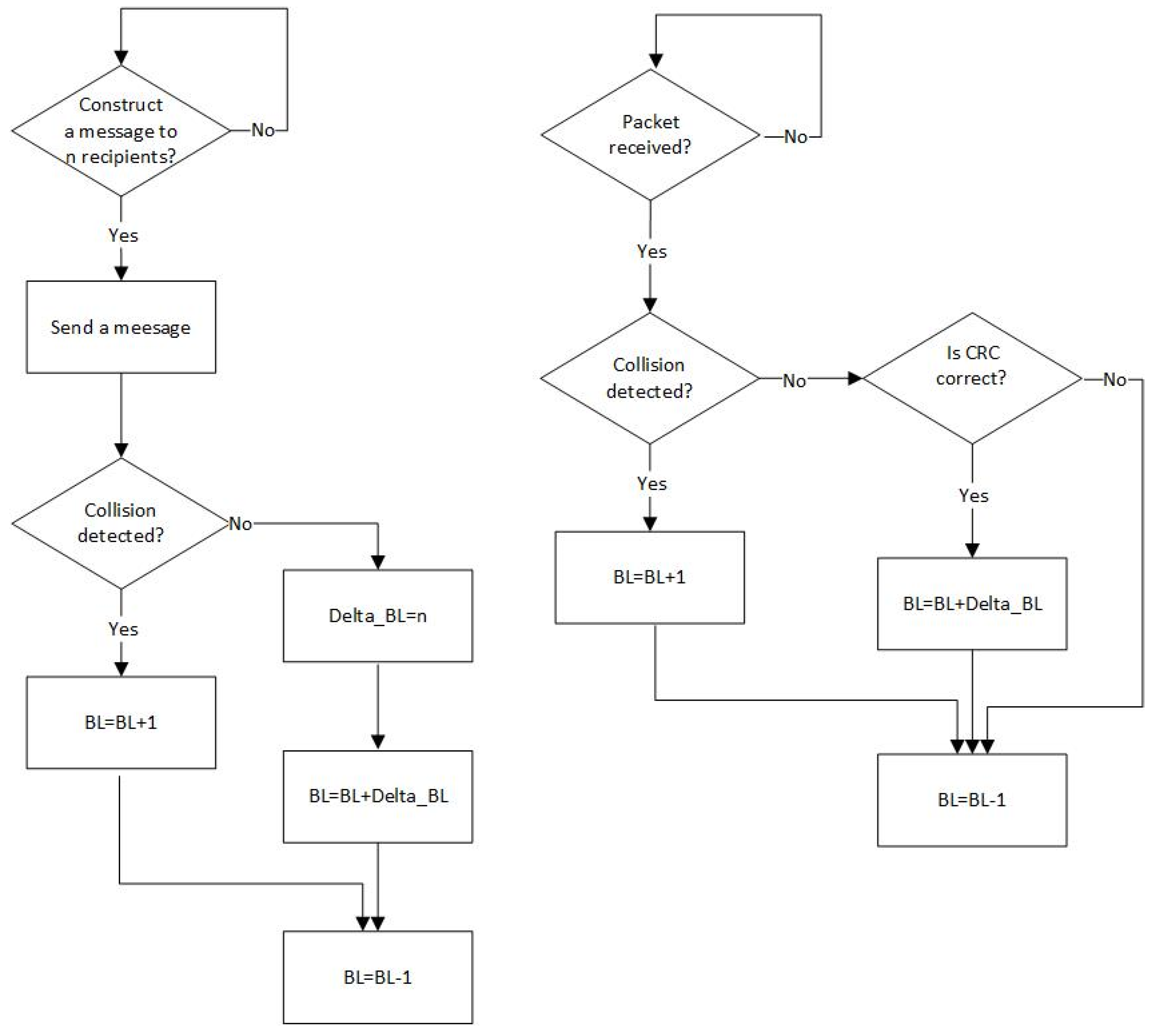
Optionally, the backlog counter might be also incremented by one in case of a collision if the nodes are equipped with the collision detection hardware [17] (Figure 2).
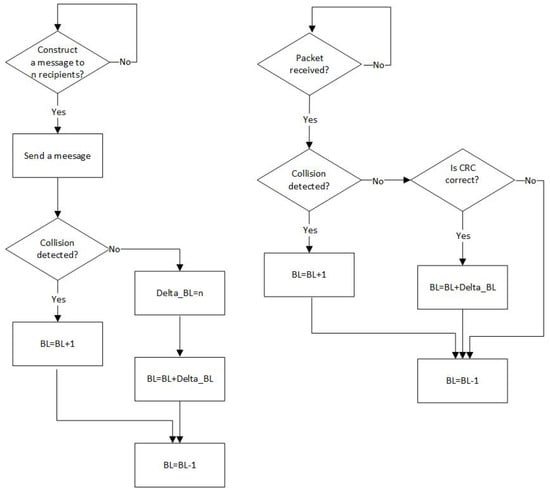
Figure 2.
Backlog counting algorithm for transmitting nodes (left diagram) and receiving nodes (right diagram) if they are able to detection collisions.
In traditional computer networks, the collision detection has been provided to avoid a waste of bandwidth by stopping as soon as possible transmissions of long data packets involved in collisions [34]. This argument is invalid in networking technologies that form Internet of Things since the size of packets transmitted through the channel is relatively small and usually does not exceed a few dozens of bytes. The motivation to use the collision detection in LON networks is different from that related to computer data networks. First, from the point of view of the packet sender, the collision detection reduces the response time because the sender does not have to wait for time-out before attempting to resend the messages. Second, in the context of global network performance, the collision detection is a part of collision avoidance mechanism that improves the network throughput due to adjustments of the contention window size to the current traffic load [17].
3. Providing Fairness in Random Access Protocols
Fairness in distributed computer systems has been studied since origins of network engineering using both qualitative and quantitative metrics. The first widely accepted quantitative measure of fairness was proposed by Jain [35]. The Jain’s fairness index evaluates the equality of user allocation and is bounded between 0 and 1. A totally fair resource allocation system has a value of Jain’s fairness index equal to 1, while a totally unfair system reaches a value of 0. Jain’s index is intended to evaluate long-term fairness but can be also used for classifying short-term fairness by applying sliding window averages of resource share [7]. Although Jain’s index reflects well the fairness of the whole system, it does not provide a deeper view to relationships between fraction of resources allocated to particular users [5]. The other measure that has been adopted for quantitative evaluation of fairness is entropy introduced in the context of information theory [36]. Entropy may be considered as expression of fairness because it is maximized when the allocation is equal [37].
Qualitative measures do not evaluate fairness by numbers but instead they give guidance for possible fair resource allocation. Two most representative qualitative measures are max-min and proportional fairness. A resource allocation is max–min fair if an attempt to increase the allocation of any flow must be at the cost of a decrease of some already smaller flow. The max-min fairness is used in various areas of networking and aims at allocating as much as possible resources to users with low rates and, at the same time, not unnecessarily wasting available resources [4]. Conversely, the proportional fairness is the ratio between the maximum and the average resource consumption [37].
The aforementioned approaches to fairness assessment that may be classified as based on Quality-of-Service (QoS) of the network are insufficient to examine fairness related to Quality-of-Experience (QoE) of end users. Although QoE of a network service user is in general dependent on QoS of the network, the notions of fairness commonly applied in the QoS domain do not translate well to the QoE domain [38]. In [39], the QoE fairness metric is defined as a linear transformation of the standard deviation of QoE of all users consuming a service to the range of [0; 1], and the system is absolutely QoE fair when all users receive the same QoE value.
Considering the time duration, fairness can be categorized into short term and long term [6,7]. A system is said to be long-term fair if all the users gain equitable access to its resources in the long-run, although there may be transient periods of unbalanced access. Short-term fairness, instead, refers to equitable share of resources in short run. Usually, short-term fairness implies long-term fairness but not vice versa [6,7].
3.1. Fairness of Random Access
To discuss a possible inequality in distributing shared resources in the random access protocols, we choose the probability of successful transmission of a given contending node as a bandwidth allocation metric. If this probability is the same for all the contending nodes in each transmission attempt, then the network access is fair. It can be also easily demonstrated that equal probability of successful transmission for each node implies even throughputs and the mean access delays among contending stations [17,27].
It is evident that the channel access according to slotted CSMA schemes with memoryless backoff is fair if all contenders choose a given contention slot used to settle the competition with equal probability. According to this observation, the probability of choosing slots within the contention window might vary among the contention slots (e.g., in the CSMA scheme with a geometrical distribution [40,41]) but particular slots have to be drawn by the contenders with the same probability. From the above condition, the following straightforward conclusion can be derived for the predictive p-persistent CSMA.
Remark 1.
Channel access according to the predictive p-persistent CSMA protocol is fair if and only if all the contending nodes have the same backlog states before each transmission attempt.
3.2. Providing Backlog Consistency in Predictive p-Persistent CSMA
As stated, there is no global coordination of states of backlog counters among the nodes. Each node computes the channel backlog autonomously based on its backlog counter. To keep the consistency of backlog states as required in Remark 1, all the nodes in the network should modify their backlog counters by the same increment or decrement synchronously before each transmission attempt.
The backlog counters consistency is guaranteed if the channel is noise-free, all the nodes are equipped with collision detection and collision detection technique allows every node to recognize each collision occurrence in a channel [17]. The backlog state is then the same for all the nodes in the network and varies randomly in time due to stochastic nature of the predictive p-persistent CSMA scheme. In the network steady state, the probability density function of backlog state is unimodal for the protocol version with collision detection, and quasi-exponential for the version without collision detection [17]. Both in the protocol version without and with collision detection, the backlog probability distribution is long-tailed. The analysis of the predictive p-CSMA performance based on queuing theory is reported in [24,25].
However, in the presence of transmission errors due to noise, or if the collision detection is absent, or if the collision detection is provided but the nodes are unable to recognize all collision occurrences in a channel, the backlog states can differ among the nodes as follows from a description of the backlog counting algorithm stated in Section 2.1.
First, the packets with an invalid CRC introduce the backlog inconsistency since all the nodes in a network segment where a packet is broadcasted reject it, and only the packet sender modifies the backlog counter according to the content of its Delta_BL field. Thus, the noise introduced by Physical Layer can break backlog consistency since recipients cannot read Delta_BL field of corrupted packets. For example, if the multicast message to 3 recipients is corrupted by the noise, the sender finally increments its counter by 2, and all the other nodes decrement their backlog counters by 1.
Second, the backlog inconsistency is introduced by Link Layer, if the nodes are unable to recognize unsuccessful transmissions (i.e., collision detection is not provided, or the nodes are unable to detect all collisions). Namely, if a packet is involved in a collision during transmission in the channel without collision detection, the modifications of backlog counters, introduced by the senders and by the remaining nodes in the network, finally differ. The senders after transmission increase their counters by the Delta_BL. However, all the other nodes in the network are unable to read the number encoded in the Delta_BL data field of the packets corrupted by collisions; thus, their backlog counters are decremented by one according to the backlog counting principles presented in Section 2.1. For example, if the multicast message addressed to two recipients collide with the unicast message, then their senders increment the corresponding counters by 1 and zero respectively, whereas all the other nodes decrement their backlog counters by 1. The senders of collided packets have a lower chance to win the contention in future since their backlog states will be larger than the backlog of the other nodes. The unfairness introduced by the collision is greater, if the multicast messages collide. In particular, the collision does not cause the unfairness if the packets involved in a collision have Delta_BL equal to zero (e.g., if the unacknowledged messages collide with the acknowledgment packets). Moreover, if the input traffic does not contain acknowledged multicast messages in the channel without collision detection, then the Link Layer does not introduce backlog inconsistency since the predictive p-persistent CSMA scheme is then reduced to the pure 0.0625-persistent CSMA where the traffic-based contention window adaptation is disabled [27]. However, the price of fair channel access in this load scenario is the absence of the collision avoidance mechanism.
The backlog inconsistency is introduced also if the collision detection is provided, but only senders of packets involved in collision are able to detect it. The senders increment their backlog counters by one but all the other nodes in the network segment decrease their backlog counters by one. Thus, such a partial collision detection also introduces backlog inconsistency. Unfortunately, the LON transceivers that were available on the market enable only senders to detect possible packet collisions (like Ethernet transceivers) and increment their backlog counters. Meanwhile, the role of collision detection in LON control networks is more extensive than in conventional LANs as stated in Section 2.3.
3.3. Short-Term and Long-Term Unfairness
The inconsistency in backlog counting is not a serious problem if a channel stays under light or medium traffic load, because idle cycles can recover the backlog consistency if the minimum window size (BL = 1) is reached for some time. More specifically, the fairness is recovered not later than after a number of idle transmission cycles equal to the highest backlog state possessed by any node. Thus, if the network is not heavily loaded, the unfairness in LON systems is short term. However, if the channel is heavy loaded, there are no idle cycles and the minimum backlog state equal to one cannot be reached. Since there is no mechanism that forces coordination of backlog counters among the nodes, the unfairness in channel access is introduced in the long run although accidentally the consistency of states may occur.
3.4. Implicit Bandwidth Allocation in Predictive p-Persistent CSMA
In a result of protocol unfairness, the bandwidth share in LON networks is dynamical and determined by the random evolution of the backlog counters in contending nodes. The relations between fractions of bandwidth available to particular nodes change in time. A node that transmits many messages is more often exposed to collisions and to decrease its chance to access the channel in future. Moreover, if it transmits many multicast messages, a reduction of allocated bandwidth may be higher. Conversely, the node that is silent, or produces unacknowledged or unicast acknowledged messages potentially has a higher chance to transmit successfully.
The process of bandwidth allocation cannot be controlled by a user but is determined implicitly by the load scenario (i.e., a specification of input traffic generated to the network by particular nodes). A fraction of available bandwidth changes in time according to stochastic dynamics of the predictive p-CSMA protocol. In Section 4, a more extensive analysis of the unfairness of the predictive p-persistent CSMA is provided.
4. Analysis of Backlog Inconsistency Model in Predictive p-Persistent CSMA
Since the problem of the protocol unfairness is related especially to the heavy network load, we choose the saturation network status as the conditions for investigation of inequality in accessing the channel. The saturation status represents the largest possible load offered by a given number of nodes.
Let us consider a LON network that contains a number of n nodes. As described, the state of backlog counters residing at particular nodes evolve stochastically with the estimated channel load. A discrete dynamical stochastic system of distributed backlog counters might be in the steady state, or in the transient state.
As already mentioned, the forthcoming model of backlog inconsistency involves analysis of multiple memoryless backoff [18,26]. The parallel analysis of inconsistency of non-memoryless backoff modeling the network attack by deviation of MAC scheme (backoff attack) in the IEEE 802.11 has been reported in [15].
4.1. Basic Backlog Inconsistency Model
At the beginning of the analysis, we propose to examine a basic backlog inconsistency model where the n nodes are distributed in two groups. One group contains n-m nodes occupying the backlog state k1, the other group includes m nodes that are in the state k2 > k1. Let us assume arbitrarily that at the beginning of the analysis, all the nodes are in the state k1 (m = 0), and then the backlog states of the nodes successively move from the state k1 to the state k2. Finally, in the proposed backlog inconsistency model, all the n nodes reach the state k2 that means in particular a recovery of backlog consistency. Since the proposed model is arbitrary, the analysis does not deal with causes that force such a backlog evolution. Thus, the analysis is valid for any protocol version (either with or without of collision detection). A transition of the backlog state from k1 to k2 may occur immediately in one transmission attempt or in a few attempts. In particular, the transition from k1 to k2 occurs in a single transmission attempt if the acknowledgement packet(s) or the unacknowledged message(s) collide with the acknowledged message addressed to (k2 − k1 + 1) recipients in a channel without collision detection.
The aim of the analysis is to examine: (1) how the distribution of bandwidth available to particular nodes changes with evolution of their backlog states; (2) what is an influence of the backlog state inconsistency on the global network performance represented by the total probability of successful transmission; (3) whether the process of implicit bandwidth allocation in LON systems is stable.
Denote by the probability that a certain node occupying the state ki, i = 1; 2 transmits a packet successfully provided that the numbers of nodes residing at the states k1 and k2 equal n − m and m, respectively. Both probabilities and are given by the following formulae [18]:
for 0 ≤ m < n.
In Formula (1), the probability is defined as the sum of products of the following partial probabilities for each one from 1, …, 16k1 slots, which are available for the node with the backlog state k1:
- probability that a winner selects a certain slot s, s = 1, …, 16k1, which equals 1/(16k1);
- probability that the other (n − m − 1) nodes occupying the state k1 select one of slots s + 1, …, 16k1 equal to [(16k1 − s)/16k1]n−m−1;
- probability that the m nodes occupying the state k2 select one from the slots s + 1, …, 16k2, which equals [(16k2 − s)/16k2]m.
In Formula (2), the probability is defined similarly, however the probability that a winner selects a certain slot s, s = 1, …, 16k2 equals 1/(16k2) since it draws from the range 1, …, 16k2.
In particular, if all the n nodes occupy the state k2 (m = 0), then [18]:
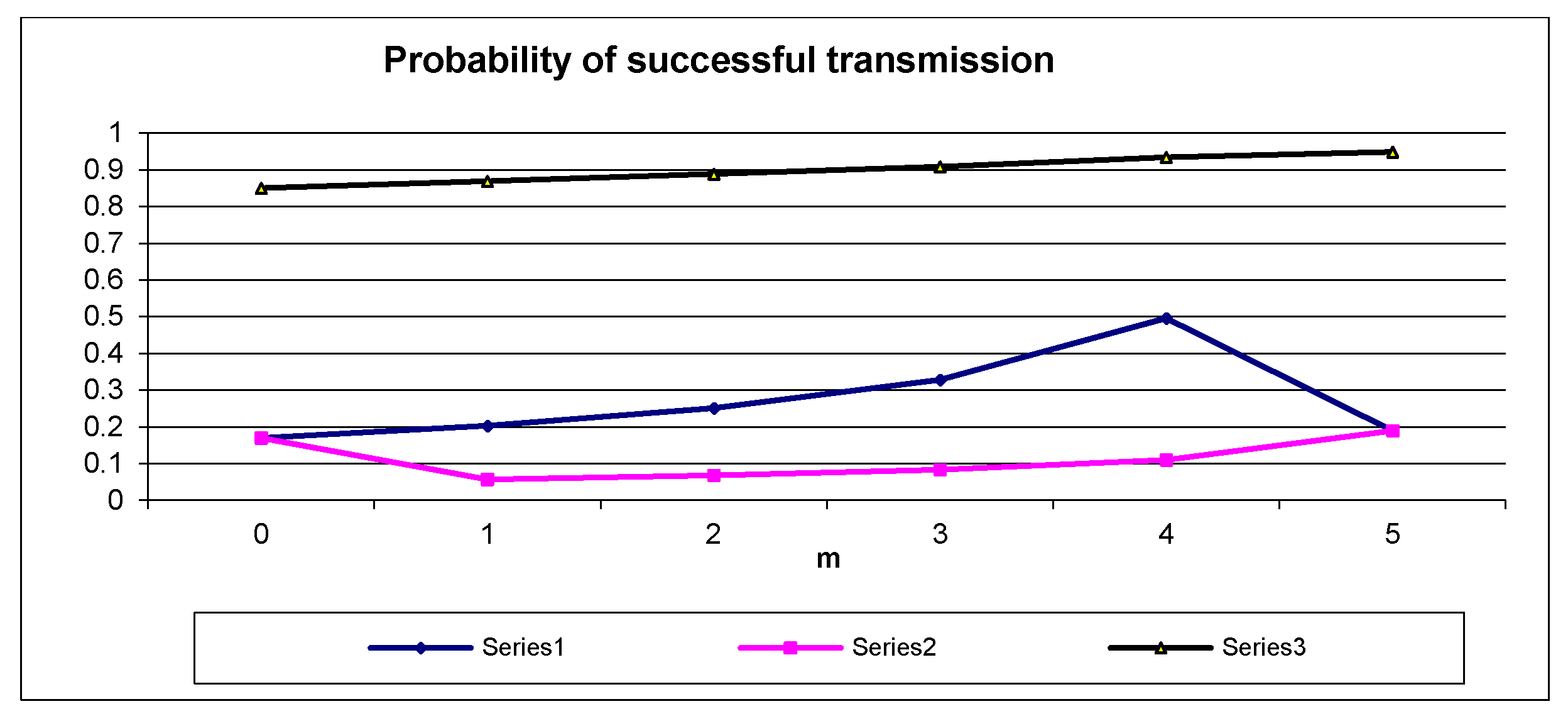
If at least one node occupies the state k1, then any successful transmission starts in a slot from the range 1, …, 16k1; thus, the true contention is reduced to 16k1 slots as expressed by (1), (2). However, if all the nodes are at the state k2, the contention is carried out within a number of 16k2 slots; thus, the sum in (3) contains 16k2 elements. The relationships , versus m together with according to (1), (2), (3) for n = 5, k1 = 1, and k2 = 3 are illustrated in Figure 3.
Comparing Formulae (1) and (2), it is evident that for 0 < m < n:
Thus, the backlog inconsistency among the nodes causes a decrease of bandwidth available to the node(s) that has higher backlog state(s), which is represented by the left inequality of (4). At the same time, the bandwidth accessed by the nodes that occupy the lower backlog state is increased as defined by the right inequality of (4).
As seen in Figure 3, the probability of successful transmission for each node that moves its state from k1 to k2 decreases because , m = 1, …, n.
The relative change of the probability of successful transmission for a node due to moving its backlog state is expressed by Remark 2 that will be defined for a general backlog inconsistency model.
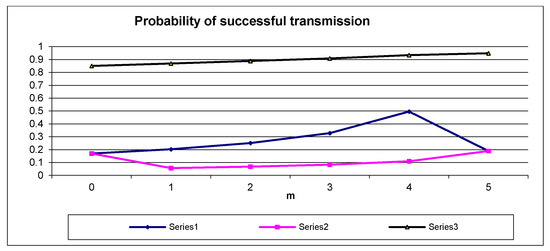
Figure 3.
Plots of , vs. number of nodes (m) that occupy backlog state k2 and according to (1), (2), (3), and according to (9) for n = 5, k1 = 1, and k2 = 3.
Figure 3.
Plots of , vs. number of nodes (m) that occupy backlog state k2 and according to (1), (2), (3), and according to (9) for n = 5, k1 = 1, and k2 = 3.
4.2. Bandwidth Share in General Backlog Inconsistency Model
Generalizing the backlog inconsistency model introduced in Section 4.1, let us assume that a number of n contending nodes occupy a number of l backlog states k1, k2, …, kl where ki < ki+1 such that ni nodes reside in the state ki, i = 1, …, l and n = n1 + … + nl. The probability that a certain node that is in the state ki transmits successfully is defined as:
Formula (5) is an extension of Formulae (1)–(3). The contention is reduced to the number of 16k1 slots defined by the lowest backlog state k1. A winner occupying the state ki selects the winning slot s with the probability 1/(16ki), the other (n − 1) nodes from the ith subset choose later slots s+1, …, 16ki with probability , and all the nodes from the jth group (i ≠ j) choose later slots s + 1, …, 16kj with probability . Remark 2 defines the bandwidth share among the nodes for the general backlog inconsistency model.
Remark 2.
The node that moves from the backlog state ki to kj, while the other nodes still occupy their states, changes its probability of a successful transmission by the factor kj/ki:
In order to prove Remark 2, let us notice that:
By dividing (7) by (8), Formula (6) is obtained.
The content of Remark 2 is surprising since the ratio of both probabilities is independent of the number of contending nodes n = n1 + … + nl and their deployment among the backlog states ki (ki = k1, …, kl). An additional result of changing the state of a distinct node is an increase (if kj > ki) or a decrease (if ki > kj) of the success probabilities for all the other nodes similarly as defined by the right inequality of (4) for the basic backlog inconsistency model. Furthermore, note that the success probability of the distinct node may change in future even if this node will stay in the same backlog state but if the other nodes will change their states. Each active node that moves from one to the other state changes its success probability by the factor equal to the ratio of both states as defined by Remark 2. Thus, the current bandwidth allocation is not determined only by the occupied backlog state but also on the deployment of the other contenders among the states.
4.3. Fairness Recovery vs. Channel Load
Let us consider the case when a certain node moves from k1 to k2 while all other nodes keep the state k1. As follows from (6), the probability that the distinct node successfully transmits reaches its maximum if the backlog state is at its minimum (k1 = 1), which corresponds to the light channel load. Thus, the most significant access unfairness is introduced if the background traffic of the network is low, and the contention window consists of 16 slots (k1 = 1). However, the fairness recovery is then faster, and may occur even after one transmission attempt. If the background backlog state k1 > 1, which corresponds to the medium or heavy load conditions, then the unfairness is lower, but the time needed to recover the access fairness is longer and may occur at least after k2 − 1 transmission attempts.
4.4. Fairness vs. Mean Channel Utilization
The backlog inconsistency has also impact on the global network performance (that may be considered as the system efficiency according to [2], or [3]) as demonstrated in the forthcoming discussion. To estimate the global network performance, we choose the total probability of successful transmission of any packet. This probability is defined as the sum of success probabilities of all the contending nodes. If a number of ni nodes reside in the state ki, i = 1, …, l where ki < ki+1, then the total probability of successful transmission equals:
where is defined by (5).
In Figure 3, the plot of the versus m according to (9) for k1 = 1, k2 = 3, n = 5 is presented. As seen, the increases with growing m. Thus, the final result of moving the backlog state of any node from k1 to k2 is an increase of total bandwidth of the communication system. The corresponding conclusion is formulated in Remark 3.
Remark 3.
If any node among the other contending nodes changes its backlog state, then the total probability of successful transmission in the system also changes. If a node moves toward higher backlog states, the total probability increases, and if a node moves toward lower backlog states, the total probability decreases. Thus, if ni < nj, then:
Remark 3 is intuitively clear because with the growing backlog state of any node, the true contention becomes lower and vice versa. The formal proof of (10) is a relative straightforward extension of the proof of Remark 3 in [18]. In particular, by setting (9) to (10), it may be shown that:
The cause of improving total bandwidth utilization represented by Remark 3 is that the decrease of the success probability of the node that moves toward higher backlog states (defined by Remark 2) is lower than the sum of increases of probabilities of successful transmissions gained by the other nodes that occupy their previous backlog states.
The following remark defines the upper bound of the increase of the total probability of successful transmission evoked by moving a number of nodes toward higher backlog states.
Remark 4.
If the backlog state of a set of ni nodes among a total number of n nodes increases significantly, then the total probability of successful transmission approaches its upper limit equal to the total probability of successful transmission for a number of n − ni contending nodes.
If the backlog state kl occupied by a set nl nodes increase significantly, then:
Remark 4 is also intuitively clear since nl nodes with growing backlog state are gradually eliminated from the contention, and the true contention is then reduced to a number of n = n1 + … + nl−1 contenders. The formal proof of (12) is a relatively straightforward extension of the proof of Remark 4 in [18].
6. Conclusions
The paper presents an analytic approach to qualitative evaluation of the media access unfairness of random media access in Local Operating Networks (LON), which is one of commercial platforms of Industrial Internet of Things (IIoT). The unfairness in accessing the LON channel is introduced by a collision avoidance mechanism in the predictive p-persistent CSMA protocol adopted at the media access control level. It has been shown that the channel access in LON systems is unfair in the short term for medium traffic load conditions, and in the long term for heavy loaded network. Furthermore, it is explained that the average bandwidth allocated to a particular node is determined implicitly by the traffic load scenario (i.e., rate and specification of input traffic generated to the network by particular nodes in the network). Finally, it is demonstrated that possibly unfair bandwidth share in LON networks determined implicitly by load scenario is stable because with lowering a fraction of actual network bandwidth accessible by a given station, the probability to decrease it in the future also drops. The presented analysis exemplifies the tradeoff between fairness and system efficiency, which is a common paradigm in communication systems. The work contributes to rapidly growing research on fairness of various network services including Internet-of-Things-based networks.
Funding
This research was funded by National Center of Science of Poland, grant number DEC- 2018/31/B/ST7/03874.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
The proofs that:
Proof.
On the basis of (13):
On the basis of Newton’s generalized binomial theorem:
Conversely:
Thus:
and next
Finally:
Thus, the proof is completed.
□
Proof.
On the basis of (13):
Since by the assumption of k2 > k1, thus:
Finally:
Thus, the proof is completed because of (A1). □
References
- Bin-Obaid, H.S.; Trafalis, T.B. Fairness in Resource Allocation: Foundation and Applications. In Network Algorithms, Data Mining, and Applications. NET 2018. Springer Proceedings in Mathematics & Statistics; Bychkov, I., Kalyagin, V., Pardalos, P., Prokopyev, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 315. [Google Scholar]
- Bertsimas, D.; Farias, V.F.; Trichakis, N. On the efficiency-fairness trade-off. Manag. Sci. 2012, 58, 2234–2250. [Google Scholar] [CrossRef]
- Bertsimas, D.; Farias, V.F.; Trichakis, N. The price of fairness. Oper. Res. 2011, 59, 17–31. [Google Scholar] [CrossRef] [Green Version]
- Radunovic, B.; Le Boudec, J.-Y. A unified framework formax-min and min-max fairness with applications. IEEE/ACM Trans. Netw. 2007, 15, 1061–1070. [Google Scholar] [CrossRef] [Green Version]
- Huaizhou, S.; Prasad, R.V.; Onur, E.; Niemegeers, I. Fairness in wireless networks: Issues, measures and challenges. IEEE Commun. Surv. Tutor. 2013, 16, 5–24. [Google Scholar] [CrossRef]
- Bottigleliengo, M.; Casetti, C.; Chiasserini, C.-F.; Meo, M. Short-term fairness for TCP flows in 802.11b WLANs. In Proceedings of the IEEE INFOCOM, Hong Kong, China, 7–11 March 2004; Volume 2, pp. 1383–1392. [Google Scholar]
- Koksal, C.E.; Kassab, H.; Balakrishnan, H. An analysis of short-term fairness in wireless media access protocols. In Proceedings of the ACM SIGMETRICS 2000, Santa Clara, CA, USA, 18–21 June 2000; pp. 118–119. [Google Scholar]
- Kim, E.-J.; Shon, T.; Park, J.J.H.; Jeong, Y.-S. Throughput Fairness Enhancement Using Differentiated Channel Access in Heterogeneous Sensor Networks. Sensors 2011, 11, 6629–6644. [Google Scholar] [CrossRef] [Green Version]
- Tuan, N.M.; Watabe, K.; Giang, P.T.; Nakagawa, K. Improving Fairness in Wireless Ad Hoc Networks by Channel Access Sensing at Link Layer and Packet Rate Control. IEICE Trans. Commun. 2017, 100, 1818–1826. [Google Scholar] [CrossRef]
- Miśkowicz, M.; Golański, R. LON Technology in Wireless Sensor Networking Applications. Sensors 2006, 6, 30–48. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Dong, L.; Yang, Q. DCN-MAC: A Dynamic Channel Negotiation MAC Mechanism for Underwater Acoustic Sensor Networks. Sensors 2020, 20, 406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, F.; Rehman, A.U.; Yahya, A.; Jan, M.A.; Chuma, J.; Tan, Z.; Hussain, K. A Quality of Service-Aware Secured Communication Scheme for Internet of Things-Based Networks. Sensors 2019, 19, 4321. [Google Scholar] [CrossRef] [Green Version]
- Lei, C.; Bie, H.; Fang, G.; Zhang, X. An Adaptive Channel Access Method for Dynamic Super Dense Wireless Sensor Networks. Sensors 2015, 15, 30221–30239. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Liu, T.; Liu, S.; Kacimi, R.; Dhaou, R. Priority-Based Data Collection for UAV-Aided Mobile Sensor Network. Sensors 2020, 20, 3034. [Google Scholar] [CrossRef] [PubMed]
- Parras, J.; Zazo, S. Repeated Game Analysis of a CSMA/CA Network under a Backoff Attack. Sensors 2019, 19, 5393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassan, H.; Ahmed, I.; Ahmad, R.; Khammari, H.; Bhatti, G.; Ahmed, W.; Alam, M.M. A Machine Learning Approach to Achieving Energy Efficiency in Relay-Assisted LTE-A Downlink System. Sensors 2019, 19, 3461. [Google Scholar] [CrossRef] [Green Version]
- Miśkowicz, M. Access delay in LonTalk MAC protocol. Comput. Stand. Interfaces 2009, 31, 548–556. [Google Scholar] [CrossRef]
- Miśkowicz, M. On the unequal bandwidth share in LonWorks control networks. In Proceedings of the IEEE International Symposium on Industrial Embedded Systems (SIES), Lausanne, Switzerland, 8–10 July 2009; pp. 28–36. [Google Scholar]
- Chetoui, Y.; Bouabdallah, N.; Othman, J.B. Improving the Bandwidth Sharing in IEEE 802.11. In Proceedings of the IEEE International Conference on Local Computer Networks (LCN), Dublin, Ireland, 15–18 October 2007; pp. 927–930. [Google Scholar]
- Ye, W.; Heidemann, J.; Estrin, D. Medium access control with coordinated adaptive sleeping for wireless sensor networks. IEEE/ACM Trans. Netw. 2004, 12, 493–506. [Google Scholar] [CrossRef] [Green Version]
- Enz, C.C.; El-Hoiydi, A.; Decotignie, J.D.; Peiris, V. WiseNET: An ultralow-power wireless sensor network solution. Computer 2004, 37, 62–70. [Google Scholar] [CrossRef]
- Van Dam, T.; Langendoen, K. An adaptive energy-efficient MAC protocol for wireless sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; pp. 171–180. [Google Scholar]
- Lin, P.; Qiao, C.; Wang, X. Medium access control with a dynamic duty cycle for sensor networks. In Proceedings of the Wireless Communications and Networking Conference, Atlanta, GA, USA, 21–25 March 2004; pp. 1534–1539. [Google Scholar]
- Buchholz, P.; Plönnigs, J. Analytical analysis of access-schemes of the CSMA. In Proceedings of the IEEE International Workshop on Factory Communication Systems (WFCS), Vienna, Austria, 22–24 September 2004; pp. 127–136. [Google Scholar]
- Buchholz, P.; Plönnigs, J.; Neugebauer, M.; Kabitzsch, K. Automated Modeling and Analysis of CSMA-Type Access Schemes for Building Automation Networks. IEEE Trans. Ind. Inform. 2006, 2, 103–111. [Google Scholar]
- Miśkowicz, M.; Szyduczyński, J.; Kościelnik, D. Analytical approach to multiple memoryless backoff contention analysis. In Proceedings of the IEEE World Conference on Factory Communication Systems (WFCS), Palma de Mallorca, Spain, 27–29 May 2015; pp. 1–4. [Google Scholar]
- Miśkowicz, M. Analysis of Mean Access Delay in Variable-Window CSMA. Sensors 2007, 7, 3535–3559. [Google Scholar] [CrossRef]
- Dadenkov, S.A. Analytical model of random multiple access protocol predictive p-persistent CSMA. Radio Electron. Comput. Sci. Control 2019, 1, 192–202. [Google Scholar] [CrossRef] [Green Version]
- Ling, X.; Cheng, Y.; Mark, J.W.; Shen, X. A Renewal Theory Based Analytical Model for the Contention Access Period of IEEE 802.15.4 MAC. IEEE Trans. Wirel. Commun. 2008, 7, 2340–2349. [Google Scholar] [CrossRef]
- Del-Valle-Soto, C.; Mex-Perera, C.; Orozco-Lugo, A.; Lara, M.; Galván-Tejada, G.M.; Olmedo, O. On the MAC/Network/Energy performance evaluation of wireless sensor networks: Contrasting MPH, AODV, DSR and ZTR routing protocols. Sensors 2014, 12, 22811–22847. [Google Scholar] [CrossRef]
- Miśkowicz, M. Reducing Communication by Event-Triggered Sampling. In Event-Based Control and Signal Processing; CRC Press: Boca Raton, FL, USA, 2016; pp. 37–58. [Google Scholar]
- Miśkowicz, M. The event-triggered sampling optimization criterion for distributed networked monitoring and control systems. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Maribor, Slovenia, 10–12 December 2003; pp. 1083–1088. [Google Scholar]
- Consumer Electronics Association. ANSI/CEA 709.1-D-2014: Control Network Protocol Specification; Consumer Electronics Association: Washington, DC, USA, 2014. [Google Scholar]
- Metcalfe, R.; Boggs, D. Ethernet: Distributed Packet Switching for Local Computer Networks. Commun. ACM 1976, 19, 395–404. [Google Scholar] [CrossRef]
- Jain, R.K.; Chiu, D.M.W.; Hawe, W.R. A Quantitative Measure of Fairness and Discrimination; Technical Report DEC-TR-301; Digital Equipment Corporation: Hudson, MA, USA, 1984. [Google Scholar]
- Shannon, C. The mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Lan, T.; Kao, D.; Chiang, M.; Sabharwal, A. An axiomatic theory of fairness. In Proceedings of the IEEE INFOCOM 2010, San Diego, CA, USA, 15–19 March 2010; pp. 1–9. [Google Scholar]
- Hoßfeld, T.; Skorin-Kapov, L.; Heegaard, P.E.; Varela, M. A new QoE fairness index for QoE management. Qual. User Exp. 2018, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Hoßfeld, T.; Skorin-Kapov, L.; Heegaard, P.E.; Varela, M. Definition of QoE Fairness in Shared Systems. IEEE Commun. Lett. 2017, 21, 184–187. [Google Scholar] [CrossRef] [Green Version]
- Tay, Y.C.; Jamieson, K.; Balakrishnan, H. Collision-minimizing CSMA and its applications to wireless sensor networks. IEEE J. Sel. Areas Commun. 2004, 22, 1048–1057. [Google Scholar] [CrossRef]
- Miśkowicz, M. Average channel utilization of CSMA with geometric distribution under varying workload. IEEE Trans. Ind. Inform. 2009, 6, 123–131. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).