Analysis of Air-Coupled Transducer-Based Elastic Waves Generation in CFRP Plates
Abstract
:1. Introduction
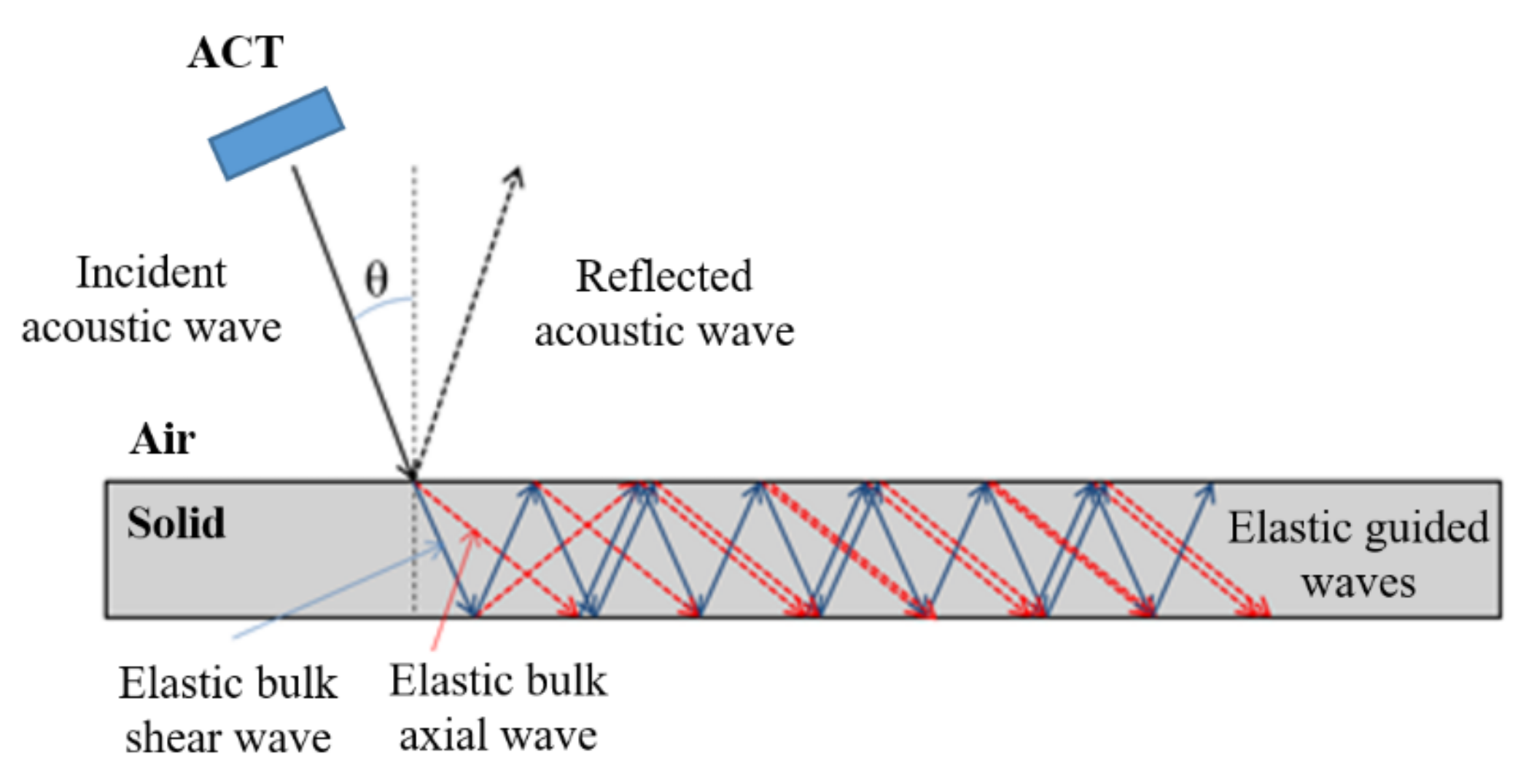
2. Air-Coupled Transducer-Based Elastic Waves Generation
3. Numerical Analysis
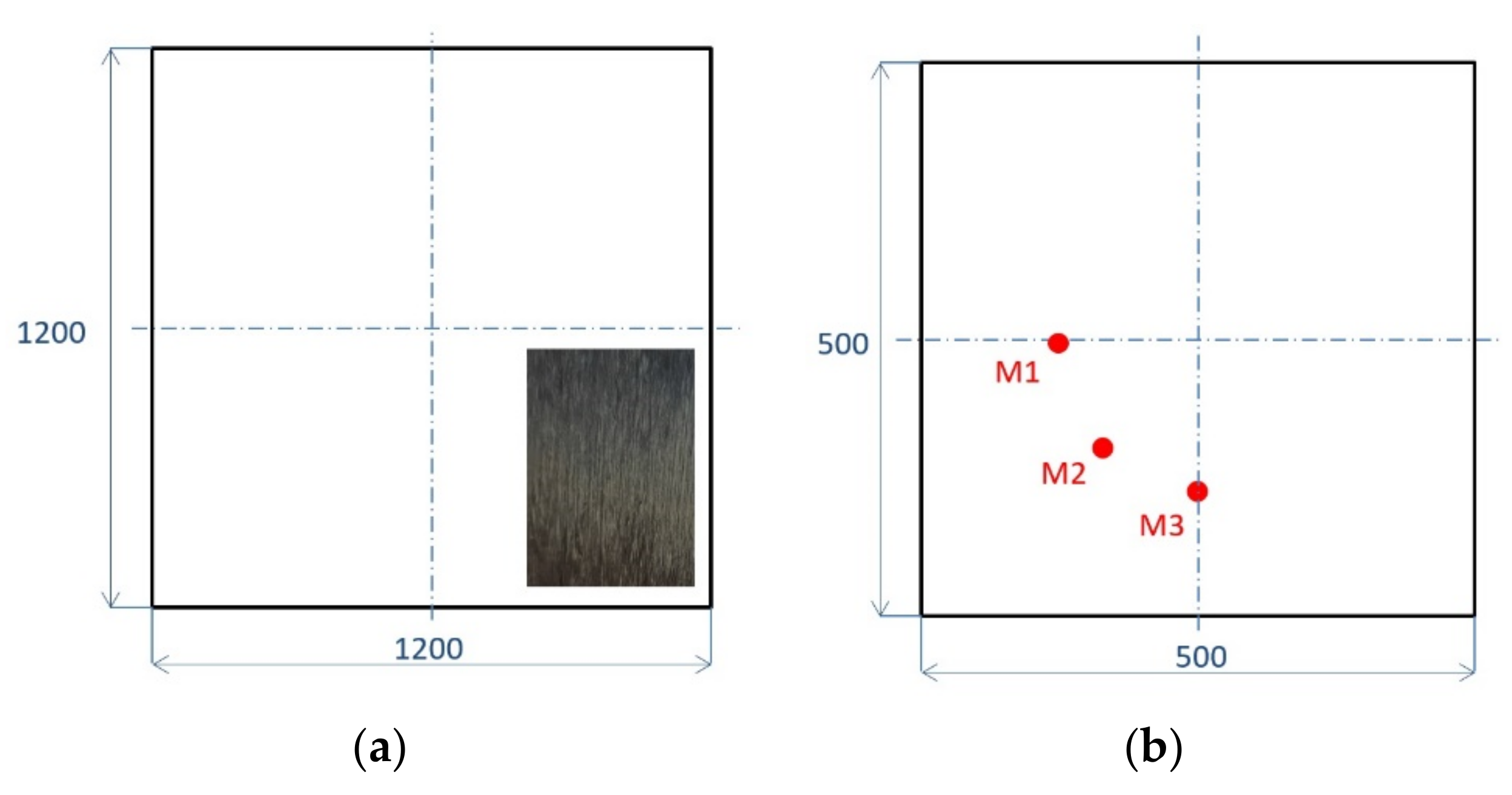
4. Experimental Setup
- the distance between the transducer (ACT) and the specimen (plate);
- the frequency of the excitation (in a relatively narrow range, specified later);
- the slope angle of the ACT on the effectiveness of elastic wave mode generation;
- the orientation of the reinforcing fibers (ACT direction across and along the reinforcing fibers) on the effectiveness of elastic wave mode generation and the coverage area of the plate with waves with high amplitude/energy.
5. Experimental Results
5.1. Dispersion Curves
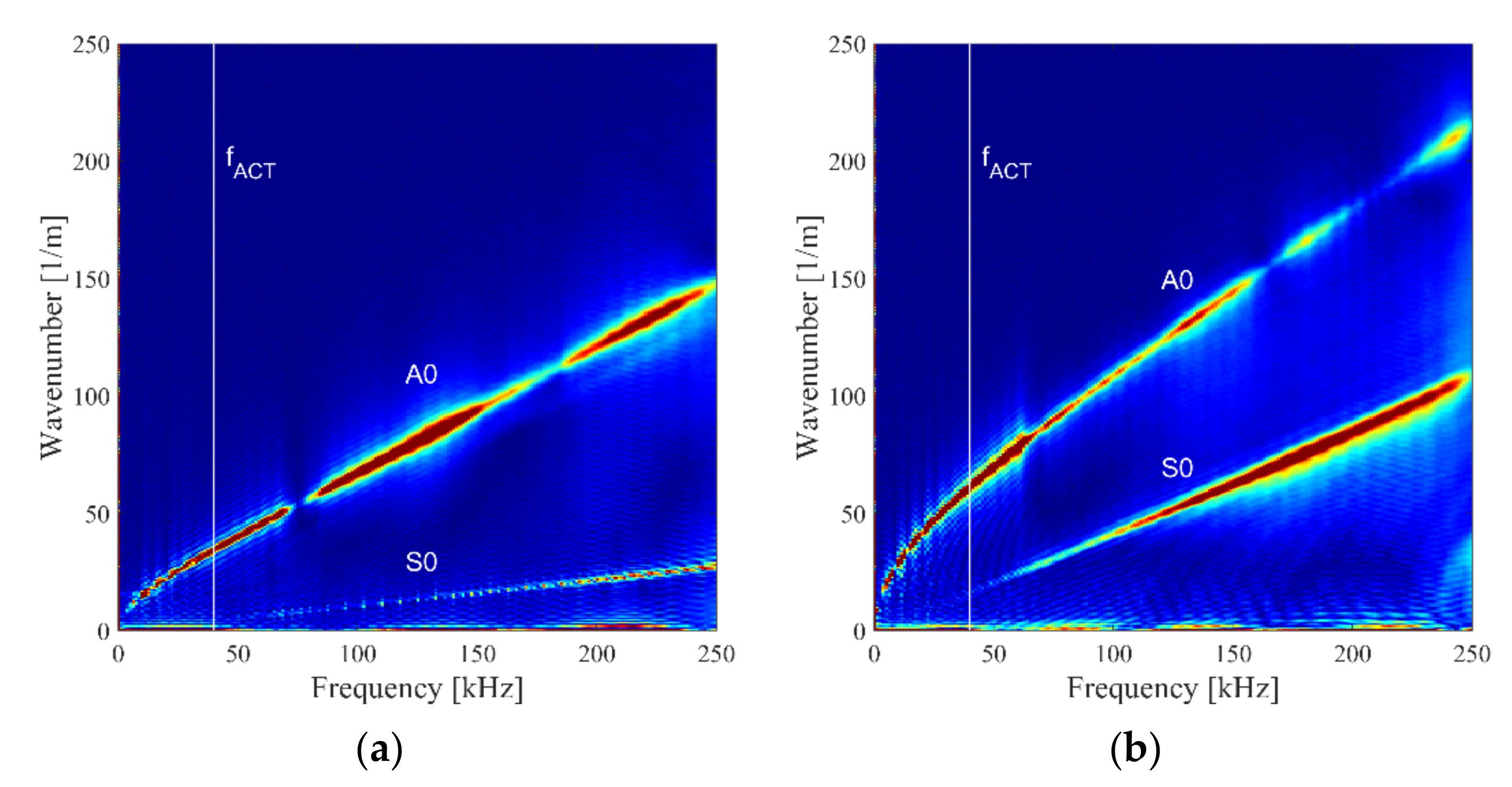
5.2. Non-Contact ACT-Based Elastic Waves Generation
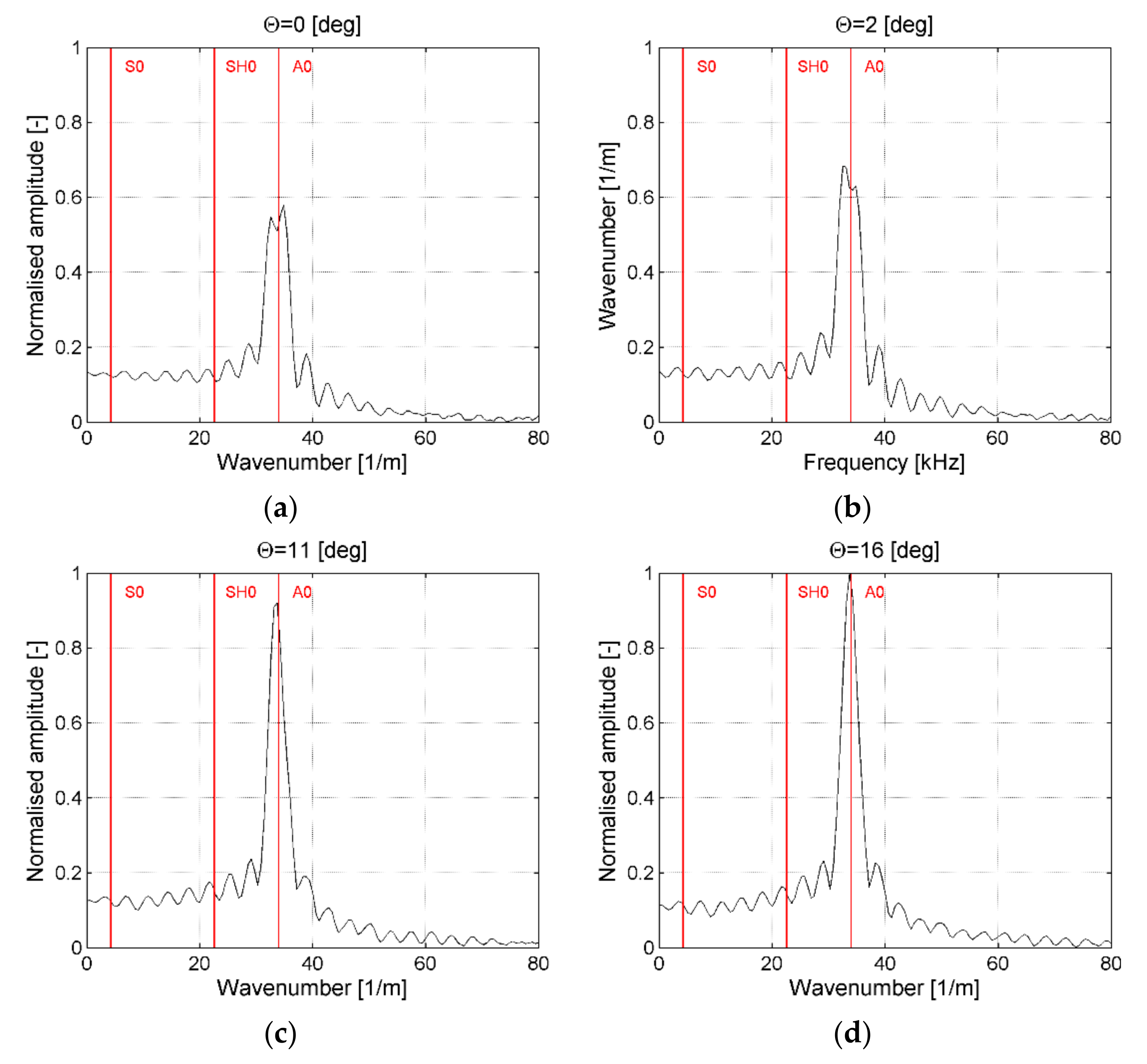
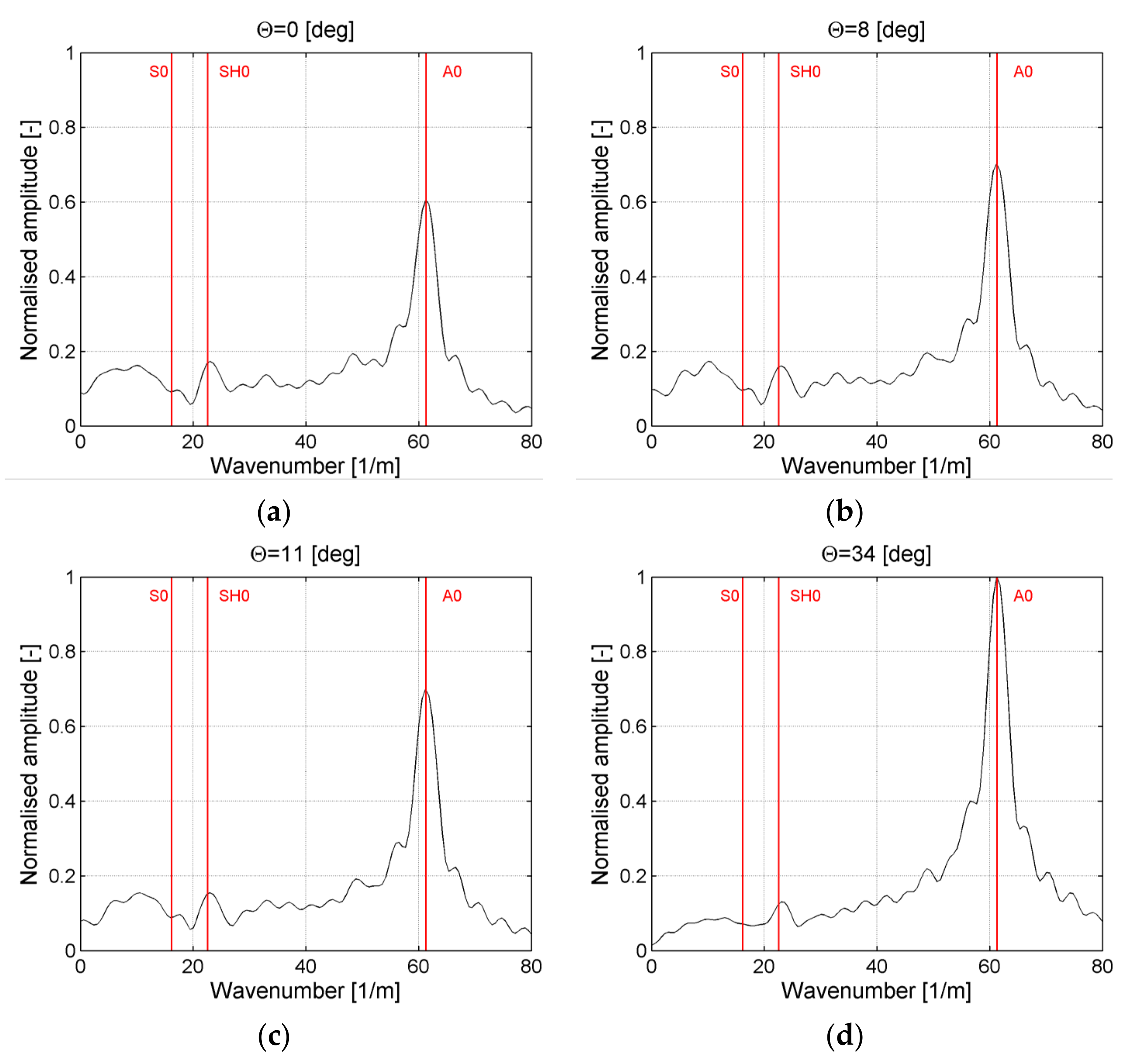
5.2.1. Point-Wise Measurements
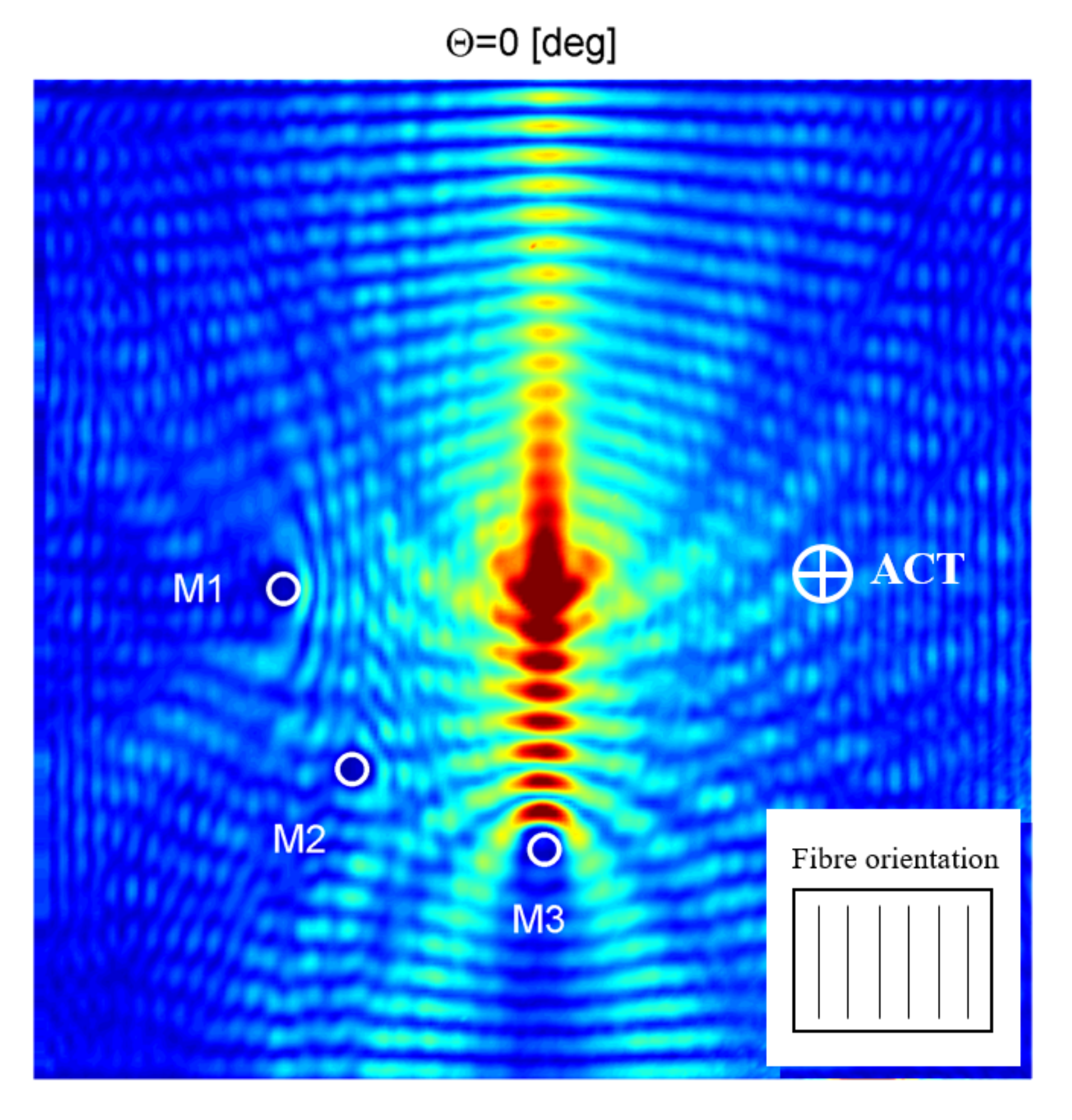
5.2.2. Full Wavefield Measurements
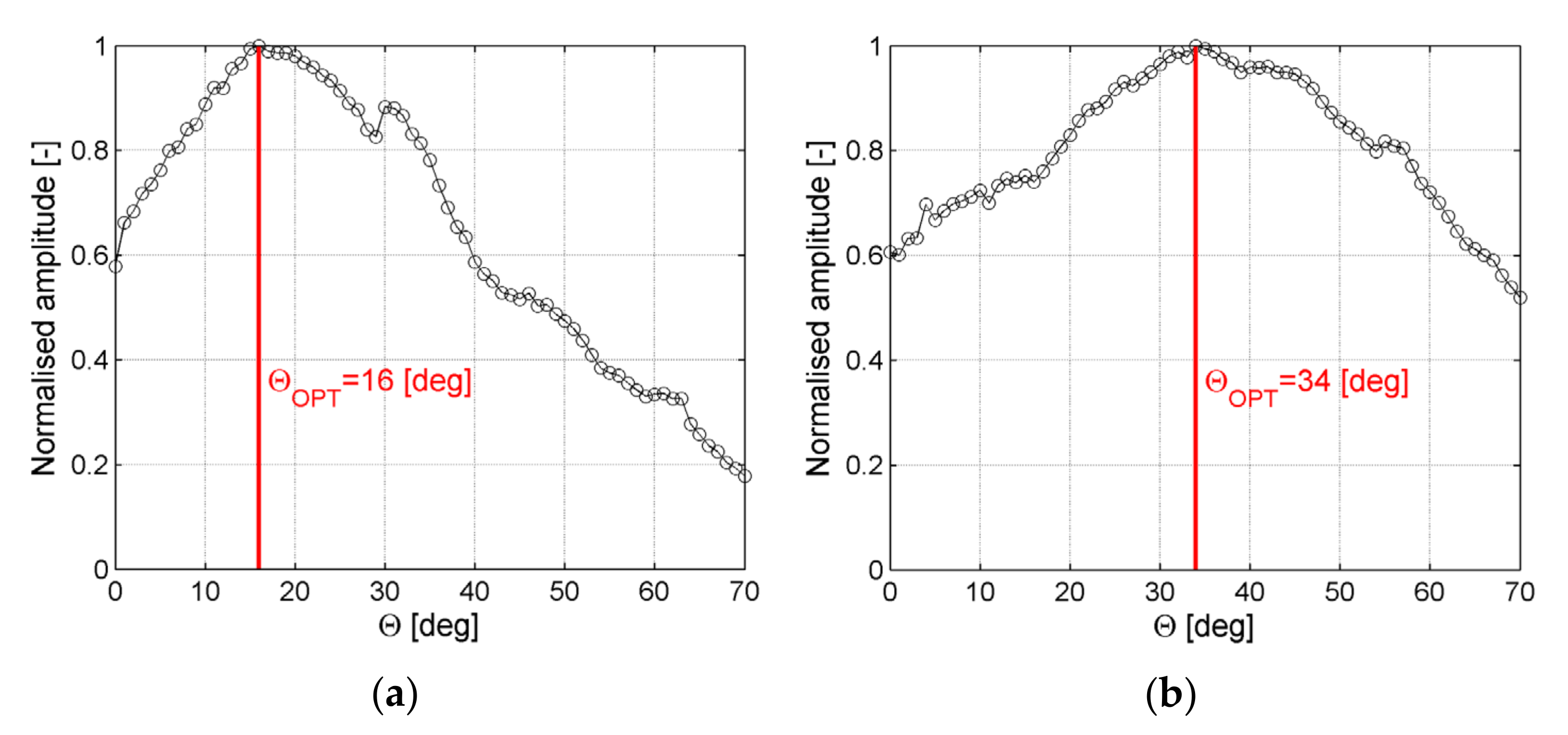
5.2.3. Determination of the Optimal Incidence Angles
6. Discontinuity Localization
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Segers, J.; Poelman, G.; Hedayatrasa, S.; Verboven, E.; Van Paepegem, W.; Kersemans, M. The state-of-the-art and beyond in non-destructive testing of a complex cfrp component. In Proceedings of the 11th Symposium on NDT in Aerospace, Paris-Saclay, France, 13–15 November 2019. [Google Scholar]
- Cai, J.; Qiu, L.; Liang, D. Structural Health Monitoring for Composite Materials; Intech: London, UK, 2012. [Google Scholar]
- Wang, B.; Zhong, S.; Lee, T.; Fancey, K.; Mi, J. Non-destructive testing and evaluation of composite materials/structures: A state-of-the-art-review. Adv. Mech. Eng. 2020, 12. [Google Scholar] [CrossRef] [Green Version]
- Eremin, A.; Glushkov, E.; Glushkova, N.; Lammering, R. Evaluation of effective elastic properties of layered composite fiber-reinforced plastic plates by piezoelectrically induced guided waves and laser Doppler vibrometry. Compos. Struct. 2015, 125, 449–458. [Google Scholar] [CrossRef]
- Jeyaprakash, N.; Bustamante, L. Evaluation of defect detection in aluminium, cfrp and epoxy resin plates using non-contact air coupled ultrasonic waves. Int. J. Precis. Eng. Manuf. 2020, 21, 1843–1856. [Google Scholar]
- Bernhardt, Y.; Kreutzbruck, M. Integrated defect sensor for the inspection of fiber-reinforced plastics using air-coupled ultrasound. J. Sens. Sens. Syst. 2020, 9, 127–132. [Google Scholar] [CrossRef]
- Bustamante, L.; Jeyaprakash, N.; Yang, C.-H. Hybrid laser and Air-coupled ultrasonic defect detection of aluminium and CFRP plates by means of Lamb mode. Results Phys. 2020, 19, 103438. [Google Scholar] [CrossRef]
- Kažys, R.; Šliteris, R.; Mažeika, L. Attenuation of a Slow Subsonic A0 Mode Ultrasonic Guided Wave in Thin Plastic Films. Materials 2019, 12, 1648. [Google Scholar] [CrossRef] [Green Version]
- Kažys, R.J.; Tumšys, O. Simultaneous Measurement of Thickness and Elastic Properties of Thin Plastic Films by Means of Ultrasonic Guided Waves. Sensors 2021, 21, 6779. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.C.; Eaton, M.J.; Marks, R.; Clarke, A.; Featherston, C.A.; Kawashita, L.F.; Hallett, S.R. An integrated numerical model for investigating guided waves in impact-damaged composite laminates. Compos. Struct. 2017, 176, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Kudela, P.; Radzienski, M.; Ostachowicz, W. Impact induced damage assessment by means of lamb wave image processing. Mech. Syst. Signal Process. 2018, 102, 23–36. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, B.; Hao, W.; Luo, Y.; Chen, H. Localization and characterization of delamination in laminates using the local wavenumber method. Compos. Struct. 2020, 238, 111972. [Google Scholar] [CrossRef]
- Segers, J.; Hedayatrasa, S.; Poelman, G.; Paepegem, W.; Kersemans, M. Robust and baseline-free full-field defect detection in complex composite parts through weighted broadband energy mapping of mode-removed guided waves. Mech. Syst. Signal Process. 2020, 151, 107360. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, L.; Leckey, C. Delamination detection using guided wave phased arrays. In Proceedings of the American Society for Composite (ASC) Technical Conference, Williamsburg, VA, USA, 19–22 September 2016. [Google Scholar]
- Leckey, C.; Yu, L.; Tian, Z. Rapid guided wave delamination detection and quantification in composites using global-local sensing. Smart Mater. Struct. 2016, 25, 085042. [Google Scholar]
- Taheri, H.; Hassen, A. Nondestructive ultrasonic inspection of composite materials: A comparative advantage of phased array ultrasonic. Sensors 2019, 9, 1628. [Google Scholar] [CrossRef] [Green Version]
- Shevtsov, S.; Chebanenko, V.; Shevtsova, M.; Chang, S.-H.; Kirillova, E.; Rozhkov, E. On the Directivity of Lamb Waves Generated by Wedge PZT Actuator in Thin CFRP Panel. Materials 2020, 13, 907. [Google Scholar] [CrossRef] [Green Version]
- Mei, H.; James, R.; Haider, M.F.; Giurgiutiu, V. Multimode guided wave detection for various composite damage types. Appl. Sci. 2020, 10, 484. [Google Scholar] [CrossRef] [Green Version]
- Rao, C.; Duan, L. Bidirectional, bimodal ultrasonic Lamb wave sensing in a composite plate using a polarization-maintaining fiber bragg grating. Sensors 2019, 19, 1375. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Howden, S.; Xiao, W. Composite bond quality nondestructive evaluation with noncontact lamb wave system. Proc. SPIE 2020, 11380, 11380M. [Google Scholar] [CrossRef] [Green Version]
- Rus, J.; Kulla, D.; Grager, J.; Grosse, C. Air-coupled ultrasonic inspection of fiber-reinforced plates using an optical microphone. DAGA 2019, 2019, 763–766. [Google Scholar]
- Balasubramaniam, K.; Rajagopal, P.; Panda, R. Rapid guided wave inspection of complex stiffened composite structural components using non-contact air-coupled ultrasound. Compos. Struct. 2018, 206, 247–260. [Google Scholar]
- Radzienski, M.; Kudela, P.; Marzani, A.; Marchi, L.; Ostachowicz, W. Damage identification in various types of composite plates using guided waves excited by a piezoelectric transducer and measured by a laser vibrometer. Sensors 2019, 19, 1958. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Falzon, B.; Tan, W. Experimental and numerical studies on the impact response of damage-tolerant hybrid unidirectional/woven carbon-fibre reinforced composite laminates. Compos. Part B Eng. 2018, 136, 101–118. [Google Scholar] [CrossRef] [Green Version]
- Mei, H.; Giurgiutiu, V. Numerical and experimental investigation of multilayer delamination detection in composites. Struct. Health Monit. 2019. [Google Scholar] [CrossRef]
- Timucin, D.; Hafiychuk, H.; Hafiychuk, V.; Wheeler, K.; Leckey, C. Simulation of guided-wave ultrasound propagation in composite laminates: Benchmark comparisons of numerical codes and experiment. Ultrasonics 2017, 84, 187–200. [Google Scholar]
- Gupta, S.; Rajagopal, P. Feasibility of ultrasonic guided waves for detecting surface-breaking cracks in laminated composite plate structures. ISSS J. Micro Smart Syst. 2020, 9, 97–102. [Google Scholar] [CrossRef]
- Liu, H.; Chen, X.; Michaels, J.E. Incremental scattering of the A0 Lamb wave mode from a notch emanating from a through-hole. Ultrasonics 2019, 91, 220–230. [Google Scholar] [CrossRef]
- Mori, N.; Biwa, S.; Kusaka, T. Damage localization method for plates based on the time reversal of the mode-converted Lamb waves. Ultrasonics 2019, 91, 19–29. [Google Scholar] [CrossRef]
- Ghose, B.; Panda, R.S.; Balasubramaniam, K. Guided A0 wave mode interaction with interfacial disbonds in an elastic-viscoelastic bilayer structure. NDT E Int. 2021, 124, 102543. [Google Scholar] [CrossRef]
- Teramoto, K.; Rabbi, M.S.; Khan, M.d.T.I. Detection of Sub-surface Delamination based on the Spatio-temporal Gradient Analysis over the A0-mode Lamb wave Fields. Phys. Procedia 2015, 70, 368–371. [Google Scholar] [CrossRef] [Green Version]
- Lugovtsova, Y.; Bulling, J.; Mesnil, O. Damage quantification in an aluminium-CFRP composite structure using guided wave wavenumber mapping: Comparison of instantaneous and local wavenumber analyses. NDT E Int. 2021, 122, 102472. [Google Scholar] [CrossRef]
- Hosoya, N.; Katsumata, T.; Kajiwara, I. Measurements of S0 mode Lamb waves using a high-speed polarization camera to detect damage in transparent materials during non-contact excitation based on a laser-induced plasma shock wave. Opt. Lasers Eng. 2022, 148, 106770. [Google Scholar] [CrossRef]
- Mei, H.; Haider, M.F.; James, R.; Giurgiutiu, V. Pure S0 and SH0 detections of various damage types in aerospace composites. Compos. Part B Eng. 2020, 189, 107906. [Google Scholar] [CrossRef]
- Howard, R.; Cegla, F. Detectability of corrosion damage with circumferential guided waves in reflection and transmission. NDT E Int. 2017, 91, 108–119. [Google Scholar] [CrossRef]
- Nazeer, N.; Ratassepp, M.; Fan, Z. Damage detection in bent plates using shear horizontal guided waves. Ultrasonics 2017, 75, 155–163. [Google Scholar] [CrossRef]
- Barski, M.; Muc, A.; Stawiarski, A. The influence of the configuration of the fiber-metal laminates on the dispersion relations of the elastic wave modes. Vib. Phys. Syst. 2020, 31, 2020202. [Google Scholar]
- Bartoli, I.; Marzani, A.; di Scalea, F.L.; Viola, E. Modeling wave propagation in damped waveguides of arbitrary cross-section. J. Sound Vib. 2006, 295, 685–707. [Google Scholar] [CrossRef]
- Kudela, P.; Radzienski, M.; Fiborek, P.; Wandowski, T. Elastic constants identification of woven fabric reinforced composites by using guided wave dispersion curves and genetic algorithm. Compos. Struct. 2020, 249, 112569. [Google Scholar] [CrossRef]
- Mindykowski, D.; Wandowski, T.; Radzieński, M.; Kudela, P. Analysis of elastic wave propagation excited by acoustic non-contact method. Proc. SPIE 2021, 11593, 115930T. [Google Scholar]
- Harb, M.S.; Yuan, F.G. A rapid, fully non-contact, hybrid system for generating Lamb wave dispersion curves. Ultrasonics 2015, 61, 62–70. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, H.; Fan, J.; Hu, Y.; He, C.; Wu, B. Baseline-free delamination inspection in composite plates by synthesizing noncontact air-coupled Lamb wave scan method and virtual time reversal algorithm. Smart Mater. Struct. 2015, 24, 045014. [Google Scholar] [CrossRef]
- Hakoda, C.; Hasanian, M.; Lissenden, C.J. On the Use of Oblique Acoustic Leakage to Measure the Wavenumber Spectrum of Propagating Lamb Waves. Sensors 2019, 19, 1391. [Google Scholar] [CrossRef] [Green Version]
- Álvarez-Arenas, T.G.; Camacho, J. Air-Coupled and Resonant Pulse-Echo Ultrasonic Technique. Sensors 2019, 19, 2221. [Google Scholar] [CrossRef] [Green Version]
- Álvarez-Arenas, T.E.G.; Camacho, J.; Fritsch, C. Passive focusing techniques for piezoelectric air-coupled ultrasonic transducers. Ultrasonics 2016, 67, 85–93. [Google Scholar] [CrossRef]
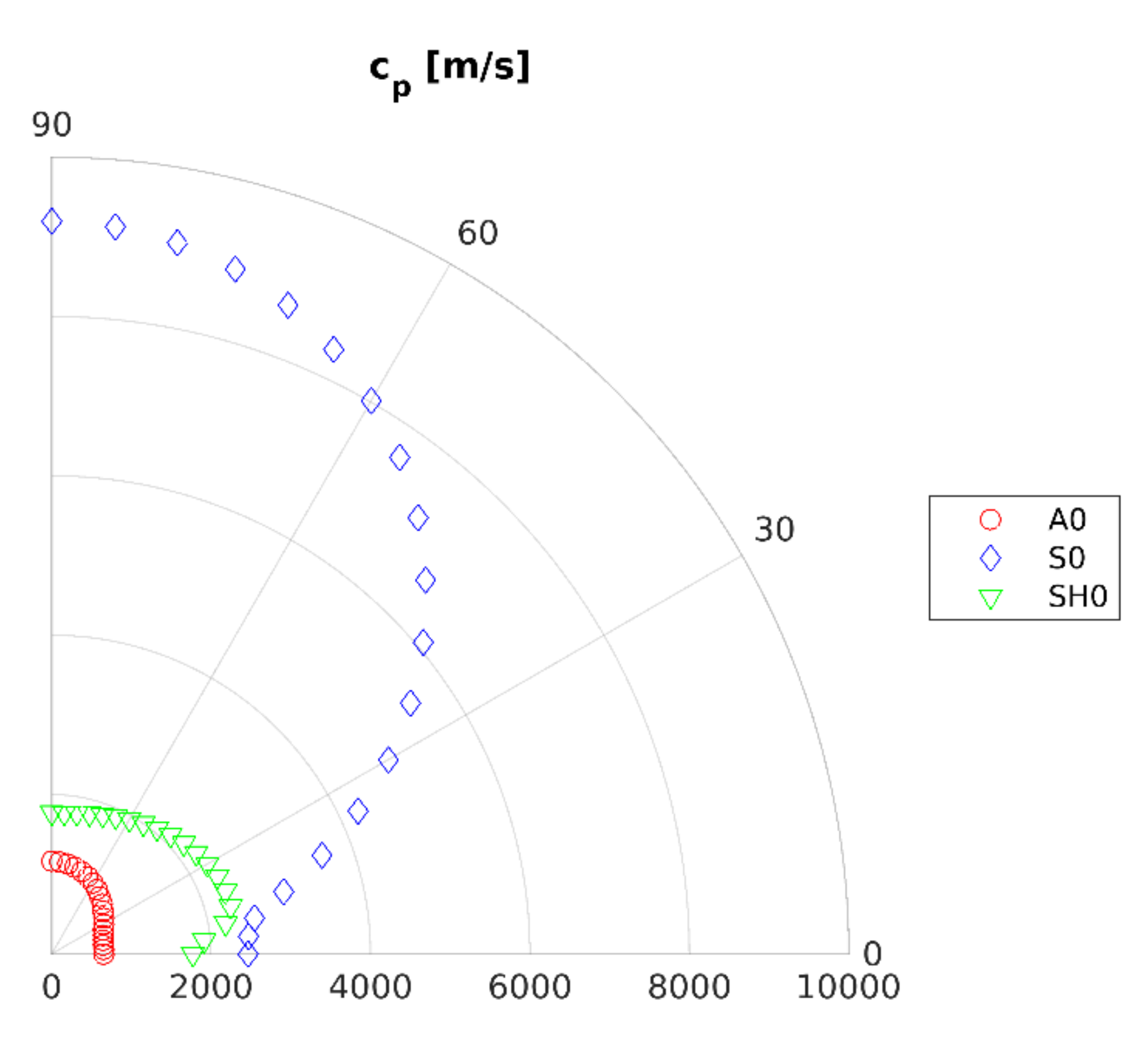


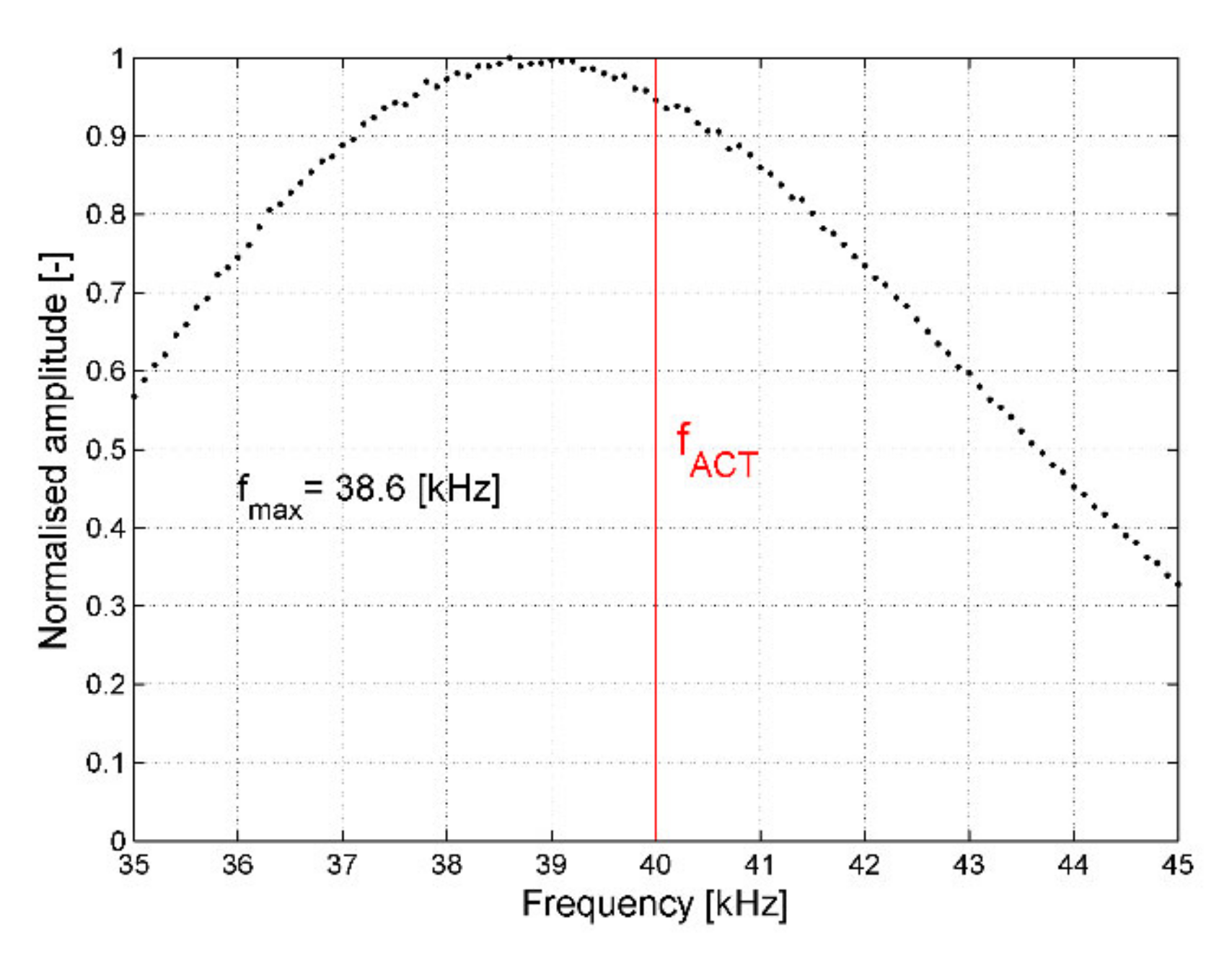
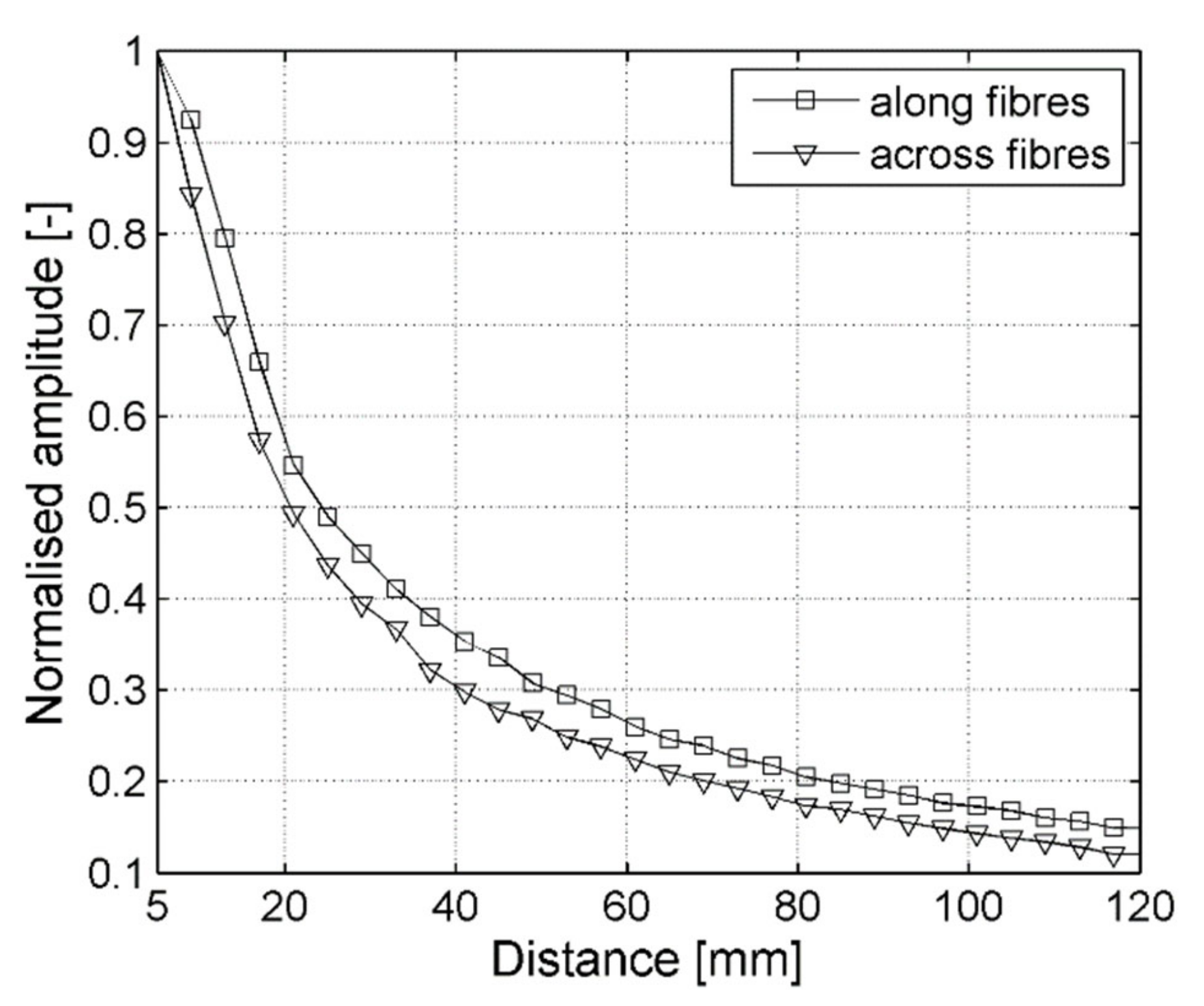
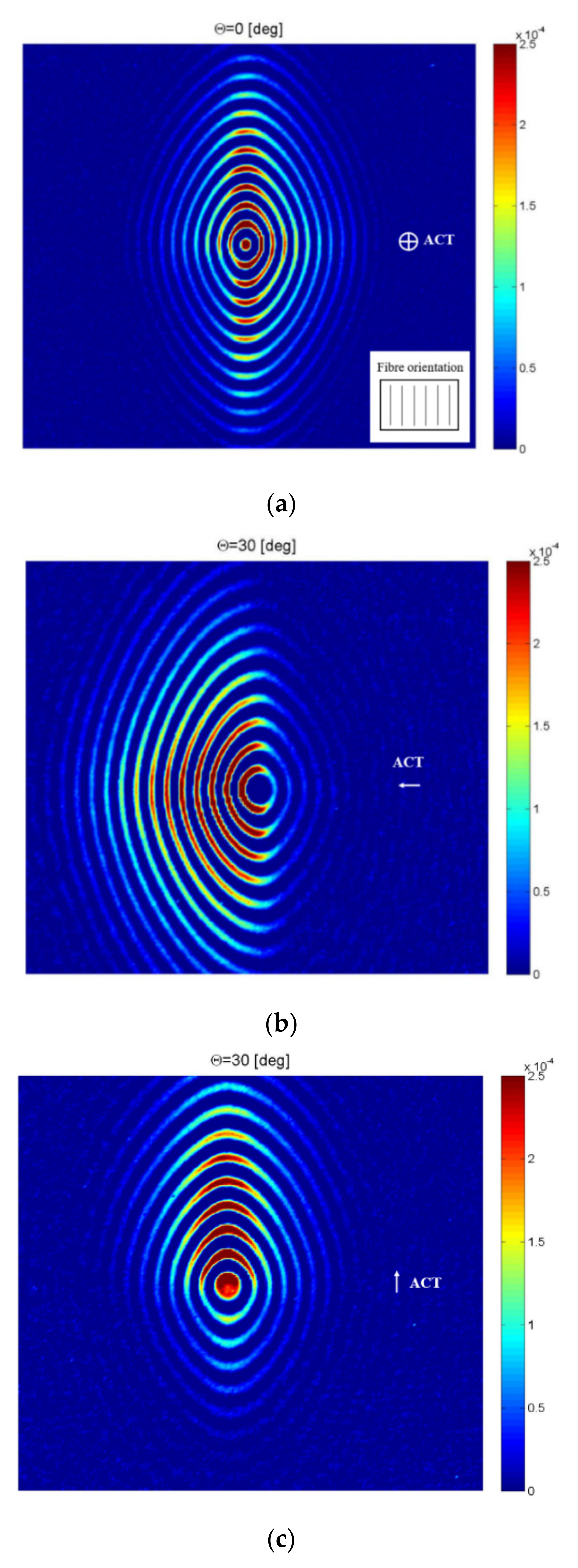
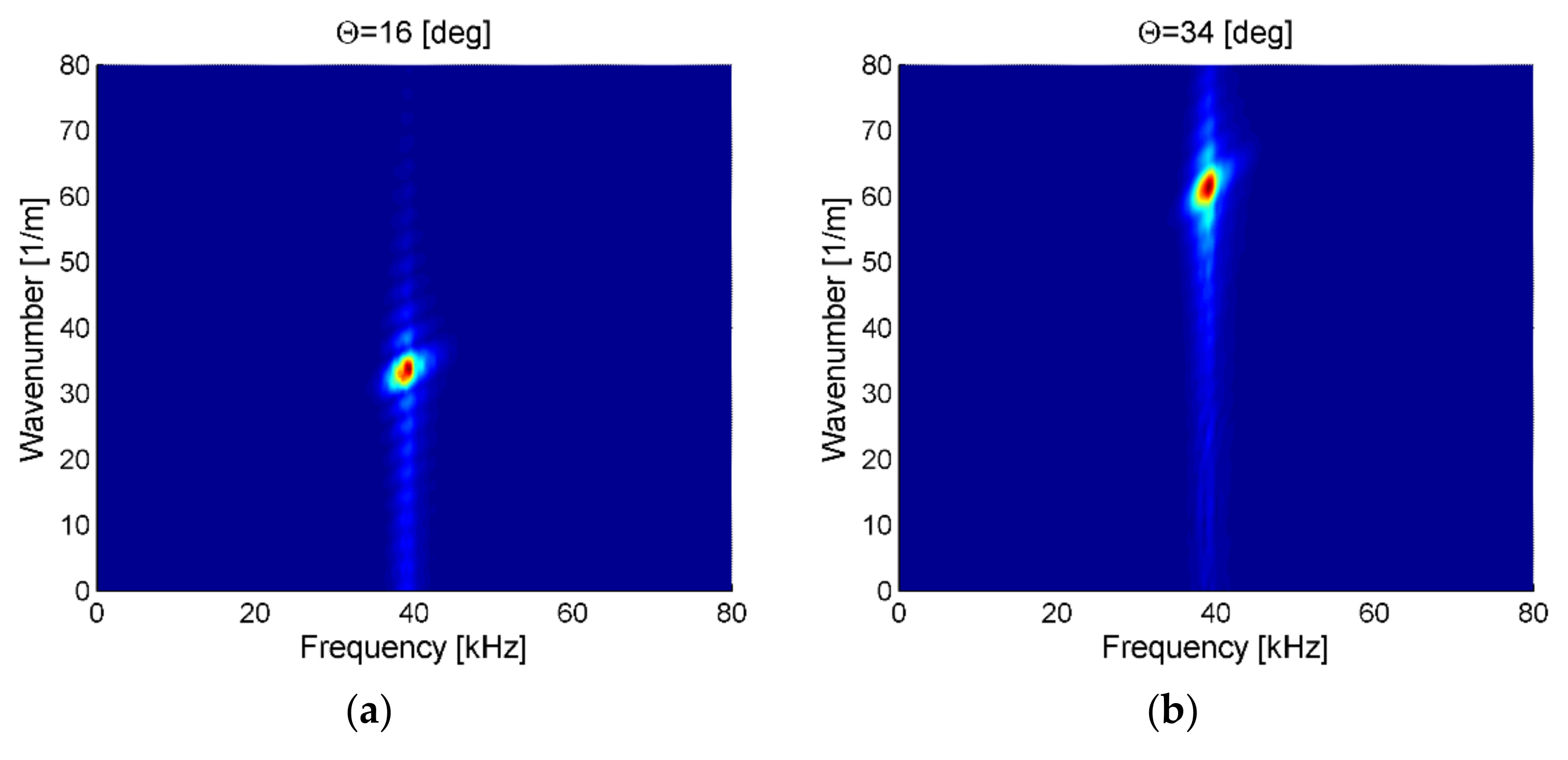

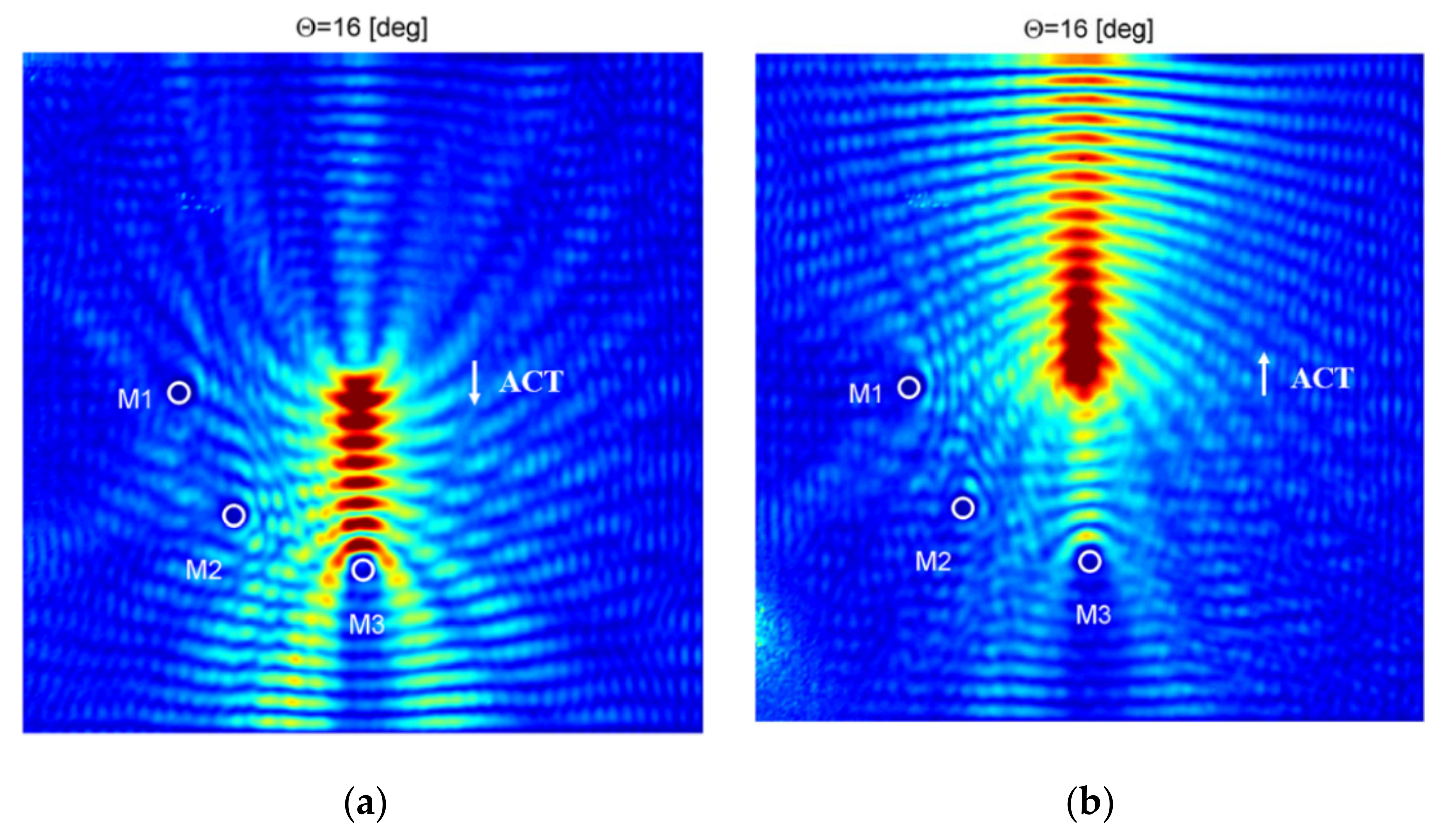
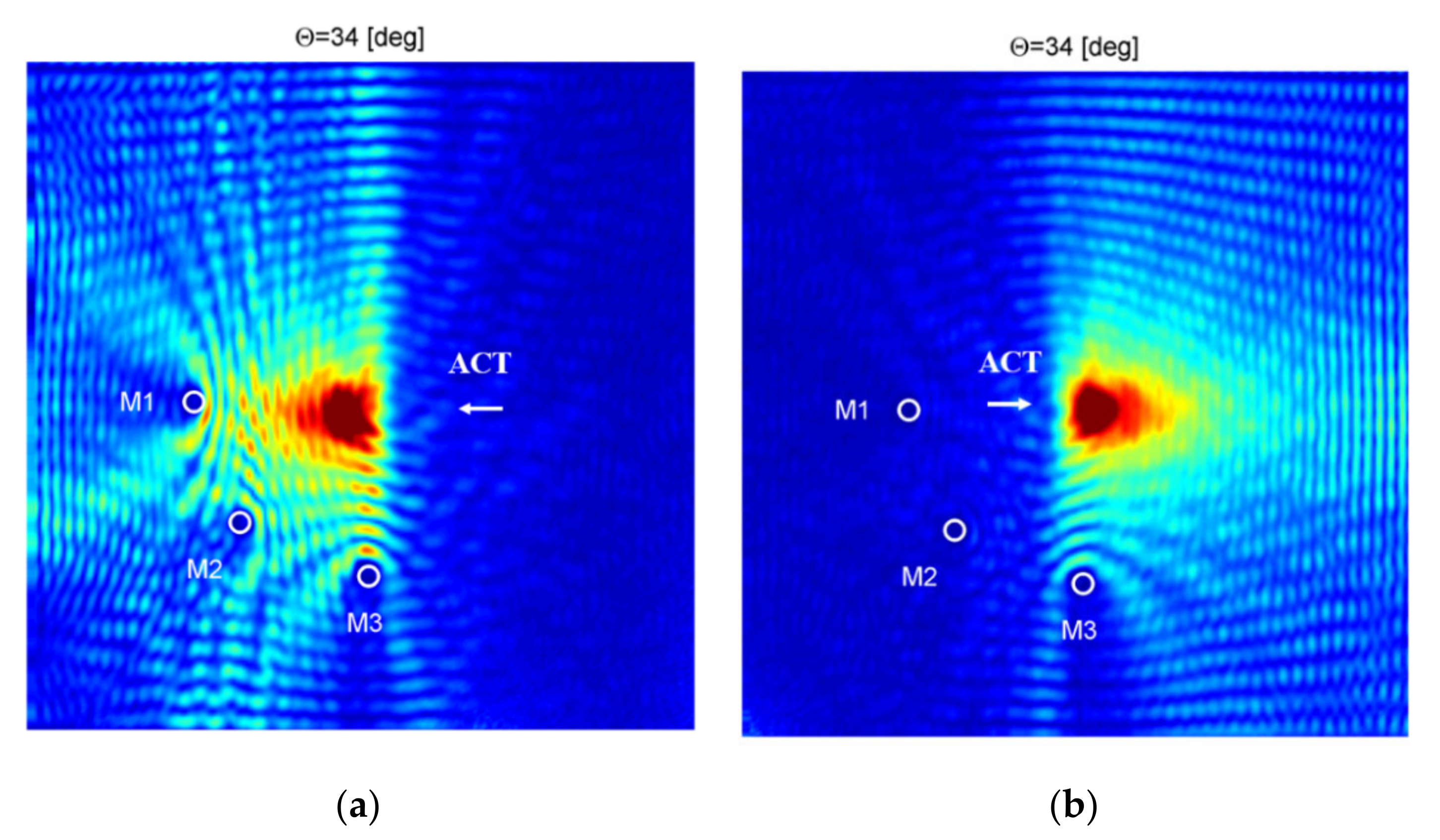
| Wave Mode | Wavenumber [1/m] | Phase Velocity [m/s] | Optimal ACT Angle θ [deg] |
|---|---|---|---|
| direction along fibres | |||
| A0 | 34.0 | 1176.5 | 16.9 |
| S0 | 4.3 | 9302.3 | 2.1 |
| SH0 | 22.58 | 1771.5 | 11.2 |
| direction across fibres | |||
| A0 | 61.3 | 652.52 | 31.7 |
| S0 | 16.24 | 2461.31 | 8 |
| SH0 | 22.58 | 1771.5 | 11.2 |
| Wave Mode | Wavenumber [1/m] | Phase Velocity [m/s] | Optimal ACT Angle [deg] |
|---|---|---|---|
| direction along fibres | |||
| A0 | 34.2 ± 1 | 1169.6 ± 33 | 17 ± 0.5 |
| S0 | 4.4 ± 0.13 | 9091 ± 261 | 2.1 ± 0.05 |
| direction across fibres | |||
| A0 | 61.2 ± 1.8 | 653.59 ± 19 | 31.6 ± 1 |
| S0 | 14.7 ± 0.4 | 2706.4 ± 72 | 7.2 ± 0.2 |
| Wave Mode | Optimal ACT Slope Angle [deg] | ||
|---|---|---|---|
| Numerical Results | PZT Measurements | ACT Measurements | |
| direction along fibres | |||
| A0 | 16.9 | 17 ± 0.5 | 16 ± 1 |
| S0 | 2.1 | 2.1 ± 0.05 | - |
| SH0 | 11.2 | - | - |
| direction across fibres | |||
| A0 | 31.7 | 31.6 ± 1 | 34 ± 1 |
| S0 | 8 | 7.2 ± 0.2 | - |
| SH0 | 11.2 | - | 10 ± 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wandowski, T.; Mindykowski, D.; Kudela, P.; Radzienski, M. Analysis of Air-Coupled Transducer-Based Elastic Waves Generation in CFRP Plates. Sensors 2021, 21, 7134. https://doi.org/10.3390/s21217134
Wandowski T, Mindykowski D, Kudela P, Radzienski M. Analysis of Air-Coupled Transducer-Based Elastic Waves Generation in CFRP Plates. Sensors. 2021; 21(21):7134. https://doi.org/10.3390/s21217134
Chicago/Turabian StyleWandowski, Tomasz, Damian Mindykowski, Pawel Kudela, and Maciej Radzienski. 2021. "Analysis of Air-Coupled Transducer-Based Elastic Waves Generation in CFRP Plates" Sensors 21, no. 21: 7134. https://doi.org/10.3390/s21217134
APA StyleWandowski, T., Mindykowski, D., Kudela, P., & Radzienski, M. (2021). Analysis of Air-Coupled Transducer-Based Elastic Waves Generation in CFRP Plates. Sensors, 21(21), 7134. https://doi.org/10.3390/s21217134







