Predictive Maintenance: An Autoencoder Anomaly-Based Approach for a 3 DoF Delta Robot
Abstract
:1. Introduction
- Given the semi-supervised nature of the method, there is no need for R2F data for training the model, which is vital when gathering such data can be dangerous or economically infeasible.
- The proposed method does not require hand designed features for training the models, which makes the training stage easier when no or too little domain knowledge about the system is available or when a large, high-dimensional dataset must be tackled.
- The proposed method can also be used to classify the task and determine which task is going to fail, based on the similarity of distribution of the signal sequence.
- By having the output of the proposed method, a probability can be assigned, which describes how probable it is that the system is going to fail. This probability includes a slack variable which determines how much deviation from reference values is allowed. Additionally, it is also possible to determine the sensitivity and rate of changes of the proposed method to deviation from the reference values or find optimal values by solving a minimax problem.
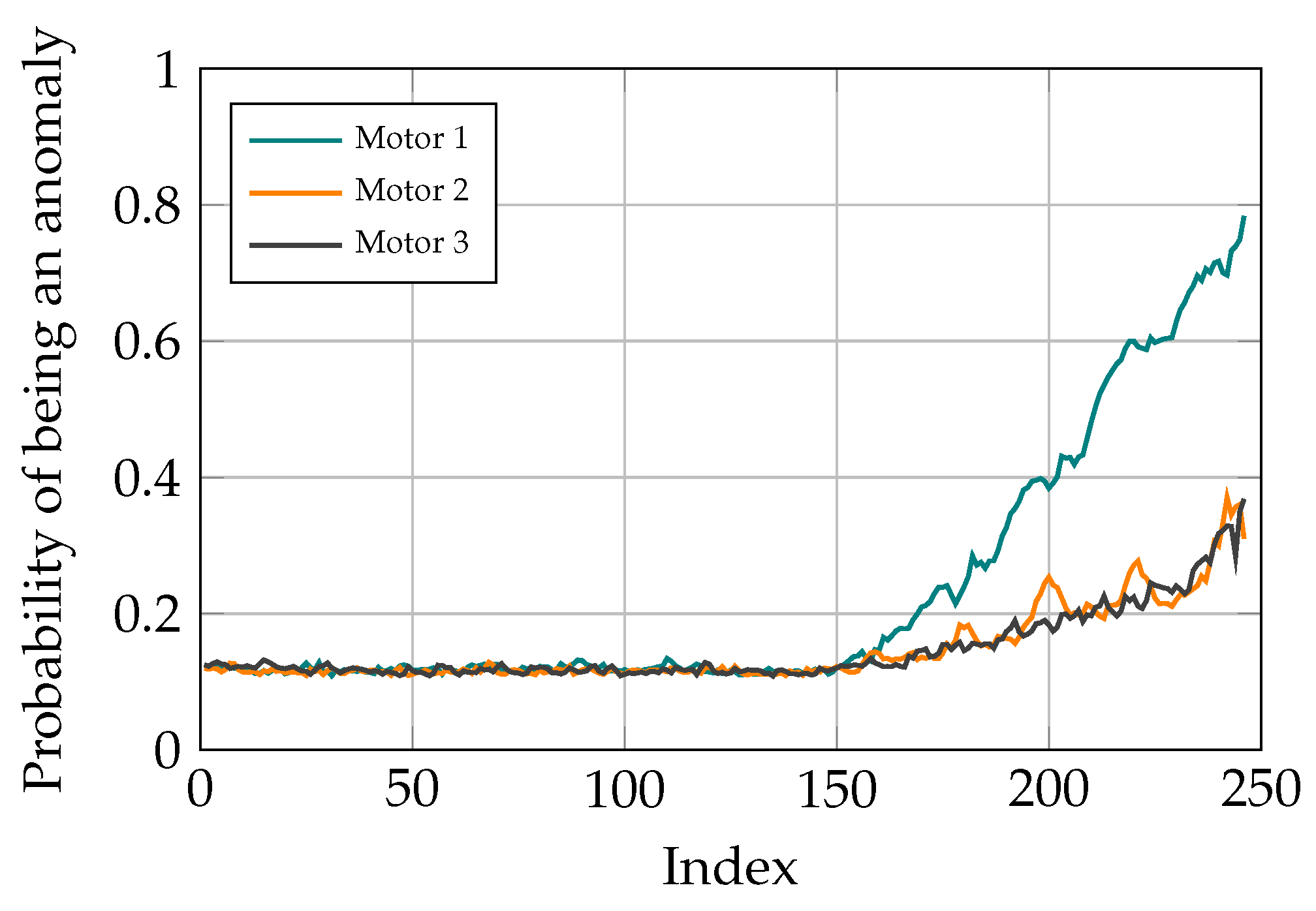
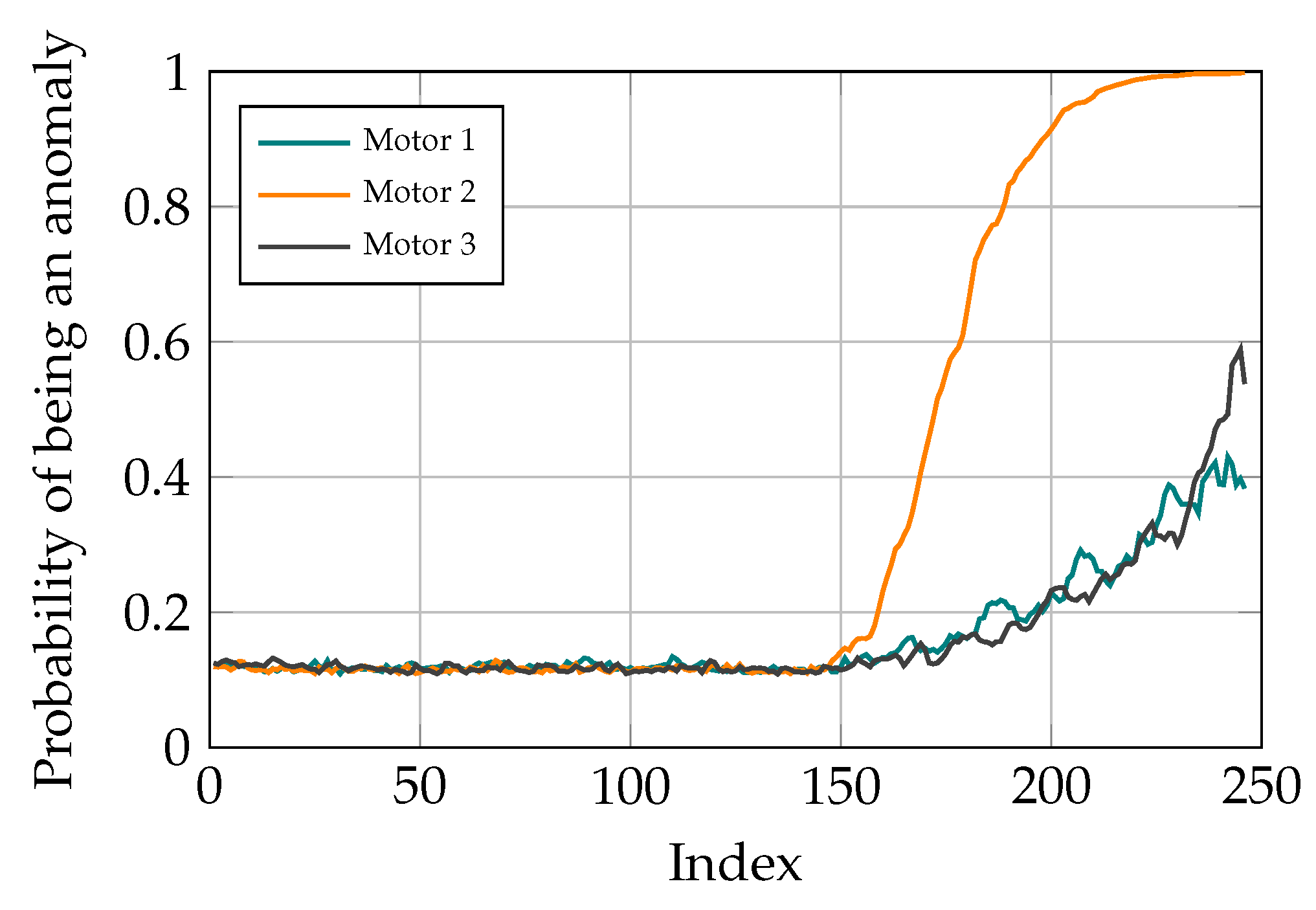
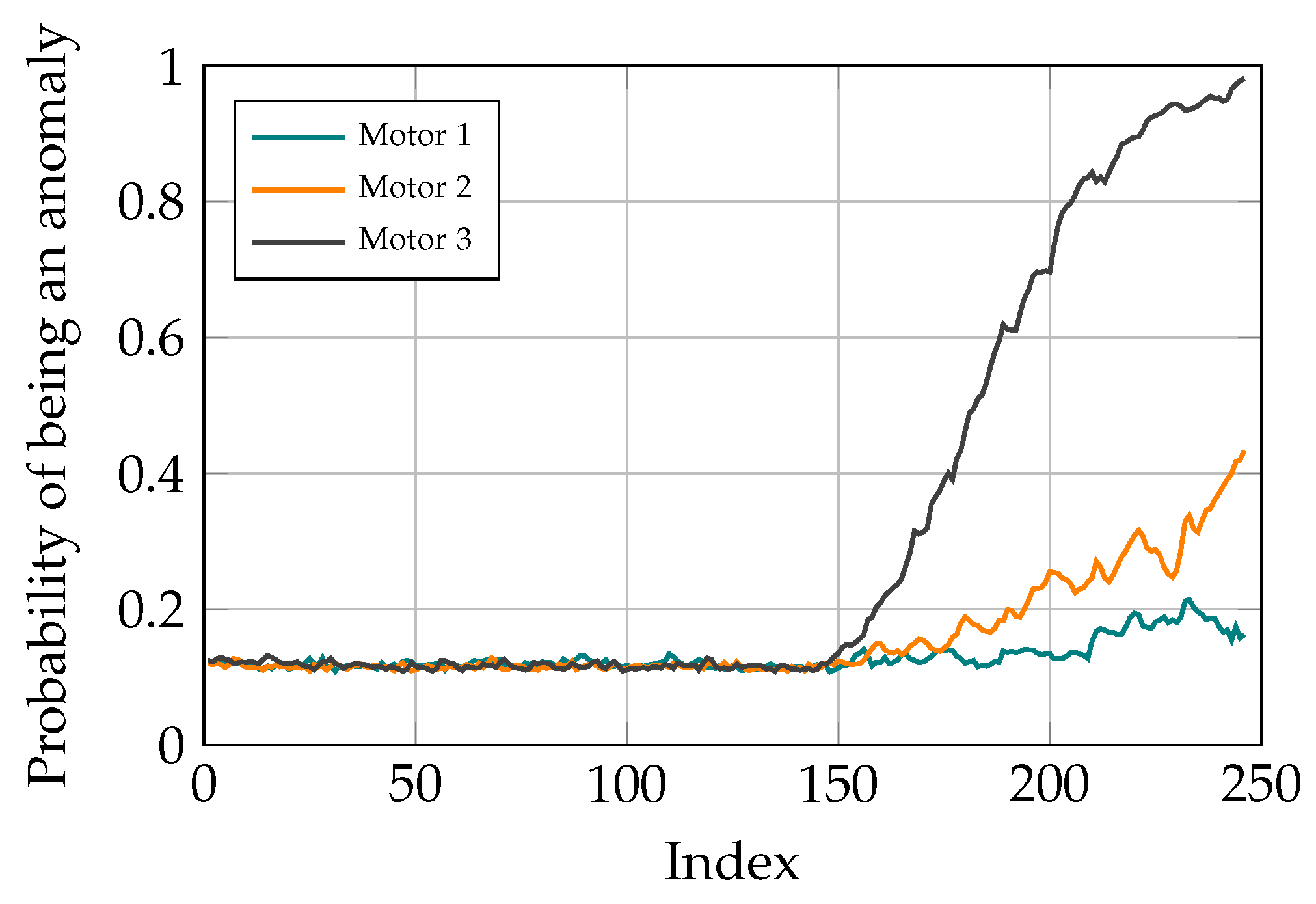
- Given the studied system, the proposed method is capable of pinpointing where the problem originates from, regardless of the number of motors misbehaving. Moreover, the output of fault localization shows that the trained model has learned some correlations between different parameters of the studied system.
- The trained GP does not require numerous data points to predict the anomaly values. Moreover, the dedicated GP for regression does not require a long time to be (re)trained. These characteristics make GP ideal for online prediction of anomaly values.
2. Material and Methods
2.1. Autoencoder (AE)
- encoder f
- internal representation z
- decoder g
- AE does not require any labels as the input is the output of the neural network.
- AE can capture the underlying error-free signal sequence distribution.
- Data shifts from the learned distributions can easily be acquired from the reconstruction error at the output of the AE.
2.2. Convolutional Layer
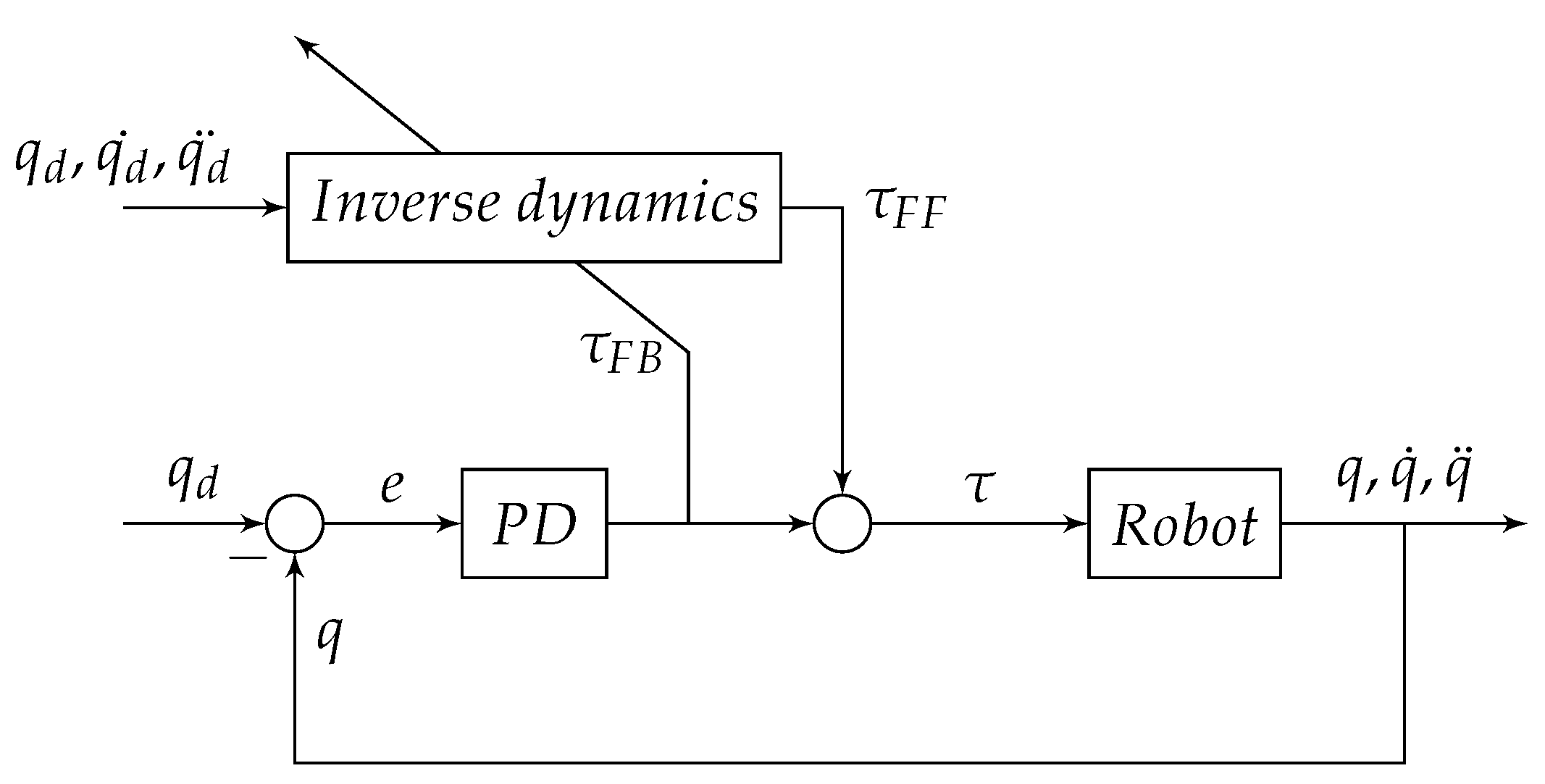
2.3. Delta Robot Dynamics and Parameters
2.4. Gathering and Preprocessing Data from Delta Robot
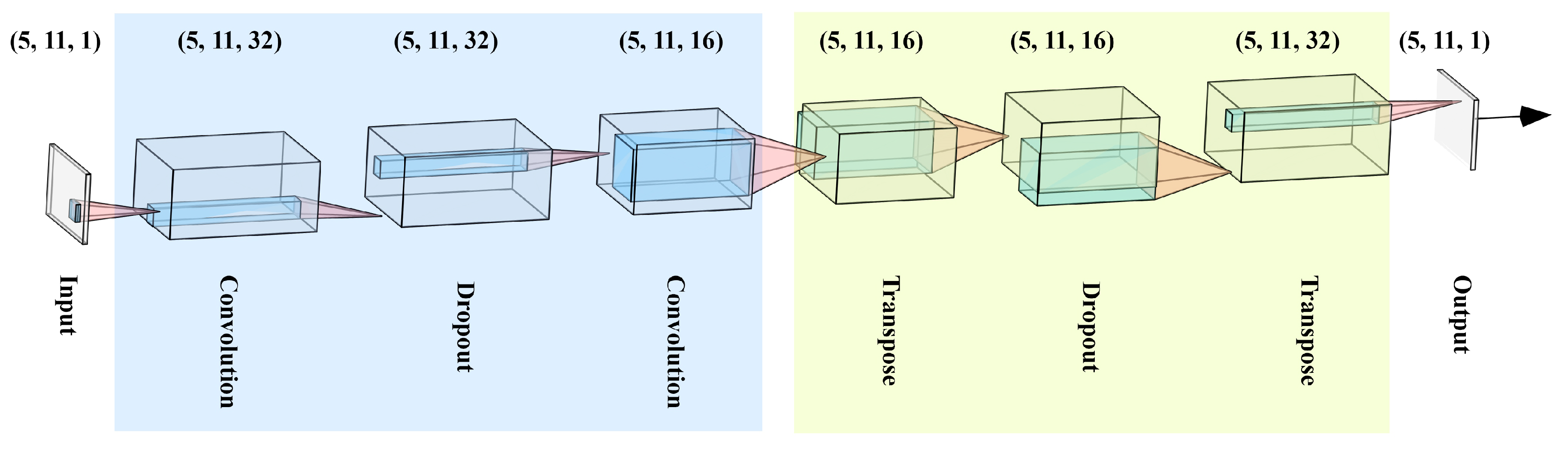
2.5. Architecture of the Proposed Method
- Convolution with 32 filters and kernel size of
- Dropout
- Convolution with 16 filters and kernel size of
- Transpose (a.k.a. deconvolution) with 16 filters and kernel size of
- Dropout
- Transpose with 32 filters and kernel size of
2.6. GP
3. Results
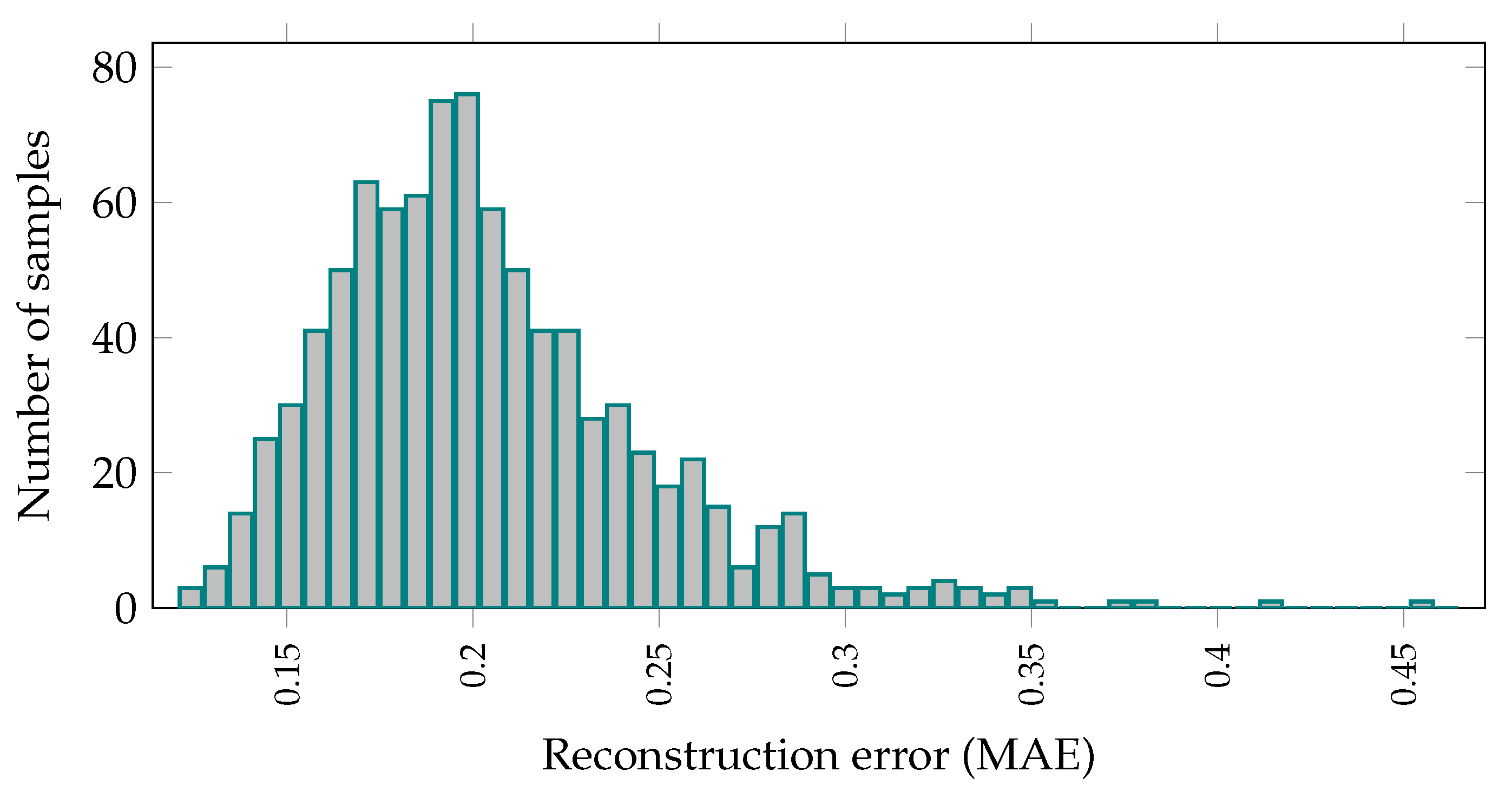
3.1. Setting up the Model
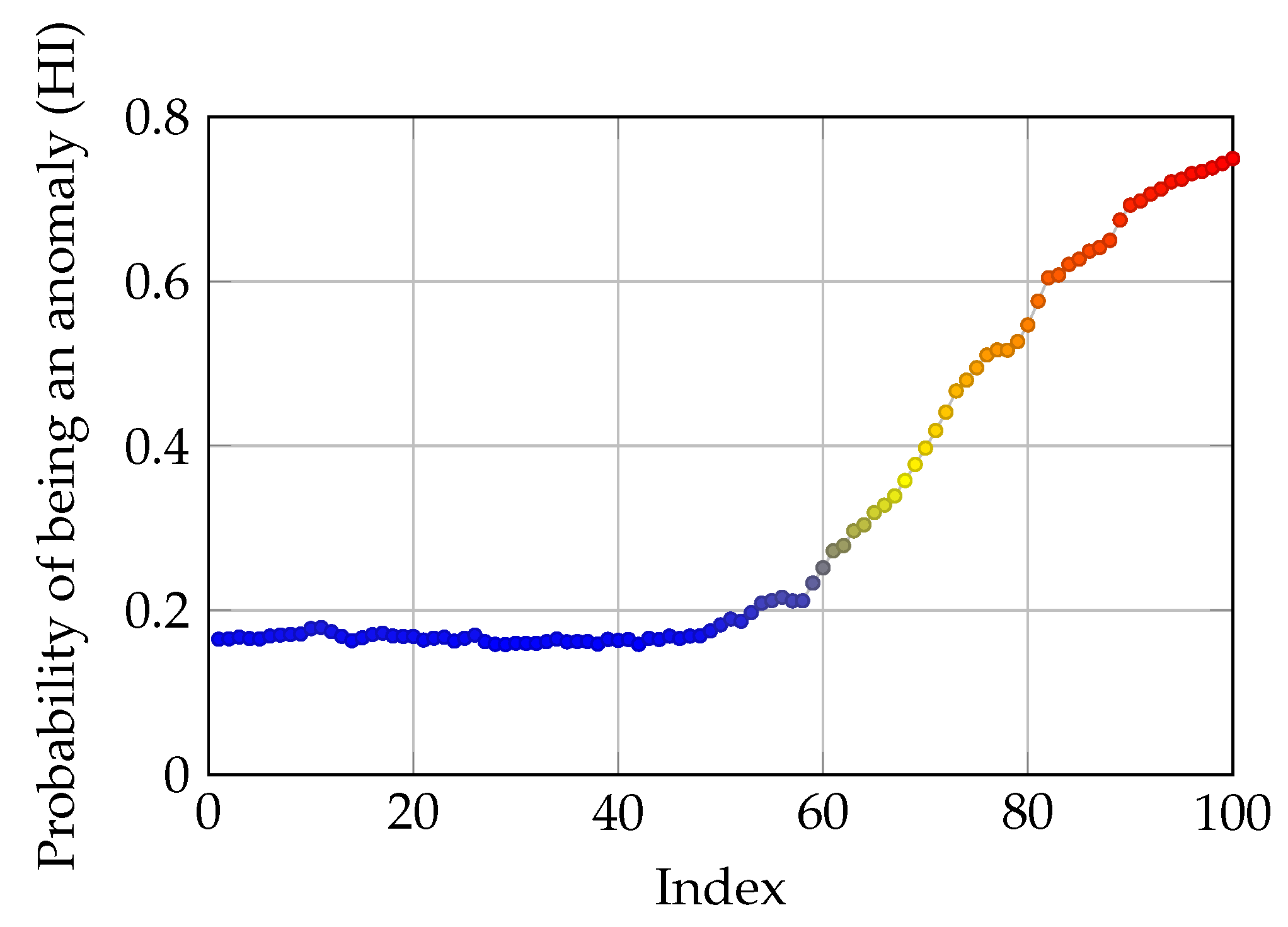
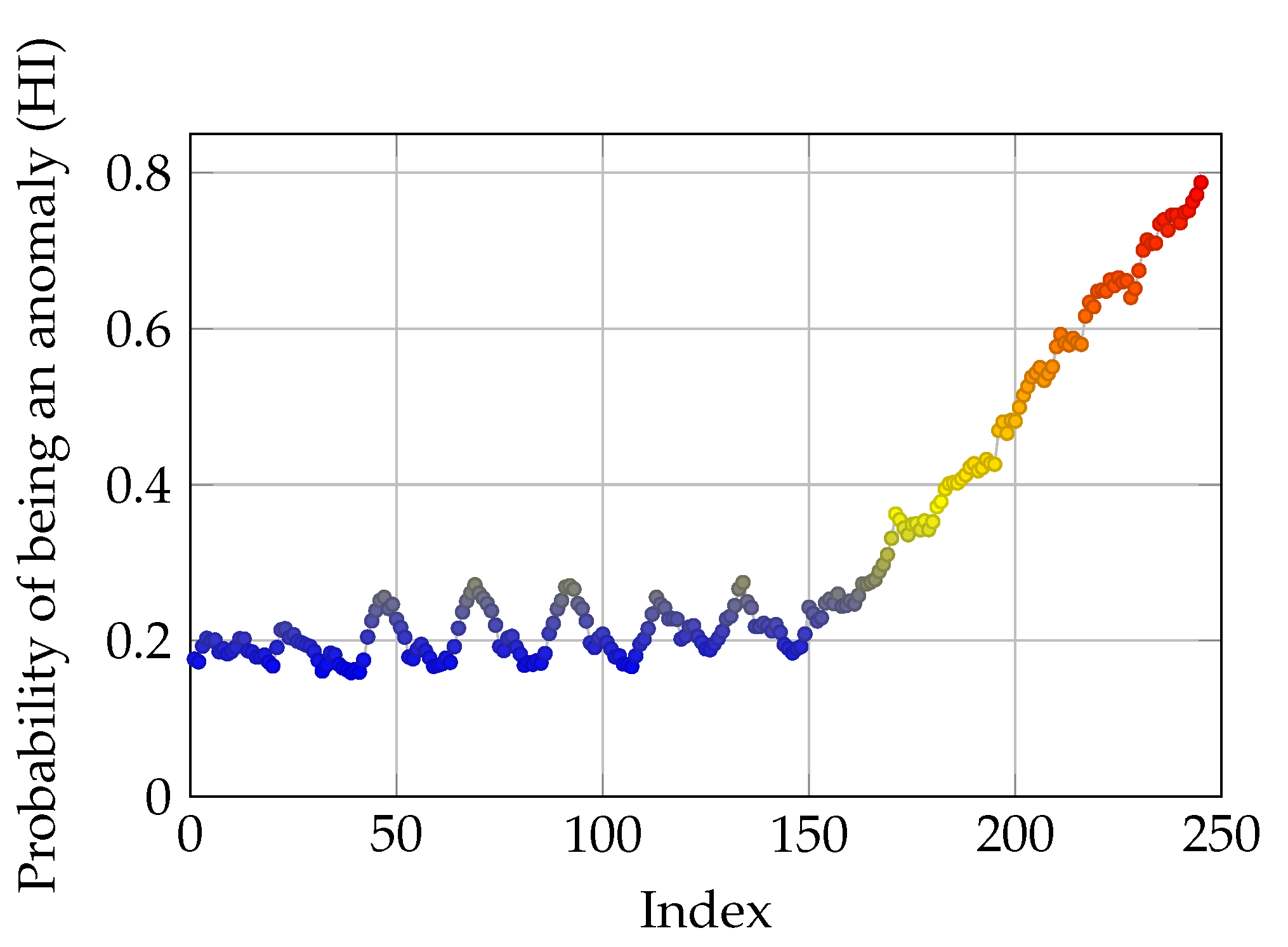
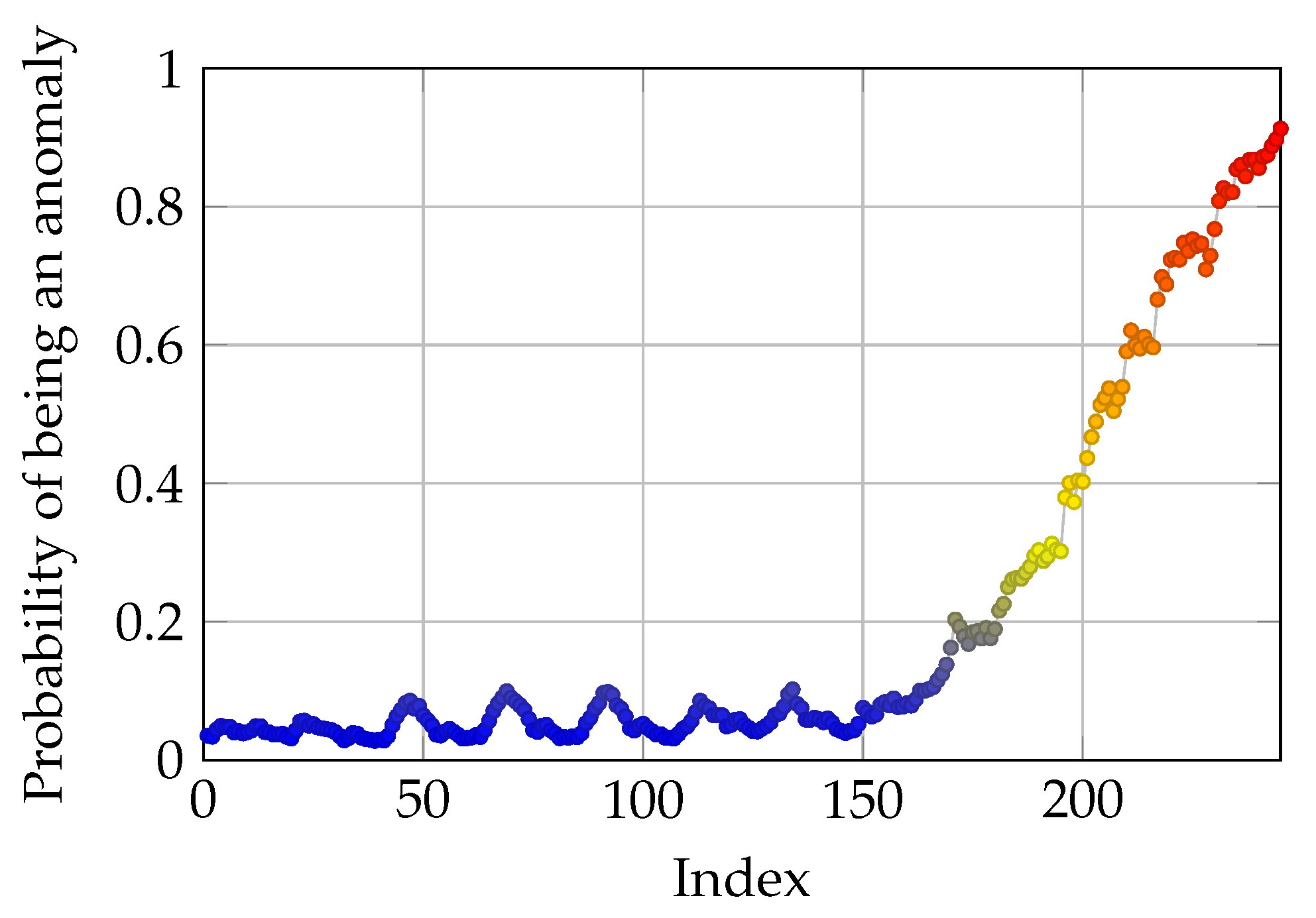
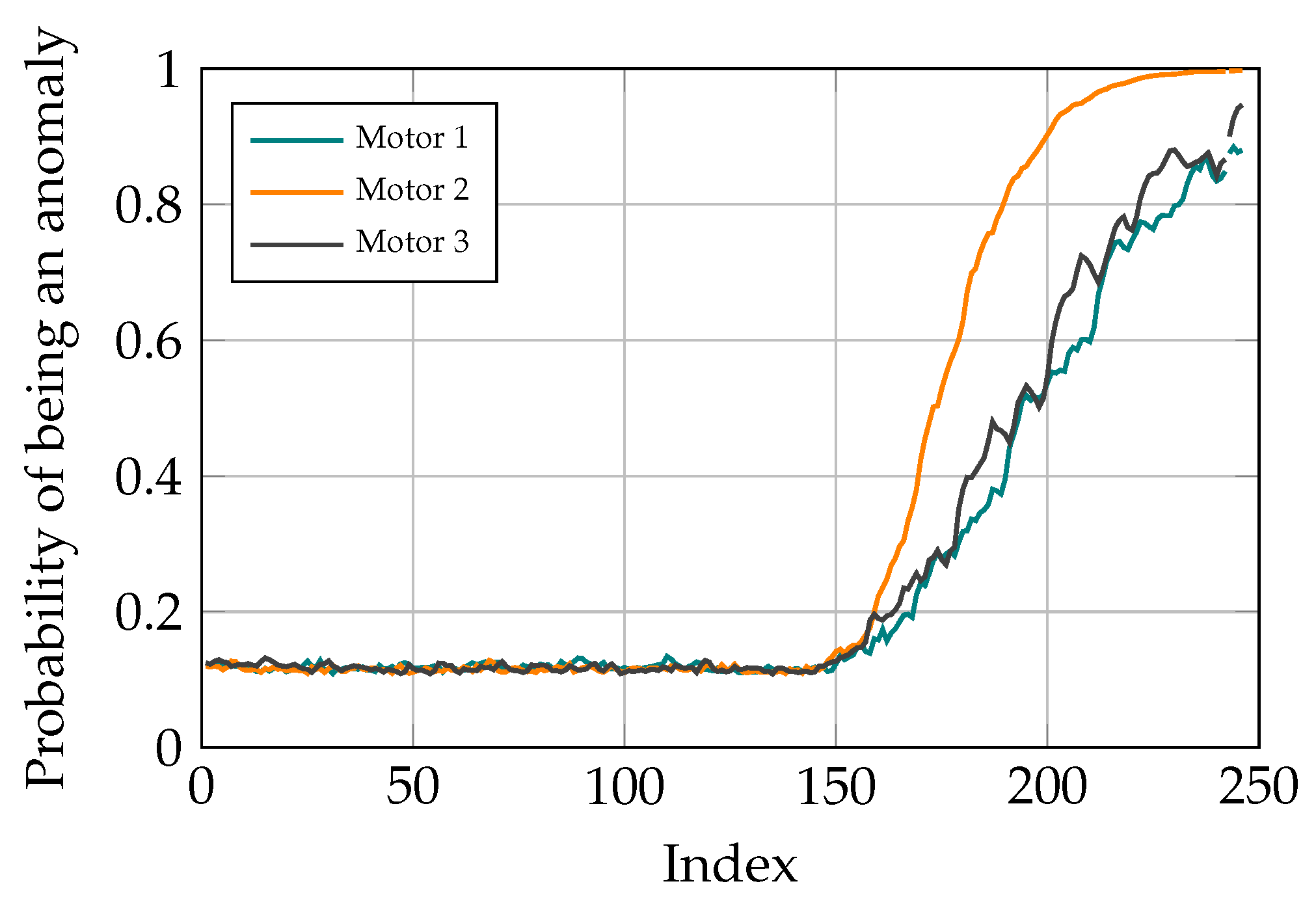
3.2. Binary Classification and Predicting Anomaly Probability
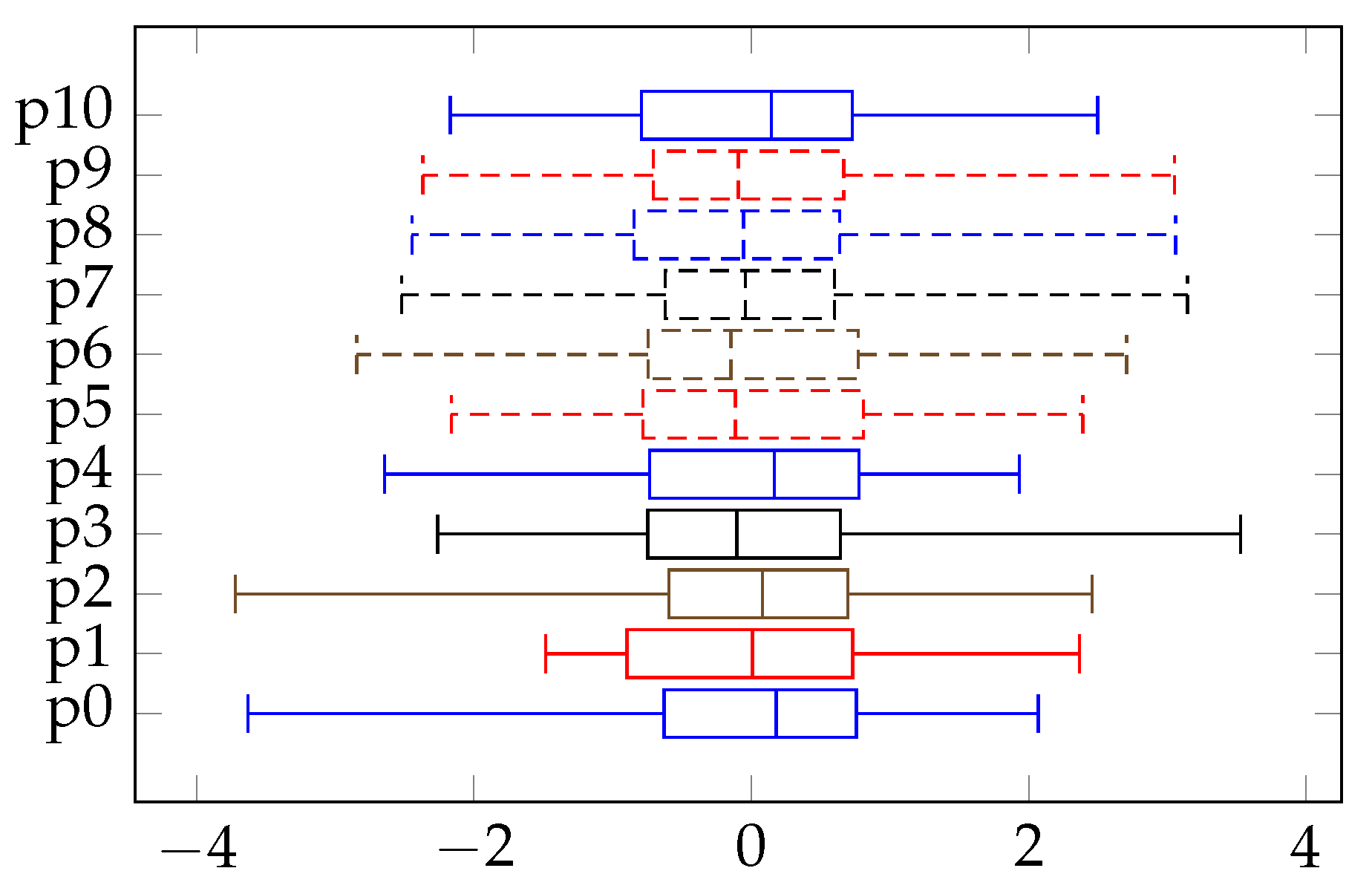
3.3. Robustness Testing
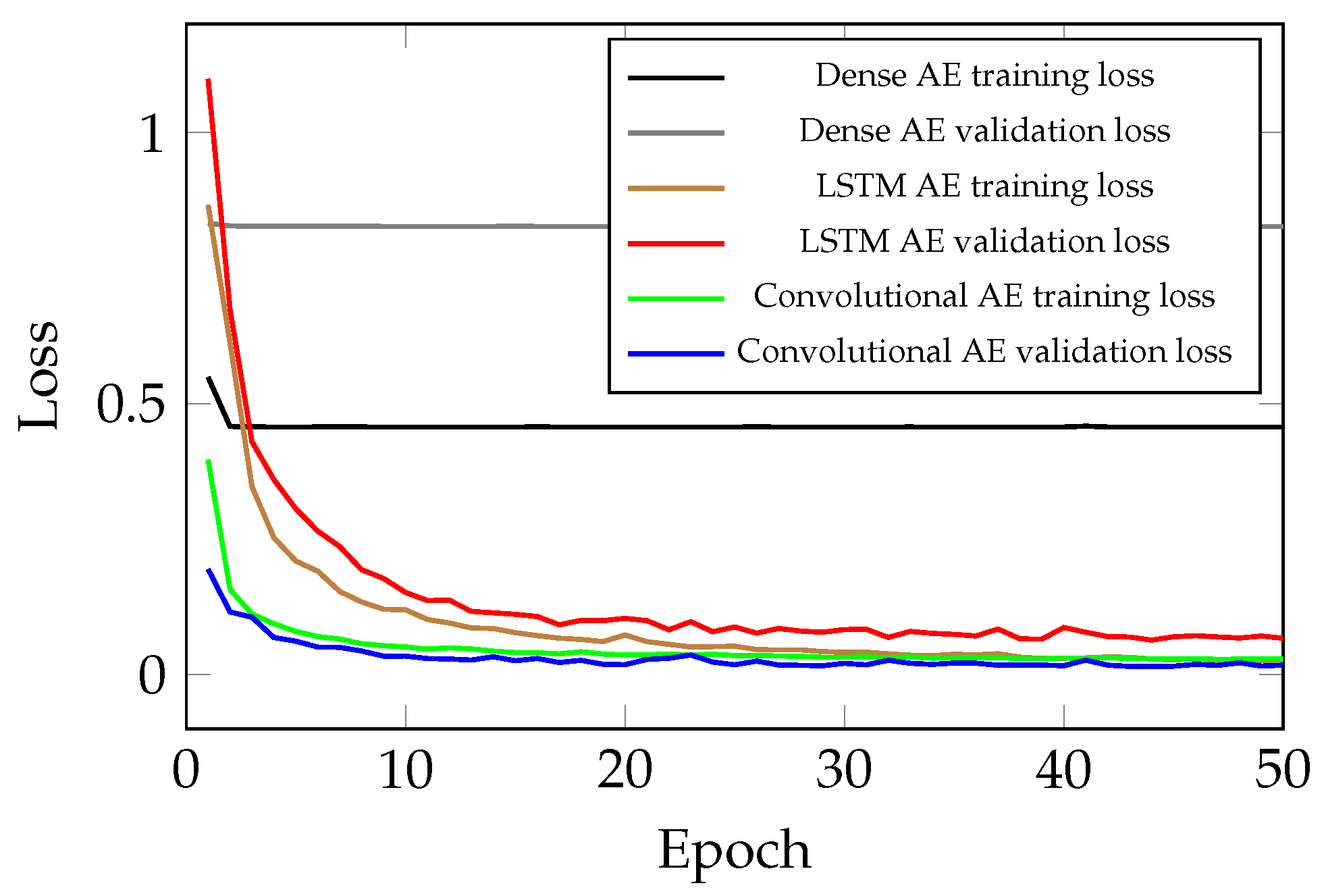
3.4. Comparison of the Convolutional, LSTM and Dense AE
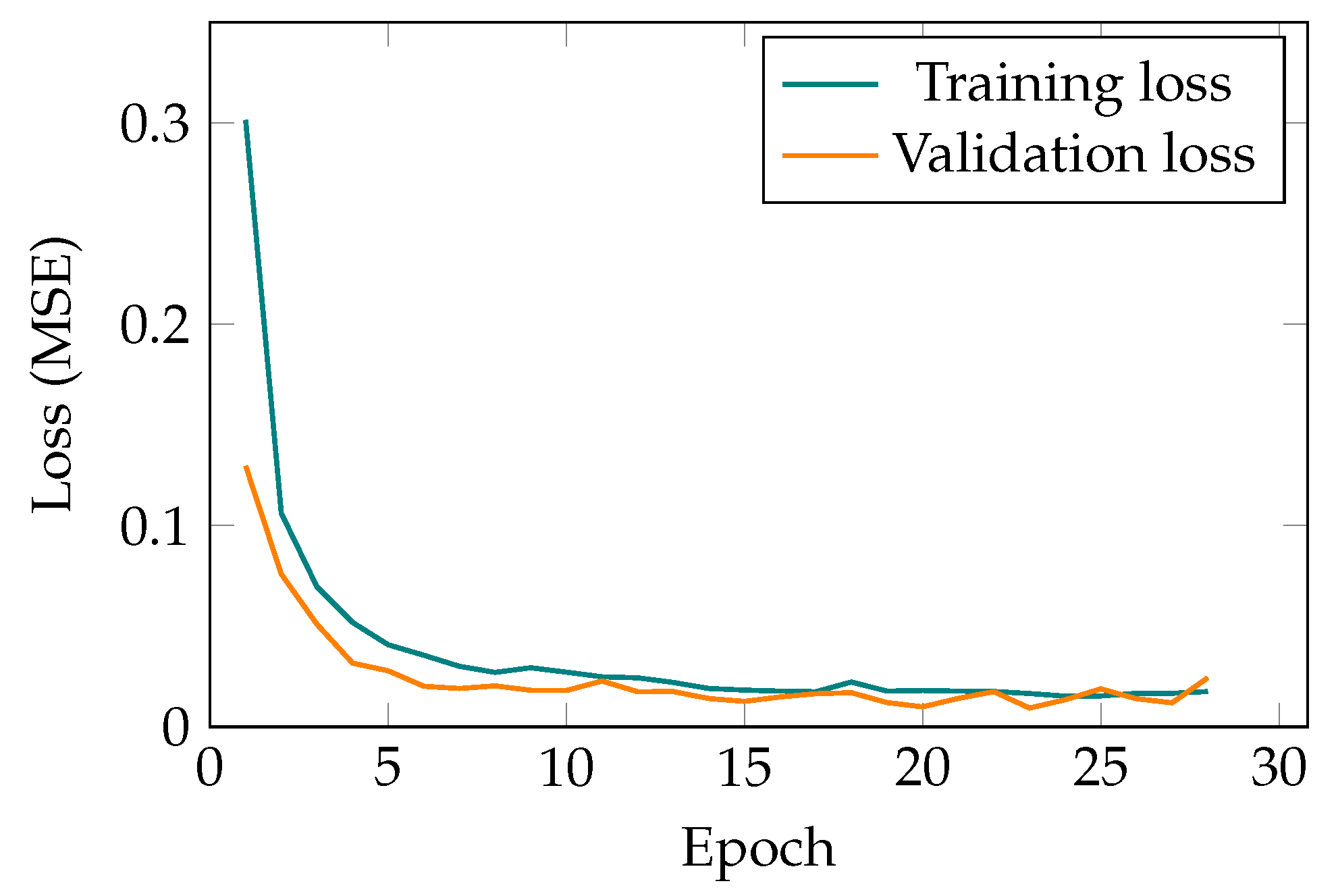
- AE with dense feed-forward layers: This architecture has the lowest performance and simply is not capable of handling sequential data. Even by increasing the model complexity, this architecture does not show any improvement in the performance. The number of trainable parameters in this case is 475,200. Moreover, the minimum validation loss for this structure is 0.8266.
- AE with LSTM layers: This model has a much better performance than the previous scenario. However, this model cannot outperform the results of the AE with convolutional layers. This simulation results proves that as expected, this structure is capable of handling sequential data, but not as good as the AE with convolutional layers. In this case, the number of trainable parameters is 254,347. It is worth noting that the minimum validation loss for AE with LSTM layers is .
- AE with convolutional layers: The best performing among the test models with the fewest parameters. The proposed method has successfully found all the spatial information and acquired features for reconstructing the given signal sequences. The number of parameters in this case is 125,665. Lastly, the minimum validation loss for the chosen AE structure is 0.0281
3.5. Optimization of Sigmoid Function
3.6. Fault Localization
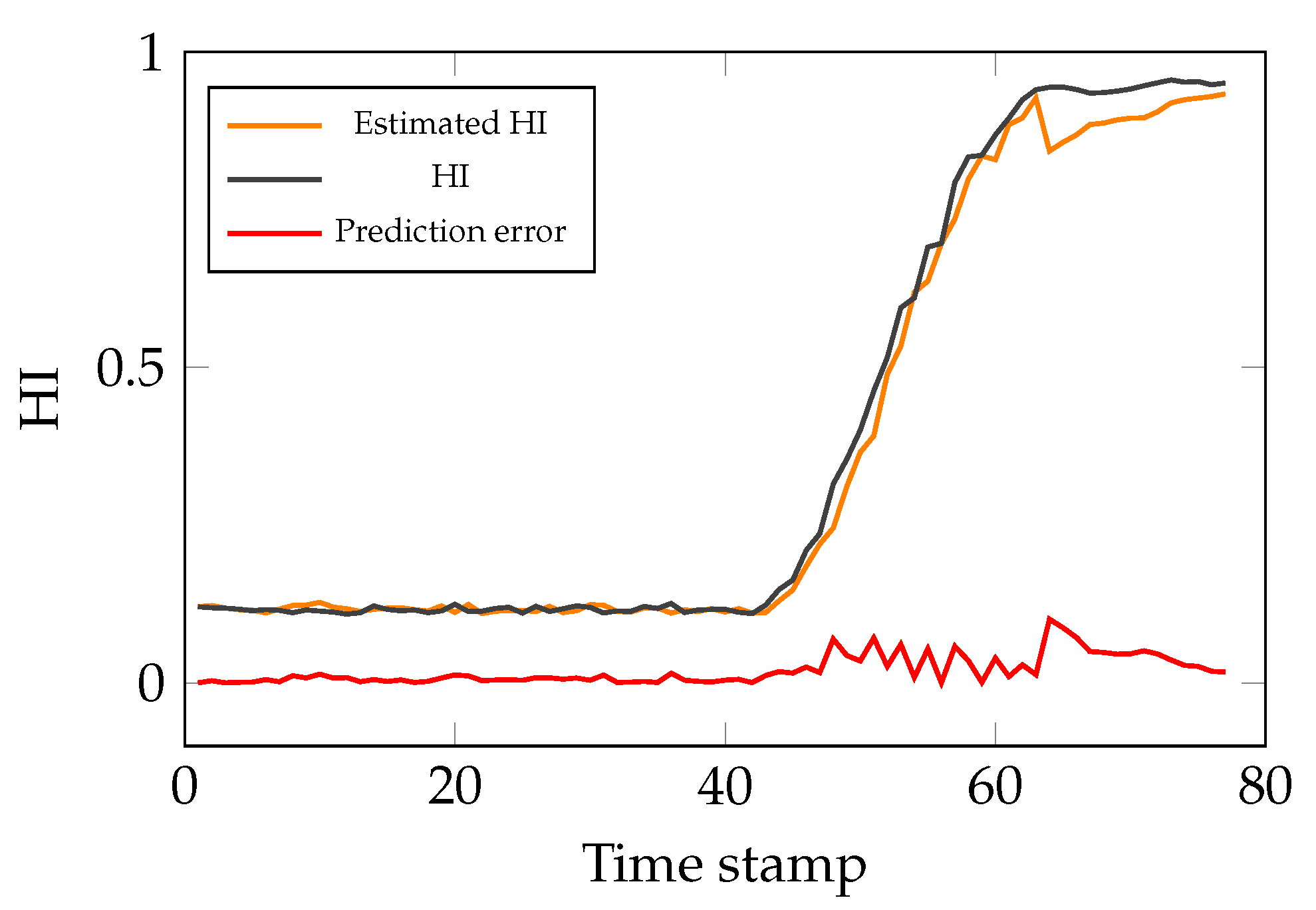
3.7. RUL
- Exp-Sine-Squared kernel
- Radial basis function
- Matern
- Constant kernelwhere is the Euclidean distance between two data points x and . Additionally, p is the periodicity parameter, l is the length scale, controls the smoothness of the kernel, is a modified Bessel function and finally, is the gamma function. It is worth noting that the implementation of the degradation model is done using the library [56].
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PdM | Predictive maintenance |
| R2F | Run-to-failure |
| CI | Condition indicator |
| HI | Health index |
| RUL | Remaining useful lifetime |
| AE | Autoencoder |
| GP | Gaussian process |
| LSTM | Long short-term memory |
| MSE | Mean squared error |
| AFFC | Adaptive feed-forward controller |
| MAE | Mean absolute error |
References
- Mobley, R.K. An Introduction to Predictive Maintenance; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Schmidt, B.; Wang, L. Cloud-enhanced predictive maintenance. Int. J. Adv. Manuf. Technol. 2018, 99, 5–13. [Google Scholar] [CrossRef]
- Krupitzer, C.; Wagenhals, T.; Züfle, M.; Lesch, V.; Schäfer, D.; Mozaffarin, A.; Edinger, J.; Becker, C.; Kounev, S. A survey on predictive maintenance for industry 4.0. arXiv 2020, arXiv:2002.08224. [Google Scholar]
- Luo, W.; Hu, T.; Ye, Y.; Zhang, C.; Wei, Y. A hybrid predictive maintenance approach for CNC machine tool driven by Digital Twin. Robot. Comput. Integr. Manuf. 2020, 65, 101974. [Google Scholar] [CrossRef]
- Butler, K.L. An expert system based framework for an incipient failure detection and predictive maintenance system. In Proceedings of the International Conference on Intelligent System Application to Power Systems, Orlando, FL, USA, 28 January–2 February 1996; pp. 321–326. [Google Scholar]
- Shimada, J.; Sakajo, S. A statistical approach to reduce failure facilities based on predictive maintenance. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 5156–5160. [Google Scholar]
- Li, C.; Zhang, Y.; Xu, M. Reliability-based maintenance optimization under imperfect predictive maintenance. Chin. J. Mech. Eng. 2012, 25, 160–165. [Google Scholar] [CrossRef]
- Ortiz, J.; Carrasco, R.A. Model-based fault detection and diagnosis in ALMA subsystems. In Observatory Operations: Strategies, Processes, and Systems VI; International Society for Optics and Photonics: Bellingham, WA, USA, 2016. [Google Scholar]
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A model-based method for remaining useful life prediction of machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Canizo, M.; Onieva, E.; Conde, A.; Charramendieta, S.; Trujillo, S. Real-time predictive maintenance for wind turbines using Big Data frameworks. In Proceedings of the 2017 IEEE international conference on prognostics and health management (ICPHM), Dallas, TX, USA, 19–21 June 2017; pp. 70–77. [Google Scholar]
- Wang, J.; Fu, P.; Zhang, L.; Gao, R.X.; Zhao, R. Multilevel information fusion for induction motor fault diagnosis. IEEE/ASME Trans. Mechatron. 2019, 24, 2139–2150. [Google Scholar] [CrossRef]
- Levitt, J. Complete Guide to Preventive and Predictive Maintenance; Industrial Press Inc.: New York, NY, USA, 2003. [Google Scholar]
- Goyal, D.; Pabla, B.S. Condition based maintenance of machine tools—A review. IRP J. Manuf. Sci. Technol. 2015, 10, 24–35. [Google Scholar] [CrossRef]
- Lughofer, E.; Sayed-Mouchaweh, M. Predictive Maintenance in Dynamic Systems: Advanced Methods, Decision Support Tools and Real-World Applications; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Cheng, J.C.; Chen, W.; Chen, K.; Wang, Q. Data-driven predictive maintenance planning framework for MEP components based on BIM and IoT using machine learning algorithms. Autom. Constr. 2020, 112, 87–103. [Google Scholar] [CrossRef]
- Baptista, M.; Sankararaman, S.; de Medeiros, I.P.; Nascimento, C., Jr.; Prendinger, H.; Henriques, E.M. Forecasting fault events for predictive maintenance using data-driven techniques and ARMA modeling. Comput. Ind. Eng. 2018, 115, 41–53. [Google Scholar] [CrossRef]
- Yu, W.; Kim, I.Y.; Mechefske, C. An improved similarity-based prognostic algorithm for RUL estimation using an RNN autoencoder scheme. Reliab. Eng. Syst. Saf. 2020, 199, 106926. [Google Scholar] [CrossRef]
- Da Xu, L.; He, W.; Li, S. Internet of things in industries: A survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar]
- Li, X.; Li, D.; Wan, J.; Vasilakos, A.V.; Lai, C.F.; Wang, S. A review of industrial wireless networks in the context of industry 4.0. Wirel. Netw. 2017, 23, 23–41. [Google Scholar] [CrossRef]
- Yan, J.; Meng, Y.; Lu, L.; Li, L. Industrial Big Data in an Industry 4.0 Environment: Challenges, Schemes, and Applications for Predictive Maintenance. IEEE Access 2017, 5, 23484–23491. [Google Scholar] [CrossRef]
- Kiangala, K.S.; Wang, Z. Initiating predictive maintenance for a conveyor motor in a bottling plant using industry 4.0 concepts. Int. J. Adv. Manuf. Technol. 2018, 97, 3251–3271. [Google Scholar] [CrossRef]
- Cattaneo, L.; Macchi, M. A Digital Twin Proof of Concept to Support Machine Prognostics with Low Availability of Run-To-Failure Data. IFAC-PapersOnLine 2019, 2, 37–42. [Google Scholar] [CrossRef]
- Rengasamy, D.; Jafari, M.; Rothwell, B.; Chen, X.; Figueredo, G.P. Deep Learning with Dynamically Weighted Loss Function for Sensor-Based Prognostics and Health Management. Sensors 2020, 20, 723. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rengasamy, D.; Morvan, H.P.; Figueredo, G.P. Deep learning approaches to aircraft maintenance, repair and overhaul: A review. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 150–156. [Google Scholar]
- Jogin, M.; Madhulika, M.S.; Divya, G.D.; Meghana, R.K.; Apoorva, S. Feature extraction using Convolution Neural Networks (CNN) and Deep Learning. In Proceedings of the 2018 3rd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 18–19 May 2018; pp. 2319–2323. [Google Scholar]
- Reddy, K.K.; Sarkar, S.; Venugopalan, V.; Giering, M. Anomaly detection and fault disambiguation in large flight data: A multi-modal deep auto-encoder approach. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Denver, CO, USA, 3–6 October 2016. [Google Scholar]
- Sarkar, S.; Reddy, K.K.; Giering, M. Deep learning for structural health monitoring: A damage characterization application. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Denver, CO, USA, 3–6 October 2016; pp. 176–182. [Google Scholar]
- Yuan, M.; Wu, Y.; Lin, L. Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 135–140. [Google Scholar]
- Susto, G.A.; Schirru, A.; Pampuri, S.; McLoone, S.; Beghi, A. Machine learning for predictive maintenance: A multiple classifier approach. IEEE Trans. Ind. Inform. 2014, 11, 812–820. [Google Scholar] [CrossRef] [Green Version]
- Kiangala, K.S.; Wang, Z. An Effective Predictive Maintenance Framework for Conveyor Motors Using Dual Time-Series Imaging and Convolutional Neural Network in an Industry 4.0 Environment. IEEE Access 2020, 8, 121033–121049. [Google Scholar] [CrossRef]
- Fan, C.; Sun, Y.; Zhao, Y.; Song, M.; Wang, J. Deep learning-based feature engineering methods for improved building energy prediction. Appl. Energy 2019, 240, 35–45. [Google Scholar] [CrossRef]
- Rutagarama, M. Deep Learning for Predictive Maintenance in Impoundment Hydropower Plants. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2019. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2014; pp. 3104–3112. [Google Scholar]
- Que, Z.; Liu, Y.; Guo, C.; Niu, X.; Zhu, Y.; Luk, W. Real-time Anomaly Detection for Flight Testing using AutoEncoder and LSTM. In Proceedings of the 2019 International Conference on Field-Programmable Technology (ICFPT), Tianjin, China, 9–13 December 2019; pp. 379–382. [Google Scholar]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Yang, J.; Nguyen, M.N.; San, P.P.; Li, X.L.; Krishnaswamy, S. Deep convolutional neural networks on multichannel time series for human activity recognition. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; Volume 15, pp. 3995–4001. [Google Scholar]
- Mishra, K.M.; Krogerus, T.R.; Huhtala, K.J. Fault detection of elevator systems using deep autoencoder feature extraction. In Proceedings of the 2019 13th International Conference on Research Challenges in Information Science (RCIS), Brussels, Belgium, 29–31 May 2019; pp. 1–6. [Google Scholar]
- Sakurada, M.; Yairi, T. Anomaly detection using autoencoders with nonlinear dimensionality reduction. In Proceedings of the MLSDA 2014 2nd Workshop on Machine Learning for Sensory Data Analysis, Gold Coast, Australia, 2 December 2014; pp. 4–11. [Google Scholar]
- Essien, A.; Giannetti, C. A deep learning model for smart manufacturing using convolutional LSTM neural network autoencoders. IEEE Trans. Ind. Inform. 2020, 16, 6069–6078. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zhao, Z.; Sun, C.; Yan, R.; Chen, X. Fault-attention generative probabilistic adversarial autoencoder for machine anomaly detection. IEEE Trans. Ind. Inform. 2020, 16, 7479–7488. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Yan, J.; Koc, M.; Lee, J. A prognostic algorithm for machine performance assessment and its application. Prod. Plan. Control 2004, 8, 796–801. [Google Scholar] [CrossRef]
- Charu, C.A. Neural Networks and Deep Learning: A Textbook; Springer: New York, NY, USA, 2018. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1, Number 2. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Sci. Am. Assoc. Adv. Sci. 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brownlee, J. Deep Learning for Time Series Forecasting: Predict the Future with MLPs, CNNs and LSTMs in Python; Machine Learning Mastery: San Juan, PR, USA, 2018. [Google Scholar]
- Arrazate, R.T. Development of a URDF File for Simulation and Programming of a Delta Robot Using ROS. Master’s Thesis, Aachen University of Applied Sciences, Aachen, Germany, 2017. [Google Scholar]
- Honegger, M.; Codourey, A.; Burdet, E. Adaptive control of the hexaglide, a 6 dof parallel manipulator. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25–25 April 1997; Volume 1, pp. 543–548. [Google Scholar]
- Codourey, A.; Burdet, E. A body-oriented method for finding a linear form of the dynamic equation of fully parallel robots. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 25–25 April 1997; Volume 2, pp. 1612–1618. [Google Scholar]
- Raschka, S.; Mirjalili, V. Python Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- LeNail, A. Nn-svg: Publication-ready neural network architecture schematics. J. Open Source Softw. 2019, 4, 747. [Google Scholar] [CrossRef]
- Ide, H.; Kurita, T. Improvement of learning for CNN with ReLU activation by sparse regularization. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2684–2691. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the ICML 2010, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- François, C. Keras. 2015. Available online: https://keras.io (accessed on 23 October 2020).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]





| Parameter | Learning Rate |
|---|---|
| Motor inertia [gm] | 0.0005 |
| Gravity [mN] | 0.08 |
| Mass [g] | 0.09 |
| Spring offset [mN m] | 0.07 |
| Coulomb friction 0 [mNm] | 0.1 |
| Coulomb friction 1 [mNm] | 0.1 |
| Coulomb friction 2 [mNm] | 0.1 |
| Spring constant [mNm/rad] | 0.2 |
| Viscose friction 0 [mNm s/rad] | 0.01 |
| Viscose friction 1 [mNm s/rad] | 0.01 |
| Viscose friction 2 [mNm s/rad] | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathi, K.; van de Venn, H.W.; Honegger, M. Predictive Maintenance: An Autoencoder Anomaly-Based Approach for a 3 DoF Delta Robot. Sensors 2021, 21, 6979. https://doi.org/10.3390/s21216979
Fathi K, van de Venn HW, Honegger M. Predictive Maintenance: An Autoencoder Anomaly-Based Approach for a 3 DoF Delta Robot. Sensors. 2021; 21(21):6979. https://doi.org/10.3390/s21216979
Chicago/Turabian StyleFathi, Kiavash, Hans Wernher van de Venn, and Marcel Honegger. 2021. "Predictive Maintenance: An Autoencoder Anomaly-Based Approach for a 3 DoF Delta Robot" Sensors 21, no. 21: 6979. https://doi.org/10.3390/s21216979
APA StyleFathi, K., van de Venn, H. W., & Honegger, M. (2021). Predictive Maintenance: An Autoencoder Anomaly-Based Approach for a 3 DoF Delta Robot. Sensors, 21(21), 6979. https://doi.org/10.3390/s21216979







