Estimation of Walking Speed and Its Spatiotemporal Determinants Using a Single Inertial Sensor Worn on the Thigh: From Healthy to Hemiparetic Walking
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Gait Evaluation and Data Collection
2.3. Data Processing
2.4. Analysis
2.4.1. Stride Time Measurement Using a Thigh IMU
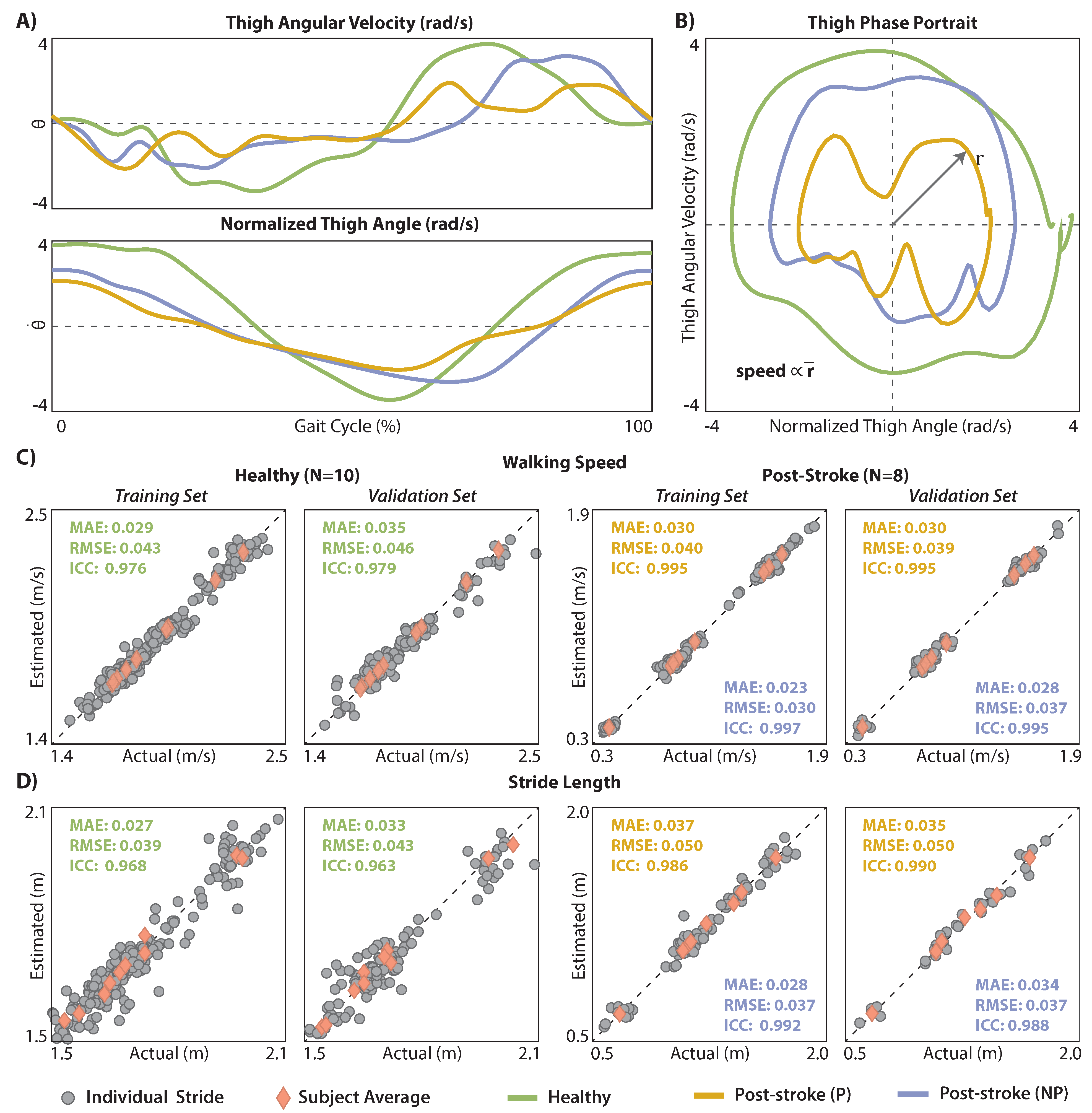
2.4.2. Walking Speed and Stride Length Estimation Using a Thigh IMU
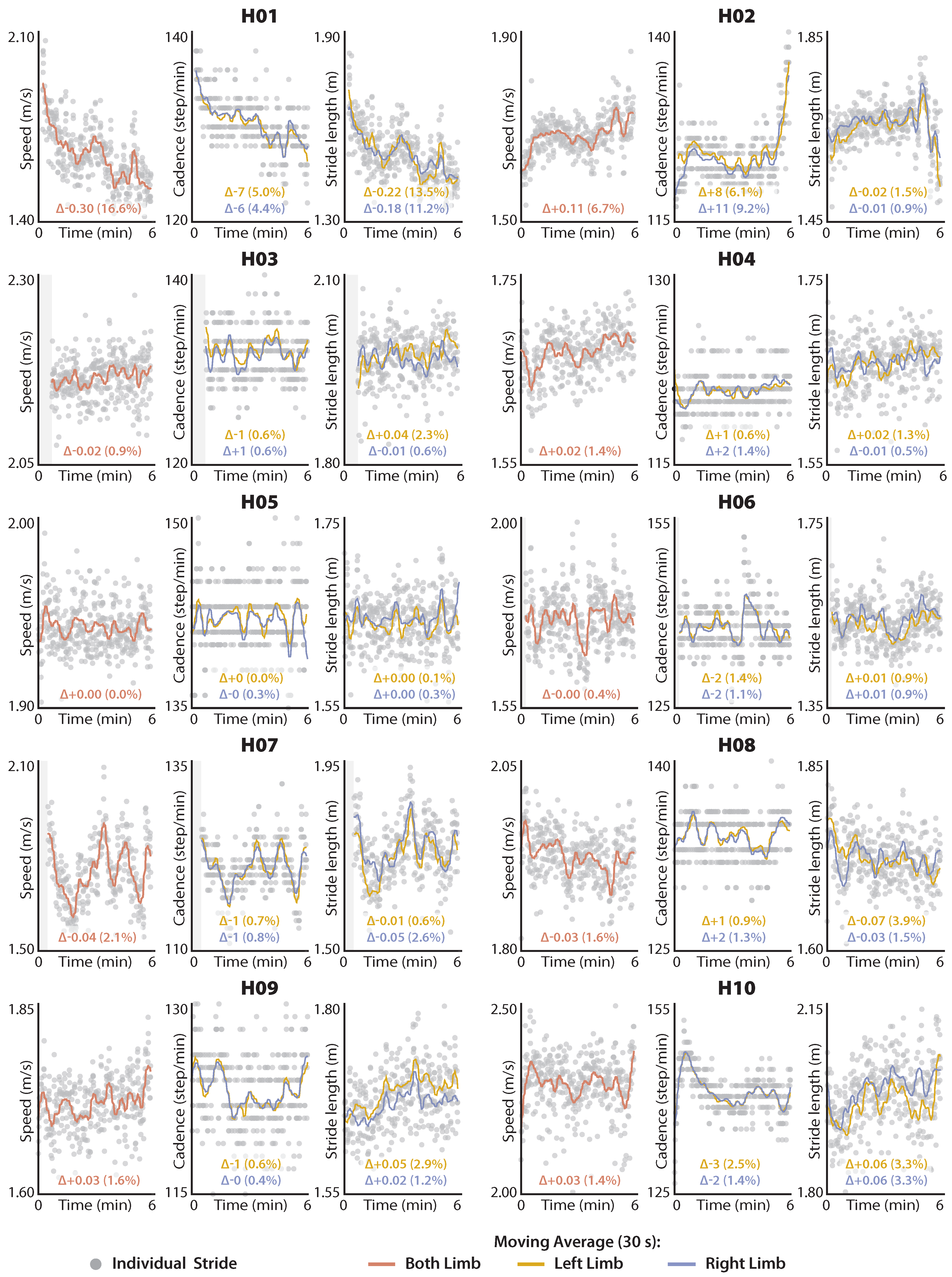
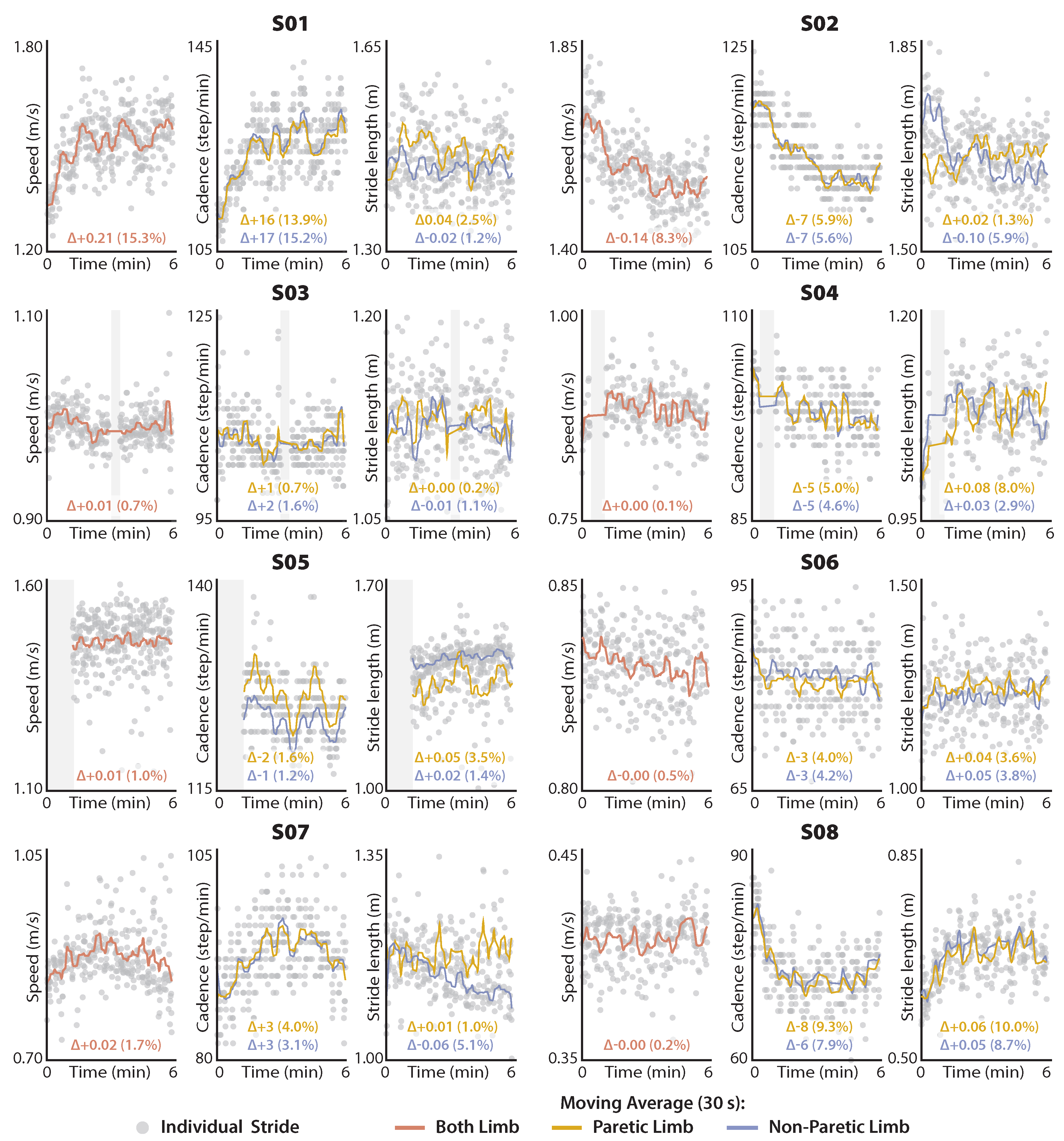
2.4.3. Exploratory Application 1: Distance-Induced Changes in Speed and Its Determinants
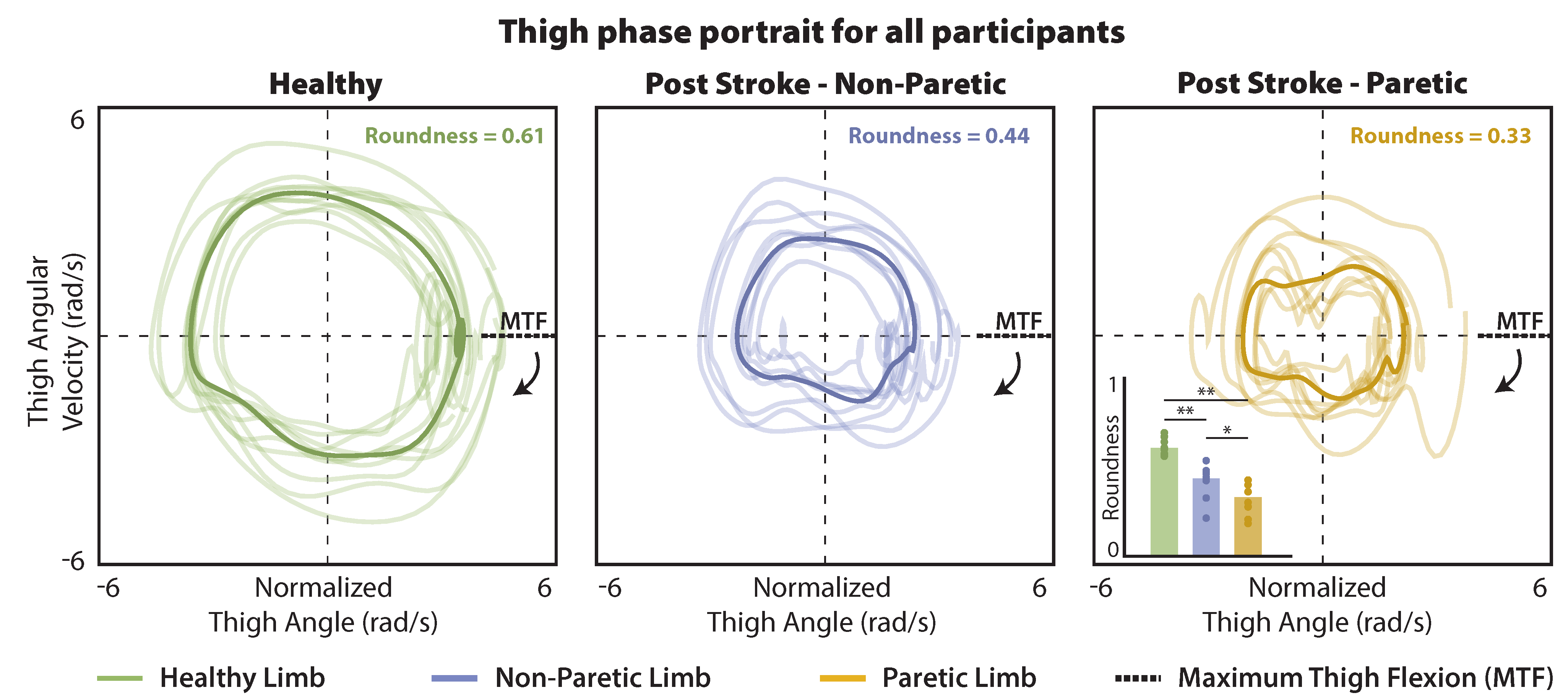
2.4.4. Exploratory Application 2: Phase Portrait Roundness as a Movement Biomarker
2.4.5. Statistical Analysis
3. Results
3.1. Stride Time Measurement Using a Thigh IMU
3.2. Walking Speed and Stride Length Estimation Using a Thigh IMU
3.3. Distance-Induced Changes in Walking Speed and Spatiotemporal Determinants
3.4. Phase Portrait Roundness
4. Discussion
4.1. Estimating Walking Speed and Stride Length Using Thigh Phase Portraits
4.2. Measuring Stride Time Using a Thigh IMU
4.3. Distance-Induced Changes in Walking Speed and Its Spatiotemporal Determinants
4.4. Phase Portrait Roundness
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IMU | inertial measurement units |
| 6MWT | 6-min walk test |
| MAE | mean absolute error |
| RMSE | root mean square error |
| ICC | inter-class correlation |
| MTF | maximum thigh flexion |
| SL | stride length |
| ST | stride time |
Appendix A. Effects of Filtering Method and Polar Radius Selection on Walking Speed Estimation Accuracy
| Approach A [26] | Approach B | Difference | |
|---|---|---|---|
| Healthy | |||
| MAE: | 0.037 | 0.035 | 0.002 (6%) |
| RMSE: | 0.047 | 0.046 | 0.001 (2%) |
| ICC: | 0.97 | 0.98 | - |
| Stroke—Paretic | |||
| MAE: | 0.041 | 0.030 | 0.011 (37%) |
| RMSE: | 0.054 | 0.039 | 0.015 (38%) |
| ICC: | 0.99 | 1.0 | - |
| Stroke—Non-Paretic | |||
| MAE: | 0.033 | 0.028 | 0.008 (29%) |
| RMSE: | 0.042 | 0.037 | 0.005 (14%) |
| ICC: | 0.99 | 1.0 | - |
References
- Schmid, A.A.; Van Puymbroeck, M.; Altenburger, P.A.; Dierks, T.A.; Miller, K.K.; Damush, T.M.; Williams, L.S. Balance and balance self-efficacy are associated with activity and participation after stroke: A cross-sectional study in people with chronic stroke. Arch. Phys. Med. Rehabil. 2012, 93, 1101–1107. [Google Scholar] [CrossRef] [PubMed]
- Fulk, G.D.; Reynolds, C.; Mondal, S.; Deutsch, J.E. Predicting Home and Community Walking Activity in People with Stroke. Arch. Phys. Med. Rehabil. 2010, 91, 1582–1586. [Google Scholar] [CrossRef] [PubMed]
- Pohl, P.S.; Duncan, P.W.; Perera, S.; Liu, W.; Lai, S.M.; Studenski, S.; Long, J. Influence of stroke-related impairments on performance in 6-minute walk test. J. Rehabil. Res. Dev. 2002, 39, 439–444. [Google Scholar] [PubMed]
- Awad, L.; Reisman, D.; Binder-Macleod, S. Distance-Induced Changes in Walking Speed after Stroke: Relationship to Community Walking Activity. J. Neurol. Phys. Ther. 2019, 43, 220–223. [Google Scholar] [CrossRef] [PubMed]
- Schinkel-Ivy, A.; Inness, E.L.; Mansfield, A. Relationships between fear of falling, balance confidence, and control of balance, gait, and reactive stepping in individuals with sub-acute stroke. Gait Posture 2016, 43, 154–159. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schinkel-Ivy, A.; Wong, J.S.; Mansfield, A. Balance Confidence Is Related to Features of Balance and Gait in Individuals with Chronic Stroke. J. Stroke Cerebrovasc. Dis. 2017, 26, 237–245. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.J.; Winston, K.D.; Mitchell, J.; Girlinghouse, J.; Crochet, K. Physical activity, functional capacity, and step variability during walking in people with lower-limb amputation. Gait Posture 2014, 40, 140–144. [Google Scholar] [CrossRef]
- Zukowski, L.A.; Feld, J.A.; Giuliani, C.A.; Plummer, P. Relationships between gait variability and ambulatory activity post stroke. Top. Stroke Rehabil. 2019, 26, 255–260. [Google Scholar] [CrossRef]
- Mansfield, A.; Wong, J.; McIlroy, W.; Biasin, L.; Brunton, K.; Bayley, M.; Inness, E. Do measures of reactive balance control predict falls in people with stroke returning to the community? Physiotherapy 2015, 101, 373–380. [Google Scholar] [CrossRef]
- Moore, S.A.; Hickey, A.; Lord, S.; Del Din, S.; Godfrey, A.; Rochester, L. Comprehensive measurement of stroke gait characteristics with a single accelerometer in the laboratory and community: A feasibility, validity and reliability study. J. Neuroeng. Rehabil. 2017, 14, 130. [Google Scholar] [CrossRef]
- Chen, S.; Lach, J.; Lo, B.; Yang, G.Z. Toward Pervasive Gait Analysis With Wearable Sensors: A Systematic Review. IEEE J. Biomed. Health Inform. 2016, 20, 1521–1537. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 1–367. [Google Scholar]
- Prasanth, H.; Caban, M.; Keller, U.; Courtine, G.; Ijspeert, A.; Vallery, H.; von Zitzewitz, J. Wearable Sensor-Based Real-Time Gait Detection: A Systematic Review. Sensors 2021, 21, 2727. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Li, Q. Inertial sensor-based methods in walking speed estimation: A systematic review. Sensors 2012, 12, 6102–6116. [Google Scholar] [CrossRef] [Green Version]
- Barker, S.; Craik, R.; Freedman, W.; Herrmann, N.; Hillstrom, H. Accuracy, reliability, and validity of a spatiotemporal gait analysis system. Med. Eng. Phys. 2006, 28, 460–467. [Google Scholar] [CrossRef]
- MejiaCruz, Y.; Franco, J.; Hainline, G.; Fritz, S.; Jiang, Z.; Caicedo, J.M.; Davis, B.; Hirth, V. Walking Speed Measurement Technology: A Review. Curr. Geriatr. Rep. 2021, 10, 32–41. [Google Scholar] [CrossRef]
- Arumukhom Revi, D.; Alvarez, A.M.; Walsh, C.J.; De Rossi, S.M.; Awad, L.N. Indirect measurement of anterior-posterior ground reaction forces using a minimal set of wearable inertial sensors: From healthy to hemiparetic walking. J. Neuroeng. Rehabil. 2020, 17, 82. [Google Scholar] [CrossRef]
- Dobkin, B.H.; Dorsch, A.K. The Evolution of Personalized Behavioral Intervention Technology. Stroke 2017, 48, 2329–2334. [Google Scholar] [CrossRef]
- Steinhubl, S.R.; Muse, E.D.; Topol, E.J. The emerging field of mobile health. Sci. Transl. Med. 2015, 7, 283rv3. [Google Scholar] [CrossRef] [Green Version]
- Fritz, S.; Lusardi, M. White Paper: “Walking Speed: The Sixth Vital Sign”. J. Geriatr. Phys. Ther. 2009, 32, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Sabatini, A.M. Quaternion-based strap-down integration method for applications of inertial sensing to gait analysis. Med. Biol. Eng. Comput. 2005, 43, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhang, J.T.; Novak, A.C.; Brouwer, B.; Li, Q. Estimation of spatio-temporal parameters for post-stroke hemiparetic gait using inertial sensors. Gait Posture 2013, 37, 354–358. [Google Scholar] [CrossRef]
- Li, Q.; Young, M.; Naing, V.; Donelan, J.M. Walking speed estimation using a shank-mounted inertial measurement unit. J. Biomech. 2010, 43, 1640–1643. [Google Scholar] [CrossRef] [PubMed]
- Laudanski, A.; Yang, S.; Li, Q. A concurrent comparison of inertia sensor-based walking speed estimation methods. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Boston, MA, USA, 30 August–3 September 2011; pp. 3484–3487. [Google Scholar] [CrossRef]
- Zijlstra, W.; Hof, A.L. Assessment of spatio-temporal gait parameters from trunk accelerations during human walking. Gait Posture 2003, 18, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Quintero, D.; Lambert, D.J.; Villarreal, D.J.; Gregg, R.D. Real-Time continuous gait phase and speed estimation from a single sensor. In Proceedings of the 1st Annual IEEE Conference on Control Technology and Applications, CCTA 2017, Kohala, HI, USA, 27–30 August 2017; pp. 847–852. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, J.; Xu, X.; Wu, X.; Pottie, G.; Kasier, W. Inertial Sensor Based Motion Trajectory Visualization and Quantitative Quality Assessment of Hemiparetic Gait. In Proceedings of the 8th International Conference on Body Area Networks, ACM, Boston, MA, USA, 30 September–2 October 2013; Volume 1, pp. 169–172. [Google Scholar] [CrossRef]
- Arens, P.; Siviy, C.; Bae, J.; Choe, D.K.; Karavas, N.; Baker, T.C.; Ellis, T.D.; Awad, L.N.; Walsh, C.J. Real-time Gait Metric Estimation for Everyday Gait Training with Wearable Devices in People Poststroke Philipp. Wearable Technol. 2020, 2, 1–14. [Google Scholar] [CrossRef]
- Trojaniello, D.; Cereatti, A.; Pelosin, E.; Avanzino, L.; Mirelman, A.; Hausdorff, J.M.; Della Croce, U. Estimation of step-by-step spazio-temporal parameters of normal and impaired gait using shank-mounted magneto-inertial sensors. J. Neuroeng. Rehabil. 2014, 11, 152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woolley, S.M. Characteristics of Gait in Hemiplegia. Top. Stroke Rehabil. 2001, 7, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Titianova, E.B.; Pitkänen, K.; Pääkkönen, A.; Sivenius, J.; Tarkka, I.M. Gait Characteristics and Functional Ambulation Profile in Patients with Chronic Unilateral Stroke. Am. J. Phys. Med. Rehabil. 2003, 82, 778–786. [Google Scholar] [CrossRef] [PubMed]
- Papagelopoulos, P.J.; Sim, F.H. Limited Range of Motion After Total Knee Arthroplasty: Etiology, Treatment, and Prognosis. Orthopedics 1997, 20, 1061–1065. [Google Scholar] [CrossRef]
- Amstutz, H.C.; Lodwig, R.M.; Schurman, D.J.; Hodgson, A.G. Range of motion studies for total hip replacements. A comparative study with a new experimental apparatus. Clin. Orthop. Relat. Res. 1975, 111, 124–130. [Google Scholar] [CrossRef]
- Kramert De Quervain, I.A.; Simon, S.R.; Leurgans, S.; Pease, W.S.; McAllister, D. Gait Pattern in the Early Recovery Period after Stroke*. J. Bone Jt. Surg. 1996, 78, 1506–1514. [Google Scholar] [CrossRef] [Green Version]
- Porciuncula, F.; Nuckols, R.; Karavas, N.; Chang, C.K.; Baker, T.C.; Orzel, D.; Perry, D.; Ellis, T.; Awad, L.; Walsh, C. Assisting Limb Advancement during Walking after Stroke Using a Wearable Soft Hip Exosuit: A Proof-of-Concept. In Converging Clinical and Engineering Research on Neurorehabilitation III; Masia, L., Micera, S., Akay, M., Pons, J.L., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 312–316. [Google Scholar]
- Kim, J.; Lee, G.; Heimgartner, R.; Arumukhom Revi, D.; Karavas, N.; Nathanson, D.; Galiana, I.; Eckert-Erdheim, A.; Murphy, P.; Perry, D.; et al. Reducing the metabolic rate of walking and running with a versatile, portable exosuit. Science 2019, 365, 668–672. [Google Scholar] [CrossRef]
- Daley, M.A.; Felix, G.; Biewener, A.A. Running stability is enhanced by a proximo-distal gradient in joint neuromechanical control. J. Exp. Biol. 2007, 210, 383–394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villarreal, D.J.; Poonawala, H.A.; Gregg, R.D. A Robust Parameterization of Human Gait Patterns Across Phase-Shifting Perturbations. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 265–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xsens Technologies B. MTi User Manual; Technical Report; Xsens: Enschede, The Netherlands, 2019. [Google Scholar]
- Liu, T.; Inoue, Y.; Shibata, K. Development of a wearable sensor system for quantitative gait analysis. Measurement 2009, 42, 978–988. [Google Scholar] [CrossRef]
- Takeda, R.; Lisco, G.; Fujisawa, T.; Gastaldi, L.; Tohyama, H.; Tadano, S. Drift Removal for Improving the Accuracy of Gait Parameters Using Wearable Sensor Systems. Sensors 2014, 14, 23230–23247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamilton, W.; Hamilton, W. Elements of Quaternions; Longmans, Green, & Company: London, UK, 1866. [Google Scholar]
- Henderson, M.D. Euler Angles, Quaternions, and Transformation Matrics for Space Shuttle Analysis; Technical Report; McDonnell-Douglas Technical Services Co., Inc., Astronautics Div: Houston, TX, USA, 1977. [Google Scholar]
- Zeni, J.A.; Richards, J.G.; Higginson, J.S. Two simple methods for determining gait events during treadmill and overground walking using kinematic data. Gait Posture 2008, 27, 710–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiu, S.L.; Chou, L.S. Variability in inter-joint coordination during walking of elderly adults and its association with clinical balance measures. Clin. Biomech. 2013, 28, 454–458. [Google Scholar] [CrossRef]
- Quintero, D.; Villarreal, D.J.; Lambert, D.J.; Kapp, S.; Gregg, R.D. Continuous-Phase Control of a Powered Knee–Ankle Prosthesis: Amputee Experiments Across Speeds and Inclines. IEEE Trans. Robot. 2018, 34, 686–701. [Google Scholar] [CrossRef]
- José, J.V.; Saletan, E.J.; Mayer, M.E. Classical Dynamics: A Contemporary Approach. Am. J. Phys. 1999, 52, 66. [Google Scholar] [CrossRef]
- DIN EN ISO. Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out; Standard, International Organization for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [Green Version]
- McGraw, K.O.; Wong, S.P. “Forming inferences about some intraclass correlations coefficients”: Correction. Psychol. Methods 1996, 1, 390. [Google Scholar] [CrossRef]
- Soumaré, A.; Tavernier, B.; Alpérovitch, A.; Tzourio, C.; Elbaz, A. A cross-sectional and longitudinal study of the relationship between walking speed and cognitive function in community-dwelling elderly people. J. Gerontol. Ser. Biol. Sci. Med. Sci. 2009, 64, 1058–1065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Middleton, A.; Braun, C.H.; Lewek, M.D.; Fritz, S.L. Balance impairment limits ability to increase walking speed in individuals with chronic stroke. Disabil. Rehabil. 2017, 39, 497–502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grau-Pellicer, M.; Chamarro-Lusar, A.; Medina-Casanovas, J.; Serdà Ferrer, B.C. Walking speed as a predictor of community mobility and quality of life after stroke. Top. Stroke Rehabil. 2019, 26, 349–358. [Google Scholar] [CrossRef] [PubMed]
- Fulk, G.D.; He, Y.; Boyne, P.; Dunning, K. Predicting Home and Community Walking Activity Poststroke. Stroke 2017, 48, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Middleton, A.; Fritz, S.L.; Lusardi, M. Walking speed: The functional vital sign. J. Aging Phys. Act. 2015, 23, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Hollman, J.H.; Watkins, M.K.; Imhoff, A.C.; Braun, C.E.; Akervik, K.A.; Ness, D.K. A comparison of variability in spatiotemporal gait parameters between treadmill and overground walking conditions. Gait Posture 2016, 43, 204–209. [Google Scholar] [CrossRef]
- Balasubramanian, C.K.; Neptune, R.R.; Kautz, S.A. Variability in spatiotemporal step characteristics and its relationship to walking performance post-stroke. Gait Posture 2009, 29, 408–414. [Google Scholar] [CrossRef] [Green Version]
- Alexander, R.M. Walking and running: Legs and leg movements are subtly adapted to minimize the energy costs of locomotion. Am. Sci. 1984, 72, 348–354. [Google Scholar]
- O’Connor, S.M.; Xu, H.Z.; Kuo, A.D. Energetic cost of walking with increased step variability. Gait Posture 2012, 36, 102–107. [Google Scholar] [CrossRef] [Green Version]
- Olney, S.J.; Richards, C.L. Hemiparetic gait following stroke. Part I: Characteristics. Gait Posture 1996, 4, 136–148. [Google Scholar] [CrossRef]
- Combs, S.A.; Van Puymbroeck, M.; Altenburger, P.A.; Miller, K.K.; Dierks, T.A.; Schmid, A.A. Is walking faster or walking farther more important to persons with chronic stroke? Disabil. Rehabil. 2013, 35, 860–867. [Google Scholar] [CrossRef] [PubMed]
- Farris, D.; Hampton, A.; Lewek, M.D.; Sawicki, G.S. Revisiting the mechanics and energetics of walking in individuals with chronic hemiparesis following stroke: From individual limbs to lower limb joints. J. Neuroeng. Rehabil. 2015, 12, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roemmich, R.T.; Leech, K.A.; Gonzalez, A.J.; Bastian, A.J. Trading Symmetry for Energy Cost During Walking in Healthy Adults and Persons Poststroke. Neurorehabilit. Neural Repair 2019, 33, 602–613. [Google Scholar] [CrossRef]
- Ferraris, F. Procedure for effortless in-field calibration of three-axis rate gyros and accelerometers. Sens. Mater. 1995, 7, 311–330. [Google Scholar]

| Participant Number | Side of Paresis | Stroke Onset (y) | Sex | Age (y) | Height (cm) | Weight (kg) | CWS (m/s) | 6MWT Distance (m) |
|---|---|---|---|---|---|---|---|---|
| Healthy study participants | ||||||||
| H01 | - | - | F | 33 | 155 | 54.0 | 1.10 | 583 |
| H02 | - | - | F | 25 | 164 | 46.9 | 1.29 | 602 |
| H03 | - | - | F | 24 | 174 | 64.6 | 1.64 | 764 |
| H04 | - | - | M | 29 | 179 | 63.9 | 1.19 | 595 |
| H05 | - | - | F | 23 | 154 | 55.6 | 1.55 | 705 |
| H06 | - | - | F | 25 | 162 | 64.4 | 1.36 | 651 |
| H07 | - | - | M | 21 | 179 | 57.6 | 1.25 | 653 |
| H08 | - | - | M | 27 | 179 | 101.2 | 1.22 | 703 |
| H09 | - | - | M | 30 | 177 | 91.2 | 1.23 | 579 |
| H10 | - | - | M | 25 | 183 | 78.0 | 1.42 | 834 |
| Average | - | - | - | 26 ± 4 | 171 ± 11 | 68 ± 17 | 1.33 ± 0.17 | 667 ± 85 |
| Study participants with post-stroke hemiparesis | ||||||||
| S01 | Left | 8.08 | M | 61 | 180 | 72.6 | 0.97 | 495 |
| S02 | Right | 5.92 | M | 35 | 184 | 93.0 | 1.47 | 546 |
| S03 | Left | 7.92 | M | 78 | 181 | 100.8 | 1.00 | 314 |
| S04 | Right | 7.25 | M | 56 | 180 | 88.0 | 0.80 | 343 |
| S05 | Left | 6.08 | M | 62 | 176 | 99.8 | 1.27 | 516 |
| S06 | Right | 3.67 | M | 62 | 176 | 83.0 | 0.70 | 295 |
| S07 | Left | 1.75 | M | 67 | 175 | 87.2 | 0.83 | 303 |
| S08 | Right | 2.33 | M | 65 | 171 | 77.1 | 0.39 | 142 |
| Average | - | 5.4 ± 2.5 | - | 61 ± 12 | 178 ± 4.1 | 88 ± 10 | 0.93 ± 0.33 | 369 ± 138 |
| () | Healthy (N = 335) | Stroke-Paretic Limb (N = 126) | Stroke-Non-Paretic Limb (N = 129) |
|---|---|---|---|
| Below −50 ms | 0% | 0% | 7.0% |
| −50 to −30 ms | 0.3% | 4.0% | 3.1% |
| −30 to −10 ms | 25.1% | 21.4% | 24.0% |
| −10 to +10 ms | 45.4% | 28.6% | 24.0% |
| +10 to +30 ms | 28.7% | 32.5% | 29.5% |
| +30 to +50 ms | 0.6% | 10.3% | 6.2% |
| Above +50 ms | 0% | 3.2% | 6.2% |
| MAE: | 7 ms | 15 ms | 28 ms |
| RMSE: | 9 ms | 21 ms | 56 ms |
| ICC: | 0.986 | 0.996 | 0.971 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arumukhom Revi, D.; De Rossi, S.M.M.; Walsh, C.J.; Awad, L.N. Estimation of Walking Speed and Its Spatiotemporal Determinants Using a Single Inertial Sensor Worn on the Thigh: From Healthy to Hemiparetic Walking. Sensors 2021, 21, 6976. https://doi.org/10.3390/s21216976
Arumukhom Revi D, De Rossi SMM, Walsh CJ, Awad LN. Estimation of Walking Speed and Its Spatiotemporal Determinants Using a Single Inertial Sensor Worn on the Thigh: From Healthy to Hemiparetic Walking. Sensors. 2021; 21(21):6976. https://doi.org/10.3390/s21216976
Chicago/Turabian StyleArumukhom Revi, Dheepak, Stefano M. M. De Rossi, Conor J. Walsh, and Louis N. Awad. 2021. "Estimation of Walking Speed and Its Spatiotemporal Determinants Using a Single Inertial Sensor Worn on the Thigh: From Healthy to Hemiparetic Walking" Sensors 21, no. 21: 6976. https://doi.org/10.3390/s21216976
APA StyleArumukhom Revi, D., De Rossi, S. M. M., Walsh, C. J., & Awad, L. N. (2021). Estimation of Walking Speed and Its Spatiotemporal Determinants Using a Single Inertial Sensor Worn on the Thigh: From Healthy to Hemiparetic Walking. Sensors, 21(21), 6976. https://doi.org/10.3390/s21216976






