Sensor and Component Fault Detection and Diagnosis for Hydraulic Machinery Integrating LSTM Autoencoder Detector and Diagnostic Classifiers
Abstract
1. Introduction
Our Contribution
2. Related Work
Autoencoder Approaches for FDD in Hydraulic Machinery
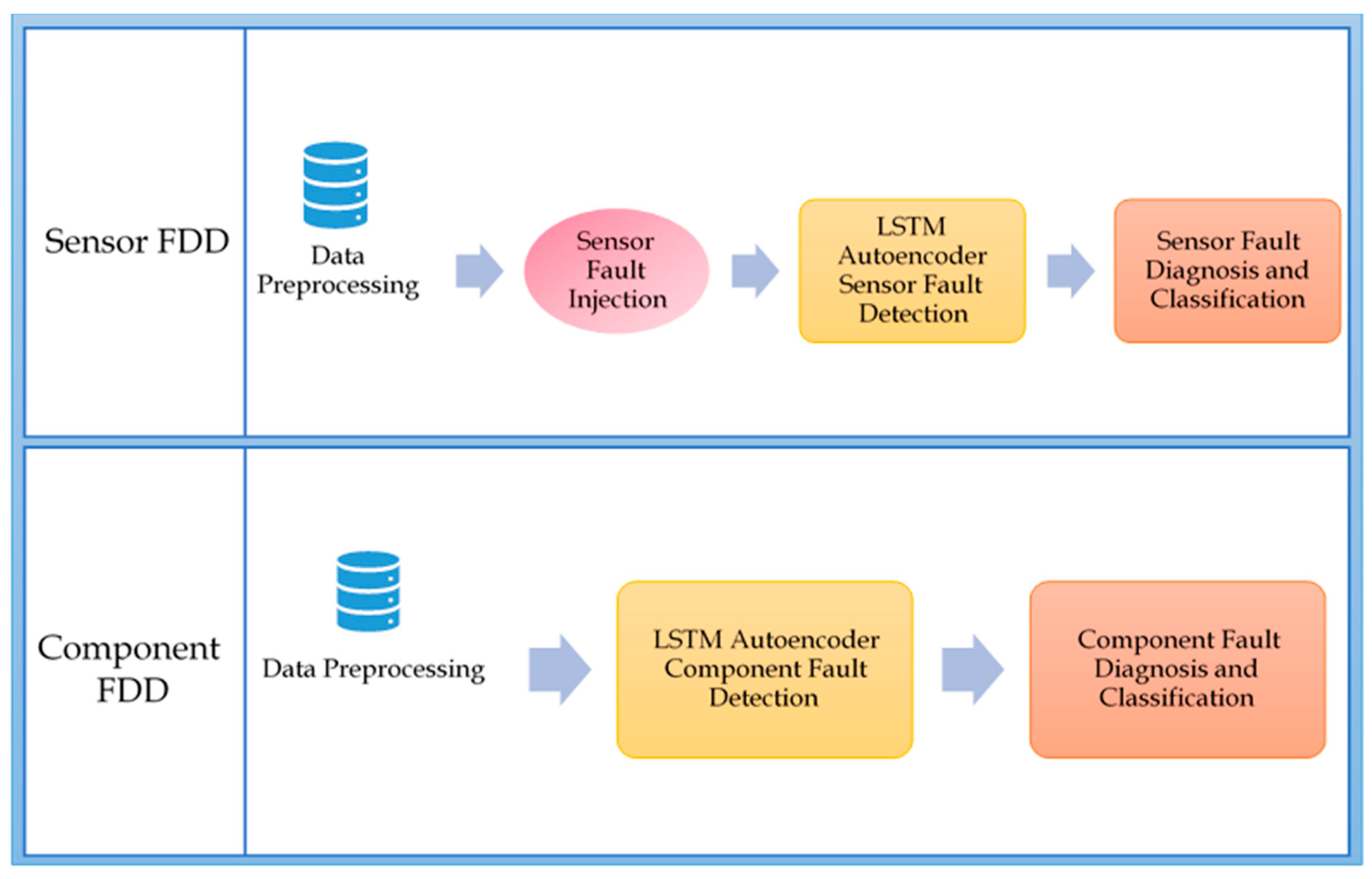
3. Hydraulic System FDD Overview
4. Analysis and Experimental Results
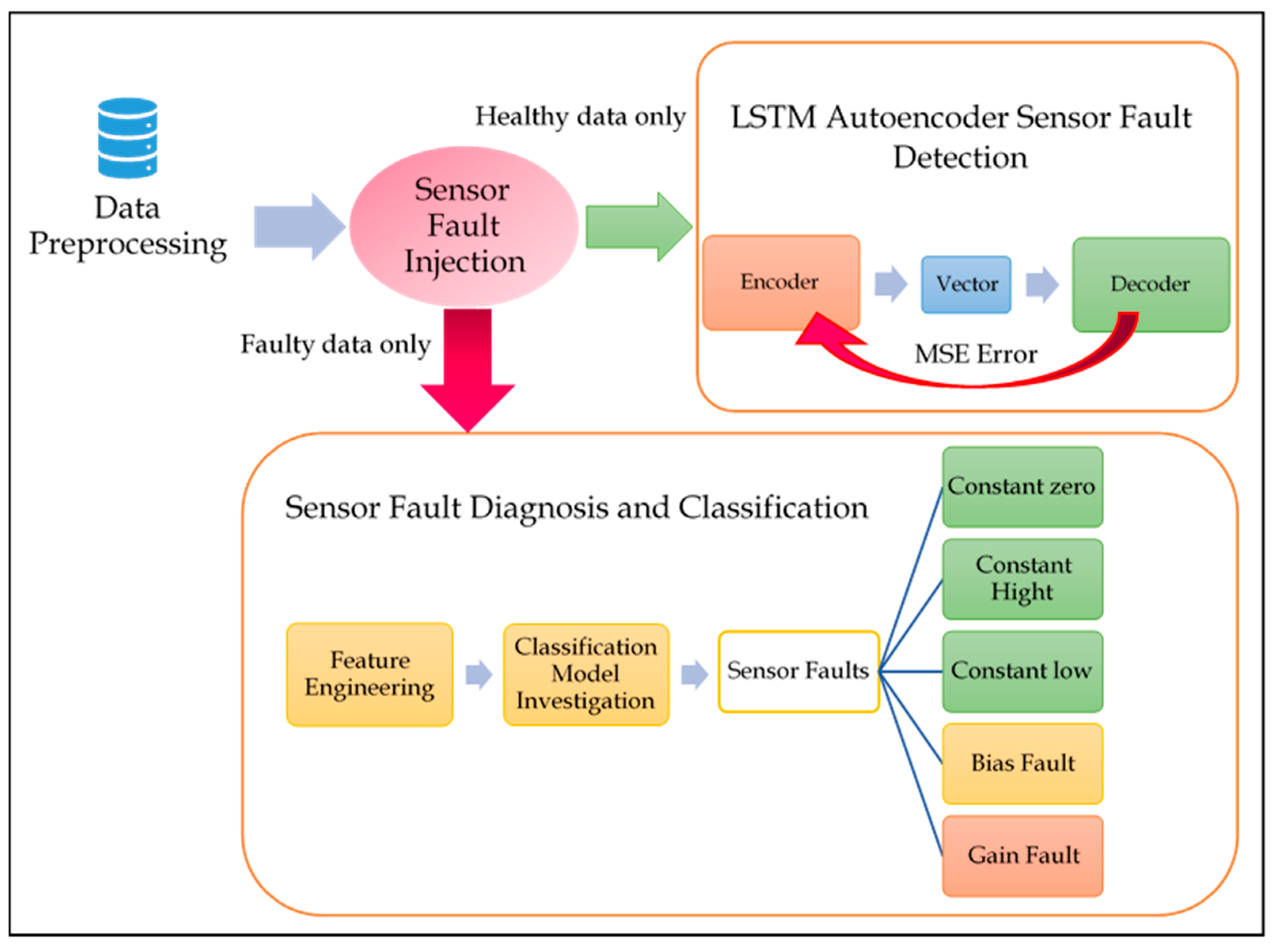
4.1. Experiment One: Sensor FDD Using the Joint LSTM Autoencoder and Classifier Approach
4.1.1. LSTM Autoencoder for Sensor Signal Reconstruction
4.1.2. Sensor Fault Diagnosis—Classification Schema
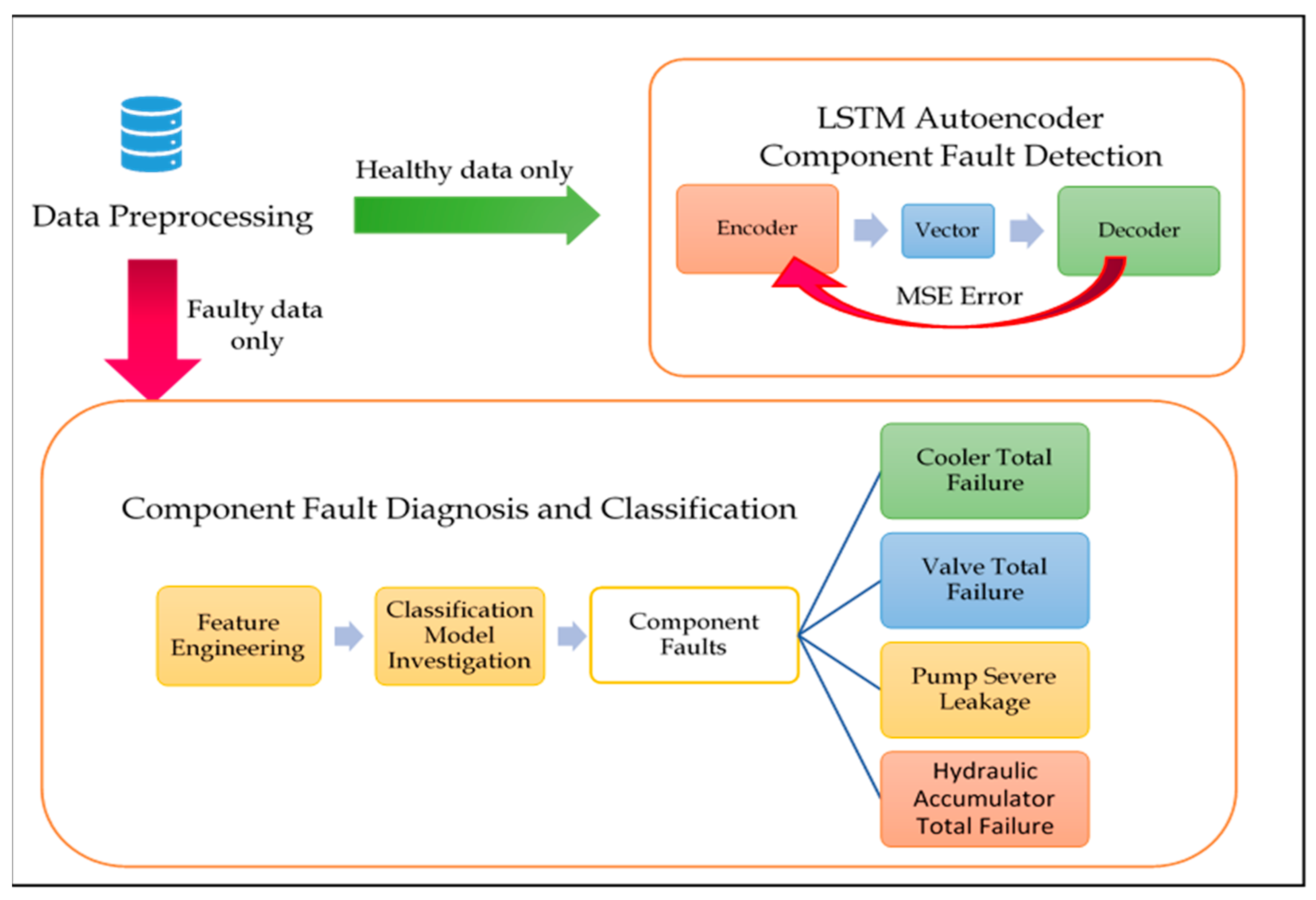
4.2. Experiment Two: Component FDD Using the Joint LSTM Autoencoder and Classifier Approach
4.2.1. Component Fault Detection—LSTM Autoencoder
4.2.2. Component Fault Diagnosis—Classification Schema
5. Conclusion and Discussion
- The proposed method is applied into two entirely different experiments, with different data pre-processing, acquisition, and structuring; different DL algorithmic designs; and above all for detecting two different fault types—sensor faults and component faults. The methods proposed in the literature only focused on one fault type, either component faults or sensor faults. However, it was rarely seen that any work showed comprehension in detecting or diagnosing different fault types at once.
- In the detection phase, using the LSTM autoencoder, some changes were made from the existing related work. The most important addition was using the sequence difference calculated by subtracting the Pearson’s autocorrelation from one. The detection results using the complement of Pearson’s autocorrelation comparing to the traditional signal difference measure applied in the state-of-the-art research was experimentally proved. In experiment one, to detect sensor faults, the detection accuracy using signal difference was observed as 62%. As compared to the detection accuracy, when applying our proposed measurement of signal difference, the detection accuracy was observed as 71%. Moreover, in experiment two for component fault detection, the accuracies observed using traditional signal difference and the proposed one were 69% and 71%, respectively. The results of the detection phase in the two conducted experiments proved to be the superior of the proposed signal difference measurement, as compared to the traditional subtraction of signals, to provide signal difference.
- Various feature engineering approaches were investigated and paired with numerous ML and DL methods in the diagnosis phase, to determine the most suitable feature engineering method, to classifiers of different functionality and design. Furthermore, this pairing gave the opportunity to see how each classifier reacted with different feature engineering methods of different procedure, which would help future researchers to select the best match pair or avoid the worst pair for both data structures, windows univariate, or no window multi-variate. For example, in experiment one when dealing with sensor faults in a sliding window data structure, it could be seen that the chosen time-domain features showed the highest diagnosis accuracy of almost all classifiers, i.e., LDA, KNN, CART, RF, and LSTM. The mean accuracy of all classifiers using PCA was computed to be a maximum of 82%, which was justified by the consistency PCA shows with all the classifiers regardless their functionality. However, time-domain extracted features showed extremely low diagnosis accuracies when applied to some classifiers, such as LR and NB, with the detection accuracies of only 24.25% and 48.21%, respectively. This explains why the time-domain extraction technique did not have the highest mean accuracy, even though it provided the highest accuracy to the majority of the supervised methods. On the other hand, in experiment two when the component faults were classified using multi-variate sensor readings without the application of sliding windows, FI showed the highest diagnosis accuracy for all ML classifiers, and PCA showed the highest diagnosis accuracy when combined with DL, such as CNN and LSTM.
- In the related work, the diagnosis phase was represented by some chosen type of classifiers combined with a chosen set of features, without any analysis or investigation with respect to other classifiers or features. In this work, after careful experimental observations and calculations, the appropriate features and their suitable classifier was used to represent the diagnosis phase for our algorithm. In experiment one (univariate sliding window structure), the diagnosis phase was chosen using the time-domain extracted features combined with either CART or LSTM classifiers, with diagnosis accuracies of 99.51% and 96.84%. However, in experiment two, when dealing with multi-variate features without the application of sliding windows, FI combined with almost all ML classifiers showed extremely high accuracies exceeding 98%. Thus, RF combined with FI was the best combo used to perform multi-variate diagnosis, especially when FI could be done implicitly during the RF training stage, based on the FI nature, which could help in reducing time and computational complexities.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Isermann, R.; Ballé, P. Trends in the application of model-based fault detection and diagnosis of technical processes. Control Eng. Pract. 1997, 5, 709–719. [Google Scholar] [CrossRef]
- Precup, R.-E.; Angelov, P.; Costa, B.S.J.; Sayed-Mouchaweh, M. An overview on fault diagnosis and nature-inspired optimal control of industrial process applications. Comput. Ind. 2015, 74, 75–94. [Google Scholar] [CrossRef]
- Kanev, S.K. Robust Fault-Tolerant Control; FEBO-DRUK: Enschede, Holland, 2004. [Google Scholar]
- Wang, P.; Guo, C. Based on the coal mine ’s essential safety management system of safety accident cause analysis. Am. J. Environ. Energy Power Res. 2013, 1, 62–68. [Google Scholar]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. Acm Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Ni, K.; Ramanathan, N.; Chehade, M.N.H.; Balzano, L.; Nair, S.; Zahedi, S.; Kohler, E.; Pottie, G.; Hansen, M.; Srivastava, M. Sensor network data fault types. ACM Trans. Sen. Netw. 2009, 5, 25:1–25:29. [Google Scholar] [CrossRef]
- Doddannavar, R.; Barnard, A.; Ganesh, J. Practical Hydraulic Systems: Operation and Troubleshooting for Engineers and Technicians; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- UCI Machine Learning Repository: Citation Policy. Available online: https://archive.ics.uci.edu/ml/citation_policy.html (accessed on 4 February 2020).
- Helwig, N.; Pignanelli, E.; Schütze, A. Condition monitoring of a complex hydraulic system using multivariate statistics. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, Pisa, Italy, 11–14 May 2015; pp. 210–215. [Google Scholar] [CrossRef]
- Schneider, T.; Helwig, N.; Schütze, A. Automatic feature extraction and selection for classification of cyclical time series data. TM Tech. Mess. 2017, 84, 198–206. [Google Scholar] [CrossRef]
- Learning Internal Representations by Error Propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MITP: Cambridge, MA, USA, 1987; pp. 318–362.
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Park, P.; Marco, P.D.; Shin, H.; Bang, J. Fault detection and diagnosis using combined autoencoder and long short-term memory network. Sensors (Basel) 2019, 19, 4612. [Google Scholar] [CrossRef]
- Chen, X. Tennessee Eastman Simulation Dataset. 2019. Available online: https://ieee-dataport.org/documents/tennessee-eastman-simulation-dataset (accessed on 4 February 2020).
- Minsky, M.; Papert, S. Perceptrons: An Introduction to Computational Geometry; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Lu, C.; Wang, Z.-Y.; Qin, W.-L.; Ma, J. Fault diagnosis of rotary machinery components using a stacked denoising autoencoder-based health state identification. Signal Process. 2017, 130, 377–388. [Google Scholar] [CrossRef]
- Pearson, K. LIII. on lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach Learn 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach Learn 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Wang, Y.; Wang, K. A deep learning approach for anomaly detection based on SAE and LSTM in mechanical equipment. Int. J. Adv. Manuf. Technol. 2019, 103, 499–510. [Google Scholar] [CrossRef]
- Altman, N.S. An introduction to kernel and nearest-neighbor nonparametric regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Chen, Z.; Deng, S.; Chen, X.; Li, C.; Sanchez, R.-V.; Qin, H. Deep neural networks-based rolling bearing fault diagnosis. Microelectron. Reliab. 2017, 75, 327–333. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. A Novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Junbo, T.; Weining, L.; Juneng, A.; Xueqian, W. Fault diagnosis method study in roller bearing based on wavelet transform and stacked auto-encoder. In Proceedings of the The 27th Chinese Control and Decision Conference (2015 CCDC), Qingdao, China, 23–25 May 2015; pp. 4608–4613. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Wang, F.; Zhao, H. An enhancement deep feature fusion method for rotating machinery fault diagnosis. Knowl. Based Syst. 2017, 119, 200–220. [Google Scholar] [CrossRef]
- Verma, N.K.; Gupta, V.K.; Sharma, M.; Sevakula, R.K. Intelligent condition based monitoring of rotating machines using sparse auto-encoders. In Proceedings of the 2013 IEEE Conference on Prognostics and Health Management (PHM), Gaithersburg, MD, USA, 24–27 June 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W. Multisensor feature fusion for bearing fault diagnosis using sparse autoencoder and deep belief network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Sun, W.; Shao, S.; Zhao, R.; Yan, R.; Zhang, X.; Chen, X. A sparse auto-encoder-based deep neural network approach for induction motor faults classification. Measurement 2016, 89, 171–178. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Lin, Y.; Li, X. A novel method for intelligent fault diagnosis of rolling bearings using ensemble deep auto-encoders. Mech. Syst. Signal Process. 2018, 102, 278–297. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, C.-H.; Huang, C.-J. Motor fault detection and feature extraction using RNN-based variational autoencoder. IEEE Access 2019, 7, 139086–139096. [Google Scholar] [CrossRef]
- Medsker, L.; Jain, L.C.; Jain, L.C. Recurrent Neural Networks: Design and Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar] [CrossRef]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Ann. Eugen. 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Welcome to the Case Western Reserve University Bearing Data Center Website|Bearing Data Center. Available online: https://csegroups.case.edu/bearingdatacenter/pages/welcome-case-western-reserve-university-bearing-data-center-website (accessed on 19 October 2020).
- NASA|Open Data|NASA Open Data Portal. Available online: https://nasa.github.io/data-nasa-gov-frontpage/ (accessed on 19 October 2020).
- Hui-jie, Z.; Ting, R.; Xin-qing, W.; You, Z.; Hu-sheng, F. Fault diagnosis of hydraulic pump based on stacked autoencoders. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015. [Google Scholar] [CrossRef]
- Mallak, A.; Fathi, M. Unsupervised feature selection using recursive K-means silhouette elimination (RkSE): A two-scenario case study for fault classification of high-dimensional sensor data. Preprints 2020. [Google Scholar] [CrossRef]
- Noshad, Z.; Javaid, N.; Saba, T.; Wadud, Z.; Saleem, M.Q.; Alzahrani, M.E.; Sheta, O.E. Fault detection in wireless sensor networks through the random forest classifier. Sensors 2019, 19, 1568. [Google Scholar] [CrossRef]
- Jan, S.U.; Lee, Y.; Shin, J.; Koo, I. Sensor fault classification based on support vector machine and statistical time-domain features. IEEE Access 2017, 5, 8682–8690. [Google Scholar] [CrossRef]
- Wang, Z.; Anand, D.M.; Moyne, J.; Tilbury, D.M. Improved sensor fault detection, isolation, and mitigation using multiple observers approach. Int. J. Syst. Sci. 2017, 5, 70–96. [Google Scholar] [CrossRef]
| Reference | Autoencoding Method | Mechanical Equipment | Fault Type/Purpose | Dataset |
|---|---|---|---|---|
| [13] | LSTM Autoencoder + LSTM Classifier | Chemical Reactor | Component Faults of Tennessee Eastman benchmark. | Tennessee Eastman benchmark [14]. |
| [20] | Stacked Autoencoder LSTM + KNN | Rotating equipment | Injected Component faults to a physical simulation | Data collected from Bently Nevada Rotor Kit RK3 to simulate rotating device. |
| [16] | Stacked Denoised Autoencoder | Rotary machinery | Component faults in a bearing test-rig | Data extracted from physical bearing test-rig. |
| [22] | Stacked deep autoencoders | Rolling bearings | Component faults in rolling bearings. | Gathered from UPS. |
| [23] | Another architecture deep autoencoder | Gearboxes and electrical locomotive roller bearings | Component faults in rolling bearings and electrical locomotive. | From a physical test rig. |
| [24] | Wavelet transform + stacked autoencoders | Roller bearing systems | Component faults in rolling bearings. | From case western reserve university (CWRU). |
| [25] | Another architecture of deep autoencoders | Rotating machinery | Component faults in rotating machinery | Physical rotor fault test, CWRU [33] and NASA datasets [34]. |
| [26] | Another architecture of sparse autoencoders | Motors and air compressors | Component faults in motors and air compressors | Actual air compressor and motor |
| [27] | SAE-DBN (sparse autoencoder + Deep Belief Networks) | Rotating machines | Component faults in rotating machinery | Extracted from an experimental system. |
| [28] | Another architecture of sparse autoencoders | Induction motors | Component faults in induction motors | Fault simulator. |
| [29] | Ensemble deep autoencoder | Rolling bearings | Component fault diagnosis in rolling bearings | CWRU [33]. |
| [35] | Another architecture of stacked autoencoders | Hydraulic pumps | Detect component faults in hydraulic pumps | Hydraulic pump of type axial piston pump (25MCY14-1B). |
| [30] | Autoencoding schema of RNN networks | Motors | Component fault detection and feature extraction in motors | Physical motor. |
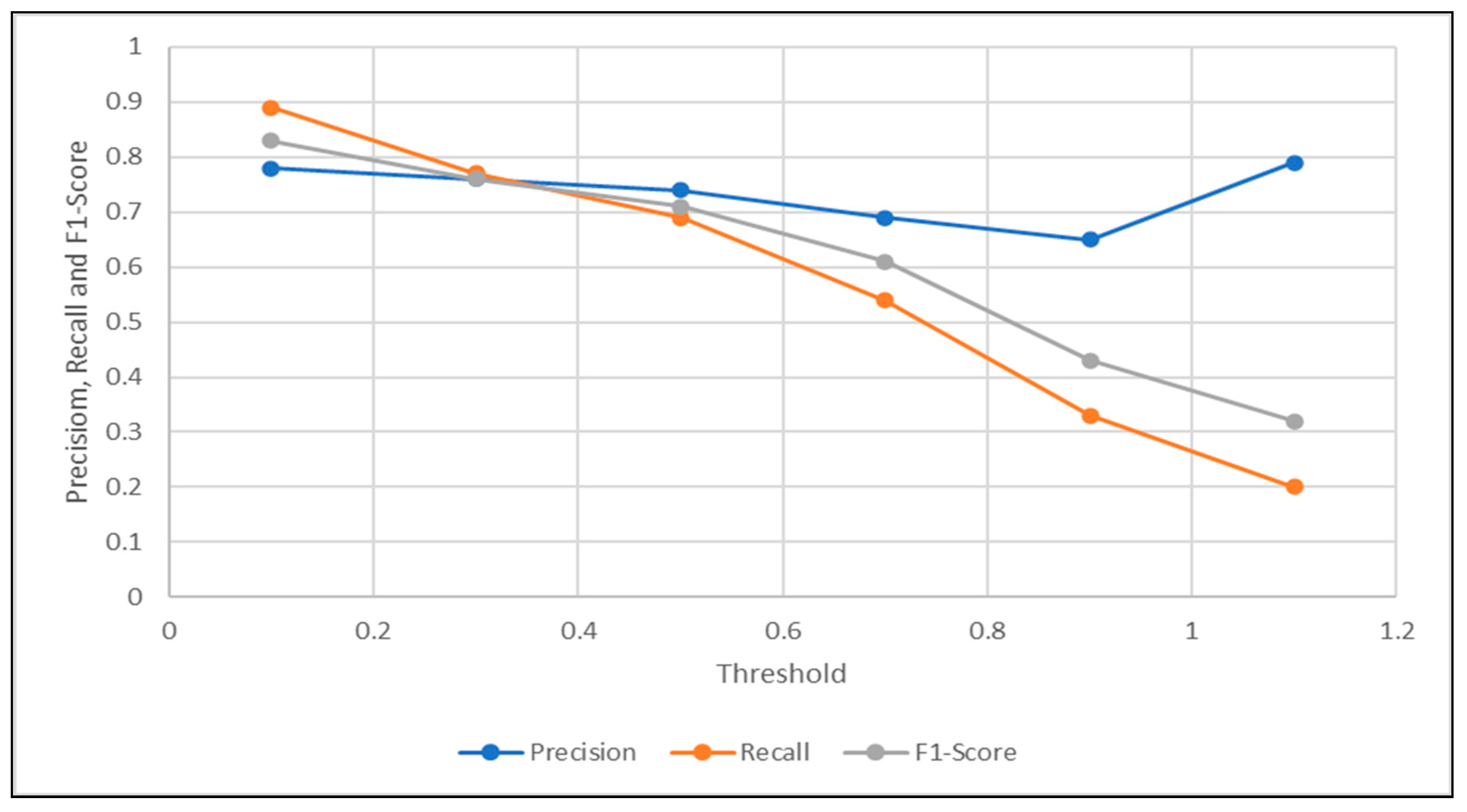
| Threshold | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | 1.1 |
|---|---|---|---|---|---|---|
| Precision | 0.78 | 0.76 | 0.74 | 0.69 | 0.65 | 0.79 |
| Recall | 0.89 | 0.77 | 0.69 | 0.54 | 0.33 | 0.2 |
| F1-Score | 0.83 | 0.76 | 0.71 | 0.61 | 0.43 | 0.32 |
| Accuracy | 0.71 | 0.62 | 0.55 | 0.44 | 0.32 | 0.32 |
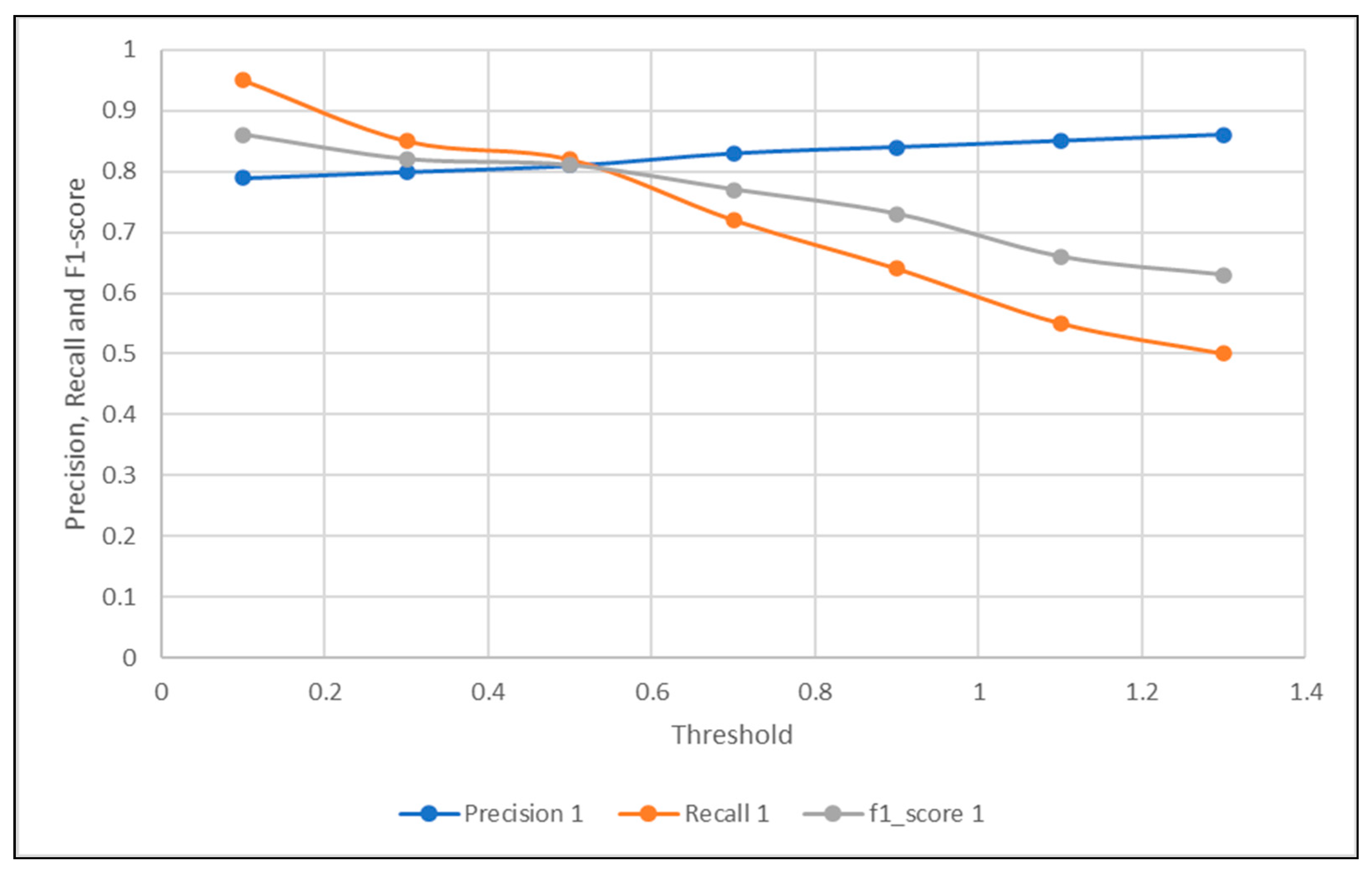
| Threshold | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | 1.1 | 1.3 |
|---|---|---|---|---|---|---|---|
| Precision | 0.79 | 0.8 | 0.81 | 0.83 | 0.84 | 0.85 | 0.86 |
| Recall | 0.95 | 0.85 | 0.82 | 0.72 | 0.64 | 0.55 | 0.5 |
| f1-score | 0.86 | 0.82 | 0.81 | 0.77 | 0.73 | 0.66 | 0.63 |
| Accuracy | 0.76 | 0.71 | 0.7 | 0.66 | 0.61 | 0.56 | 0.53 |
| Classifier | No Feature Selection | PCA | Time-Domain Features | FI | RkSE |
|---|---|---|---|---|---|
| LR | 0.6911 | 0.6356 | 0.2425 | 0.7019 | 0.6882 |
| LDA | 0.7053 | 0.6535 | 0.7859 | 0.7038 | 0.7068 |
| KNN | 0.8747 | 0.9128 | 0.9625 | 0.8758 | 0.8816 |
| CART | 0.8972 | 0.9818 | 0.9951 | 0.9126 | 0.9116 |
| NB | 0.7089 | 0.6919 | 0.4821 | 0.6930 | 0.6824 |
| SVM | 0.9125 | 0.8827 | 0.7298 | 0.9112 | 0.9142 |
| RF | 0.8189 | 0.8390 | 0.9402 | 0.8196 | 0.8193 |
| CNN | 0.8773 | 0.8486 | 0.7575 | 0.8385 | 0.8562 |
| LSTM | 0.8352 | 0.9568 | 0.9684 | 0.7278 | 0.7499 |
| Mean Feature Accuracy | 0.81 | 0.82 | 0.76 | 0.80 | 0.80 |
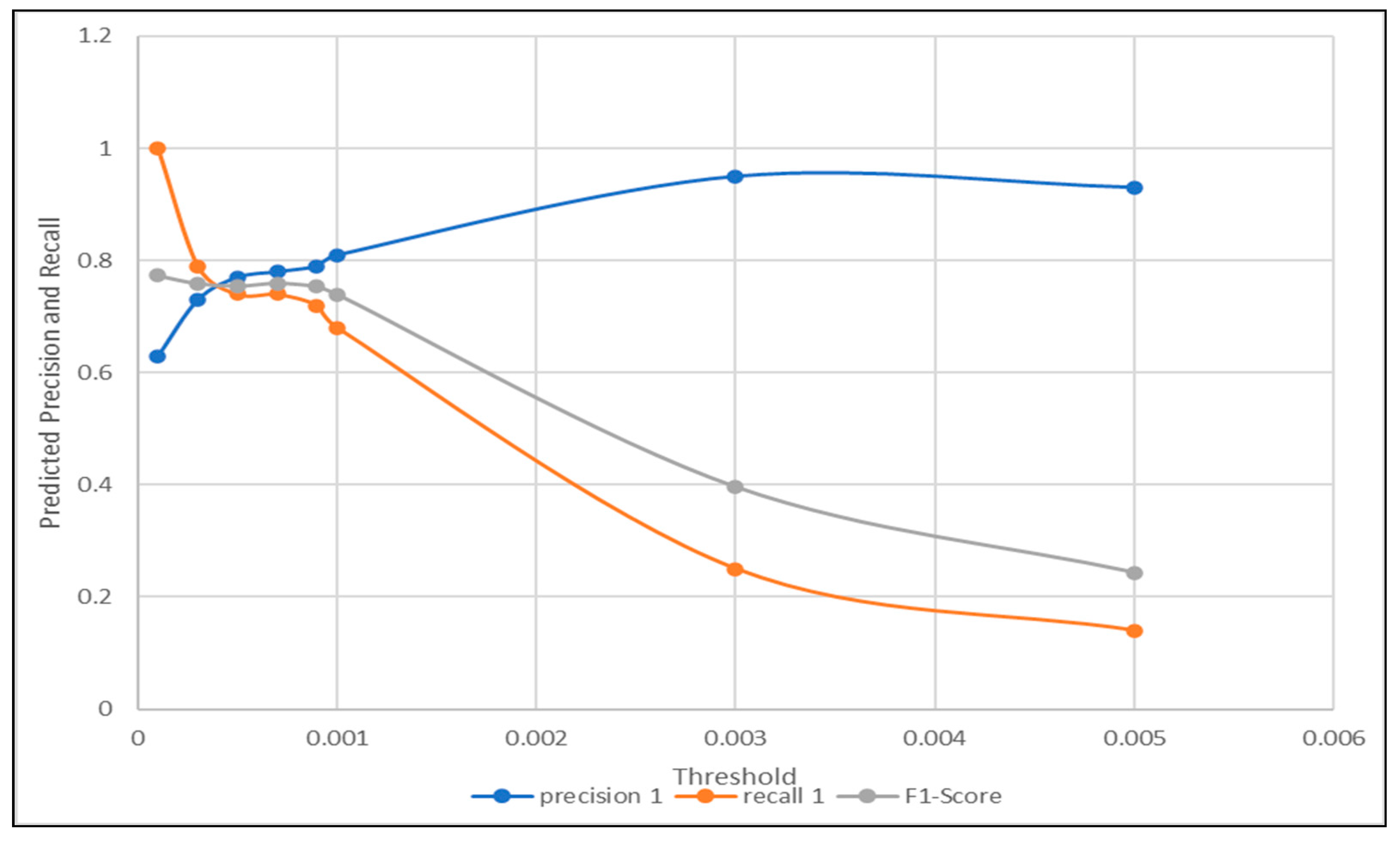
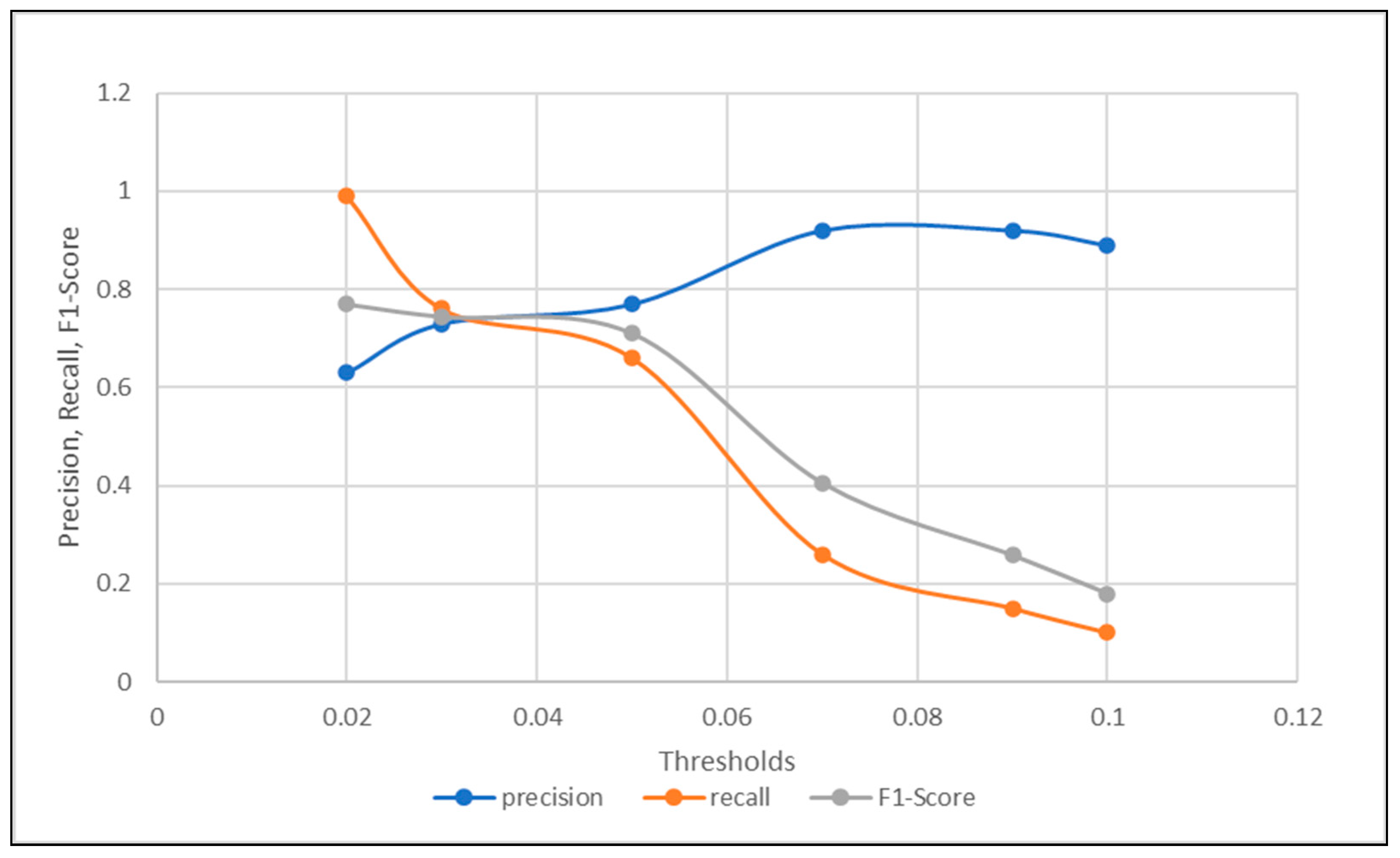
| Threshold | 0.0001 | 0.0003 | 0.0005 | 0.0007 | 0.0009 | 0.001 | 0.003 | 0.005 |
|---|---|---|---|---|---|---|---|---|
| precision | 0.63 | 0.73 | 0.77 | 0.78 | 0.79 | 0.81 | 0.95 | 0.93 |
| recall | 1 | 0.79 | 0.74 | 0.74 | 0.72 | 0.68 | 0.25 | 0.14 |
| F1-Score | 0.77 | 0.76 | 0.75 | 0.76 | 0.75 | 0.74 | 0.39 | 0.24 |
| Accuracy | 0.63 | 0.69 | 0.7 | 0.71 | 0.7 | 0.69 | 0.52 | 0.46 |
| Method Name | FI | PCA | RkSE | Time-Domain Features | No Feature Selection |
|---|---|---|---|---|---|
| LR | 0.9962 | 0.7300 | 0.7823 | 0.37599 | 0.6832 |
| LDA | 0.7634 | 0.7490 | 0.7528 | 0.370521 | 0.7031 |
| KNN | 0.9940 | 0.9229 | 0.9320 | 0.831458 | 0.8677 |
| CART | 0.9932 | 0.9435 | 0.9912 | 0.928594 | 0.6849 |
| NB | 0.9924 | 0.7510 | 0.7122 | 0.39526 | 0.9035 |
| SVM | 0.9859 | 0.9337 | 0.9310 | 0.833281 | 0.8139 |
| RF | 0.9930 | 0.9013 | 0.9910 | 0.871042 | 0.9042 |
| CNN | 0.7343 | 0.8427 | 0.7343 | 0.3971 | 0.7385 |
| LSTM | 0.7375 | 0.8770 | 0.7375 | 0.3981 | 0.73124 |
| MEAN ACCURACY | 0.910 | 0.850 | 0.840 | 0.600 | 0.781 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallak, A.; Fathi, M. Sensor and Component Fault Detection and Diagnosis for Hydraulic Machinery Integrating LSTM Autoencoder Detector and Diagnostic Classifiers. Sensors 2021, 21, 433. https://doi.org/10.3390/s21020433
Mallak A, Fathi M. Sensor and Component Fault Detection and Diagnosis for Hydraulic Machinery Integrating LSTM Autoencoder Detector and Diagnostic Classifiers. Sensors. 2021; 21(2):433. https://doi.org/10.3390/s21020433
Chicago/Turabian StyleMallak, Ahlam, and Madjid Fathi. 2021. "Sensor and Component Fault Detection and Diagnosis for Hydraulic Machinery Integrating LSTM Autoencoder Detector and Diagnostic Classifiers" Sensors 21, no. 2: 433. https://doi.org/10.3390/s21020433
APA StyleMallak, A., & Fathi, M. (2021). Sensor and Component Fault Detection and Diagnosis for Hydraulic Machinery Integrating LSTM Autoencoder Detector and Diagnostic Classifiers. Sensors, 21(2), 433. https://doi.org/10.3390/s21020433





