A Prosthetic Socket with Active Volume Compensation for Amputated Lower Limb
Abstract
1. Introduction
2. Materials and Methods
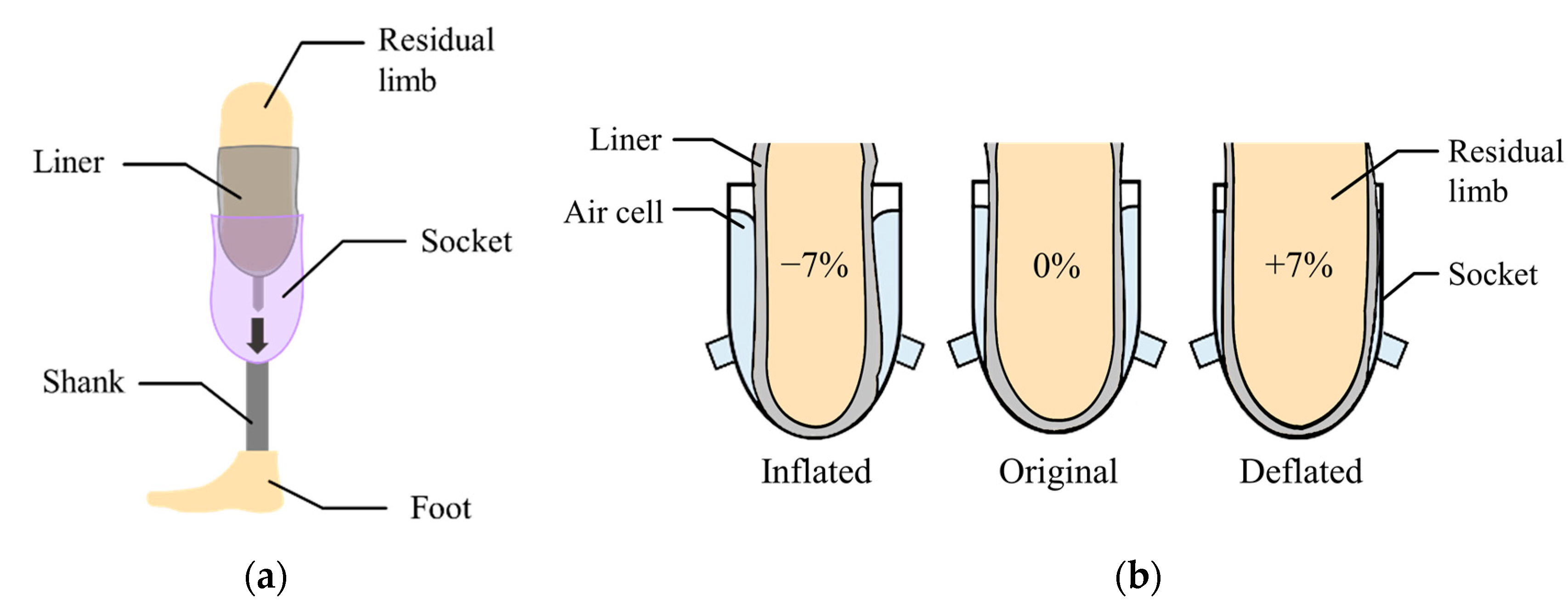
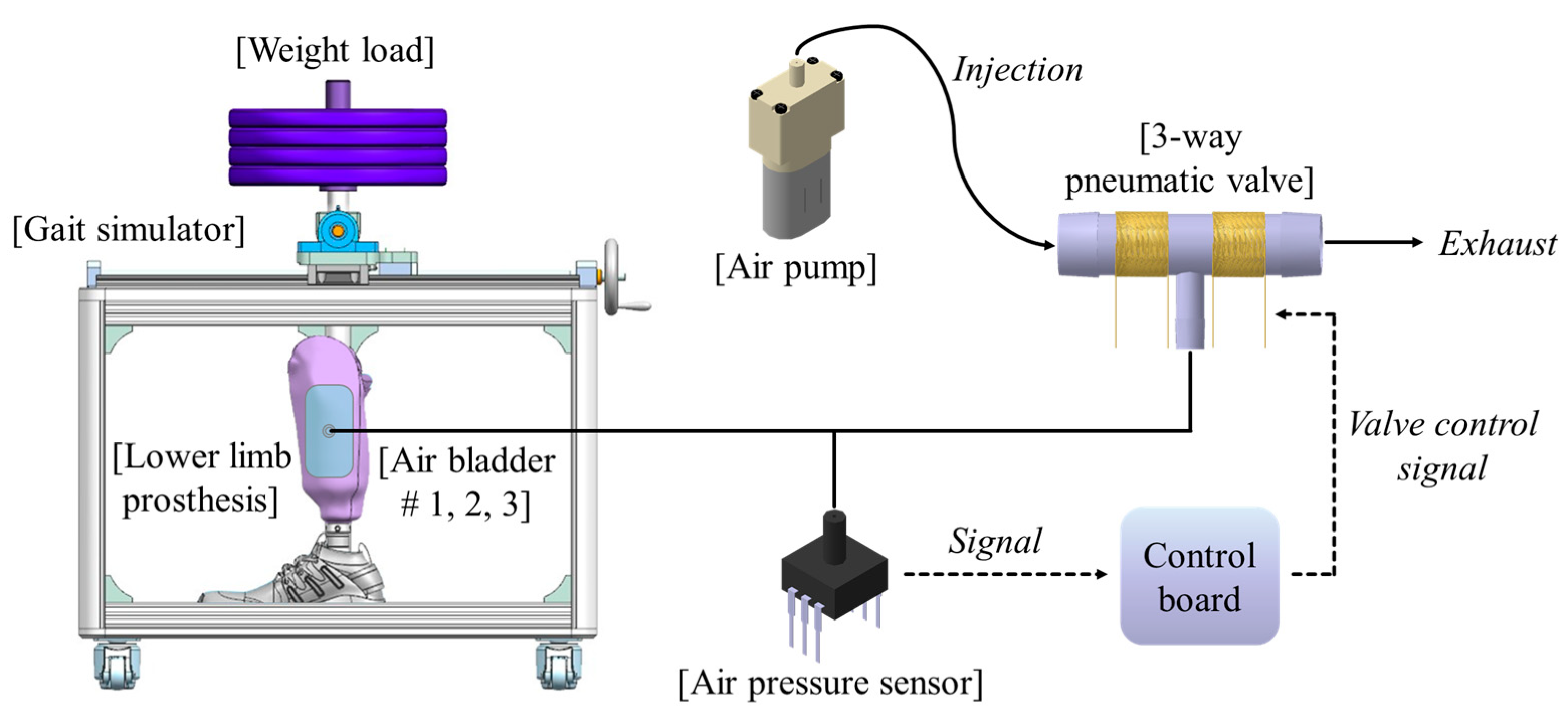
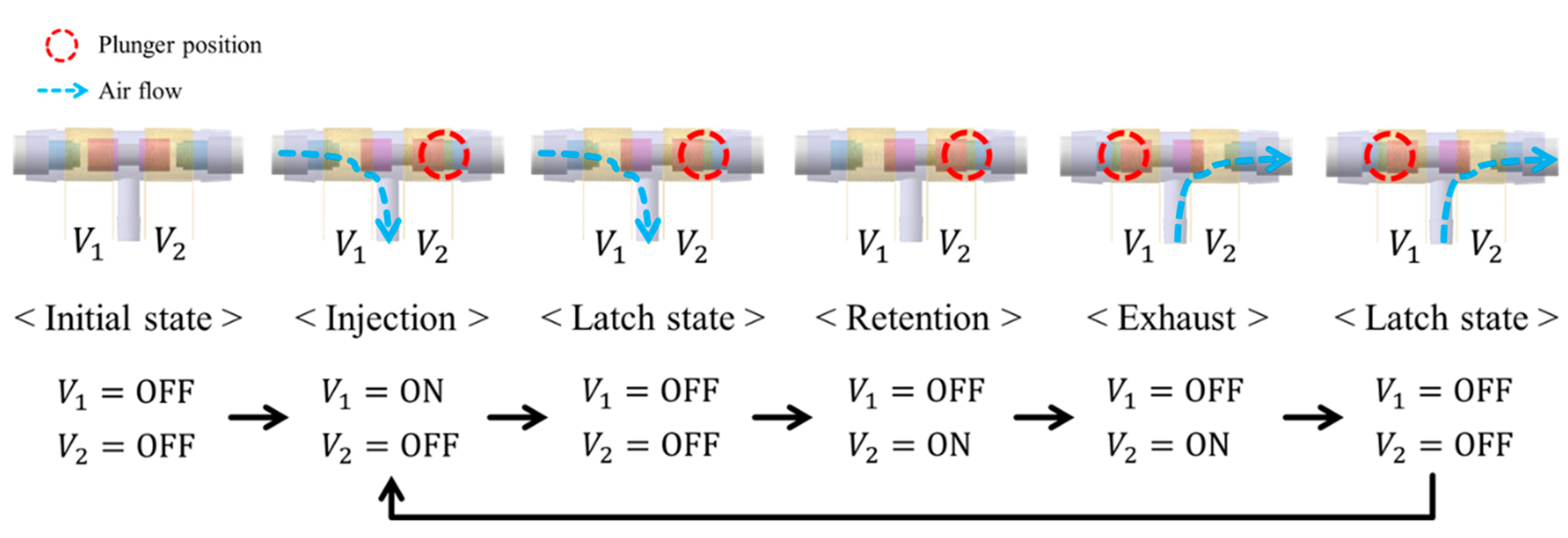
2.1. System Structure and Operation Principle
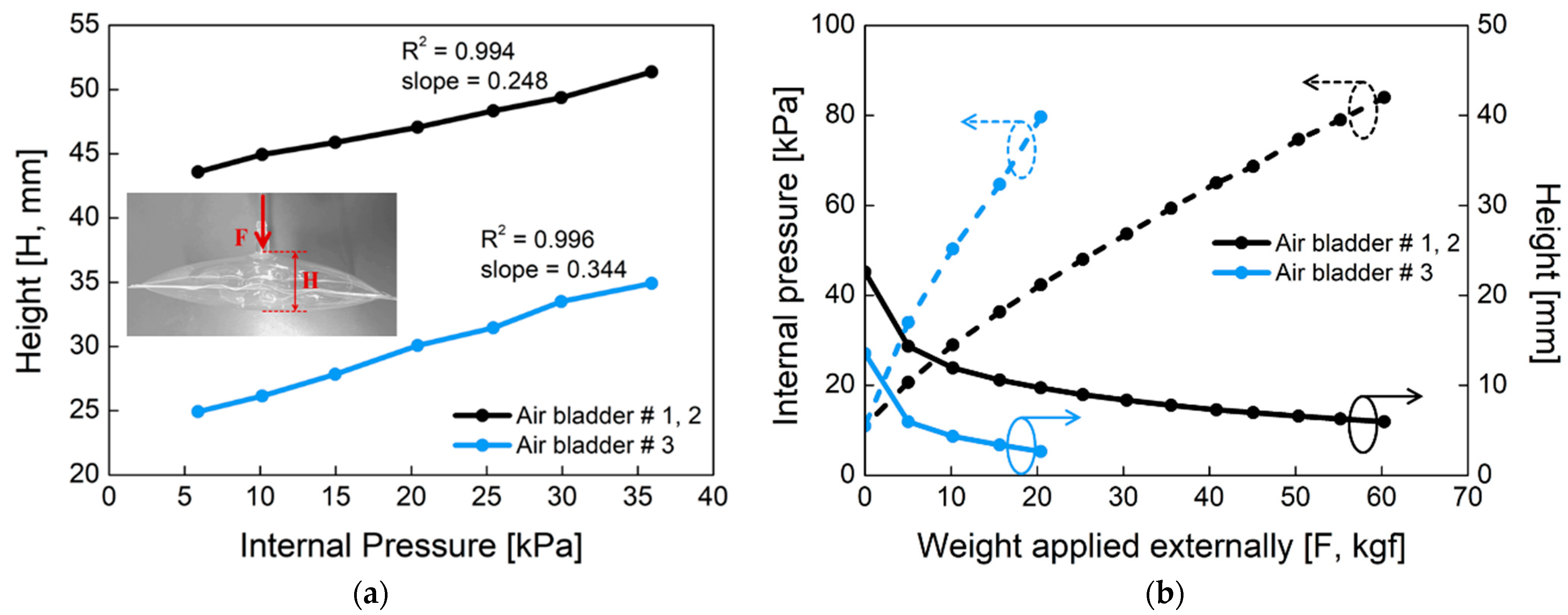
2.2. Characterization of an Inflatable Air Bladder
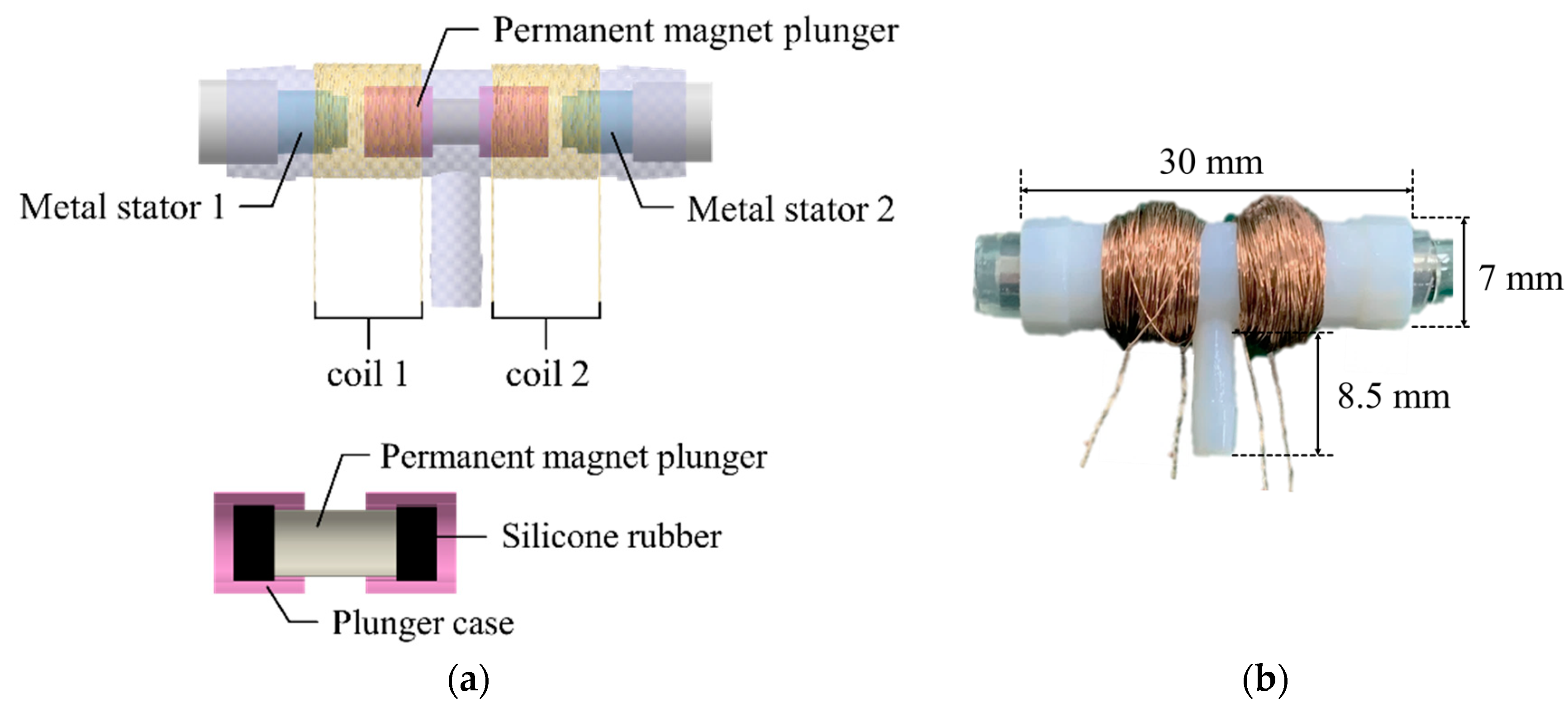
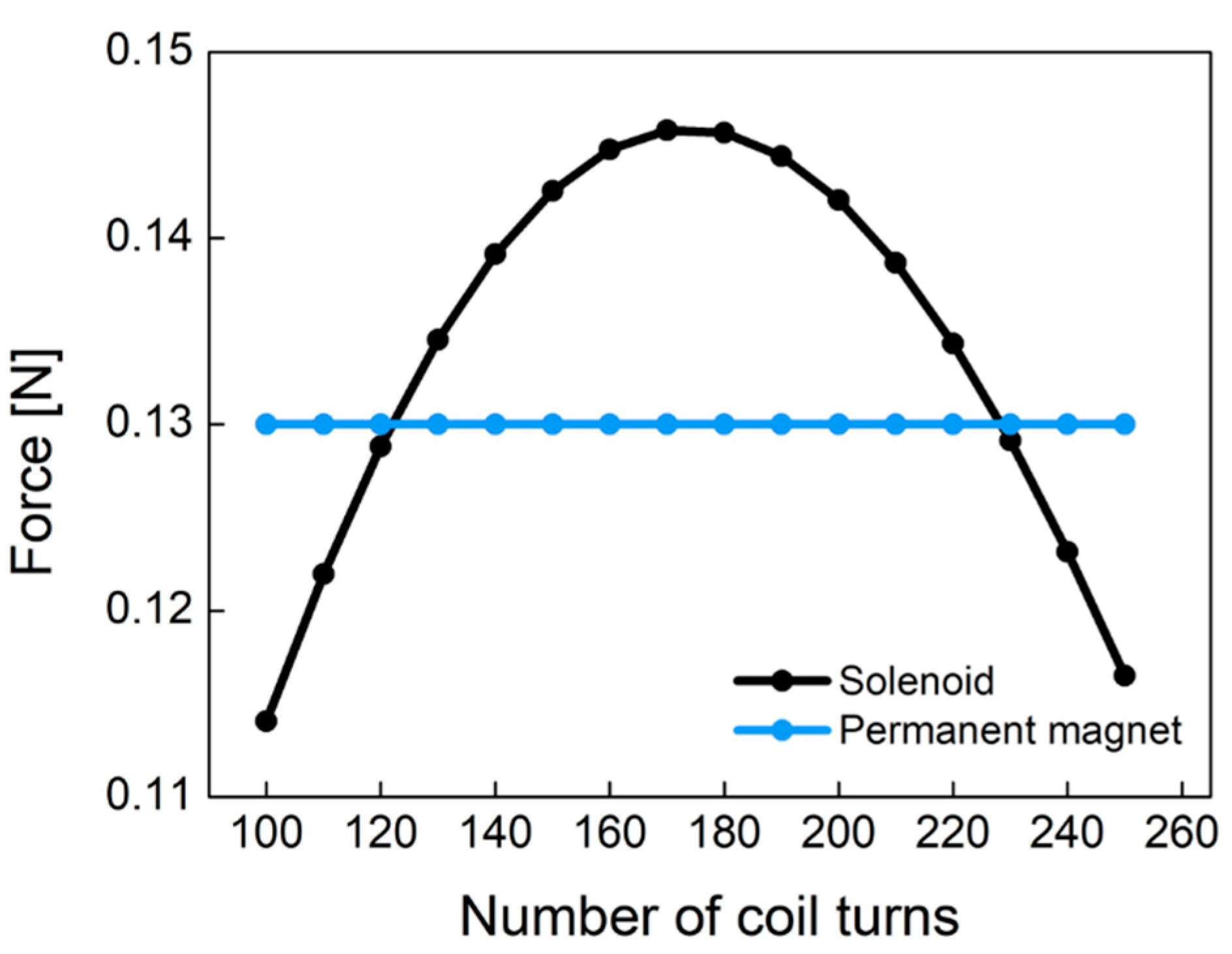
2.3. Design of the 3-Way Pneumatic Valve
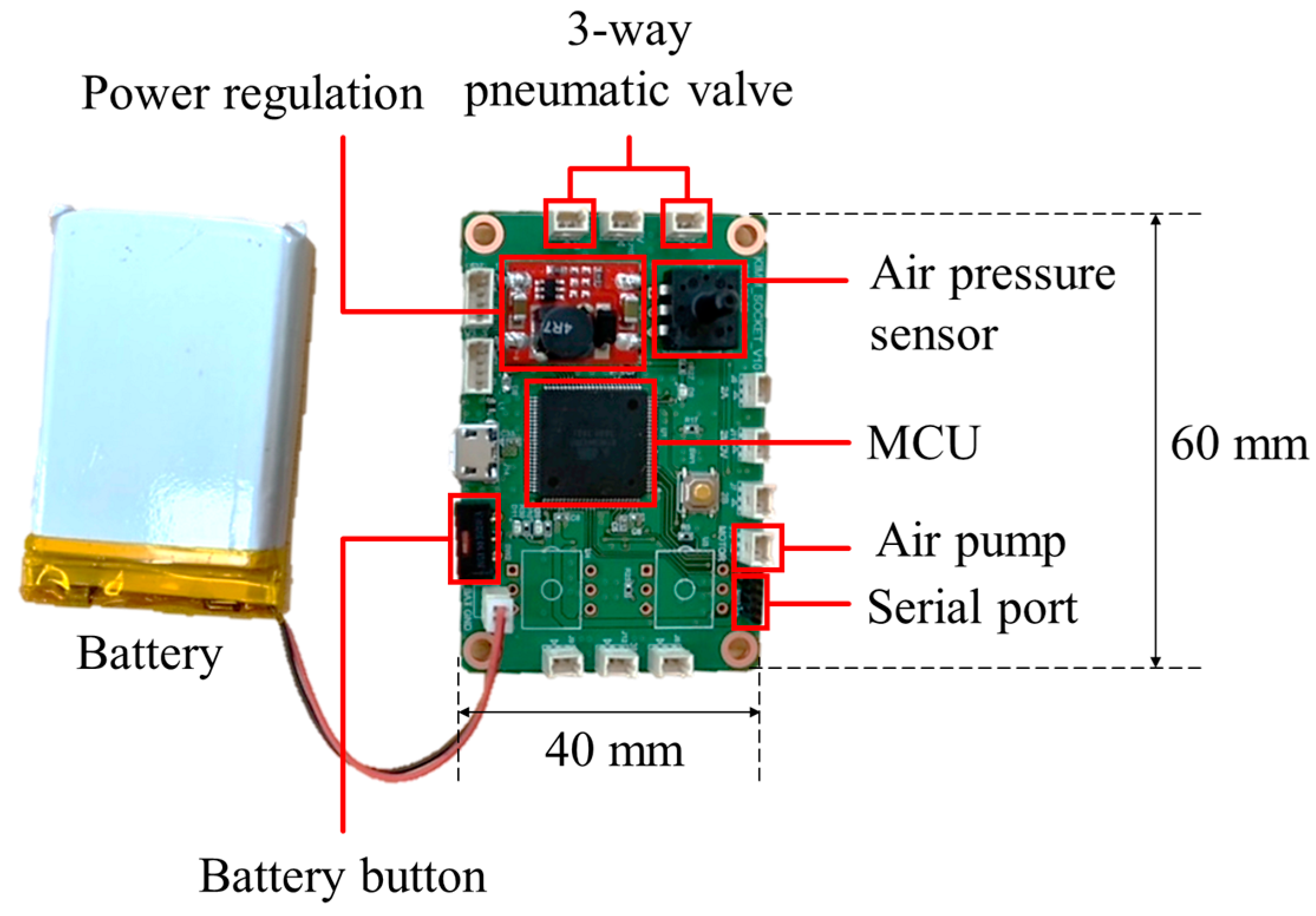
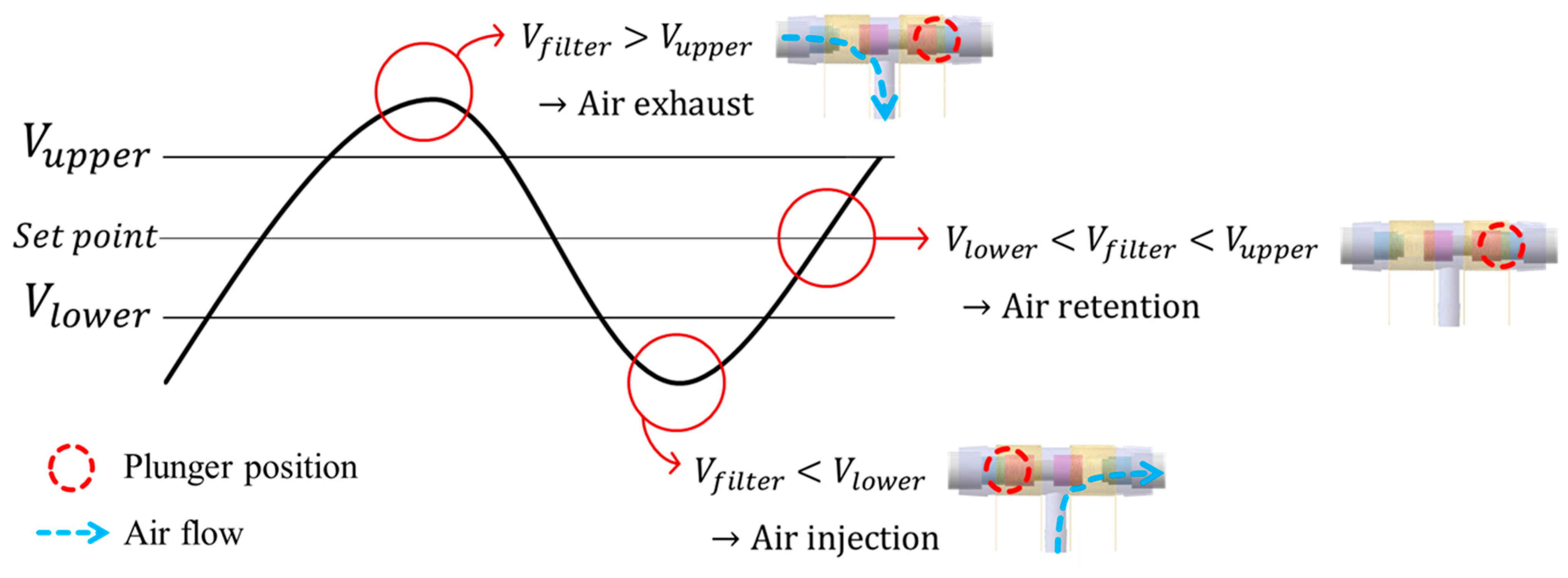
2.4. Closed-Loop Control Strategy
3. Results and Discussion
3.1. Leg Limb Model with Volume Changes
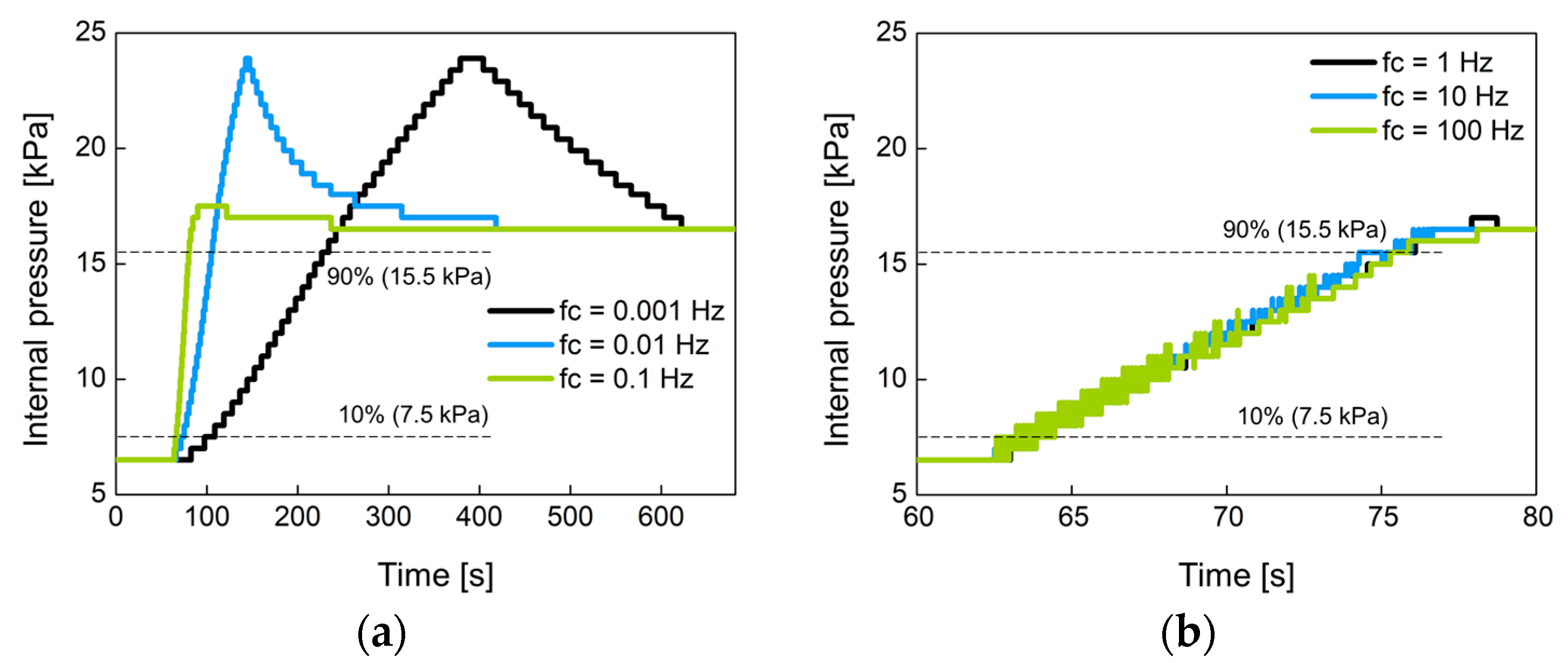
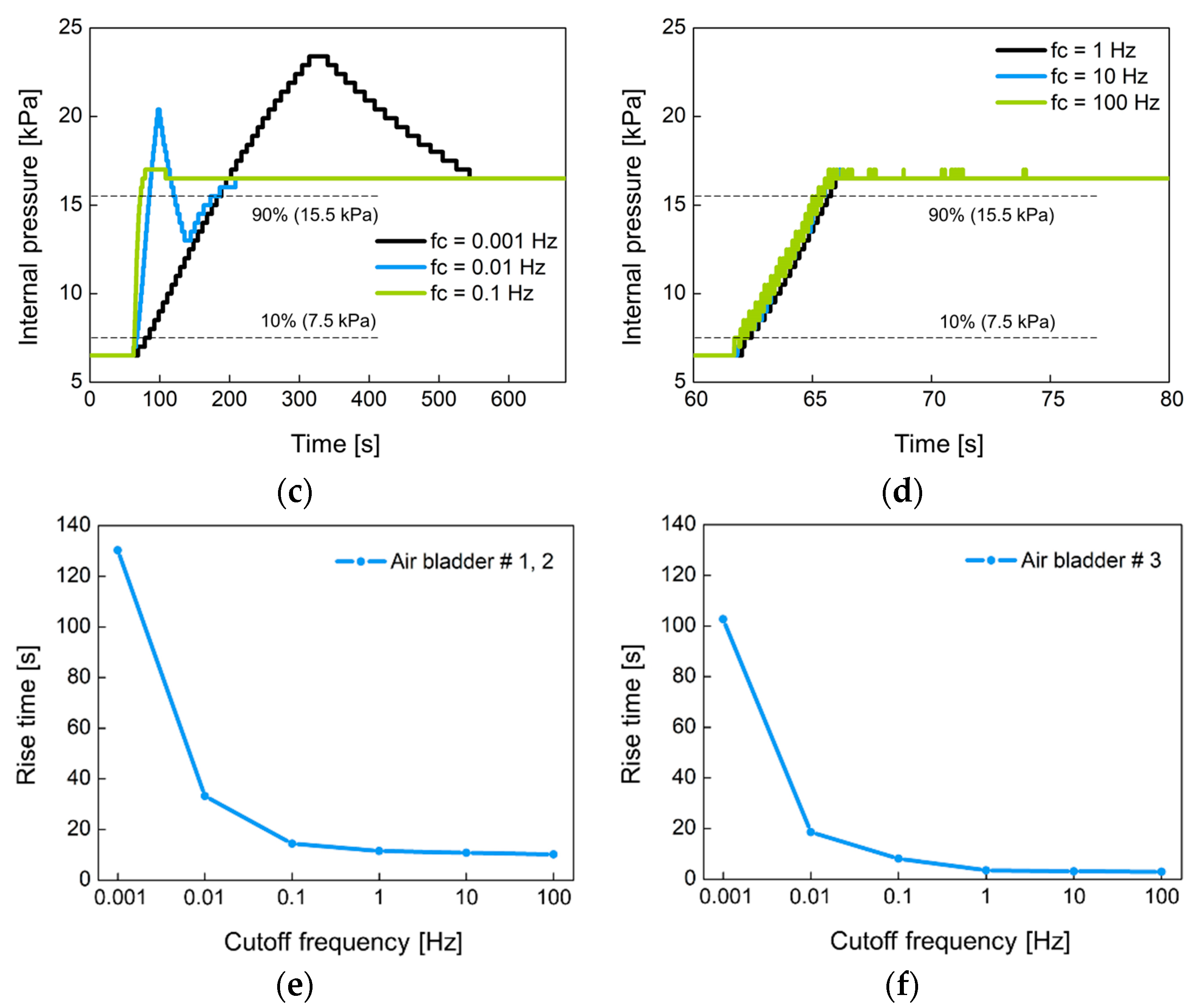
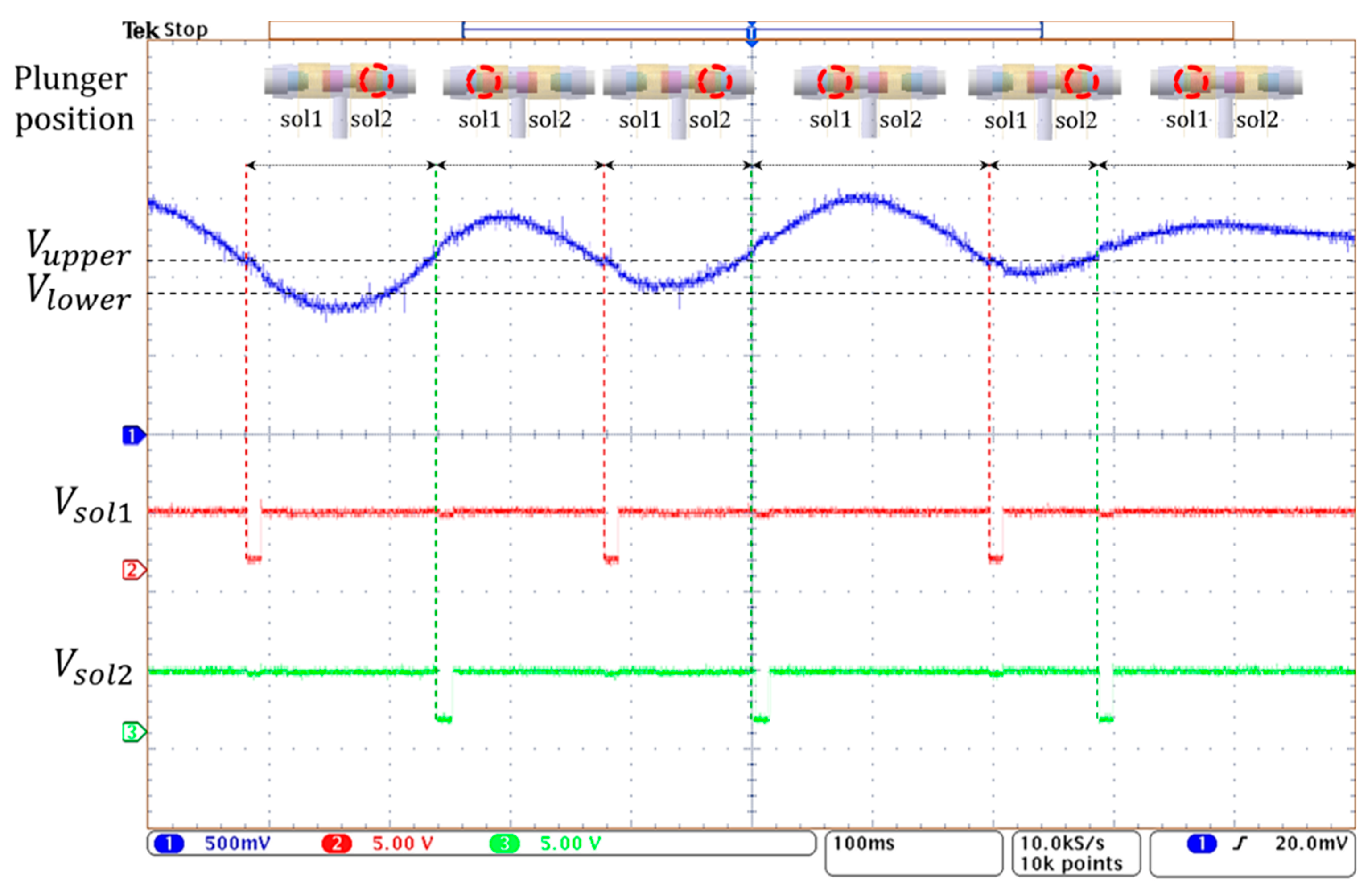
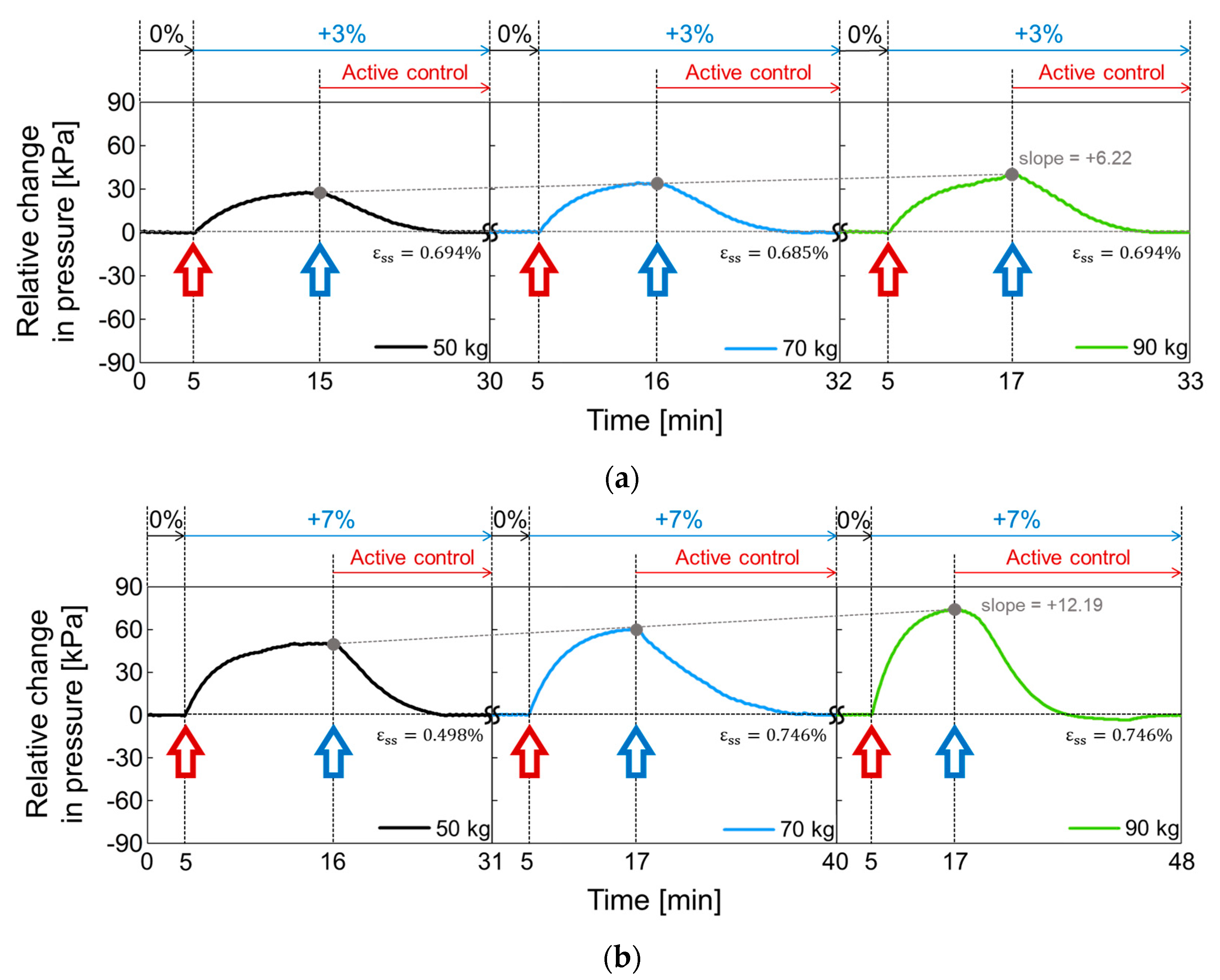
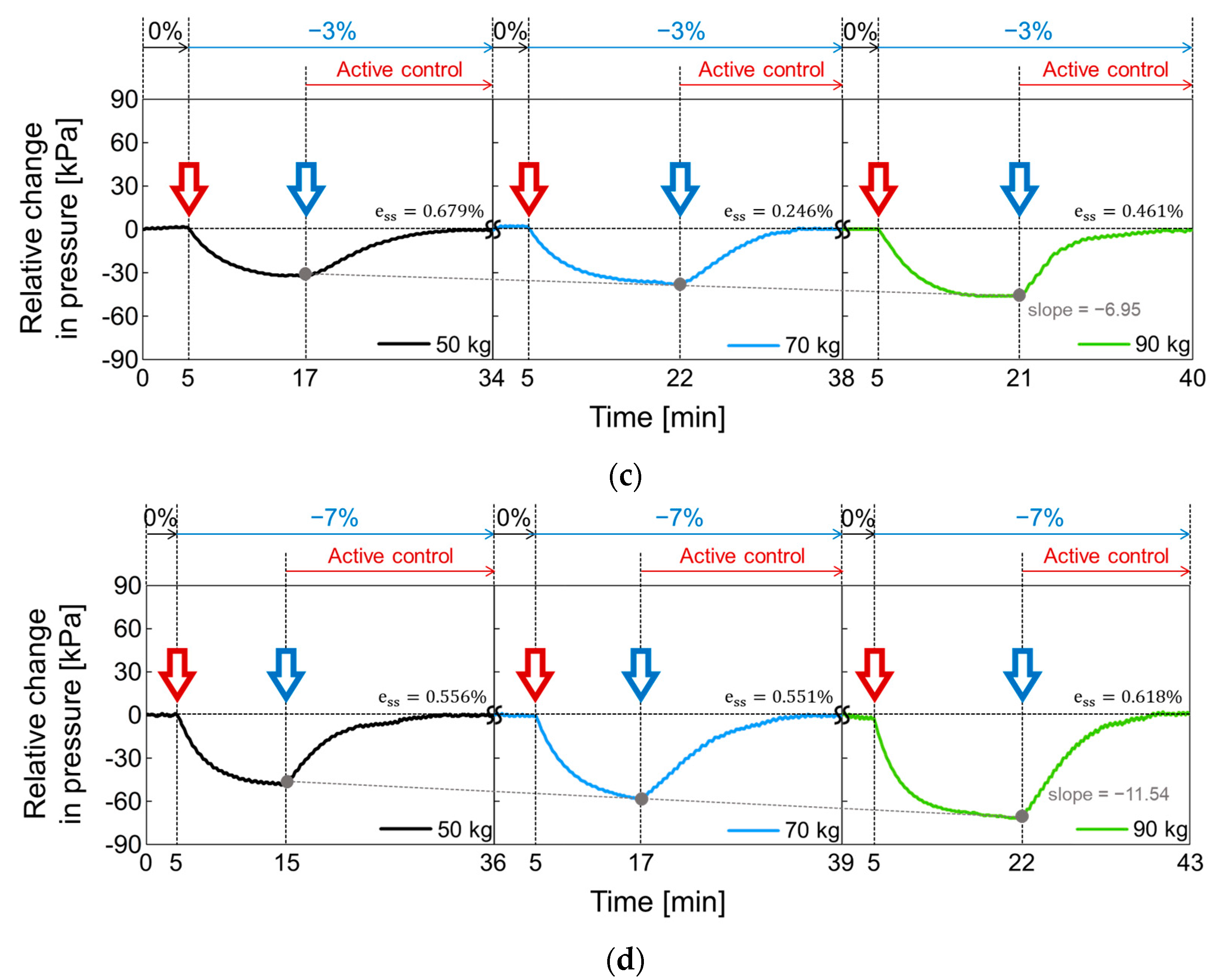
3.2. Performance of a Closed-Loop Control
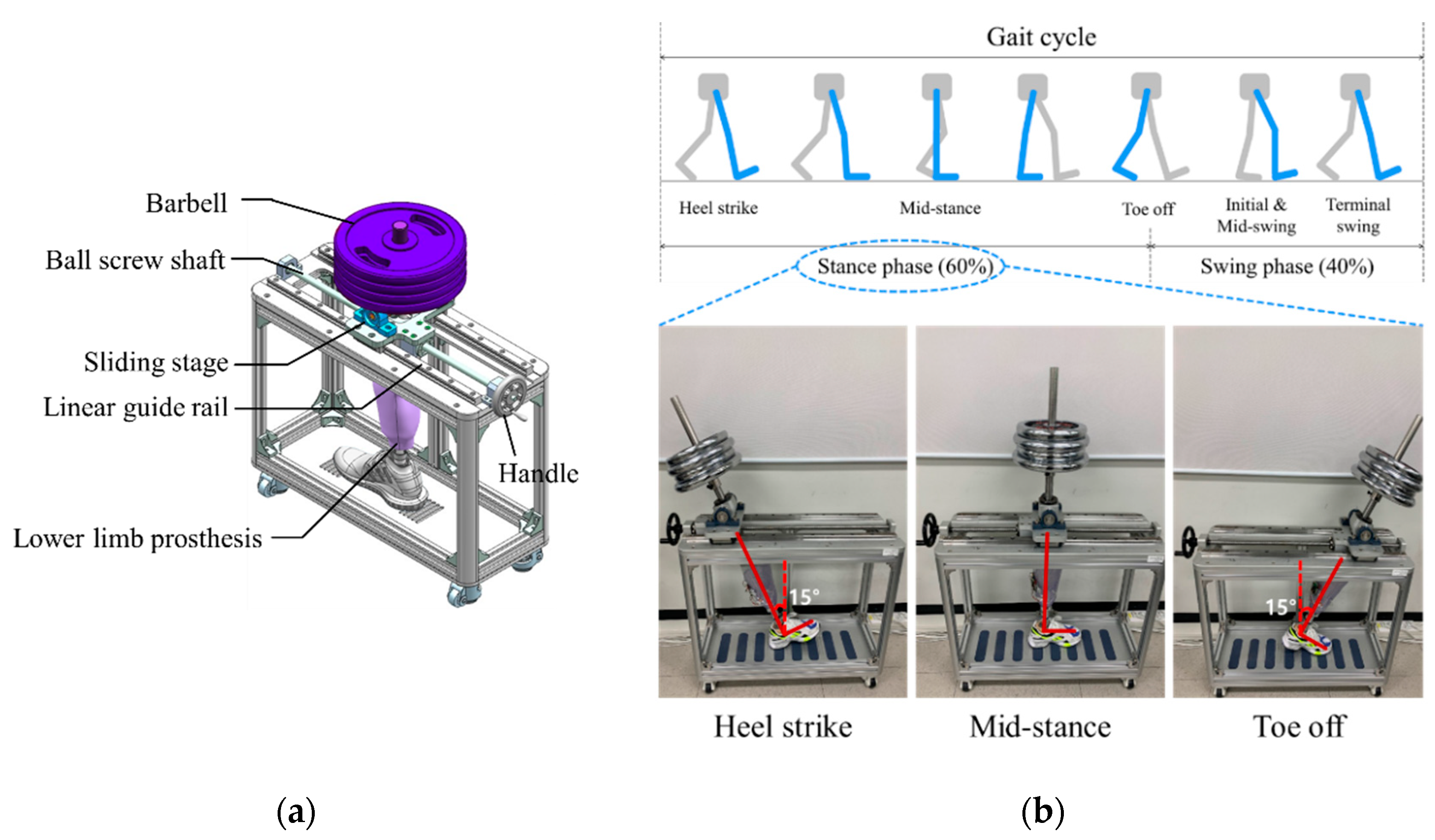
3.3. Verification of Closed-Loop Control during Gait Cycle
3.4. Active Volume Compensation during Gait Cycle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Berhe, G.; Kibrom, G.; Reiye, E. Patterns and causes of amputation in ayder referral hospital, mekelle, ethiopia: A three-year experience. Ethiop. J. Health Sci. 2018, 28, 31–36. [Google Scholar]
- Harding, J.L.; Andes, L.J.; Rolka, D.B.; Imperatore, G.; Gregg, E.W.; Li, Y.; Albright, A. National and State-Level Trends in Nontraumatic Lower-Extremity Amputation Among U.S. Medicare Beneficiaries with Diabetes, 2000–2017. Diabetes Care 2020, 43, 2453–2459. [Google Scholar] [CrossRef] [PubMed]
- Chadwell, A.; Diment, L.; Micó-Amigo, M.; Ramírez, D.Z.M.; Dickinson, A.S.; Granat, M.; Kenney, L.; Kheng, S.; Sobuh, M.; Ssekitoleko, R.; et al. Technology for monitoring everyday prosthesis use: A systematic review. J. Neuroeng. Rehabil. 2020, 17, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Haleem, S.; Yousaf, S.; Hamid, T.; Nagappa, S.; Parker, M.J. Characteristics and outcomes of hip fractures in lower limb amputees. Injury 2020. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Wong, D.W.-C.; Zhang, M.; Leung, A.K.L. Analysis of compression/release stabilized transfemoral prosthetic socket by finite element modelling method. Med. Eng. Phys. 2020, 83, 123–129. [Google Scholar] [CrossRef] [PubMed]
- Paterno, L.; Ibrahimi, M.; Gruppioni, E.; Menciassi, A.; Ricotti, L. Sockets for Limb Prostheses: A Review of Existing Technologies and Open Challenges. IEEE Trans. Biomed. Eng. 2018, 65, 1996–2010. [Google Scholar] [CrossRef]
- Montgomery, J.T.; Vaughan, M.R.; Crawford, R.H. Design of an actively actuated prosthetic socket. Rapid Prototyp. J. 2010, 16, 194–201. [Google Scholar] [CrossRef]
- Youngblood, R.T.; Hafner, B.J.; Allyn, K.; Cagle, J.C.; Hinrichs, P.; Redd, C.; Vamos, A.C.; Ciol, M.A.; Bean, N.; Sanders, J.E. Effects of activity intensity, time, and intermittent doffing on daily limb fluid volume change in people with transtibial am-putation. Prosthet. Orthot. Int. 2019, 43, 28–38. [Google Scholar] [CrossRef]
- Weathersby, E.J.; Gurrey, C.J.; McLean, J.B.; Sanders, B.N.; Larsen, B.G.; Carter, R.V.; Garbini, J.L.; Sanders, J.E. Thin Magnetically Permeable Targets for Inductive Sensing: Application to Limb Prosthetics. Sensors 2019, 19, 4041. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Abu Osman, N.A.; Lúvíksdóttir, Á.G.; Eshraghi, A.; Kamyab, M.; Abas, W.A.B.W. A new approach for the pistoning measurement in transtibial prosthesis. Prosthet. Orthot. Int. 2011, 35, 360–364. [Google Scholar] [CrossRef]
- Henrikson, K.M.; Weathersby, E.J.; Larsen, B.G.; Cagle, J.C.; McLean, J.B.; Sanders, J.E. An Inductive Sensing System to Measure In-Socket Residual Limb Displacements for People Using Lower-Limb Prostheses. Sensors 2018, 18, 3840. [Google Scholar] [CrossRef] [PubMed]
- Dakhil, N.; Evin, M.; Llari, M.; Mo, F.; Thefenne, L.; Liu, T.; Behr, M. Is skin pressure a relevant factor for socket assessment in patients with lower limb amputation? Technol. Health Care 2019, 27, 669–677. [Google Scholar] [CrossRef] [PubMed]
- El-Sayed, A.M.; Hamzaid, N.A.; Abu Osman, N.A. Piezoelectric Bimorphs’ Characteristics as In-Socket Sensors for Transfemoral Amputees. Sensors 2014, 14, 23724–23741. [Google Scholar] [CrossRef] [PubMed]
- Al-Fakih, E.A.; Osman, N.A.; Adikan, F.R.M. Techniques for Interface Stress Measurements within Prosthetic Sockets of Transtibial Amputees: A Revies of the Past 50 Years of Research. Sensors 2016, 16, 1119. [Google Scholar] [CrossRef]
- Jasni, F.; Hamzaid, N.A.; Muthalif, A.G.; Zakaria, Z.; Shasmin, H.N.; Ng, S.C. In-Socket Sensory System for Transfemoral Amputees Using Piezoelectric Sensors: An Efficacy Study. IEEE/ASME Trans. Mechatron. 2016, 21, 2466–2476. [Google Scholar] [CrossRef]
- Carrigan, W.; Nothnagle, C.; Savant, P.; Gao, F.; Wijesundara, M.B.J. Pneumatic Actuator Inserts for Interface Pressure Mapping and Fit Improvement in Lower Extremity Prosthetics. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016. [Google Scholar]
- Pirouzi, G.; Abu Osman, N.A.; Oshkour, A.A.; Ali, S.; Gholizadeh, H.; Abas, W.A.B.W. Development of an Air Pneumatic Suspension System for Transtibial Prostheses. Sensors 2014, 14, 16754–16765. [Google Scholar] [CrossRef]
- Weathersby, E.J.; Garbini, J.L.; Larsen, B.G.; McLean, J.B.; Vamos, A.C.; Sanders, J. Automatic Control of Prosthetic Socket Size for People with Transtibial Amputation: Implementation and Evaluation. IEEE Trans. Biomed. Eng. 2021, 68, 36–46. [Google Scholar] [CrossRef]
- Kharb, A.; Saini, V.; Jain, Y.K.; Dhiman, S. A review of gait cycle and its parameters. Int. J. Comput. Eng. Manag. 2011, 13, 78–83. [Google Scholar]
- Zahradka, N.; Behboodi, A.; Wright, H.; Bodt, B.; Lee, S.C.K. Evaluation of Gait Phase Detection Delay Compensation Strategies to Control a Gyroscope-Controlled Functional Electrical Stimulation System During Walking. Sensors 2019, 19, 2471. [Google Scholar] [CrossRef]
- Aqueveque, P.; Germany, E.; Osorio, R.; Pastene, F. Gait Segmentation Method Using a Plantar Pressure Measurement System with Custom-Made Capacitive Sensors. Sensors 2020, 20, 656. [Google Scholar] [CrossRef]
- Nagaoka, S. Compact latching-type single-mode-fiber switches fabricated by a fiber-micromachining technique and their practical applications. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 36–45. [Google Scholar] [CrossRef]
- Wang, H.; El Wahed, A.K. Development of a Novel Latching-Type Electromagnetic Actuator for Applications in Minimally Invasive Surgery. Actuators 2020, 9, 41. [Google Scholar] [CrossRef]
- Song, C.-W.; Lee, S.-Y. Design of a Solenoid Actuator with a Magnetic Plunger for Miniaturized Segment Robots. Appl. Sci. 2015, 5, 595–607. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Schimpf, P.; Jafari, A. Design optimization of a solenoid-based electromagnetic soft actuator with permanent magnet core. Sens. Actuators A Phys. 2018, 284, 276–285. [Google Scholar] [CrossRef]
- Kouzou, A. Power Factor Correction Circuits. In Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2018; pp. 529–569. [Google Scholar]
- Ellis, G. Nonlinear Behavior and Time Variation. In Control System Design Guide; Kollmorgen Corporation: Radford, VA, USA, 2012; pp. 235–260. [Google Scholar]
- Li, Y.; Zhao, H. A Space Vector Switching Pattern Hysteresis Control Strategy in VIENNA Rectifier. IEEE Access 2020, 8, 60142–60151. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, J.-H.; Lee, H.-J.; Seo, D.-W.; Lee, D.-K.; Kwon, O.-W.; Kwak, M.-K.; Lee, K.-H. A Prosthetic Socket with Active Volume Compensation for Amputated Lower Limb. Sensors 2021, 21, 407. https://doi.org/10.3390/s21020407
Seo J-H, Lee H-J, Seo D-W, Lee D-K, Kwon O-W, Kwak M-K, Lee K-H. A Prosthetic Socket with Active Volume Compensation for Amputated Lower Limb. Sensors. 2021; 21(2):407. https://doi.org/10.3390/s21020407
Chicago/Turabian StyleSeo, Ji-Hyeon, Hyuk-Jin Lee, Dong-Wook Seo, Dong-Kyu Lee, Oh-Won Kwon, Moon-Kyu Kwak, and Kang-Ho Lee. 2021. "A Prosthetic Socket with Active Volume Compensation for Amputated Lower Limb" Sensors 21, no. 2: 407. https://doi.org/10.3390/s21020407
APA StyleSeo, J.-H., Lee, H.-J., Seo, D.-W., Lee, D.-K., Kwon, O.-W., Kwak, M.-K., & Lee, K.-H. (2021). A Prosthetic Socket with Active Volume Compensation for Amputated Lower Limb. Sensors, 21(2), 407. https://doi.org/10.3390/s21020407






