Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning
Abstract
1. Introduction
2. Rapidly Exploring Random Tree (RRT) Algorithm
3. RRT-Connect Algorithm
3.1. Pseudocode of the RRT-Connect Algorithm
| Algorithm 1 Pseudocode of the RRT-Connect Algorithm | |
| Input: qstart ← Start Point Position qgoal ← Goal Point Position λ ← Step Length C ← Position Set of All Boundary Points in All Obstacles Ν ← Number of Random Samples Output: R ← Result of Path R Initialize: Ta ← Null Tree Tb ← Null Tree dshorter ← 0 | |
| BeginRRT-ConnectProcedure | |
| 1 | Ta ← Insert Root Node<qstart> to Ta |
| 2 | Tb ← Insert Root Node<qgoal> to Tb |
| 3 | While 1 ← n to N do |
| 4 | Generate n-th Random Sample |
| 5 | qrand ← Position of n-th Random Sample |
| 6 | If Not Extend(Ta, Tb, qnewB ← Null, qrand, λ, C) then |
| 7 | If Connect(Preach ← Null Path, Ta, Tb, qnewB, λ) then |
| 8 | dreach ← Distance of Preach |
| 9 | If dshorter = 0 or dshorter > dreach then |
| 10 | R ← Preach |
| 11 | dshorter ← dreach |
| 12 | Swap(Ta, Tb) |
| EndRRT-ConnectProcedure | |
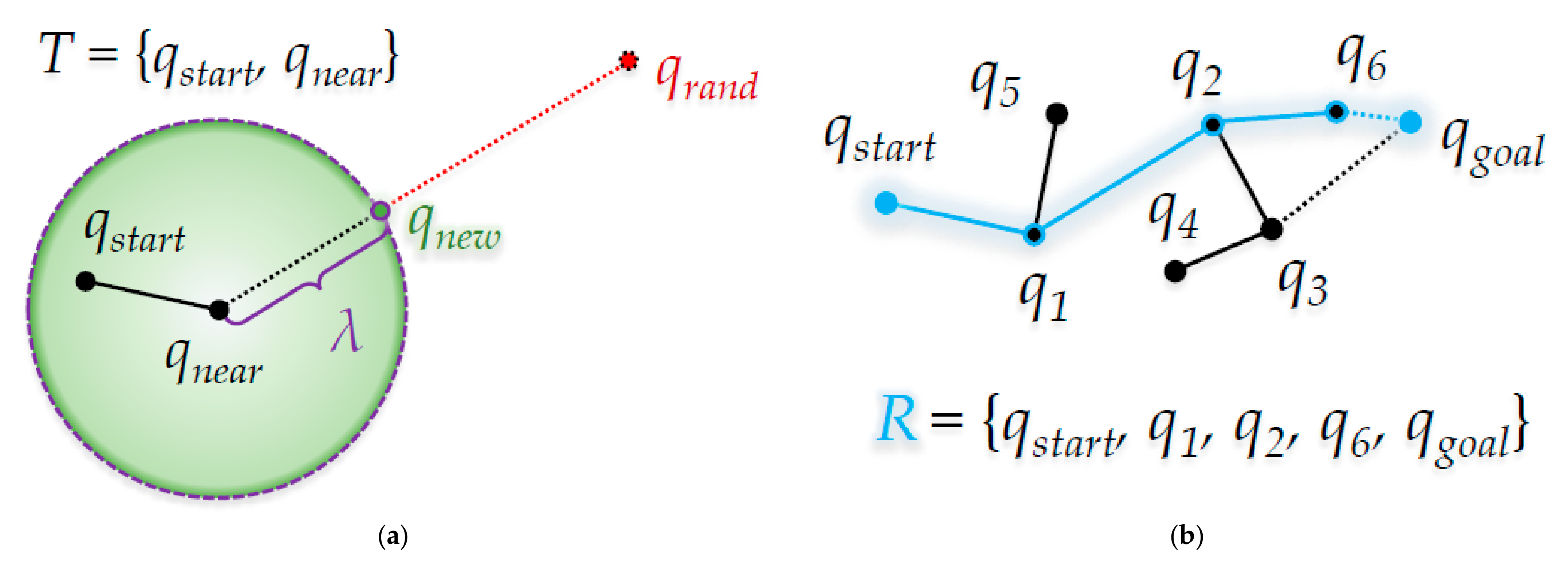
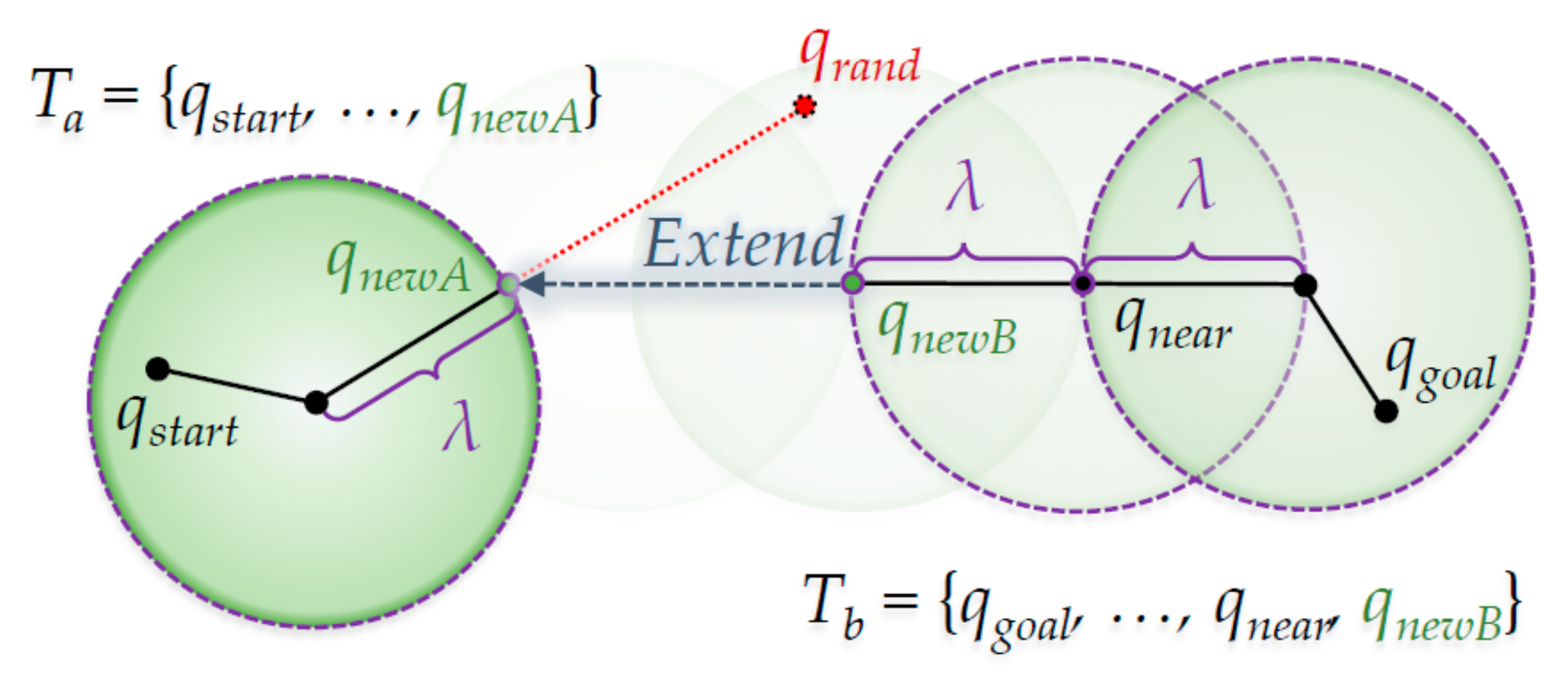
3.2. Pseudocode of the Extend Method from the RRT-Connect Algorithm
| Algorithm 2 Pseudocode of the original ‘Extend’ method from the RRT-Connect Algorithm | |
| Input: Ta ← Tree Ta from RRT-Connect Tb ← Tree Tb from RRT-Connect qnewB ← Position qnewB from RRT-Connect qrand ← Position qrand from RRT-Connect λ ← Step Length λ from RRT-Connect C ← Position Set C from RRT-Connect Output: ftrap ← Result of Boolean ftrap Ta ← Result of Tree Ta //Return by Reference Tb ← Result of Tree Tb //Return by Reference qnewB ← Result of Position qnewB //Return by Reference Initialize: ftrap ← False | |
| Begin ExtendProcedure fromRRT-Connect | |
| 1 | qnear ← Find Position of Nearest Node in Ta from qrand |
| 2 | If NotisInside(qnear, qrand, λ) then |
| 3 | qnewA ← Position of the Intersection Point between the Line Segment connecting qrand and qnear and a Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 4 | Else |
| 5 | qnewA ← qrand |
| 6 | IfisTrapped(qnewA, qnear, C) then |
| 7 | ftrap ← True |
| 8 | Else |
| 9 | Ta ← Insert Node<qnewA> and Edge<qnewA, qnear> to Ta |
| 10 | qnear ← Find Position of Nearest Node in Tb from qnewA |
| 11 | If isInside(qnear, qnewA, λ) then |
| 12 | qnewB ← qnear |
| 13 | Else |
| 14 | qnewB ← Position of Intersection Point between Line Segment connecting qnewA and qnear, and Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 15 | While Not isTrapped(qnewB, qnear, C) do |
| 16 | Tb ← Insert Node<qnewB> and Edge<qnewB, qnear> to Tb |
| 17 | If Not isInside(qnewA, qnewB, λ) then |
| 18 | qnear ← qnewB |
| 19 | qnewB ← Position of Intersection Point between Line Segment connecting qnewA and qnear, and Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 20 | Else |
| 21 | Break |
| EndExtendProcedure fromRRT-Connect | |
3.3. Pseudocode of the Connect Method from the RRT-Connect Algorithm
| Algorithm 3 Pseudocode of the Original ‘Connect’ Method from the RRT-Connect Algorithm | |
| Input: Preach ← Path Preach from RRT-Connect Ta ← Tree Ta from RRT-Connect Tb ← Tree Tb from RRT-Connect qnewB ← Position qnewB from RRT-Connect λ ← Step Length λ from RRT-Connect Output: freach ← Result of Boolean freach Preach ← Result of Path Pmerged //Return by Reference Initialize: freach ← False | |
| BeginConnectProcedure fromRRT-Connect | |
| 1 | IfisInside(qnewA, qnewB, λ) then |
| 2 | Pa ← Path from Root Node [qstart] to Last Inserted Node [qnewA] in Ta |
| 3 | Pb ← Path from qnewB to Root Node [qgoal] in Tb |
| 4 | Pconnect ← Path from Last Inserted Node [qnewA] in Ta to qnewB in Tb |
| 5 | Pmerged ← Merge Path Pa to Pb via Pconnect |
| 6 | freach ← True |
| EndConnectProcedure fromRRT-Connect | |
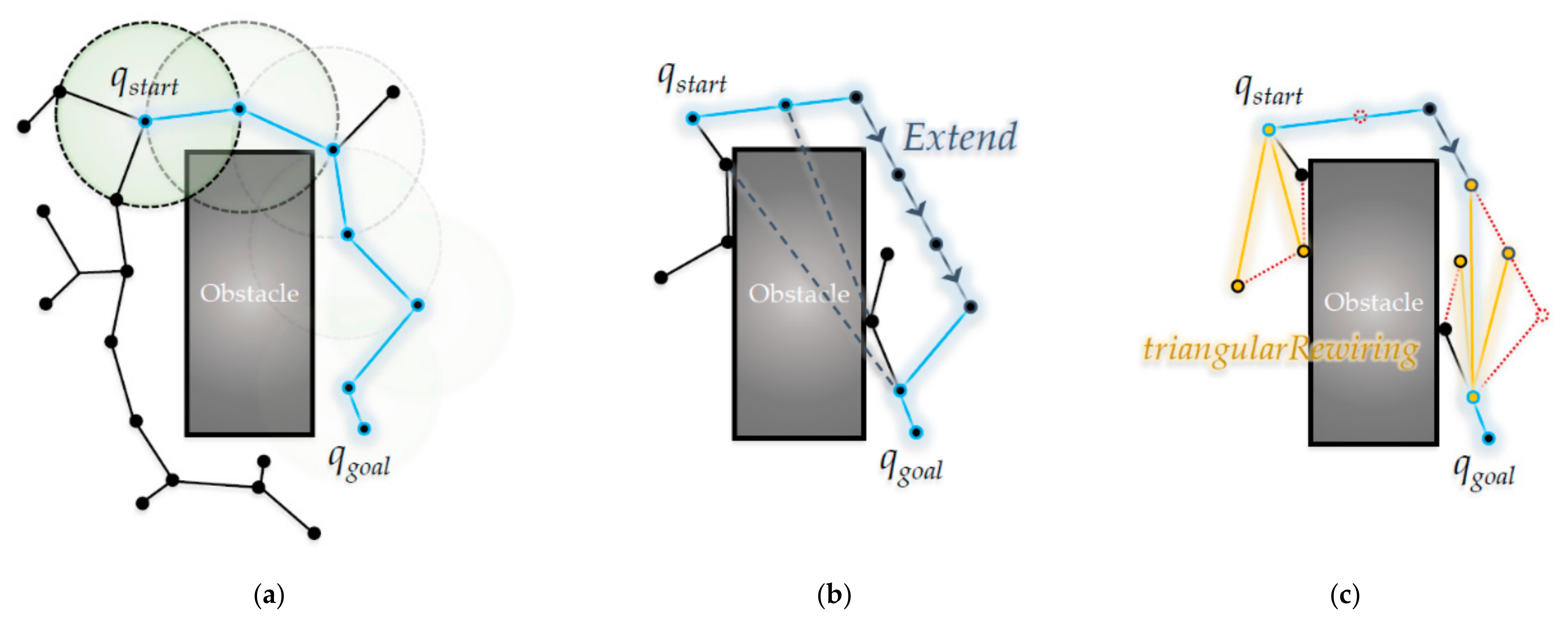
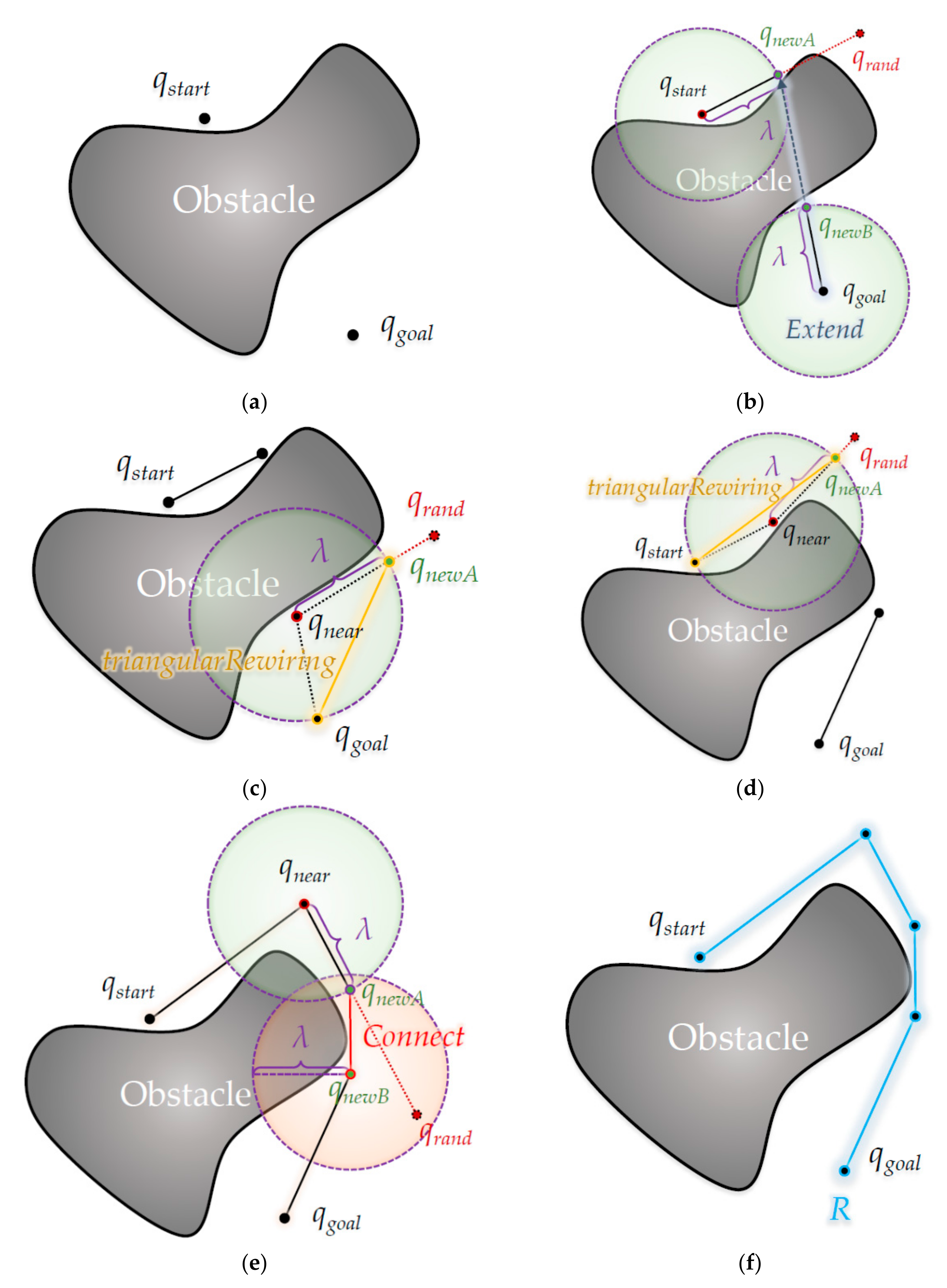
4. Proposed Triangular Inequality-Based RRT-Connect Algorithm
- There is only one start point and one goal point even though the goal point may be changed incrementally as time goes on.
- The robot is capable of omnidirectional motion.
4.1. Pseudocode of the Proposed Triangular-Rewiring Method for the Improved RRT-Connect Algorithm
| Algorithm 4 Pseudocode of the Proposed ‘Triangular-Rewiring’ Method for the RRT-Connect Algorithm | |
| Input: qchild ← Position {qnew/qnewA/qnewB} from {Extend/Connect} qparent ← Position qnear from {Extend/Connect} T ← Tree {Tmerged/Ta/Tb} from {Extend/Connect} C ← Position Set C from {Extend/Connect} Output: {Tmerged/Ta/Tb} ← Result of T | |
| BegintriangularRewiringProcedure fromExtend, Connect | |
| 1 | qancestor ← Position of Parent Node of qparent in T |
| 2 | If NotisTrapped(qancestor, qchild, C) then |
| 3 | T ← Delete Node<qparent>, Edge<qparent, qchild> and Edge<qparent, qancestor> from T |
| 4 | qparent ← qancestor |
| 5 | qancestor ← Position of Parent Node of qancestor in T |
| 6 | While Not qancestor = Null do |
| 7 | If Not isTrapped(qancestor, qchild, C) then |
| 8 | T ← Delete Node<qparent> and Edge<qparent, qancestor> from T |
| 9 | qparent ← qancestor |
| 10 | qancestor ← Position of Parent Node of qancestor in T |
| 11 | Else |
| 12 | Break |
| 13 | T ← Insert Edge<qparent, qchild> to T |
| 14 | Else |
| 15 | T ← Insert Node<qchild> and Edge<qchild, qparent> to T |
| EndtriangularRewiringProcedure fromExtend, Connect | |
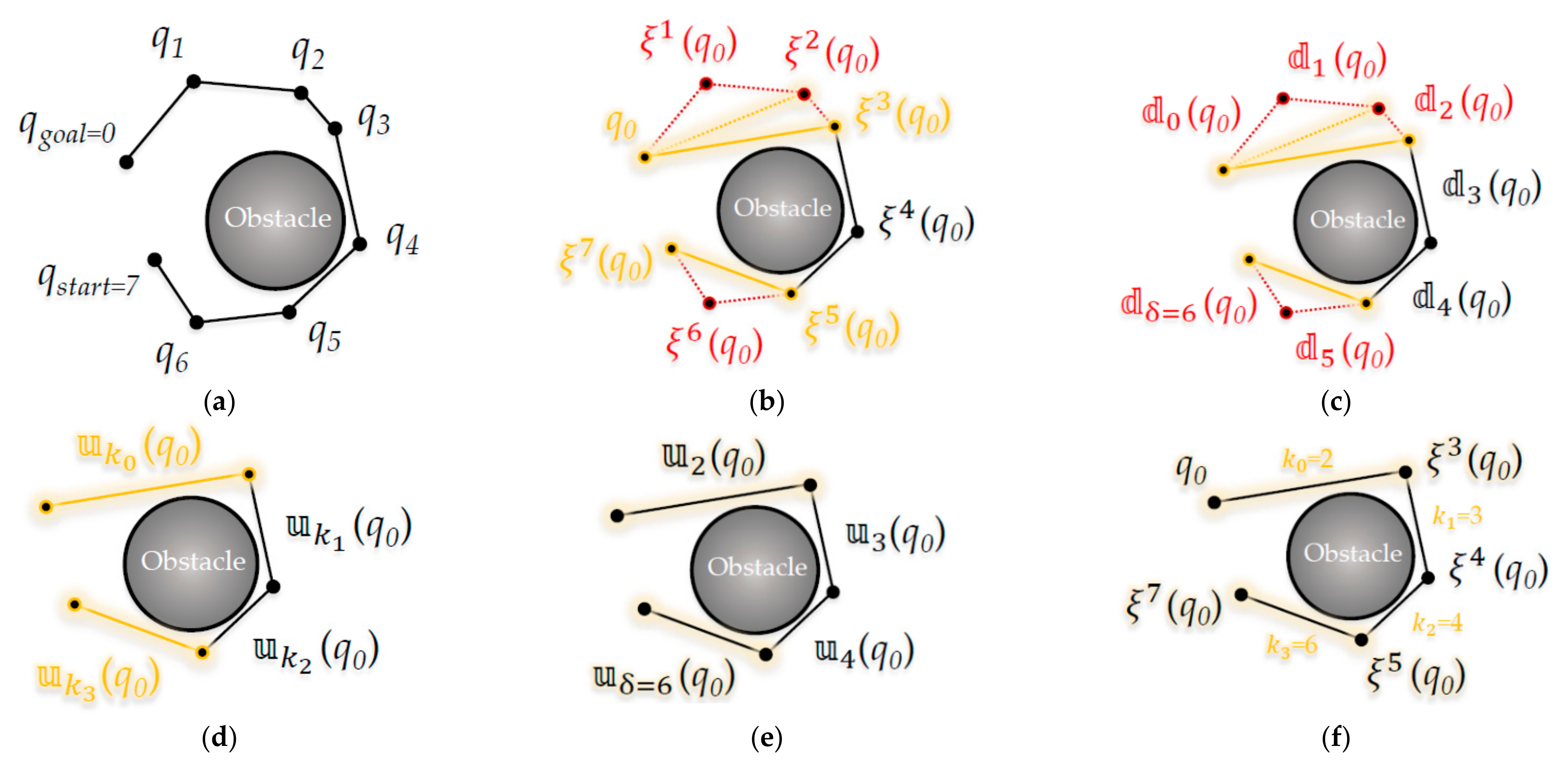
4.2. Mathematical Modeling of the Proposed Triangular Inequality-Based RRT-Connect Algorithm
4.3. Pseudocode of Proposed Extend Method for the Improved RRT-Connect Algorithm
| Algorithm 5 Pseudocode of the Proposed ‘Extend’ Method for the RRT-Connect Algorithm | |
| Input: Ta ← Tree Ta from RRT-Connect Tb ← Tree Tb from RRT-Connect qnewB ← Position qnewB from RRT-Connect qrand ← Position qrand from RRT-Connect λ ← Step Length λ from RRT-Connect C ← Position Set C from RRT-Connect Output: ftrap ← Result of Boolean ftrap Ta ← Result of Tree Ta //Return by Reference Tb ← Result of Tree Tb //Return by Reference qnewB ← Result of Position qnewB //Return by Reference Initialize: ftrap ← False | |
| BeginExtendProcedure fromRRT-Connect | |
| 1 | qnear ← Find Position of Nearest Node in Ta from qrand |
| 2 | If NotisInside(qnear, qrand, λ) then |
| 3 | qnewA ← Position of Intersection Point between Line Segment connecting qrand and qnear, and Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 4 | Else |
| 5 | qnewA ← qrand |
| 6 | IfisTrapped(qnewA, qnear, C) then |
| 7 | ftrap ← True |
| 8 | Else |
| 9 | Ta ← triangularRewiring(qnewA, qnear, Ta, C) |
| 10 | qnear ← Find Position of Nearest Node in Tb from qnewA |
| 11 | If isInside(qnear, qnewA, λ) then |
| 12 | qnewB ← qnear |
| 13 | Else |
| 14 | qnewB ← Position of Intersection Point between Line Segment connecting qnewA and qnear, and Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 15 | While Not isTrapped(qnewB, qnear, C) do |
| 16 | Tb ← triangularRewiring(qnewB, qnear, Tb, C) |
| 17 | If Not isInside(qnewA, qnewB, λ) then |
| 18 | qnear ← qnewB |
| 19 | qnewB ← Position of Intersection Point between Line Segment connecting qnewA and qnear, and Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 20 | Else |
| 21 | Break |
| EndExtendProcedure fromRRT-Connect | |
4.4. Pseudocode of the Proposed Connect Method for the RRT-Connect Algorithm
| Algorithm 6 Pseudocode of the Proposed ‘Connect’ Method for the RRT-Connect Algorithm | |
| Input: Preach ← Path Preach from RRT-Connect Ta ← Tree Ta from RRT-Connect Tb ← Tree Tb from RRT-Connect qnewB ← Position qnewB from RRT-Connect λ ← Step Length λ from RRT-Connect Output: freach ← Result of Boolean freach Preach ← Result of Path Pmerged //Return by Reference Initialize: freach ← False | |
| BeginConnectProcedure fromRRT-Connect | |
| 1 | IfisInside(qnewA, qnewB, λ) then |
| 2 | Pa ← Path from Root Node [qstart] to Last Inserted Node [qnewA] in Ta |
| 3 | Pb ← Path from qnewB to Root Node [qgoal] in Tb |
| 4 | Pconnect ← Path from Last Inserted Node [qnewA] in Ta to qnewB in Tb |
| 5 | Tmerged ← Tree Structure with Merge Path Pa to Pb via Pconnect //1st Insert: qstart, …, n-th Insert: qnewA, (n + 1)-th Insert: qnewB, …, Last Insert: qgoal to Tmerged |
| 6 | For i ← Inserted Index of qnewA in Tmerged to (Number of Node in Tmerged) – 1 do |
| 7 | qnew ← (i – 1)-th Inserted Node in Tmerged |
| 8 | qnear ← i-th Inserted Node in Tmerged |
| 9 | Tmerged ← triangularRewiring(qnew, qnear, Tmerged, C) |
| 10 | Pmerged ← Path from Root Node [qstart] to Last Inserted Node [qgoal] in Tmerged |
| 11 | freach ← True |
| EndConnectProcedure fromRRT-Connect | |
4.5. Process of the Proposed Triangular Inequality-Based RRT-Connect Algorithm
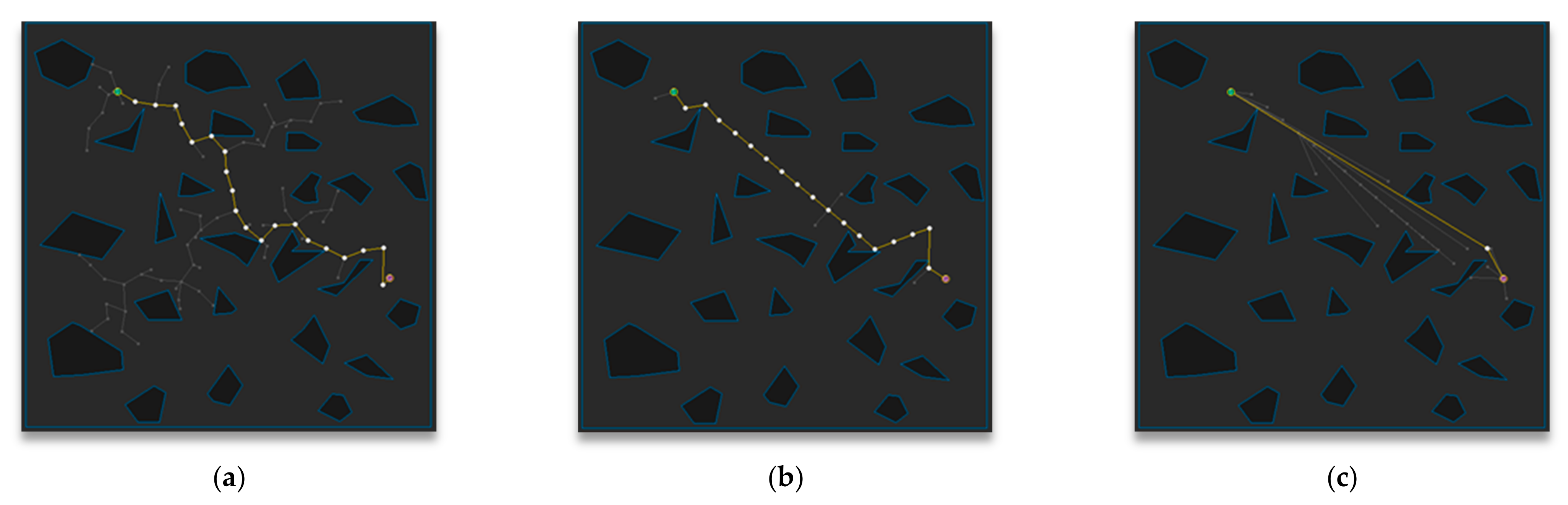
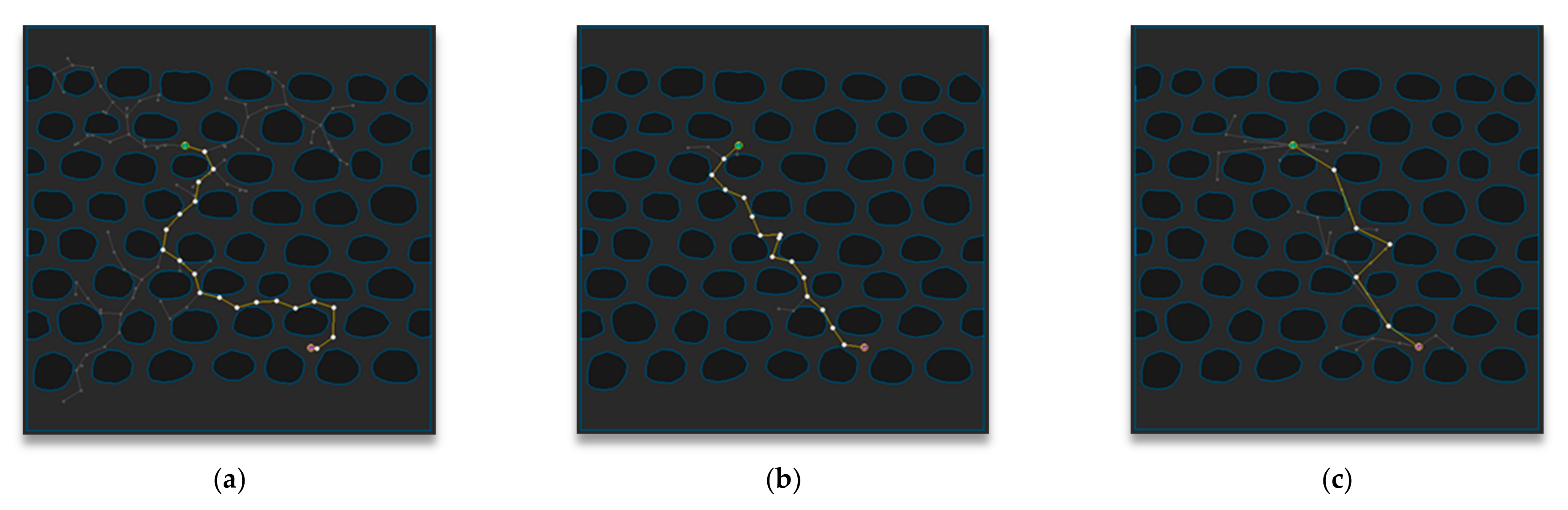
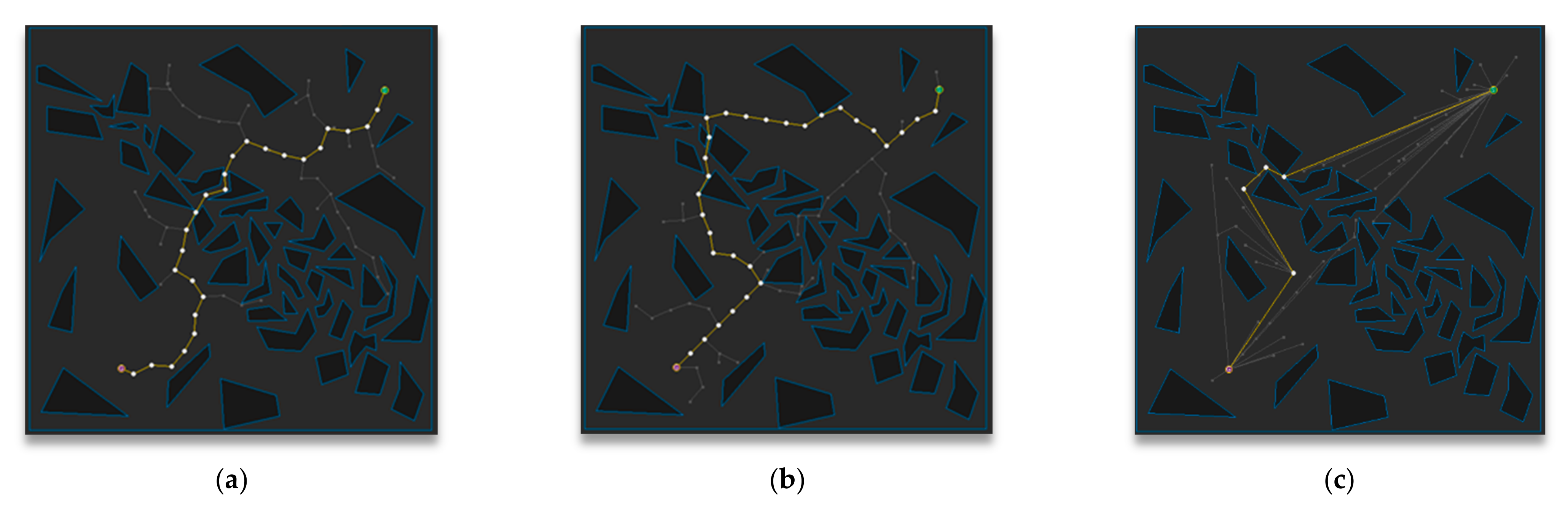
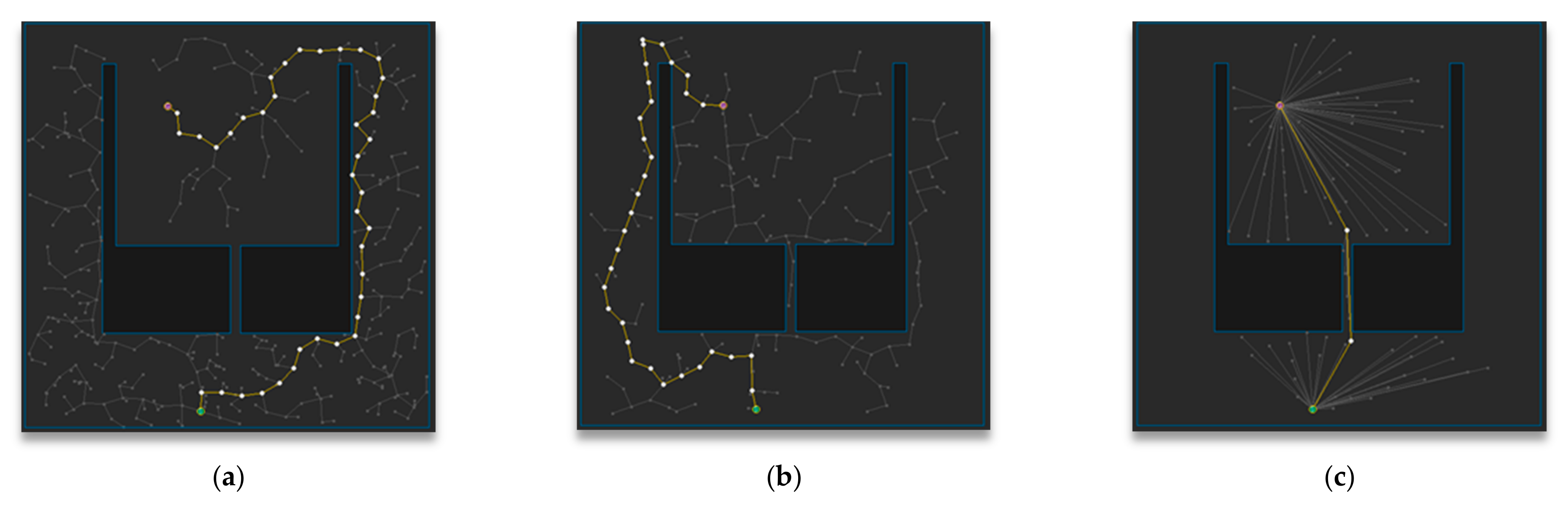
5. Experimental Results
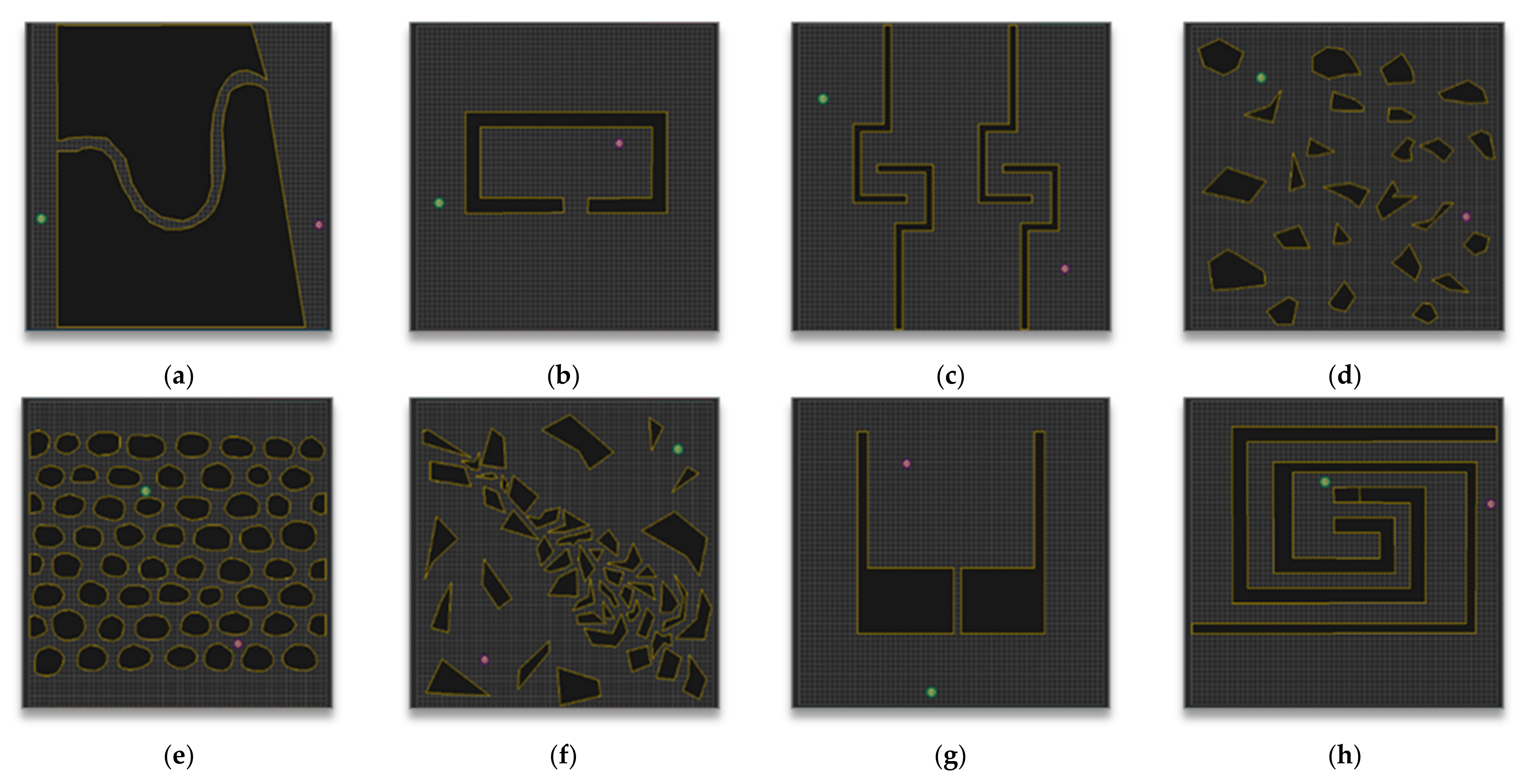
5.1. Experimental Environment
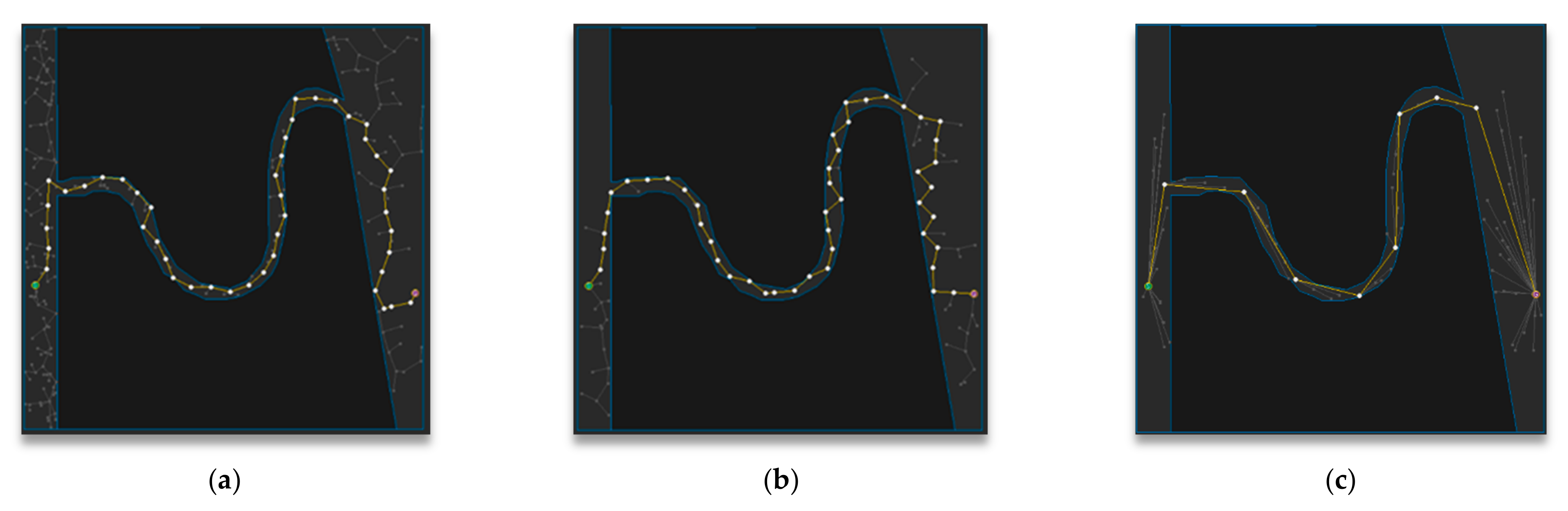
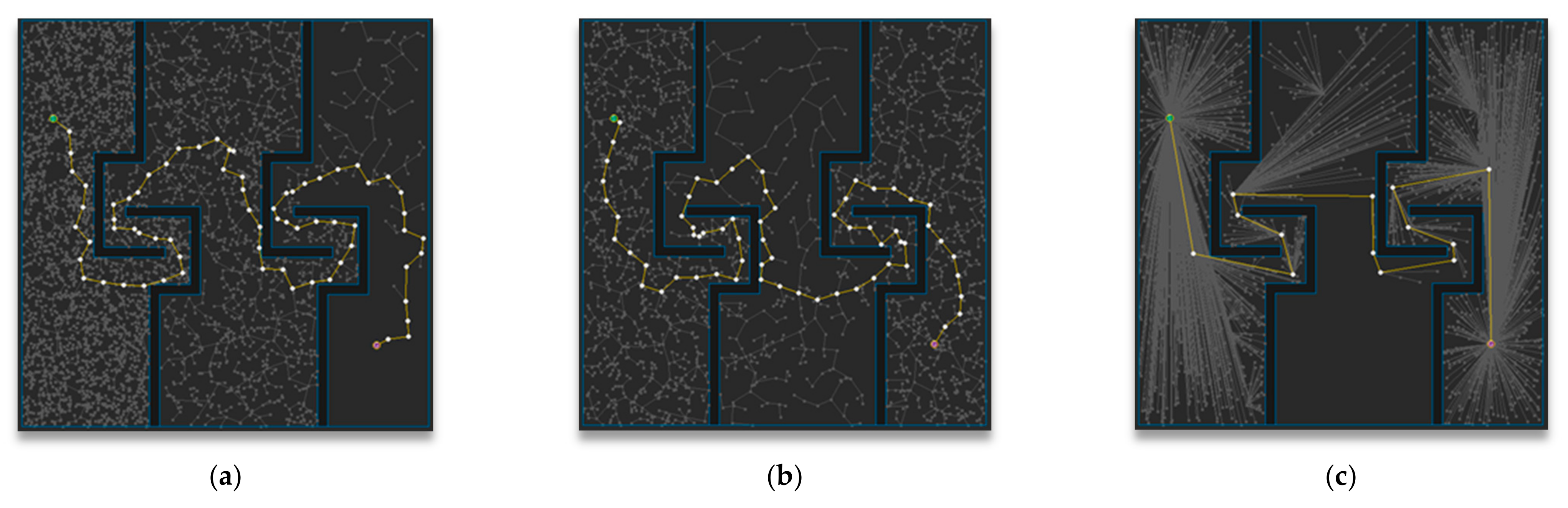
5.2. Experimental Results and Analysis for Each Map
5.3. Experimental Results and Analysis in Total
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Details of the RRT Algorithm
Appendix A.1. Pseudocode of the RRT Algorithm
| Algorithm A1 Pseudocode of the RRT Algorithm | |
| Input: qstart ← Position of Start Point qgoal ← Position of Goal Point λ ← Step Length C ← Position Set of All Boundary Points in All Obstacles N ← Number of Random Samples Output: R ← Result of Path R Initialize: T ← Null Tree dshorter ← 0 | |
| BeginRRTProcedure | |
| 1 | T ← Insert Root Node<qstart> to T |
| 2 | While 1 ← n to N do |
| 3 | Generaten-th Random Sample |
| 4 | qrand ← Position of n-th Random Sample |
| 5 | qnear ← Find Position of Nearest Node in T from qrand |
| 6 | If Not isInside(qnear, qrand, λ) then |
| 7 | qnew ← Position of Intersection Point between Line Segment connecting qrand and qnear, and Circle with Radius λ centered at qnear //2D: Circle, 3D: Sphere, … |
| 8 | Else |
| 9 | qnew ← qrand |
| 10 | If Not isTrapped(qnew, qnear, C) then |
| 11 | T ← Insert Node<qnew> and Edge<qnew, qnear> to T |
| 12 | If isInside(qnew, qgoal, λ) then |
| 13 | T ← Insert Node<qgoal> and Edge<qnew, qgoal> to T |
| 14 | Preach ← Path from Last Inserted Node [qgoal] to Root Node [qstart] in T |
| 15 | dreach ← Distance of Preach |
| 16 | If dshorter = 0 or dshorter > dreach then |
| 17 | R ← Preach |
| 18 | dshorter ← dreach |
| 19 | T ← Delete Node<qgoal> and Edge<qnew, qgoal> from T |
| EndRRTProcedure | |
Appendix A.2. Pseudocode of the Functions Used in the RRT Algorithm
| Algorithm A2 Pseudocode of the isInside Function from the RRT Algorithm | |
| Input: qcenter ← Position {qnear/qnew} from RRT qtarget ← Position {qrand/qgoal} from RRT λ ← Step Length λ from RRT Output: f ← Result of Boolean f Initialize: f ← False | |
| BeginisInsideProcedure fromRRT | |
| 1 | d ← Distance of qcenter to qtarget |
| 2 | Ifλ ≥ d then |
| 3 | f ← True |
| EndisInsideProcedure fromRRT | |
| Algorithm A3 Pseudocode of the isTrapped Function from the RRT Algorithm | |
| Input: qnew ← Position qnew from RRT qnear ← Position qnear from RRT C ← Position Set of All Boundary Points in All Obstacles C from RRT Output: f ← Result of Boolean f Initialize: n ← 1 f ← True | |
| BeginisTrappedProcedure fromRRT | |
| 1 | lq ← Line Segment connecting qnew and qnear |
| 2 | c ← Position Set of All Boundary Points of n-th Inserted Obstacle in C |
| 3 | lc ← Line Segment connecting Last Inserted Position and 1st Inserted Position in c |
| 4 | i ← 1 |
| 5 | While Not Intersect between lq and lc do |
| 6 | lc ← Line Segment connecting i-th Inserted Position and (i + 1)-th Inserted Position in c |
| 7 | i ← i + 1 |
| 8 | If i = (Number of Position in c) – 1 then |
| 9 | If Intersect between lq and lc then |
| 10 | Break |
| 11 | n ← n + 1 |
| 12 | If n > (Number of Position Set in C) then |
| 13 | f ← False |
| 14 | Break |
| 15 | Else |
| 16 | c ← Position Set of All Boundary Points of n-th Inserted Obstacle in C |
| 17 | lc ← Line Segment connecting Last Inserted Position and 1st Inserted Position in c |
| 18 | i ← 1 |
| EndisTrappedProcedure fromRRT | |
Appendix A.3. Basic Mathematical Modeling of the RRT Algorithm
References
- Schwab, K. The Fourth Industrial Revolution; Crown Business: New York, NY, USA, 2017. [Google Scholar]
- Sariff, N.; Buniyamin, N. An overview of autonomous mobile robot path planning algorithms. In Proceedings of the IEEE 4th Student Conference on Research and Development, Selangor, Malaysia, 28–29 June 2006; pp. 183–188. [Google Scholar]
- Roy, D. Visibility graph based spatial path planning of robots using configuration space algorithms. Int. J. Robot. Autom. 2009, 24, 1–9. [Google Scholar] [CrossRef]
- Katevas, N.I.; Tzafestas, S.G.; Pnevmatikatos, C.G. The approximate cell decomposition with local node refinement global path planning method: Path nodes refinement and curve parametric interpolation. J. Intell. Robot. Syst. 1998, 22, 289–314. [Google Scholar] [CrossRef]
- Warren, C.W. Global Path Planning using Artificial Potential Fields. In Proceedings of the International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; Volume 1, pp. 316–321. [Google Scholar]
- LaValle, S.M. Motion planning part II: Wild frontiers. IEEE Robot. Autom. Mag. 2011, 18, 108–118. [Google Scholar]
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A survey of motion planning and control techniques for self-driving urban vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Incremental sampling based algorithms for optimal motion planning. arXiv 2010, arXiv:1005.0416. [Google Scholar]
- Brunner, M.; Bruggemann, B.; Schulz, D. Hierarchical Rough Terrain Motion Planning using an Optimal Sampling based Method. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5539–5544. [Google Scholar]
- Adiyatov, O.; Varol, H.A. Rapidly-exploring Random Tree Based Memory Efficient Motion Planning. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 4–7 August 2013; pp. 354–359. [Google Scholar]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Springer: London, UK, 1998. [Google Scholar]
- Englot, B.; Hover, F.S. Sampling based coverage path planning for inspection of complex structures. In Proceedings of the ICAPS 2012, 22nd International Conference on Automated Planning and Scheduling, Atibaia, Sao Paulo, Brazil, 25–29 June 2012. [Google Scholar]
- Kuffner, J.J., Jr.; LaValle, S.M. RRT-connect: An Efficient Approach to Single-query Path Planning. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 995–1001. [Google Scholar]
- Islam, F.; Nasir, J.; Malik, U.; Ayaz, Y.; Hasan, O. Rrt*-smart: Rapid Convergence Implementation of rrt* towards Optimal Solution. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 1651–1656. [Google Scholar]
- Jeong, I.-B.; Lee, S.-J.; Kim, J.-H. Quick-RRT*: Triangular inequality based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal Sampling based Path Planning Focused via Direct Sampling of an Admissible Ellipsoidal Heuristic. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Klemm, S.; Oberländer, J.; Hermann, A.; Roennau, A.; Schamm, T.; Zollner, J.M.; Dillmann, R. RRT*-Connect: Faster, Asymptotically Optimal Motion Planning. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Zhuhai, China, 6–9 December 2015; pp. 1670–1677. [Google Scholar]
- Choudhury, S.; Scherer, S.; Singh, S. RRT*-AR: Sampling based Alternate Routes Planning with Applications to Autonomous Emergency Landing of a Helicopter. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3947–3952. [Google Scholar]
- Noreen, I.; Amna, K.; Zulfiqar, H. A comparison of RRT, RRT* and RRT*-smart path planning algorithms. Int. J. Comput. Sci. Netw. Secur. 2016, 16, 20. [Google Scholar]
- Da Silva Arantes, M.; Toledo, C.F.M.; Williams, B.C.; Ono, M. Collision-free encoding for chance-constrained nonconvex path planning. IEEE Trans. Robot. 2019, 35, 433–448. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Sung, I.; Choi, B.; Nielsen, P. On the training of a neural network for online path planning with offline path planning algorithms. Int. J. Inf. Manag. 2020, 102142. [Google Scholar] [CrossRef]
- Jeon, G.-Y.; Jung, J.-W. Water sink model for robot motion planning. Sensors 2019, 19, 1269. [Google Scholar] [CrossRef] [PubMed]
- Han, J. Mobile robot path planning with surrounding point set and path improvement. Appl. Soft Comput. 2017, 57, 35–47. [Google Scholar] [CrossRef]
- Yoon, H.U.; Lee, D.-W. Subplanner algorithm to escape from local minima for artificial potential function based robotic path planning. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 263–275. [Google Scholar] [CrossRef]
- Jung, J.-W.; So, B.-C.; Kang, J.-G.; Lim, D.-W.; Son, Y. Expanded Douglas–Peucker polygonal approximation and opposite angle based exact cell decomposition for path planning with curvilinear obstacles. Appl. Sci. 2019, 9, 638. [Google Scholar] [CrossRef]








| H/W | Specification |
|---|---|
| CPU | Intel Core i7-6700k 4.00 GHz (8 CPUs) |
| RAM | 32,768 MB (32 GB DDR4) |
| VGA | Nvidia GeForce GTX 1080 (VRAM 8 GB) SLI (x2) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 1216 (100) | 729 (60) | 823 (68) |
| Avg. path length (px) | 1341 (100) | 1343 (100) | 1200 (89) |
| Avg. planning time (ms) | 12 (100) | 7 (58) | 10 (83) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 271 (100) | 101 (37) | 113 (42) |
| Avg. path length (px) | 598 (100) | 613 (98) | 484 (81) |
| Avg. planning time (ms) | 6 (100) | 3 (50) | 3 (50) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 6106 (100) | 4574 (75) | 4679 (77) |
| Avg. path length (px) | 1934 (100) | 1871 (97) | 1489 (77) |
| Avg. planning time (ms) | 866 (100) | 299 (35) | 313 (36) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 290 (100) | 28 (10) | 32 (11) |
| Avg. path length (px) | 711 (100) | 588 (83) | 534 (75) |
| Avg. planning time (ms) | 3 (100) | 3 (100) | 4 (133) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 371 (100) | 68 (18) | 74 (20) |
| Avg. path length (px) | 554 (100) | 588 (106) | 465 (84) |
| Avg. planning time (ms) | 13 (100) | 2 (15) | 2 (15) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 541 (100) | 184 (34) | 140 (26) |
| Avg. path length (px) | 886 (100) | 778 (88) | 668 (75) |
| Avg. planning time (ms) | 9 (100) | 6 (67) | 4 (44) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 436 (100) | 235 (54) | 244 (56) |
| Avg. path length (px) | 898 (100) | 862 (96) | 674 (75) |
| Avg. planning time (ms) | 5 (100) | 4 (80) | 3 (60) |
| RRT | RRT-Connect | Proposed Algorithm | |
|---|---|---|---|
| Avg. num. of samples (samples) | 17,033 (100) | 3031 (18) | 2954 (17) |
| Avg. path length (px) | 1611 (100) | 1576 (98) | 1358 (84) |
| Avg. planning time (ms) | 4501 (100) | 119 (3) | 125 (3) |
| Algorithm (cmp) | Performance Ratio Based on RRT | Avg. | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Map 1 | Map 2 | Map 3 | Map 4 | Map 5 | Map 6 | Map 7 | Map 8 | ||
| RRT | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| RRT-Connect | 60 | 37 | 75 | 10 | 18 | 34 | 54 | 18 | 38 |
| Proposed | 68 | 42 | 77 | 11 | 20 | 26 | 56 | 17 | 40 |
| Algorithm (cmp) | Performance Ratio Based on RRT | Avg. | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Map 1 | Map 2 | Map 3 | Map 4 | Map 5 | Map 6 | Map 7 | Map 8 | ||
| RRT | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
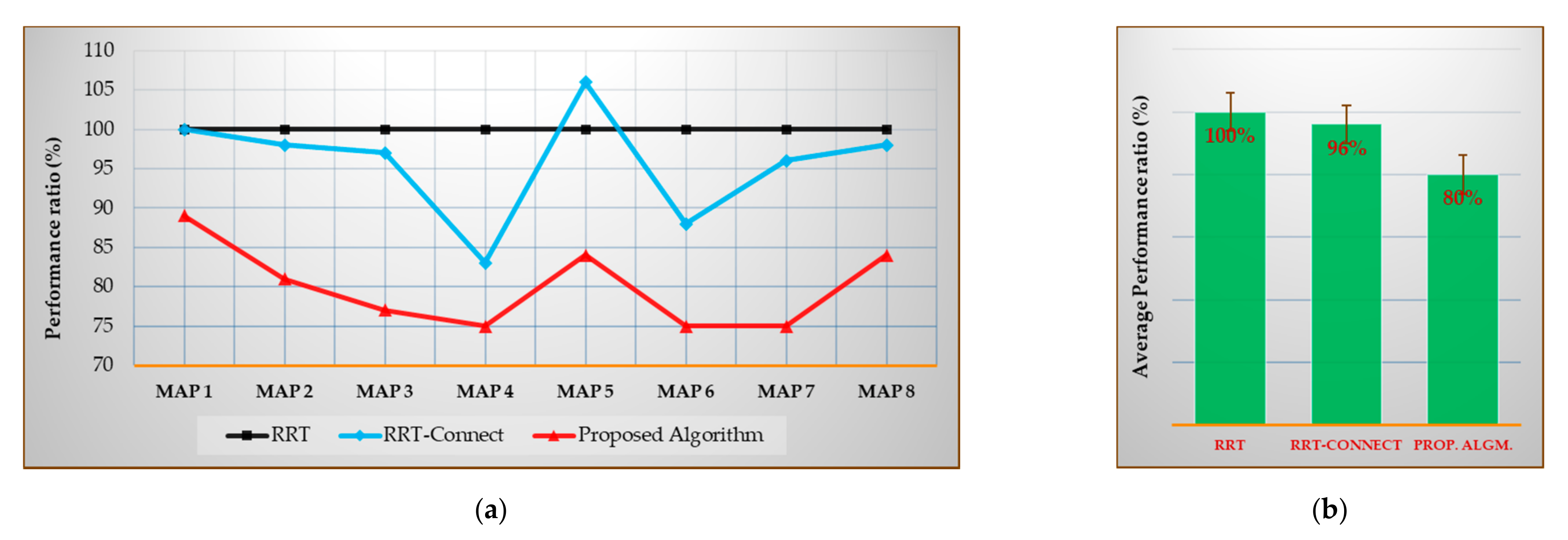
| RRT-Connect | 100 | 98 | 97 | 83 | 106 | 88 | 96 | 98 | 96 |
| Proposed | 89 | 81 | 77 | 75 | 84 | 75 | 75 | 84 | 80 |
| Algorithm (cmp) | Performance Ratio Based on RRT | Avg. | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Map 1 | Map 2 | Map 3 | Map 4 | Map 5 | Map 6 | Map 7 | Map 8 | ||
| RRT | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| RRT-Connect | 58 | 50 | 35 | 100 | 15 | 67 | 80 | 3 | 51 |
| Proposed | 83 | 50 | 36 | 133 | 15 | 44 | 60 | 3 | 53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.-G.; Lim, D.-W.; Choi, Y.-S.; Jang, W.-J.; Jung, J.-W. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors 2021, 21, 333. https://doi.org/10.3390/s21020333
Kang J-G, Lim D-W, Choi Y-S, Jang W-J, Jung J-W. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors. 2021; 21(2):333. https://doi.org/10.3390/s21020333
Chicago/Turabian StyleKang, Jin-Gu, Dong-Woo Lim, Yong-Sik Choi, Woo-Jin Jang, and Jin-Woo Jung. 2021. "Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning" Sensors 21, no. 2: 333. https://doi.org/10.3390/s21020333
APA StyleKang, J.-G., Lim, D.-W., Choi, Y.-S., Jang, W.-J., & Jung, J.-W. (2021). Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors, 21(2), 333. https://doi.org/10.3390/s21020333







