Joint Torque Prediction via Hybrid Neuromusculoskeletal Modelling during Gait Using Statistical Ground Reaction Estimates: An Exploratory Study
Abstract
:1. Introduction
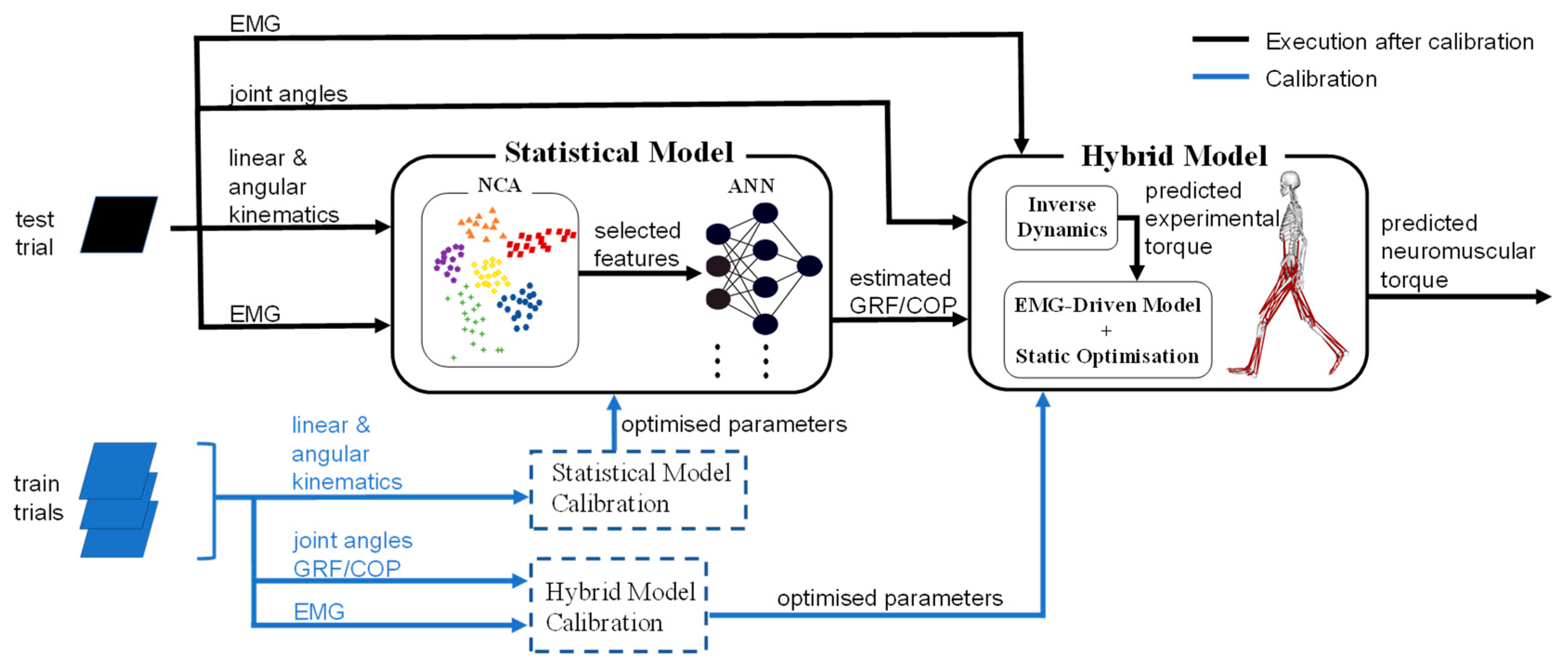
2. Materials and Methods
2.1. Data Collection and Preprocessing
2.2. Musculoskeletal Modelling
2.3. EMG-Assisted Musculoskeletal Modeling
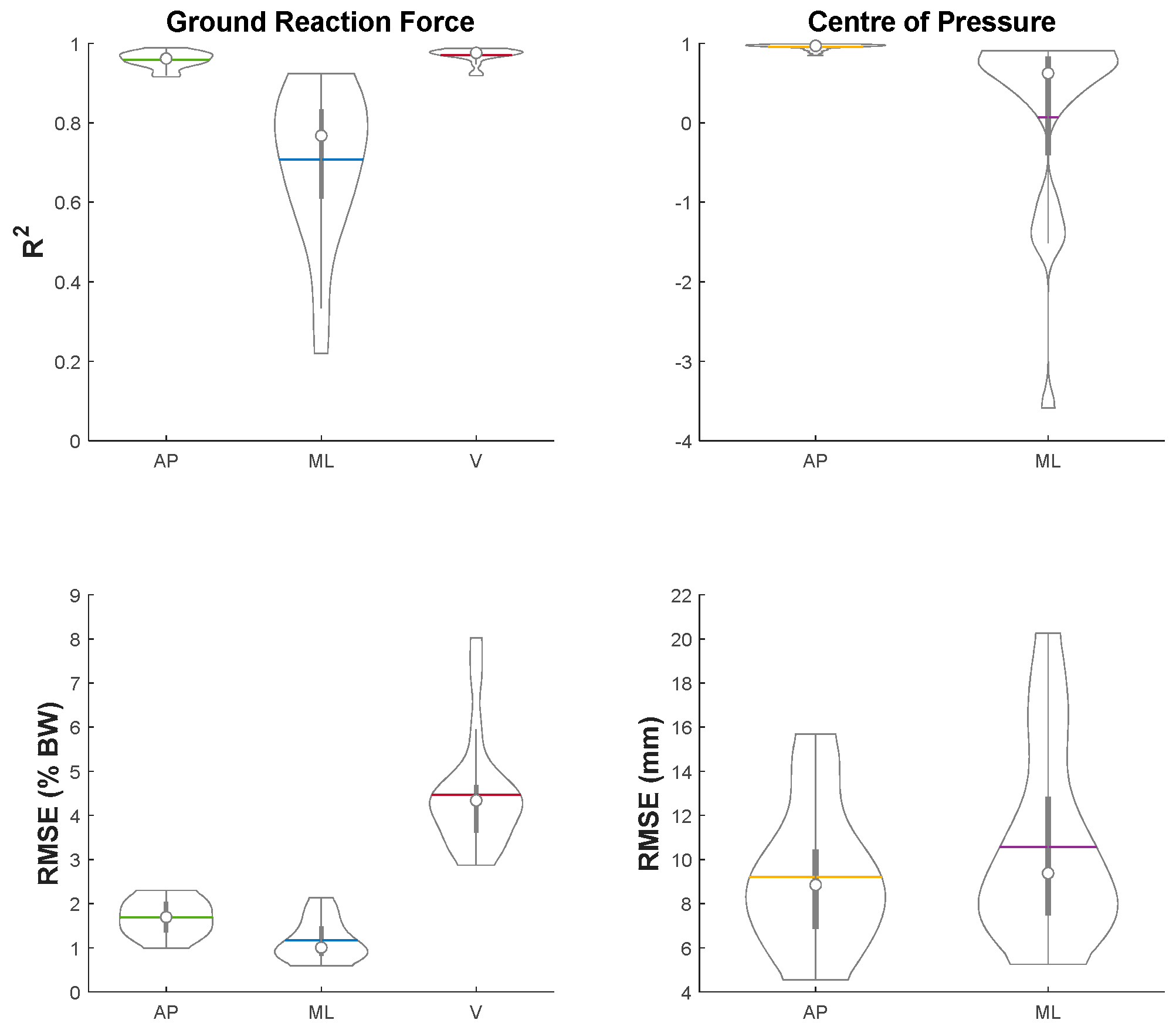
2.4. Ground Reaction Force and Centre of Pressure Estimation
2.4.1. Feature Selection by Neighbourhood Component Analysis
2.4.2. Estimation by Artificial Neural Network
2.5. Experimental Conditions and Model Performance Analysis
2.6. Statistical Analysis
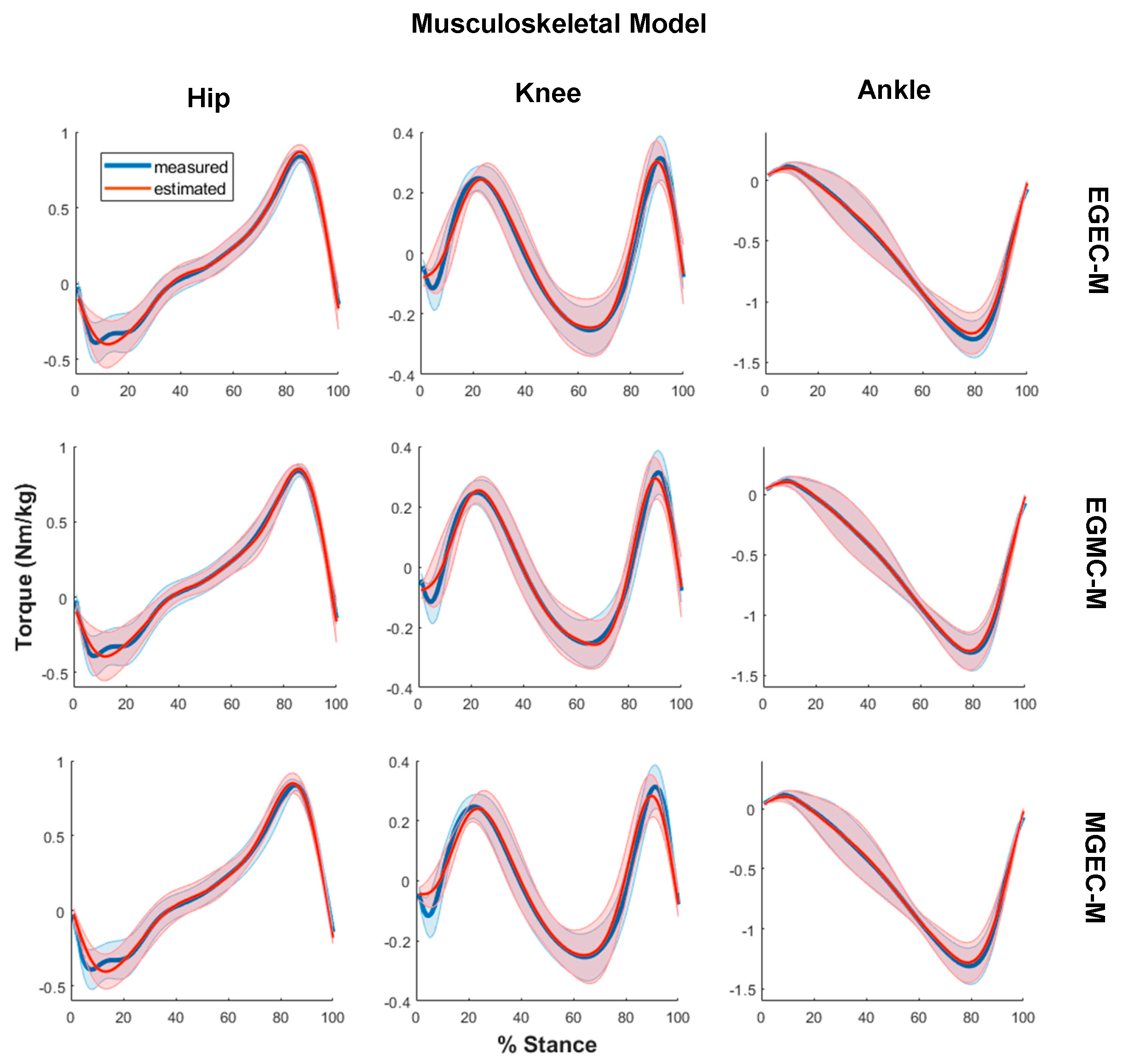
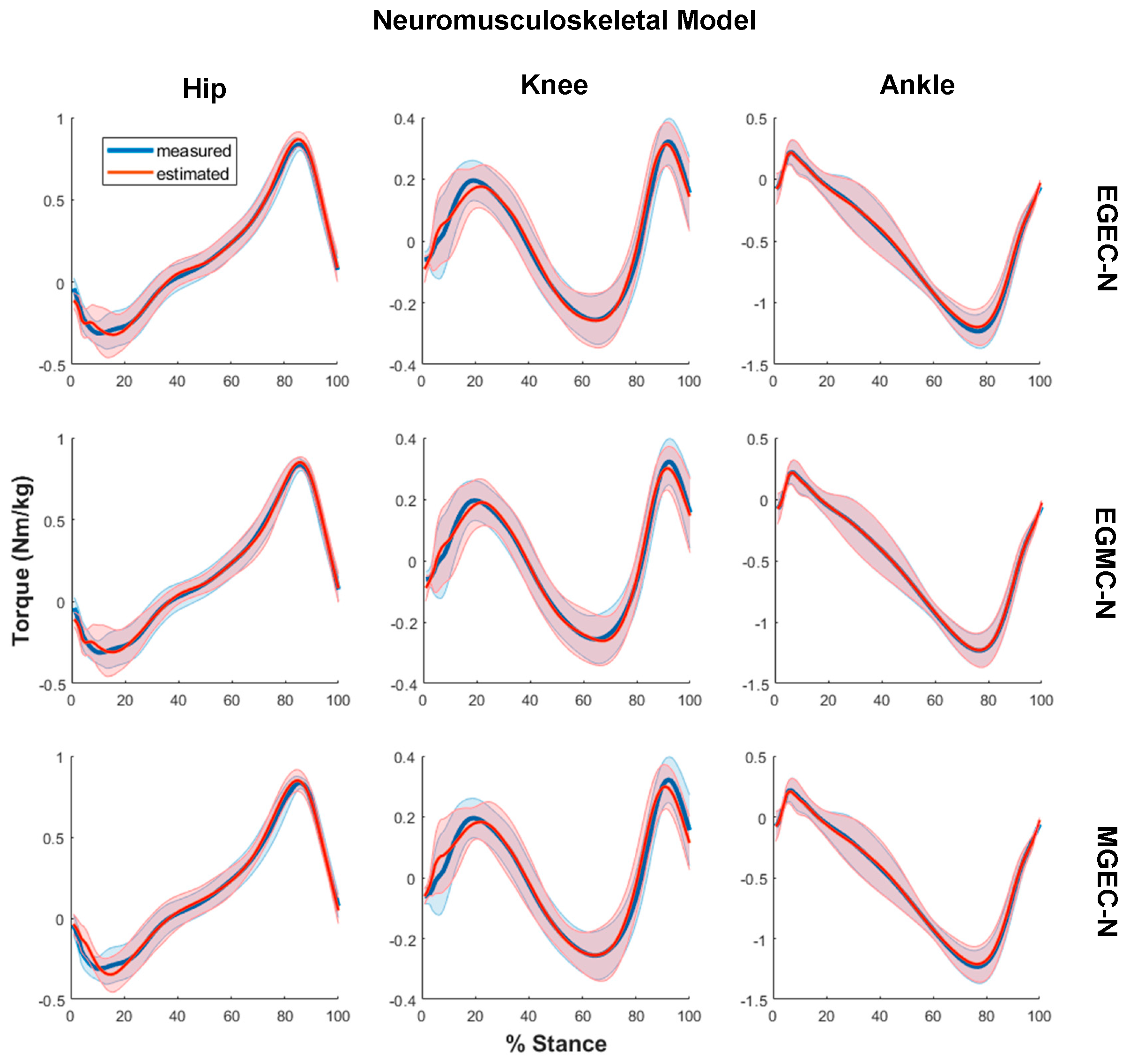
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ai, Q.; Ding, B.; Liu, Q.; Meng, W. A Subject-Specific EMG-Driven Musculoskeletal Model for Applications in Lower-Limb Rehabilitation Robotics. Int. J. Hum. Robot. 2016, 13, 1650005. [Google Scholar] [CrossRef]
- Neckel, N.D.; Blonien, N.; Nichols, D.; Hidler, J. Abnormal joint torque patterns exhibited by chronic stroke subjects while walking with a prescribed physiological gait pattern. J. Neuroeng. Rehabil. 2008, 5, 19. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Xie, S.; Zhang, Y. Muscle Force Estimation Model for Gait Rehabilitation. In Biomechatronics in Medical Rehabilitation; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 147–170. [Google Scholar]
- Lewinson, R.T.; Worobets, J.T.; Stefanyshyn, D.J. Calculation of external knee adduction moments: A comparison of an inverse dynamics approach and a simplified lever-arm approach. Knee 2015, 22, 292–297. [Google Scholar] [CrossRef]
- Rutherford, D.J.; Baker, M. Knee moment outcomes using inverse dynamics and the cross product function in moderate knee osteoarthritis gait: A comparison study. J. Biomech. 2018, 78, 150–154. [Google Scholar] [CrossRef]
- Elftman, H. FORCES AND ENERGY CHANGES IN THE LEG DURING WALKING. Am. J. Physiol. Content 1939, 125, 339–356. [Google Scholar] [CrossRef] [Green Version]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 978-047-054-914-8. [Google Scholar]
- Thelen, D.G.; Anderson, F.C.; Delp, S.L. Generating dynamic simulations of movement using computed muscle control. J. Biomech. 2003, 36, 321–328. [Google Scholar] [CrossRef]
- Crowninshield, R.D.; Brand, R.A. A physiologically based criterion of muscle force prediction in locomotion. J. Biomech. 1981, 14, 793–801. [Google Scholar] [CrossRef]
- Anderson, F.C.; Pandy, M. Static and dynamic optimization solutions for gait are practically equivalent. J. Biomech. 2001, 34, 153–161. [Google Scholar] [CrossRef]
- Lloyd, D.G.; Besier, T. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Shao, Q.; MacLeod, T.; Manal, K.; Buchanan, T.S. Estimation of Ligament Loading and Anterior Tibial Translation in Healthy and ACL-Deficient Knees During Gait and the Influence of Increasing Tibial Slope Using EMG-Driven Approach. Ann. Biomed. Eng. 2010, 39, 110–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rao, G.; Berton, E.; Amarantini, D.; Vigouroux, L.; Buchanan, T.S. An EMG-Driven Biomechanical Model That Accounts for the Decrease in Moment Generation Capacity During a Dynamic Fatigued Condition. J. Biomech. Eng. 2010, 132, 071003. [Google Scholar] [CrossRef]
- Winby, C.R.; Lloyd, D.G.; Besier, T.F.; Kirk, T.B. Muscle and External Load Contribution to Knee Joint Contact Loads dur-ing Normal Gait. J. Biomech. 2009, 42, 2294–2300. [Google Scholar] [CrossRef] [PubMed]
- Sartori, M.; Reggiani, M.; Farina, D.; Lloyd, D. EMG-Driven Forward-Dynamic Estimation of Muscle Force and Joint Moment about Multiple Degrees of Freedom in the Human Lower Extremity. PLoS ONE 2012, 7, e52618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farina, D.; Negro, F. Accessing the Neural Drive to Muscle and Translation to Neurorehabilitation Technologies. IEEE Rev. Biomed. Eng. 2012, 5, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Hussain, I.; Park, S.-J. Prediction of Myoelectric Biomarkers in Post-Stroke Gait. Sensors 2021, 21, 5334. [Google Scholar] [CrossRef] [PubMed]
- Costa, A.; Itkonen, M.; Yamasaki, H.; Alnajjar, F.; Shimoda, S. Importance of muscle selection for EMG signal analysis during upper limb rehabilitation of stroke patients. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Korea, 11–15 July 2017; Volume 2017, pp. 2510–2513. [Google Scholar]
- Steele, K.M.; Rozumalski, A.; Schwartz, M. Muscle synergies and complexity of neuromuscular control during gait in cerebral palsy. Dev. Med. Child Neurol. 2015, 57, 1176–1182. [Google Scholar] [CrossRef] [Green Version]
- Sartori, M.; Llyod, D.G.; Farina, D. Neural Data-Driven Musculoskeletal Modeling for Personalized Neurorehabilitation Technologies. IEEE Trans. Biomed. Eng. 2016, 63, 879–893. [Google Scholar] [CrossRef] [Green Version]
- Farina, D.; Merletti, R.; Enoka, R.M. The extraction of neural strategies from the surface EMG. J. Appl. Physiol. 2004, 96, 1486–1495. [Google Scholar] [CrossRef] [Green Version]
- De Luca, C.J.; Donald Gilmore, L.; Kuznetsov, M.; Roy, S.H. Filtering the Surface EMG Signal: Movement Artifact and Base-line Noise Contamination. J. Biomech. 2010, 43, 1573–1579. [Google Scholar] [CrossRef]
- Sartori, M.; Farina, D.; Lloyd, D. Hybrid neuromusculoskeletal modeling to best track joint moments using a balance between muscle excitations derived from electromyograms and optimization. J. Biomech. 2014, 47, 3613–3621. [Google Scholar] [CrossRef]
- Rouhani, H.; Favre, J.; Crevoisier, X.; Aminian, K. Ambulatory assessment of 3D ground reaction force using plantar pressure distribution. Gait Posture 2010, 32, 311–316. [Google Scholar] [CrossRef]
- Forner-Cordero, A.; Koopman, H.F.; Van Der Helm, F. Use of pressure insoles to calculate the complete ground reaction forces. J. Biomech. 2004, 37, 1427–1432. [Google Scholar] [CrossRef]
- Jung, Y.; Jung, M.; Lee, K.; Koo, S. Ground Reaction Force Estimation Using an Insole-Type Pressure Mat and Joint Kinemat-ics during Walking. J. Biomech. 2014, 47, 2693–2699. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Inoue, Y.; Shibata, K. A wearable force plate system for the continuous measurement of triaxial ground reaction force in biomechanical applications. Meas. Sci. Technol. 2010, 21, 085804. [Google Scholar] [CrossRef]
- Veltink, P.; Liedtke, C.; Droog, E. Ambulatory measurement of ground reaction forces. In Proceedings of the 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No. 04CH37583), The Hague, The Netherlands, 10–13 October 2004; Volume 1, pp. 701–703. [Google Scholar]
- Low, D.; Dixon, S. Footscan pressure insoles: Accuracy and reliability of force and pressure measurements in running. Gait Posture 2010, 32, 664–666. [Google Scholar] [CrossRef]
- Chen, J.-P.; Chung, M.-J.; Wu, C.-Y.; Cheng, K.-W.; Wang, M.-J. Comparison of Barefoot Walking and Shod Walking Between Children with and without Flat Feet. J. Am. Podiatr. Med. Assoc. 2015, 105, 218–225. [Google Scholar] [CrossRef]
- Leporace, G.; Batista, L.A.; Nadal, J. Prediction of 3D ground reaction forces during gait based on accelerometer data. Res. Biomed. Eng. 2018, 34, 211–216. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.E.; Choi, A.; Mun, J.H. Prediction of ground reaction forces during gait based on kinematics and a neural network model. J. Biomech. 2013, 46, 2372–2380. [Google Scholar] [CrossRef]
- Dorschky, E.; Nitschke, M.; Martindale, C.F.; Bogert, A.V.D.; Koelewijn, A.D.; Eskofier, B.M. CNN-Based Estimation of Sagittal Plane Walking and Running Biomechanics From Measured and Simulated Inertial Sensor Data. Front. Bioeng. Biotechnol. 2020, 8, 604. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.R.; Mian, A.; Donnelly, C.J.; Lloyd, D.; Alderson, J. Predicting athlete ground reaction forces and moments from motion capture. Med. Biol. Eng. Comput. 2018, 56, 1781–1792. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnson, W.R.; Mian, A.; Donnelly, C.J.; Lloyd, D.; Alderson, J. Prediction of Ground Reaction Forces and Moments via Supervised Learning Is Independent of Participant Sex, Height and Mass. In Proceedings of the 35th Conference of the International Society of Bio-mechanics in Sports, Cologne, Germany, 14–18 June 2017. [Google Scholar]
- Johnson, W.R.; Mian, A.; Robinson, M.A.; Verheul, J.; Lloyd, D.G.; Alderson, J.A. Multidimensional Ground Reaction Forces and Moments From Wearable Sensor Accelerations via Deep Learning. IEEE Trans. Biomed. Eng. 2021, 68, 289–297. [Google Scholar] [CrossRef]
- Lim, H.; Kim, B.; Park, S. Prediction of Lower Limb Kinetics and Kinematics during Walking by a Single IMU on the Lower Back Using Machine Learning. Sensors 2019, 20, 130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Komaris, D.-S.; Perez-Valero, E.; Jordan, L.; Barton, J.; Hennessy, L.; O’Flynn, B.; Tedesco, S. Predicting Three-Dimensional Ground Reaction Forces in Running by Using Artificial Neural Networks and Lower Body Kinematics. IEEE Access 2019, 7, 156779–156786. [Google Scholar] [CrossRef]
- Lee, M.; Park, S. Estimation of Three-Dimensional Lower Limb Kinetics Data during Walking Using Machine Learning from a Single IMU Attached to the Sacrum. Sensors 2020, 20, 6277. [Google Scholar] [CrossRef] [PubMed]
- Ardestani, M.M.; Zhang, X.; Wang, L.; Lian, Q.; Liu, Y.; He, J.; Li, D.; Jin, Z. Human Lower Extremity Joint Moment Predic-tion: A Wavelet Neural Network Approach. Expert Syst. Appl. 2014, 41, 4422–4433. [Google Scholar] [CrossRef]
- Mundt, M.; Koeppe, A.; Bamer, F.; Potthast, W.; Pforzheim, A.C. Prediction of Joint Kinetics Based On Joint Kinematics Using Neural Networks. In Proceedings of the 36th Conference of the International Society of Biomechanics in Sports, Auckland, New Zealand, 10–14 September 2018; pp. 794–797. [Google Scholar]
- Schreiber, C.; Moissenet, F. A multimodal dataset of human gait at different walking speeds established on injury-free adult participants. Sci. Data 2019, 6, 111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pizzolato, C.; Lloyd, D.G.; Sartori, M.; Ceseracciu, E.; Besier, T.F.; Fregly, B.J.; Reggiani, M. CEINMS: A Toolbox to Inves-tigate the Influence of Different Neural Control Solutions on the Prediction of Muscle Excitation and Joint Moments during Dynamic Motor Tasks. J. Biomech. 2015, 48, 3929–3936. [Google Scholar] [CrossRef] [PubMed]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [Green Version]
- Hamner, S.R.; Seth, A.; Delp, S.L. Muscle contributions to propulsion and support during running. J. Biomech. 2010, 43, 2709–2716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Modenese, L.; Ceseracciu, E.; Reggiani, M.; Lloyd, D. Estimation of musculotendon parameters for scaled and subject specific musculoskeletal models using an optimization technique. J. Biomech. 2016, 49, 141–148. [Google Scholar] [CrossRef] [Green Version]
- Fernando, T.; Maier, H.; Dandy, G. Selection of input variables for data driven models: An average shifted histogram partial mutual information estimator approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- Goldberger, J.; Roweis, S.; Hinton, G.; Salakhutdinov, R. Neighbourhood Components Analysis. Adv. Neural Inf. Process. Syst. 2004, 17, 513–520. [Google Scholar]
- Jiménez-Grande, D.; Atashzar, S.F.; Martinez-Valdes, E.; De Nunzio, A.M.; Falla, D. Kinematic biomarkers of chronic neck pain measured during gait: A data-driven classification approach. J. Biomech. 2021, 118, 110190. [Google Scholar] [CrossRef]
- Malan, N.S.; Sharma, S. Feature Selection Using Regularized Neighbourhood Component Analysis to Enhance the Classi-fication Performance of Motor Imagery Signals. Comput. Biol. Med. 2019, 107, 118–126. [Google Scholar] [CrossRef]
- Kwon, S.; Ro, D.; Song, M.; Han, H.-S.; Lee, M.; Kim, H. Identifying key gait features associated with the radiological grade of knee osteoarthritis. Osteoarthr. Cartil. 2019, 27, 1755–1760. [Google Scholar] [CrossRef]
- Raghu, S.; Sriraam, N. Classification of focal and non-focal EEG signals using neighborhood component analysis and machine learning algorithms. Expert Syst. Appl. 2018, 113, 18–32. [Google Scholar] [CrossRef]
- Manit, J.; Youngkong, P. Neighborhood components analysis in sEMG signal dimensionality reduction for gait phase pattern recognition. In Proceedings of the 7th International Conference on Broadband Communications and Biomedical Applications, Melbourne, VIC, Australia, 21–24 November 2011; pp. 86–90. [Google Scholar]
- Yang, Z.; Laaksonen, J. Regularized Neighborhood Component Analysis. In Image Analysis; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 2007; Volume 4522, pp. 253–262. [Google Scholar]
- Favre, J.; Hayoz, M.; Erhart-Hledik, J.C.; Andriacchi, T.P. A neural network model to predict knee adduction moment during walking based on ground reaction force and anthropometric measurements. J. Biomech. 2012, 45, 692–698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagan, M.T.; Demuth, H.; Beale, M. Neural Network Design; PWS Publishing, Co.: Boston, MA, USA, 1997. [Google Scholar]
- Podobnik, J.; Kraljić, D.; Zadravec, M.; Munih, M. Centre of Pressure Estimation during Walking Using Only Iner-tial-Measurement Units and End-to-End Statistical Modelling. Sensors (Switzerland) 2020, 20, 6136. [Google Scholar] [CrossRef] [PubMed]
- Hullfish, T.J.; Drazan, J.F.; Baxter, J.R. Experimental recommendations for estimating lower extremity loading based on joint and activity. J. Biomech. 2021, 127, 110688. [Google Scholar] [CrossRef] [PubMed]
- John, C.T.; Seth, A.; Schwartz, M.H.; Delp, S.L. Contributions of muscles to mediolateral ground reaction force over a range of walking speeds. J. Biomech. 2012, 45, 2438–2443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veerkamp, K.; Schallig, W.; Harlaar, J.; Pizzolato, C.; Carty, C.P.; Lloyd, D.G.; van der Krogt, M.M. The Effects of Electro-myography-Assisted Modelling in Estimating Musculotendon Forces during Gait in Children with Cerebral Palsy. J. Biomech. 2019, 92, 45–53. [Google Scholar] [CrossRef]
- Scheys, L.; Van Campenhout, A.; Spaepen, A.; Suetens, P.; Jonkers, I. Personalized MR-Based Musculoskeletal Models Com-pared to Rescaled Generic Models in the Presence of Increased Femoral Anteversion: Effect on Hip Moment Arm Lengths. Gait Posture 2008, 28, 358–365. [Google Scholar] [CrossRef] [PubMed]


| Neuromusculoskeletal Model Parameter | Range | |
|---|---|---|
| Minimum | Maximum | |
| Tendon slack length | 0.95 | 1.05 |
| Optimal fibre length | 0.975 | 1.025 |
| Muscle strength coefficient | 0.5 | 2 |
| MTU activation filtering coefficients | −1 | 1 |
| Shape factor | −5 | 0 |
| Experimental EMG | MTU of the Model |
|---|---|
| Soleus | soleus |
| Tibialis anterior | tib_ant |
| Gastrocnemius medialis | med_gas, lat_gas |
| Rectus femoris | rect_fem |
| Vastus medialis | vas_lat, vas_med, vas_int |
| Semitendinosus | semimem, semiten |
| Gluteus maximus | glut_max1, glut_max2, glut_max3 |
| Gluteus medius | glut_med1, glut_med2, glut_med3, glut_min1, glut_min2, glut_min3 |
| ANN Model Parameter | Range | |
|---|---|---|
| Minimum | Maximum | |
| Neuron number | 2 | 20 |
| Learning rate | 0.0005 | 1 |
| Epochs | 500 | 1000 |
| Condition | Joint | ||
|---|---|---|---|
| Hip | Knee | Ankle | |
| EGEC-M | 0.84 ± 0.089 | 0.70 ± 0.17 | 0.97 ± 0.029 |
| EGEC-N | 0.80 ± 0.094 | 0.73 ± 0.12 | 0.97 ± 0.024 |
| EGMC-M | 0.87 ± 0.048 | 0.84 ± 0.059 | 0.99 ± 0.0027 |
| EGMC-N | 0.83 ± 0.090 | 0.84 ± 0.051 | 1.0 ± 0.0013 |
| MGEC-M | 0.95 ± 0.028 | 0.78 ± 0.14 | 0.97 ± 0.023 |
| MGEC-N | 0.94 ± 0.028 | 0.82 ± 0.12 | 0.97 ± 0.021 |
| Condition | Joint | ||
|---|---|---|---|
| Hip | Knee | Ankle | |
| EGEC-M | 0.14 ± 0.032 | 0.094 ± 0.024 | 0.081 ± 0.023 |
| EGEC-N | 0.15 ± 0.030 | 0.091 ± 0.016 | 0.069 ± 0.026 |
| EGMC-M | 0.13 ± 0.019 | 0.070 ± 0.010 | 0.032 ± 0.0073 |
| EGMC-N | 0.14 ± 0.029 | 0.070 ± 0.011 | 0.022 ± 0.0045 |
| MGEC-M | 0.081 ± 0.018 | 0.079 ± 0.021 | 0.073 ± 0.029 |
| MGEC-N | 0.078 ± 0.018 | 0.073 ± 0.017 | 0.065 ± 0.023 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, S.K.; Vujaklija, I. Joint Torque Prediction via Hybrid Neuromusculoskeletal Modelling during Gait Using Statistical Ground Reaction Estimates: An Exploratory Study. Sensors 2021, 21, 6597. https://doi.org/10.3390/s21196597
Lam SK, Vujaklija I. Joint Torque Prediction via Hybrid Neuromusculoskeletal Modelling during Gait Using Statistical Ground Reaction Estimates: An Exploratory Study. Sensors. 2021; 21(19):6597. https://doi.org/10.3390/s21196597
Chicago/Turabian StyleLam, Shui Kan, and Ivan Vujaklija. 2021. "Joint Torque Prediction via Hybrid Neuromusculoskeletal Modelling during Gait Using Statistical Ground Reaction Estimates: An Exploratory Study" Sensors 21, no. 19: 6597. https://doi.org/10.3390/s21196597
APA StyleLam, S. K., & Vujaklija, I. (2021). Joint Torque Prediction via Hybrid Neuromusculoskeletal Modelling during Gait Using Statistical Ground Reaction Estimates: An Exploratory Study. Sensors, 21(19), 6597. https://doi.org/10.3390/s21196597






