A Deep Learning Approach for Foot Trajectory Estimation in Gait Analysis Using Inertial Sensors
Abstract
:1. Introduction
2. Materials and Methods
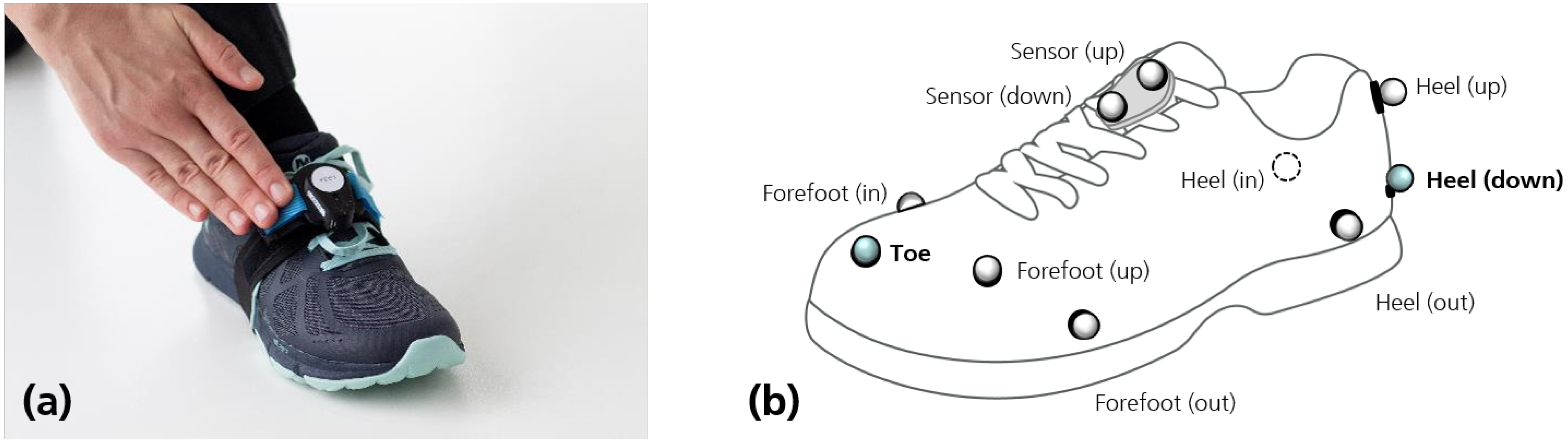
2.1. Dataset
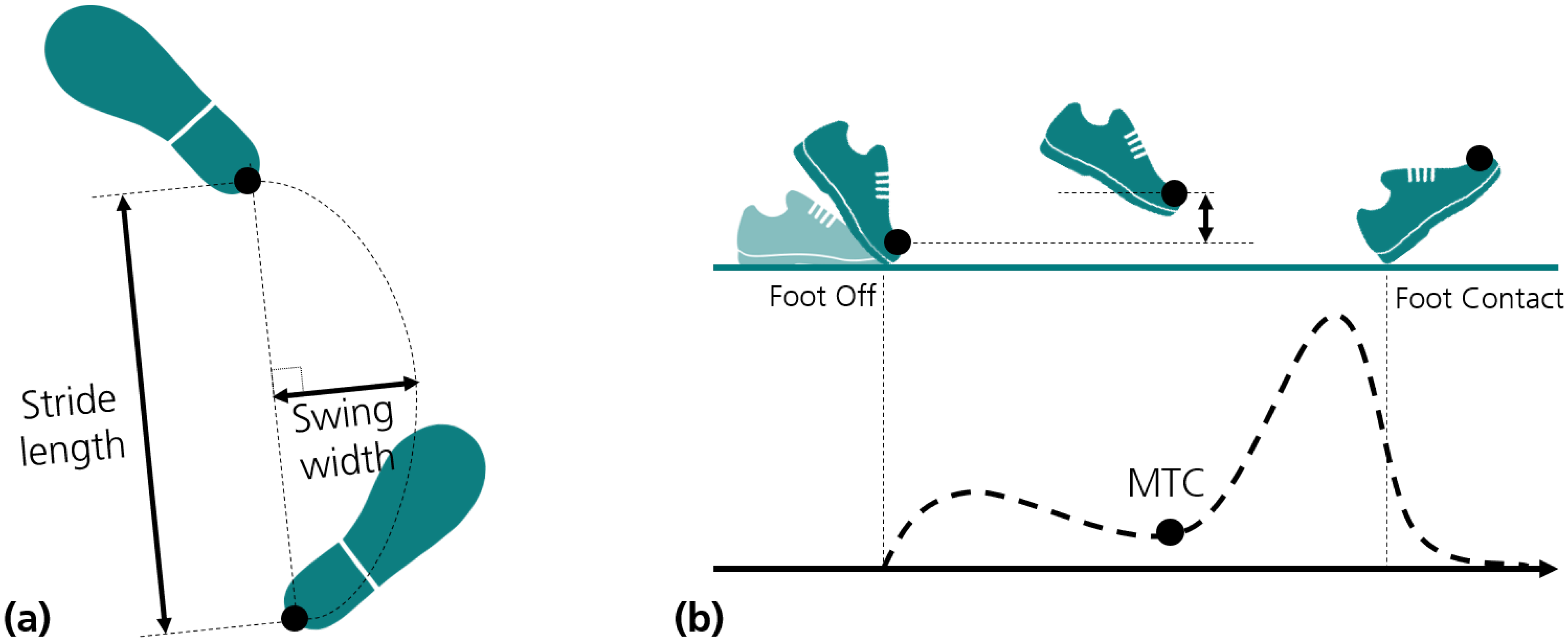
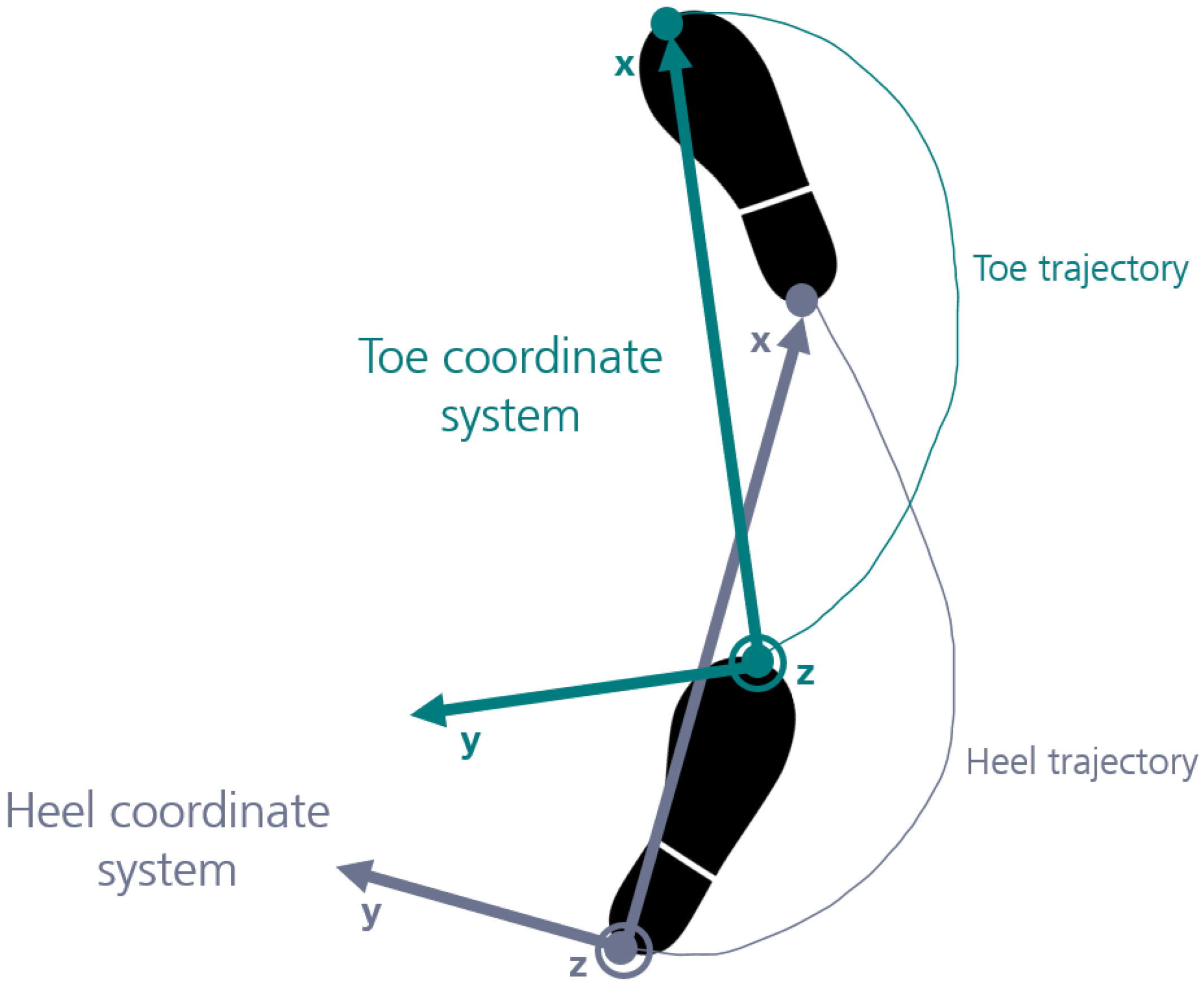
2.2. Reference Trajectories and Gait Parameters
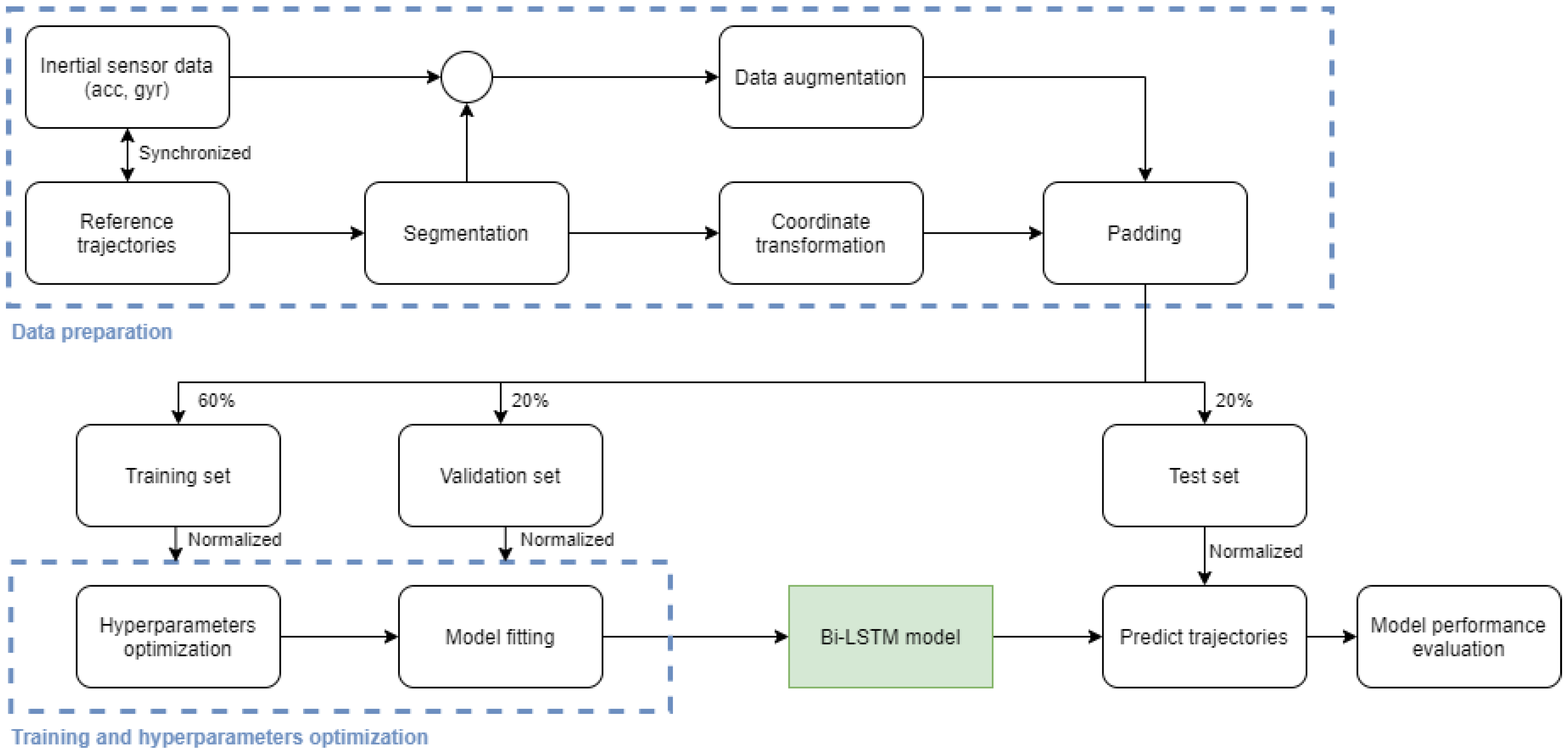
2.3. Data Preparation
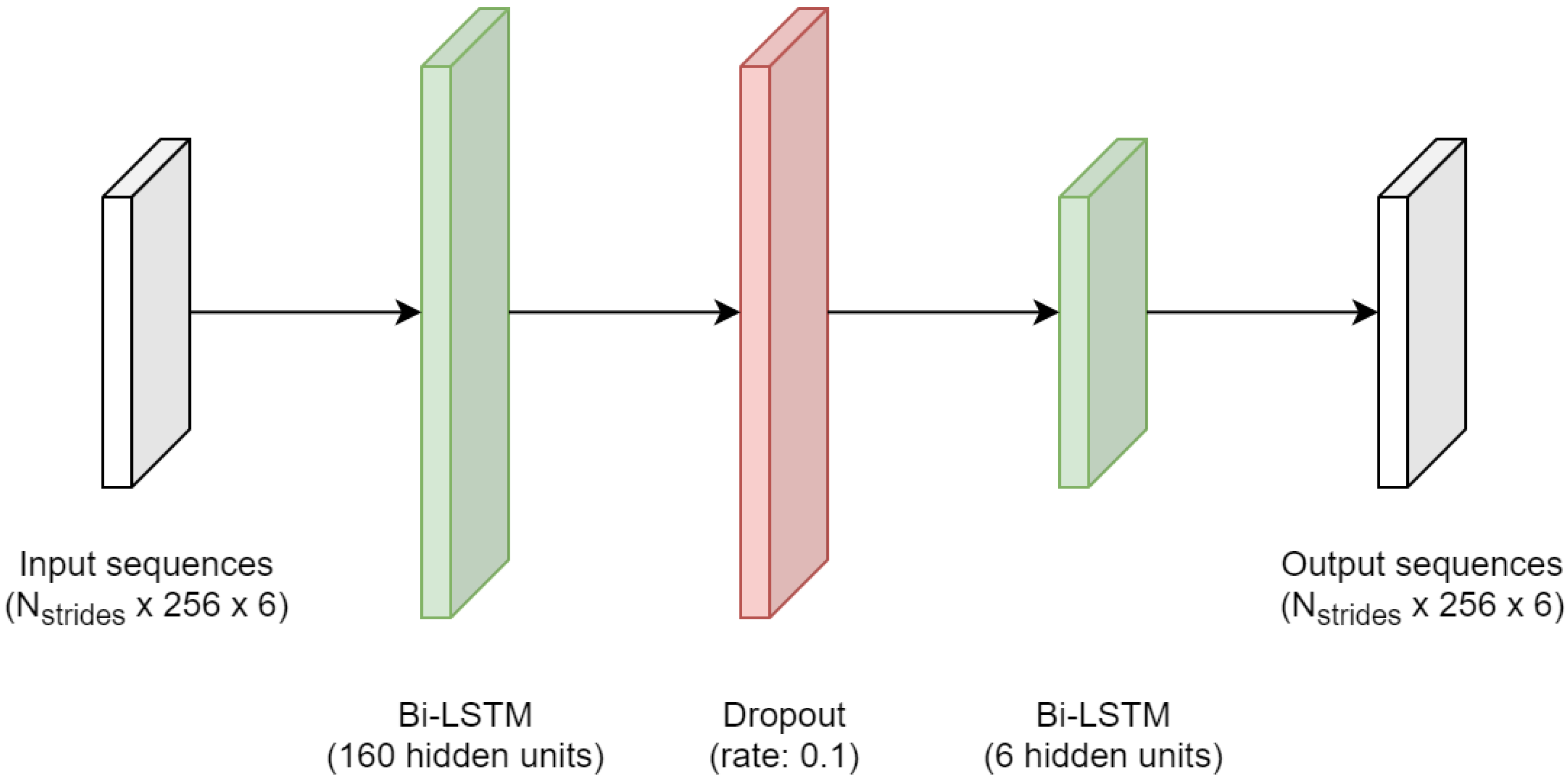
2.4. Network Architecture
2.5. Training and Hyperparameters Optimization
2.6. Model Performance Evaluation
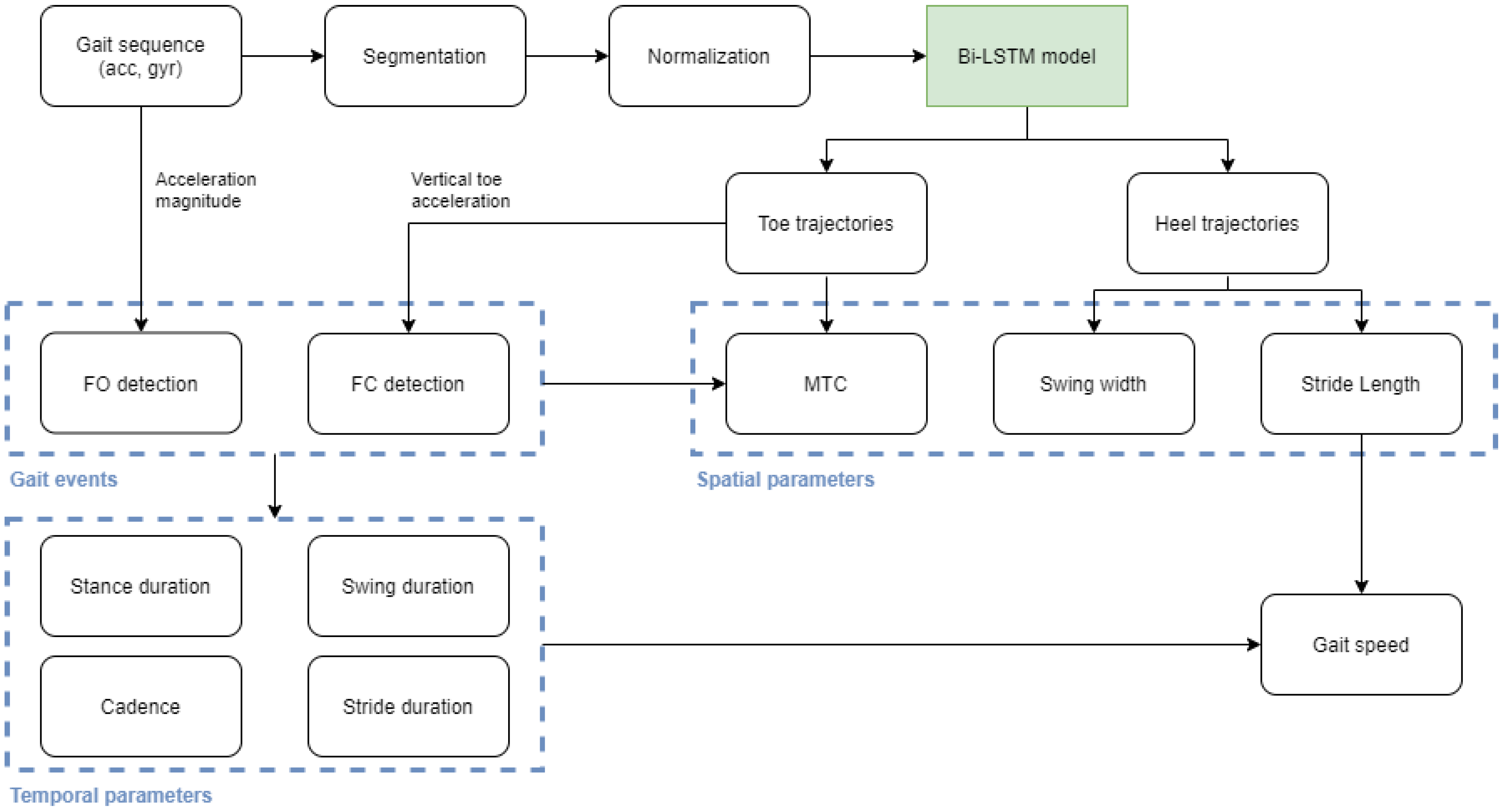
2.7. Gait Parameters from Predictions
2.8. Instrument Comparison and Validation
2.9. Comparison with the Conventional Gait Analysis Approach
3. Results
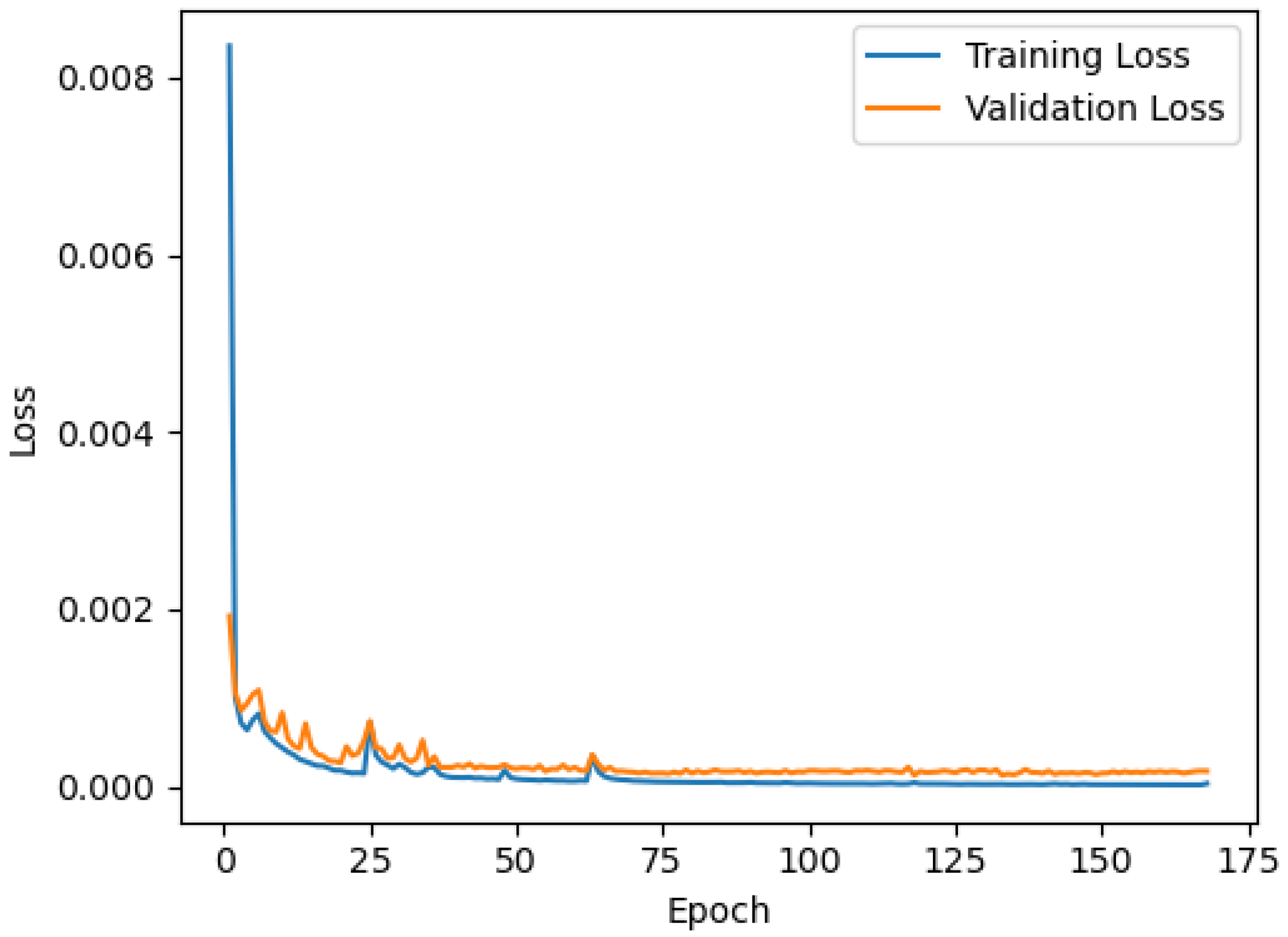
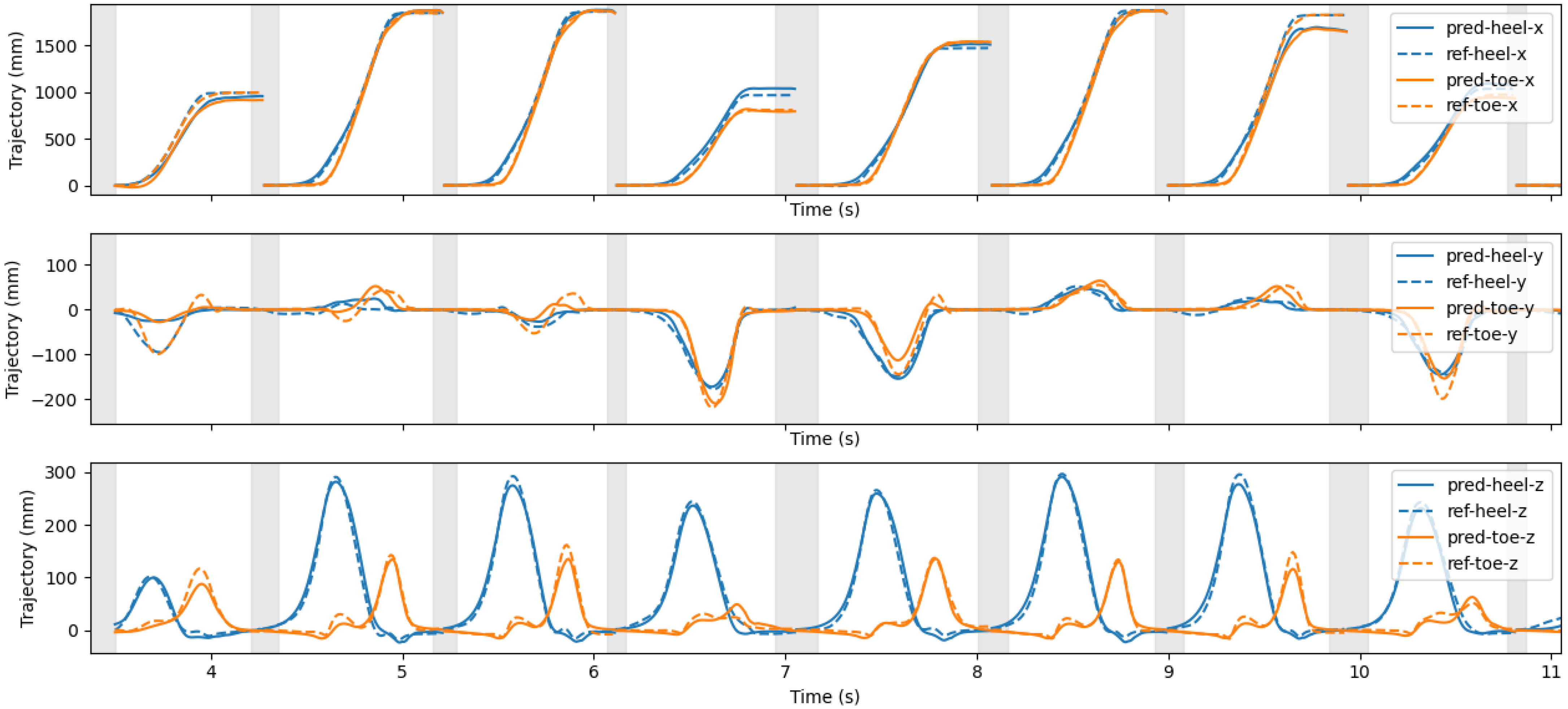
3.1. Network Training and Trajectories Estimation
3.2. Gait Parameters Using the Deep Learning Approach
3.3. Robustness to Changes in Orientation
3.4. Comparison with the Conventional Gait Analysis Approach
4. Discussion
4.1. Problem Formulation
4.2. Deep Learning-Based Gait Analysis Performance
4.3. Comparison with the Conventional Gait Analysis Approach
4.4. Framing our Method within the State-of-the-Art
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Freiberger, E.; Sieber, C.C.; Kob, R. Mobility in Older Community-Dwelling Persons: A Narrative Review. Front. Physiol. 2020, 11, 881. [Google Scholar] [CrossRef]
- Grande, G.; Triolo, F.; Nuara, A.; Welmer, A.K.; Fratiglioni, L.; Vetrano, D.L. Measuring gait speed to better identify prodromal dementia. Exp. Gerontol. 2019, 124, 110625. [Google Scholar] [CrossRef]
- Liu, B.; Hu, X.; Zhang, Q.; Fan, Y.; Li, J.; Zou, R.; Zhang, M.; Wang, X.; Wang, J. Usual walking speed and all-cause mortality risk in older people: A systematic review and meta-analysis. Gait Posture 2016, 44, 172–177. [Google Scholar] [CrossRef]
- Bridenbaugh, S.A.; Kressig, R.W. Laboratory Review: The Role of Gait Analysis in Seniors’ Mobility and Fall Prevention. Gerontology 2011, 57, 256–264. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Si, H.; Qiao, X.; Jin, Y.; Ji, L.; Liu, Q.; Bian, Y.; Wang, W.; Wang, C. Predictive value of intrinsic capacity on adverse outcomes among community-dwelling older adults. Geriatr. Nurs. 2021, 42, 1257–1263. [Google Scholar] [CrossRef]
- De Cock, A.M.; Fransen, E.; Perkisas, S.; Verhoeven, V.; Beauchet, O.; Vandewoude, M.; Remmen, R. Comprehensive Quantitative Spatiotemporal Gait Analysis Identifies Gait Characteristics for Early Dementia Subtyping in Community Dwelling Older Adults. Front. Neurol. 2019, 10, 313. [Google Scholar] [CrossRef] [Green Version]
- Ravi, D.K.; Gwerder, M.; König Ignasiak, N.; Baumann, C.R.; Uhl, M.; van Dieën, J.H.; Taylor, W.R.; Singh, N.B. Revealing the optimal thresholds for movement performance: A systematic review and meta-analysis to benchmark pathological walking behaviour. Neurosci. Biobehav. Rev. 2020, 108, 24–33. [Google Scholar] [CrossRef]
- Lindemann, U. Spatiotemporal gait analysis of older persons in clinical practice and research: Which parameters are relevant? Z. FüR Gerontol. Und Geriatr. 2020, 53, 171–178. [Google Scholar] [CrossRef]
- Chen, S.; Lach, J.; Lo, B.; Yang, G.Z. Toward Pervasive Gait Analysis With Wearable Sensors: A Systematic Review. IEEE J. Biomed. Health Inform. 2016, 20, 1521–1537. [Google Scholar] [CrossRef]
- Guimarães, V.; Sousa, I.; Correia, M.V. Gait events detection from heel and toe trajectories: Comparison of methods using multiple datasets. In Proceedings of the 2021 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Lausanne, Switzerland, 23–25 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mariani, B.; Jiménez, M.C.; Vingerhoets, F.J.G.; Aminian, K. On-Shoe Wearable Sensors for Gait and Turning Assessment of Patients with Parkinson’s Disease. IEEE Trans. Biomed. Eng. 2013, 60, 155–158. [Google Scholar] [CrossRef]
- Huxham, F.; Gong, J.; Baker, R.; Morris, M.; Iansek, R. Defining spatial parameters for non-linear walking. Gait Posture 2006, 23, 159–163. [Google Scholar] [CrossRef]
- Hori, K.; Mao, Y.; Ono, Y.; Ora, H.; Hirobe, Y.; Sawada, H.; Inaba, A.; Orimo, S.; Miyake, Y. Inertial Measurement Unit-Based Estimation of Foot Trajectory for Clinical Gait Analysis. Front. Physiol. 2020, 10, 1530. [Google Scholar] [CrossRef] [Green Version]
- Caldas, R.; Mundt, M.; Potthast, W.; Buarque de Lima Neto, F.; Markert, B. A systematic review of gait analysis methods based on inertial sensors and adaptive algorithms. Gait Posture 2017, 57, 204–210. [Google Scholar] [CrossRef]
- Conte Alcaraz, J.; Moghaddamnia, S.; Peissig, J. Efficiency of deep neural networks for joint angle modeling in digital gait assessment. EURASIP J. Adv. Signal Process. 2021, 2021, 10. [Google Scholar] [CrossRef]
- Mariani, B.; Hoskovec, C.; Rochat, S.; Büla, C.; Penders, J.; Aminian, K. 3D gait assessment in young and elderly subjects using foot-worn inertial sensors. J. Biomech. 2010, 43, 2999–3006. [Google Scholar] [CrossRef]
- Rampp, A.; Barth, J.; Schülein, S.; Gaßmann, K.G.; Klucken, J.; Eskofier, B.M. Inertial sensor-based stride parameter calculation from gait sequences in geriatric patients. IEEE Trans. Bio. Med. Eng. 2015, 62, 1089–1097. [Google Scholar] [CrossRef]
- Hamacher, D.; Hamacher, D.; Schega, L. Towards the importance of minimum toe clearance in level ground walking in a healthy elderly population. Gait Posture 2014, 40, 727–729. [Google Scholar] [CrossRef]
- Hannink, J.; Ollenschläger, M.; Kluge, F.; Roth, N.; Klucken, J.; Eskofier, B.M. Benchmarking Foot Trajectory Estimation Methods for Mobile Gait Analysis. Sensors 2017, 17, 1940. [Google Scholar] [CrossRef]
- Mariani, B.; Rochat, S.; Büla, C.J.; Aminian, K. Heel and Toe Clearance Estimation for Gait Analysis Using Wireless Inertial Sensors. IEEE Trans. Biomed. Eng. 2012, 59, 3162–3168. [Google Scholar] [CrossRef]
- Kanzler, C.M.; Barth, J.; Rampp, A.; Schlarb, H.; Rott, F.; Klucken, J.; Eskofier, B.M. Inertial sensor based and shoe size independent gait analysis including heel and toe clearance estimation. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5424–5427. [Google Scholar] [CrossRef]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Barth, J.; Schulein, S.; Gassmann, K.G.; Klucken, J.; Eskofier, B.M. Mobile Stride Length Estimation With Deep Convolutional Neural Networks. IEEE J. Biomed. Health Inform. 2018, 22, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Hannink, J.; Kautz, T.; Pasluosta, C.F.; Gasmann, K.G.; Klucken, J.; Eskofier, B.M. Sensor-Based Gait Parameter Extraction with Deep Convolutional Neural Networks. IEEE J. Biomed. Health Inform. 2017, 21, 85–93. [Google Scholar] [CrossRef] [Green Version]
- Silva do Monte Lima, J.P.; Uchiyama, H.; Taniguchi, R.I. End-to-End Learning Framework for IMU-Based 6-DOF Odometry. Sensors 2019, 19, 3777. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Lu, C.X.; Wahlstrom, J.; Markham, A.; Trigoni, N. Deep Neural Network Based Inertial Odometry Using Low-Cost Inertial Measurement Units. IEEE Trans. Mob. Comput. 2021, 20, 1351–1364. [Google Scholar] [CrossRef]
- Wang, Q.; Ye, L.; Luo, H.; Men, A.; Zhao, F.; Huang, Y. Pedestrian Stride-Length Estimation Based on LSTM and Denoising Autoencoders. Sensors 2019, 19, 840. [Google Scholar] [CrossRef] [Green Version]
- Asraf, O.; Shama, F.; Klein, I. PDRNet: A Deep-Learning Pedestrian Dead Reckoning Framework. IEEE Sens. J. 2021, 1, 1–8. [Google Scholar] [CrossRef]
- Guimarães, V.; Sousa, I.; Correia, M.V. Orientation-Invariant Spatio-Temporal Gait Analysis Using Foot-Worn Inertial Sensors. Sensors 2021, 21, 3940. [Google Scholar] [CrossRef]
- Shoemake, K. Uniform Random Rotations. In Graphics Gems III (IBM Version); Elsevier: Amsterdam, The Netherlands, 1992; pp. 124–132. [Google Scholar] [CrossRef]
- Tunca, C.; Salur, G.; Ersoy, C. Deep Learning for Fall Risk Assessment with Inertial Sensors: Utilizing Domain Knowledge in Spatio-Temporal Gait Parameters. IEEE J. Biomed. Health Inform. 2020, 24, 1994–2005. [Google Scholar] [CrossRef]
- Mundt, M.; Thomsen, W.; Witter, T.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of lower limb joint angles and moments during gait using artificial neural networks. Med. Biol. Eng. Comput. 2020, 58, 211–225. [Google Scholar] [CrossRef]
- Weber, D.; Gühmann, C.; Seel, T. Neural Networks Versus Conventional Filters for Inertial-Sensor-based Attitude Estimation. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Mundt, M.; Johnson, W.R.; Potthast, W.; Markert, B.; Mian, A.; Alderson, J. A Comparison of Three Neural Network Approaches for Estimating Joint Angles and Moments from Inertial Measurement Units. Sensors 2021, 21, 4535. [Google Scholar] [CrossRef]
- Mundt, M.; Koeppe, A.; Bamer, F.; David, S.; Markert, B. Artificial Neural Networks in Motion Analysis—Applications of Unsupervised and Heuristic Feature Selection Techniques. Sensors 2020, 20, 4581. [Google Scholar] [CrossRef]
- Esfahani, M.A.; Wang, H.; Wu, K.; Yuan, S. OriNet: Robust 3-D Orientation Estimation with a Single Particular IMU. IEEE Robot. Autom. Lett. 2020, 5, 399–406. [Google Scholar] [CrossRef]
- Xia, K.; Huang, J.; Wang, H. LSTM-CNN Architecture for Human Activity Recognition. IEEE Access 2020, 8, 56855–56866. [Google Scholar] [CrossRef]
- Zebin, T.; Sperrin, M.; Peek, N.; Casson, A.J. Human activity recognition from inertial sensor time-series using batch normalized deep LSTM recurrent networks. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Alawneh, L.; Mohsen, B.; Al-Zinati, M.; Shatnawi, A.; Al-Ayyoub, M. A Comparison of Unidirectional and Bidirectional LSTM Networks for Human Activity Recognition. In Proceedings of the 2020 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Austin, TX, USA, 23–27 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Martelloni, C.; Scapellato, S.; Cavallo, F. Assessment of walking features from foot inertial sensing. IEEE Trans.-Bio-Med. Eng. 2005, 52, 486–494. [Google Scholar] [CrossRef] [Green Version]
- Kluge, F.; Gaßner, H.; Hannink, J.; Pasluosta, C.; Klucken, J.; Eskofier, B. Towards Mobile Gait Analysis: Concurrent Validity and Test-Retest Reliability of an Inertial Measurement System for the Assessment of Spatio-Temporal Gait Parameters. Sensors 2017, 17, 1522. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L.; de Marmiesse, G.; Fu, Y.; Podivìn, J.; Schäfer, F.; et al. Keras Tuner. 2019. Available online: https://github.com/keras-team/keras-tuner (accessed on 7 July 2021).
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Skog, I.; Nilsson, J.O.; Handel, P. Evaluation of zero-velocity detectors for foot-mounted inertial navigation systems. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Altman, D.G.; Bland, J.M. Measurement in Medicine: The Analysis of Method Comparison Studies. Statistician 1983, 32, 307. [Google Scholar] [CrossRef]
- Mukaka, M. A guide to appropriate use of Correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Ornelas-Vences, C.; Sanchez-Fernandez, L.P.; Sanchez-Perez, L.A.; Garza-Rodriguez, A.; Villegas-Bastida, A. Fuzzy inference model evaluating turn for Parkinson’s disease patients. Comput. Biol. Med. 2017, 89, 379–388. [Google Scholar] [CrossRef]
- Delgado-Escano, R.; Castro, F.M.; Cozar, J.R.; Marin-Jimenez, M.J.; Guil, N. An End-to-End Multi-Task and Fusion CNN for Inertial-Based Gait Recognition. IEEE Access 2019, 7, 1897–1908. [Google Scholar] [CrossRef]
- Santhiranayagam, B.K.; Lai, D.T.; Sparrow, W.; Begg, R.K. A machine learning approach to estimate Minimum Toe Clearance using Inertial Measurement Units. J. Biomech. 2015, 48, 4309–4316. [Google Scholar] [CrossRef]
- Peyer, K.E.; Brassey, C.A.; Rose, K.A.; Sellers, W.I. Locomotion pattern and foot pressure adjustments during gentle turns in healthy subjects. J. Biomech. 2017, 60, 65–71. [Google Scholar] [CrossRef] [Green Version]
- Bonnyaud, C.; Pradon, D.; Bensmail, D.; Roche, N. Dynamic Stability and Risk of Tripping during the Timed Up and Go Test in Hemiparetic and Healthy Subjects. PLoS ONE 2015, 10, e0140317. [Google Scholar] [CrossRef] [Green Version]
- Tunca, C.; Pehlivan, N.; Ak, N.; Arnrich, B.; Salur, G.; Ersoy, C. Inertial Sensor-Based Robust Gait Analysis in Non-Hospital Settings for Neurological Disorders. Sensors 2017, 17, 825. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Wang, X.; Liu, X.; Liu, Q.; Song, J.; Sebe, N.; Kim, B. Explainable deep learning for efficient and robust pattern recognition: A survey of recent developments. Pattern Recognit. 2021, 120, 108102. [Google Scholar] [CrossRef]
- Tran, L.; Choi, D. Data Augmentation for Inertial Sensor-Based Gait Deep Neural Network. IEEE Access 2020, 8, 12364–12378. [Google Scholar] [CrossRef]
- Camargo, J.; Ramanathan, A.; Csomay-Shanklin, N.; Young, A. Automated gap-filling for marker-based biomechanical motion capture data. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 1180–1189. [Google Scholar] [CrossRef]
- Meyer, J.; Kuderer, M.; Muller, J.; Burgard, W. Online marker labeling for fully automatic skeleton tracking in optical motion capture. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5652–5657. [Google Scholar] [CrossRef]

| Partition | Number of Subjects | Number of Strides |
|---|---|---|
| Training set (60%) | 14 | 31,470 |
| Validation set (20%) | 6 | 13,872 |
| Test set (20%) | 6 | 12,474 |
| Parameter | Configuration Space | Optimal Configuration |
|---|---|---|
| Number of Units | 32–160 | 160 |
| Dropout | 0–0.30 | 0.1 |
| Learning Rate | – | |
| Batch Size | 100–400 | 100 |
| Metric | Validation Set | Test Set | ||
|---|---|---|---|---|
| Heel Traj. | Toe Traj. | Heel Traj. | Toe Traj. | |
| MSE (mm2) | ||||
| MAE (mm) | ||||
| RMSE (mm) | ||||
| Eucl. Dist. (mm) | ||||
| Parameter | IMU | VICON | Rel. Error | Abs. Error | Lim. Agr. | RMSE | Corr. † | Equival. ‡ |
|---|---|---|---|---|---|---|---|---|
| Stride dur. (s) | ||||||||
| Swing dur. (s) | ||||||||
| Stance dur. (s) | ||||||||
| Cad. (st/min) | ||||||||
| SL (cm) | ||||||||
| Speed (cm/s) | ||||||||
| SW (cm) | ||||||||
| MTC (cm) |
| Parameter | IMU | VICON | Rel. Error | Abs. Error | Lim. Agr. | RMSE | Corr. † | Equival. ‡ |
|---|---|---|---|---|---|---|---|---|
| Stride dur. (s) | ||||||||
| Swing dur. (s) | ||||||||
| Stance dur. (s) | ||||||||
| Cad. (st/min) | ||||||||
| SL (cm) | ||||||||
| Speed (cm/s) | ||||||||
| SW (cm) | ||||||||
| MTC (cm) |
| Parameter | Original Orientation | Random Orientation | RMSD | Correlation † | Equivalence ‡ |
|---|---|---|---|---|---|
| Stride dur. (s) | |||||
| Swing dur. (s) | |||||
| Stance dur. (s) | |||||
| Cad. (st/min) | |||||
| SL (cm) | |||||
| Speed (cm/s) | |||||
| SW (cm) | |||||
| MTC (cm) |
| Parameter | Including Turns | Excluding Turns | ||
|---|---|---|---|---|
| Deep Learning Approach | Conventional Approach | Deep Learning Approach | Conventional Approach | |
| Trajectories (mm) | (heel) (toe) | (sensor) | (heel) (toe) | (sensor) |
| Stride dur. (s) | ||||
| Swing dur. (s) | ||||
| Stance dur. (s) | ||||
| Cad. (st/min) | ||||
| SL (cm) | ||||
| Speed (cm/s) | ||||
| SW (cm) | ||||
| MTC (cm) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guimarães, V.; Sousa, I.; Correia, M.V. A Deep Learning Approach for Foot Trajectory Estimation in Gait Analysis Using Inertial Sensors. Sensors 2021, 21, 7517. https://doi.org/10.3390/s21227517
Guimarães V, Sousa I, Correia MV. A Deep Learning Approach for Foot Trajectory Estimation in Gait Analysis Using Inertial Sensors. Sensors. 2021; 21(22):7517. https://doi.org/10.3390/s21227517
Chicago/Turabian StyleGuimarães, Vânia, Inês Sousa, and Miguel Velhote Correia. 2021. "A Deep Learning Approach for Foot Trajectory Estimation in Gait Analysis Using Inertial Sensors" Sensors 21, no. 22: 7517. https://doi.org/10.3390/s21227517
APA StyleGuimarães, V., Sousa, I., & Correia, M. V. (2021). A Deep Learning Approach for Foot Trajectory Estimation in Gait Analysis Using Inertial Sensors. Sensors, 21(22), 7517. https://doi.org/10.3390/s21227517







