An Inertial Sensor-Based Gait Analysis Pipeline for the Assessment of Real-World Stair Ambulation Parameters
Abstract
:1. Introduction
- We present a new algorithmic pipeline that can extract stride-level temporal parameters from continuous IMU data, including level-walking and, specifically, stair-ambulation sequences.
- To enable a robust detection of individual strides within mixed gait-related activities, we extended an HMM-based segmentation approach by adding additional stride models to detect stair strides along with level-walking strides in continuous IMU data.
- The stride segmentation was combined with an adapted gait event detection algorithm to reliably estimate terminal and initial contact in the absence of a heel strike, which is often missing during stair walking.
- Stride-type classification was achieved through spatial features derived from a Kalman filter-based walking bout trajectory reconstruction and a subsequent walking bout assembly to ensure the high precision of the classification.
- Each individual pipeline step was evaluated on a new recorded dataset of 20 healthy participants walking on various stair configurations and at different speeds to enable a wide variety of strides, as expected during real-world studies. In total, around 16,000 stair strides and 13,000 level-walking strides, including pressure insole reference and video annotations, were available for evaluation.
- The entire pipeline was additionally validated end-to-end on the 20 healthy participants and additionally on an independent dataset of 13 PD patients.
2. Materials and Methods
2.1. Dataset
2.1.1. Evaluation Dataset
2.1.2. Validation Dataset
2.2. Sensor System and Measurement Setup
2.3. Coordinate Transformation
2.4. Reference Labels
2.4.1. Stride Borders
2.4.2. Stride Class Labels
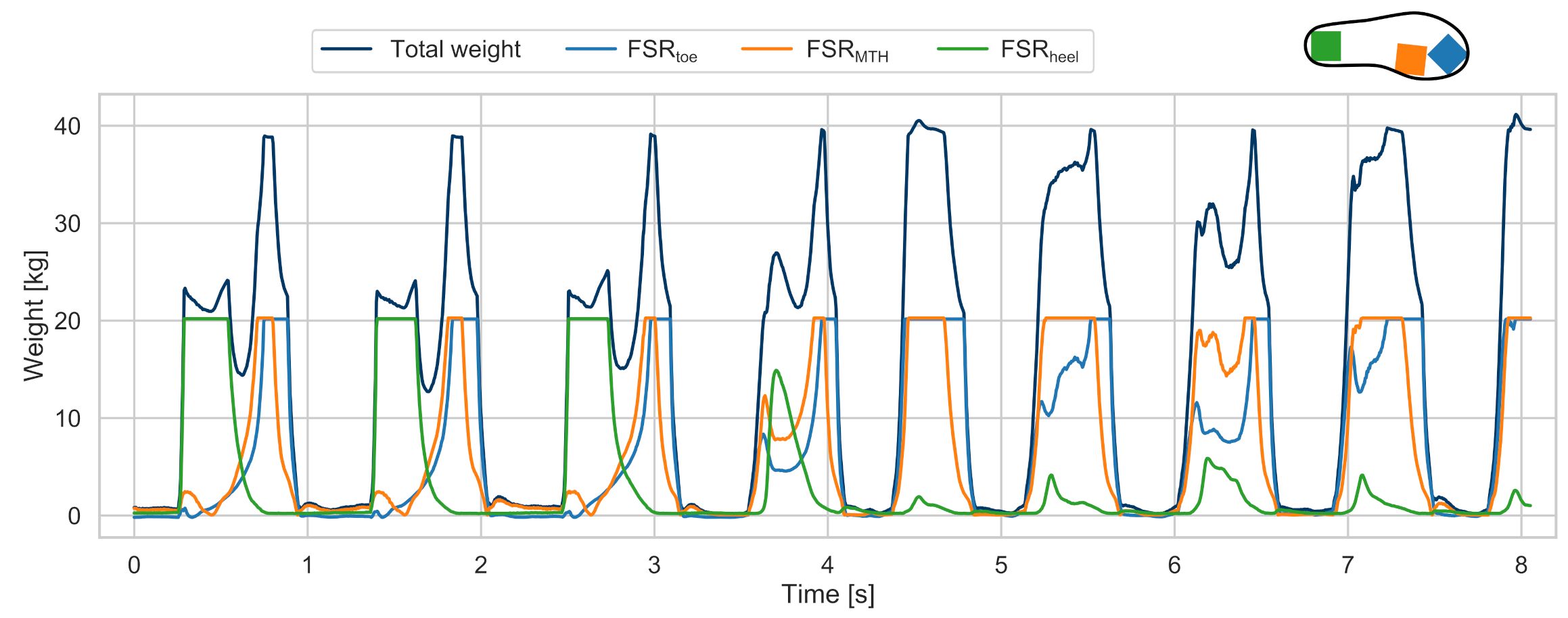
2.4.3. Pressure Insole Reference
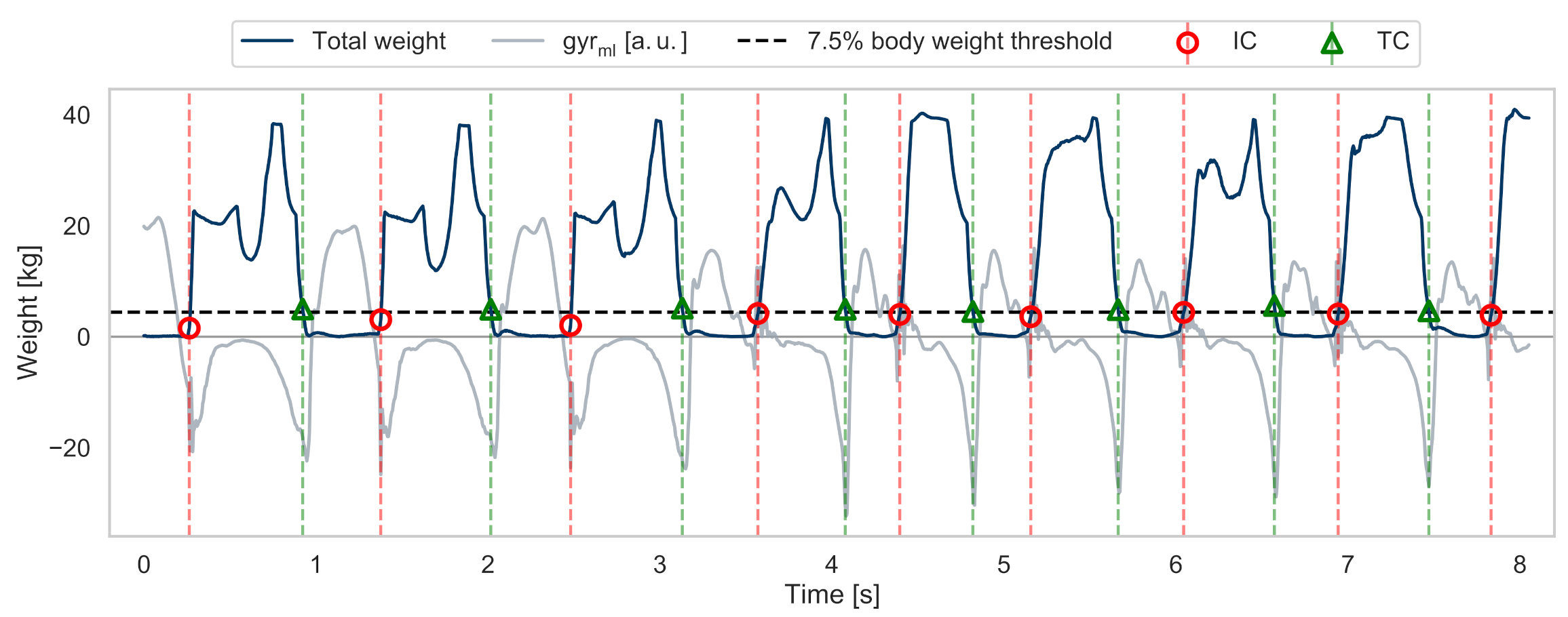
2.4.4. Reference Gait Events
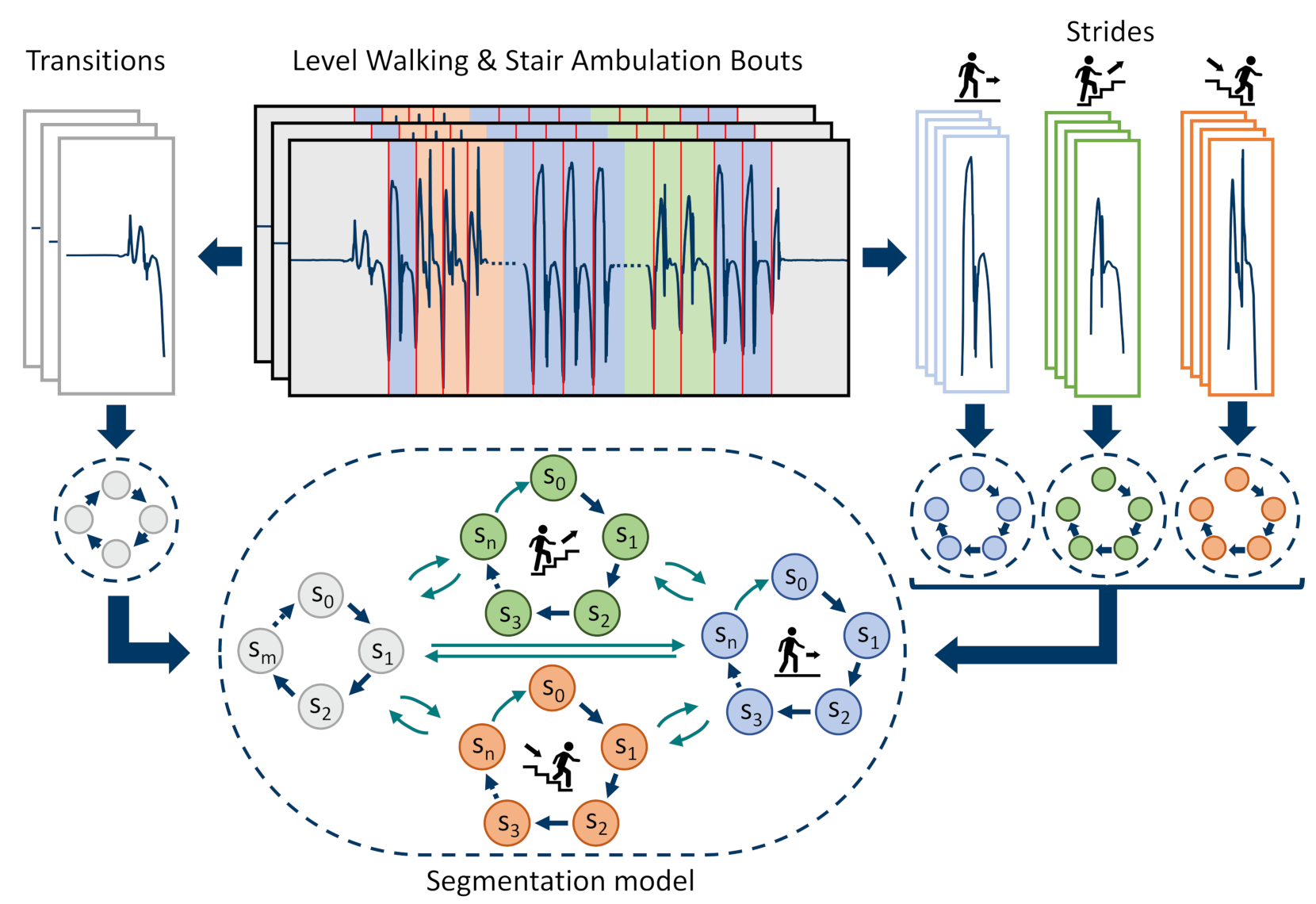
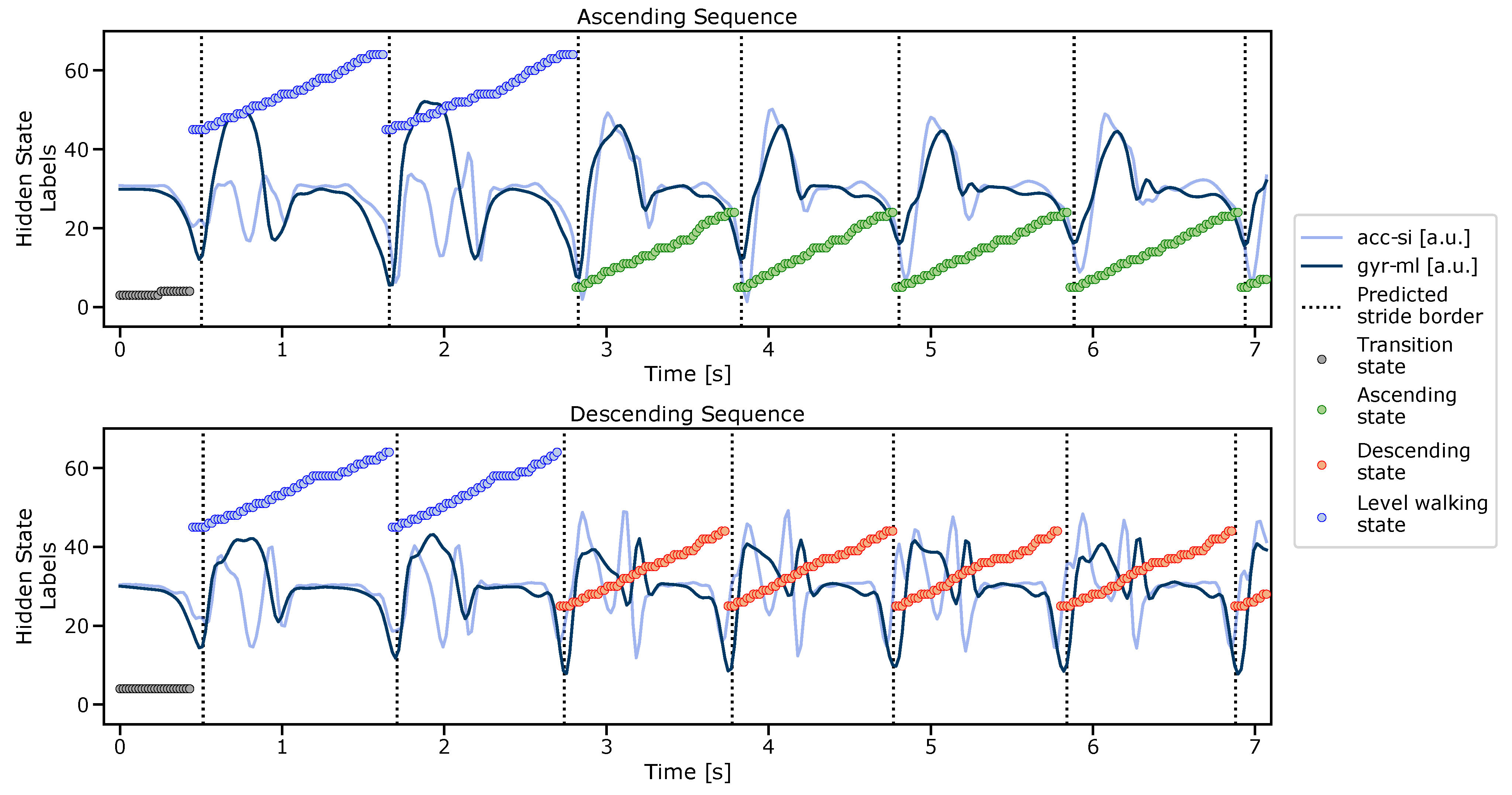
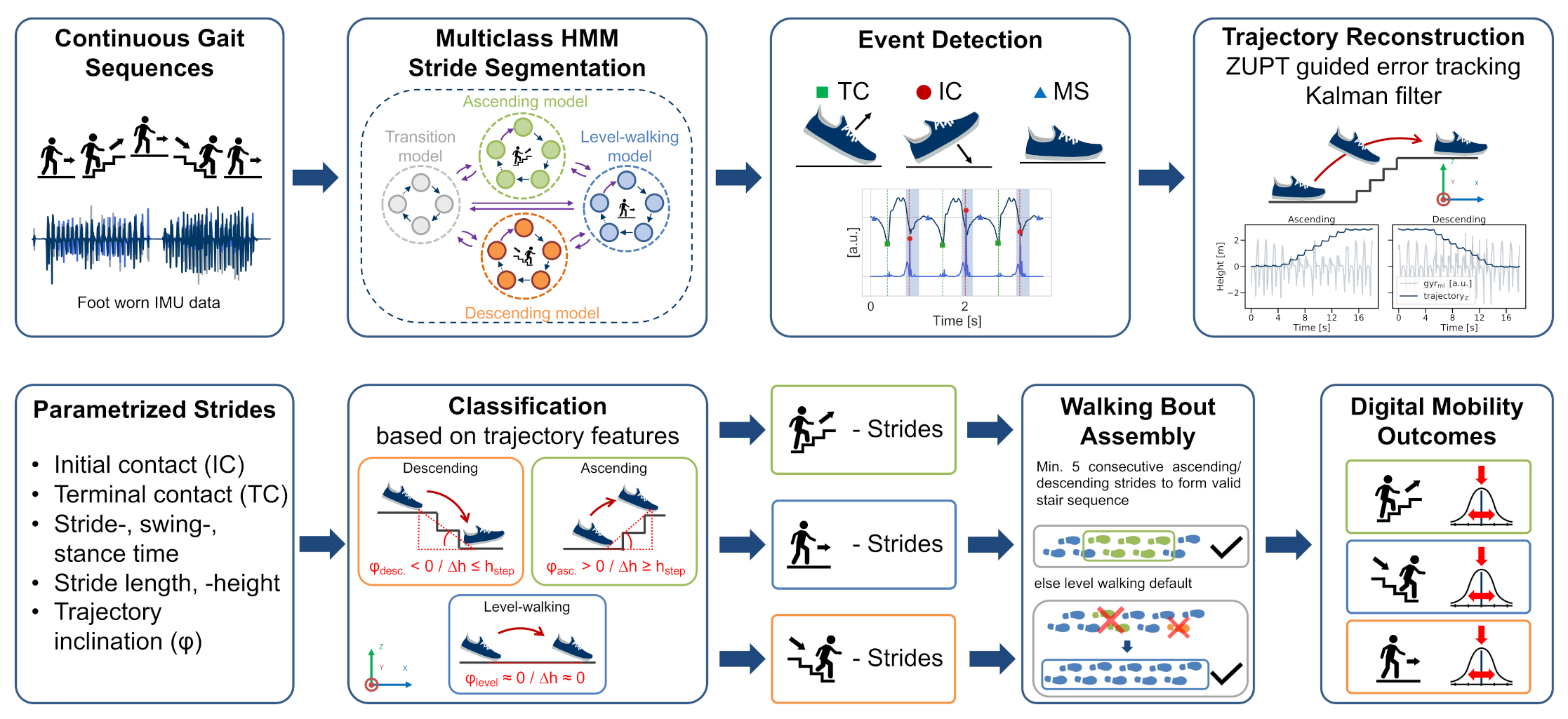
2.5. Multiclass Hidden Markov Model
2.5.1. Model Architecture
2.5.2. Model Training
2.5.3. Stride Border Prediction
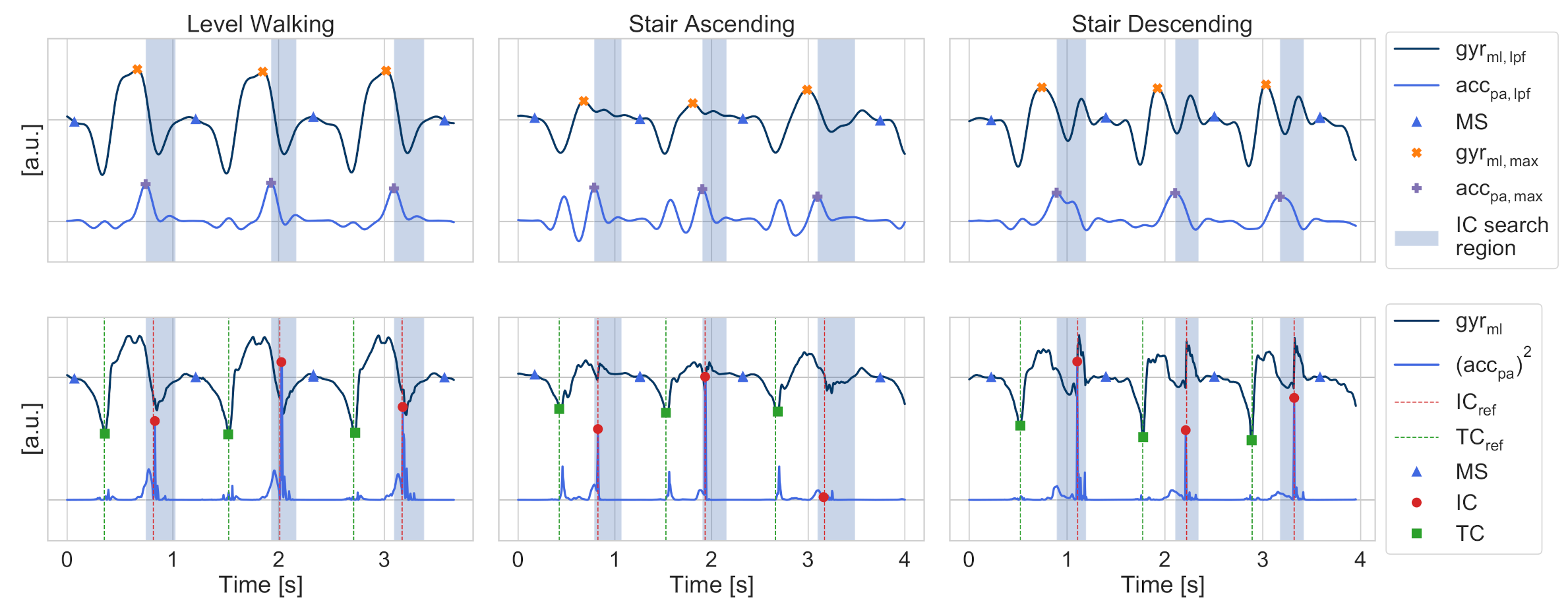
2.6. Event Detection and Parameter Extraction
2.6.1. Terminal Contact (TC)
2.6.2. Mid Stance (MS)
2.6.3. Swing and Forward Acceleration Maximum
2.6.4. Initial Contact (IC)
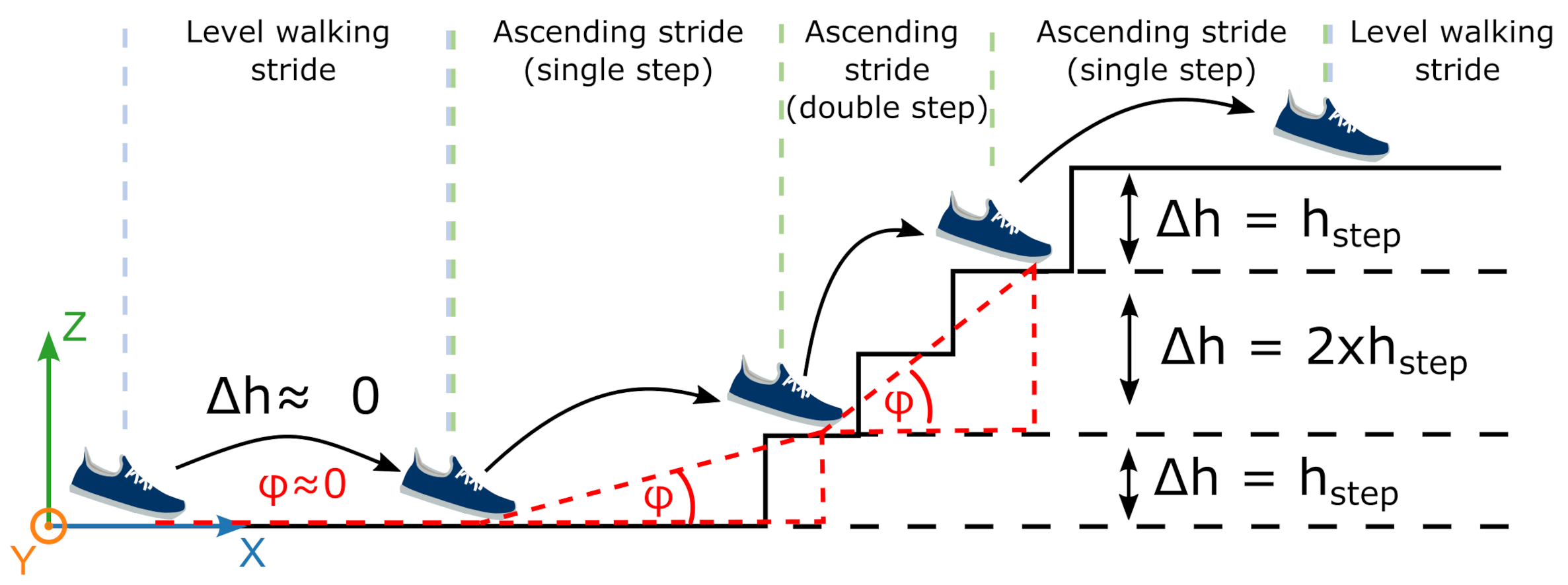
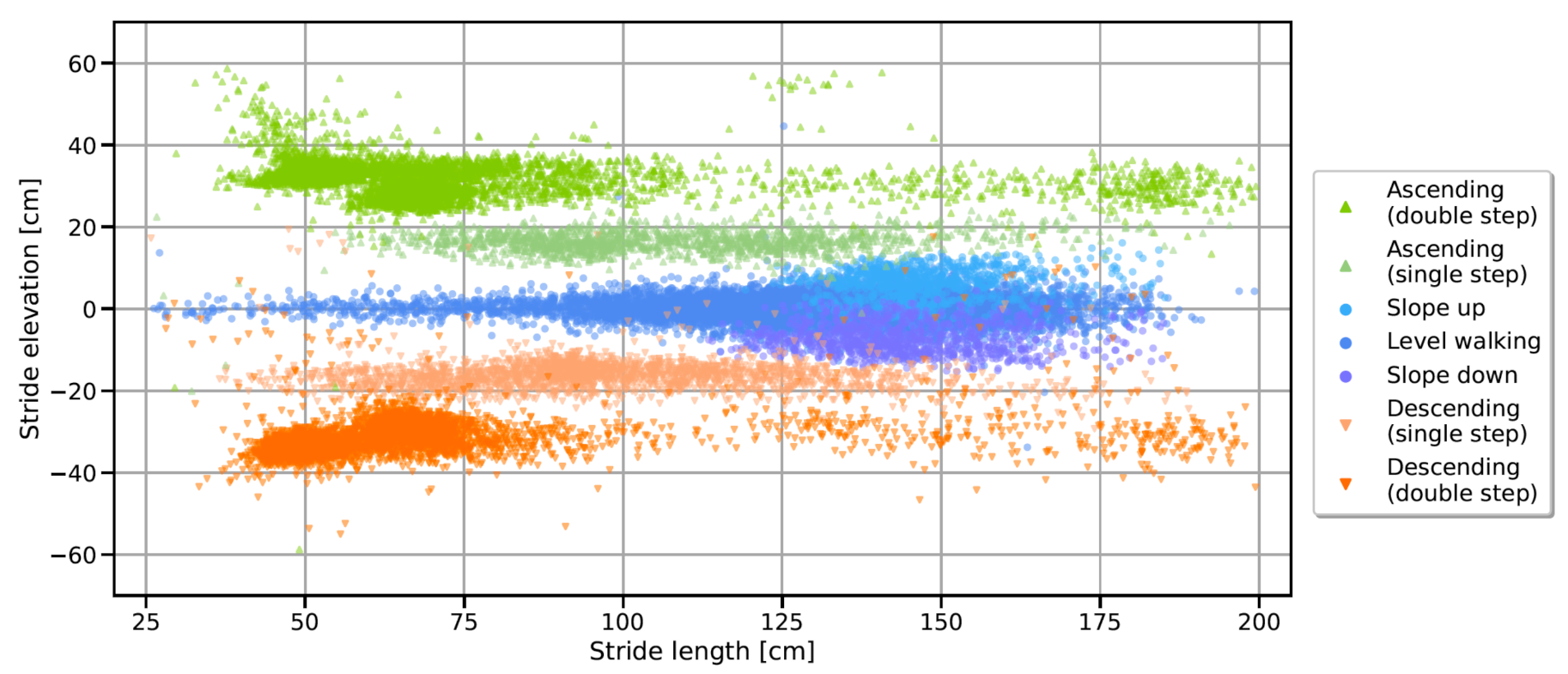
2.7. Stride-Type Classification
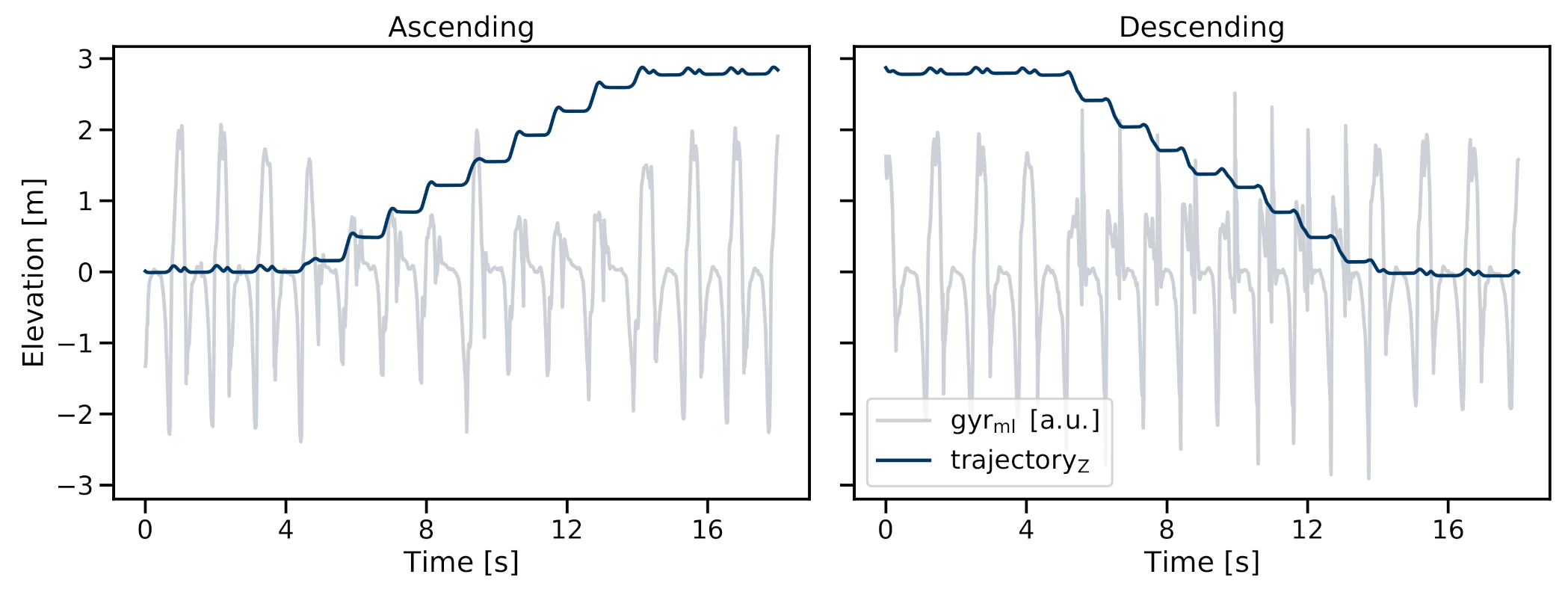
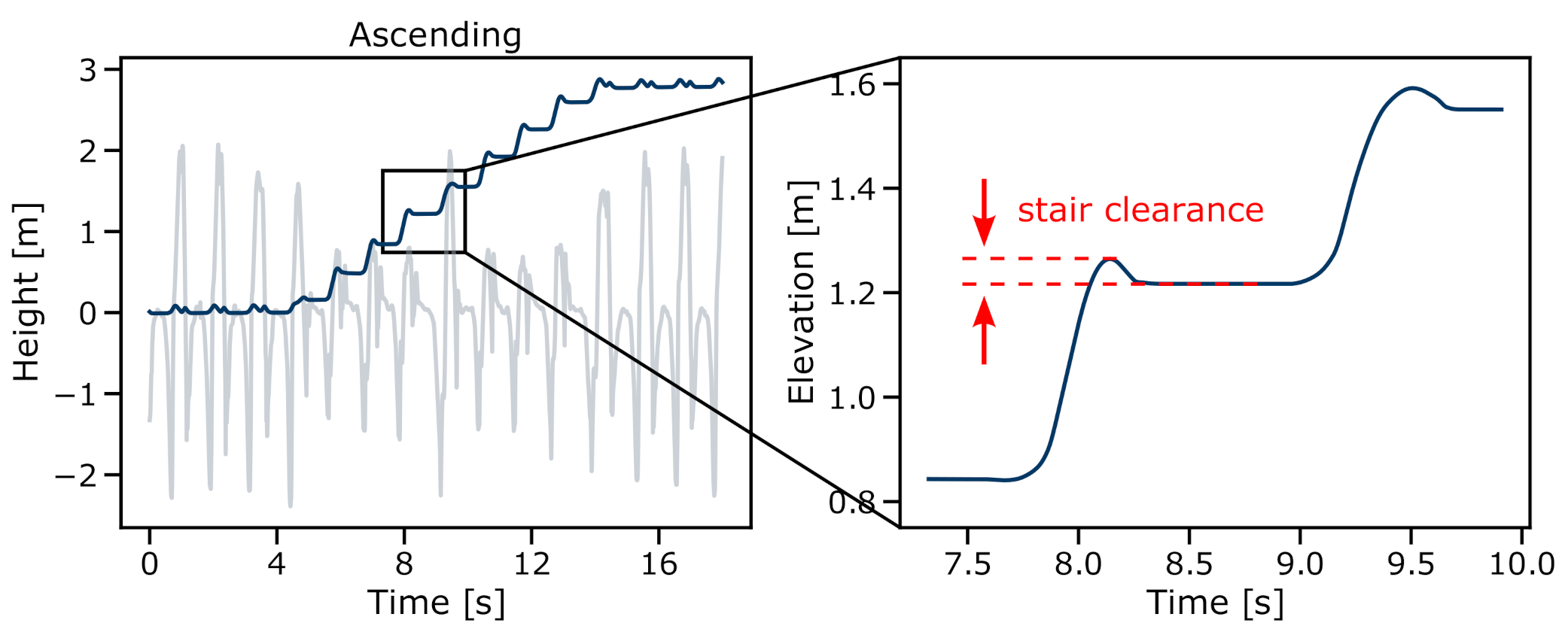
2.8. Walking Bout Trajectory Reconstruction
2.8.1. Zero Velocity Update
2.8.2. Error-Tracking Kalman Filter
2.8.3. Spatial Stride Features
2.9. Walking Bout Assembly
3. Evaluation
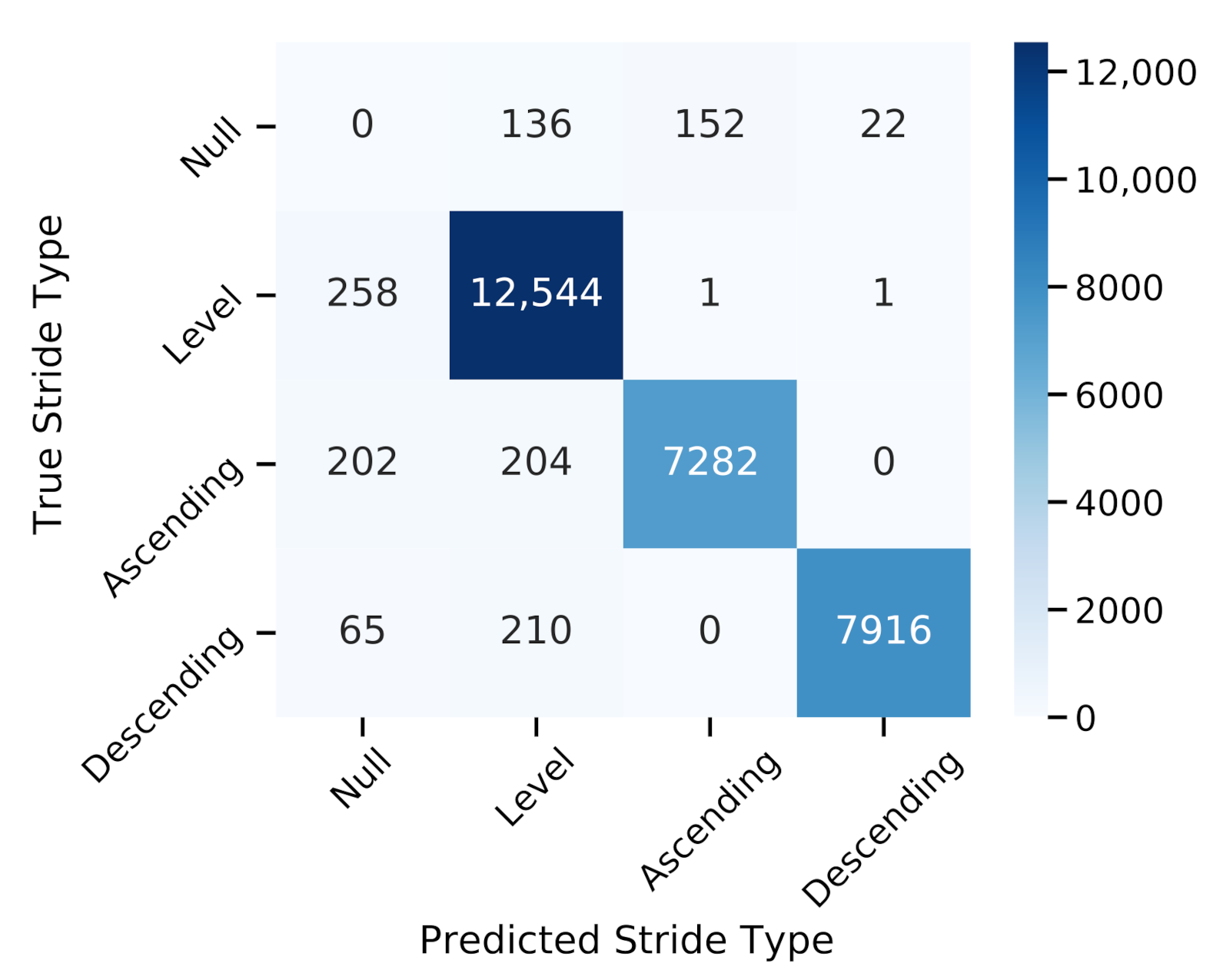
3.1. Stride Segmentation
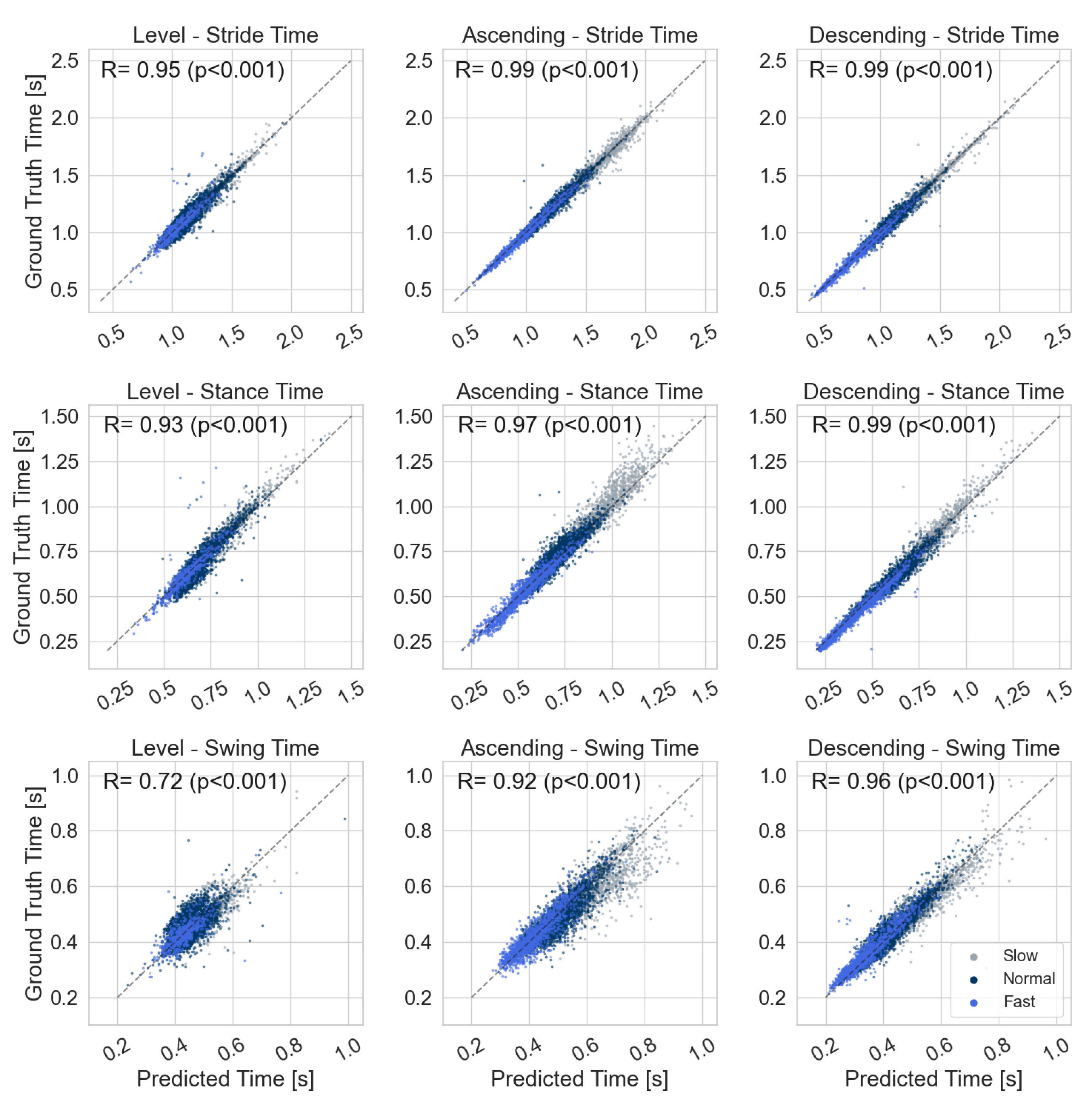
3.2. Event Detection
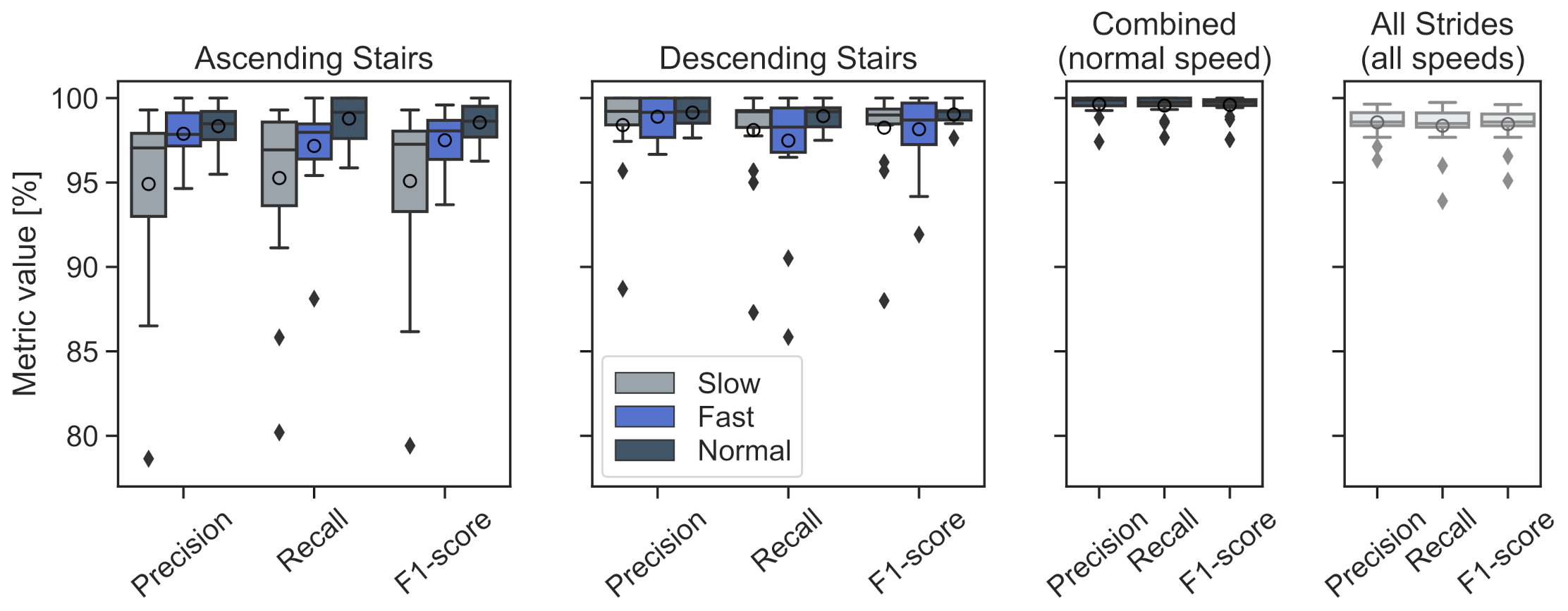
3.3. Stride-Type Classification
3.4. Full Pipeline Validation
4. Results
4.1. Stride Segmentation
4.2. Event Detection
4.3. Spatial Stride Features
4.4. Stride-Type Classification
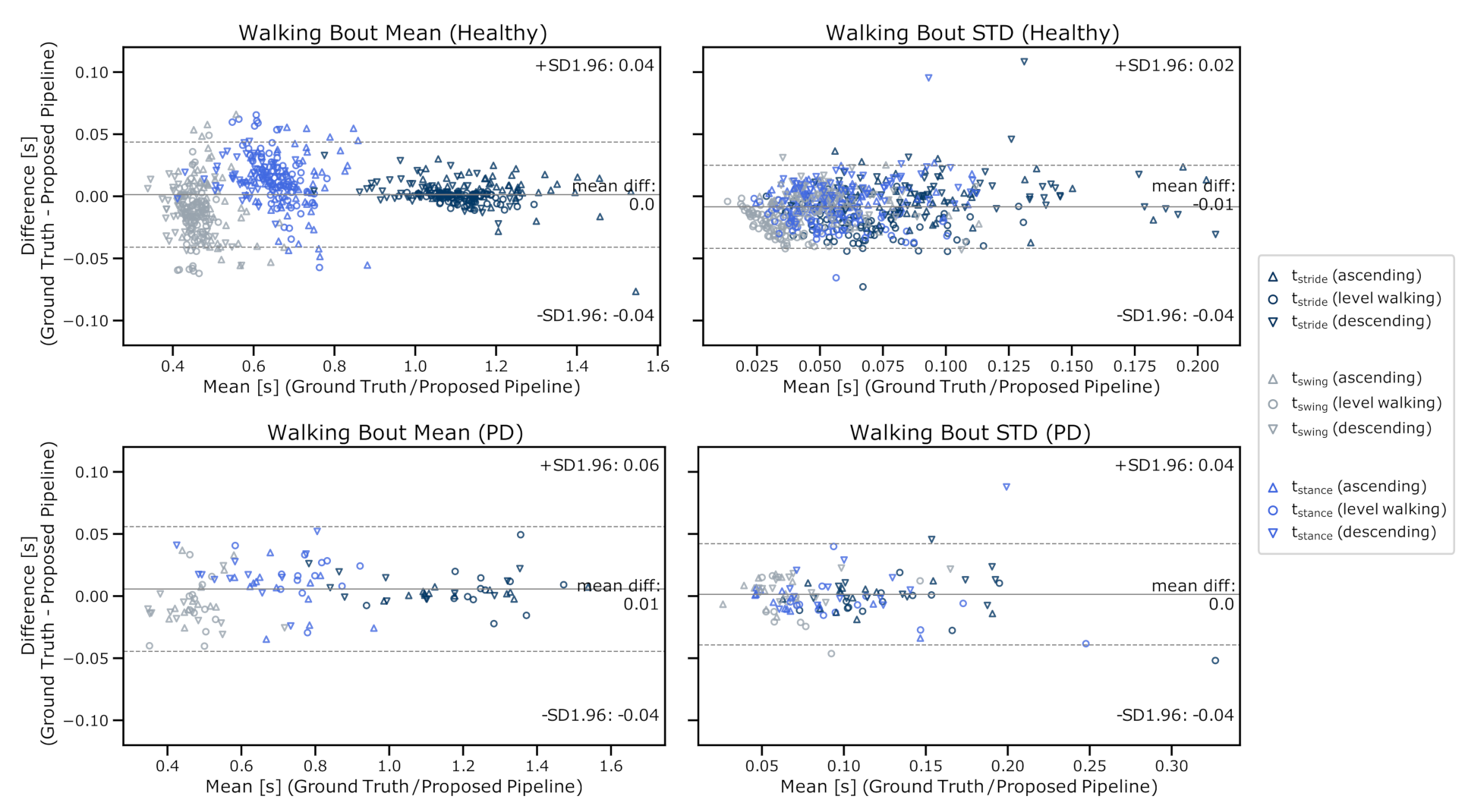
4.5. Full Pipeline Validation
5. Discussion
5.1. Datasets
5.2. Stride Segmentation
5.3. Gait Event Detection
5.4. Spatial Features and Stride-Type Classification
5.5. Full Pipeline Validation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DMO | Digital mobility outcome |
| ETKF | Error tracking Kalman filter |
| FN | False negative |
| FP | False positive |
| HMM | Hidden Markov model |
| IC | Initial contact |
| IRQ | Interquartile range |
| MS | Mid stance |
| PD | Parkinson’s disease |
| TC | Terminal contact |
| UPDRS | Unified Parkinson’s disease rating scale |
| ZUPT | Zero velocity update |
References
- Alzahrani, M.A.; Dean, C.M.; Ada, L. Ability to negotiate stairs predicts free-living physical activity in community-dwelling people with stroke: An observational study. Aust. J. Physiother. 2009, 55, 277–281. [Google Scholar] [CrossRef] [Green Version]
- Conway, Z.J.; Silburn, P.A.; Blackmore, T.; Cole, M.H. Evidence of compensatory joint kinetics during stair ascent and descent in Parkinson’s disease. Gait Posture 2017, 52, 33–39. [Google Scholar] [CrossRef]
- Nadeau, S.; McFadyen, B.J.; Malouin, F. Frontal and sagittal plane analyses of the stair climbing task in healthy adults aged over 40 years: What are the challenges compared to level walking? Clin. Biomech. 2003, 18, 950–959. [Google Scholar] [CrossRef]
- Jacobs, J.V. A review of stairway falls and stair negotiation: Lessons learned and future needs to reduce injury. Gait Posture 2016, 49, 159–167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tiedemann, A.C.; Sherrington, C.; Lord, S.R. Physical and psychological factors associated with stair negotiation performance in older people. J. Gerontol. Ser. Biol. Sci. Med. Sci. 2007, 62, 1259–1265. [Google Scholar] [CrossRef] [PubMed]
- van Iersel, M.B.; Rikkert, M.G.O.; Mulley, G.P. Is stair negotiation measured appropriately in functional assessment scales? Clin. Rehabil. 2003, 17, 325–333. [Google Scholar] [CrossRef] [PubMed]
- Beghi, E.; Gervasoni, E.; Pupillo, E.; Bianchi, E.; Montesano, A.; Aprile, I.; Agostini, M.; Rovaris, M.; Cattaneo, D.; Iacobone, G.; et al. Prediction of falls in subjects suffering from Parkinson disease, multiple sclerosis, and stroke. Arch. Phys. Med. Rehabil. 2018, 99, 641–651. [Google Scholar] [CrossRef] [PubMed]
- Muro-De-La-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait analysis methods: An overview of wearable and non-wearable systems, highlighting clinical applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef] [Green Version]
- Benson, L.C.; Clermont, C.A.; Bošnjak, E.; Ferber, R. The use of wearable devices for walking and running gait analysis outside of the lab: A systematic review. Gait Posture 2018, 63, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Sica, M.; Tedesco, S.; Crowe, C.; Kenny, L.; Moore, K.; Timmons, S.; Barton, J.; O’Flynn, B.; Komaris, D.S. Continuous home monitoring of Parkinson’s disease using inertial sensors: A systematic review. PLoS ONE 2021, 16, e0246528. [Google Scholar] [CrossRef]
- Del Din, S.; Godfrey, A.; Mazzà, C.; Lord, S.; Rochester, L. Free-living monitoring of Parkinson’s disease: Lessons from the field. Mov. Disord. 2016, 31, 1293–1313. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Godfrey, A.; Galna, B.; Lord, S.; Rochester, L. Free-living gait characteristics in ageing and Parkinson’s disease: Impact of environment and ambulatory bout length. J. Neuroeng. Rehabil. 2016, 13, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Del Din, S.; Galna, B.; Godfrey, A.; Bekkers, E.M.; Pelosin, E.; Nieuwhof, F.; Mirelman, A.; Hausdorff, J.M.; Rochester, L. Analysis of free-living gait in older adults with and without Parkinson’s disease and with and without a history of falls: Identifying generic and disease-specific characteristics. J. Gerontol. Ser. A 2019, 74, 500–506. [Google Scholar] [CrossRef] [PubMed]
- Lueken, M.; ten Kate, W.; Batista, J.P.; Ngo, C.; Bollheimer, C.; Leonhardt, S. Peak detection algorithm for gait segmentation in long-term monitoring for stride time estimation using inertial measurement sensors. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical, Chicago, IL, USA, 19–22 May 2019, Health Informatics (BHI); pp. 1–4.
- Barth, J.; Oberndorfer, C.; Pasluosta, C.; Schülein, S.; Gassner, H.; Reinfelder, S.; Kugler, P.; Schuldhaus, D.; Winkler, J.; Klucken, J.; et al. Stride segmentation during free walk movements using multi-dimensional subsequence dynamic time warping on inertial sensor data. Sensors 2015, 15, 6419–6440. [Google Scholar] [CrossRef] [PubMed]
- Mannini, A.; Trojaniello, D.; Della Croce, U.; Sabatini, A.M. Hidden markov model-based strategy for gait segmentation using inertial sensors: Application to elderly, hemiparetic patients and huntington’s disease patients. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5179–5182. [Google Scholar]
- Haji Ghassemi, N.; Hannink, J.; Martindale, C.F.; Gaßner, H.; Müller, M.; Klucken, J.; Eskofier, B.M. Segmentation of gait sequences in sensor-based movement analysis: A comparison of methods in Parkinson’s disease. Sensors 2018, 18, 145. [Google Scholar] [CrossRef] [Green Version]
- Roth, N.; Küderle, A.; Ullrich, M.; Gladow, T.; Marxreiter, F.; Klucken, J.; Eskofier, B.M.; Kluge, F. Hidden Markov Model based stride segmentation on unsupervised free-living gait data in Parkinson’s disease patients. J. Neuroeng. Rehabil. 2021, 18, 1–15. [Google Scholar] [CrossRef]
- Steinmetzer, T.; Bönninger, I.; Reckhardt, M.; Reinhardt, F.; Erk, D.; Travieso, C.M. Comparison of algorithms and classifiers for stride detection using wearables. Neural Comput. Appl. 2020, 32, 17857–17868. [Google Scholar] [CrossRef]
- Gadaleta, M.; Cisotto, G.; Rossi, M.; Rehman, R.Z.U.; Rochester, L.; Del Din, S. Deep learning techniques for improving digital gait segmentation. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 1834–1837. [Google Scholar]
- Rueterbories, J.; Spaich, E.G.; Larsen, B.; Andersen, O.K. Methods for gait event detection and analysis in ambulatory systems. Med. Eng. Phys. 2010, 32, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Coley, B.; Najafi, B.; Paraschiv-Ionescu, A.; Aminian, K. Stair climbing detection during daily physical activity using a miniature gyroscope. Gait Posture 2005, 22, 287–294. [Google Scholar] [CrossRef]
- Formento, P.C.; Acevedo, R.; Ghoussayni, S.; Ewins, D. Gait event detection during stair walking using a rate gyroscope. Sensors 2014, 14, 5470–5485. [Google Scholar] [CrossRef] [Green Version]
- Figueiredo, J.; Felix, P.; Costa, L.; Moreno, J.C.; Santos, C.P. Gait event detection in controlled and real-life situations: Repeated measures from healthy subjects. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 1945–1956. [Google Scholar] [CrossRef] [PubMed]
- Preece, S.J.; Goulermas, J.Y.; Kenney, L.P.; Howard, D.; Meijer, K.; Crompton, R. Activity identification using body-mounted sensors—a review of classification techniques. Physiol. Meas. 2009, 30, R1. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Yan, J.; Xu, Y. Gait pattern classification with integrated shoes. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 833–839. [Google Scholar]
- Bartlett, H.L.; Goldfarb, M. A phase variable approach for IMU-based locomotion activity recognition. IEEE Trans. Biomed. Eng. 2017, 65, 1330–1338. [Google Scholar] [CrossRef]
- Song, M.; Kim, J. An ambulatory gait monitoring system with activity classification and gait parameter calculation based on a single foot inertial sensor. IEEE Trans. Biomed. Eng. 2017, 65, 885–893. [Google Scholar] [CrossRef]
- Wang, K.; Delbaere, K.; Brodie, M.A.; Lovell, N.H.; Kark, L.; Lord, S.R.; Redmond, S.J. Differences between gait on stairs and flat surfaces in relation to fall risk and future falls. IEEE J. Biomed. Health Informatics 2017, 21, 1479–1486. [Google Scholar] [CrossRef]
- Schlachetzki, J.C.; Barth, J.; Marxreiter, F.; Gossler, J.; Kohl, Z.; Reinfelder, S.; Gassner, H.; Aminian, K.; Eskofier, B.M.; Winkler, J.; et al. Wearable sensors objectively measure gait parameters in Parkinson’s disease. PLoS ONE 2017, 12, e0183989. [Google Scholar] [CrossRef]
- Ferraris, F.; Grimaldi, U.; Parvis, M. Procedure for effortless in-field calibration of three-axis rate gyros and accelerometers. Sens. Mater. 1995, 7, 311. [Google Scholar]
- Riener, R.; Rabuffetti, M.; Frigo, C. Stair ascent and descent at different inclinations. Gait Posture 2002, 15, 32–44. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Ladin, Z.; Wei, J.Y. Footswitch system for measurement of the temporal parameters of gait. J. Biomech. 1995, 28, 347–351. [Google Scholar] [CrossRef]
- Pappas, I.P.; Popovic, M.R.; Keller, T.; Dietz, V.; Morari, M. A reliable gait phase detection system. IEEE Trans. Neural Syst. Rehabil. Eng. 2001, 9, 113–125. [Google Scholar] [CrossRef]
- Bobić, V.N.; Djurić-Jovièić, M.D.; Radovanović, S.M.; Dragaević, N.T.; Kostić, V.S.; Popović, M.B. Challenges of stride segmentation and their implementation for impaired gait. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 2284–2287. [Google Scholar]
- Catalfamo, P.; Moser, D.; Ghoussayni, S.; Ewins, D. Detection of gait events using an F-Scan in-shoe pressure measurement system. Gait Posture 2008, 28, 420–426. [Google Scholar] [CrossRef] [PubMed]
- Rampp, A.; Barth, J.; Schülein, S.; Gaßmann, K.G.; Klucken, J.; Eskofier, B.M. Inertial sensor-based stride parameter calculation from gait sequences in geriatric patients. IEEE Trans. Biomed. Eng. 2014, 62, 1089–1097. [Google Scholar] [CrossRef] [PubMed]
- MacDougall, H.G.; Moore, S.T. Marching to the beat of the same drummer: The spontaneous tempo of human locomotion. J. Appl. Physiol. 2005, 99, 1164–1173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tunca, C.; Pehlivan, N.; Ak, N.; Arnrich, B.; Salur, G.; Ersoy, C. Inertial sensor-based robust gait analysis in non-hospital settings for neurological disorders. Sensors 2017, 17, 825. [Google Scholar] [CrossRef] [Green Version]
- Skog, I.; Handel, P.; Nilsson, J.O.; Rantakokko, J. Zero-velocity detection—An algorithm evaluation. IEEE Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef]
- Colomar, D.S.; Nilsson, J.O.; Händel, P. Smoothing for ZUPT-aided INSs. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, Australia, 13–15 November 2012; pp. 1–5. [Google Scholar]
- Kluge, F.; Del Din, S.; Cereatti, A.; Gassner, H.; Hansen, C.; Helbostad, J.L.; Klucken, J.; Kuederle, A.; Mueller, A.; Rochester, L.; et al. Consensus based framework for digital mobility monitoring. PLoS ONE 2021, 16, e0256541. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef] [Green Version]
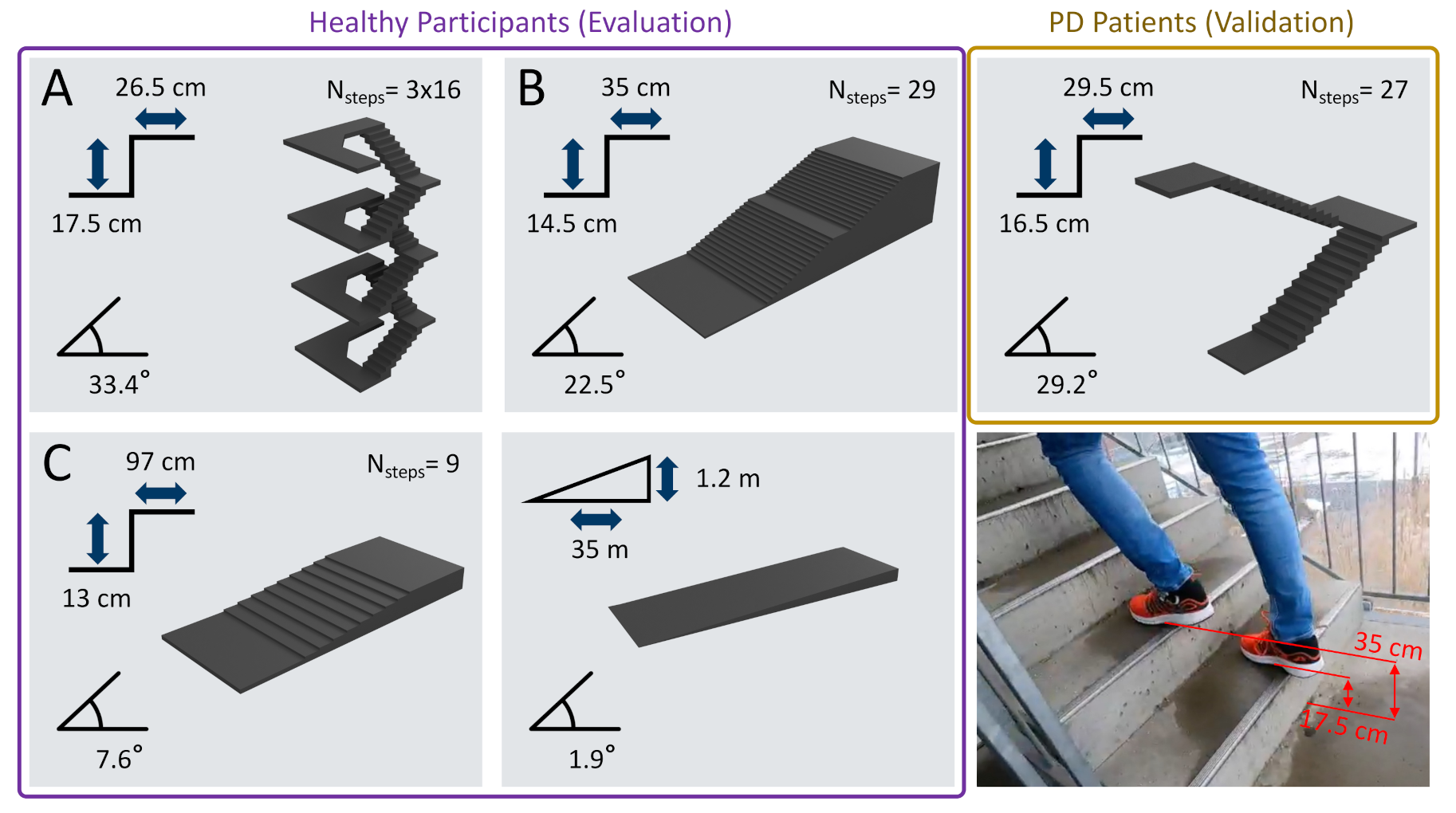
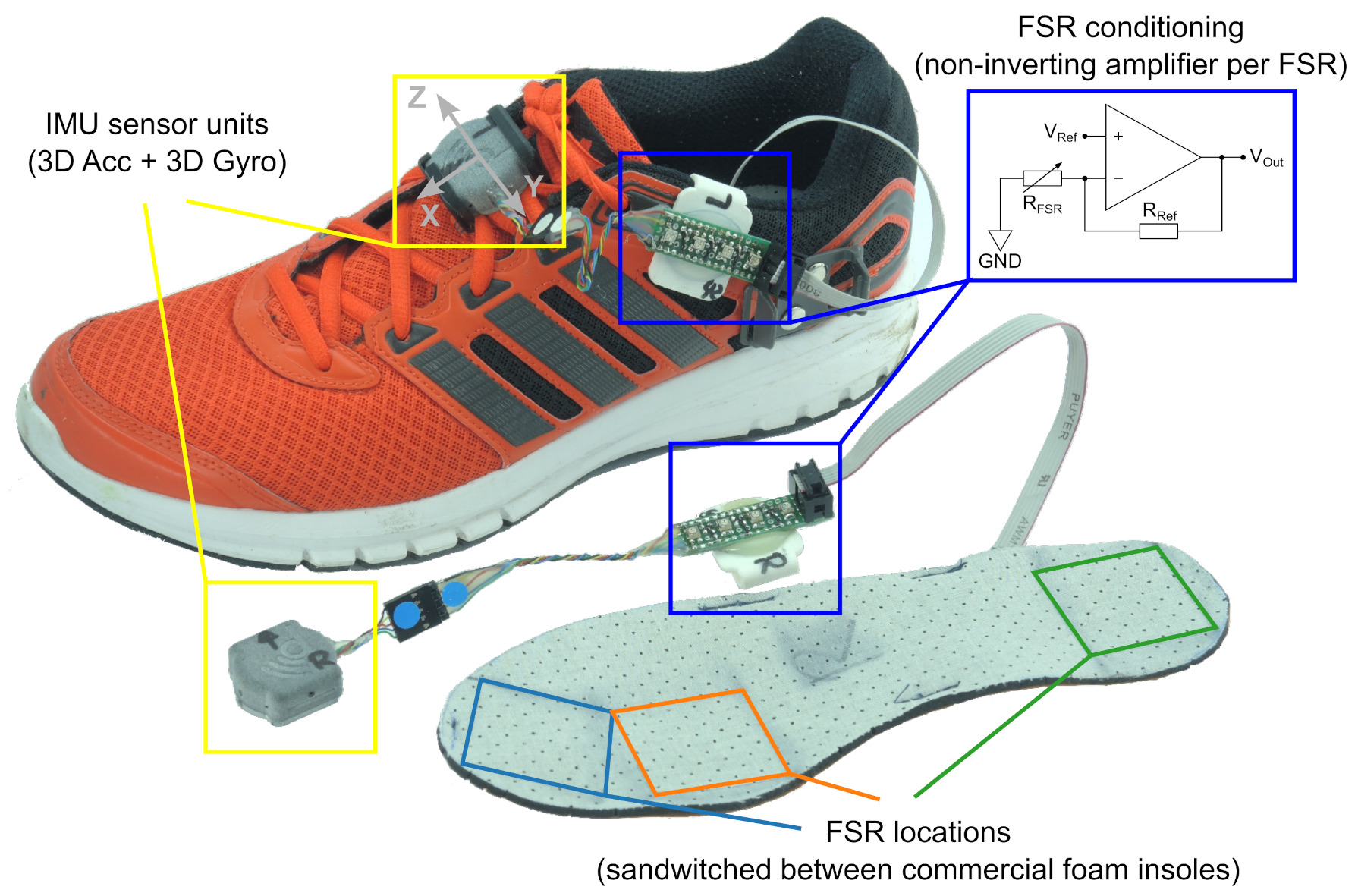
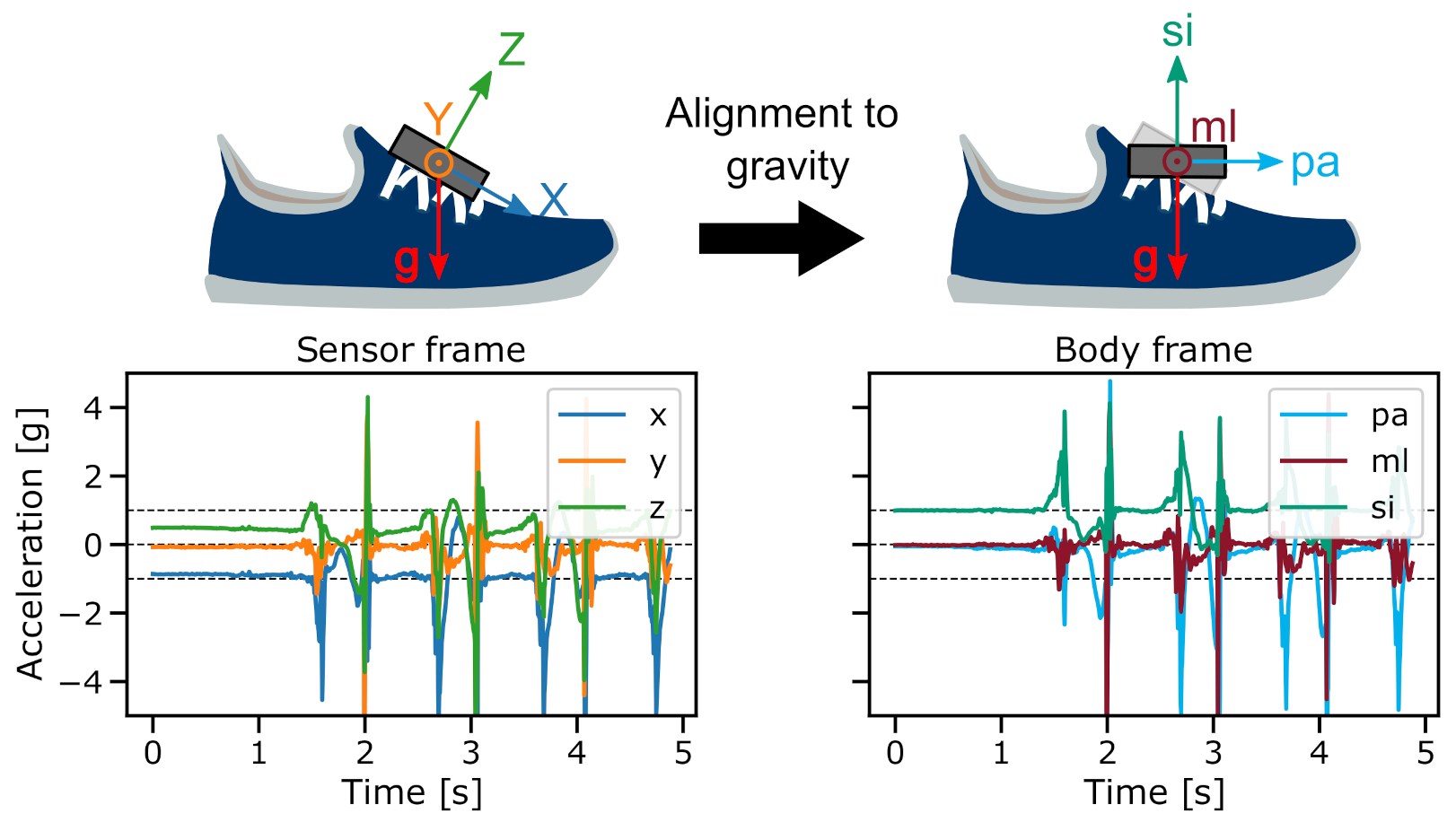
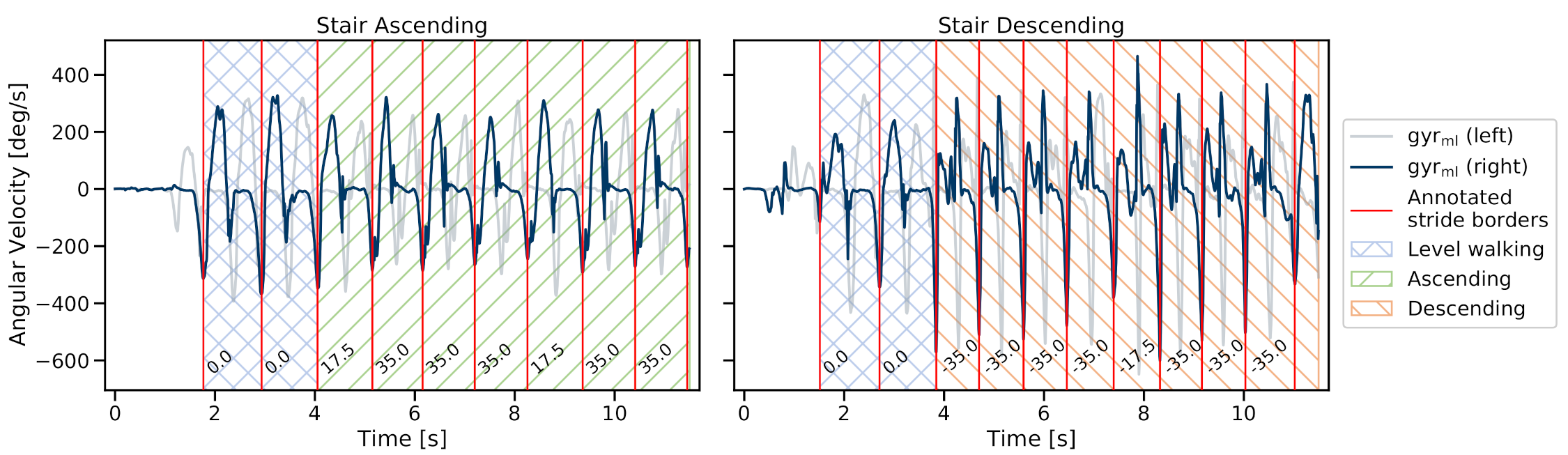
| Characteristic | Healthy Participants | PD Patients |
|---|---|---|
| Gender [f/m] | 10/10 | 3/10 |
| Age [years] | 27.1 ± 11.3 | 61.1 ± 9.0 |
| Height [cm] | 173.4 ± 7.1 | 174.1 ± 8.6 |
| Weight [kg] | 68.1 ± 8.6 | 82.3 ± 15.1 |
| UPDRS-III | - | 16.3 ± 7.8 |
| Hoehn & Yahr | - | 2.1 ± 0.7 |
| Stride Type | Label | State Transitions | |||
|---|---|---|---|---|---|
| Level walking | start | ||||
| Level walking | end | ||||
| Ascending | start | ||||
| Ascending | end | ||||
| Descending | start | ||||
| Descending | end | ||||
| Stride Type | Level | Ascending | Descending | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean Error | Mean Abs. Error | Mean Error | Mean Abs. Error | Mean Error | Mean Abs. Error | |||||||||||||
| IC [ms] | −0.5 | ± | 28.3 | 15.1 | ± | 26.4 | 9.8 | ± | 26.9 | 19.5 | ± | 22.0 | 1.9 | ± | 23.6 | 14.9 | ± | 20.5 |
| TC [ms] | −4.0 | ± | 25.9 | 11.2 | ± | 23.7 | −0.8 | ± | 26.2 | 17.8 | ± | 19.2 | 6.4 | ± | 14.6 | 12.0 | ± | 10.4 |
| Swing time [ms] | 1.4 | ± | 28.4 | 19.6 | ± | 20.7 | 11.2 | ± | 39.2 | 28.9 | ± | 28.7 | −4.5 | ± | 26.3 | 18.6 | ± | 19.1 |
| Stance time [ms] | −1.8 | ± | 29.5 | 19.3 | ± | 22.3 | −11.0 | ± | 39.6 | 28.7 | ± | 29.3 | 4.4 | ± | 26.9 | 19.1 | ± | 19.5 |
| Stride time [ms] | −0.3 | ± | 31.7 | 17.5 | ± | 26.4 | 0.3 | ± | 28.6 | 18.3 | ± | 22.0 | −0.1 | ± | 25.0 | 14.2 | ± | 20.5 |
| Stride-Type Class | |||
|---|---|---|---|
| Metric | Level Walking | Ascending | Descending |
| Precision | 96.8% | 100.0% | 100.0% |
| Recall | 100.0% | 97.3% | 97.4% |
| F1 score | 98.4% | 98.6% | 98.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roth, N.; Küderle, A.; Prossel, D.; Gassner, H.; Eskofier, B.M.; Kluge, F. An Inertial Sensor-Based Gait Analysis Pipeline for the Assessment of Real-World Stair Ambulation Parameters. Sensors 2021, 21, 6559. https://doi.org/10.3390/s21196559
Roth N, Küderle A, Prossel D, Gassner H, Eskofier BM, Kluge F. An Inertial Sensor-Based Gait Analysis Pipeline for the Assessment of Real-World Stair Ambulation Parameters. Sensors. 2021; 21(19):6559. https://doi.org/10.3390/s21196559
Chicago/Turabian StyleRoth, Nils, Arne Küderle, Dominik Prossel, Heiko Gassner, Bjoern M. Eskofier, and Felix Kluge. 2021. "An Inertial Sensor-Based Gait Analysis Pipeline for the Assessment of Real-World Stair Ambulation Parameters" Sensors 21, no. 19: 6559. https://doi.org/10.3390/s21196559
APA StyleRoth, N., Küderle, A., Prossel, D., Gassner, H., Eskofier, B. M., & Kluge, F. (2021). An Inertial Sensor-Based Gait Analysis Pipeline for the Assessment of Real-World Stair Ambulation Parameters. Sensors, 21(19), 6559. https://doi.org/10.3390/s21196559









