The Validity and Reliability of a Tire Pressure-Based Power Meter for Indoor Cycling
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Design
2.3. Material
2.4. Data Processing and Statistical Analysis
2.4.1. Data Processing
2.4.2. Data Processing
2.4.3. Validity Analysis
2.4.4. Reliability Analysis
3. Results
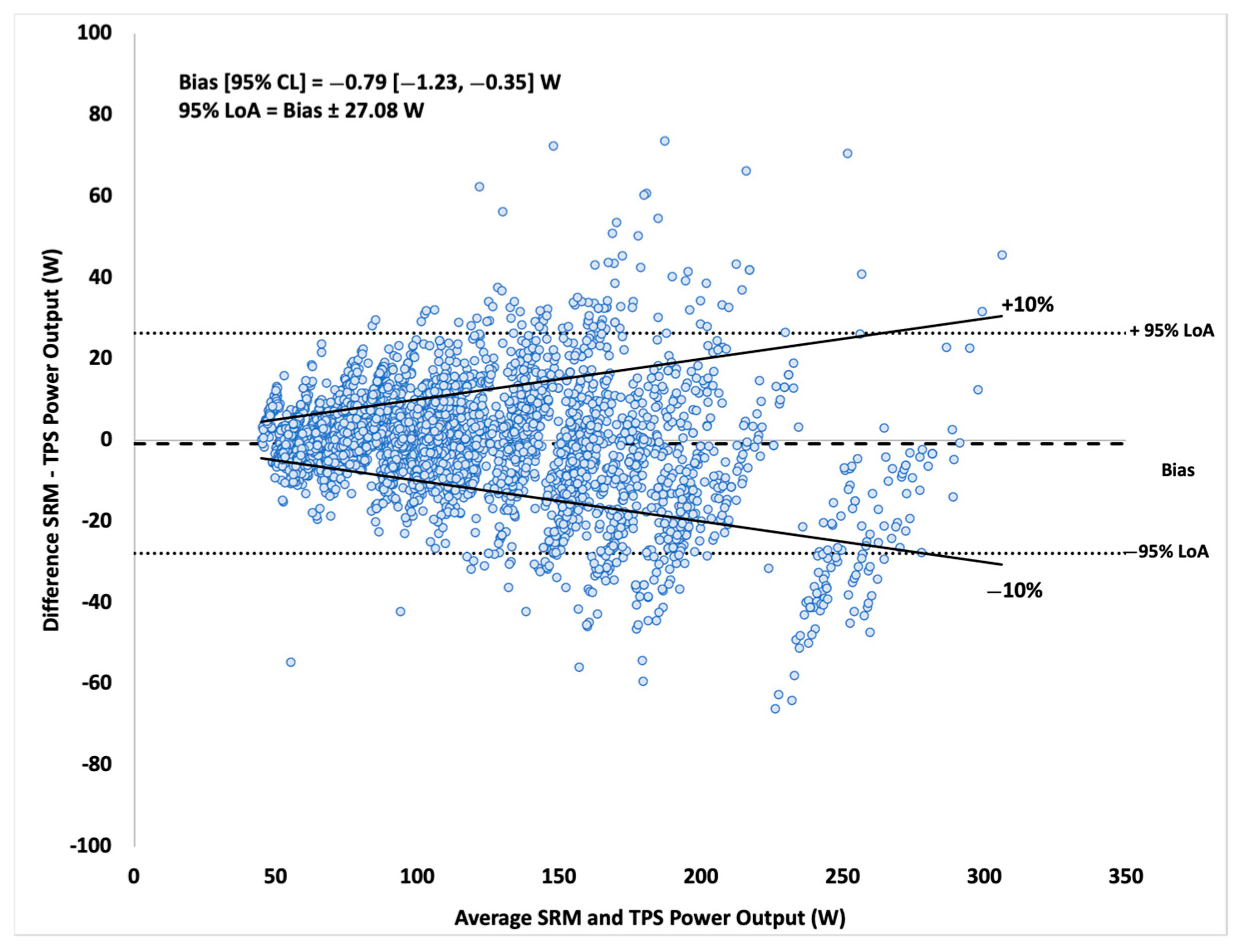
3.1. Validity Analysis 1-S Data
3.2. Validity Analysis of 1 min Average Trials
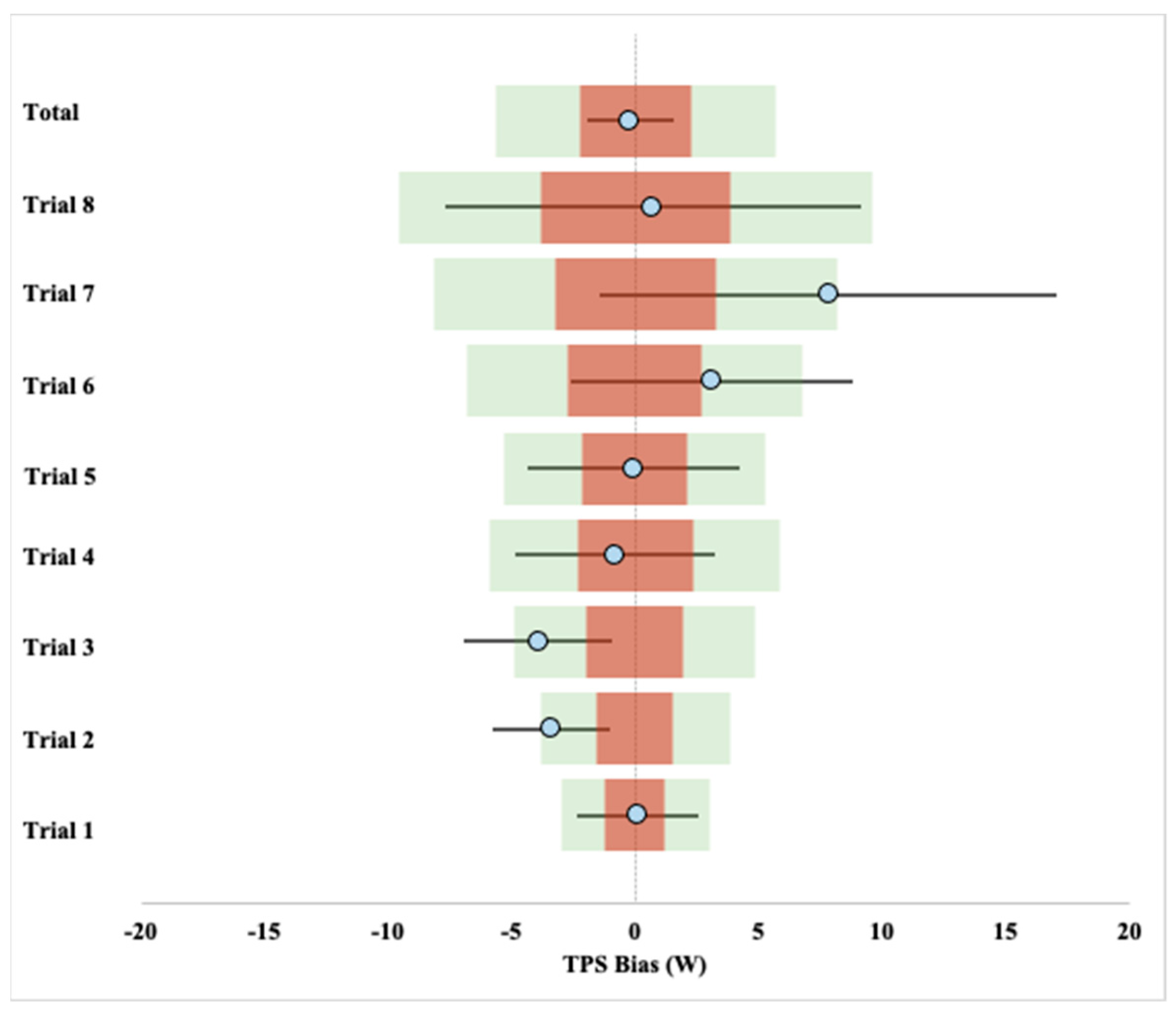
3.3. Reliability of 1 min Average Trials
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Halson, S.L. Monitoring Training Load to Understand Fatigue in Athletes. Sports Med. 2014, 44, 139–147. [Google Scholar] [CrossRef]
- Bourdon, P.C.; Cardinale, M.; Murray, A.; Gastin, P.; Kellmann, M.; Varley, M.; Gabbett, T.J.; Coutts, A.J.; Burgess, D.J.; Gregson, W.; et al. Monitoring Athlete Training Loads: Consensus Statement. Int. J. Sports Physiol. Perform. 2017, 12, S2-161–S2-170. [Google Scholar] [CrossRef]
- Garber, C.E.; Blissmer, B.; Deschenes, M.R.; Franklin, B.A.; Lamonte, M.J.; Lee, I.-M.; Nieman, D.C.; Swain, D.P. Quantity and Quality of Exercise for Developing and Maintaining Cardiorespiratory, Musculoskeletal, and Neuromotor Fitness in Apparently Healthy Adults: Guidance for Prescribing Exercise. Med. Sci. Sports Exerc. 2011, 43, 1334–1359. [Google Scholar] [CrossRef] [PubMed]
- Passfield, L.; Hopker, J.; Jobson, S.; Friel, D.; Zabala, M. Knowledge is power: Issues of measuring training and performance in cycling. J. Sports Sci. 2017, 35, 1426–1434. [Google Scholar] [CrossRef]
- Jones, A.M.; Vanhatalo, A.; Burnley, M.; Morton, R.H.; Poole, D.C. Critical Power: Implications for Determination of V˙O2max and Exercise Tolerance. Med. Sci. Sports Exerc. 2010, 42, 1876–1890. [Google Scholar] [CrossRef]
- Jones, S.L.P.; Passfield, L. The dynamic calibration of bicycle power measuring cranks. Eng. Sport. 1998, 265–274. Available online: https://kar.kent.ac.uk/id/eprint/27863 (accessed on 11 September 2021).
- Bouillod, A.; Pinot, J.; Soto-Romero, G.; Bertucci, W.; Grappe, F. Validity, Sensitivity, Reproducibility, and Robustness of the PowerTap, Stages, and Garmin Vector Power Meters in Comparison With the SRM Device. Int. J. Sports Physiol. Perform. 2017, 12, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Pallares, J.G.; Lillo-Bevia, J.R. Validity and Reliability of the PowerTap P1 Pedals Power Meter. J. sports Sci. Med. 2018, 17, 305–311. [Google Scholar] [PubMed]
- Rodríguez-Rielves, V.; Lillo-Beviá, J.; Buendía-Romero, Á.; Martínez-Cava, A.; Hernández-Belmonte, A.; Courel-Ibáñez, J.; Pallarés, J. Are the Assioma Favero Power Meter Pedals a Reliable Tool for Monitoring Cycling Power Output? Sensors 2021, 21, 2789. [Google Scholar] [CrossRef]
- Duc, S.; Villerius, V.; Bertucci, W.; Grappe, F. Validity and Reproducibility of the Ergomo®Pro Power Meter Compared With the SRM and Powertap Power Meters. Int. J. Sports Physiol. Perform. 2007, 2, 270–281. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bertucci, W.; Duc, S.; Villerius, V.; Pernin, J.N.; Grappe, F. Validity and Reliability of the PowerTap Mobile Cycling Powermeter when Compared with the SRM Device. Int. J. Sports Med. 2005, 26, 868–873. [Google Scholar] [CrossRef]
- Abbiss, C.; Quod, M.J.; Levin, G.; Martin, D.T.; Laursen, P.B. Accuracy of the Velotron Ergometer and SRM Power Meter. Int. J. Sports Med. 2009, 30, 107–112. [Google Scholar] [CrossRef]
- Czajkowski, M.; Bouillod, A.; Dauriannes, A.; Soto-Romero, G.; Grappe, F. Validity and reproducibility of the Powertap P1 power meter when compared with SRM device. J. Sci. Cycl. 2016. Available online: https://www.jsc-journal.com/index.php/JSC/article/view/257 (accessed on 2 September 2021).
- Paton, C.D.; Hopkins, W.G. Tests of Cycling Performance. Sports Med. 2001, 31, 489–496. [Google Scholar] [CrossRef]
- Hutchison, R.; Klapthor, G.; Edwards, K.; Bruneau, K.; Mocko, G.; Vahidi, A. Validity and Reproducibility of the Garmin Vector Power Meter When Compared to the SRM Device. J. Sports Sci. 2017, 5, 235–241. [Google Scholar] [CrossRef]
- Novak, A.R.; Dascombe, B.J. Agreement of Power Measures between Garmin Vector and SRM Cycle Power Meters. Meas. Phys. Educ. Exerc. Sci. 2016, 20, 167–172. [Google Scholar] [CrossRef]
- Nimmerichter, A.; Schnitzer, L.; Prinz, B.; Simon, D.; Wirth, K. Validity and Reliability of the Garmin Vector Power Meter in Laboratory and Field Cycling. Int. J. Sports Med. 2017, 38, 439–446. [Google Scholar] [CrossRef]
- Hurst, H.; Atkins, S.; Sinclair, J.; Metcalfe, J. Agreement Between the Stages Cycling and SRM Powermeter Systems during Field-Based Off-Road Climbing. J. Sci. Cycl. 2015, 4, 21–27. [Google Scholar]
- Granier, C.; Hausswirth, C.; Dorel, S.; Le Meur, Y. Validity and Reliability of the Stages Cycling Power Meter. J. Strength Cond. Res. 2020, 34, 3554–3559. [Google Scholar] [CrossRef]
- Sparks, A.; Dove, B.; Bridge, C.; Midgley, A.; Mc Naughton, L. Validity and Reliability of the Look Keo Power Pedal System for Measuring Power Output During Incremental and Repeated Sprint Cycling. Int. J. Sports Physiol. Perform. 2015, 10, 39–45. [Google Scholar] [CrossRef]
- Millet, G.; Tronche, C.; Fuster, N.; Bentley, D.J.; Candau, R. Validity and Reliability of the Polar®S710 Mobile Cycling Powermeter. Int. J. Sports Med. 2003, 24, 156–161. [Google Scholar] [CrossRef]
- Oja, P.; Titze, S.; Bauman, A.; De Geus, B.; Krenn, P.; Reger-Nash, B.; Kohlberger, T. Health benefits of cycling: A systematic review. Scand. J. Med. Sci. Sports 2011, 21, 496–509. [Google Scholar] [CrossRef]
- Hopkins, W.; Marshall, S.; Batterham, A.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef]
- Hopkins, W.G. Spreadsheets for analysis of validity and reliability. Sportscience 2015, 21, 36–42. [Google Scholar]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Hopker, J.G.; Myers, S.; Jobson, S.; Bruce, W.; Passfield, L. Validity and Reliability of the Wattbike Cycle Ergometer. Int. J. Sports Med. 2010, 31, 731–736. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Schabort, E.J.; Hawley, J.A. Reliability of Power in Physical Performance Tests. Sports Med. 2001, 31, 211–234. [Google Scholar] [CrossRef]
- Stevens, C.; Dascombe, B.J. The Reliability and Validity of Protocols for the Assessment of Endurance Sports Performance: An Updated Review. Meas. Phys. Educ. Exerc. Sci. 2015, 19, 177–185. [Google Scholar] [CrossRef]
- Currell, K.; Jeukendrup, A.E. Validity, Reliability and Sensitivity of Measures of Sporting Performance. Sports Med. 2008, 38, 297–316. [Google Scholar] [CrossRef]
- Borszcz, F.K.; Tramontin, A.F.; Costa, V.P. Reliability of the Functional Threshold Power in Competitive Cyclists. Int. J. Sports Med. 2020, 41, 175–181. [Google Scholar] [CrossRef]
- Lamberts, R.P.; Swart, J.; Noakes, T.D.; Lambert, M. A novel submaximal cycle test to monitor fatigue and predict cycling performance. Br. J. Sports Med. 2009, 45, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.A. Is there a large sample size problem? Ophthalmic Physiol. Opt. 2019, 39, 129–130. [Google Scholar] [CrossRef]
- Kyle, C.R.; Caiozzo, V.J. Experiments in Human Ergometry as Applied to the Design of Human Powered Vehicles. Int. J. Sport Biomech. 1986, 2, 6–19. [Google Scholar] [CrossRef]
- Martin, J.; Milliken, D.L.; Cobb, J.E.; McFadden, K.L.; Coggan, A.R. Validation of a Mathematical Model for Road Cycling Power. J. Appl. Biomech. 1998, 14, 276–291. [Google Scholar] [CrossRef] [PubMed]



| Trial | Gearing | RPM |
|---|---|---|
| 1 | 53 × 15 a | 50 |
| 2 | 60 | |
| 3 | 75 | |
| 4 | 90 | |
| 5 | 53 × 11 a | 60 |
| 6 | 75 | |
| 7 | 90 | |
| 8 | 100 |
| Trial | n | Correlation | SEE (W) 95% CI [LL, UL] | TEE (%) 95% CI [LL, UL] |
|---|---|---|---|---|
| Trial 1 | 12 | r = 0.96, p < 0.001 | 3.19 [2.23, 5.61] | 5.90 [4.11, 10.65] |
| Trial 2 | 12 | r = 0.97, p < 0.001 | 3.90 [2.72, 6.85] | 5.48 [3.80, 9.82] |
| Trial 3 | 12 | r = 0.96, p < 0.001 | 4.98 [3.48, 8.73] | 5.59 [3.88,10.02] |
| Trial 4 | 12 | r = 0.96, p < 0.001 | 5.87 [4.10, 10.30] | 4.90 [3.40, 8.76] |
| Trial 5 | 12 | r = 0.97, p < 0.001 | 4.51 [3.15, 7.92] | 4.80 [3.33, 8.58] |
| Trial 6 | 12 | r = 0.95, p < 0.001 | 6.96 [4.86, 12.21] | 5.61 [3.89, 10.06] |
| Trial 7 | 12 | r = 0.92, p < 0.001 | 11.92 [8.26, 20.74] | 8.23 [5.68, 14.89] |
| Trial 8 | 10 | r = 0.96, p < 0.001 | 10.27 [6.94, 19.68] | 6.18 [4.13, 12.17] |
| Total | 94 | r = 0.99, p < 0.001 | 7.55 [6.60, 8.82)] | 6.43 [5.60, 7.56] |
| Mean (SD) | |||
|---|---|---|---|
| Trial | TPS (W) | SRM (W) | Group Differences |
| Trial 1 | 60.74 (12.80) | 59.90 (10.96) | d = 0.21 s, p = 0.48 a |
| Trial 2 | 73.14 (14.51) | 76.51 (14.49) | d = −0.90 m, p < 0.01 a |
| Trial 3 | 93.68 (17.46) | 97.61 (17.84) | d = −0.93 m, p < 0.05 a |
| Trial 4 | 116.91 (22.15) | 117.74 (19.92) | d = −0.13 t, p = 0.66 a |
| Trial 5 | 105.61 (21.50) | 105.67 (16.91) | d = −0.01 t, p = 0.98 a |
| Trial 6 | 139.01 (27.00) | 135.92 (21.96) | d = 0.34 s, p = 0.26 a |
| Trial 7 | 171.73 (36.23) | 163.23 (29.22) | d = 0.58 s, p = 0.07 a |
| Trial 8 | 192.28 (40.71) | 191.57 (35.32) | d = 0.06 s, p = 0.86 a |
| Total | 113.32 (48.02) | 113.11 (44.55) | < 0.01, p = 0.83 b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiolo, N.J.; Lu, H.-Y.; Chen, C.-H.; Fuchs, P.X.; Chen, W.-H.; Shiang, T.-Y. The Validity and Reliability of a Tire Pressure-Based Power Meter for Indoor Cycling. Sensors 2021, 21, 6117. https://doi.org/10.3390/s21186117
Fiolo NJ, Lu H-Y, Chen C-H, Fuchs PX, Chen W-H, Shiang T-Y. The Validity and Reliability of a Tire Pressure-Based Power Meter for Indoor Cycling. Sensors. 2021; 21(18):6117. https://doi.org/10.3390/s21186117
Chicago/Turabian StyleFiolo, Nicholas J., Hai-Ying Lu, Chia-Hsiang Chen, Philip X. Fuchs, Wei-Han Chen, and Tzyy-Yuang Shiang. 2021. "The Validity and Reliability of a Tire Pressure-Based Power Meter for Indoor Cycling" Sensors 21, no. 18: 6117. https://doi.org/10.3390/s21186117
APA StyleFiolo, N. J., Lu, H.-Y., Chen, C.-H., Fuchs, P. X., Chen, W.-H., & Shiang, T.-Y. (2021). The Validity and Reliability of a Tire Pressure-Based Power Meter for Indoor Cycling. Sensors, 21(18), 6117. https://doi.org/10.3390/s21186117








