The Undoped Polycrystalline Diamond Film—Electrical Transport Properties
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
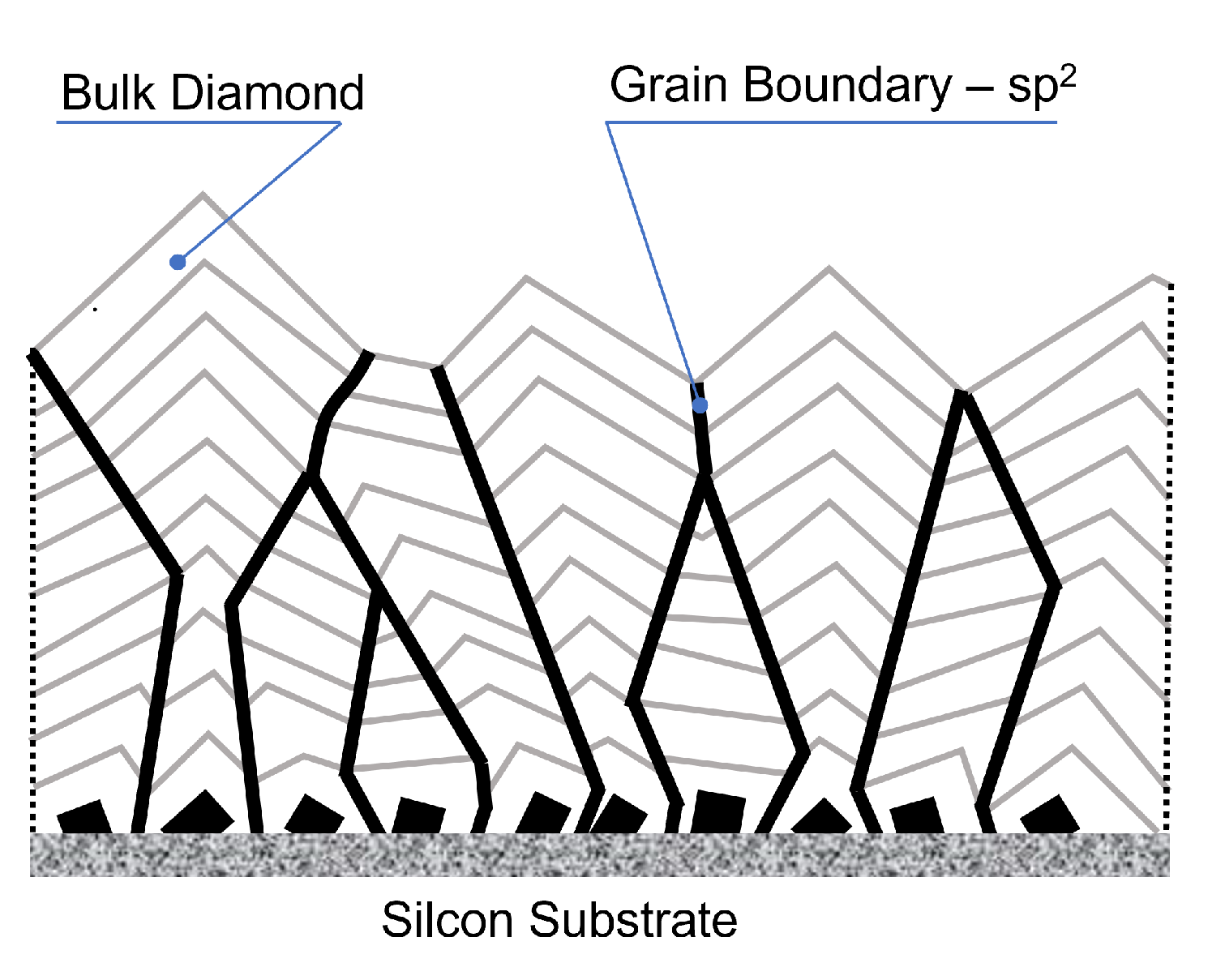
3.1. SEM Analysis
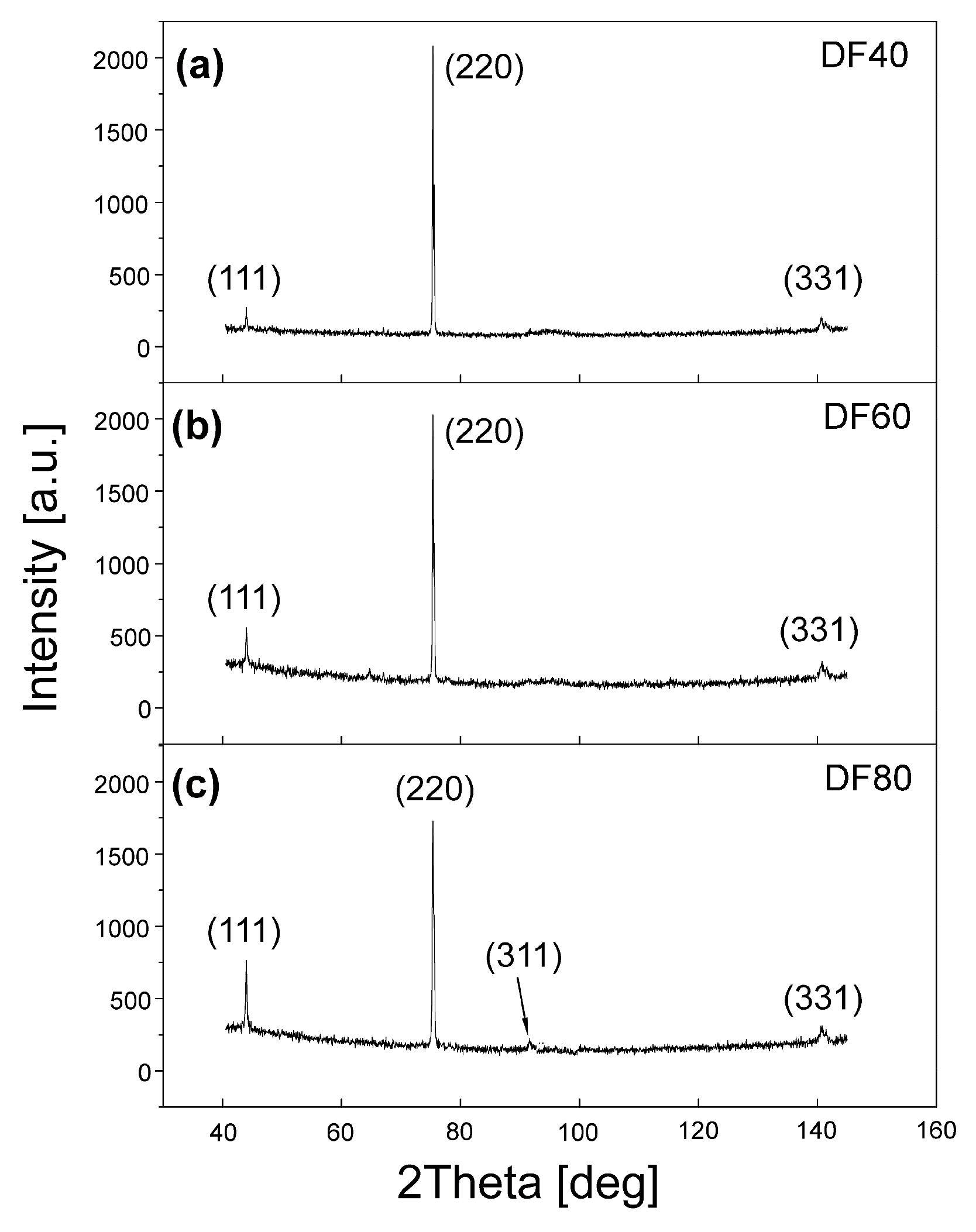
3.2. X-ray Diffraction Measurements
3.3. Raman Spectroscopy Measurements
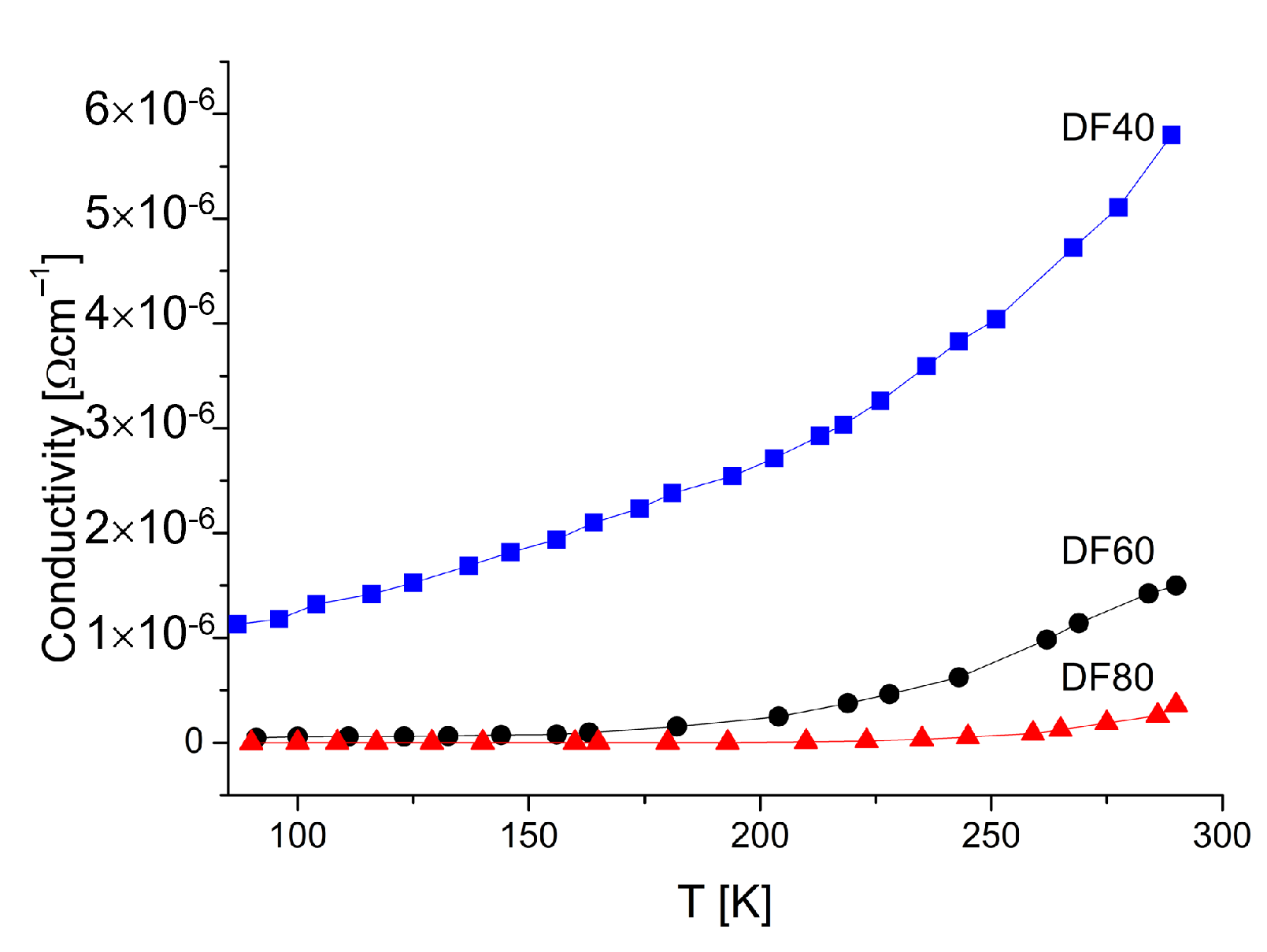
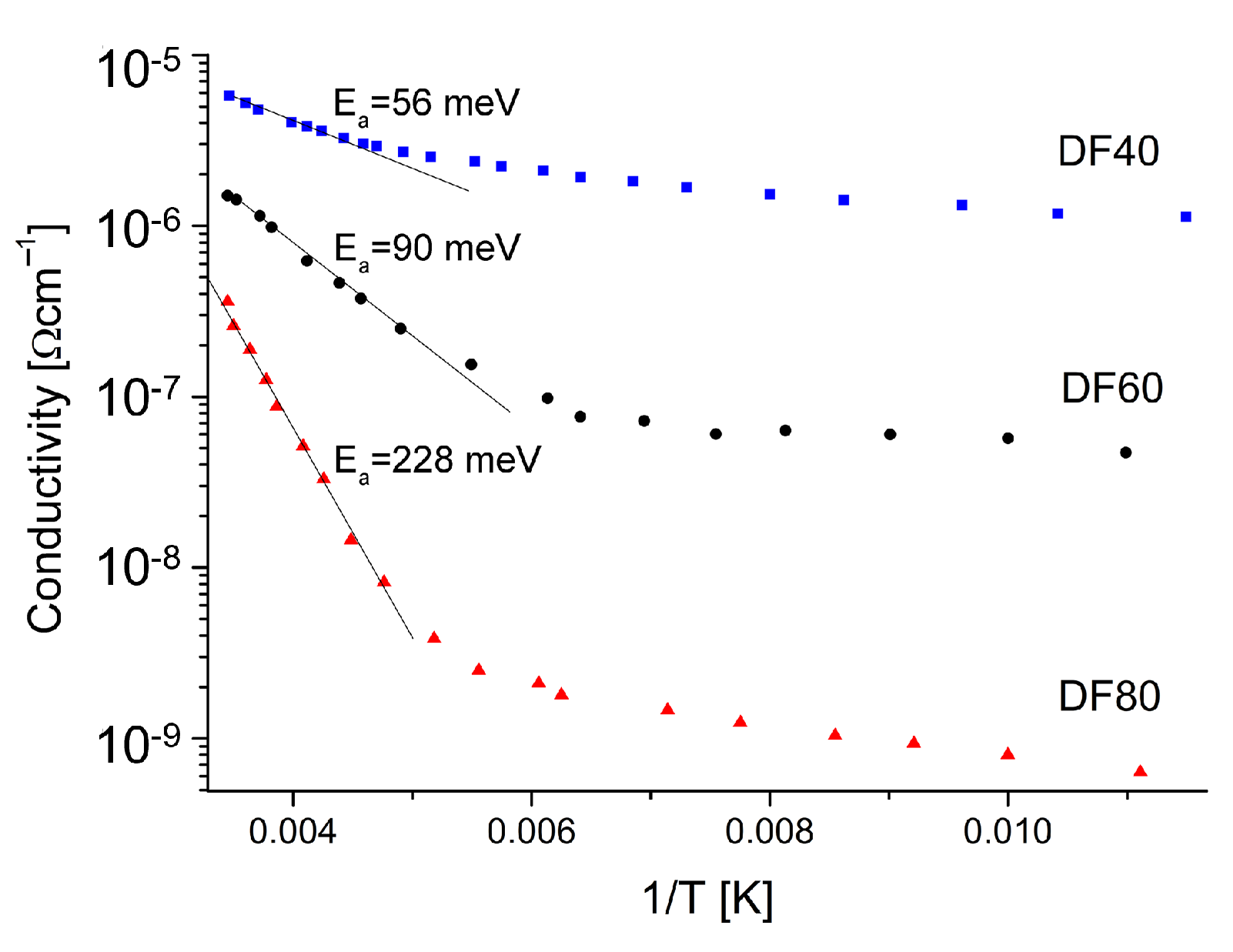
3.4. DC-Conductivity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HF CVD | hot filament chemical vapor deposition |
| M-VRH | Mott variable range hopping |
| ES-VRH | Efrost-Shklovskii variable range hopping |
| I-V-T | current voltage characteristics versus temperature |
| RT | room temperature |
| GB | grain boundary |
| N(E) | density of states near Fermi energy |
| grain boundary’s potential | |
| DF | diamond film |
| SEM | scanning electron microscopy |
| FWHW | full width at half maximum |
References
- Yoder, M.N. Diamond properties and applications. Diamond Films and Coatings: Development, Properties, and Applications; Noyes Publications: Park Ridge, NJ, USA, 1993; pp. 1–30. [Google Scholar]
- Davydova, M.; Kulha, P.; Babchenko, O.; Kromka, A. Hydrogen-terminated diamond surface as gas sensing layer working at room temperature. In Proceedings of the Nanoconference, Brno, Czech Republic, 14–16 October 2015. [Google Scholar]
- Ižák, T.; Novotná, K.; Kopová, I.; Bačáková, L.; Rezek, B.; Kromka, A. H-terminated diamond as optically transparent impedance sensor for real-time monitoring of cell growth. Phys. Status Solidi (b) 2013, 250, 2741–2746. [Google Scholar] [CrossRef]
- Sasaki, Y.; Kawarada, H. Low drift and small hysteresis characteristics of diamond electrolyte-solution-gate FET. J. Phys. D Appl. Phys. 2010, 43, 374020. [Google Scholar] [CrossRef]
- Kowalska, M.; Paprocki, K.; Szybowicz, M.; Wrzyszczyński, A.; Łoś, S.; Fabisiak, K. Electrochemical sensitivity of undoped CVD diamond films as function of their crystalline quality. J. Electroanal. Chem. 2020, 859, 113811. [Google Scholar] [CrossRef]
- Crawford, K.G.; Maini, I.; Macdonald, D.A.; Moran, D.A. Surface transfer doping of diamond: A review. Prog. Surf. Sci. 2021, 96, 100613. [Google Scholar] [CrossRef]
- Kočí, M.; Kromka, A.; Bouřa, A.; Szabó, O.; Husák, M. Hydrogen-Terminated Diamond Surface as a Gas Sensor: A Comparative Study of Its Sensitivities. Sensors 2021, 21, 5390. [Google Scholar] [CrossRef] [PubMed]
- Landstrass, M.I.; Ravi, K.V. Resistivity of chemical vapor deposited diamond films. Appl. Phys. Lett. 1989, 55, 975. [Google Scholar] [CrossRef]
- Denisenko, A.; Aleksov, A.; Pribil, A.; Gluche, P.; Ebert, W.; Kohn, E. Hypothesis on the conductivity mechanism in hydrogen terminated diamond films. Diam. Relat. Mater. 2000, 9, 1138–1142. [Google Scholar] [CrossRef]
- Łoś, S.; Paprocki, K.; Fabisiak, K.; Szybowicz, M. The influence of the space charge on The Ohm’s law conservation in CVD diamond layers. Carbon 2019, 143, 413–418. [Google Scholar] [CrossRef]
- Chevallier, J.; Aucoutuier, M. Hydrogen in crystaline semiconductors. Annu. Rev. Mater. Sci. 1988, 18, 219–256. [Google Scholar] [CrossRef]
- de Walle, C.V.; Neugebaue, J. Hydrogen in semiconductors. Annu. Rev. Mater. Res. 2006, 36, 179–198. [Google Scholar] [CrossRef]
- Maier, F.; Riedel, M.; Mantel, B.; Ristein, J.; Ley, L. Origin of surface conductivity in diamond. Phys. Rev. Lett. 2000, 85, 3472. [Google Scholar] [CrossRef]
- Sque, S.; Jones, R.; Briddon, P. Structure, electronics, and interaction of hydrogen and oxygen on diamond surfaces. Phys. Rev. B 2006, 73, 085313. [Google Scholar] [CrossRef]
- Krainsky, I.; Asnin, V. Negative electron affinity mechanism for diamond surfaces. Appl. Phys. Lett. 1998, 72, 2574–2576. [Google Scholar] [CrossRef] [Green Version]
- Seto, J. The electrical properties of polycrystalline silicon films. J. Appl. Phys. 1975, 46, 5247–5254. [Google Scholar] [CrossRef]
- Pandey, S.; Cavalcoli, D.; Minj, A.; Fraboni, B.; Cavallini, A.; Skuridina, D.; Vogt, P.; Kneissl, M. Mobility-limiting mechanisms in polar semiconductor heterostructures. Acta Mater. 2012, 60, 3176–3180. [Google Scholar] [CrossRef]
- Look, D.C.; Sizelove, J. Dislocation scattering in GaN. Phys. Rev. Lett. 1999, 82, 1237–1240. [Google Scholar] [CrossRef] [Green Version]
- Łoś, S.; Paprocki, K.; Szybowicz, M.; Fabisiak, K. The n–Si/p–CVD Diamond Heterojunction. Materials 2020, 13, 3530. [Google Scholar] [CrossRef]
- Rodrigues, A.; Gomes, H.L.; Stallinga, P.; Pereira, L.; Pereira, E. Electrical characterization of CVD diamond–n+ silicon junctions. Diam. Relat. Mater. 2001, 10, 858–862. [Google Scholar] [CrossRef]
- Madaleno, J.; Pereira, L. The modulation of electrical carrier transport in metal-MPCVD diamond due to the microcrystalline inhomogeneous barriers. Diam. Relat. Mater. 2005, 14, 584–588. [Google Scholar] [CrossRef]
- Mendes, J.; Gomes, H.; Trippe, S.; Mukherjee, D.; Pereira, L. Small signal analysis of MPCVD diamond Schottky diodes. Diam. Relat. Mater. 2019, 93, 131–138. [Google Scholar] [CrossRef]
- Salvatori, S.; Vincenzoni, R.; Rossi, M.; Galluzzi, F.; Pinzari, F.; Mattei, G.; Cappelli, E.; Ascarelli, P. Electrical and photoelectrical characterization of diamond-on-silicon structures. Appl. Surf. Sci. 1996, 102, 125–129. [Google Scholar] [CrossRef]
- Trucchi, D.; Cappelli, E.; Conte, G.; Mattei, G.; Gramaccioni, C.; Ascarelli, P. The influence of grain-boundaries on the electronic performance of CVD diamond films. Diam. Relat. Mater. 2005, 14, 575–579. [Google Scholar] [CrossRef]
- Hayashi, K.; Yamanaka, S.; Watanabe, H.; Sekiguchi, T.; Okushi, H.; Kajimura, K. Investigation of the effect of hydrogen on electrical and optical properties in chemical vapor deposited on homoepitaxial diamond films. J. Appl. Phys. 1997, 81, 744–753. [Google Scholar] [CrossRef]
- Williams, O.A.; Jackman, R.B. Surface conductivity on hydrogen terminated diamond. Semicond. Sci. Technol. 2003, 18, S34. [Google Scholar] [CrossRef]
- Fabisiak, K.; Kowalska, M.; Szybowicz, M.; Paprocki, K.; Popielarski, P.; Wrzyszczyński, A.; Mosińska, L.; Zhusupkalieva, G.K. The undoped CVD diamond electrode: The effect of surface pretreatment on its electrochemical properties. Adv. Eng. Mater. 2013, 15, 935–940. [Google Scholar] [CrossRef]
- Fabisiak, K.; Torz-Piotrowska, R.; Staryga, E.; Szybowicz, M.; Paprocki, K.; Banaszak, A.; Popielarski, P. The influence of working gas on CVD diamond quality. Mater. Sci. Eng. B 2012, 177, 1352–1357. [Google Scholar] [CrossRef]
- Cullity, B.; Stock, S. Elements of X-ray Diffraction, 2nd ed.; Assison-Wesley Publishing Company: Boston, MA, USA, 1978. [Google Scholar]
- Łoś, S.; Duclaux, L.; Kempiński, W.; Połomska, M. Size effect in the characterization of microporous activated nanostructured carbon. Microporous Mesoporous Mater. 2010, 130, 21–25. [Google Scholar] [CrossRef]
- Łoś, S.; Duclaux, L.; Alvarez, L.; Łukasz, H.; Duber, S.; Kempiński, W. Cleavage and size reduction of graphite crystal using ultrasound radiation. Carbon 2013, 55, 53–61. [Google Scholar] [CrossRef]
- Shroder, R.; Nemanich, R.; Glass, J. Analysis of the composite structures in diamond thin films by Raman spectroscopy. Phys. Rev. B 1990, 41, 3738. [Google Scholar] [CrossRef]
- Bąk, G.; Fabisiak, K.; Klimek, L.; Kozanecki, M.; Staryga, E. Investigation of biaxial stresses in diamond films deposited on a silicon substrate by the HF CVD method. Opt. Mater. 2008, 30, 770–773. [Google Scholar] [CrossRef]
- Casiraghi, C.; Ferrari, A.; Robertson, J. Raman spectroscopy of hydrogenated amorphous carbons. Phys. Rev. B 2005, 72, 085401. [Google Scholar] [CrossRef] [Green Version]
- Prawer, S.; Nemanich, R.J. Raman spectroscopy of diamond and doped diamond. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 2537–2565. [Google Scholar] [CrossRef]
- Solin, S.; Ramdas, A. Raman spectrum of diamond. Phys. Rev. B 1970, 1, 1687. [Google Scholar] [CrossRef]
- Srivastava, G. The Physics of Phonons; Taylor & Francis: New York, NY, USA, 1990. [Google Scholar]
- Kazmerski, L.L. Electrical properties of polycrystalline semiconductor thin films. Polycryst. Amorph. Thin Film. Devices 1980, 59–133. [Google Scholar] [CrossRef]
- Pankove, J.I.; Johnson, N.M. Introduction to hydrogen in semiconductors. In Semiconductors and Semimetals; Elsevier: Amsterdam, The Netherlands, 1991; Volume 34, pp. 1–15. [Google Scholar] [CrossRef]
- Tsugawa, K.; Umezawa, H.; Kawarada, H. Characterization of diamond surface-channel metal-semiconductor field-effect transistor with device simulation. Jpn. J. Appl. Phys. 2001, 40, 3101. [Google Scholar] [CrossRef]
- Shklovskii, B.I.; Efros, A.L. Variable-range hopping conduction. In Electronic Properties of Doped Semiconductors; Springer: Berlin/Heidelberg, Germany, 1984; pp. 202–227. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Shklovskii, B.; Spivak, B. Hopping Transport in Solids; Elsevier: Amsterdam, The Netherlands, 1991; p. 271. [Google Scholar]
- Errai, M.; Kaaouachi, A.E.; Idrissi, H.E. Variable range hopping conduction in n-CdSe samples at very low temperature. J. Semicond. 2015, 36, 122001. [Google Scholar] [CrossRef]
- Mott, N.F. Conduction in non-crystalline materials: III. Localized states in a pseudogap and near extremities of conduction and valence bands. Philos. Mag. 1969, 19, 835–852. [Google Scholar] [CrossRef]
- Hassanien, A.; Akl, A.A. Electrical transport properties and Mott’s parameters of chalcogenide cadmium sulphoselenide bulk glasses. J.-Non-Cryst. Solids 2016, 432, 471–479. [Google Scholar] [CrossRef]
- Davis, E.; Mott, N. Conduction in non-crystalline systems V. Conductivity, optical absorption and photoconductivity in amorphous semiconductors. Philos. Mag. 1970, 22, 0903–0922. [Google Scholar] [CrossRef]
- Zhang, X.; Shao, Z.; Zhang, X.; He, Y.; Jie, J. Surface Charge Transfer Doping of Low-Dimensional Nanostructures toward High-Performance Nanodevices. Adv. Mater. 2016, 28, 10409–10442. [Google Scholar] [CrossRef] [PubMed]



| Films | Pressure | Peak Position | FWHM | C | H | L |
|---|---|---|---|---|---|---|
| [hPa] | [cm] | [cm] | [a. u.] | [at.%] | [nm] | |
| DF40 | 40 | 1331.9 | 6.8 | 0.99 | 26 | 66 |
| DF60 | 60 | 1331.7 | 7.9 | 0.98 | 24 | 52 |
| DF80 | 80 | 1331.6 | 9.2 | 0.96 | 17 | 35 |
| Films | Peak Position | FWHM | Integral Intensity | m-Slope |
|---|---|---|---|---|
| [cm] | [cm] | [a. u.] | m | |
| DF40 | 1531 | 243 | 53,125 | 103,000 |
| DF60 | 1534 | 185 | 45,180 | 64,000 |
| DF80 | 1534 | 125 | 25,030 | 13,000 |
| Films | N(E) | R | W | |
|---|---|---|---|---|
| [cm] | [cm] | [meV] | [meV] | |
| DF40 | 9.2 | 4.2 | 32 | 60 |
| DF60 | 2.6 | 2.5 | 33 | 110 |
| DF80 | 4.7 | 1.23 | 57 | 257 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łoś, S.; Fabisiak, K.; Paprocki, K.; Szybowicz, M.; Dychalska, A. The Undoped Polycrystalline Diamond Film—Electrical Transport Properties. Sensors 2021, 21, 6113. https://doi.org/10.3390/s21186113
Łoś S, Fabisiak K, Paprocki K, Szybowicz M, Dychalska A. The Undoped Polycrystalline Diamond Film—Electrical Transport Properties. Sensors. 2021; 21(18):6113. https://doi.org/10.3390/s21186113
Chicago/Turabian StyleŁoś, Szymon, Kazimierz Fabisiak, Kazimierz Paprocki, Mirosław Szybowicz, and Anna Dychalska. 2021. "The Undoped Polycrystalline Diamond Film—Electrical Transport Properties" Sensors 21, no. 18: 6113. https://doi.org/10.3390/s21186113
APA StyleŁoś, S., Fabisiak, K., Paprocki, K., Szybowicz, M., & Dychalska, A. (2021). The Undoped Polycrystalline Diamond Film—Electrical Transport Properties. Sensors, 21(18), 6113. https://doi.org/10.3390/s21186113










