Precision Magnetometers for Aerospace Applications: A Review
Abstract
1. Introduction
2. Existing Applications
2.1. Interplanetary Science Missions
2.1.1. Mars Atmosphere and Volatile Evolution (MAVEN)
2.1.2. Cassini

2.1.3. Juno
2.2. Future Interplanetary Missions
2.3. Applications in Earth Atmosphere and Orbit
2.3.1. Geostationary Operational Environmental Satellites (GOES)
2.3.2. Magnetometers Onboard Micro- and Nanosatellites
2.3.3. Navigation in the Earth’s Atmosphere
2.3.4. Magnetometers in Manned Aerial Vehicles
2.3.5. Magnetometers in Unmanned Aerial Vehicles
3. Emerging Magnetometers
3.1. Atomic Magnetometers (Including SERF)
3.2. Optomechanical Magnetometers
3.3. Magnetometers Based on Atomic Defects in Solids
4. Brief Summary
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kintner, P.M.; Ledvina, B.M.; de Paula, E.R. GPS and ionospheric scintillations. Space Weather 2007, 5, 1–23. [Google Scholar] [CrossRef]
- Boteler, D.H. Geomagnetic Hazards to Conducting Networks. Nat. Hazards 2003, 28, 537–561. [Google Scholar] [CrossRef]
- Frissell, N.A.; Vega, J.S.; Markowitz, E.; Gerrard, A.J.; Engelke, W.D.; Erickson, P.J.; Miller, E.S.; Luetzelschwab, R.C.; Bortnik, J. High-Frequency Communications Response to Solar Activity in September 2017 as Observed by Amateur Radio Networks. Space Weather 2019, 17, 118–132. [Google Scholar] [CrossRef]
- Santis, A.D.; Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory worldwide signatures of earthquake occurrences on Swarm satellite data. Sci. Rep. 2019, 9, 1135–1145. [Google Scholar] [CrossRef]
- Liu, H.; Dong, H.; Ge, J.; Liu, Z. An Overview of Technologies for Geophysical Vector Magnetic Survey: A Case Study of the Instrumentation and Future Directions. arXiv 2020, arXiv:2007.05198. [Google Scholar]
- Johnson, C.L.; Mittelholz, A.; Langlais, B.; Russell, C.T.; Ansan, V.; Banfield, D.; Chi, P.J.; Fillingim, M.O.; Forget, F.; Haviland, H.F.; et al. Crustal and time-varying magnetic fields at the InSight landing site on Mars. Nat. Geosci. 2020, 13, 199–204. [Google Scholar] [CrossRef]
- Connerney, J.E.P.; Benn, M.; Bjarno, J.B.; Denver, T.; Espley, J.; Jorgensen, J.L.; Jorgensen, P.S.; Lawton, P.; Malinnikova, A.; Merayo, J.M.; et al. The Juno Magnetic Field Investigation. Space Sci. Rev. 2017, 213, 138–213. [Google Scholar] [CrossRef]
- Dougherty, M.K.; Kellock, S.; Southwood, D.J.; Balogh, A.; Smith, E.J.; Tsurutani, B.T.; Gerlach, B.; Glassmeier, K.H.; Gleim, F.; Russell, C.T.; et al. The Cassini Magnetic Field Investigation. Space Sci. Rev. 2004, 114, 331–383. [Google Scholar] [CrossRef]
- Hart, W.; Brown, G.M.; Collins, S.M.; De Soria-Santacruz Pich, M.; Fieseler, P.; Goebel, D.; Marsh, D.; Oh, D.Y.; Snyder, S.; Warner, N.; et al. Overview of the spacecraft design for the Psyche mission concept. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–20. [Google Scholar] [CrossRef]
- Owens, M.J.; Forsyth, R.J. The Heliospheric Magnetic Field. Living Rev. Sol. Phys. 2013, 10, 5. [Google Scholar] [CrossRef]
- Matthews, J.; Bukshpun, L.; Pradhan, R. A novel photonic magnetometer for detection of low frequency magnetic fields. In Photonic Fiber and Crystal Devices: Advances in Materials and Innovations in Device Applications V; Yin, S., Guo, R., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2011; Volume 8120, pp. 405–415. [Google Scholar] [CrossRef]
- Carletta, S.; Teofilatto, P.; Farissi, S. A Magnetometer-Only Attitude Determination Strategy for Small Satellites: Design of the Algorithm and Hardware-in-the-Loop Testing. Aerospace 2020, 7, 3. [Google Scholar] [CrossRef]
- Maus, S.; Barckhausen, U.; Berkenbosch, H.; Bournas, N.; Brozena, J.; Childers, V.; Dostaler, F.; Fairhead, J.D.; Finn, C.; von Frese, R.R.B.; et al. EMAG2: A 2-arc min resolution Earth Magnetic Anomaly Grid compiled from satellite, airborne, and marine magnetic measurements. Geochem. Geophys. Geosyst. 2009, 10, 1–12. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Z.; Liu, S.; Liu, Y.; Bin, J.; Shi, F.; Dong, H. A Nonlinear Regression Application via Machine Learning Techniques for Geomagnetic Data Reconstruction Processing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 128–140. [Google Scholar] [CrossRef]
- Acuña, M.H. Space-based magnetometers. Rev. Sci. Instrum. 2002, 73, 3717–3736. [Google Scholar] [CrossRef]
- Díaz-Michelena, M. Small Magnetic Sensors for Space Applications. Sensors 2009, 9, 2271–2288. [Google Scholar] [CrossRef]
- Balogh, A. Planetary Magnetic Field Measurements: Missions and Instrumentation. Space Sci. Rev. 2010, 152, 23–97. [Google Scholar] [CrossRef]
- Kitching, J. Chip-scale atomic devices. Appl. Phys. Rev. 2018, 5, 031302. [Google Scholar] [CrossRef]
- Fescenko, I.; Jarmola, A.; Savukov, I.; Kehayias, P.; Smits, J.; Damron, J.; Ristoff, N.; Mosavian, N.; Acosta, V.M. Diamond magnetometer enhanced by ferrite flux concentrators. Phys. Rev. Res. 2020, 2, 023394. [Google Scholar] [CrossRef] [PubMed]
- Li, B.B.; Brawley, G.; Greenall, H.; Forstner, S.; Sheridan, E.; Rubinsztein-Dunlop, H.; Bowen, W.P. Ultrabroadband and sensitive cavity optomechanical magnetometry. Photon. Res. 2020, 8, 1064–1071. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Turtle, E.P.; Barnes, J.W.; Trainer, M.G.; Adams, D.S.; Hibbard, K.E.; Sheldon, C.Z.; Zacny, K.; Peplowski, P.N.; Lawrence, D.J.; et al. Dragonfly: A Rotorcraft Lander Concept for Scientific Exploration at Titan. John Hopkins APL Tech. Dig. 2018, 34, 374–387. [Google Scholar]
- Rodriguez, S.; Vinatier, S.; Cordier, D.; Carrasco, N.; Charnay, B.; Cornet, T.; Coustenis, A.; de Kok, R.; Freissinet, C.; Galand, M.; et al. Science Goals and Mission Concepts for a Future Orbital and In Situ Exploration of Titan; White Paper; Planetary and Space Science Group, Université de Paris: Paris, France, 2019. [Google Scholar]
- Choblet, G.; Buch, A.; Cadek, O.; Camprubi-Casas, E.; Freissinet, C.; Hedman, M.; Jones, G.; Lainey, V.; Gall, A.L.; Lucchetti, A.; et al. Enceladus as a Potential Oasis for Life: Science Goals and Investigations for Future Explorations; White Paper; Laboratoire de Planétologie et Géodynamique, Nantes Université: Nantes, France, 2019. [Google Scholar]
- Jakosky, B.M.; Lin, R.P.; Grebowsky, J.M.; Luhmann, J.G.; Mitchell, D.F.; Beutelschies, G.; Priser, T.; Acuna, M.; Andersson, L.; Baird, D.; et al. The Mars Atmosphere and Volatile Evolution (MAVEN) Mission. Space Sci. Rev. 2015, 195, 3–48. [Google Scholar] [CrossRef]
- Connerney, J.E.P.; Espley, J.; Lawton, P.; Murphy, S.; Odom, J.; Oliversen, R.; Sheppard, D. The MAVEN Magnetic Field Investigation. Space Sci. Rev. 2015, 195, 1572–9672. [Google Scholar] [CrossRef]
- Ness, N.F. Space Exploration of Planetary Magnetism. Space Sci. Rev. 2010, 152, 5–22. [Google Scholar] [CrossRef]
- Cochrane, C.J.; Blacksberg, J.; Anders, M.A.; Lenahan, P.M. Vectorized magnetometer for space applications using electrical readout of atomic scale defects in silicon carbide. Sci. Rep. 2016, 6, 37077. [Google Scholar] [CrossRef]
- Candidi, M.; Orfei, R.; Palutan, F.; Vannaroni, G. FFT Analysis of a Space Magnetometer Noise. IEEE Trans. Geosci. Electron. 1974, 12, 23–28. [Google Scholar] [CrossRef]
- Lu, C.C.; Huang, J.; Chiu, P.K.; Chiu, S.L.; Jeng, J.T. High-sensitivity low-noise miniature fluxgate magnetometers using a flip chip conceptual design. Sensors 2014, 14, 13815–13829. [Google Scholar] [CrossRef]
- Can, H.; Topal, U. Design of Ring Core Fluxgate Magnetometer as Attitude Control Sensor for Low and High Orbit Satellites. J. Supercond. Nov. Magn. 2015, 28, 1093–1096. [Google Scholar] [CrossRef]
- Miles, D.M.; Mann, I.R.; Ciurzynski, M.; Barona, D.; Narod, B.B.; Bennest, J.R.; Pakhotin, I.P.; Kale, A.; Bruner, B.; Nokes, C.D.A.; et al. A miniature, low-power scientific fluxgate magnetometer: A stepping-stone to cube-satellite constellation missions. J. Geophys. Res. Space Phys. 2016, 121, 11839–11860. [Google Scholar] [CrossRef]
- Zhi, M.; Tang, L.; Cao, X.; Qiao, D. Digital Fluxgate Magnetometer for Detection of Microvibration. J. Sens. 2017, 2017, 6453243. [Google Scholar] [CrossRef]
- Herčík, D.; Auster, H.; Blum, J.; Fornaçon, K.H.; Fujimoto, M.; Gebauer, K.; Guttler, C.; Hillenmaier, O.; Hordt, A.; Liebert, E.; et al. The MASCOT Magnetometer. Space Sci. Rev. 2017, 208, 433–449. [Google Scholar] [CrossRef]
- Frandsen, A.M.A.; Connor, B.V.; Amersfoort, J.V.; Smith, E.J. The ISEE-C Vector Helium Magnetometer. IEEE Trans. Geosci. Electron. 1978, 16, 195–198. [Google Scholar] [CrossRef]
- Guttin, C.; Leger, J.; Stoeckel, F. An isotropic earth field scalar magnetometer using optically pumped helium 4. J. Phys. IV Proc. EDP Sci. 1994, 4, C4-655–C4-659. [Google Scholar] [CrossRef][Green Version]
- Rutkowski, J.; Fourcault, W.; Bertrand, F.; Rossini, U.; Gétin, S.; Le Calvez, S.; Jager, T.; Herth, E.; Gorecki, C.; Le Prado, M.; et al. Towards a miniature atomic scalar magnetometer using a liquid crystal polarization rotator. Sens. Actuators A Phys. 2014, 216, 386–393. [Google Scholar] [CrossRef]
- Léger, J.M.; Jager, T.; Bertrand, F.; Hulot, G.; Brocco, L.; Vigneron, P.; Lalanne, X.; Chulliat, A.; Fratter, I. In-flight performance of the Absolute Scalar Magnetometer vector mode on board the Swarm satellites. Earth Planets Space 2015, 67, 57. [Google Scholar] [CrossRef]
- Lieb, G.; Jager, T.; Palacios-Laloy, A.; Gilles, H. All-optical isotropic scalar 4He magnetometer based on atomic alignment. Rev. Sci. Instrum. 2019, 90, 075104. [Google Scholar] [CrossRef] [PubMed]
- Balogh, A.; Beek, T.J.; Forsyth, R.J.; Hedgecock, P.C.; Marquedant, R.J.; Smith, E.J.; Southwood, D.J.; Tsurutani, B.T. The magnetic field investigation on the ULYSSES mission—Instrumentation and preliminary scientific results. Astron. Astrophys. Suppl. Ser. 1992, 92, 221–236, Provided by the SAO/NASA Astrophysics Data System. [Google Scholar]
- Moore, K.M.; Yadav, R.K.; Kulowski, L.; Cao, H.; Bloxham, J.; Connerney, J.E.P.; Kotsiaros, S.; Jørgensen, J.L.; Merayo, J.M.G.; Stevenson, D.J.; et al. A complex dynamo inferred from the hemispheric dichotomy of Jupiter’s magnetic field. Nature 2018, 561, 76–78. [Google Scholar] [CrossRef]
- Russel, C.T.; Anderson, B.J.; Baumjohann, W.; Bromund, K.R.; Dearborn, D.; Fischer, D.; Le, G.; Leinweber, H.K.; Leneman, D.; Magnes, W.; et al. The Magnetospheric Multiscale Magnetometers. Space Sci. Rev. 2016, 199, 189–256. [Google Scholar] [CrossRef]
- Grasset, O.; Dougherty, M.; Coustenis, A.; Bunce, E.; Erd, C.; Titov, D.; Blanc, M.; Coates, A.; Drossart, P.; Fletcher, L.; et al. JUpiter ICy moons Explorer (JUICE): An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 2013, 78, 1–21. [Google Scholar] [CrossRef]
- Howell, S.; Pappalardo, R. NASA’s Europa Clipper—A mission to a potentially habitable ocean world. Nat. Commun. 2020, 11, 1311. [Google Scholar] [CrossRef]
- Klesh, A.T.; Baker, J.D.; Bellardo, J.; Castillo-Rogez, J.; Cutler, J.; Halatek, L.; Lightsey, E.G.; Murphy, N.; Raymond, C. INSPIRE: Interplanetary NanoSpacecraft Pathfinder in Relevant Environment. In Proceedings of the AIAA SPACE 2013 Conference and Exposition, San Diego, CA, USA, 10–12 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Balaram, J.; Aung, M.; Golombek, M.P. The Ingenuity Helicopter on the Perseverance Rover. Space Sci. Rev. 2021, 217, 56. [Google Scholar] [CrossRef]
- King-Hele, D. Progress of the Russian Earth Satellite Sputnik 3. Nature 1958, 182, 1409–1411. [Google Scholar] [CrossRef]
- Langel, R.A.; Estes, R.H. The near-Earth magnetic field at 1980 determined from Magsat data. J. Geophys. Res. Solid Earth 1985, 90, 2495–2509. [Google Scholar] [CrossRef]
- Huang, T.; Lühr, H.; Wang, H.; Xiong, C. The Relationship of High-Latitude Thermospheric Wind With Ionospheric Horizontal Current, as Observed by CHAMP Satellite. J. Geophys. Res. Space Phys. 2017, 122, 12378–12392. [Google Scholar] [CrossRef]
- Neubert, T.; Mandea, M.; Hulot, G.; von Frese, R.; Primdahl, F.; Jørgensen, J.L.; Friis-Christensen, E.; Stauning, P.; Olsen, N.; Risbo, T. Ørsted satellite captures high-precision geomagnetic field data. EOS Trans. Am. Geophys. Union 2001, 82, 81–88. [Google Scholar] [CrossRef]
- Leger, J.M.; Bertrand, F.; Jager, T.; Fratter, I. Spaceborn scalar magnetometers for Earth’s field studies. In Proceedings of the 62nd International Astronautical Congress 2011, Cape Town, South Africa, 3–7 October 2011; Volume 4, pp. 2671–2676. [Google Scholar]
- Fedrizzi, M.; Fuller-Rowell, T.J.; Codrescu, M.V. Global Joule heating index derived from thermospheric density physics-based modeling and observations. Space Weather 2012, 10, 1–13. [Google Scholar] [CrossRef]
- Singer, H.; Matheson, L.; Grubb, R.; Newman, A.; Bouwer, D. Monitoring space weather with the GOES magnetometers. In GOES-8 and Beyond; Washwell, E.R., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 1996; Volume 2812, pp. 299–308. [Google Scholar] [CrossRef]
- NOAA NASA Boeing. GOES N Series Data Book Revision C; Technical Report CDRL PM-1-1-03; NASA Goddard Space Flight Center: Greenbelt Rd, MD, USA, 2009.
- Loto’aniu, T.M.; Redmon, R.; Califf, S.; Singer, H.J.; Rowland, W.; Macintyre, S.; Chastain, C.; Dence, R.; Bailey, R.; Shoemaker, E.; et al. The GOES-16 Spacecraft Science Magnetometer. Space Sci. Rev. 2019, 215, 32. [Google Scholar] [CrossRef]
- NASA (JPL). Global Earthquake Satellite System: A 20-Year Plan to Enable Earthquake Prediction; Technical Report; Jet Propulsion Laboratory, National Aeronautics and Space Administration: La Kenyada, CA, USA, 2003.
- Chmyrev, V.; Smith, A.; Kataria, D.; Nesterov, B.; Owen, C.; Sammonds, P.; Sorokin, V.; Vallianatos, F. Detection and monitoring of earthquake precursors: TwinSat, a Russia–UK satellite project. Adv. Space Res. 2013, 52, 1135–1145. [Google Scholar] [CrossRef]
- Inamori, T.; Nakasuka, S. Application of Magnetic Sensors to Nano and Micro-Satellite Attitude Control Systems. In Magnetic Sensors—Principles and Applications; Kuang, K., Ed.; InTech: Amsterdam, The Netherlands, 2012; pp. 85–102. [Google Scholar] [CrossRef]
- Amorim, J.d.; Martins-Filho, L.S. Experimental Magnetometer Calibration for Nanosatellites Navigation System. J. Aerosp. Technol. Manag. 2016, 8, 103–112. [Google Scholar]
- Inamori, T.; Sako, N.; Nakasuka, S. Strategy of magnetometer calibration for nano-satellite missions and in-orbit performance. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 13. [Google Scholar] [CrossRef]
- Hughes, P.; Baird, D.; Goldbaum, E.; Johnson, T.; Keesey, L. Mission-Saving Instrument Secures New Flight Opportunity; Slated for Significant Upgrade. Cut. Edge Goddard’s Emerg. Technol. 2019, 15, 8. [Google Scholar]
- Hughes, P.; Baird, D.; Goldbaum, E.; Johnson, T.; Keesey, L. Fluxgate and Magneto Inductive Magnetometers. Cut. Edge Goddard’s Emerg. Technol. 2020, 16, 7. [Google Scholar]
- Prance, R.; Clark, T.; Prance, H. Ultra low noise induction magnetometer for variable temperature operation. Sens. Actuators A Phys. 2000, 85, 361–364. [Google Scholar] [CrossRef]
- Torbert, R.B.; Russell, C.T.; Magnes, W.; Ergun, R.E.; Lindqvist, P.A.; LeContel, O.; Vaith, H.; Macri, J.; Myers, S.; Rau, D.; et al. The FIELDS Instrument Suite on MMS: Scientific Objectives, Measurements, and Data Products. Space Sci. Rev. 2016, 199, 105–135. [Google Scholar] [CrossRef]
- Ennen, I.; Kappe, D.; Rempel, T.; Glenske, C.; Hutten, A. Giant Magnetoresistance: Basic Concepts, Microstructure, Magnetic Interactions and Applications. Sensors 2016, 16, 904. [Google Scholar] [CrossRef] [PubMed]
- Reig, C.; Cubells-Beltrán, M.D.; Ramírez Muñoz, D. Magnetic Field Sensors Based on Giant Magnetoresistance (GMR) Technology: Applications in Electrical Current Sensing. Sensors 2009, 9, 7919–7942. [Google Scholar] [CrossRef]
- Daughton, J. GMR applications. J. Magn. Magn. Mater. 1999, 192, 334–342. [Google Scholar] [CrossRef]
- Brown, P.; Whiteside, B.J.; Beek, T.J.; Fox, P.; Horbury, T.S.; Oddy, T.M.; Archer, M.O.; Eastwood, J.P.; Sanz-Hernández, D.; Sample, J.G.; et al. Space magnetometer based on an anisotropic magnetoresistive hybrid sensor. Rev. Sci. Instrum. 2014, 85, 125117. [Google Scholar] [CrossRef] [PubMed]
- Archer, M.O.; Horbury, T.S.; Brown, P.; Eastwood, J.P.; Oddy, T.M.; Whiteside, B.J.; Sample, J.G. The MAGIC of CINEMA: First in-flight science results from a miniaturised anisotropic magnetoresistive magnetometer. Ann. Geophys. 2015, 33, 725–735. [Google Scholar] [CrossRef]
- Edelstein, A.S.; Fischer, G.; Benard, W.; Nowak, E.; Cheng, S.F. The MEMS flux concentrator: Potential low-cost, high sensitivity magnetometer. US Army Res. 2006, 361, 1–7. [Google Scholar]
- Hui, Y.; Nan, T.; Sun, N.X.; Rinaldi, M. High Resolution Magnetometer Based on a High Frequency Magnetoelectric MEMS-CMOS Oscillator. J. Microelectromechan. Syst. 2015, 24, 134–143. [Google Scholar] [CrossRef]
- Li, M.; Rouf, V.T.; Thompson, M.J.; Horsley, D.A. Three-Axis Lorentz-Force Magnetic Sensor for Electronic Compass Applications. J. Microelectromechan. Syst. 2012, 21, 1002–1010. [Google Scholar] [CrossRef]
- Pala, S.; Çiçek, M.; Azgın, K. A Lorentz force MEMS magnetometer. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Rasson, J.L. Geomagnetic Measurements for Aeronautics. In Geomagnetics for Aeronautical Safety; Rasson, J.L., Delipetrov, T., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 213–230. [Google Scholar]
- Isac, A.; Dobrica, V.; Greculeasa, R.; Iancu, L. Geomagnetic Measurements and Maps for National Aeronautical Safety. Rev. Roimaine Géophys. 2016, 60, 27–33. [Google Scholar]
- Shapiro, I.R.; Stolarik, J.D.; Heppner, J.P. Thye Vector Field Proton Magnetometer for IGY Satellite Ground Stations. J. Geophys. Res. 1960, 65, 913–920. [Google Scholar] [CrossRef]
- Lilley, F.E.M. An experimental detailed magnetic survey by light aircraft. Proc. Australas. Inst. Min. Metall. 1964, 210, 59–69. [Google Scholar]
- Overhauser, A.W. Polarization of Nuclei in Metals. Phys. Rev. 1953, 92, 411–415. [Google Scholar] [CrossRef]
- Duret, D.; Bonzom, J.; Brochier, M.; Frances, M.; Leger, J.; Odru, R.; Salvi, C.; Thomas, T.; Perret, A. Overhauser magnetometer for the Danish Oersted satellite. IEEE Trans. Magn. 1995, 31, 3197–3199. [Google Scholar] [CrossRef]
- Duret, D.; Leger, J.; Frances, M.; Bonzom, J.; Alcouffe, F.; Perret, A.; Llorens, J.; Baby, C. Performances of the OVH magnetometer for the Danish Oersted satellite. IEEE Trans. Magn. 1996, 32, 4935–4937. [Google Scholar] [CrossRef]
- Hardy, J.; Strader, J.; Gross, J.N.; Gu, Y.; Keck, M.; Douglas, J.; Taylor, C.N. Unmanned aerial vehicle relative navigation in GPS denied environments. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 344–352. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Taylor, B. Impact and Mitigation of GPS-Unavailability on Small UAV Navigation, Guidance and Control White Paper; Technical Report; Department of Aerospace Engineering & Mechanics, University of Minnesota: Minneapolis, MN, USA, 2012. [Google Scholar]
- Chen, S.; Jiang, H.; Zhu, J.; Qiu, Y.; Zhang, S. Classification of unexploded ordnance-like targets with characteristic response in transient electromagnetic sensing. J. Instrum. 2019, 14, P10011. [Google Scholar] [CrossRef]
- Salem, A.; Ushijima, K.; Gamey, T.; Ravat, D. Automatic Detection of UXO from Airborne Magnetic Data Using a Neural Network. Subsurf. Sens. Technol. Appl. 2001, 2, 191–213. [Google Scholar] [CrossRef]
- Wiegert, R.; Oeschger, J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; Volume 2, pp. 1325–1332. [Google Scholar] [CrossRef]
- Linzen, S.; Chwala, A.; Schultze, V.; Schulz, M.; Schuler, T.; Stolz, R.; Bondarenko, N.; Meyer, H. A LTS-SQUID System for Archaeological Prospection and Its Practical Test in Peru. IEEE Trans. Appl. Supercond. 2007, 17, 750–755. [Google Scholar] [CrossRef]
- Doll, W.; Gamey, T.; Beard, L.; Bell, D.; Holladay, J. Recent advances in airborne survey technology yield performance approaching ground-based surveys. Lead. Edge 2003, 22, 420–425. [Google Scholar] [CrossRef]
- Hardwick, C. Important Design Considerations for Inboard Airborne Magnetic Gradiometers. Explor. Geophys. 1984, 15, 266. [Google Scholar] [CrossRef]
- Weiss, E.; Ginzburg, B.; Cohen, T.R.; Zafrir, H.; Alimi, R.; Salomonski, N.; Sharvit, J. High Resolution Marine Magnetic Survey of Shallow Water Littoral Area. Sensors 2007, 7, 1697–1712. [Google Scholar] [CrossRef] [PubMed]
- Boyce, J.; Reinhardt, E.G.; Raban, A.; Pozza, M. Marine Magnetic Survey of a Submerged Roman Harbour, Caesarea Maritima, Israel. Int. J. Naut. Archaeol. 2004, 33, 122–136. [Google Scholar] [CrossRef]
- German, C.R.; Yoerger, D.R.; Jakuba, M.; Shank, T.M.; Langmuir, C.H.; ichi Nakamura, K. Hydrothermal exploration with the Autonomous Benthic Explorer. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2008, 55, 203–219. [Google Scholar] [CrossRef]
- Gamey, T.J.; Doll, W.E.; Beard, L.P. Initial design and testing of a full-tensor airborne SQUID magnetometer for detection of unexploded ordnance. In SEG Technical Program Expanded Abstracts 2004; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005; pp. 798–801. [Google Scholar] [CrossRef]
- Drung, D.; Abmann, C.; Beyer, J.; Kirste, A.; Peters, M.; Ruede, F.; Schurig, T. Highly Sensitive and Easy-to-Use SQUID Sensors. IEEE Trans. Appl. Supercond. 2007, 17, 699–704. [Google Scholar] [CrossRef]
- Kirtley, J.R.; Ketchen, M.B.; Stawiasz, K.G.; Sun, J.Z.; Gallagher, W.J.; Blanton, S.H.; Wind, S.J. High-resolution scanning SQUID microscope. Appl. Phys. Lett. 1995, 66, 1138–1140. [Google Scholar] [CrossRef]
- Hao, H.; Wang, H.; Chen, L.; Wu, J.; Qiu, L.; Rong, L. Initial Results from SQUID Sensor: Analysis and Modeling for the ELF/VLF Atmospheric Noise. Sensors 2017, 17, 371. [Google Scholar] [CrossRef] [PubMed]
- Baudenbacher, F.; Fong, L.E.; Holzer, J.R.; Radparvar, M. Monolithic low-transition-temperature superconducting magnetometers for high resolution imaging magnetic fields of room temperature samples. Appl. Phys. Lett. 2003, 82, 3487–3489. [Google Scholar] [CrossRef]
- Zhang, Y.; Yi, H.R.; Schubert, J.; Zander, W.; Krause, H.; Bousack, H.; Braginski, A.I. Operation of rf SQUID magnetometers with a multi-turn flux transformer integrated with a superconducting labyrinth resonator. IEEE Trans. Appl. Supercond. 1999, 9, 3396–3400. [Google Scholar] [CrossRef]
- Storm, J.H.; Hömmen, P.; Drung, D.; Körber, R. An ultra-sensitive and wideband magnetometer based on a superconducting quantum interference device. Appl. Phys. Lett. 2017, 110, 072603. [Google Scholar] [CrossRef]
- Cho, E.Y.; Li, H.; LeFebvre, J.C.; Zhou, Y.W.; Dynes, R.C.; Cybart, S.A. Direct-coupled micro-magnetometer with Y-Ba-Cu-O nano-slit SQUID fabricated with a focused helium ion beam. Appl. Phys. Lett. 2018, 113, 162602. [Google Scholar] [CrossRef]
- Trabaldo, E.; Pfeiffer, C.; Andersson, E.; Chukharkin, M.; Arpaia, R.; Montemurro, D.; Kalaboukhov, A.; Winkler, D.; Lombardi, F.; Bauch, T. SQUID Magnetometer Based on Grooved Dayem Nanobridges and a Flux Transformer. IEEE Trans. Appl. Supercond. 2020, 30, 1–4. [Google Scholar] [CrossRef]
- Jenks, W.G.; Sadeghi, S.S.H.; Wikswo, J.P. SQUIDs for nondestructive evaluation. J. Phys. D Appl. Phys. 1997, 30, 293–323. [Google Scholar] [CrossRef]
- Clarke, J.; Braginski, A.I. The SQUID Handbook; Wiley Online Library: Hoboken, NJ, USA, 2004; Volume 1. [Google Scholar]
- Faley, M.I.; Kostyurina, E.A.; Kalashnikov, K.V.; Maslennikov, Y.V.; Koshelets, V.P.; Dunin-Borkowski, R.E. Superconducting Quantum Interferometers for Nondestructive Evaluation. Sensors 2017, 17, 2798. [Google Scholar] [CrossRef]
- Anahory, Y.; Reiner, J.; Embon, L.; Halbertal, D.; Yakovenko, A.; Myasoedov, Y.; Rappaport, M.L.; Huber, M.E.; Zeldov, E. Three-Junction SQUID-on-Tip with Tunable In-Plane and Out-of-Plane Magnetic Field Sensitivity. Nano Lett. 2014, 14, 6481–6487. [Google Scholar] [CrossRef]
- Talanov, V.V.; Lettsome, N.M., Jr.; Borzenets, V.; Gagliolo, N.; Cawthorne, A.B.; Orozco, A. A scanning SQUID microscope with 200 MHz bandwidth. Supercond. Sci. Technol. 2014, 27, 044032. [Google Scholar] [CrossRef][Green Version]
- Schultze, V.; Linzen, S.; Schüler, T.; Chwala, A.; Stolz, R.; Schulz, M.; Meyer, H.G. Rapid and sensitive magnetometer surveys of large areas using SQUIDs—the measurement system and its application to the Niederzimmern Neolithic double-ring ditch exploration. Archaeol. Prospect. 2008, 15, 113–131. [Google Scholar] [CrossRef]
- Schmelz, M.; Stolz, R. Superconducting Quantum Interference Device (SQUID) Magnetometers. In High Sensitivity Magnetometers; Grosz, A., Haji-Sheikh, M.J., Mukhopadhyay, S.C., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 279–311. [Google Scholar] [CrossRef]
- Finkler, A.; Segev, Y.; Myasoedov, Y.; Rappaport, M.L.; Ne’eman, L.; Vasyukov, D.; Zeldov, E.; Huber, M.E.; Martin, J.; Yacoby, A. Self-Aligned Nanoscale SQUID on a Tip. Nano Lett. 2010, 10, 1046–1049. [Google Scholar] [CrossRef] [PubMed]
- Carr, C.; Eulenburg, A.; Romans, E.J.; Pegrum, C.M.; Donaldson, G.B. High-temperature superconducting YBCO dc SQUID gradiometers fabricated on STO bicrystal substrate. Supercond. Sci. Technol. 1998, 11, 1317–1322. [Google Scholar] [CrossRef]
- Du, J.; Lazar, J.Y.; Lam, S.K.H.; Mitchell, E.E.; Foley, C.P. Fabrication and characterisation of series YBCO step-edge Josephson junction arrays. Supercond. Sci. Technol. 2014, 27, 095005. [Google Scholar] [CrossRef]
- Coustenis, A. Titan. In Encyclopedia of the Solar System; Spohn, T., Breuer, D., Johnson, T.V., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2014; pp. 831–849. [Google Scholar] [CrossRef]
- Chen, H.; Wan, Z. SQUID-Based Internal Defect Detection of Three-Dimensional Braided Composite Material. In Communications in Computer and Information Science; Computing and Intelligent Systems, ICCIC 2011; Springer: Berlin/Heidelber, Germany, 2011; Volume 233, pp. 9–16. [Google Scholar] [CrossRef]
- Snider, E.; Dasenbrock-Gammon, N.; McBride, R.; Debessai, M.; Vindana, H.; Vencatasamy, K.; Lawler, K.V.; Salamat, A.; Dias, R.P. Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature 2020, 586, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Macharet, D.G.; Perez-Imaz, H.I.A.; Rezeck, P.A.F.; Potje, G.A.; Benyosef, L.C.C.; Wiermann, A.; Freitas, G.M.; Garcia, L.G.U.; Campos, M.F.M. Autonomous Aeromagnetic Surveys Using a Fluxgate Magnetometer. Sensors 2016, 16, 2169. [Google Scholar] [CrossRef]
- Calou, P.; Munschy, M. Airborne Magnetic Surveying With a Drone and Determination of the Total Magnetization of a Dipole. IEEE Trans. Magn. 2020, 56, 1–9. [Google Scholar] [CrossRef]
- Oh, S. Multisensor fusion for autonomous UAV navigation based on the Unscented Kalman Filter with Sequential Measurement Updates. In Proceedings of the 2010 IEEE Conference on Multisensor Fusion and Integration, Salt Lake City, UT, USA, 5–7 September 2010; pp. 217–222. [Google Scholar]
- Brzozowski, B.; Rochala, Z.; Wojtowicz, K. Overview of the research on state-of-the-art measurement sensors for UAV navigation. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 565–570. [Google Scholar]
- Youn, W. Magnetic Fault–Tolerant Navigation Filter for a UAV. IEEE Sens. J. 2020, 20, 13480–13490. [Google Scholar] [CrossRef]
- Parshin, A.; Morozov, V.; Blinov, A.; Kosterev, A.; Budyak, A. Low-altitude geophysical magnetic prospecting based on multirotor UAV as a promising replacement for traditional ground survey. Geo Spat. Inf. Sci. 2018, 21, 67–74. [Google Scholar] [CrossRef]
- Raquet, J.F.; Shockley, J.; Fisher, K. Determining Absolute Position Using 3-Axis Magnetometers and the Need for Self-Building World Models; Technical Report STO-EN-SET-197; Air Force Institute of Technology, AFIT/ENG: Hobson Way, OH, USA, 2013. [Google Scholar]
- Gavazzi, B.; Le Maire, P.; Mercier de Lépinay, J.; Calou, P.; Munschy, M. Fluxgate three-component magnetometers for cost-effective ground, UAV and airborne magnetic surveys for industrial and academic geoscience applications and comparison with current industrial standards through case studies. Geomech. Energy Environ. 2019, 20, 100117. [Google Scholar] [CrossRef]
- Mitchell, M.W.; Palacios Alvarez, S. Colloquium: Quantum limits to the energy resolution of magnetic field sensors. Rev. Mod. Phys. 2020, 92, 021001. [Google Scholar] [CrossRef]
- Schultz, G.; Mhaskar, R.; Prouty, M.; Miller, J. Integration of micro-fabricated atomic magnetometers on military systems. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXI; Bishop, S.S., Isaacs, J.C., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2016; Volume 9823, pp. 358–367. [Google Scholar] [CrossRef]
- Li, B.B.; Bulla, D.; Prakash, V.; Forstner, S.; Dehghan-Manshadi, A.; Rubinsztein-Dunlop, H.; Foster, S.; Bowen, W.P. Invited Article: Scalable high-sensitivity optomechanical magnetometers on a chip. APL Photonics 2018, 3, 120806. [Google Scholar] [CrossRef]
- Chung, R.; Weber, R.; Jiles, D.C. The magnetostrictive laser diode magnetometer for personal magnetic field dosimetry. J. Appl. Phys. 1993, 73, 5638. [Google Scholar] [CrossRef]
- Osiander, R.; Ecelberger, S.A.; Givens, R.B.; Wickenden, D.K.; Murphy, J.C.; Kistenmacher, T.J. A microelectromechanical-based magnetostrictive magnetometer. Appl. Phys. Lett. 1996, 69, 2930–2931. [Google Scholar] [CrossRef]
- Calkins, F.T.; Flatau, A.B.; Dapino, M.J. Overview of Magnetostrictive Sensor Technology. J. Intell. Mater. Syst. Struct. 2007, 18, 1057–1066. [Google Scholar] [CrossRef]
- Wickenden, D.K.; Kistenmacher, T.J.; Osiander, R.; Ecelberger, S.A.; Givens, R.B.; Murphy, J.C. Development of Miniature Magnetometers. John Hopkins APL Tech. Dig. 1997, 18, 271–278. [Google Scholar]
- Viehmann, W. Magnetometer Based on the Hall Effect. Rev. Sci. Instrum. 1962, 33, 537–539. [Google Scholar] [CrossRef]
- Popovic, R.S. High resolution Hall magnetic sensors. In Proceedings of the 2014 29th International Conference on Microelectronics Proceedings—MIEL 2014, Belgrade, Serbia, 12–14 May 2014; pp. 69–74. [Google Scholar] [CrossRef]
- Korth, H.; Strohbehn, K.; Tejada, F.; Andreou, A.G.; Kitching, J.; Knappe, S.; Lehtonen, S.J.; London, S.M.; Kafel, M. Miniature atomic scalar magnetometer for space based on the rubidium isotope 87Rb. JGR Space Phys. 2016, 121, 7870–7880. [Google Scholar] [CrossRef]
- Li, B.B.; Bílek, J.; Hoff, U.B.; Madsen, L.S.; Forstner, S.; Prakash, V.; Schäfermeier, C.; Gehring, T.; Bowen, W.P.; Andersen, U.L. Quantum enhanced optomechanical magnetometry. Optica 2018, 5, 850–856. [Google Scholar] [CrossRef]
- Webb, J.L.; Clement, J.D.; Troise, L.; Ahmadi, S.; Johansen, G.J.; Hucka, A.; Andersen, U.L. Nanotesla sensitivity magnetic field sensing using a compact diamond nitrogen-vacancy magnetometer. Appl. Phys. Lett. 2019, 114, 231103. [Google Scholar] [CrossRef]
- Alem, O.; Sauer, K.L.; Romalis, M.V. Spin damping in an rf atomic magnetometer. Phys. Rev. A 2013, 87, 013413. [Google Scholar] [CrossRef]
- IJsselsteijn, R.; Kielpinski, M.; Woetzel, S.; Scholtes, T.; Kessler, E.; Stolz, R.; Schultze, V.; Meyer, H.G. A full optically operated magnetometer array: An experimental study. Rev. Sci. Instrum. 2012, 83, 113106. [Google Scholar] [CrossRef]
- Pyragius, T.; Florez, H.M.; Fernholz, T. Voigt-effect-based three-dimensional vector magnetometer. Phys. Rev. A 2019, 100, 023416. [Google Scholar] [CrossRef]
- Schwindt, P.D.D.; Lindseth, B.; Knappe, S.; Shah, V.; Kitching, J. Chip-scale atomic magnetometer with improved sensitivity by use of the Mx technique. Appl. Phys. Lett. 2007, 90, 081102. [Google Scholar] [CrossRef]
- Patton, B.; Zhivun, E.; Hovde, D.C.; Budker, D. All-Optical Vector Atomic Magnetometer. Phys. Rev. Lett. 2014, 113, 013001. [Google Scholar] [CrossRef]
- Ley, L.Y.; Crepaz, H.; Dumke, R. Cavity enhanced atomic magnetometry. Sci. Rep. 2015, 5, 15448. [Google Scholar] [CrossRef]
- Fu, K.M.C.; Iwata, G.Z.; Wickenbrock, A.; Budker, D. Sensitive magnetometry in challenging environments. AVS Quantum Sci. 2020, 2, 044702. [Google Scholar] [CrossRef]
- GEM Systems. GSMP Potassium Magnetometer for High Precision and Accuracy. 2018. Available online: https://www.gemsys.ca/ultra-high-sensitivity-potassium/ (accessed on 13 May 2021).
- Ledbetter, M.P.; Savukov, I.M.; Budker, D.; Shah, V.; Knappe, S.; Kitching, J.; Michalak, D.J.; Xu, S.; Pines, A. Zero-field remote detection of NMR with a microfabricated atomic magnetometer. Proc. Natl. Acad. Sci. USA 2008, 105, 2286–2290. [Google Scholar] [CrossRef] [PubMed]
- Sarty, G.E.; Obenaus, A. Magnetic resonance imaging of astronauts on the international space station and into the solar system. Can. Aeronaut. Space J. 2012, 58, 60–68. [Google Scholar] [CrossRef]
- Van Ombergen, A.; Laureys, S.; Sunaert, S.; Tomilovskaya, E.; Parizel, P.M.; Wuyts, F.L. Spaceflight-induced neuroplasticity in humans as measured by MRI: What do we know so far? NPJ Microgravity 2017, 3, 2373–8065. [Google Scholar] [CrossRef] [PubMed]
- Forstner, S.; Prams, S.; Knittel, J.; van Ooijen, E.D.; Swaim, J.D.; Harris, G.I.; Szorkovszky, A.; Bowen, W.P.; Rubinsztein-Dunlop, H. Cavity Optomechanical Magnetometer. Phys. Rev. Lett. 2012, 108, 120801. [Google Scholar] [CrossRef]
- Wu, M.; Wu, N.L.Y.; Firdous, T.; Sani, F.F.; Losby, J.E.; Freeman, M.R.; Barclay, P.E. Nanocavity optomechanical torque magnetometry and radiofrequency susceptometry. Nat. Nanotechnol. 2017, 12, 127–131. [Google Scholar] [CrossRef] [PubMed]
- Forstner, S.; Sheridan, E.; Knittel, J.; Humphreys, C.L.; Brawley, G.A.; Rubinsztein-Dunlop, H.; Bowen, W.P. Ultrasensitive optomechanical magnetometry. Adv. Mater. 2014, 26, 6348–6353. [Google Scholar] [CrossRef]
- Yu, C.; Janousek, J.; Sheridan, E.; McAuslan, D.L.; Rubinsztein-Dunlop, H.; Lam, P.K.; Zhang, Y.; Bowen, W.P. Optomechanical magnetometry with a macroscopic resonator. Phys. Rev. Appl. 2016, 5, 044007. [Google Scholar] [CrossRef]
- Davis, J.P.; Vick, D.; Fortin, D.C.; Burgess, J.A.J.; Hiebert, W.K.; Freeman, M.R. Nanotorsional resonator torque magnetometry. Appl. Phys. Lett. 2010, 96, 072513. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, G.; Savukov, I.; Yang, L. Polymer encapsulated microcavity optomechanical magnetometer. Sci. Rep. 2017, 7, 8896. [Google Scholar] [CrossRef]
- Hajisalem, G.; Losby, J.E.; de Oliveira Luiz, G.; Sauer, V.T.; Barclay, P.E.; Freeman, M.R. Two-axis cavity optomechanical torque characterization of magnetic microstructures. New J. Phys. 2019, 21, 095005. [Google Scholar] [CrossRef]
- Burgess, J.; Fraser, A.; Sani, F.F.; Vick, D.; Hauer, B.; Davis, J.; Freeman, M. Quantitative magneto-mechanical detection and control of the Barkhausen effect. Science 2013, 339, 1051–1054. [Google Scholar] [CrossRef]
- Davis, J.; Vick, D.; Li, P.; Portillo, S.; Fraser, A.; Burgess, J.; Fortin, D.; Hiebert, W.; Freeman, M. Nanomechanical torsional resonator torque magnetometry. J. Appl. Phys. 2011, 109, 07D309. [Google Scholar] [CrossRef]
- Colombano, M.F.; Arregui, G.; Bonell, F.; Capuj, N.E.; Chavez-Angel, E.; Pitanti, A.; Valenzuela, S.O.; Sotomayor-Torres, C.M.; Navarro-Urrios, D.; Costache, M.V. Ferromagnetic Resonance Assisted Optomechanical Magnetometer. Phys. Rev. Lett. 2020, 125, 147201. [Google Scholar] [CrossRef] [PubMed]
- Purdy, T.; Yu, P.L.; Kampel, N.; Peterson, R.; Cicak, K.; Simmonds, R.; Regal, C. Optomechanical Raman-ratio thermometry. Phys. Rev. A 2015, 92, 031802. [Google Scholar] [CrossRef]
- Purdy, T.; Grutter, K.; Srinivasan, K.; Taylor, J. Quantum correlations from a room-temperature optomechanical cavity. Science 2017, 356, 1265–1268. [Google Scholar] [CrossRef]
- Singh, R.; Purdy, T.P. Detecting Acoustic Blackbody Radiation with an Optomechanical Antenna. Phys. Rev. Lett. 2020, 125, 120603. [Google Scholar] [CrossRef]
- Basiri-Esfahani, S.; Armin, A.; Forstner, S.; Bowen, W.P. Precision ultrasound sensing on a chip. Nat. Commun. 2019, 10, 132. [Google Scholar] [CrossRef]
- Westerveld, W.J.; Mahmud-Ul-Hasan, M.; Shnaiderman, R.; Ntziachristos, V.; Rottenberg, X.; Severi, S.; Rochus, V. Sensitive, small, broadband and scalable optomechanical ultrasound sensor in silicon photonics. Nat. Photonics 2021, 15, 341–345. [Google Scholar] [CrossRef]
- Zhao, X.; Tsai, J.; Cai, H.; Ji, X.; Zhou, J.; Bao, M.; Huang, Y.; Kwong, D.; Liu, A.Q. A nano-opto-mechanical pressure sensor via ring resonator. Opt. Express 2012, 20, 8535–8542. [Google Scholar] [CrossRef] [PubMed]
- Gavartin, E.; Verlot, P.; Kippenberg, T.J. A hybrid on-chip optomechanical transducer for ultrasensitive force measurements. Nat. Nanotechnol. 2012, 7, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Harris, G.I.; McAuslan, D.L.; Stace, T.M.; Doherty, A.C.; Bowen, W.P. Minimum requirements for feedback enhanced force sensing. Phys. Rev. Lett. 2013, 111, 103603. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Bao, Y.; Madugani, R.; Long, D.A.; Gorman, J.J.; LeBrun, T.W. Broadband thermomechanically limited sensing with an optomechanical accelerometer. Optica 2021, 8, 350–356. [Google Scholar] [CrossRef]
- Krause, A.G.; Winger, M.; Blasius, T.D.; Lin, Q.; Painter, O. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 2012, 6, 768. [Google Scholar] [CrossRef]
- Guzmán Cervantes, F.; Kumanchik, L.; Pratt, J.; Taylor, J.M. High sensitivity optomechanical reference accelerometer over 10 kHz. Appl. Phys. Lett. 2014, 104, 221111. [Google Scholar] [CrossRef]
- Gerberding, O.; Cervantes, F.G.; Melcher, J.; Pratt, J.R.; Taylor, J.M. Optomechanical reference accelerometer. Metrologia 2015, 52, 654. [Google Scholar] [CrossRef]
- Thanalakshme, R.P.; Kanj, A.; Kim, J.; Wilken-Resman, E.; Jing, J.; Grinberg, I.H.; Bernhard, J.T.; Tawfick, S.; Bahl, G. Magneto-Mechanical Transmitters for Ultra-Low Frequency Near-field Communication. arXiv 2021, arXiv:2012.14548. [Google Scholar]
- Simin, D.; Soltamov, V.A.; Poshakinskiy, A.V.; Anisimov, A.N.; Babunts, R.A.; Tolmachev, D.O.; Mokhov, E.N.; Trupke, M.; Tarasenko, S.A.; Sperlich, A.; et al. All-Optical dc Nanotesla Magnetometry Using Silicon Vacancy Fine Structure in Isotopically Purified Silicon Carbide. Phys. Rev. X 2016, 6, 031014. [Google Scholar] [CrossRef]
- Niethammer, M.; Widmann, M.; Lee, S.Y.; Stenberg, P.; Kordina, O.; Ohshima, T.; Son, N.T.; Janzén, E.; Wrachtrup, J. Vector Magnetometry Using Silicon Vacancies in 4H-SiC Under Ambient Conditions. Phys. Rev. Appl. 2016, 6, 034001. [Google Scholar] [CrossRef]
- Wolf, T.; Neumann, P.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; Wrachtrup, J. Subpicotesla Diamond Magnetometry. Phys. Rev. X 2015, 5, 041001. [Google Scholar] [CrossRef]
- Chatzidrosos, G.; Wickenbrock, A.; Bougas, L.; Leefer, N.; Wu, T.; Jensen, K.; Dumeige, Y.; Budker, D. Miniature Cavity-Enhanced Diamond Magnetometer. Phys. Rev. Appl. 2017, 8, 044019. [Google Scholar] [CrossRef]
- Grinolds, M.; Hong, S.; Maletinsky, P.; Luan, L.; Lukin, M.D.; Walsworth, R.L.; Yacoby, A. Nanoscale magnetic imaging of a single electron spin under ambient conditions. Nat. Phys. 2013, 9, 215–219. [Google Scholar] [CrossRef]
- Kuwahata, A.; Kitaizumi, T.; Saichi, K.; Sato, T.; Igarashi, R.; Ohshima, T.; Masuyama, Y.; Iwasaki, T.; Hatano, M.; Jelezko, F.; et al. Magnetometer with nitrogen-vacancy center in a bulk diamond for detecting magnetic nanoparticles in biomedical applications. Sci. Rep. 2020, 10, 2483. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.; Leefer, N.; Jarmola, A.; Dumeige, Y.; Acosta, V.M.; Kehayias, P.; Patton, B.; Budker, D. Cavity-Enhanced Room-Temperature Magnetometry Using Absorption by Nitrogen-Vacancy Centers in Diamond. Phys. Rev. Lett. 2014, 112, 160802. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, P.; Osterkamp, C.; Chen, Y.; Chen, X.; Teraji, T.; Wu, E.; Naydenov, B.; Jelezko, F. dc Magnetometry with Engineered Nitrogen-Vacancy Spin Ensembles in Diamond. Nano Lett. 2019, 19, 6681–6686. [Google Scholar] [CrossRef]
- Sánchez, E.D.C.; Pessoa, A.R.; Amaral, F.; Menezes, L.D.S. Microcontroller-based magnetometer using a single nitrogen-vacancy defect in a nanodiamond. AIP Adv. 2020, 10, 025323. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.P.; Hingant, T.; Roch, J.F.; Maletinsky, P.; Jacques, V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014, 77, 056503. [Google Scholar] [CrossRef]
- Balasubramanian, G.; Chan, I.Y.; Kolesov, R.; Al-Hmoud, M.; Tisler, J.; Shin, C.; Kim, C.; Wojcik, A.; Hemmer, P.R.; Krueger, A.; et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 2008, 455, 648–651. [Google Scholar] [CrossRef]
- Le Sage, D.; Arai, K.; Glenn, D.R.; DeVience, S.J.; Pham, L.M.; Rahn-Lee, L.; Lukin, M.D.; Yacoby, A.; Komeili, A.; Walsworth, R.L. Optical magnetic imaging of living cells. Nature 2013, 496, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Clevenson, H.; Pham, L.M.; Teale, C.; Johnson, K.; Englund, D.; Braje, D. Robust high-dynamic-range vector magnetometry with nitrogen-vacancy centers in diamond. Appl. Phys. Lett. 2018, 112, 252406. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, H.; Zhao, R.; Du, F.; Li, Z.; Wang, L.; Wu, D.; Chen, Y.; Tang, J.; Liu, J. High-Sensitivity Three-Axis Vector Magnetometry Using Electron Spin Ensembles in Single-Crystal Diamond. IEEE Magn. Lett. 2019, 10, 1–4. [Google Scholar] [CrossRef]
- Yahata, K.; Matsuzaki, Y.; Saito, S.; Watanabe, H.; Ishi-Hayase, J. Demonstration of vector magnetic field sensing by simultaneous control of nitrogen-vacancy centers in diamond using multi-frequency microwave pulses. Appl. Phys. Lett. 2019, 114, 022404. [Google Scholar] [CrossRef]
- Van der Sar, T.; Casola, F.; Walsworth, R.; Yacoby, A. Nanometre-scale probing of spin waves using single electron spins. Nat. Commun. 2015, 6, 7886. [Google Scholar] [CrossRef]
- Glenn, D.R.; Fu, R.R.; Kehayias, P.; Sage, D.L.; Lima, E.A.; Weiss, B.P.; Walsworth, R.L. Micrometer-scale magnetic imaging of geological samples using a quantum diamond microscope. Geochem. Geophys. Geosyst. 2017, 18, 3254–3267. [Google Scholar] [CrossRef]
- Mamin, H.J.; Kim, M.; Sherwood, M.H.; Rettner, C.T.; Ohno, K.; Awschalom, D.D.; Rugar, D. Nanoscale Nuclear Magnetic Resonance with a Nitrogen-Vacancy Spin Sensor. Science 2013, 339, 557–560. [Google Scholar] [CrossRef]
- Kittmann, A.; Durdaut, P.; Zabel, S.; Reermann, J.; Schmalz, J.; Spetzler, B.; Meyners, D.; Sun, N.X.; McCord, J.; Gerken, M.; et al. Wide Band Low Noise Love Wave Magnetic Field Sensor System. Sci. Rep. 2018, 8, 278. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Y.; Li, M.; Shen, Y.; Li, J.; Viehland, D. Quasi-static (f<10-2 Hz) frequency response of magnetoelectric composites based magnetic sensor. Mater. Lett. 2012, 85, 84–87. [Google Scholar] [CrossRef]
- Li, M.; Gao, J.; Wang, Y.; Gray, D.; Li, J.; Viehland, D. Enhancement in magnetic field sensitivity and reduction in equivalent magnetic noise by magnetoelectric laminate stacks. J. Appl. Phys. 2012, 111, 104504. [Google Scholar] [CrossRef]
- Balevicius, S.; Zurauskiene, N.; Stankevic, V.; Kersulis, S.; Baskys, A.; Bleizgys, V.; Dilys, J.; Lucinskis, A.; Tyshko, A.; Brazil, S. Hand-Held Magnetic Field Meter Based on Colossal Magnetoresistance-B-Scalar Sensor. IEEE Trans. Instrum. Meas. 2020, 69, 2808–2816. [Google Scholar] [CrossRef]
- Guedes, A.; Almeida, J.M.; Cardoso, S.; Ferreira, R.; Freitas, P.P. Improving Magnetic Field Detection Limits of Spin Valve Sensors Using Magnetic Flux Guide Concentrators. IEEE Trans. Magn. 2007, 43, 2376–2378. [Google Scholar] [CrossRef]
- Qiu, F.; Wang, J.; Zhang, Y.; Yang, G.; Weng, C. Resolution limit of anisotropic magnetoresistance (AMR) based vector magnetometer. Sens. Actuators A Phys. 2018, 280, 61–67. [Google Scholar] [CrossRef]
- Affolderbach, C.; Stähler, M.; Knappe, S.; Wynands, R. An all-optical, high-sensitivity magnetic gradiometer. Appl. Phys. B 2002, 75, 605–612. [Google Scholar] [CrossRef]
- Griffith, W.C.; Knappe, S.; Kitching, J. Femtotesla atomic magnetometry in a microfabricated vapor cell. Opt. Express 2010, 18, 27167–27172. [Google Scholar] [CrossRef]
- Sander, T.H.; Preusser, J.; Mhaskar, R.; Kitching, J.; Trahms, L.; Knappe, S. Magnetoencephalography with a chip-scale atomic magnetometer. Biomed. Opt. Express 2012, 3, 981–990. [Google Scholar] [CrossRef]
- Liu, G.; Tang, J.; Yin, Y.; Wang, Y.; Zhou, B.; Han, B. Single-Beam Atomic Magnetometer Based on the Transverse Magnetic-Modulation or DC-Offset. IEEE Sensors J. 2020, 20, 5827–5833. [Google Scholar] [CrossRef]
- Shah, V.; Romalis, M.V. Spin-exchange relaxation-free magnetometry using elliptically polarized light. Phys. Rev. A 2009, 80, 013416. [Google Scholar] [CrossRef]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Sheng, D.; Perry, A.R.; Krzyzewski, S.P.; Geller, S.; Kitching, J.; Knappe, S. A microfabricated optically-pumped magnetic gradiometer. Appl. Phys. Lett. 2017, 110, 031106. [Google Scholar] [CrossRef]
- Scholtes, T.; Schultze, V.; IJsselsteijn, R.; Woetzel, S.; Meyer, H.G. Light-narrowed optically pumped Mx magnetometer with a miniaturized Cs cell. Phys. Rev. A 2011, 84, 043416. [Google Scholar] [CrossRef]
- Mhaskar, R.; Knappe, S.; Kitching, J. A low-power, high-sensitivity micromachined optical magnetometer. Appl. Phys. Lett. 2012, 101, 241105. [Google Scholar] [CrossRef]
- Knappe, S.; Alem, O.; Sheng, D.; Kitching, J. Microfabricated Optically-Pumped Magnetometers for Biomagnetic Applications. J. Phys. Conf. Ser. 2016, 723, 012055. [Google Scholar] [CrossRef]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
- Albarelli, F.; Rossi, M.A.C.; Paris, M.G.A.; Genoni, M.G. Ultimate limits for quantum magnetometry via time-continuous measurements. New J. Phys. 2017, 19, 123011. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, Z.; Xiang, G.Y.; Li, C.F.; Guo, G.C.; Chen, H.; Liu, L.; Yuan, H. Minimal Tradeoff and Ultimate Precision Limit of Multiparameter Quantum Magnetometry under the Parallel Scheme. Phys. Rev. Lett. 2020, 125, 020501. [Google Scholar] [CrossRef] [PubMed]
- Hospodarsky, G.B. Spaced-based search coil magnetometers. J. Geophys. Res. Space Phys. 2016, 121, 12068–12079. [Google Scholar] [CrossRef]
- Koch, R.H.; Deak, J.G.; Grinstein, G. Fundamental limits to magnetic-field sensitivity of flux-gate magnetic-field sensors. Appl. Phys. Lett. 1999, 75, 3862–3864. [Google Scholar] [CrossRef]
- Bowen, W.P.; Yu, C. High Sensitivity Magnetometers. In High Sensitivity Magnetometers; Grosz, A., Haji-Sheikh, M.J., Mukhopadhyay, S.C., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 313–338. [Google Scholar] [CrossRef]
- Forstner, S.; Knittel, J.; Sheridan, E.; Swaim, J.D.; Rubinsztein-Dunlop, H.; Bowen, W.P. Sensitivity and performance of cavity optomechanical field sensors. Photonic Sens. 2012, 2, 259–270. [Google Scholar] [CrossRef]
- Yu, Y.; Forstner, S.; Rubinsztein-Dunlop, H.; Bowen, W.P. Modelling of cavity optomechanical magnetometers. Sensors 2018, 18, 1558. [Google Scholar] [CrossRef]
- Shah, V.; Knappe, S.; Schwindt, P.D.D.; Kitching, J. Subpicotesla atomic magnetometry with a microfabricated vapour cell. Nat. Photonics 2007, 1, 649–652. [Google Scholar] [CrossRef]
- Ludwig, C.; Kessler, C.; Steinforc, A.J.; Ludwig, W. Versatile high performance digital SQUID electronics. IEEE Trans. Appl. Supercond. 2001, 11, 1122–1125. [Google Scholar] [CrossRef]
- Meyer, H.G.; Stolz, R.; Schulz, M. SQUID technology for geophysical exploration. Phys. Status Solidi 2005, 2, 1504–1509. [Google Scholar] [CrossRef]
- Schwarz, T.; Nagel, J.; Wölbing, R.; Kemmler, M.; Kleiner, R.; Koelle, D. Low-Noise Nano Superconducting Quantum Interference Device Operating in Tesla Magnetic Fields. ACS Nano 2013, 7, 844–850. [Google Scholar] [CrossRef] [PubMed]
- Schmelz, M.; Matsui, Y.; Stolz, R.; Zakosarenko, V.; Schönau, T.; Anders, S.; Linzen, S.; Itozaki, H.; Meyer, H.G. Investigation of all niobium nano-SQUIDs based on sub-micrometer cross-type Josephson junctions. Supercond. Sci. Technol. 2014, 28, 015004. [Google Scholar] [CrossRef]
- Vettoliere, A.; Ruggiero, B.; Valentinpo, M.; Silestrini, P.; Granata, C. Fine-Tuning and Optimization of Superconducting Quantum Magnetic Sensors by Thermal Annealing. Sensors 2019, 19, 3635. [Google Scholar] [CrossRef] [PubMed]
- Stürner, F.M.; Brenneis, A.; Buck, T.; Kassel, J.; Rölver, R.; Fuchs, T.; Savitsky, A.; Suter, D.; Grimmel, J.; Hengesbach, S.; et al. Integrated and Portable Magnetometer Based on Nitrogen-Vacancy Ensembles in Diamond. Adv. Quantum Technol. 2021, 4, 2000111. [Google Scholar] [CrossRef]




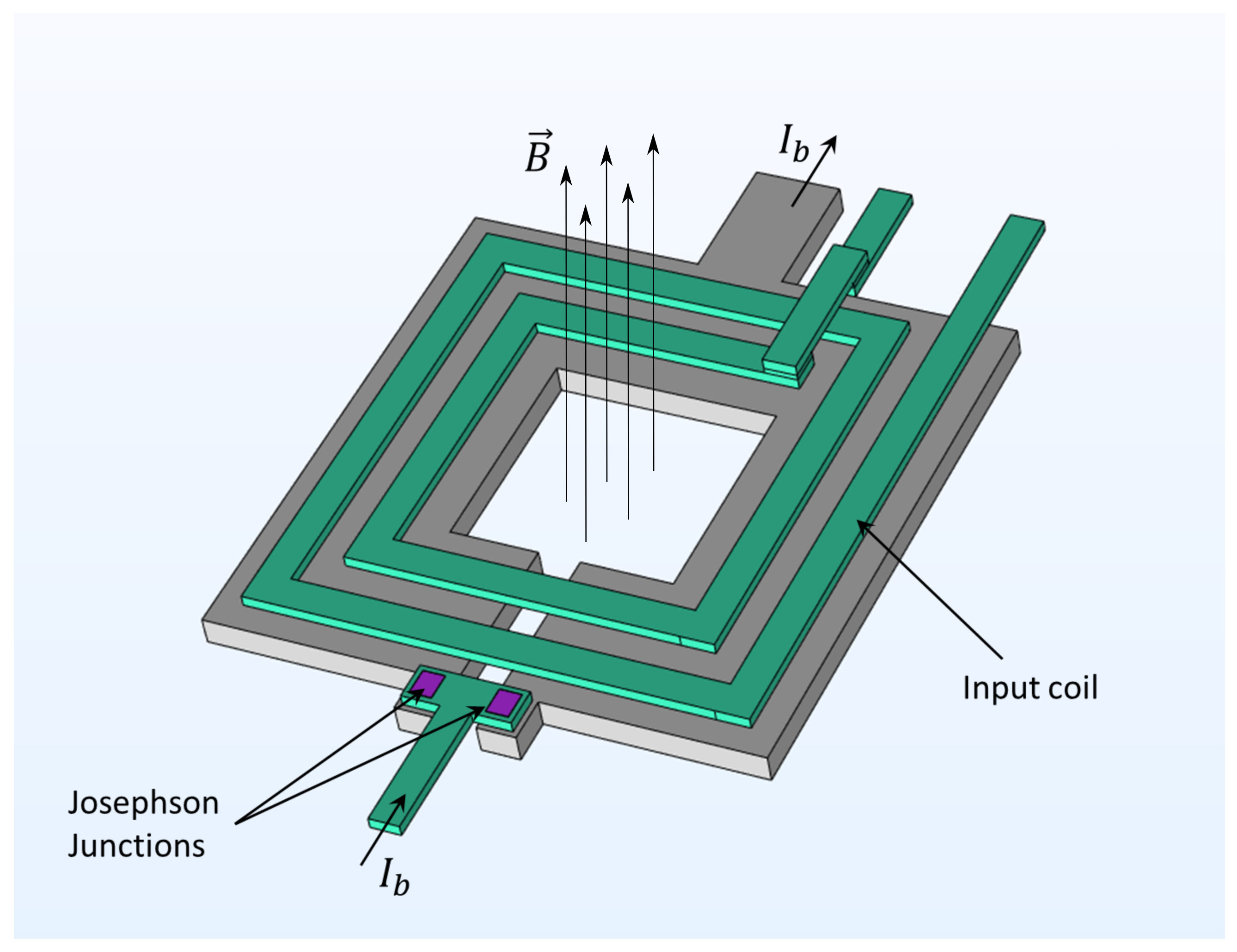

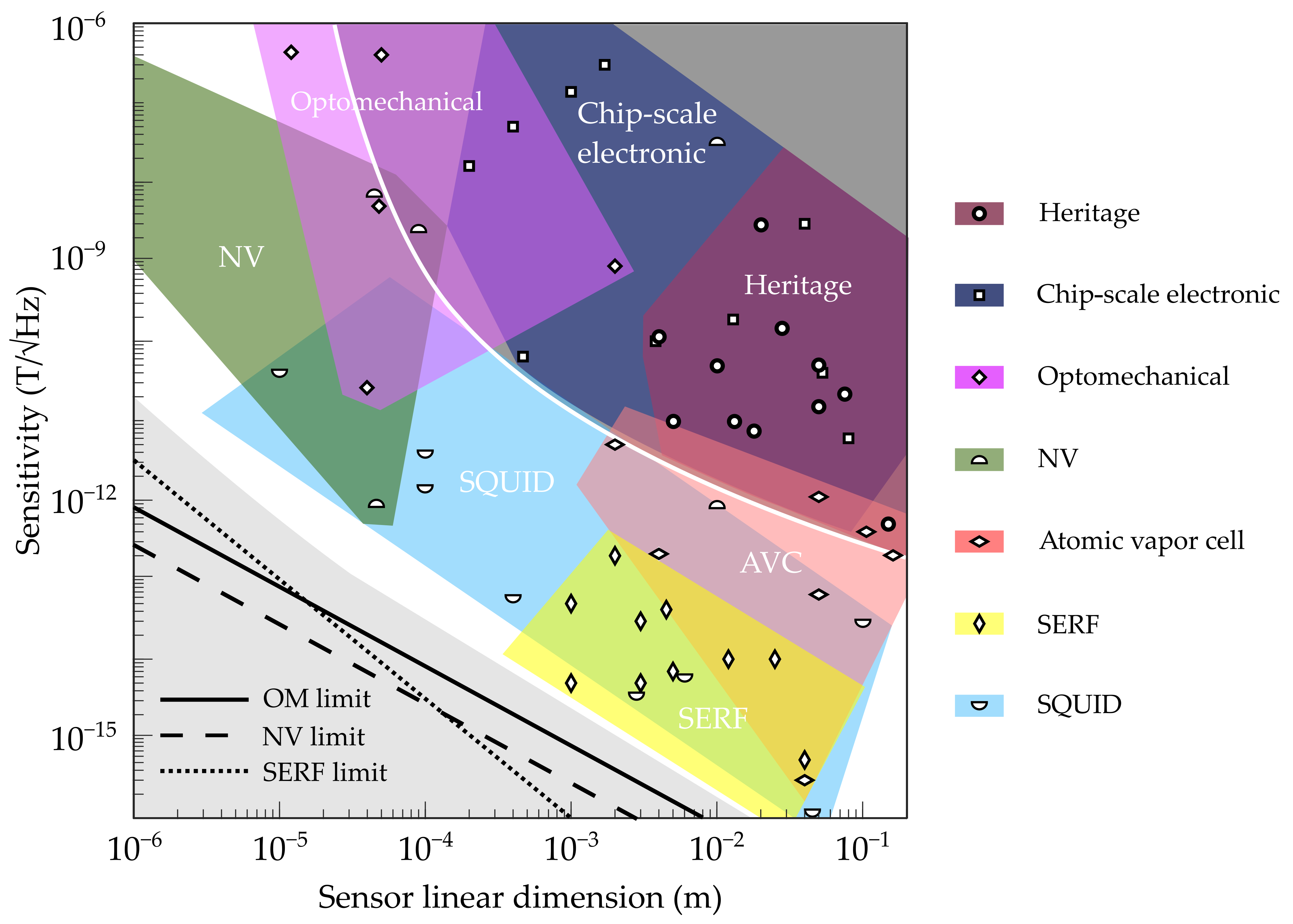
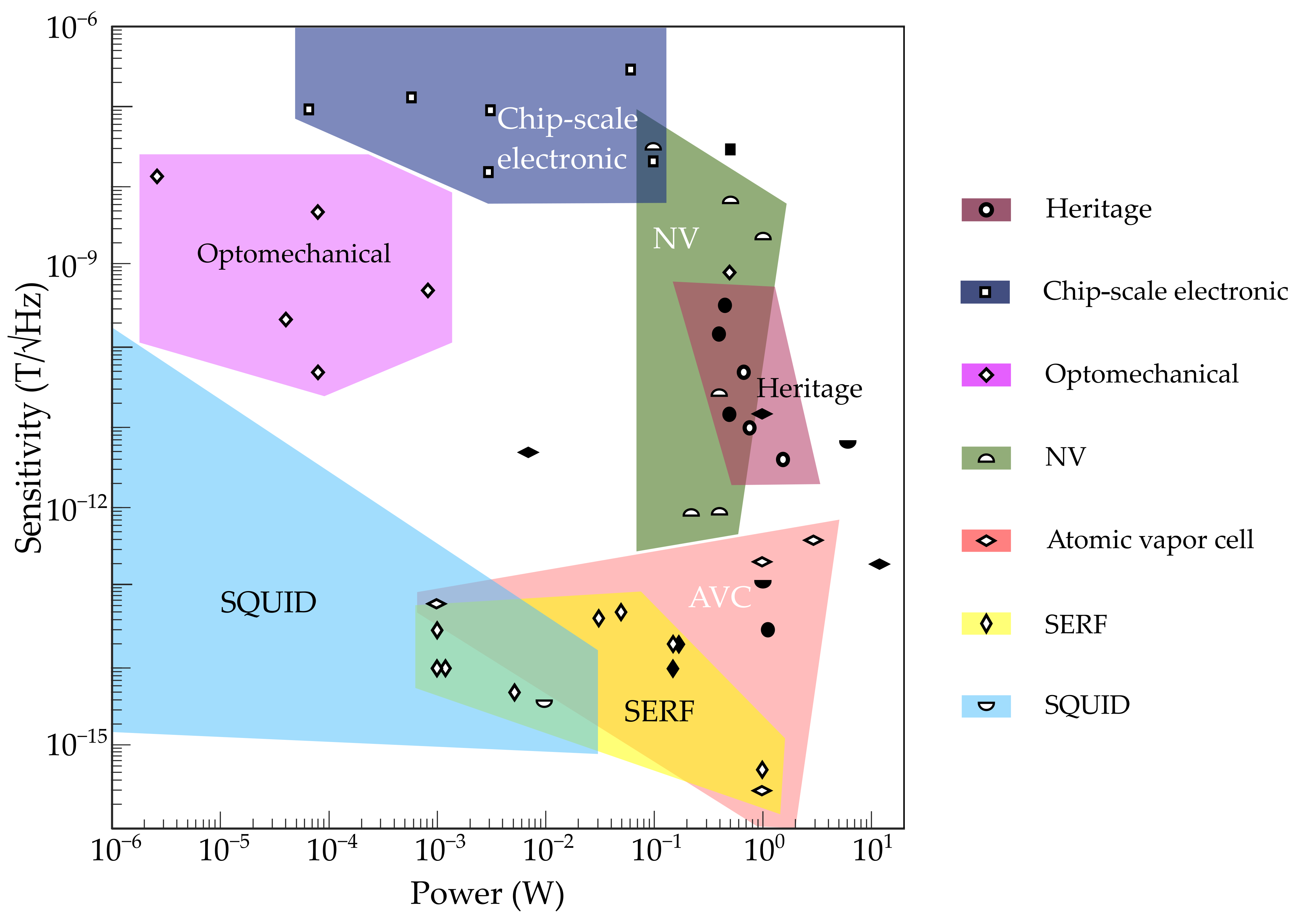

| Mission | Launch Year | Magnetometer | Dynamic Range (nT) | Resolution (pT) | Mass (kg) | Power (W) |
|---|---|---|---|---|---|---|
| GOES-1–3 | 1975–1978 | FGM (B) | 50–400 | - | - | - |
| GOES-4–7 | 1980–1987 | FGM (B) | 200 | - | - | |
| GOES-I–M | 1994–2001 | FGM (T) | 100 | - | - | |
| Cassini | 1997 | FGM (T) | 0.44 (FGM) | (sleep) | ||
| +V/SHM | (V/SHM) | (FGM + VHM) | ||||
| ±10,000 | 1200 | - | (FGM + SHM) | |||
| GOES-N–P | 2006–2010 | FGM (T) | 30 | - | - | |
| Juno | 2011 | FGM (T) | (nominal) | 48 | 5 | >4.5 |
| ± 1,638,400 (max.) | 5000 | |||||
| MAVEN | 2013 | FGM (T) | 15 | - | >1 | |
| 62 | - | |||||
| GOES-R | 2016 | FGM (T) | 16 | 2.5 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bennett, J.S.; Vyhnalek, B.E.; Greenall, H.; Bridge, E.M.; Gotardo, F.; Forstner, S.; Harris, G.I.; Miranda, F.A.; Bowen, W.P. Precision Magnetometers for Aerospace Applications: A Review. Sensors 2021, 21, 5568. https://doi.org/10.3390/s21165568
Bennett JS, Vyhnalek BE, Greenall H, Bridge EM, Gotardo F, Forstner S, Harris GI, Miranda FA, Bowen WP. Precision Magnetometers for Aerospace Applications: A Review. Sensors. 2021; 21(16):5568. https://doi.org/10.3390/s21165568
Chicago/Turabian StyleBennett, James S., Brian E. Vyhnalek, Hamish Greenall, Elizabeth M. Bridge, Fernando Gotardo, Stefan Forstner, Glen I. Harris, Félix A. Miranda, and Warwick P. Bowen. 2021. "Precision Magnetometers for Aerospace Applications: A Review" Sensors 21, no. 16: 5568. https://doi.org/10.3390/s21165568
APA StyleBennett, J. S., Vyhnalek, B. E., Greenall, H., Bridge, E. M., Gotardo, F., Forstner, S., Harris, G. I., Miranda, F. A., & Bowen, W. P. (2021). Precision Magnetometers for Aerospace Applications: A Review. Sensors, 21(16), 5568. https://doi.org/10.3390/s21165568






