A Novel Anti-Noise Fault Diagnosis Approach for Rolling Bearings Based on Convolutional Neural Network Fusing Frequency Domain Feature Matching Algorithm
Abstract
:1. Introduction
2. A Brief Theoretical Background
2.1. FFT
2.2. CNN
3. Proposed Fault Diagnosis Method
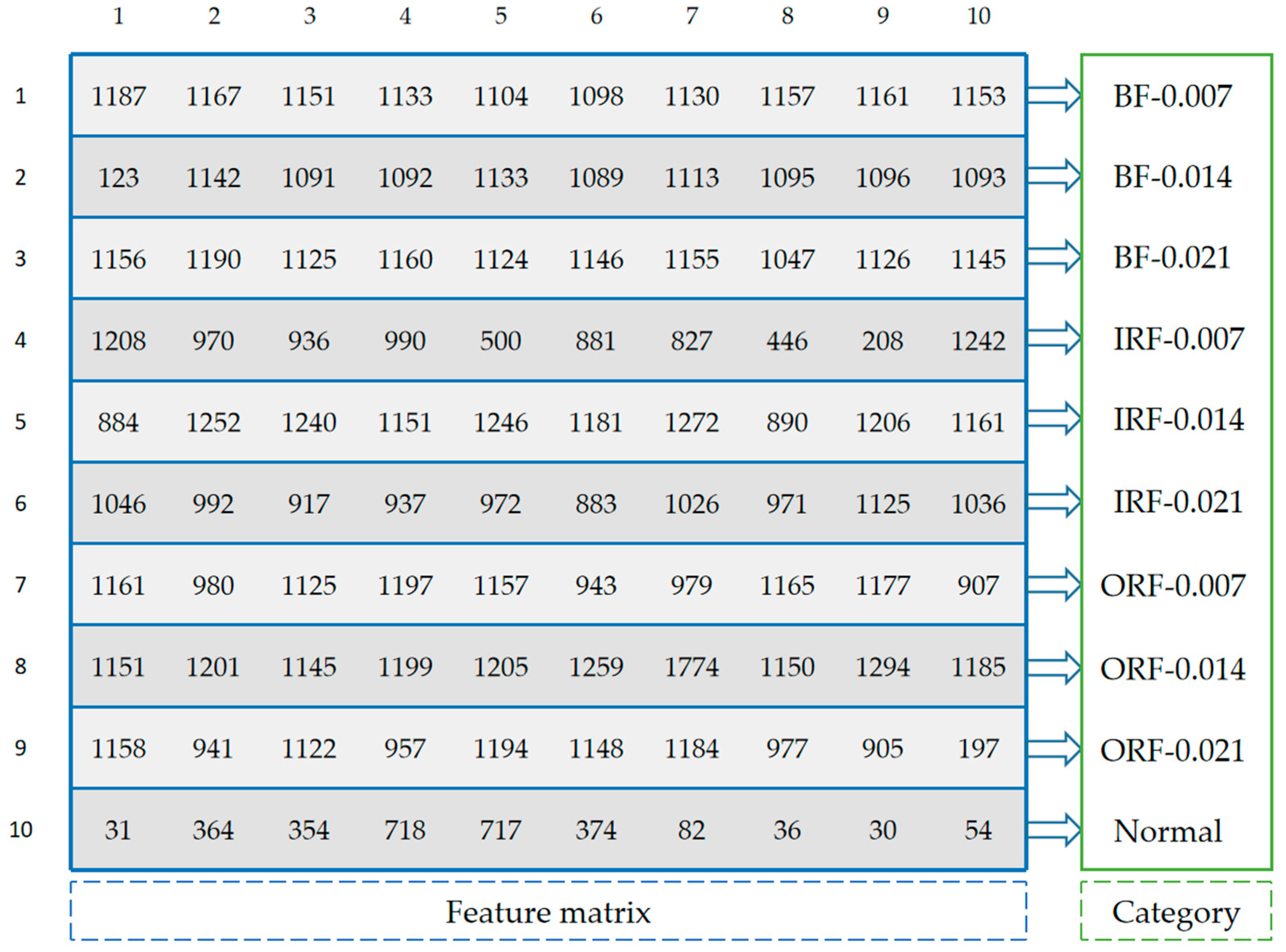
3.1. Frequency Domain Feature Matching Algorithm
- (1)
- Count the number in , and score 1 point for each number in common.
- (2)
- Count the number in , and score 1 point for each number in common.
- (3)
- Count the number in , and score 4 point for each number in common.
| Algorithm 1 | Frequency Domain Feature Matching Algorithm |
| Input: | Training dataset: ; length of training dataset:; Test dataset: ; length of test dataset:; Fast Fourier transform (FFT): ; The number of selected feature frequencies for each sample: ; The function that returns the index of the array sorted in ascending order: ; The function that reverses the array and returns the first elements:; The number of categories: ; The number of selected feature frequencies for each category: ; Scoring function with scoring rules 1, 2 and 3: ; A is feature frequencies; B is feature matrix. |
| Output: | Feature matrix with size of ; Scoreboard of all test samples. |
| Training stage: | Obtain feature matrix with size of |
| for do (Obtain the frequency spectrums of training samples by FFT); ; (Extract feature frequencies from frequency spectrum of each training sample); end for for do ; for do if then Append to the end of the list ; end if end for Count the occurrence times of feature frequencies in and sort them in descending order; The feature sequence consists of the first feature frequencies; ; end for ; return | |
| Test stage: | Calculate scoreboard of all test samples |
| ; for do (Obtain the frequency spectrums of test samples by FFT); ; (Extract feature frequencies from frequency spectrum of each test sample); (Initialize score); ; ; Append to the end of the list ; end for ; return |
3.2. 1D-CNN with Dropout in the First Layer
3.3. Fusion Strategies: Softmax with Parameter T and D-S Evidence Theory
4. Experiments
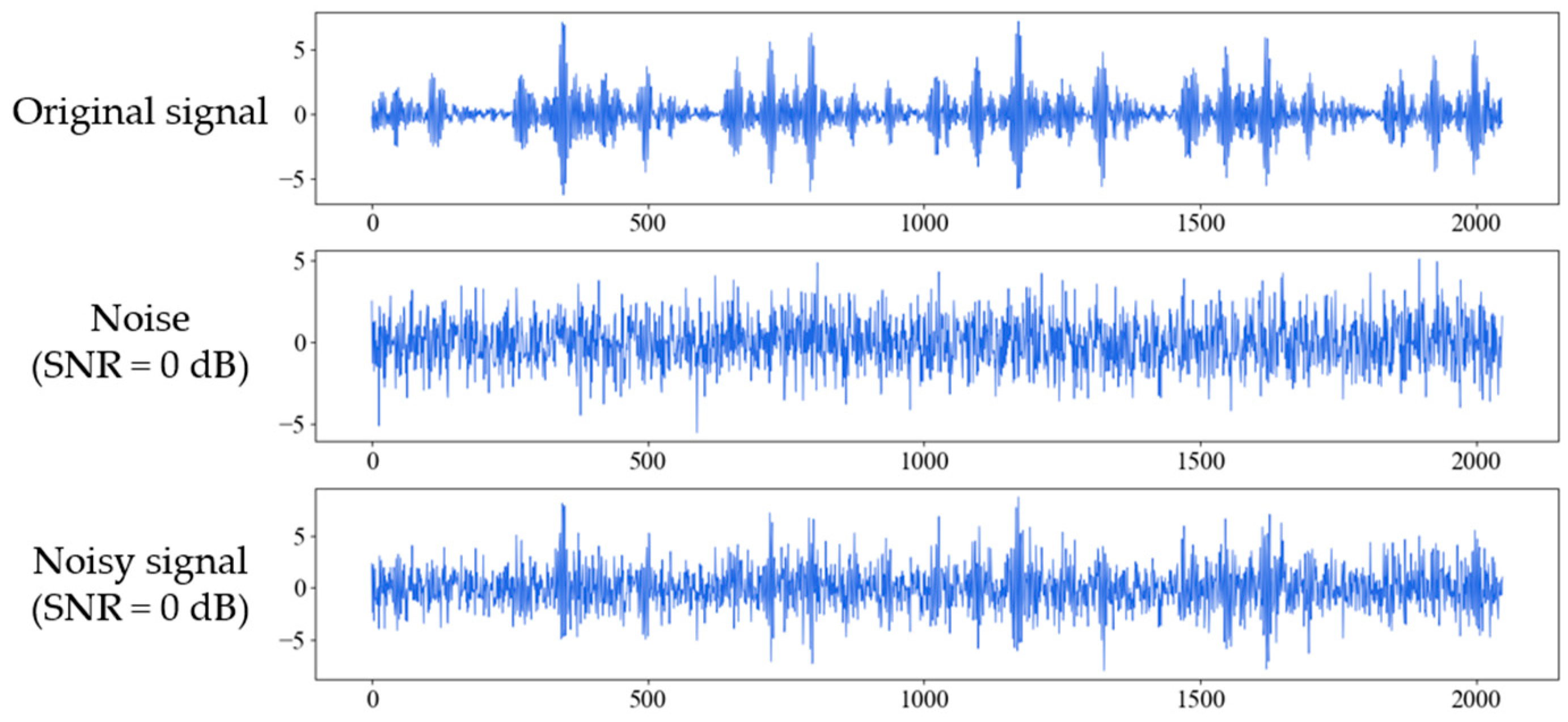
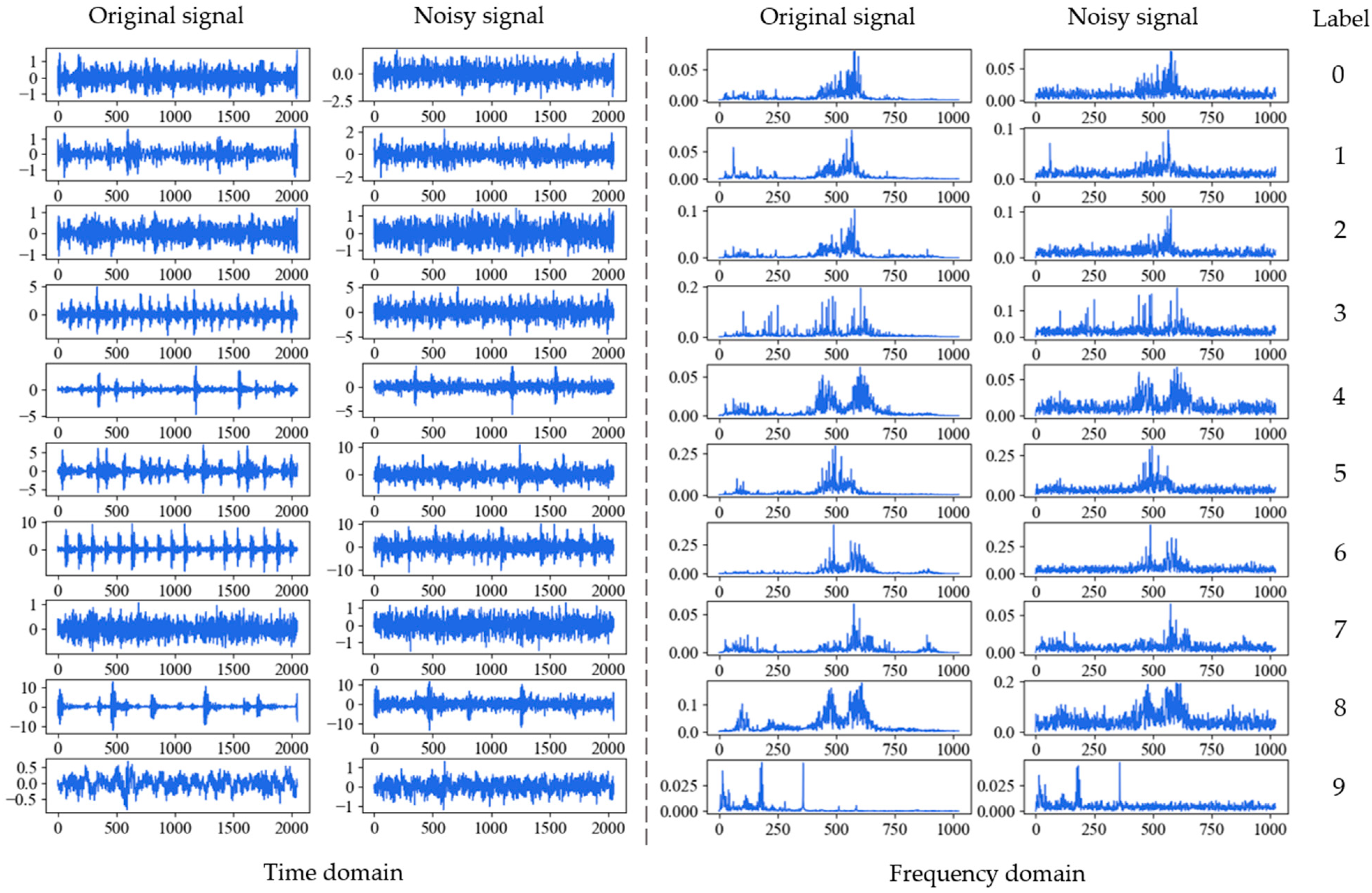
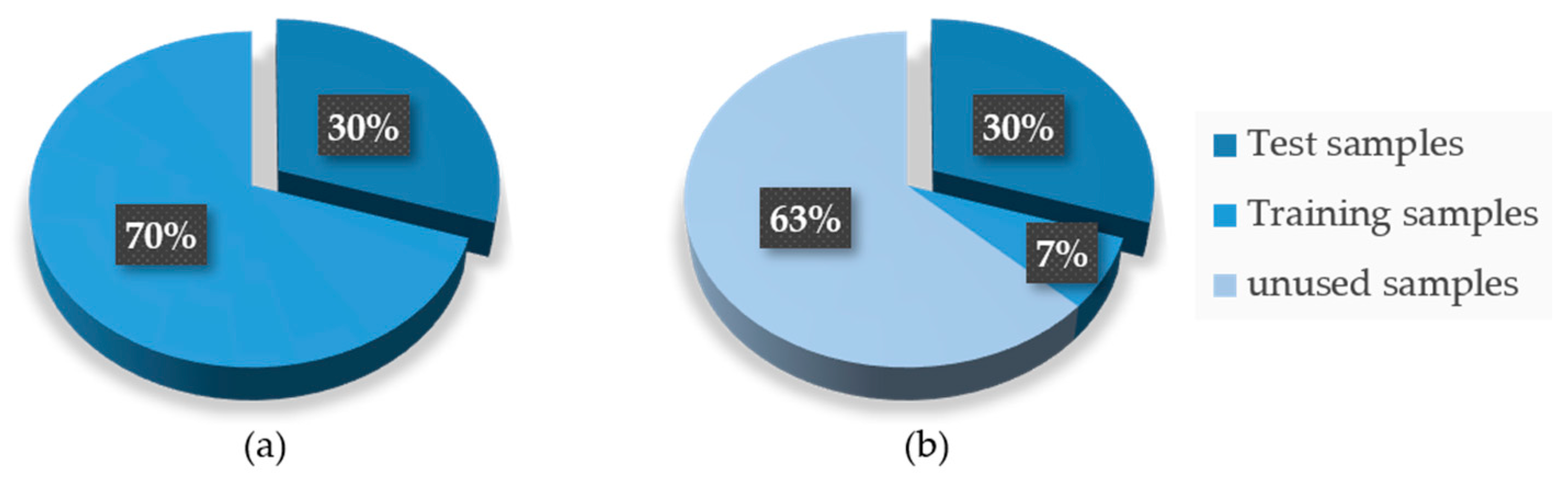
4.1. Data Description
4.2. Parameters Selection
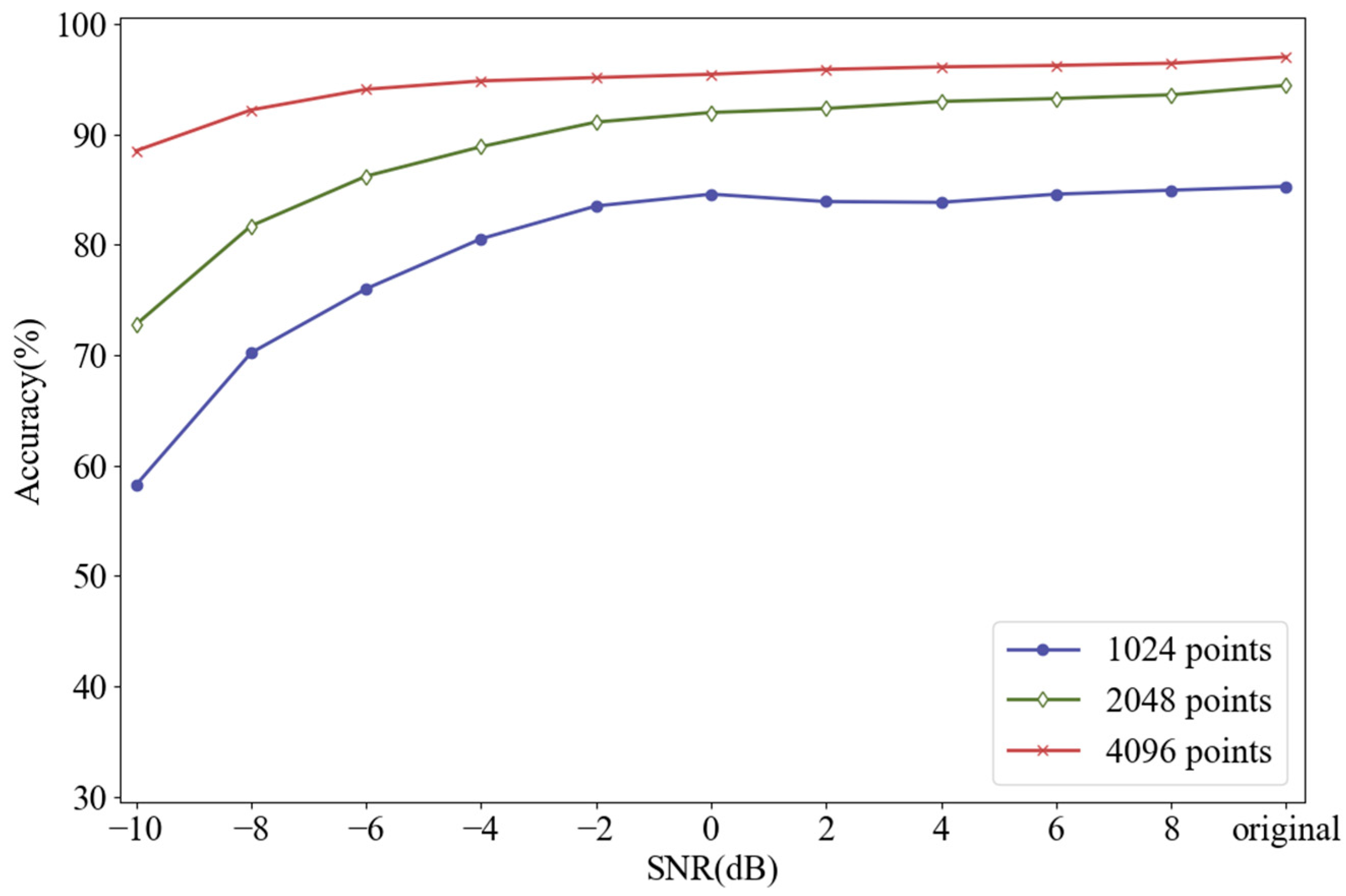
4.2.1. Sampling Points of FDFM
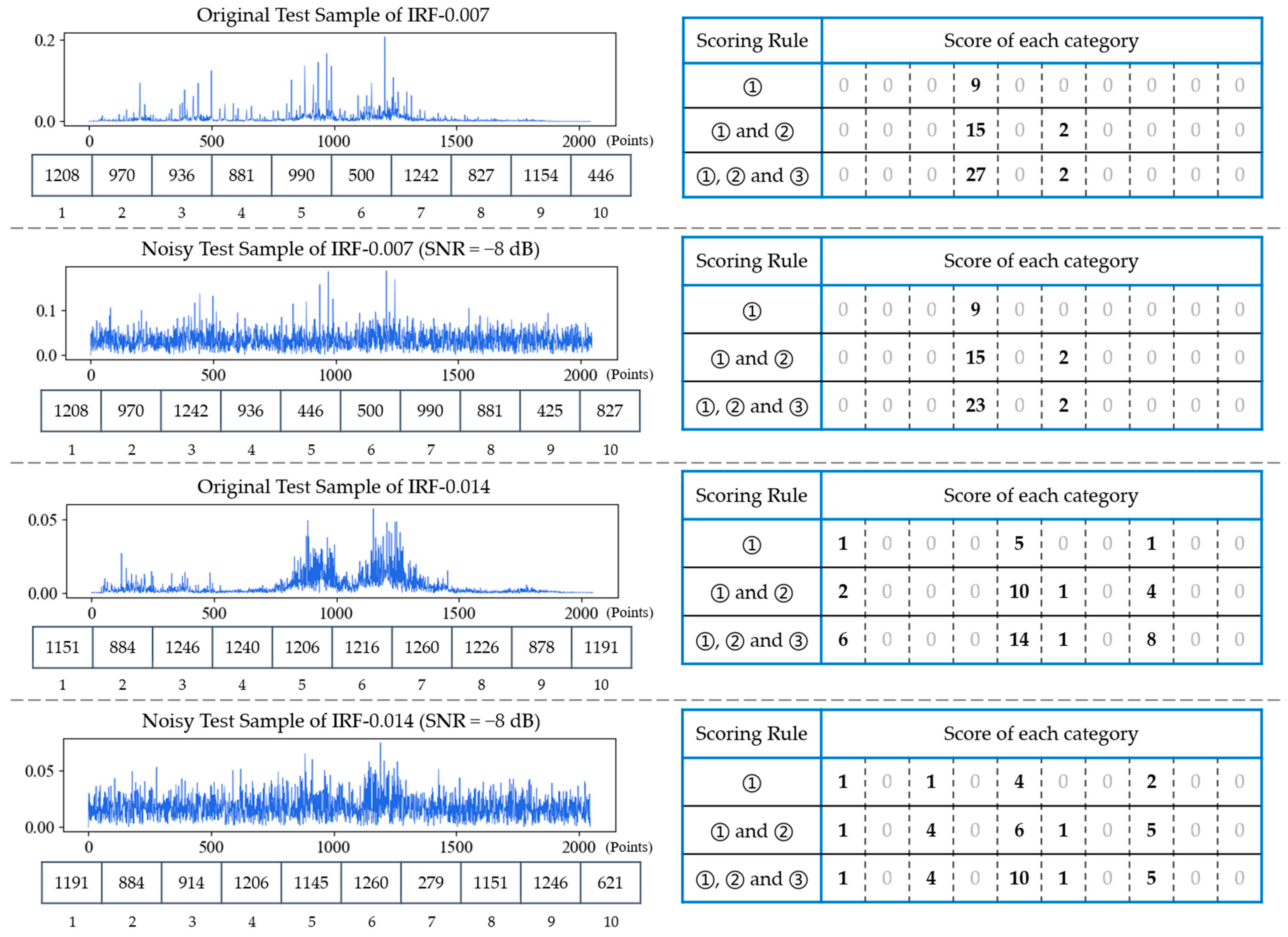
4.2.2. Scoring Rules of FDFM
4.2.3. First-Layer Kernel Size of CNN
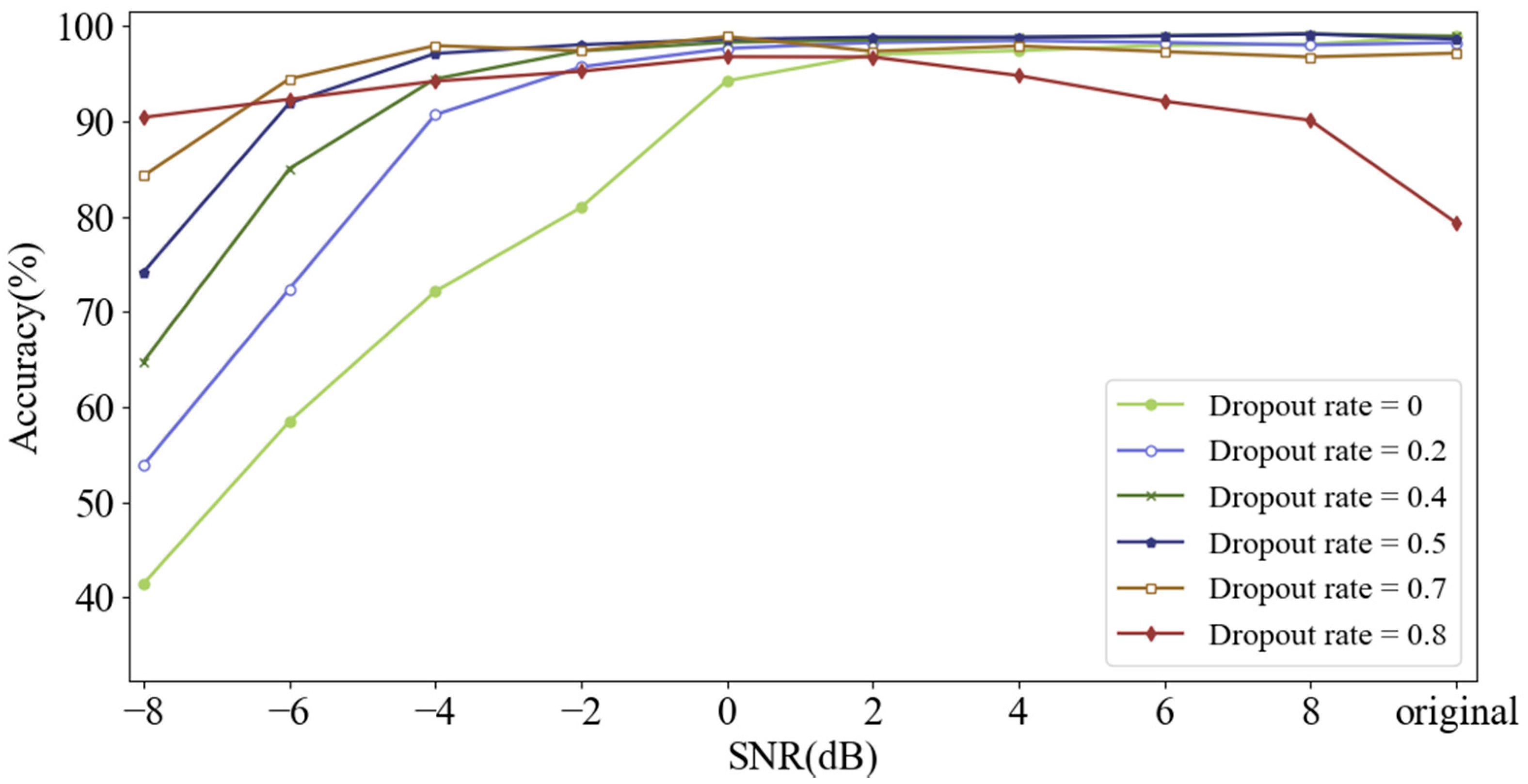
4.2.4. Dropout Rate
4.3. Performance of FDFM with Limited Sample Size
4.4. Visualization of CNN
4.5. Model Fusion
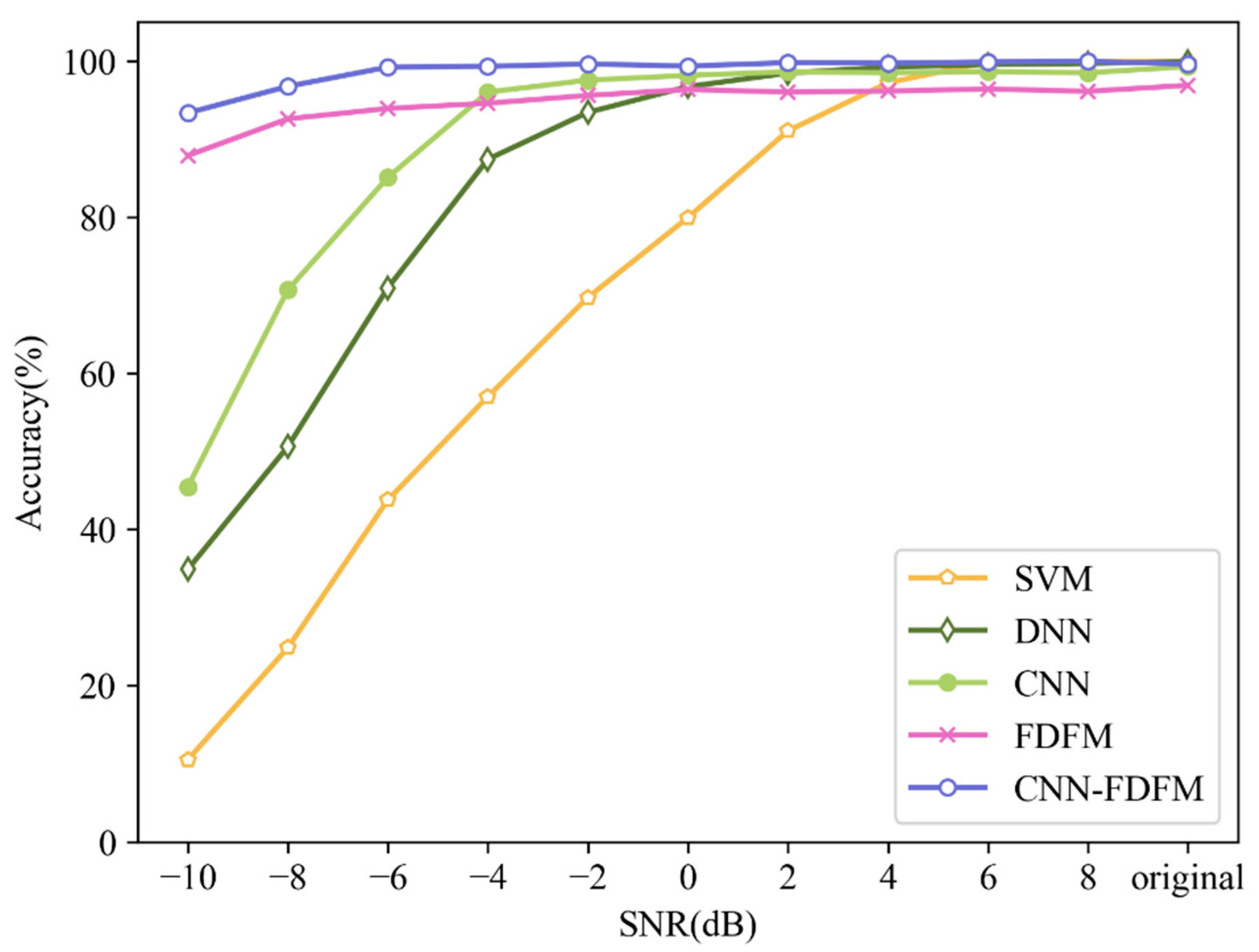
4.6. Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, C.; Zhang, W.; Peng, G.; Liu, S. Bearing Fault Diagnosis Using Fully-Connected Winner-Take-All Autoencoder. IEEE Access 2018, 6, 6103–6115. [Google Scholar] [CrossRef]
- Sun, J.; Yan, C.; Wen, J. Intelligent Bearing Fault Diagnosis Method Combining Compressed Data Acquisition and Deep Learning. IEEE Trans. Instrum. Meas. 2018, 67, 185–195. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Zi, Y.; Jiang, S. A Local Weighted Multi-Instance Multilabel Network for Fault Diagnosis of Rolling Bearings Using Encoder Signal. IEEE Trans. Instrum. Meas. 2020, 69, 8580–8589. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial Intelligence for Fault Diagnosis of Rotating Machinery: A Review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Zou, L.; Li, Y.; Xu, F. An Adversarial Denoising Convolutional Neural Network for Fault Diagnosis of Rotating Machinery under Noisy Environment and Limited Sample Size Case. Neurocomputing 2020, 407, 105–120. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H. Mean-Optimized Mode Decomposition: An Improved EMD Approach for Non-Stationary Signal Processing. ISA Trans. 2020, 106, 392–401. [Google Scholar] [CrossRef]
- Zhu, H.; He, Z.; Wei, J.; Wang, J.; Zhou, H. Bearing Fault Feature Extraction and Fault Diagnosis Method Based on Feature Fusion. Sensors 2021, 21, 2524. [Google Scholar] [CrossRef]
- Shen, C.; Wang, D.; Kong, F.; Tse, P.W. Fault Diagnosis of Rotating Machinery Based on the Statistical Parameters of Wavelet Packet Paving and a Generic Support Vector Regressive Classifier. Measurement 2013, 46, 1551–1564. [Google Scholar] [CrossRef]
- Fei, S. Fault Diagnosis of Bearing Based on Wavelet Packet Transform-Phase Space Reconstruction-Singular Value Decomposition and SVM Classifier. Arab. J. Sci. Eng. 2017, 42, 1967–1975. [Google Scholar] [CrossRef]
- Rai, V.K.; Mohanty, A.R. Bearing Fault Diagnosis Using FFT of Intrinsic Mode Functions in Hilbert–Huang Transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Guan, Z.; Liao, Z.; Li, K.; Chen, P. A Precise Diagnosis Method of Structural Faults of Rotating Machinery Based on Combination of Empirical Mode Decomposition, Sample Entropy, and Deep Belief Network. Sensors 2019, 19, 591. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Du, G.; Zhu, Z.; Shen, C.; He, Q. Fault Diagnosis of Rotating Machines Based on the EMD Manifold. Mech. Syst. Signal Process. 2020, 135, 106443. [Google Scholar] [CrossRef]
- Liang, B.; Iwnicki, S.D.; Zhao, Y. Application of Power Spectrum, Cepstrum, Higher Order Spectrum and Neural Network Analyses for Induction Motor Fault Diagnosis. Mech. Syst. Signal Process. 2013, 39, 342–360. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Li, M.; Zhang, Y. A Novel Adaptive Stochastic Resonance Method Based on Coupled Bistable Systems and Its Application in Rolling Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2019, 114, 128–145. [Google Scholar] [CrossRef]
- Zhang, B.; Miao, Y.; Lin, J.; Li, H. Weighted Envelope Spectrum Based on the Spectral Coherence for Bearing Diagnosis. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, M.; Wu, R.; Gao, H.; Yang, M.; Luo, Z.; Li, G. Silent Speech Decoding Using Spectrogram Features Based on Neuromuscular Activities. Brain Sci. 2020, 10, 442. [Google Scholar] [CrossRef]
- Samanta, B.; Nataraj, C. Use of Particle Swarm Optimization for Machinery Fault Detection. Eng. Appl. Artif. Intell. 2009, 22, 308–316. [Google Scholar] [CrossRef]
- Goyal, D.; Choudhary, A.; Pabla, B.S.; Dhami, S.S. Support Vector Machines Based Non-Contact Fault Diagnosis System for Bearings. J. Intell. Manuf. 2020, 31, 1275–1289. [Google Scholar] [CrossRef]
- Wang, D. K-Nearest Neighbors Based Methods for Identification of Different Gear Crack Levels under Different Motor Speeds and Loads: Revisited. Mech. Syst. Signal Process. 2016, 70–71, 201–208. [Google Scholar] [CrossRef]
- Xin, G.; Hamzaoui, N.; Antoni, J. Semi-Automated Diagnosis of Bearing Faults Based on a Hidden Markov Model of the Vibration Signals. Measurement 2018, 127, 141–166. [Google Scholar] [CrossRef]
- Yang, D.; Karimi, H.R.; Sun, K. Residual Wide-Kernel Deep Convolutional Auto-Encoder for Intelligent Rotating Machinery Fault Diagnosis with Limited Samples. Neural Netw. 2021, 141, 133–144. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A Novel Convolutional Neural Network Based Fault Recognition Method via Image Fusion of Multi-Vibration-Signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Xu, Z.; Li, C.; Yang, Y. Fault Diagnosis of Rolling Bearings Using an Improved Multi-Scale Convolutional Neural Network with Feature Attention Mechanism. ISA Trans. 2021, 110, 379–393. [Google Scholar] [CrossRef]
- An, Z.; Li, S.; Wang, J.; Jiang, X. A Novel Bearing Intelligent Fault Diagnosis Framework under Time-Varying Working Conditions Using Recurrent Neural Network. ISA Trans. 2020, 100, 155–170. [Google Scholar] [CrossRef] [PubMed]
- Gan, M.; Wang, C.; Zhu, C. Construction of Hierarchical Diagnosis Network Based on Deep Learning and Its Application in the Fault Pattern Recognition of Rolling Element Bearings. Mech. Syst. Signal Process. 2016, 72–73, 92–104. [Google Scholar] [CrossRef]
- Yu, J.-B. Evolutionary Manifold Regularized Stacked Denoising Autoencoders for Gearbox Fault Diagnosis. Knowl. Based Syst. 2019, 178, 111–122. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Wang, J.; Mao, K. Learning to Monitor Machine Health with Convolutional Bi-Directional LSTM Networks. Sensors 2017, 17, 273. [Google Scholar] [CrossRef]
- Cabrera, D.; Guamán, A.; Zhang, S.; Cerrada, M.; Sánchez, R.-V.; Cevallos, J.; Long, J.; Li, C. Bayesian Approach and Time Series Dimensionality Reduction to LSTM-Based Model-Building for Fault Diagnosis of a Reciprocating Compressor. Neurocomputing 2020, 380, 51–66. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Shi, H.; Chen, J.; Si, J.; Zheng, C. Fault Diagnosis of Rolling Bearings Based on a Residual Dilated Pyramid Network and Full Convolutional Denoising Autoencoder. Sensors 2020, 20, 5734. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Q.; Zhao, J.; Shen, H.; Xiong, X. Fault Diagnosis of Rotating Machinery under Noisy Environment Conditions Based on a 1-D Convolutional Autoencoder and 1-D Convolutional Neural Network. Sensors 2019, 19, 972. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Li, Y.; Zheng, H.; Wang, R.; Xu, M. A New Dynamic Model and Transfer Learning Based Intelligent Fault Diagnosis Framework for Rolling Element Bearings Race Faults: Solving the Small Sample Problem. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- Pan, T.; Chen, J.; Xie, J.; Chang, Y.; Zhou, Z. Intelligent Fault Identification for Industrial Automation System via Multi-Scale Convolutional Generative Adversarial Network with Partially Labeled Samples. ISA Trans. 2020, 101, 379–389. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A Deep Convolutional Neural Network with New Training Methods for Bearing Fault Diagnosis under Noisy Environment and Different Working Load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Pang, S.; Yang, X.; Zhang, X.; Lin, X. Fault Diagnosis of Rotating Machinery with Ensemble Kernel Extreme Learning Machine Based on Fused Multi-Domain Features. ISA Trans. 2020, 98, 320–337. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 1, ISBN 978-0-691-21469-6. [Google Scholar]
- Fan, X.; Zuo, M.J. Fault Diagnosis of Machines Based on D–S Evidence Theory. Part 1: D–S Evidence Theory and Its Improvement. Pattern Recognit. Lett. 2006, 27, 366–376. [Google Scholar] [CrossRef]
- The Case Western Reserve University Bearing Data Center. Available online: https://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 10 July 2021).
- Apparatus & Procedures | Bearing Data Center. Available online: https://csegroups.case.edu/bearingdatacenter/pages/apparatus-procedures (accessed on 10 July 2021).
- van der Maaten, L.; Hinton, G. Viualizing Data Using T-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]


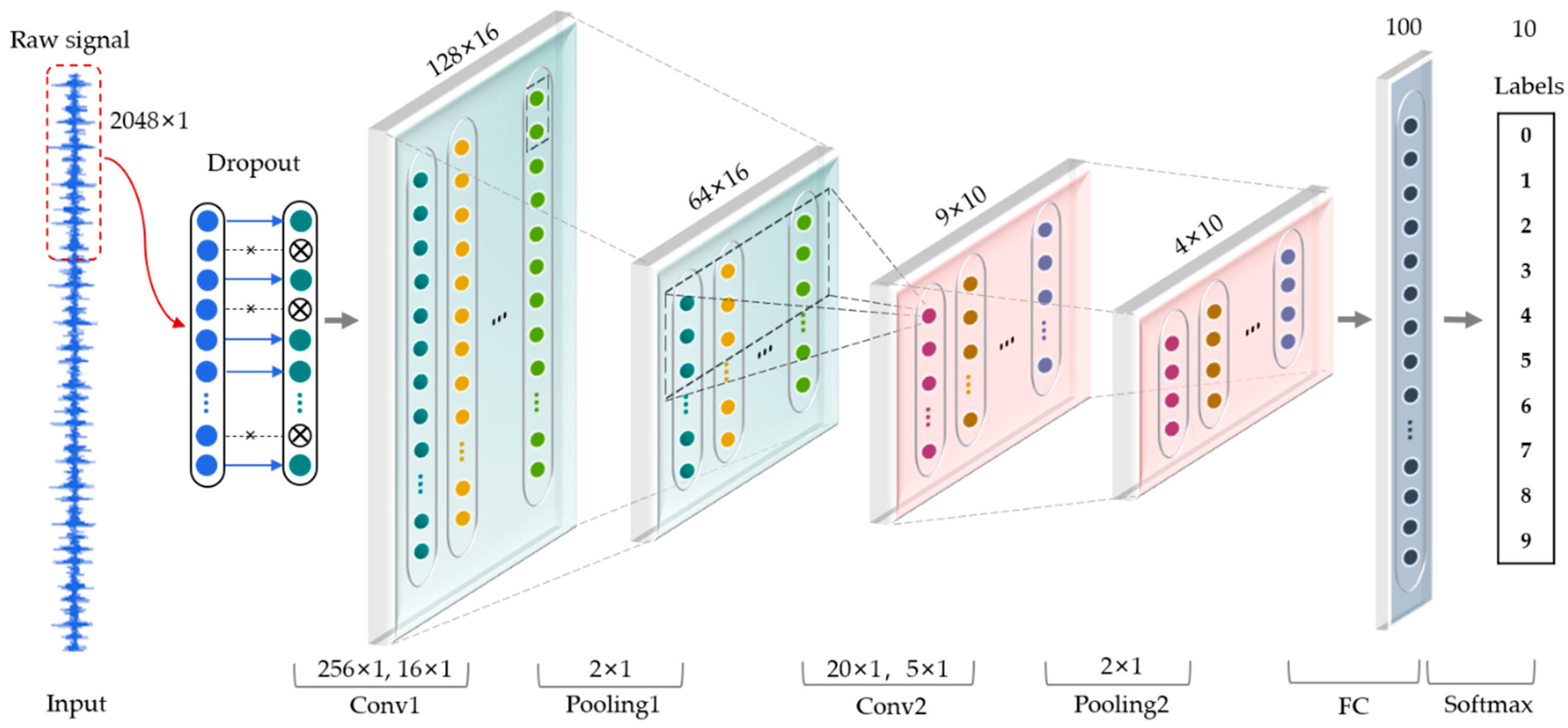



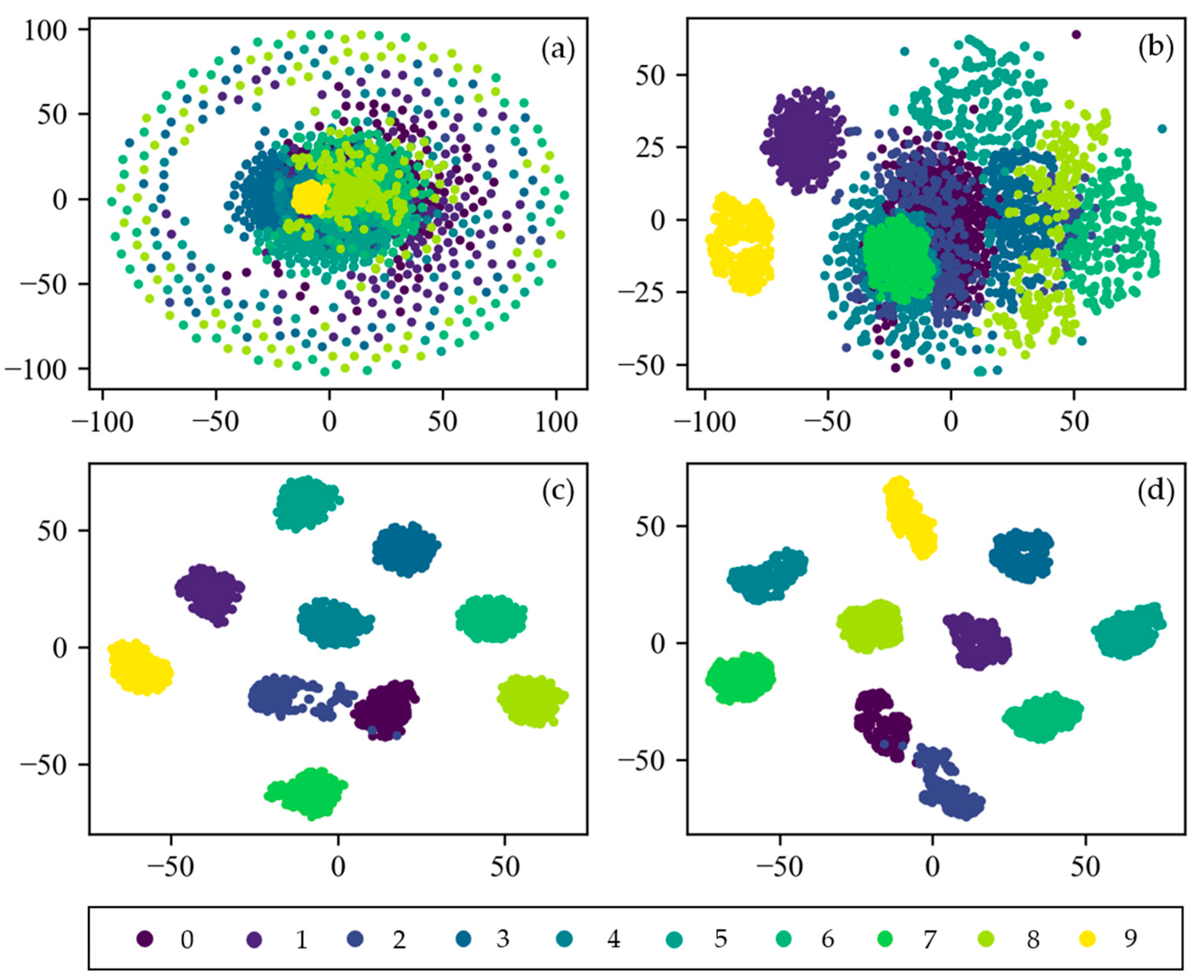
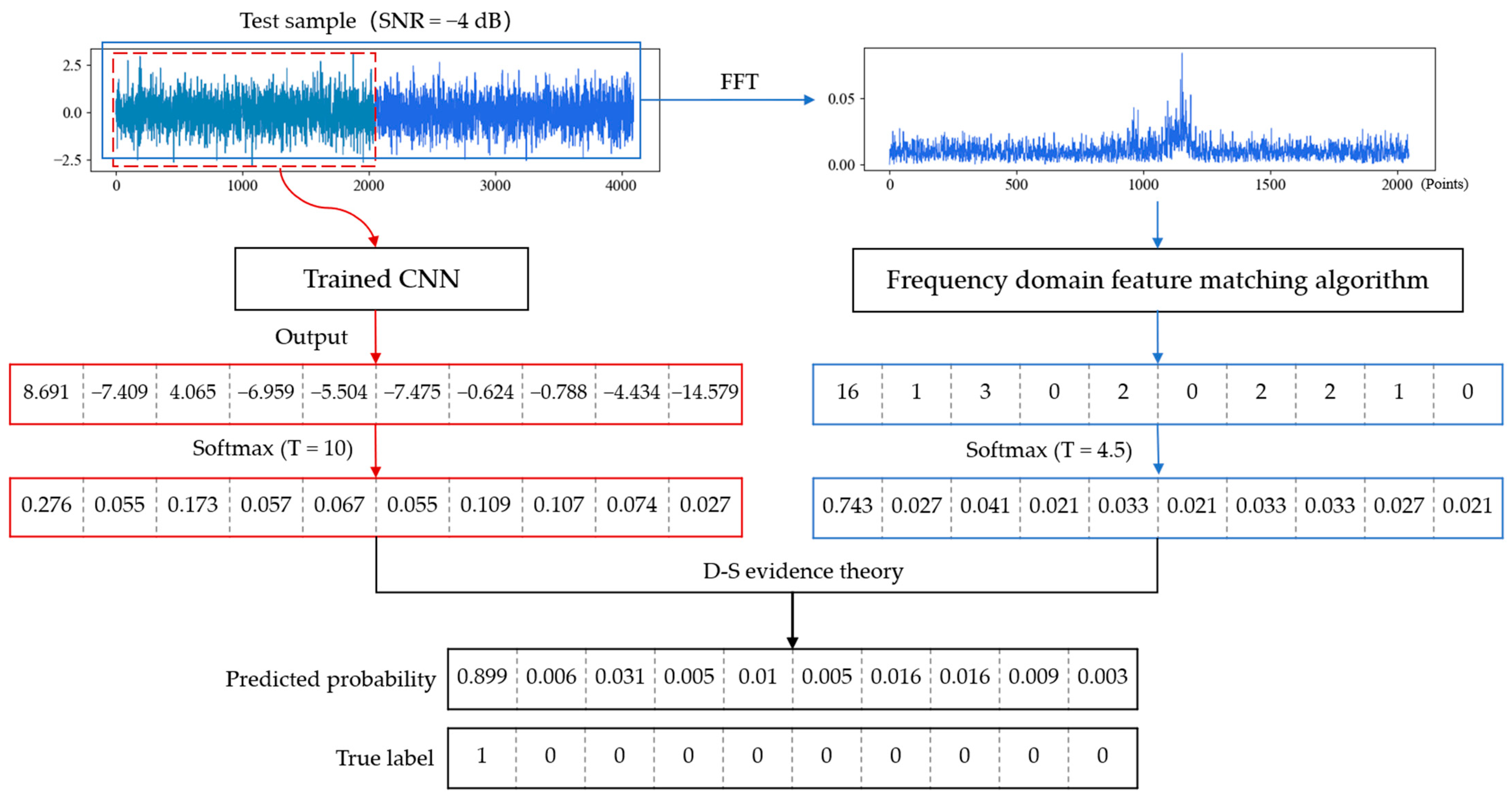
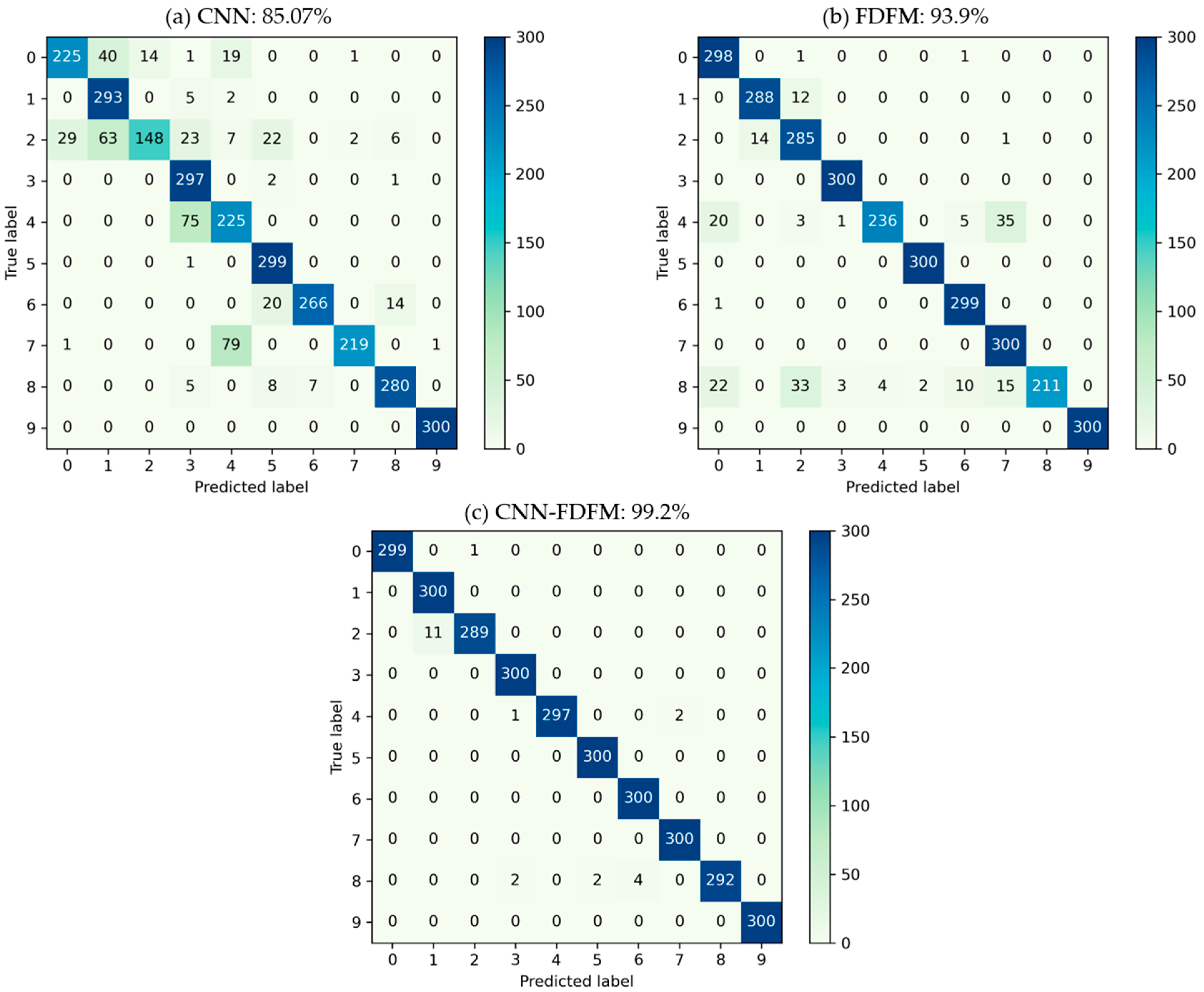

| Layer | Kernel Size/Step Size | Kernel Number | Output Size | Padding |
|---|---|---|---|---|
| Conv1 | 256 × 1/16 × 1 | 16 | 128 × 16 | YES |
| Pooling1 | 2 × 1/2 × 1 | 16 | 64 × 16 | NO |
| Conv2 | 20 × 1/5 × 1 | 10 | 9 × 10 | YES |
| Pooling2 | 2 × 1/2 × 1 | 10 | 4 × 10 | NO |
| Fully connected layer | 100 | 1 | 1 × 100 | |
| Softmax | 10 | 1 | 1 × 10 |
| Fault Location | Ball | Inner Race | Outer Race | None | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Category label | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Fault diameter(inch) | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | 0 | |
| Dataset Size | Train | 700 | 700 | 700 | 700 | 700 | 700 | 700 | 700 | 700 | 700 |
| Test | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | |
| Accuracy (%) | SNR (dB) | ||||
|---|---|---|---|---|---|
| −10 | −6 | −2 | 2 | 6 | |
| (1) | 86.77 | 93.03 | 94.23 | 94.7 | 94.83 |
| (1) and (2) | 86.9 | 93.13 | 94.3 | 94.93 | 95.23 |
| (1), (2) and (3) | 88.73 | 94.47 | 95.2 | 95.9 | 96.37 |
| Training Samples | Proportion | 1% | 5% | 10% | 20% | 50% | 100% |
|---|---|---|---|---|---|---|---|
| Number | 70 | 350 | 700 | 1400 | 3500 | 7000 | |
| Accuracy (%) | 90.33 | 90.73 | 91.2 | 92.43 | 92.83 | 93.9 | |
| Training time (s) | 0.01 | 0.14 | 0.62 | 2.66 | 19.58 | 91.86 | |
| Accuracy (%) | SNR (dB) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −10 | −8 | −6 | −4 | −2 | 0 | 2 | 4 | 6 | 8 | Original | |
| CNN | 45.43 | 70.67 | 85.07 | 96 | 97.53 | 98.13 | 98.6 | 98.47 | 99.27 | 98.63 | 98.47 |
| FDFM | 87.77 | 92.57 | 93.9 | 94.57 | 95.57 | 96.33 | 96 | 96.13 | 96.4 | 96.1 | 96.87 |
| CNN-FDFM | 93.33 | 96.73 | 99.2 | 99.3 | 99.6 | 99.33 | 99.77 | 99.7 | 99.87 | 99.93 | 99.6 |
| Method | Training Time (7000 Samples) | Testing Time (3000 Samples) | Accuracy (SNR = −4 dB) |
|---|---|---|---|
| DNN | 39.12 s | 0.125 s | 87.4% |
| CNN | 37.7 s | 0.178 s | 96% |
| FDFM | 91.86 s | 3.609 s | 94.53% |
| CNN-FDFM | 127.52 s | 4.288 s | 99.3% |
| Method | Training Time (700 Samples) | Testing Time (300 Samples) | Accuracy (SNR = −4 dB) |
|---|---|---|---|
| DNN | 7.63 s | 0.017 s | 82.67% |
| CNN | 7.68 s | 0.065 s | 86.33% |
| FDFM | 0.62 s | 0.363 s | 93.33% |
| CNN-FDFM | 8.23 s | 0.477 s | 98% |
| Method | Baseline Model | Anti-Noise Strategy | Diagnosis Accuracy on CWRU Dataset (SNR = −4 dB) |
|---|---|---|---|
| WDCNN [29] | CNN | Wide kernels in the first convolutional layer | 66.95% |
| FC-WTA [1] | SAE | Data destruction and lifetime sparsity | 71.44% |
| TICNN [34] | CNN | Kernel with changing dropout rate and small mini-batch training | 82.05% |
| CNN-FDFM | CNN | Anti-noise algorithm FDFM and information fusion between CNN and FDFM | 99.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Mao, S.; Li, M. A Novel Anti-Noise Fault Diagnosis Approach for Rolling Bearings Based on Convolutional Neural Network Fusing Frequency Domain Feature Matching Algorithm. Sensors 2021, 21, 5532. https://doi.org/10.3390/s21165532
Zhou X, Mao S, Li M. A Novel Anti-Noise Fault Diagnosis Approach for Rolling Bearings Based on Convolutional Neural Network Fusing Frequency Domain Feature Matching Algorithm. Sensors. 2021; 21(16):5532. https://doi.org/10.3390/s21165532
Chicago/Turabian StyleZhou, Xiangyu, Shanjun Mao, and Mei Li. 2021. "A Novel Anti-Noise Fault Diagnosis Approach for Rolling Bearings Based on Convolutional Neural Network Fusing Frequency Domain Feature Matching Algorithm" Sensors 21, no. 16: 5532. https://doi.org/10.3390/s21165532
APA StyleZhou, X., Mao, S., & Li, M. (2021). A Novel Anti-Noise Fault Diagnosis Approach for Rolling Bearings Based on Convolutional Neural Network Fusing Frequency Domain Feature Matching Algorithm. Sensors, 21(16), 5532. https://doi.org/10.3390/s21165532







