A Proof-of-Concept Study Using Numerical Simulations of an Acoustic Spheroid-on-a-Chip Platform for Improving 3D Cell Culture
Abstract
:1. Introduction
2. Materials and Methods
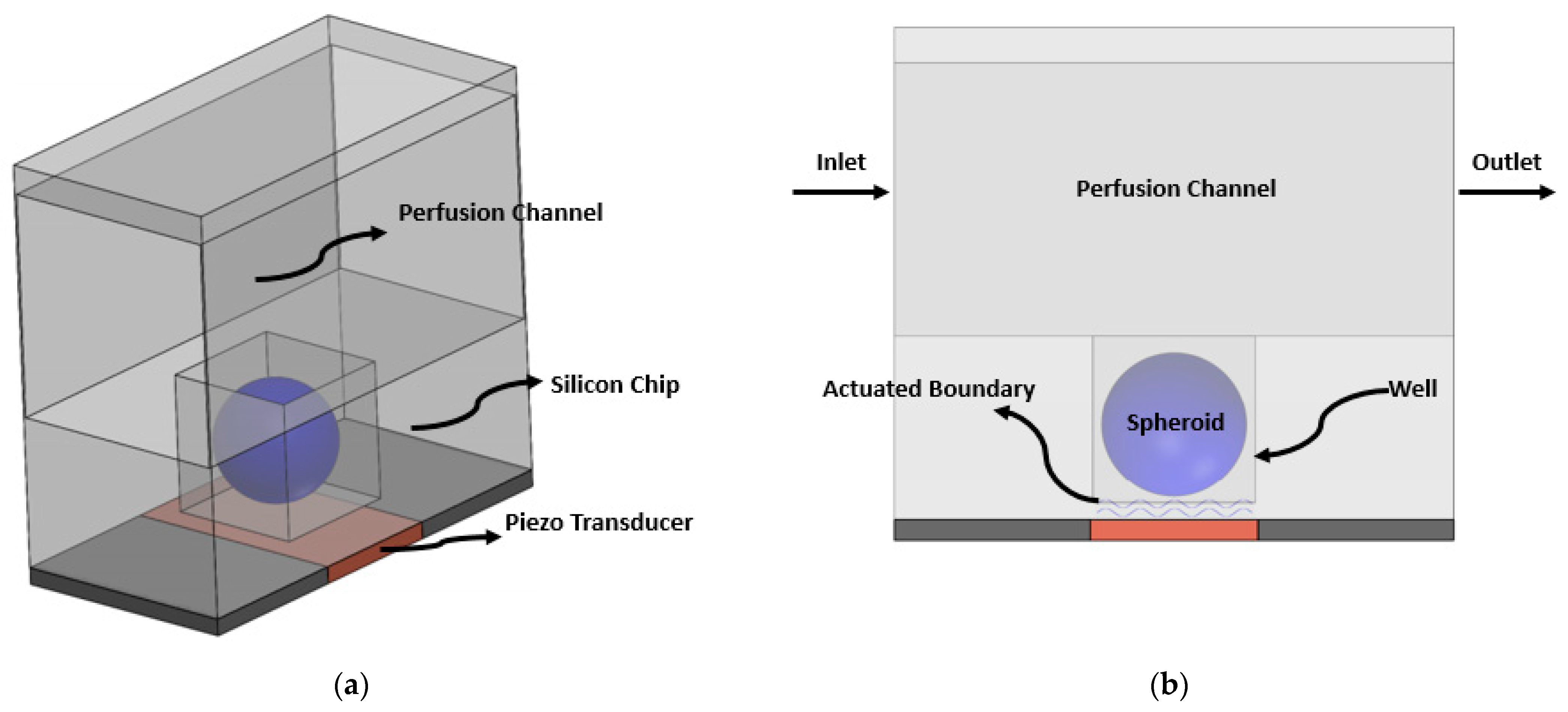
2.1. Geometry and Model Description
2.2. Governing Equations
2.2.1. Microfluidic Flow
2.2.2. Transport of Dilute Species
2.2.3. Acoustic
2.3. Boundary Conditions
2.3.1. Microfluidic Flow
2.3.2. Transport of Dilute Species
2.3.3. Acoustic
2.4. Numerical Method
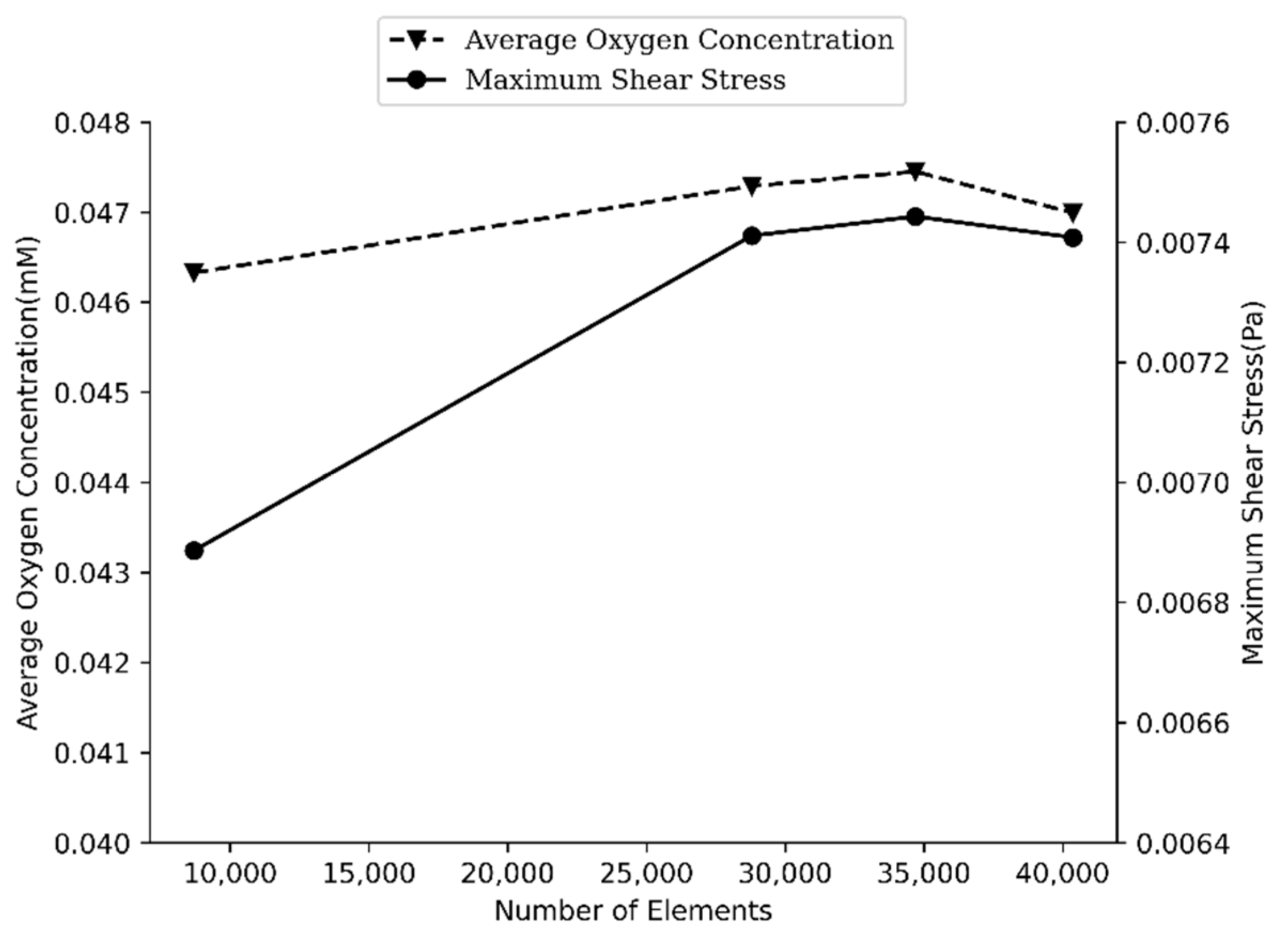
2.5. Mesh-Independent Study
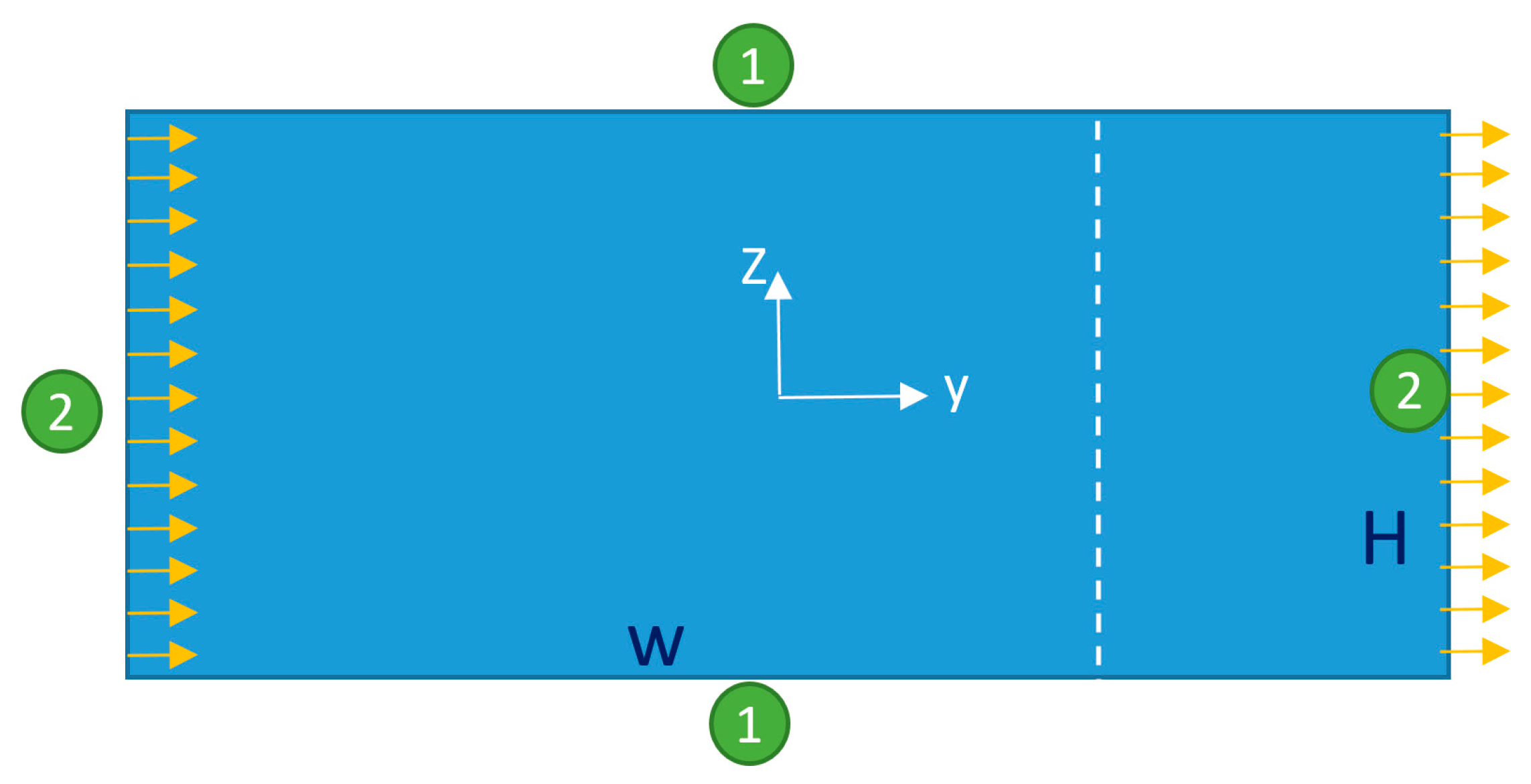
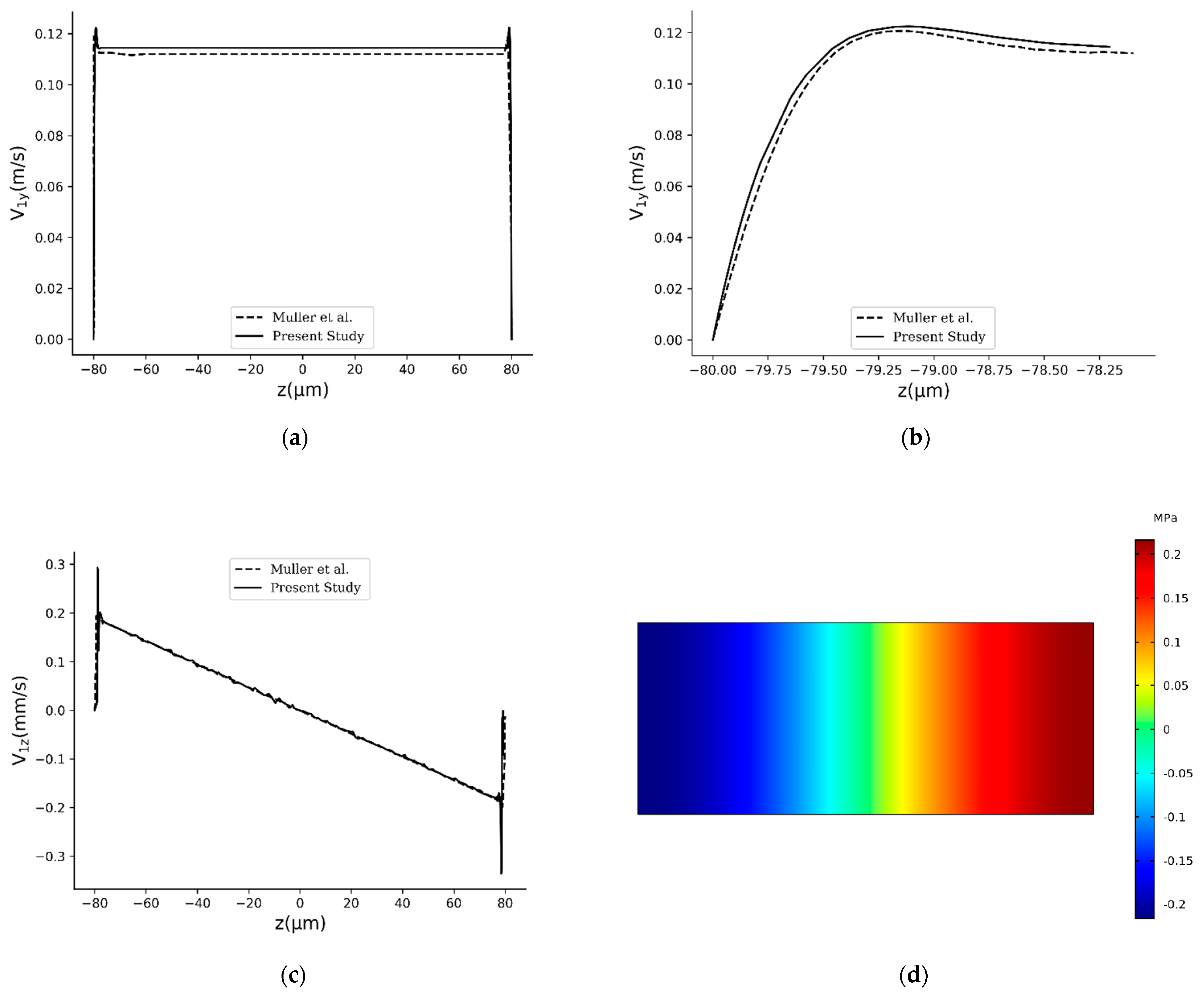
2.6. Validation of the Study
3. Results and Discussion
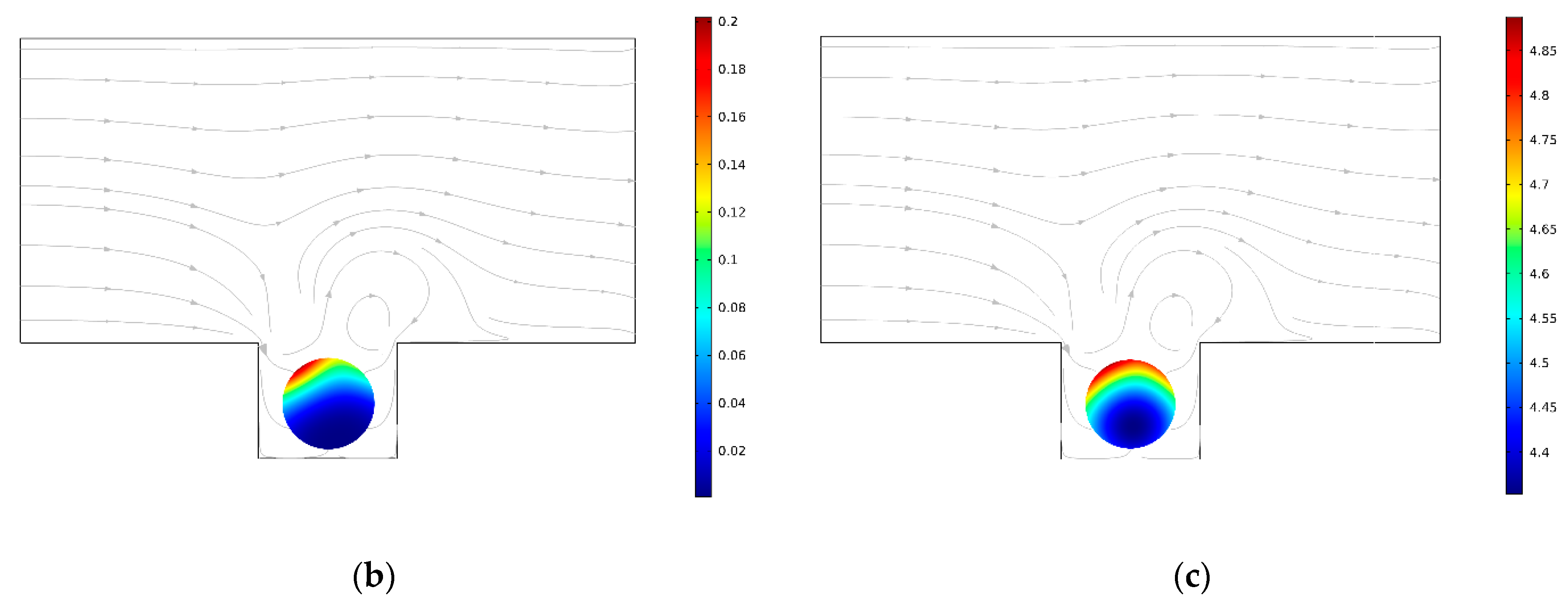
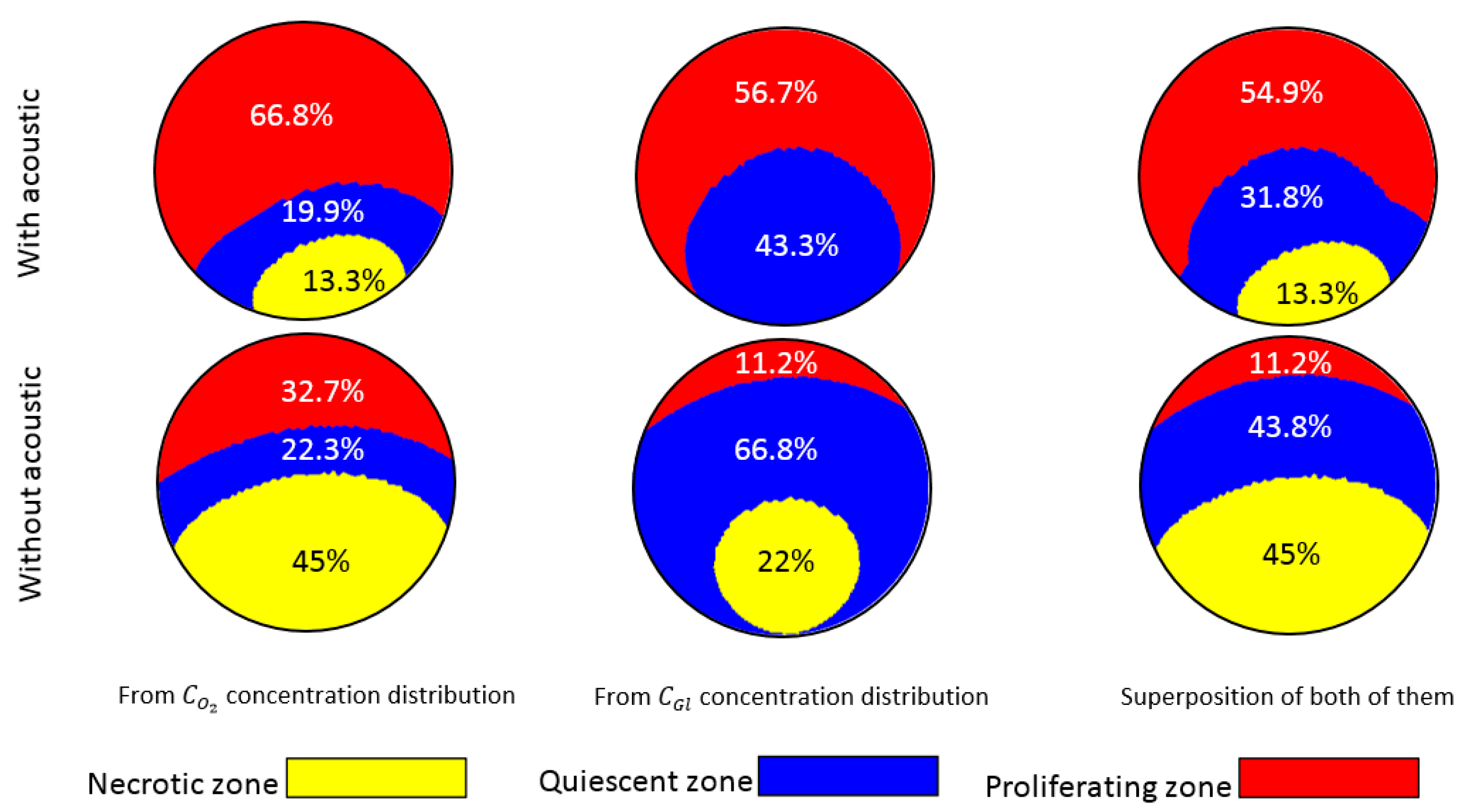
3.1. Conventional Spheroid-on-Chip Platform (No Acoustic)
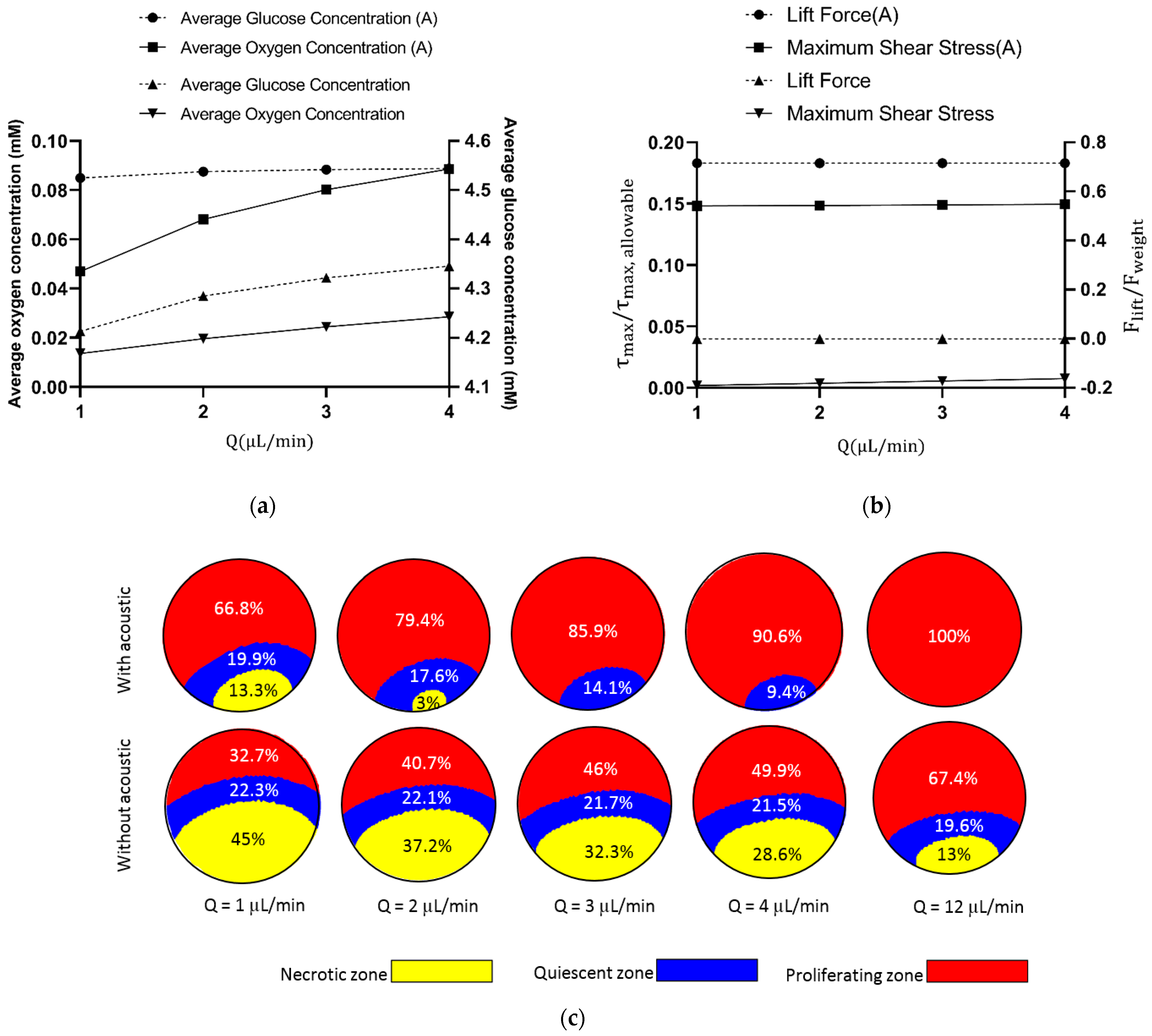
3.2. Acoustic Spheroid-on-Chip Platform
3.3. Boundary Displacement Amplitude
3.4. Flow Rate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Torre, L.A.; Bray, F.; Siegel, R.L.; Ferlay, J.; Lortet-Tieulent, J.; Jemal, A. Global cancer statistics, 2012. CA Cancer J. Clin. 2015, 65, 87–108. [Google Scholar] [CrossRef] [Green Version]
- Young, E.W. Cells, tissues, and organs on chips: Challenges and opportunities for the cancer tumor microenvironment. Integr. Biol. 2013, 5, 1096–1109. [Google Scholar] [CrossRef]
- Dhiman, N.; Shagaghi, N.; Bhave, M.; Sumer, H.; Kingshott, P.; Rath, S.N. Indirect co-culture of lung carcinoma cells with hyperthermia-treated mesenchymal stem cells influences tumor spheroid growth in a collagen-based 3-dimensional microfluidic model. Cytotherapy 2020, 23, 25–26. [Google Scholar] [CrossRef] [PubMed]
- Moghadas, H.; Saidi, M.S.; Kashaninejad, N.; Kiyoumarsioskouei, A.; Nguyen, N.-T. Fabrication and characterization of low-cost, bead-free, durable and hydrophobic electrospun membrane for 3D cell culture. Biomed. Microdevices 2017, 19, 74. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehta, G.; Hsiao, A.Y.; Ingram, M.; Luker, G.D.; Takayama, S. Opportunities and challenges for use of tumor spheroids as models to test drug delivery and efficacy. J. Control. Release 2012, 164, 192–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kashaninejad, N.; Nikmaneshi, M.R.; Moghadas, H.; Kiyoumarsi Oskouei, A.; Rismanian, M.; Barisam, M.; Saidi, M.S.; Firoozabadi, B. Organ-Tumor-on-a-Chip for Chemosensitivity Assay: A Critical Review. Micromachines 2016, 7, 130. [Google Scholar] [CrossRef] [PubMed]
- Schmeichel, K.L.; Bissell, M.J. Modeling tissue-specific signaling and organ function in three dimensions. J. Cell Sci. 2003, 116, 2377–2388. [Google Scholar] [CrossRef] [Green Version]
- Friedrich, J.; Seidel, C.; Ebner, R.; Kunz-Schughart, L.A. Spheroid-based drug screen: Considerations and practical approach. Nat. Protoc. 2009, 4, 309. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Schubert, S.; Richter, S.; Dötzel, W. Hybrid-assembled micro dosing system using silicon-based micropump/valve and mass flow sensor. Sens. Actuators A Phys. 1998, 69, 85–91. [Google Scholar] [CrossRef]
- Dinh, T.; Phan, H.-P.; Dao, D.V.; Woodfield, P.; Qamar, A.; Nguyen, N.-T. Graphite on paper as material for sensitive thermoresistive sensors. J. Mater. Chem. C 2015, 3, 8776–8779. [Google Scholar] [CrossRef] [Green Version]
- Altmann, B.; Grün, C.; Nies, C.; Gottwald, E. Advanced 3D Cell Culture Techniques in Micro-Bioreactors, Part II: Systems and Applications. Processes 2021, 9, 21. [Google Scholar] [CrossRef]
- Huang, Y.L.; Ma, Y.; Wu, C.; Shiau, C.; Segall, J.E.; Wu, M. Tumor spheroids under perfusion within a 3D microfluidic platform reveal critical roles of cell-cell adhesion in tumor invasion. Sci. Rep. 2020, 10, 9648. [Google Scholar] [CrossRef]
- Shao, C.; Chi, J.; Zhang, H.; Fan, Q.; Zhao, Y.; Ye, F. Development of cell spheroids by advanced technologies. Adv. Mater. Technol. 2020, 5, 2000183. [Google Scholar] [CrossRef]
- Bourn, M.D.; Batchelor, D.V.; Ingram, N.; McLaughlan, J.R.; Coletta, P.L.; Evans, S.D.; Peyman, S.A. High-throughput microfluidics for evaluating microbubble enhanced delivery of cancer therapeutics in spheroid cultures. J. Control. Release 2020, 326, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Moshksayan, K.; Kashaninejad, N.; Warkiani, M.E.; Lock, J.G.; Moghadas, H.; Firoozabadi, B.; Saidi, M.S.; Nguyen, N.-T. Spheroids-on-a-chip: Recent advances and design considerations in microfluidic platforms for spheroid formation and culture. Sens. Actuators B Chem. 2018, 263, 151–176. [Google Scholar] [CrossRef] [Green Version]
- Rostami, P.; Kashaninejad, N.; Moshksayan, K.; Saidi, M.S.; Firoozabadi, B.; Nguyen, N.-T. Novel approaches in cancer management with circulating tumor cell clusters. J. Sci. Adv. Mater. Devices 2019, 4, 1–18. [Google Scholar] [CrossRef]
- Wu, L.Y.; Di Carlo, D.; Lee, L.P. Microfluidic self-assembly of tumor spheroids for anticancer drug discovery. Biomed. Microdevices 2008, 10, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Yahyazadeh Shourabi, A.; Kashaninejad, N.; Saidi, M.S. An integrated microfluidic concentration gradient generator for mechanical stimulation and drug delivery. J. Sci. Adv. Mater. Devices 2021, 6, 280–290. [Google Scholar] [CrossRef]
- Lee, S.W.; Hong, S.; Jung, B.; Jeong, S.Y.; Byeon, J.H.; Jeong, G.S.; Choi, J.; Hwang, C. In vitro lung cancer multicellular tumor spheroid formation using a microfluidic device. Biotechnol. Bioeng. 2019, 116, 3041–3052. [Google Scholar] [CrossRef]
- Weiswald, L.-B.; Bellet, D.; Dangles-Marie, V. Spherical cancer models in tumor biology. Neoplasia 2015, 17, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, J.; Nakazawa, K. Orderly arrangement of hepatocyte spheroids on a microfabricated chip. Tissue Eng. 2005, 11, 1254–1262. [Google Scholar] [CrossRef] [PubMed]
- Barisam, M.; Saidi, M.S.; Kashaninejad, N.; Vadivelu, R.; Nguyen, N.-T. Numerical simulation of the behavior of toroidal and spheroidal multicellular aggregates in microfluidic devices with microwell and U-shaped barrier. Micromachines 2017, 8, 358. [Google Scholar] [CrossRef] [Green Version]
- Rocha, H.L.; Godet, I.; Kurtoglu, F.; Metzcar, J.; Konstantinopoulos, K.; Bhoyar, S.; Gilkes, D.M.; Macklin, P. A persistent invasive phenotype in post-hypoxic tumor cells is revealed by novel fate-mapping and computational modeling. bioRxiv 2021. [Google Scholar] [CrossRef]
- Kim, C.H.; Ko, A.R.; Lee, S.Y.; Jeon, H.M.; Kim, S.M.; Park, H.G.; Han, S.I.; Kang, H.S. Hypoxia switches glucose depletion-induced necrosis to phosphoinositide 3-kinase/Akt-dependent apoptosis in A549 lung adenocarcinoma cells. Int. J. Oncol. 2010, 36, 117–124. [Google Scholar] [PubMed]
- Wang, B.; Zhao, Q.; Zhang, Y.; Liu, Z.; Zheng, Z.; Liu, S.; Meng, L.; Xin, Y.; Jiang, X. Targeting hypoxia in the tumor microenvironment: A potential strategy to improve cancer immunotherapy. J. Exp. Clin. Cancer Res. 2021, 40, 24. [Google Scholar] [CrossRef]
- Barisam, M.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.-T. Prediction of necrotic core and hypoxic zone of multicellular spheroids in a microbioreactor with a u-shaped barrier. Micromachines 2018, 9, 94. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Vilanova, G.; Gomez, H. A mathematical model coupling tumor growth and angiogenesis. PLoS ONE 2016, 11, e0149422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimes, D.R.; Kelly, C.; Bloch, K.; Partridge, M. A method for estimating the oxygen consumption rate in multicellular tumour spheroids. J. R. Soc. Interface 2014, 11, 20131124. [Google Scholar] [CrossRef] [Green Version]
- Im, G.-B.; Kim, S.-W.; Bhang, S.H. Fortifying the angiogenic efficacy of adipose derived stem cell spheroids using spheroid compaction. J. Ind. Eng. Chem. 2021, 93, 228–236. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, Y.; Wang, Y.; Wang, B.; Zheng, L.; Zhang, D.; Zhuang, S. Rapid quantitative detection of chloramphenicol in milk by microfluidic immunoassay. Food Chem. 2021, 339, 127857. [Google Scholar] [CrossRef]
- Rousset, N.; Monet, F.; Gervais, T. Simulation-assisted design of microfluidic sample traps for optimal trapping and culture of non-adherent single cells, tissues, and spheroids. Sci. Rep. 2017, 7, 245. [Google Scholar] [CrossRef]
- Patra, B.; Peng, C.-C.; Liao, W.-H.; Lee, C.-H.; Tung, Y.-C. Drug testing and flow cytometry analysis on a large number of uniform sized tumor spheroids using a microfluidic device. Sci. Rep. 2016, 6, 21061. [Google Scholar] [CrossRef] [Green Version]
- Bruus, H.; Dual, J.; Hawkes, J.; Hill, M.; Laurell, T.; Nilsson, J.; Radel, S.; Sadhal, S.; Wiklund, M. Forthcoming Lab on a Chip tutorial series on acoustofluidics: Acoustofluidics—Exploiting ultrasonic standing wave forces and acoustic streaming in microfluidic systems for cell and particle manipulation. Lab Chip 2011, 11, 3579–3580. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Li, P.; Lin, S.-C.S.; Stratton, Z.S.; Nama, N.; Guo, F.; Slotcavage, D.; Mao, X.; Shi, J.; Costanzo, F. Surface acoustic wave microfluidics. Lab Chip 2013, 13, 3626–3649. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Friend, J.R. Surface acoustic wave microfluidics. Annu. Rev. Fluid Mech. 2014, 46, 379–406. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Mao, Z.; Peng, Z.; Zhou, L.; Chen, Y.; Huang, P.-H.; Truica, C.I.; Drabick, J.J.; El-Deiry, W.S.; Dao, M. Acoustic separation of circulating tumor cells. Proc. Natl. Acad. Sci. USA 2015, 112, 4970–4975. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shilton, R.; Tan, M.K.; Yeo, L.Y.; Friend, J.R. Particle concentration and mixing in microdrops driven by focused surface acoustic waves. J. Appl. Phys. 2008, 104, 014910. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Guo, F.; Chen, Y.; Ding, X.; Li, P.; Wang, L.; Cameron, C.E.; Huang, T.J. Standing surface acoustic wave based cell coculture. Anal. Chem. 2014, 86, 9853–9859. [Google Scholar] [CrossRef] [Green Version]
- Greco, G.; Agostini, M.; Tonazzini, I.; Sallemi, D.; Barone, S.; Cecchini, M. Surface-acoustic-wave (SAW)-driven device for dynamic cell cultures. Anal. Chem. 2018, 90, 7450–7457. [Google Scholar] [CrossRef]
- Wu, Y.; Ao, Z.; Chen, B.; Muhsen, M.; Bondesson, M.; Lu, X.; Guo, F. Acoustic assembly of cell spheroids in disposable capillaries. Nanotechnology 2018, 29, 504006. [Google Scholar] [CrossRef] [Green Version]
- Jeger-Madiot, N.; Arakelian, L.; Setterblad, N.; Bruneval, P.; Hoyos, M.; Larghero, J.; Aider, J.-L. Self-organization and culture of Mesenchymal Stem Cell spheroids in acoustic levitation. Sci. Rep. 2021, 11, 8355. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wu, Y.; Ao, Z.; Cai, H.; Nunez, A.; Liu, Y.; Foley, J.; Nephew, K.; Lu, X.; Guo, F. High-throughput acoustofluidic fabrication of tumor spheroids. Lab Chip 2019, 19, 1755–1763. [Google Scholar] [CrossRef]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raghavan, R.V.; Friend, J.R.; Yeo, L.Y. Particle concentration via acoustically driven microcentrifugation: microPIV flow visualization and numerical modelling studies. Microfluid. Nanofluidics 2010, 8, 73–84. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, H.; Zhang, H.; Yang, Y.; He, M.; Qu, H.; Pang, W.; Zhang, D.; Duan, X. Localized ultrahigh frequency acoustic fields induced micro-vortices for submilliseconds microfluidic mixing. Appl. Phys. Lett. 2016, 109, 253503. [Google Scholar] [CrossRef]
- Anada, T.; Fukuda, J.; Sai, Y.; Suzuki, O. An oxygen-permeable spheroid culture system for the prevention of central hypoxia and necrosis of spheroids. Biomaterials 2012, 33, 8430–8441. [Google Scholar] [CrossRef]
- Bruus, H. Acoustofluidics 2: Perturbation theory and ultrasound resonance modes. Lab Chip 2012, 12, 20–28. [Google Scholar] [CrossRef]
- Datta, M.; Via, L.E.; Chen, W.; Baish, J.W.; Xu, L.; Barry, C.E.; Jain, R.K. Mathematical model of oxygen transport in tuberculosis granulomas. Ann. Biomed. Eng. 2016, 44, 863–872. [Google Scholar] [CrossRef] [Green Version]
- Jackson, A.R.; Huang, C.-Y.C.; Brown, M.D.; Yong Gu, W. 3D finite element analysis of nutrient distributions and cell viability in the intervertebral disc: Effects of deformation and degeneration. J. Biomech. Eng. 2011, 133, 091006. [Google Scholar] [CrossRef]
- Alhourani, A.H.; Tidwell, T.R.; Bokil, A.A.; Røsland, G.V.; Tronstad, K.J.; Søreide, K.; Hagland, H.R. Metformin treatment response is dependent on glucose growth conditions and metabolic phenotype in colorectal cancer cells. Sci. Rep. 2021, 11, 10487. [Google Scholar] [CrossRef]
- Das, P.K.; Snider, A.D.; Bhethanabotla, V.R. Acoustothermal heating in surface acoustic wave driven microchannel flow. Phys. Fluids 2019, 31, 106106. [Google Scholar] [CrossRef]
- Shurbaji, S.; Anlar, G.G.; Hussein, E.A.; Elzatahry, A.; Yalcin, H.C. Effect of flow-induced shear stress in nanomaterial uptake by cells: Focus on targeted anti-cancer therapy. Cancers 2020, 12, 1916. [Google Scholar] [CrossRef] [PubMed]
- Dual, J.; Schwarz, T. Acoustofluidics 3: Continuum mechanics for ultrasonic particle manipulation. Lab. A Chip 2012, 12, 244–252. [Google Scholar] [CrossRef] [PubMed]
- Lien, S.-C.; Chang, S.-F.; Lee, P.-L.; Wei, S.-Y.; Chang, M.D.-T.; Chang, J.-Y.; Chiu, J.-J. Mechanical regulation of cancer cell apoptosis and autophagy: Roles of bone morphogenetic protein receptor, Smad1/5, and p38 MAPK. Biochim. Biophys. Acta BBA Mol. Cell Res. 2013, 1833, 3124–3133. [Google Scholar] [CrossRef] [Green Version]
- Bizik, J.; Kankuri, E.; Ristimäki, A.; Taieb, A.; Vapaatalo, H.; Lubitz, W.; Vaheri, A. Cell–cell contacts trigger programmed necrosis and induce cyclooxygenase-2 expression. Cell Death Differ. 2004, 11, 183–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Parameter | Value |
|---|---|
| Spheroid diameter | |
| Well height | |
| Well width | |
| Channel height | |
| Channel length |
| Parameters | Descriptions | Values | References |
|---|---|---|---|
| Inflow | [26] | ||
| Inlet concentration of oxygen | [22] | ||
| Inlet concentration of glucose | [50] | ||
| Diffusion coefficient of oxygen through H2O | [22] | ||
| Diffusion coefficient of oxygen through the cell aggregate | [22] | ||
| Diffusion coefficient of Glucose through H2O | [22] | ||
| Diffusion coefficient of glucose through cell aggregate | [22] | ||
| Solubility coefficient of oxygen in the cell aggregate vs. H2O | [22] | ||
| Solubility coefficient of glucose in the cell aggregate vs. H2O | [22] | ||
| Maximum reaction rate of oxygen | [22] | ||
| Maximum reaction rate of glucose | [22] | ||
| Michaelis-Menten constant of oxygen | [22] | ||
| Michaelis-Menten constant of glucose | [22] | ||
| Actuation frequency | - | ||
| Fluid density | [22] | ||
| Fluid dynamic viscosity | [22] | ||
| Fluid bulk viscosity | [43] | ||
| Fluid specific heat at constant pressure | [43] | ||
| Fluid thermal expansion | [43] | ||
| Fluid isentropic compressibility | [43] | ||
| Wall displacement amplitude (Equation (21)) | [43,51] | ||
| Sound velocity in the fluid | [43] |
| Parameter | Value |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yahyazadeh Shourabi, A.; Salajeghe, R.; Barisam, M.; Kashaninejad, N. A Proof-of-Concept Study Using Numerical Simulations of an Acoustic Spheroid-on-a-Chip Platform for Improving 3D Cell Culture. Sensors 2021, 21, 5529. https://doi.org/10.3390/s21165529
Yahyazadeh Shourabi A, Salajeghe R, Barisam M, Kashaninejad N. A Proof-of-Concept Study Using Numerical Simulations of an Acoustic Spheroid-on-a-Chip Platform for Improving 3D Cell Culture. Sensors. 2021; 21(16):5529. https://doi.org/10.3390/s21165529
Chicago/Turabian StyleYahyazadeh Shourabi, Arash, Roozbeh Salajeghe, Maryam Barisam, and Navid Kashaninejad. 2021. "A Proof-of-Concept Study Using Numerical Simulations of an Acoustic Spheroid-on-a-Chip Platform for Improving 3D Cell Culture" Sensors 21, no. 16: 5529. https://doi.org/10.3390/s21165529
APA StyleYahyazadeh Shourabi, A., Salajeghe, R., Barisam, M., & Kashaninejad, N. (2021). A Proof-of-Concept Study Using Numerical Simulations of an Acoustic Spheroid-on-a-Chip Platform for Improving 3D Cell Culture. Sensors, 21(16), 5529. https://doi.org/10.3390/s21165529








