Preview Control with Dynamic Constraints for Autonomous Vehicles
Abstract
:1. Introduction
2. Vehicle Lateral Dynamics
3. Controller Design
3.1. Preview Controller
3.2. Establishment of Vehicle Dynamic Constraints
- Mass center slip angle. Considering that the too large mass center slip angle β has a potential effect on the driving stability, the limited range of β is denoted aswhere μ is the friction coefficient of the road, and g is the acceleration of gravity.
- Tire slip angle. Due to the fact that the vehicle dynamics model is established under the small slip angle assumption, the tire slip angle beyond the linear region may incur lower model precision. Moreover, once the tire adhesion reaches saturation (namely beyond linear region), the vehicle may easily skid. For the sake of the aforementioned reasons, the following constraints are set to avoid vehicle instability:where α represents both front tire slip angle αf and rear tire slip angle αr.
- Input steering angle. This is a hard constraint based on vehicle physical limits and driving safety requirement that is imposed to ensure a reasonable range of steering angle:
3.3. Optimization on Preview Length Using SA Algorithm
- Step 1:
- Initialize temperature T, prediction length H, and energy function E. Initial T is set to 600. H is started at a random value within [1,30]; then, it is used to calculate corresponding E.
- Step 2:
- Select a neighbor of current H randomly and compute E.
- Step 3:
- If Metropolis criterion is satisfied, accept the new H and E; if not, discard them.
- Step 4:
- Come back to step 2 if the termination condition (a minimum temperature or a maximum iteration number) is not satisfied; otherwise, the procedure terminates.
4. Closed-Loop System Analysis
4.1. System Stability
4.2. Steady-State Response in the Time Domain
- The sub-optimal control coefficient λi affects the steady state ey by increasing the amplitude of γ. However, this situation only happens during system transient response. As the system reaches steady state, λi approaches 1. In other words, the sub-optimal control is able to achieve steady-state error similar to the optimal control.
- Feedback gain Kx and feedforward gain Kρ can only change the steady-state ey but independent of steady-state eψ. A higher k1 results in lowering ey. Furthermore, well-matched k3 and Kρ can lead ey to zero theoretically.
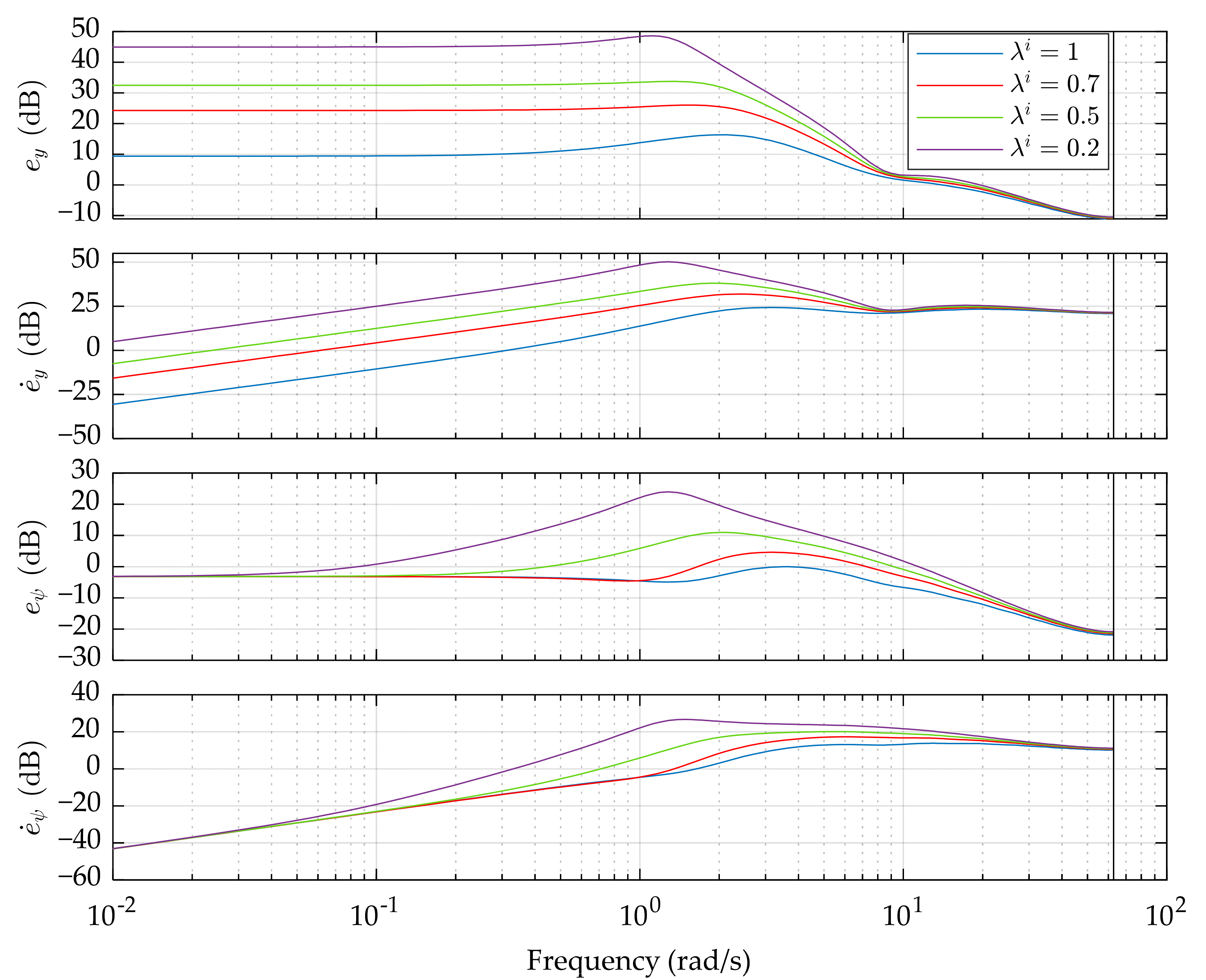
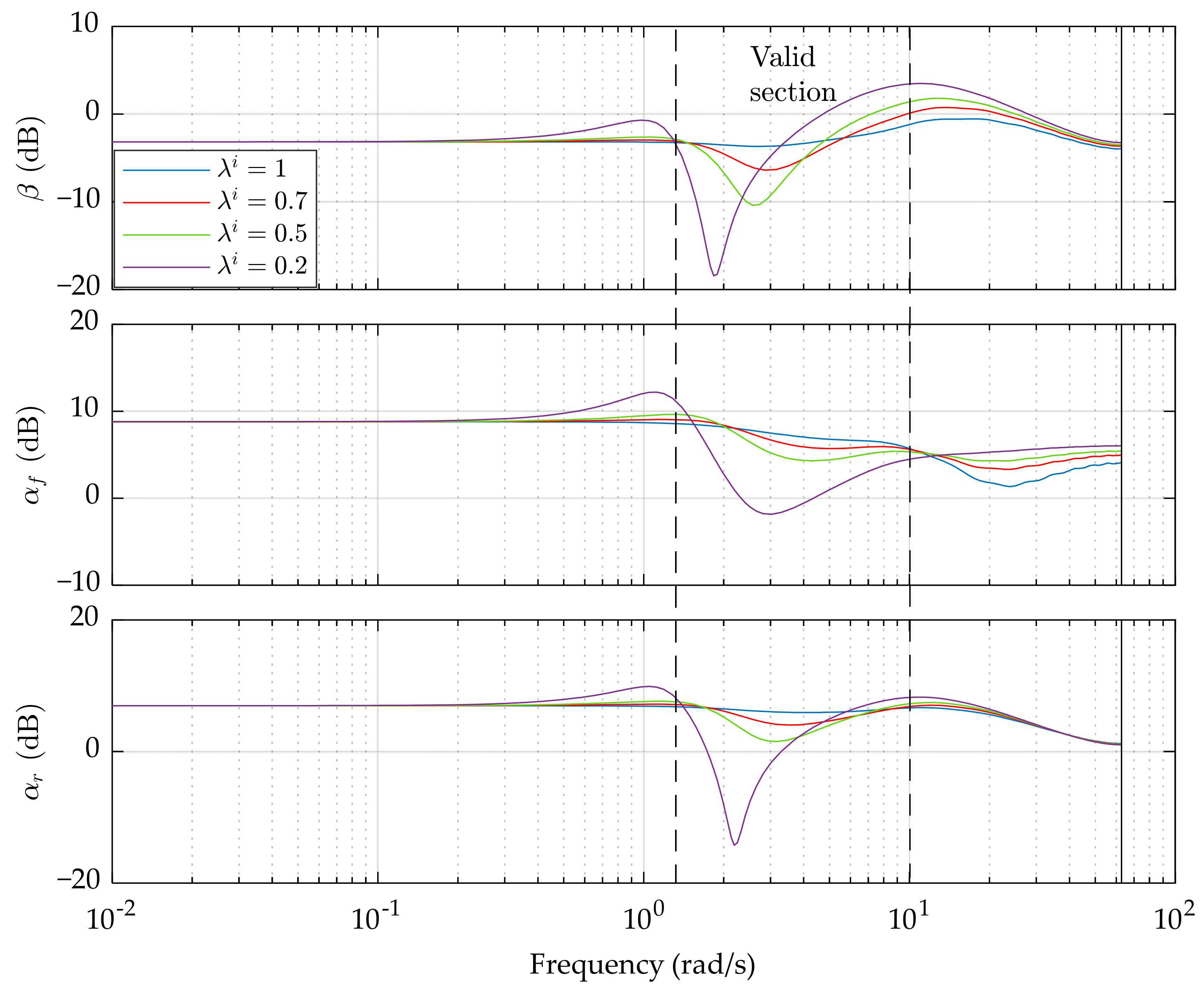
4.3. System Response in the Frequency Domain
- The sub-optimal control with constraints weakens the suppression of path tracking errors compared with the optimal preview control. A lower λi usually leads to higher errors, especially at low and medium frequency. It is worth to notice that the yaw angle error eψ is not influenced by λi at very low frequency, which is similar to the steady-state response.
- The proposed control has the capability of suppressing the constrained variables, resulting in the enhancement of vehicle stability. Unfortunately, this happens only in a limited frequency range, which is called the valid section. As the sub-optimal control coefficient λi decreases, the suppression of β, αf, and αr becomes more obvious, but at the sacrifice of the performance beyond the valid section.
5. Simulation and Results
5.1. Establishment of Simulation
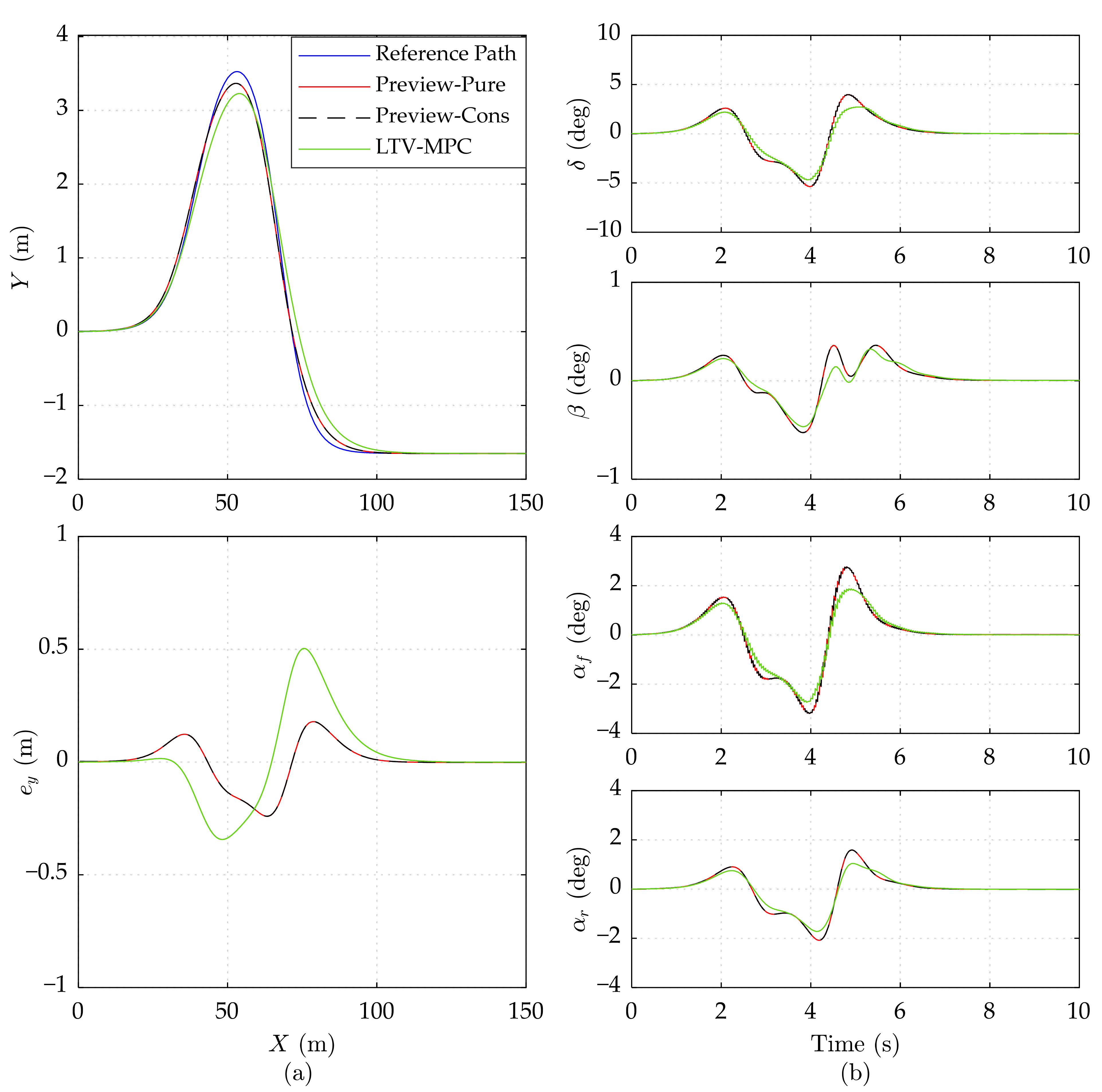
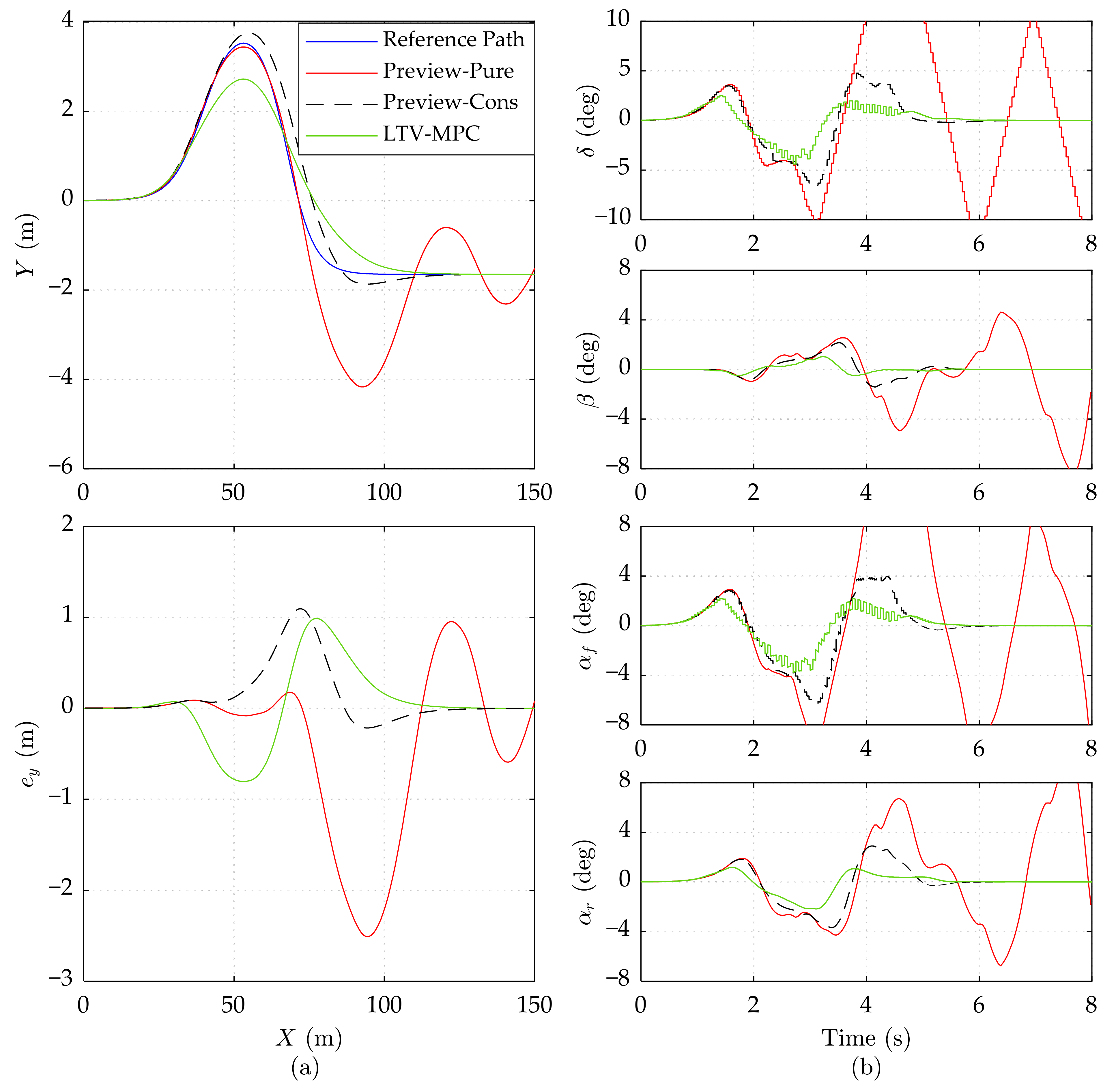
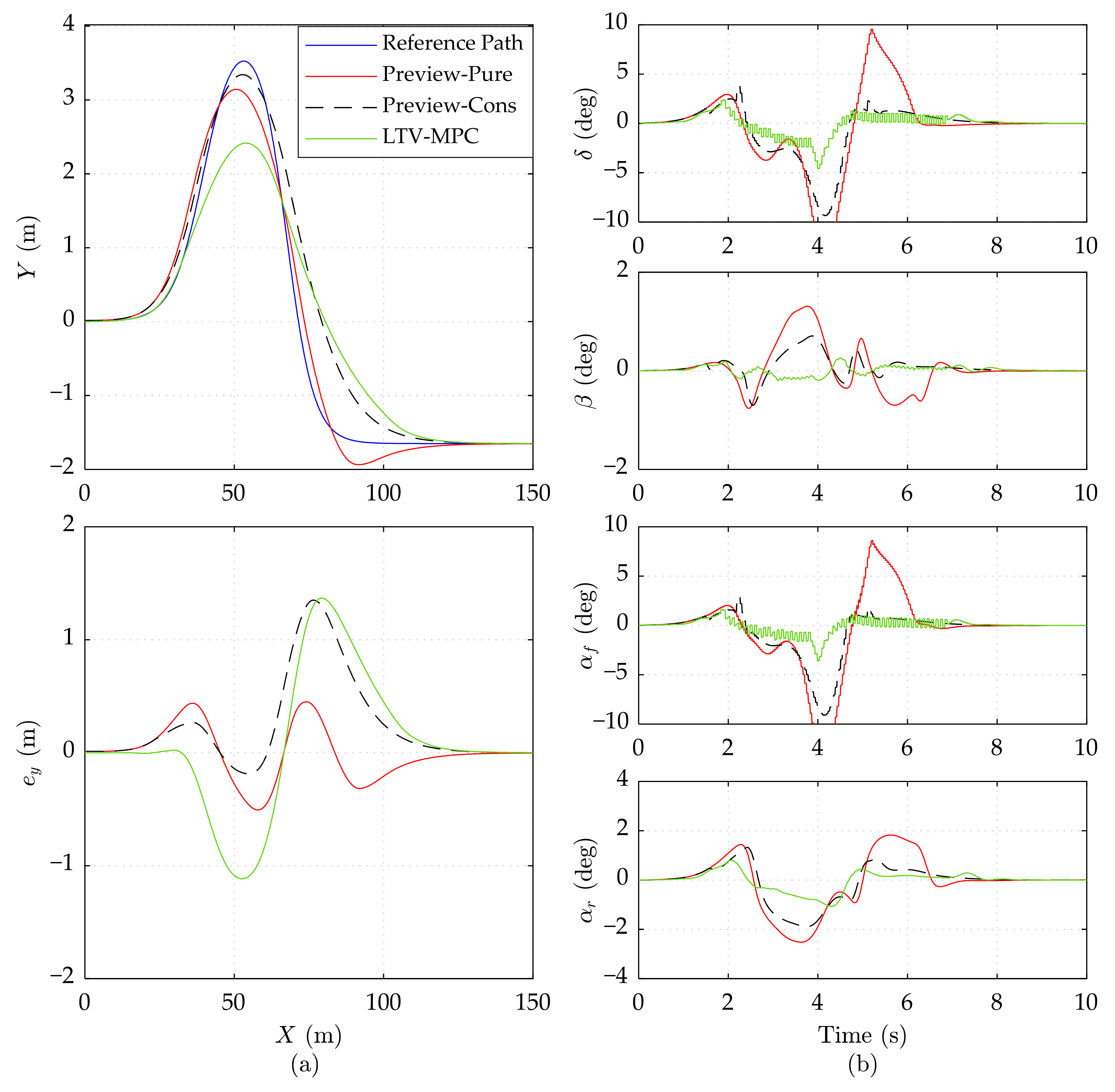
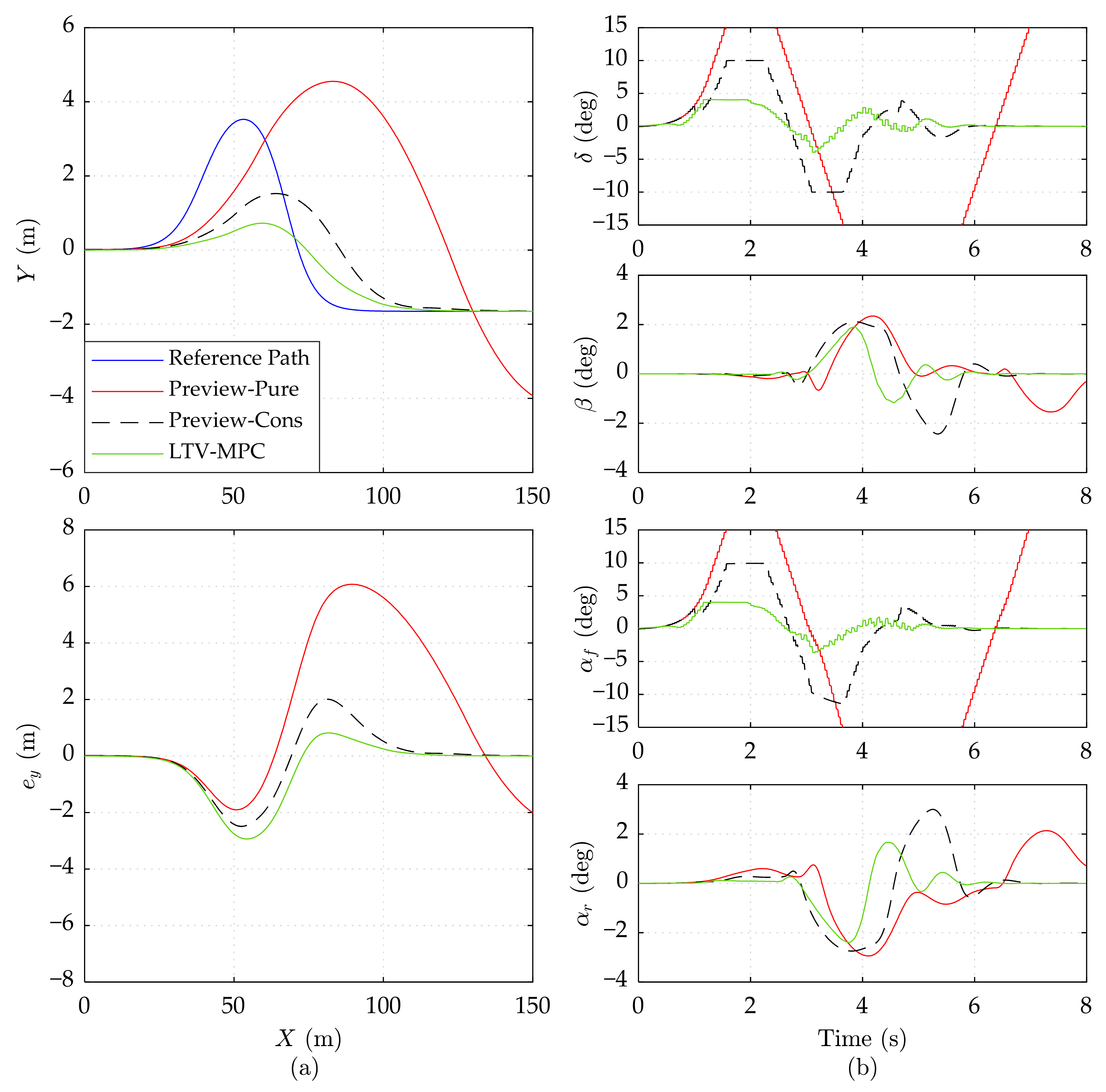
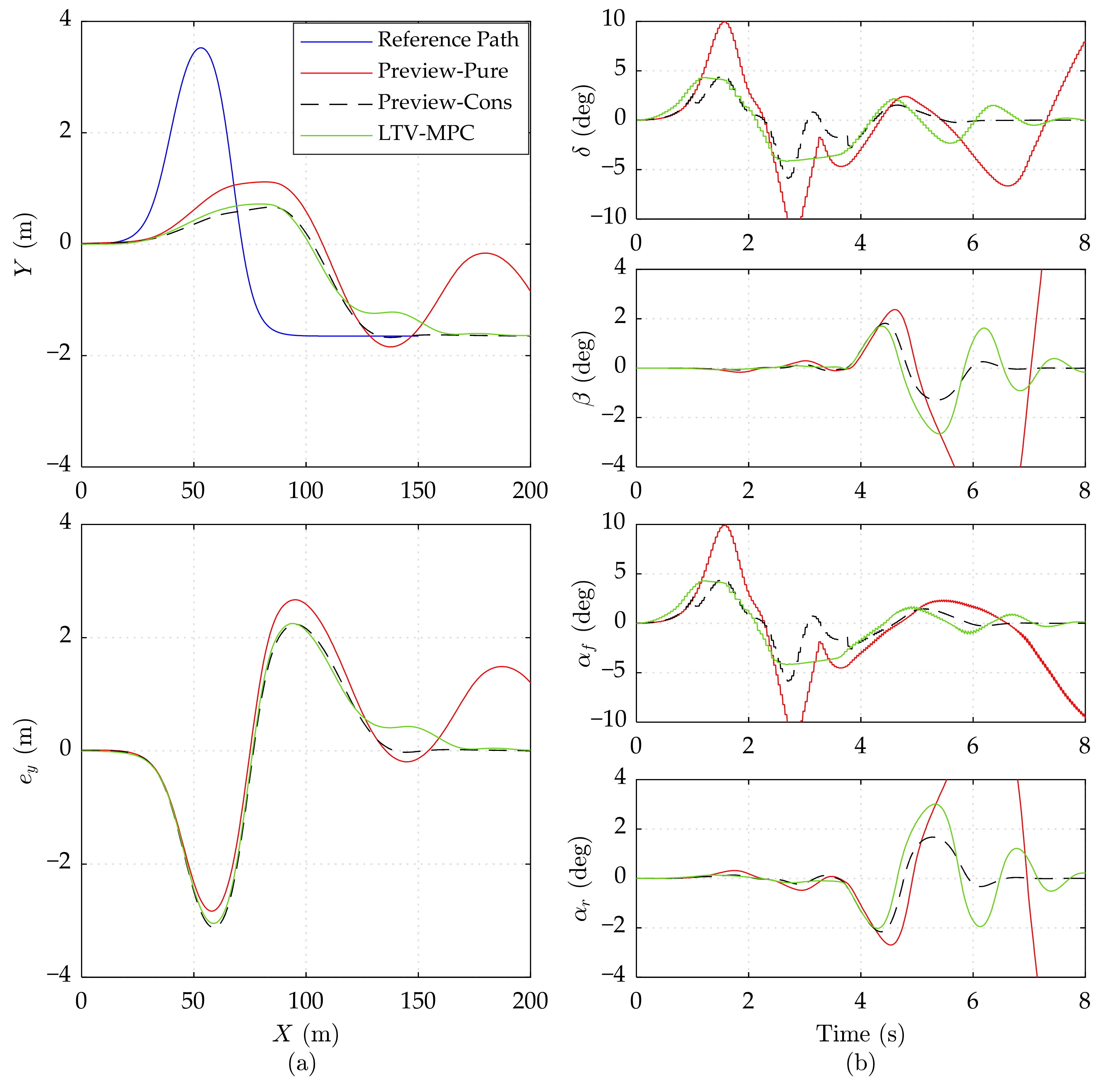
5.2. Results and Analysis
5.2.1. Performance at Different Speeds under the High Road Adhesion Condition
5.2.2. Performance at Different Speeds under the Low Road Adhesion Condition
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, A.; Sentouh, C.; Zhang, H.; Popieul, J. Fuzzy Static Output Feedback Control for Path Following of Autonomous Vehicles with Transient Performance Improvements. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3069–3079. [Google Scholar] [CrossRef]
- Liu, J.; Jayakumar, P.; Stein, J.L.; Ersal, T. A Study on Model Fidelity for Model Predictive Control-Based Obstacle Avoidance in High-Speed Autonomous Ground Vehicles. Veh. Syst. Dyn. 2016, 54, 1629–1650. [Google Scholar] [CrossRef]
- Cao, J.; Song, C.; Peng, S.; Song, S.; Zhang, X.; Xiao, F. Trajectory Tracking Control Algorithm for Autonomous Vehicle Considering Cornering Characteristics. IEEE Access 2020, 8, 59470–59484. [Google Scholar] [CrossRef]
- Samuel, M.; Hussein, M.; Mohamad, B.M. A Review of Some Pure-Pursuit Based Path Tracking Techniques for Control of Autonomous Vehicle. Int. J. Comput. Appl. 2016, 135, 35–38. [Google Scholar] [CrossRef]
- Park, M.; Lee, S.; Han, W. Development of Steering Control System for Autonomous Vehicle Using Geometry-Based Path Tracking Algorithm. ETRI J. 2015, 37, 617–625. [Google Scholar] [CrossRef]
- Wit, J.; Crane, C.D., III; Armstrong, D. Autonomous Ground Vehicle Path Tracking. J. Robot. Syst. 2004, 21, 439–449. [Google Scholar] [CrossRef]
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous Automobile Trajectory Tracking for Off-Road Driving: Controller Design, Experimental Validation and Racing. In Proceedings of the IEEE 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 2296–2301. [Google Scholar]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The Robot that Won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Kritayakirana, K.; Gerdes, J.C. Using the Centre of Percussion to Design a Steering Controller for an Autonomous Race Car. Veh. Syst. Dyn. 2012, 50, 33–51. [Google Scholar] [CrossRef]
- Kapania, N.R.; Gerdes, J.C. Design of a Feedback-Feedforward Steering Controller for Accurate Path Tracking and Stability at the Limits of Handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef] [Green Version]
- Chatzikomis, C.; Sorniotti, A.; Gruber, P.; Zanchetta, M.; Willans, D.; Balcombe, B. Comparison of Path Tracking and Torque-Vectoring Controllers for Autonomous Electric Vehicles. IEEE Trans. Intell. Veh. 2018, 3, 559–570. [Google Scholar] [CrossRef] [Green Version]
- Imine, H.; Madani, T. Sliding-mode Control for Automated Lane Guidance of Heavy Vehicle. Int. J. Robust Nonlinear Control. 2013, 23, 67–76. [Google Scholar] [CrossRef]
- Wasim, M.; Kashif, A.; Awan, A.U.; Khan, M.M.; Wasif, M.; Ali, W. H-Infinity Control via Scenario Optimization for Handling and Stabilizing Vehicle Using AFS Control. In Proceedings of the IEEE 2016 International Conference on Computing, Electronic and Electrical Engineering (ICE), Quetta, Pakistan, 11–12 April 2016; pp. 307–312. [Google Scholar]
- Mammar, S.; Koenig, D. Vehicle Handling Improvement by Active Steering. Veh. Syst. Dyn. 2002, 38, 211–242. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X.; Xi, L.; Tian, Y. Design of a Path-Tracking Steering Controller for Autonomous Vehicles. Energies 2018, 11, 1451. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Nie, L.; Yin, Z.; Huang, S. A Two-Layer Controller for Lateral Path Tracking Control of Autonomous Vehicles. Sensors 2020, 20, 3689. [Google Scholar] [CrossRef]
- Borrelli, F.; Falcone, P.; Keviczky, T.; Asgari, J.; Hrovat, D. MPC-Based Approach to Active Steering for Autonomous Vehicle Systems. Int. J. Veh. Auton. Syst. 2005, 3, 265–291. [Google Scholar] [CrossRef]
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive Active Steering Control for Autonomous Vehicle Systems. IEEE Trans. Control Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]
- Falcone, P.; Eric Tseng, H.; Borrelli, F.; Asgari, J.; Hrovat, D. MPC-Based Yaw and Lateral Stabilisation via Active Front Steering and Braking. Veh. Syst. Dyn. 2008, 46, 611–628. [Google Scholar] [CrossRef]
- Katriniok, A.; Abel, D. LTV-MPC Approach for Lateral Vehicle Guidance by Front Steering at the Limits of Vehicle Dynamics. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 6828–6833. [Google Scholar]
- Mayne, D.Q. Model Predictive Control: Recent Developments and Future Promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Birla, N.; Swarup, A. Optimal Preview Control: A Review. Optim. Control. Appl. Methods 2015, 36, 241–268. [Google Scholar] [CrossRef]
- Sharp, R.S.; Casanova, D.; Symonds, P. A Mathematical Model for Driver Steering Control, with Design, Tuning and Performance Results. Veh. Syst. Dyn. 2000, 33, 289–326. [Google Scholar]
- Xu, S.; Peng, H. Design, Analysis, and Experiments of Preview Path Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 48–58. [Google Scholar] [CrossRef]
- Xu, S.; Peng, H.; Tang, Y. Preview Path Tracking Control with Delay Compensation for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2979–2989. [Google Scholar] [CrossRef]
- Shimmyo, S.; Sato, T.; Ohnishi, K. Biped Walking Pattern Generation by Using Preview Control Based on Three-Mass Model. IEEE Trans. Ind. Electron. 2013, 60, 5137–5147. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control, 2nd ed.; Springer: New York, NY, USA, 2011; pp. 19–93. [Google Scholar]
- Laine, F.; Tomlin, C. Efficient Computation of Feedback Control for Equality-Constrained LQR. In Proceedings of the IEEE 2019 International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 6748–6754. [Google Scholar]
- Wang, J.; Alexander, L.; Rajamani, R. Friction Estimation on Highway Vehicles Using Longitudinal Measurements. J. Dyn. Syst. Meas. Control-Trans. ASME 2004, 126, 265–275. [Google Scholar] [CrossRef]
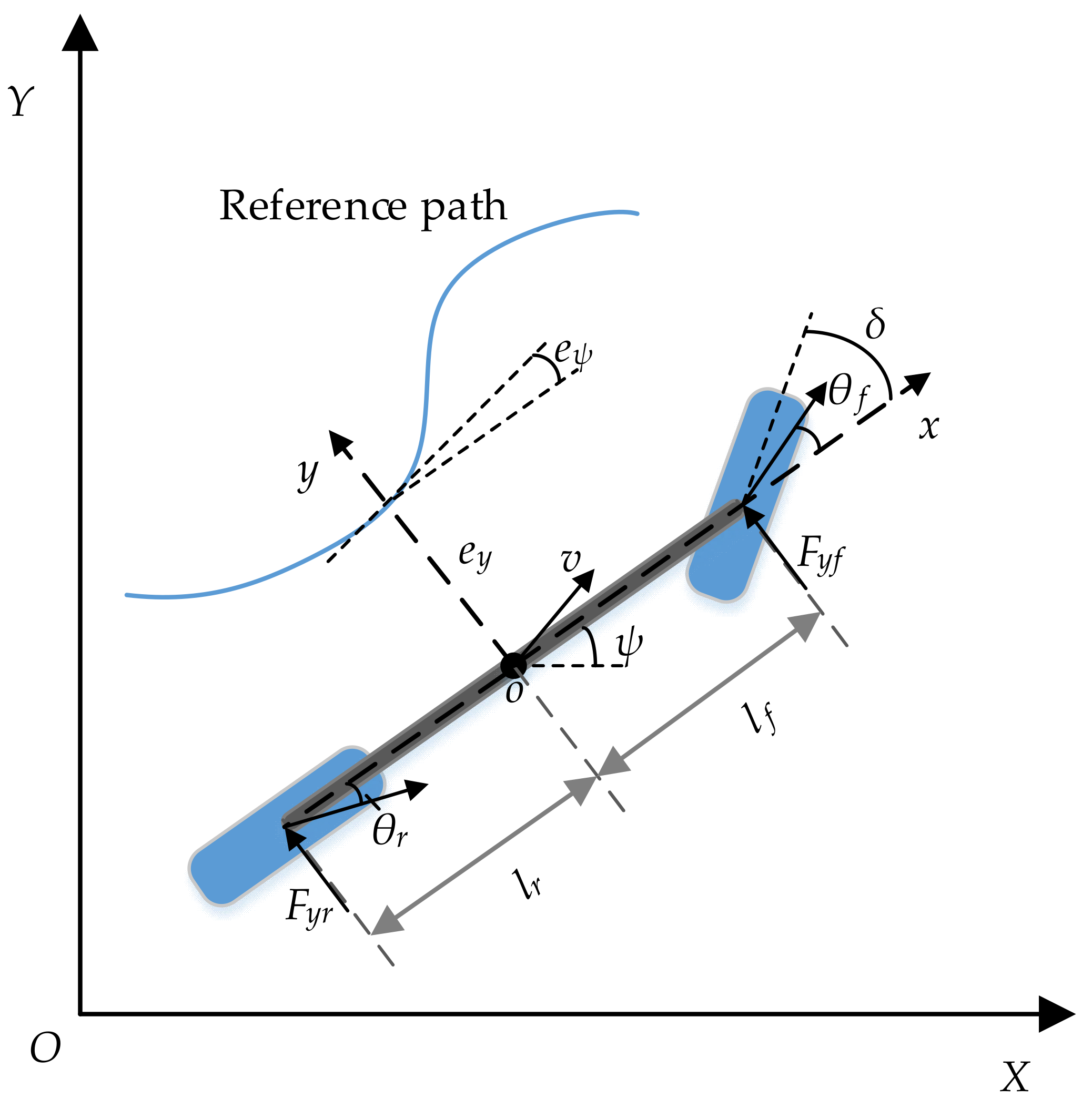

| Symbol | Definition | Unit |
|---|---|---|
| Vehicle mass | kg | |
| Yaw moment of vehicle inertia | kg·m2 | |
| Lateral tire force of the front/rear wheel (in vehicle body-fixed coordinate system, oxy) | N | |
| Lateral stiffness of the front/rear wheel | N/rad | |
| Slip angle of the front/rear wheel | rad | |
| Velocity angle of the front/rear wheel | rad | |
| Distance from center of gravity to the front/rear wheel | m | |
| Front wheel steering angle | rad | |
| Vehicle speed (in inertial coordinate system, OXY) | m/s | |
| Longitudinal speed (the projection of v in the x axis of oxy) | m/s | |
| Lateral error from center of gravity to the reference trajectory | m | |
| Yaw angle of vehicle | rad | |
| Error of yaw angle with respect to reference path | rad |
| Vehicle Speed (m/s) | Road Friction Coefficient μ | Preview Length H |
|---|---|---|
| 10 | 0.3 | 17 |
| 0.9 | 4 | |
| 15 | 0.3 | 28 |
| 0.9 | 9 | |
| 20 | 0.3 | 33 |
| 0.9 | 17 | |
| 25 | 0.3 | 35 |
| 0.9 | 19 |
| Parameter | Value/Description |
|---|---|
| Vehicle mass | 1620 kg |
| Front wheelbase | 1.165 m |
| Rear wheelbase | 1.535 m |
| Yaw inertia | 3645 kg·m2 |
| Powertrain | 125 kW front-wheel drive |
| Transmission gear ratio | 4.1:1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Ouyang, Q.; Cui, Y.; Jin, Y. Preview Control with Dynamic Constraints for Autonomous Vehicles. Sensors 2021, 21, 5155. https://doi.org/10.3390/s21155155
Li R, Ouyang Q, Cui Y, Jin Y. Preview Control with Dynamic Constraints for Autonomous Vehicles. Sensors. 2021; 21(15):5155. https://doi.org/10.3390/s21155155
Chicago/Turabian StyleLi, Rui, Qi Ouyang, Yue Cui, and Yang Jin. 2021. "Preview Control with Dynamic Constraints for Autonomous Vehicles" Sensors 21, no. 15: 5155. https://doi.org/10.3390/s21155155
APA StyleLi, R., Ouyang, Q., Cui, Y., & Jin, Y. (2021). Preview Control with Dynamic Constraints for Autonomous Vehicles. Sensors, 21(15), 5155. https://doi.org/10.3390/s21155155





