Fractional Derivative Modification of Drude Model
Abstract
1. Introduction
2. Drude Model
3. Numerical Implementation
4. Results
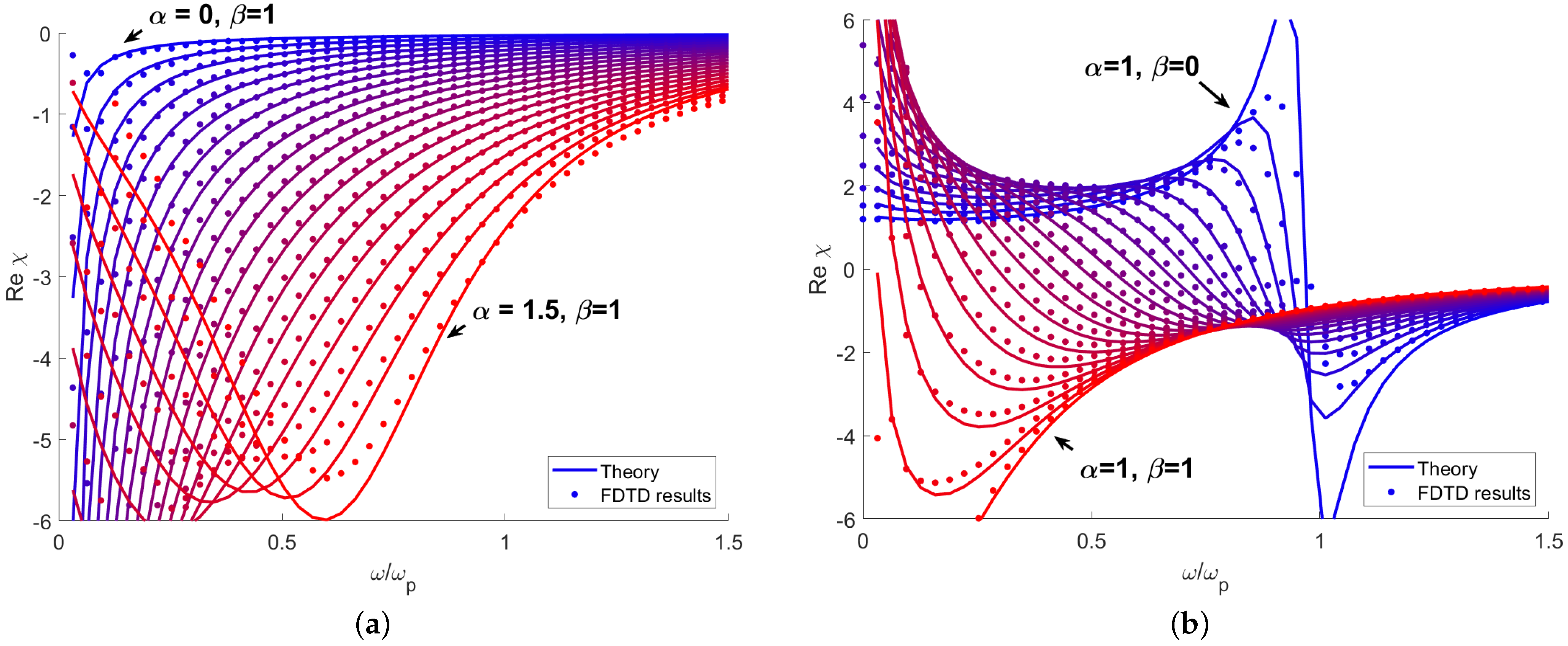
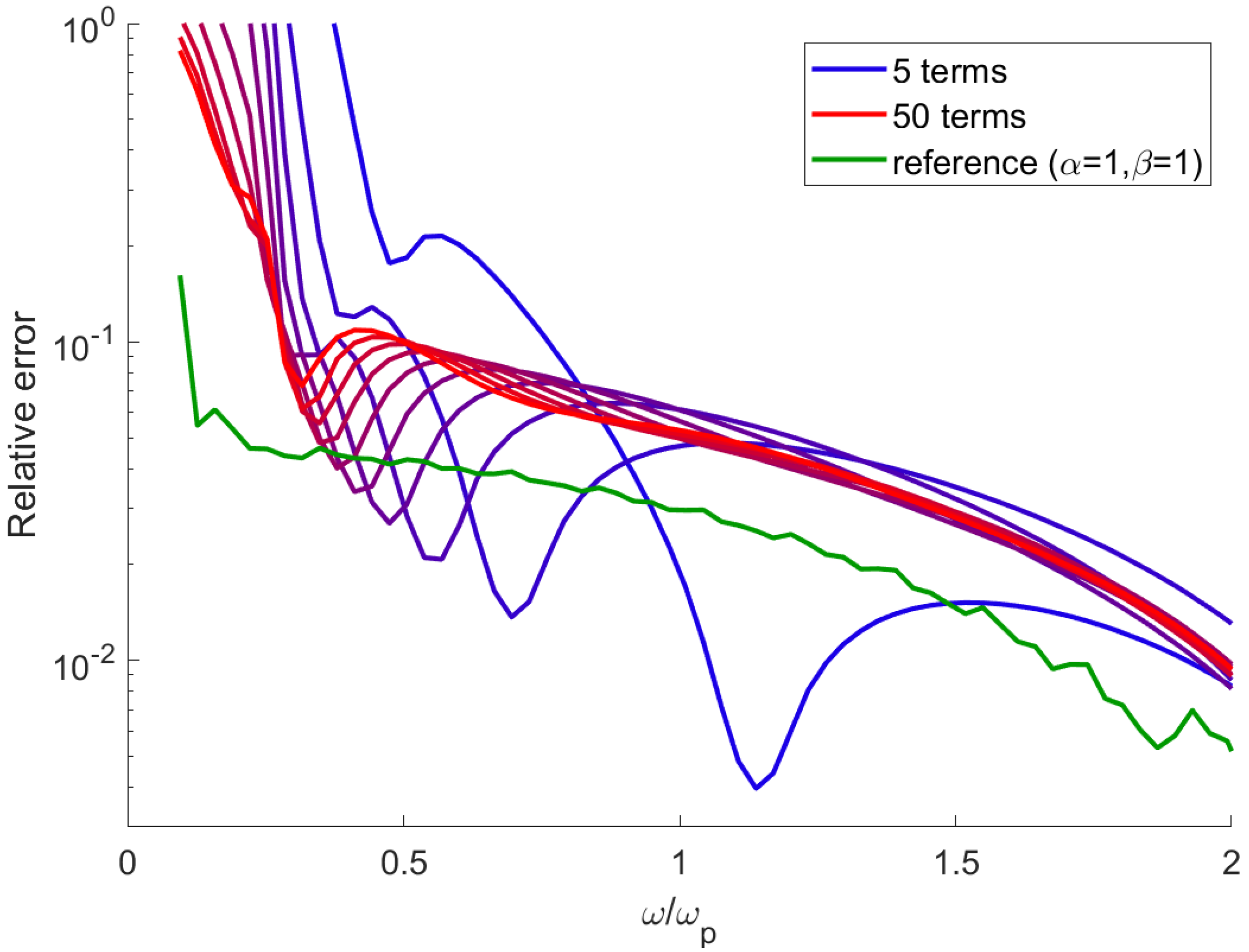
4.1. Calculation of Susceptibility
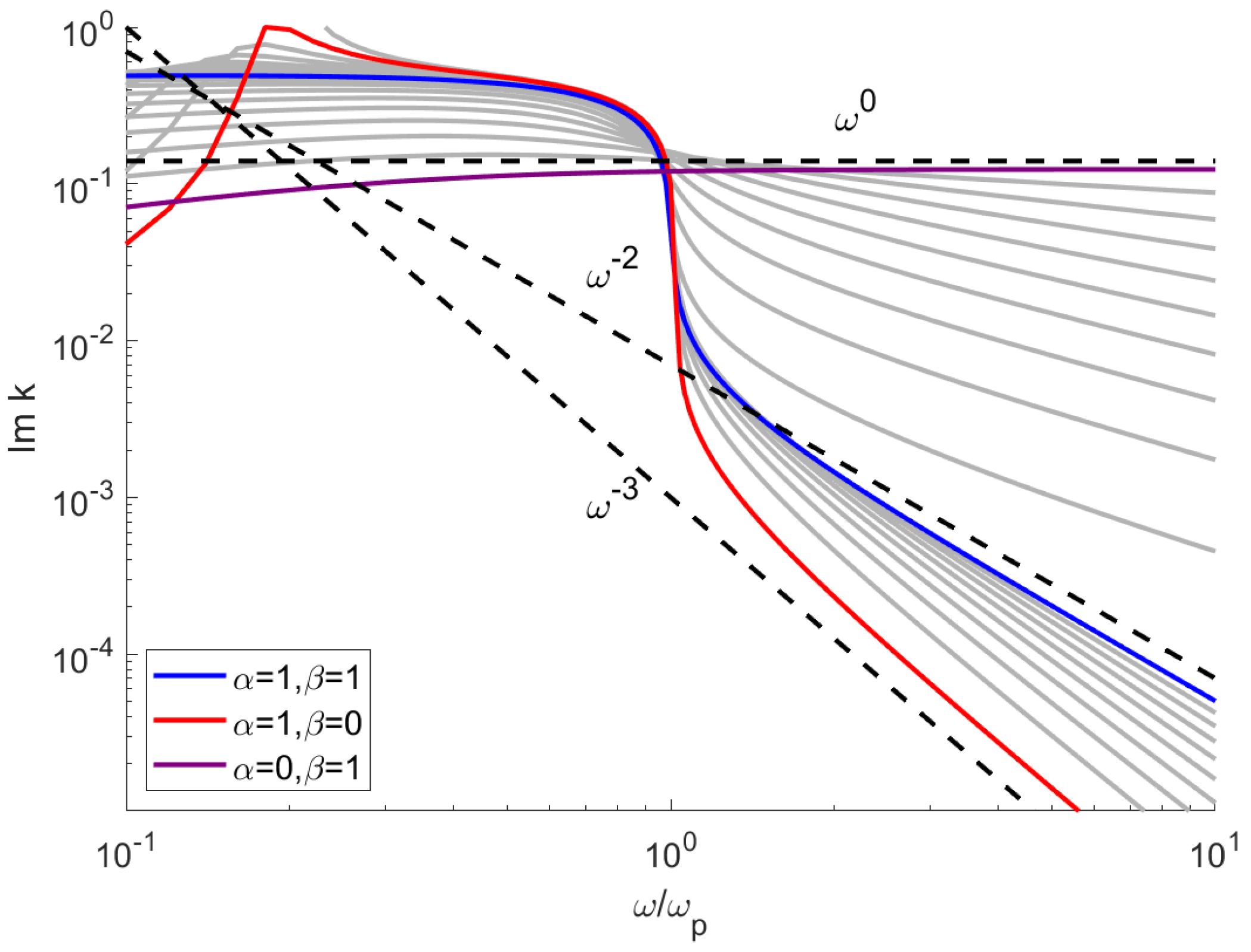
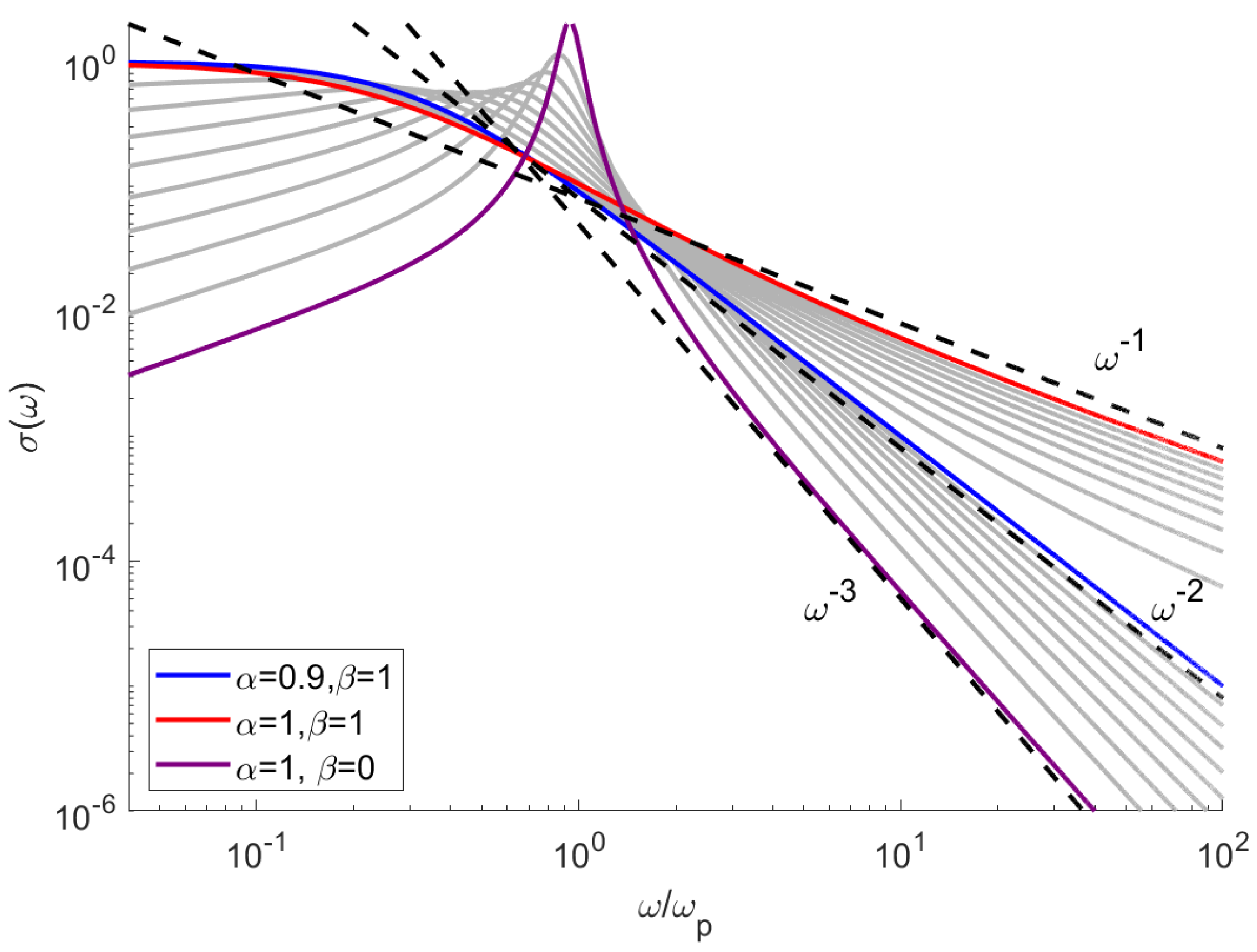
4.2. Wave Propagation in Fractional Medium
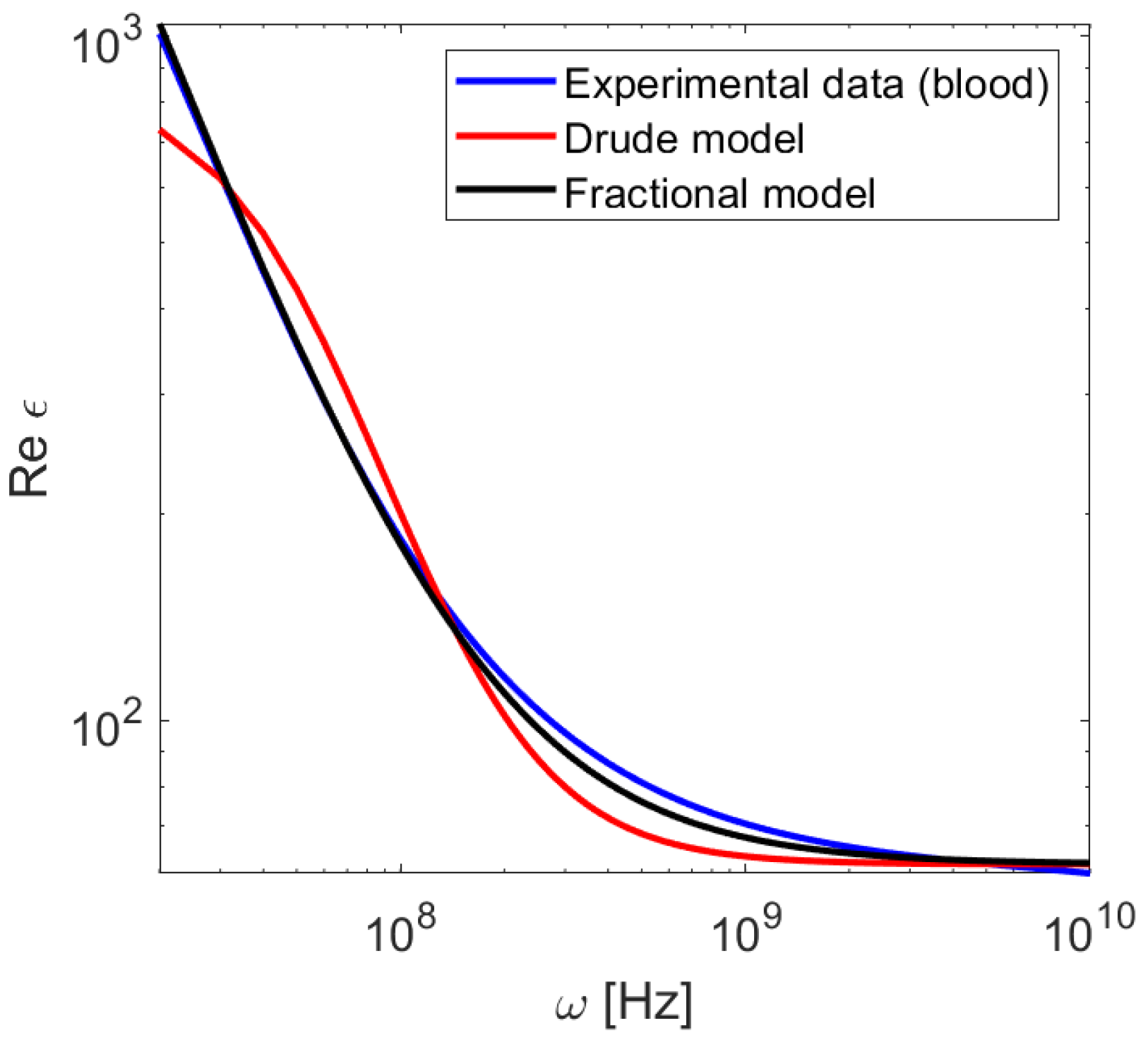
4.3. Application to Soft Tissue
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Herrmann, R. Fractional Calculus—An Introduction for Physicists; World Scientific Publishing: Singapore, 2018. [Google Scholar]
- Liang, G.; Hao, J.; Shan, D. Electromagnetic Interpretation of Fractional-Order Elements. J. Mod. Phys. 2017, 8, 2209–2218. [Google Scholar] [CrossRef][Green Version]
- Tarasov, V. Fractional integro-differential equations for electromagnetic waves in dielectric media. Theor. Math. Phys. 2009, 158, 355–359. [Google Scholar] [CrossRef]
- Machado, J.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Ray, S.; Sahoo, S.; Das, S. Formulation and solutions of fractional continuously variable order mass-spring-damper systems controlled by viscoelastic and viscous-viscoelastic dampers. Adv. Mech. Eng. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Padovan, J. Computational algorithms for FE formulations involving fractional operators. Comput. Mech. 1987, 2, 271–287. [Google Scholar] [CrossRef]
- Holm, S.; Näsholm, S. A causal and fractional all-frequency wave equation for lossy media J. Acoust. Soc. Am. 2011, 130, 2195–2202. [Google Scholar] [CrossRef]
- Chen, W.; Holm, S. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. J. Acoust. Soc. Am. 2004, 115, 1424–1430. [Google Scholar] [CrossRef]
- Song, G.; Zhang, W. Electromagnetic Field in One-Dimensional Metallic Nanoparticle Arrays. Plasmonics 2018, 13, 2369–2376. [Google Scholar] [CrossRef]
- Holm, S.; Näsholm, S. Comparison of fractional wave equations for power law attenuation in ultrasound and elastography. Ultrasound Med. Biol. 2014, 40, 695–703. [Google Scholar] [CrossRef] [PubMed]
- Rossikhin, Y.; Shitikova, M. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 1997, 50, 15–67. [Google Scholar] [CrossRef]
- Nigmatullin, R. Fractional integral and its physical interpretation. Theor. Math. Phys. 1992, 90, 242–251. [Google Scholar] [CrossRef]
- Enelund, M.; Olsson, P. Damping described by fading memory; analysis and application to fractional derivative models. Int. J. Solids Struct. 1999, 25, 939–970. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J. Novel analytical solutions of the fractional Drude model. Optik 2018, 168, 728–740. [Google Scholar] [CrossRef]
- Gantzler, N.; Dordevic, S. An alternative approach to the extended Drude model. J. Appl. Spectrosc. 2018, 85, 361–364. [Google Scholar] [CrossRef]
- Guia, M.; Rosales, J.; Martinez, L.; Alvarez, J. Fractional Drude model of electrons in a metal. Rev. Mex. Fis. 2016, 62, 155–159. [Google Scholar]
- Yee, K. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
- Mrozowski, M.; Stuhly, M. Parameterization of Media Dispersive Properties for FDTD. IEEE Trans. Antennas Propag. 1997, 45, 1438–1439. [Google Scholar] [CrossRef]
- Abdullah, H.; Elsadek, H.; ElDeeb, H.; Bagherzadeh, N. Fractional Derivatives Based Scheme for FDTD Modeling of nth-Order Cole–Cole Dispersive Media. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 281–284. [Google Scholar] [CrossRef]
- Rekanos, I. FDTD Modeling of Havriliak-Negami Media. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 49–51. [Google Scholar] [CrossRef]
- Mehrotra, P.; Chatterjee, B.; Sen, S. EM-Wave Biosensors: A Review of RF, Microwave, mm-Wave and Optical Sensing. Sensors 2019, 19, 1013. [Google Scholar] [CrossRef]
- Gomez, A.; Rus, G.; Saffari, N. Wave Propagation in a Fractional Viscoelastic Tissue Model: Application to Transluminal Procedures. Sensors 2021, 21, 2778. [Google Scholar] [CrossRef]
- Caputo, M.; Carcione, J.; Cavallini, F. Wave simulation in biologic media based on the Kelvin-Voigt fractional-derivative stress-strain relation. Ultrasound Med. Biol. 2011, 37, 996–1004. [Google Scholar] [CrossRef]
- Callejas, A.; Gomez, A.; Faris, I.; Melchor, J.; Rus, G. Kelvin-Voigt Parameters Reconstruction of Cervical Tissue-Mimicking Phantoms Using Torsional Wave Elastography. Sensors 2019, 19, 3281. [Google Scholar] [CrossRef]
- Garappa, R.; Kaslik, E.; Popolizio, M. Evaluation of Fractional Integrals and Derivatives of Elementary Functions: Overview and Tutorial. Mathematics 2019, 7, 407. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, L.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef] [PubMed]
- Alsunaidi, M.; Al-Jabr, A. A General ADE-FDTD Algorithm for the Simulation of Dispersive Structures. IEEE Photonics Technol. Lett. 2009, 21, 817–819. [Google Scholar] [CrossRef]
- Sumelka, W.; Łuczak, B.; Gajewski, T.; Voyiadjis, G. Modelling of AAA in the framework of time-fractional damage hyperelasticity. Int. J. Solids Struct. 2020, 206, 30–42. [Google Scholar] [CrossRef]
- Salinas, M.; Salas, R.; Melado, D.; Glaria, A.; Saavedra, C. A Computational Fractional Signal Derivative Method. Model. Simul. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Ziemkiewicz, D.; Słowik, K.; Zielińska-Raczyńska, S. Tunable narrowband plasmonic resonances in electromagnetically induced transparency media. J. Opt. Soc. Am. B 2017, 34, 1981–1988. [Google Scholar] [CrossRef]
| , , | |||||||||||||||||||||
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 | |
| ∞ | 89 | 37 | 26 | 19 | 16 | 13 | 11 | 9 | 6 | 4 | 3 | 1 | 2 | 5 | 9 | 16 | 27 | 48 | 110 | ∞ | |
| , , | |||||||||||||||||||||
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2 | |
| 9 | 11 | 12 | 13 | 13 | 12 | 12 | 12 | 11 | 10 | 9 | 12 | 690 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 117 | |
| , , | |||||||||||||||||||||
| 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 1 | 1.1 | |
| 0.5 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 14 | 16 | ∞ | |
| , , | |||||||||||||||||||||
| 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 | 0.55 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | 1 | 1.1 | |
| 0.5 | 0.8 | 0.7 | 0.7 | 0.6 | 0.5 | 0.1 | 0.4 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 | 14 | 17 | ∞ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpiński, K.; Zielińska-Raczyńska, S.; Ziemkiewicz, D. Fractional Derivative Modification of Drude Model. Sensors 2021, 21, 4974. https://doi.org/10.3390/s21154974
Karpiński K, Zielińska-Raczyńska S, Ziemkiewicz D. Fractional Derivative Modification of Drude Model. Sensors. 2021; 21(15):4974. https://doi.org/10.3390/s21154974
Chicago/Turabian StyleKarpiński, Karol, Sylwia Zielińska-Raczyńska, and David Ziemkiewicz. 2021. "Fractional Derivative Modification of Drude Model" Sensors 21, no. 15: 4974. https://doi.org/10.3390/s21154974
APA StyleKarpiński, K., Zielińska-Raczyńska, S., & Ziemkiewicz, D. (2021). Fractional Derivative Modification of Drude Model. Sensors, 21(15), 4974. https://doi.org/10.3390/s21154974






