Limitations of Foot-Worn Sensors for Assessing Running Power
Abstract
:1. Introduction
2. Methods
2.1. Participants and Study Design
2.2. Testing Procedures
2.2.1. Combined Incremental and Ramp Exercise Test
2.2.2. Modulation of Running Economy
- SF+10%: an increase of the step frequency by 10%. This was prescribed using a digital metronome. Participants were also verbally encouraged and supported when the target frequency was not met;
- SF−10%: a decrease in step frequency by 10%. Again, a metronome was used to help the participants keep this running form. As additional mental help, the participants were instructed to lengthen their stride, as if they were gliding;
- GCT: reduction of ground contact time. The participants were instructed to reduce the time spent in contact with the ground by around 20 ms. They were told the GCT during their self-selected running and a target GCT for this variation. Participants were instructed regularly to either keep their step exactly as is or to try and decrease their GCT further. As a mental image, participants were encouraged to imagine the treadmill to be covered in hot coals;
- Arms: The participants were instructed to run without arm swing and, thus, without counterbalance to their running motion. The arms were either held above the head or in the neck in order to avoid effective use as a counterweight to rotational movement.
2.3. Statistics
2.3.1. Oxygen Consumption during Altered Running Conditions
2.3.2. Difference in Slope of Power to Oxygen
3. Results
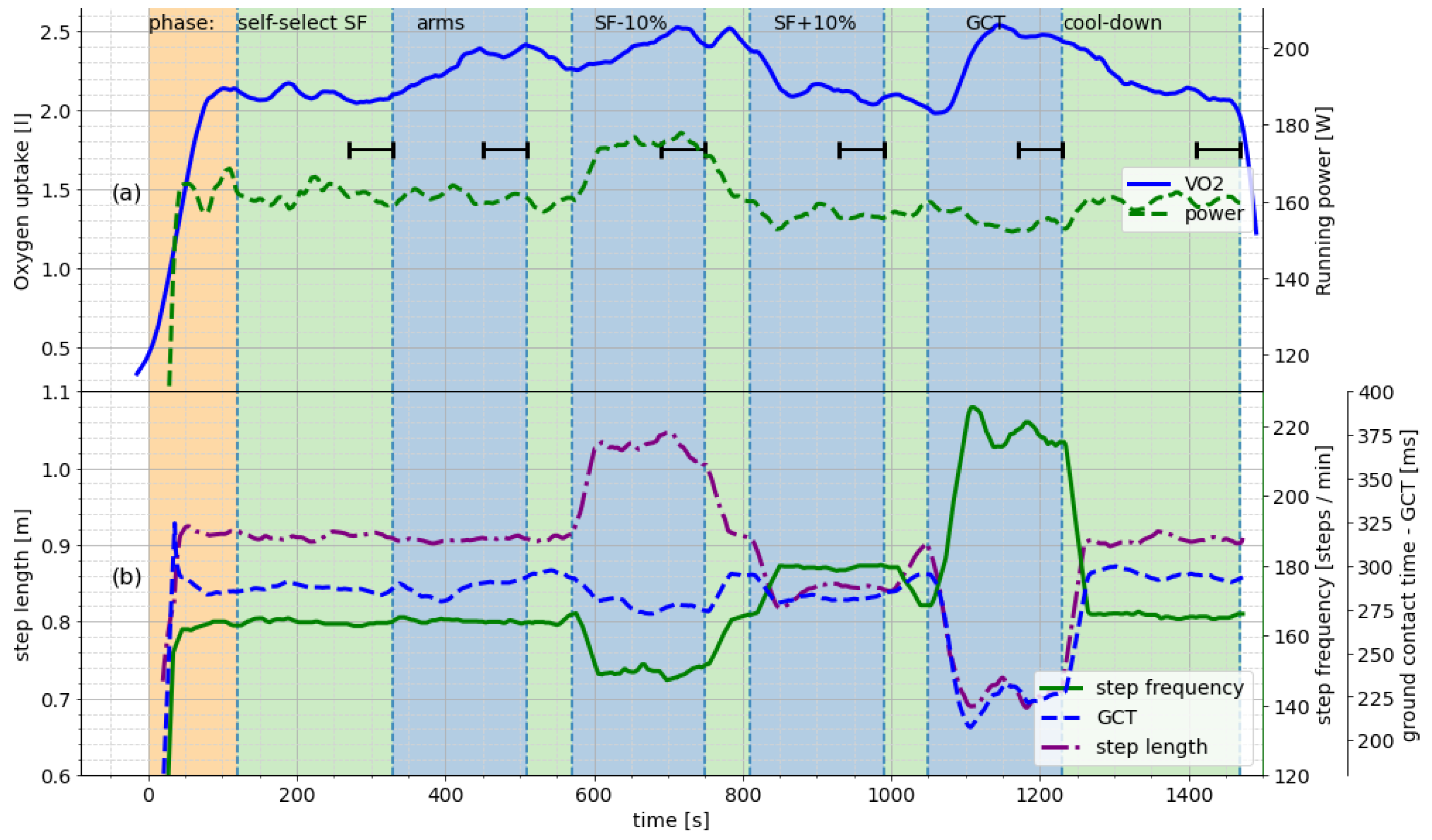
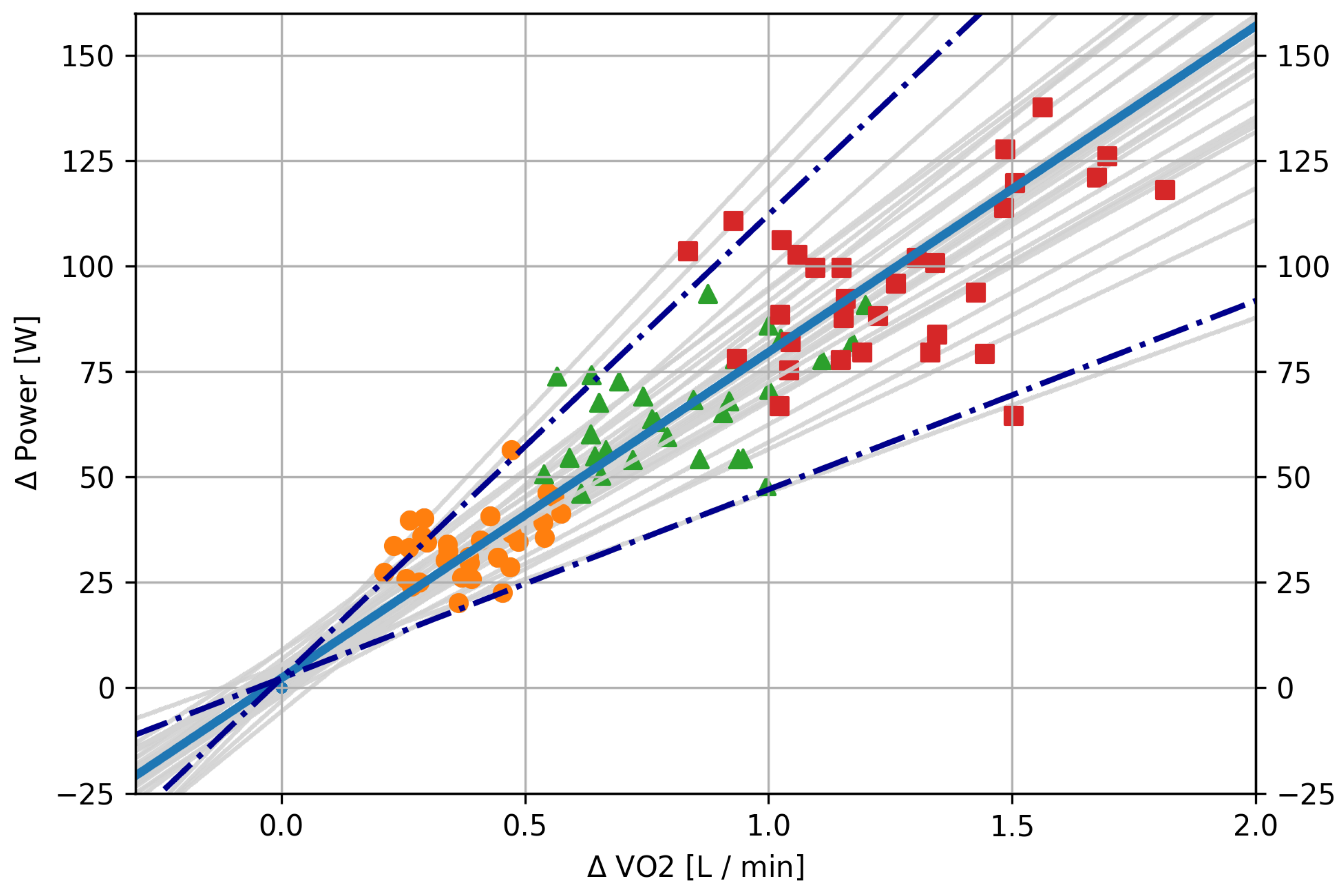
3.1. Relation of VO and Power during the Incremental/Ramp Test
3.2. Running Economy
3.3. Relation between Metabolic Cost of Running and Running Power
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Soulard, J.; Vaillant, J.; Balaguier, R.; Baillet, A.; Gaudin, P.; Vuillerme, N. Foot-Worn Inertial Sensors Are Reliable to Assess Spatiotemporal Gait Parameters in Axial Spondyloarthritis under Single and Dual Task Walking in Axial Spondyloarthritis. Sensors 2020, 20, 6453. [Google Scholar] [CrossRef]
- Huang, Y.; Jirattigalachote, W.; Cutkosky, M.R.; Zhu, X.; Shull, P.B. Novel Foot Progression Angle Algorithm Estimation via Foot-Worn, Magneto-Inertial Sensing. IEEE Trans. Biomed. Eng. 2016, 63, 2278–2285. [Google Scholar] [CrossRef]
- Falbriard, M.; Meyer, F.; Mariani, B.; Millet, G.P.; Aminian, K. Accurate Estimation of Running Temporal Parameters Using Foot-Worn Inertial Sensors. Front. Physiol. 2018, 9. [Google Scholar] [CrossRef] [Green Version]
- García-Pinillos, F.; Roche-Seruendo, L.E.; Marcén-Cinca, N.; Marco-Contreras, L.A.; Latorre-Román, P.A. Absolute Reliability and Concurrent Validity of the Stryd System for the Assessment of Running Stride Kinematics at Different Velocities. J. Strength Cond. Res. 2021, 35, 78–84. [Google Scholar] [CrossRef]
- Scataglini, S.; Cools, E.; Neyrinck, J.; Verwulgen, S. An Exploratory Analysis of User Needs and Design Issues of Wearable Technology for Monitoring Running Performances. Adv. Intell. Syst. Comput. 2021, 1206, 207–215. [Google Scholar] [CrossRef]
- Cerezuela-Espejo, V.; Hernández-Belmonte, A.; Courel-Ibáñez, J.; Conesa-Ros, E.; Mora-Rodríguez, R.; Pallarés, J.G. Are we ready to measure running power? Repeatability and concurrent validity of five commercial technologies. Eur. J. Sport Sci. 2021, 21, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Falbriard, M.; Soltani, A.; Aminian, K. Running Speed Estimation Using Shoe-Worn Inertial Sensors: Direct Integration, Linear, and Personalized Model. Front. Sports Act. Living 2021, 3, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Muniz-Pardos, B.; Sutehall, S.; Gellaerts, J.; Falbriard, M.; Mariani, B.; Bosch, A.; Asrat, M.; Schaible, J.; Pitsiladis, Y.P. Integration of Wearable Sensors into the Evaluation of Running Economy and Foot Mechanics in Elite Runners. Curr. Sports Med. Rep. 2018, 17, 480–488. [Google Scholar] [CrossRef] [PubMed]
- Snyder, K. Running Power Definition and Utility. Available online: https://blog.stryd.com/2020/12/17/running-power-definition-utility-article/ (accessed on 15 June 2021).
- Tjelta, L.I. Three Norwegian brothers all European 1500m champions: What is the secret? Int. J. Sports Sci. Coach. 2019, 14, 694–700. [Google Scholar] [CrossRef]
- Powers, S.K. Exercise Physiology: Theory and Application to Fitness and Performance, 10th ed.; McGraw-Hill: New York, NY, USA, 2018. [Google Scholar]
- Weir, J.B. New methods for calculating metabolic rate with special reference to protein metabolism. J. Physiol. 1949, 109, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Midgley, A.W.; McNaughton, L.R.; Polman, R.; Marchant, D. Criteria for Determination of Maximal Oxygen Uptake. Sports Med. 2007, 37, 1019–1028. [Google Scholar] [CrossRef] [PubMed]
- Ettema, G.; Lorås, H.W. Efficiency in cycling: A review. Eur. J. Appl. Physiol. 2009, 106, 1–14. [Google Scholar] [CrossRef] [PubMed]
- How to Lead the Pack: Running Power Meters & Quality Data. Available online: https://blog.stryd.com/2017/12/07/how-to-lead-the-pack-running-power-meters-quality-data/ (accessed on 19 May 2021).
- Moore, I.S. Is There an Economical Running Technique? A Review of Modifiable Biomechanical Factors Affecting Running Economy. Sports Med. 2016, 46, 793–807. [Google Scholar] [CrossRef] [Green Version]
- Kirkendall, D.T.; Garrett, W.E. Function and biomechanics of tendons. Scand. J. Med. Sci. Sports 2007, 7, 62–66. [Google Scholar] [CrossRef] [PubMed]
- Willems, P.; Cavagna, G.; Heglund, N. External, internal and total work in human locomotion. J. Exp. Biol. 1995, 198, 379–393. [Google Scholar] [CrossRef]
- McLaren, S.J.; Macpherson, T.W.; Coutts, A.J.; Hurst, C.; Spears, I.R.; Weston, M. The Relationships Between Internal and External Measures of Training Load and Intensity in Team Sports: A Meta-Analysis. Sports Med. 2018, 48, 641–658. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barnes, K.R.; Kilding, A.E. Running economy: Measurement, norms, and determining factors. Sports Med. Open 2015, 1, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Harriss, D.; Atkinson, G. Ethical Standards in Sport and Exercise Science Research: 2016 Update. Int. J. Sports Med. 2015, 36, 1121–1124. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, M.; Berg, A.; Kapp, R.; Wessinghage, T.; Keul, J. Correlations between Laboratory Testing and Distance Running Performance in Marathoners of Similar Performance Ability. Int. J. Sports Med. 1983, 04, 226–230. [Google Scholar] [CrossRef]
- de Ruiter, C.J.; Verdijk, P.W.; Werker, W.; Zuidema, M.J.; de Haan, A. Stride frequency in relation to oxygen consumption in experienced and novice runners. Eur. J. Sport Sci. 2014, 14, 251–258. [Google Scholar] [CrossRef]
- D’Agostino, R.; Pearson, E.S. Tests for Departure from Normality. Biometrika 1973, 60, 613. [Google Scholar] [CrossRef]
- Saunders, P.U.; Pyne, D.B.; Telford, R.D.; Hawley, J.A. Factors Affecting Running Economy in Trained Distance Runners. Sports Med. 2004, 34, 465–485. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.R.; Esau, S.P.; MacIntosh, B.R. Changes in tendon stiffness and running economy in highly trained distance runners. Eur. J. Appl. Physiol. 2010, 110, 1037–1046. [Google Scholar] [CrossRef]
- Morgan, D.; Martin, P.; Craib, M.; Caruso, C.; Clifton, R.; Hopewell, R. Effect of step length optimization on the aerobic demand of running. J. Appl. Physiol. 1994, 77, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Moore, I.S.; Ashford, K.J.; Cross, C.; Hope, J.; Jones, H.S.R.; McCarthy-Ryan, M. Humans Optimize Ground Contact Time and Leg Stiffness to Minimize the Metabolic Cost of Running. Front. Sports Act. Living 2019, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joyner, M.J. Modeling: Optimal marathon performance on the basis of physiological factors. J. Appl. Physiol. 1991, 70, 683–687. [Google Scholar] [CrossRef] [Green Version]
- Austin, C.; Hokanson, J.; McGinnis, P.; Patrick, S. The Relationship between Running Power and Running Economy in Well-Trained Distance Runners. Sports 2018, 6, 142. [Google Scholar] [CrossRef] [Green Version]
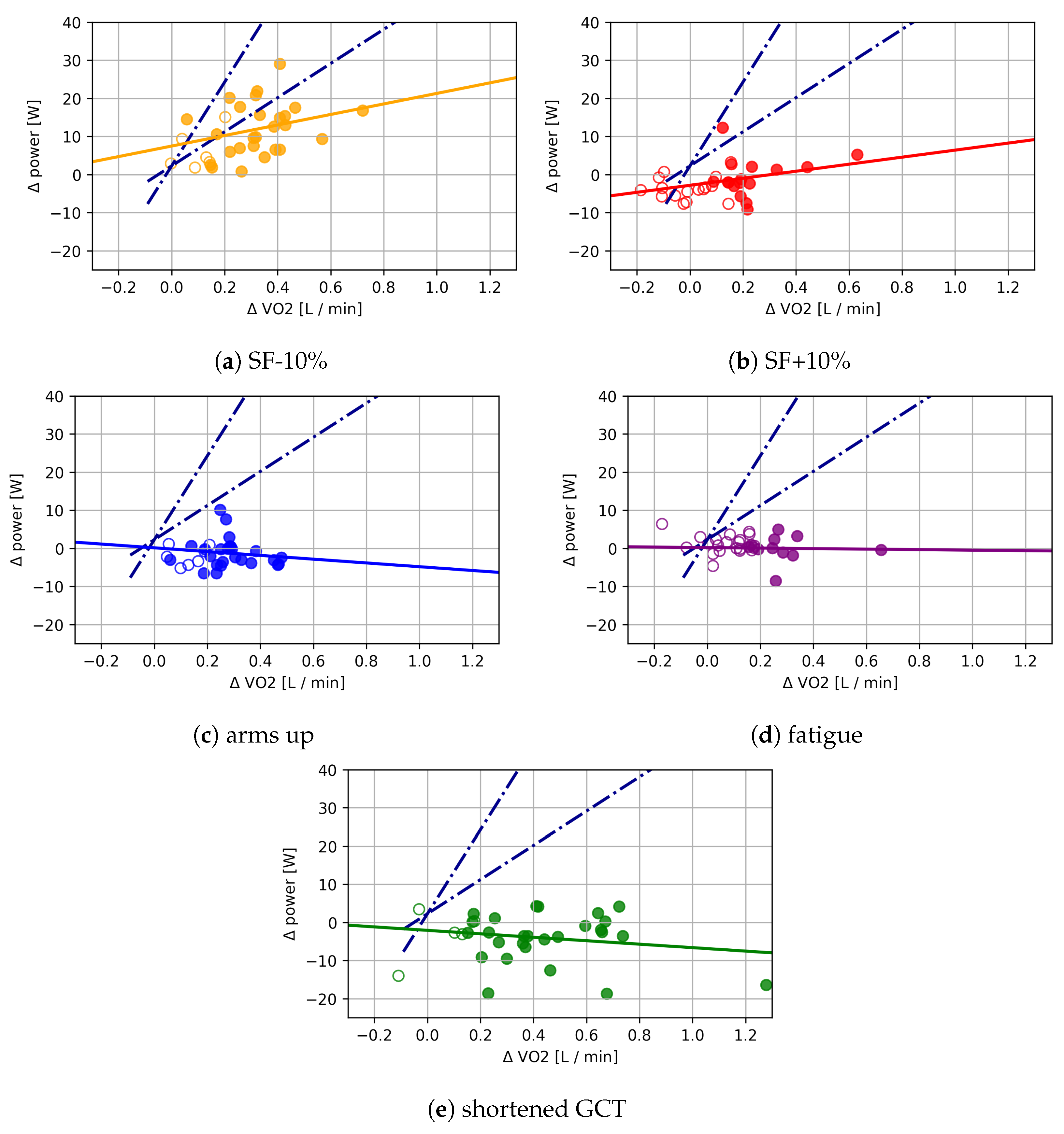
| Figure 3 | Condition | F | p | SMD | |
|---|---|---|---|---|---|
| a | SF − 10% | 36.89 | <0.0001 | 0.24 | 1.15 |
| b | SF + 10% | 193.47 | <0.0001 | 0.64 | 3.33 |
| c | arms up | 368.93 | <0.0001 | 0.76 | 4.62 |
| d | fatigued | 160.18 | <0.0001 | 0.61 | 4.98 |
| e | GCT | 429.89 | <0.0001 | 0.78 | 4.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baumgartner, T.; Held, S.; Klatt, S.; Donath, L. Limitations of Foot-Worn Sensors for Assessing Running Power. Sensors 2021, 21, 4952. https://doi.org/10.3390/s21154952
Baumgartner T, Held S, Klatt S, Donath L. Limitations of Foot-Worn Sensors for Assessing Running Power. Sensors. 2021; 21(15):4952. https://doi.org/10.3390/s21154952
Chicago/Turabian StyleBaumgartner, Tobias, Steffen Held, Stefanie Klatt, and Lars Donath. 2021. "Limitations of Foot-Worn Sensors for Assessing Running Power" Sensors 21, no. 15: 4952. https://doi.org/10.3390/s21154952
APA StyleBaumgartner, T., Held, S., Klatt, S., & Donath, L. (2021). Limitations of Foot-Worn Sensors for Assessing Running Power. Sensors, 21(15), 4952. https://doi.org/10.3390/s21154952






