Non-Orthogonal Multiple Access for Unicast and Multicast D2D: Channel Assignment, Power Allocation and Energy Efficiency
Abstract
1. Introduction
2. Related Work
- 1.
- The investigated system models in the literature assume a single/group of D2D pairs can share CUs resource blocks. In this unicast communication model, a transmitter sends data to a single receiver. However, in our system model, devices with a common interest form a group, where a single transmitter multicasts data to a set of receivers (the MD2D group). Note that the MD2D mode also includes the particular case of unicast D2D communications (when the groups just include one receiver).
- 2.
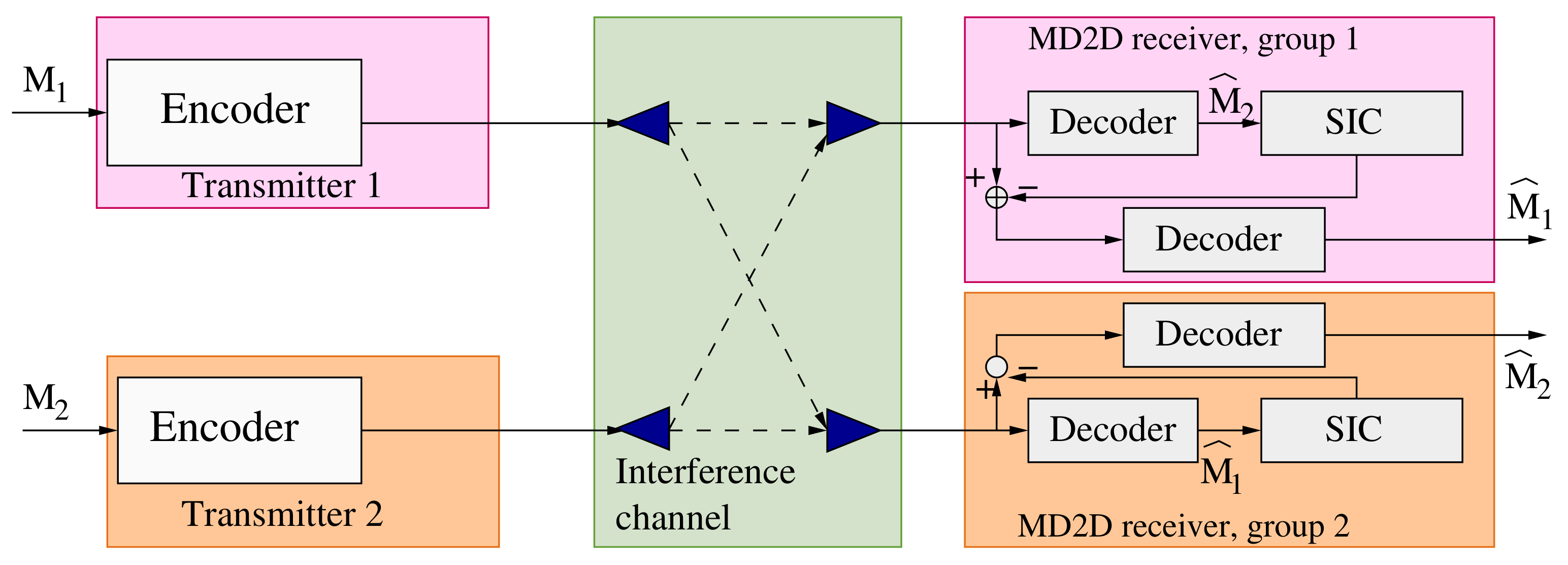
- In multicast communications, group data rate is determined according to the receiver with the poorest channel quality (CQ). Therefore, we assume that the receivers in a MD2D group as well as the CUs are able to apply SIC to the stronger interference signal. This would reduce the received interference to a minimum value leading to enhancements in MD2D communication quality.
- 3.
- We model the resource allocation sub-problem in underlay MD2D using matching theory and overlapping coalition formation game to minimize harmful mutual interference as the means to maximize energy efficiency for both the system as a whole and for individual users, metrics not considered in other related works.
- 4.
- The resource allocation approach involves two design parameters (the reuse degree and the split factor) which allow considering all the possible RB sharing variants when analyzing the system behavior.
- 5.
- The power control sub-problem is optimally solved using fractional programming. In this work, we assume that a central entity is in charge of assigning transmission power to each transmitter in the network.
- 6.
- We evaluate the performance of NOMA-based systems under a broad range of resource sharing scenarios. As performance metrics, we analyze both EE and transmission rate for the whole system (global EE and sum-rate). A potential drawback of this approach is that global performance measures do not properly capture the service fairness among users. Thus, we also formulate and analyze the MMF EE and the rate for individual users.
- Scenario 1
- (): Each CU shares its communication channel with a single D2D pair/MD2D group. Similarly, each D2D pair/MD2D group uses only one channel.
- Scenario 2
- (, ): A D2D pair/MD2D group takes advantage of multiple cellular channels and distributes its message over them. Here, a D2D pair/MD2D group may disperse its transmission power budget or rate among the occupied channels. However, a channel cannot support more than one D2D pair/MD2D group.
- Scenario 3
- (, ): Each cellular communication channel can support up to r D2D pairs/MD2D groups, which are allowed to use one cellular channel, at most. Compared to the previous scenarios, having r devices using the same channel leads to mutual interference accumulation over the CU and each D2D pair/MD2D group per channel.
- Scenario 4
- (, ): Each D2D pair/MD2D group uses up to s different cellular channels. Moreover, each channel can support r D2D pairs/MD2D groups. As in Scenario 3, the accumulated mutual interference among the channel’s devices may negatively affect both type of communications and limit the benefits of D2D pairs/MD2D groups in term of spectral and energy efficiency.
3. Problem Formulation
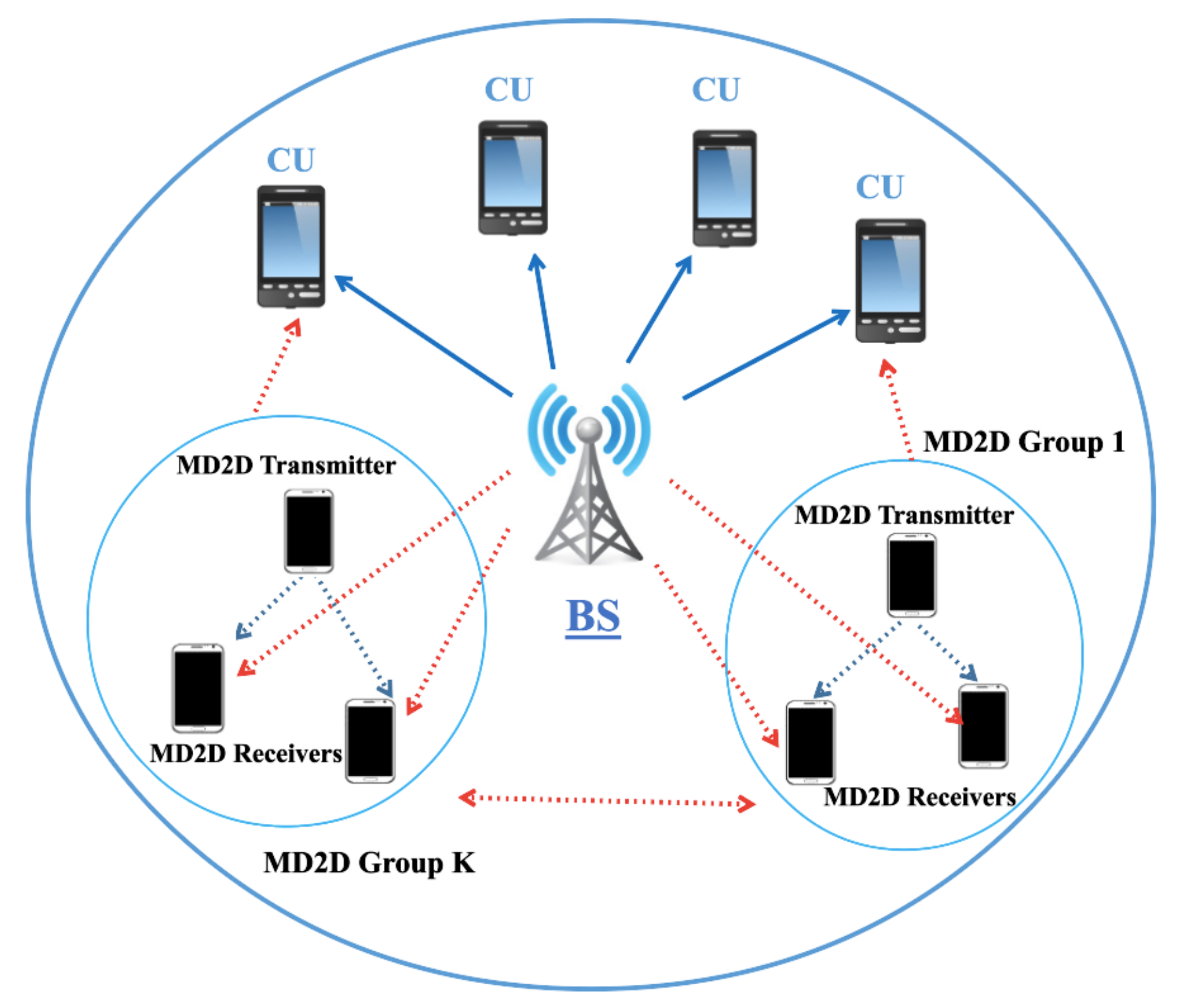
3.1. System Model
- The CU interference is caused by the BS transmissions to the CU(s) over the channel(s) used by the MD2D group at the same time.
- The inter-groups interference is caused by the transmitters on those MD2D groups that are reusing the channel(s) the MD2D group is also accessing.
3.2. Channel Model
3.3. Resource Allocation Problem
4. Resource Allocation: Power Control and Channel Assignment
4.1. Power Control Algorithm
| Algorithm 1: Optimal power control for GEE and MMF-EE (Dinkelbach’s algorithm). |
|
4.2. Centralized Channel Assignment: Matching Theory
4.2.1. Channel Assignment Algorithm
- One-to-One Matching: A one-to-one match is a mapping from to itself such that, for any , if , then , and, if for some , then . The partner is referred to as if . The preference function for setting the matching uses the received aggregate interference on each MD2D group given byfor channel m. In an analogous form, the aggregated interference seen by each CU user isSince is additive, we isolate the contribution of the MD2D group by denoting , or, equivalently, setting and , in (12). Then, the preference relationship is defined as follows: (i) group prefers channel to if ; and (ii) user prefers group to if . Note that, if a channel m is empty, then , and, when group is forbidden to transmit on any channel, .
- Many-to-One Matching: A many-to-one match is a mapping from to itself such that, for each , if , then , and, if for some , then . The partner is referred to as if . For many-to-one matches, the preference relationship is similarly defined as follows: (i) transmitter in prefers channel to channel if ; and (ii) user prefers to if ; (iii) , where r is channel m’s reuse factor.
- Many-to-Many Matching: For matches between arbitrary subsets of and , the following preference relationship is defined by: (i) prefers channel to if ; (ii) user prefers to if ; (iii) , where r is channel m’s reuse factor; and (iv) , where s is group ’s split factor.
| Algorithm 2: NOMA interference-based matching algorithm. |
|
4.2.2. Stability
4.3. Distributed Channel Assignment: Coalition Formation
- 1.
- is the set of players, with and denoting the sets of CUs and MD2D groups.
- 2.
- is the valuation function that gives the value of a coalition in a game. This is a set function that maps each to real non-negative number interpreted as the absolute value of the coalition.
- 3.
- is the set of formed coalitions namely the coalition structure. Here, each coalition is a subset of (, for ).
- Merge coalitions
- Any subset of coalitions may be merged whenever the merged form is preferred by the players. The preference relationship is the same defined in Section 4.2.1 for the centralized solution approach.
- Split coalitions
- Any coalition may be split whenever the split form is preferred by the players.
- 1.
- The weakest receiver in group suffers less individual interference if the group is moved to (recall the the receiver with the poorest channel sets the transmission rate for the group).
- 2.
- The total mutual interference of coalition does not increase: . This condition is essential for guaranteeing convergence of the algorithm. It simply states that movements among coalitions are allowed only if they improve the local value of the coalition.
- 3.
- The new coalition structure results in less total interference than the current one: is preferred to . In other words, only movements that also improve the total value of the network are approved.
4.4. Algorithmic Complexity
| Algorithm 3: NOMA based merge-and-split for the coalitional game. |
|
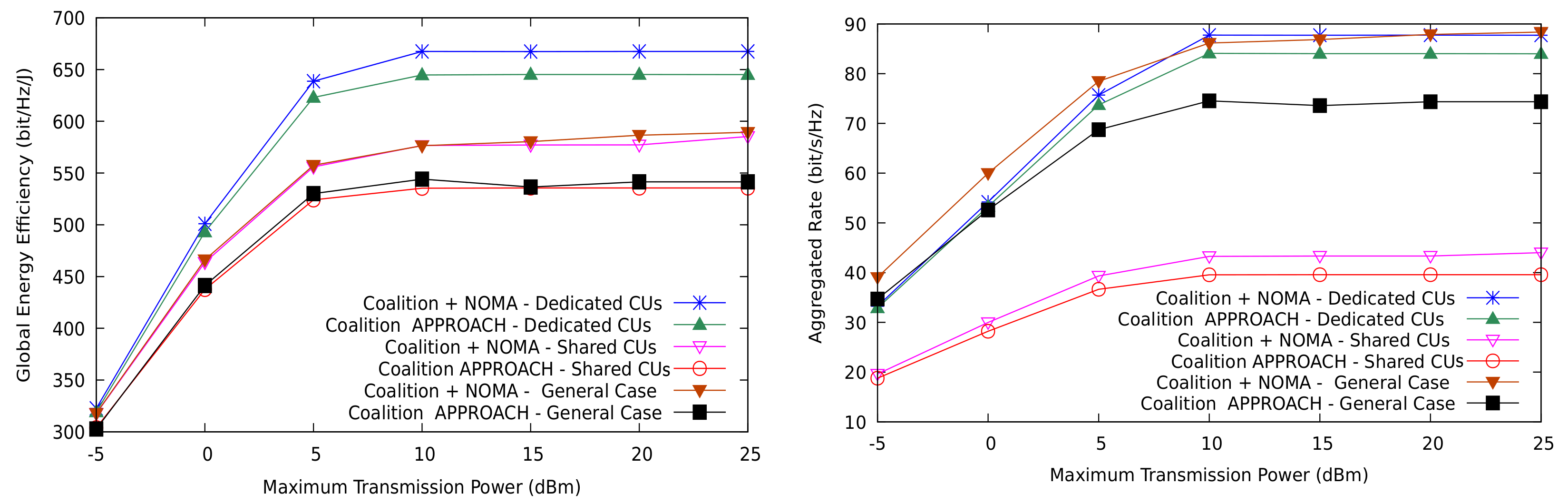
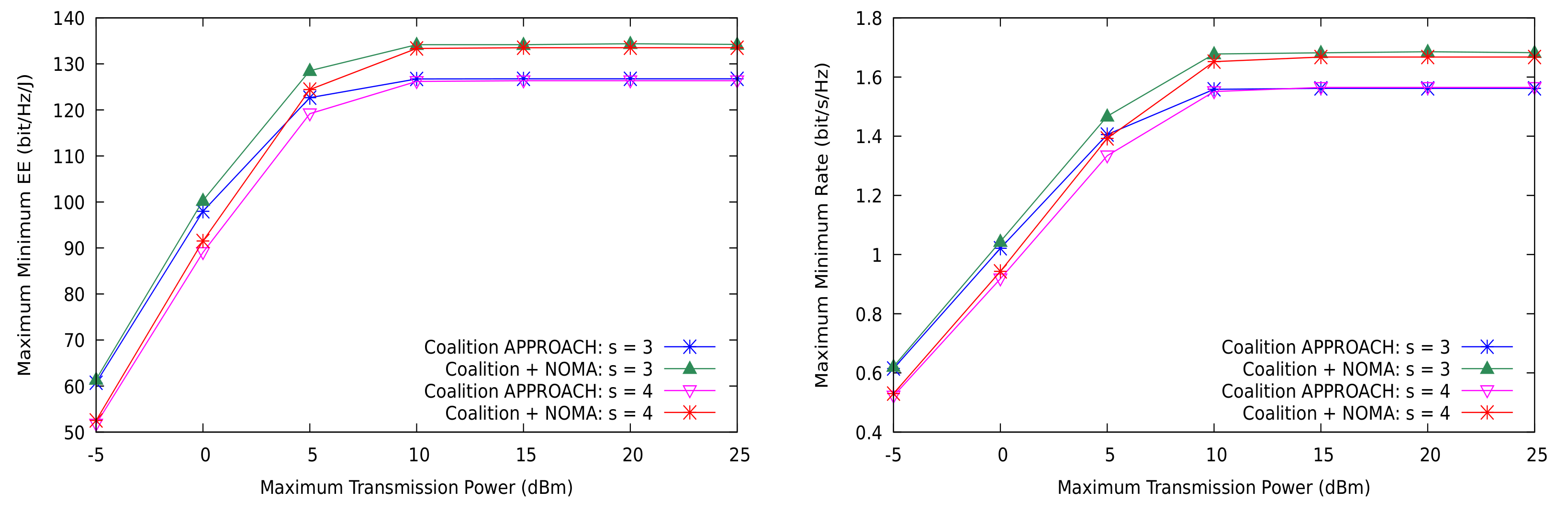
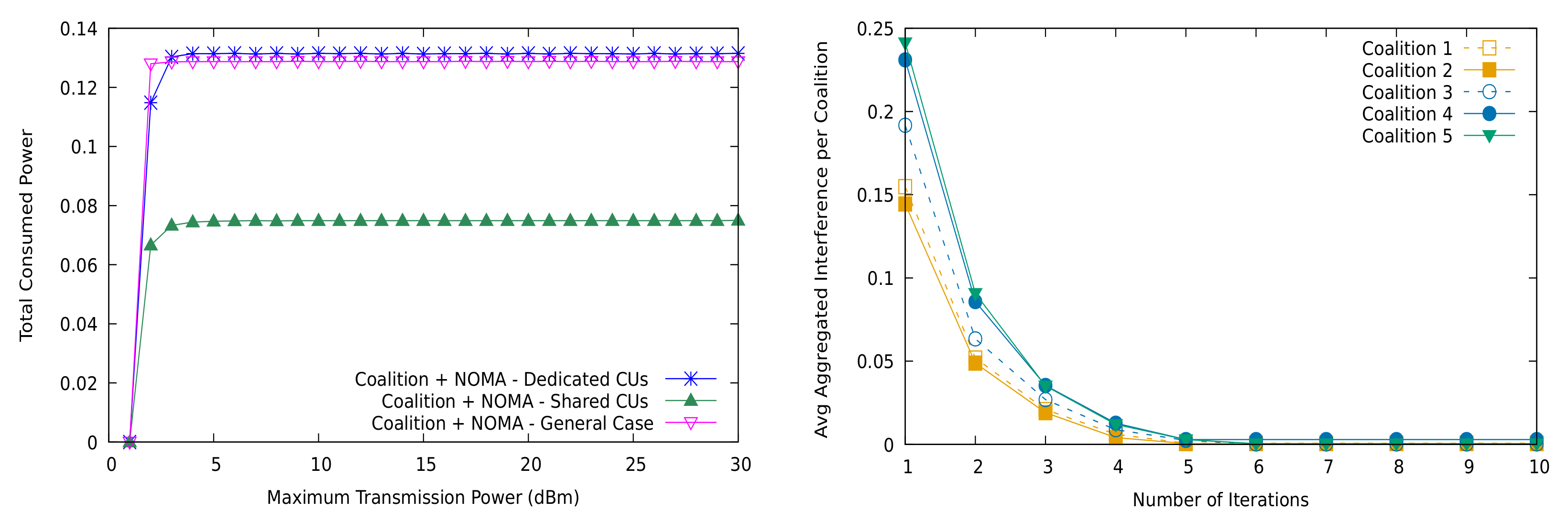
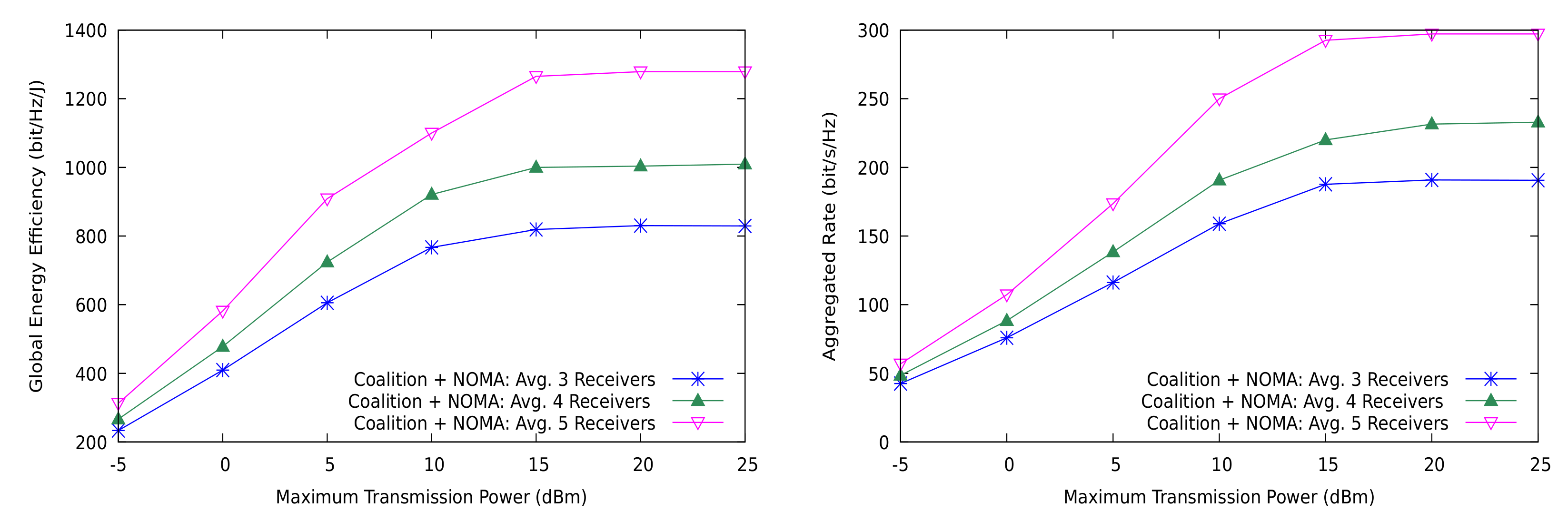
5. Numerical Results
5.1. Distributed Resource Allocation
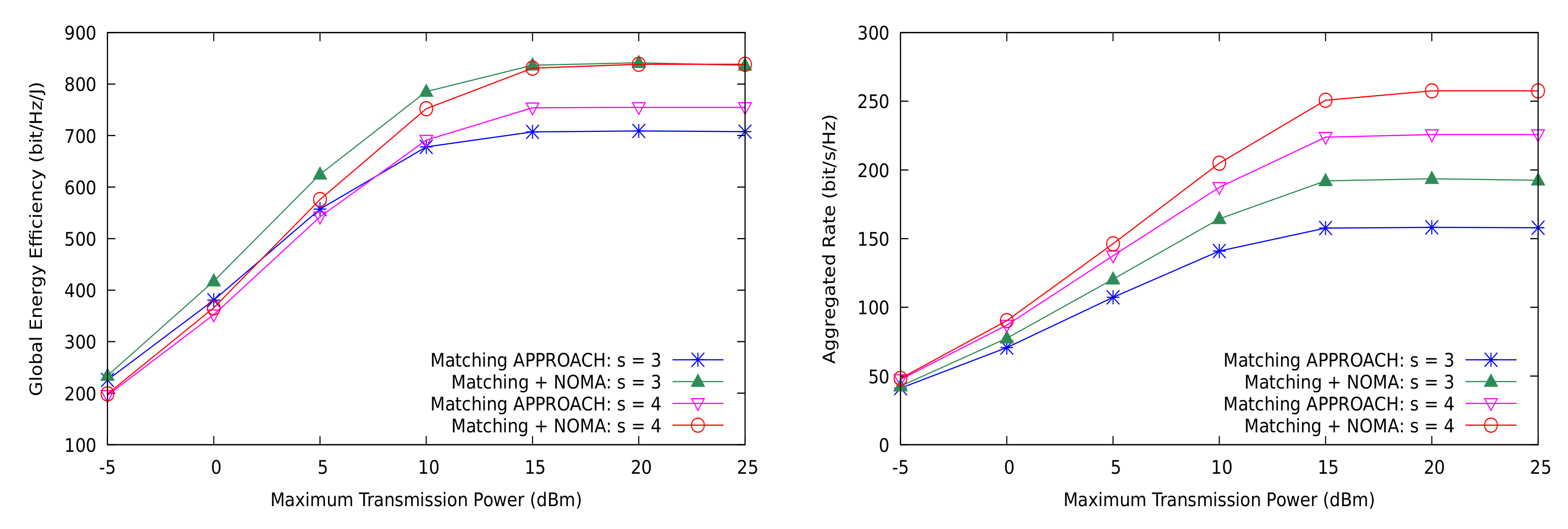
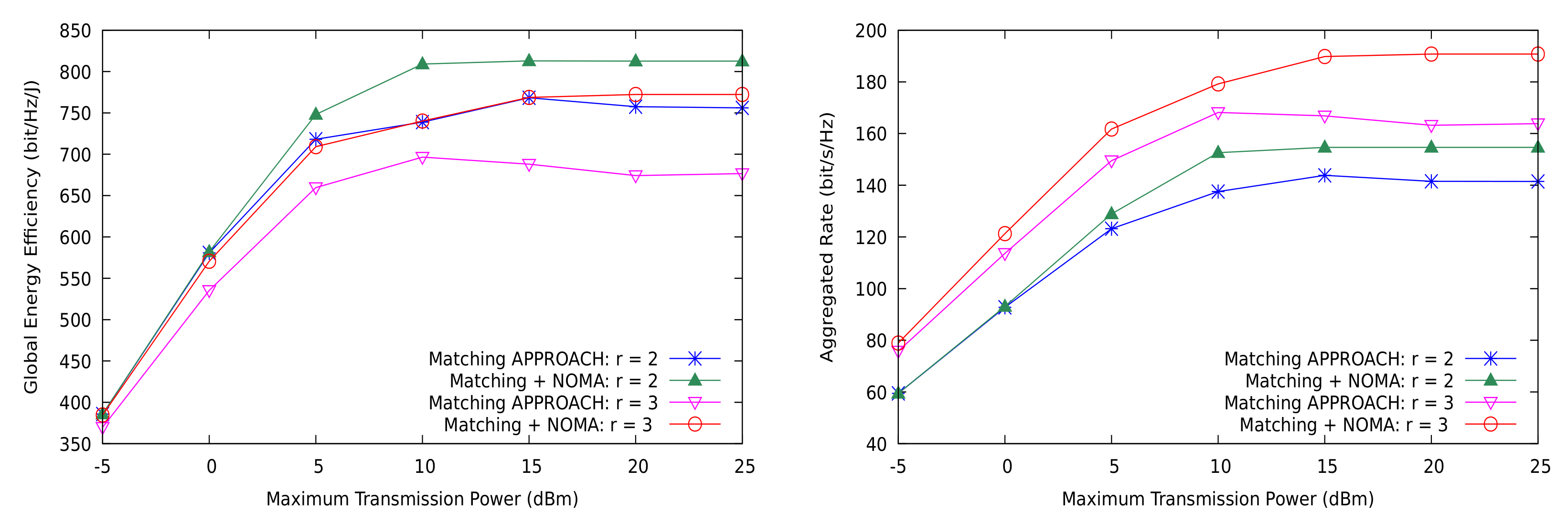
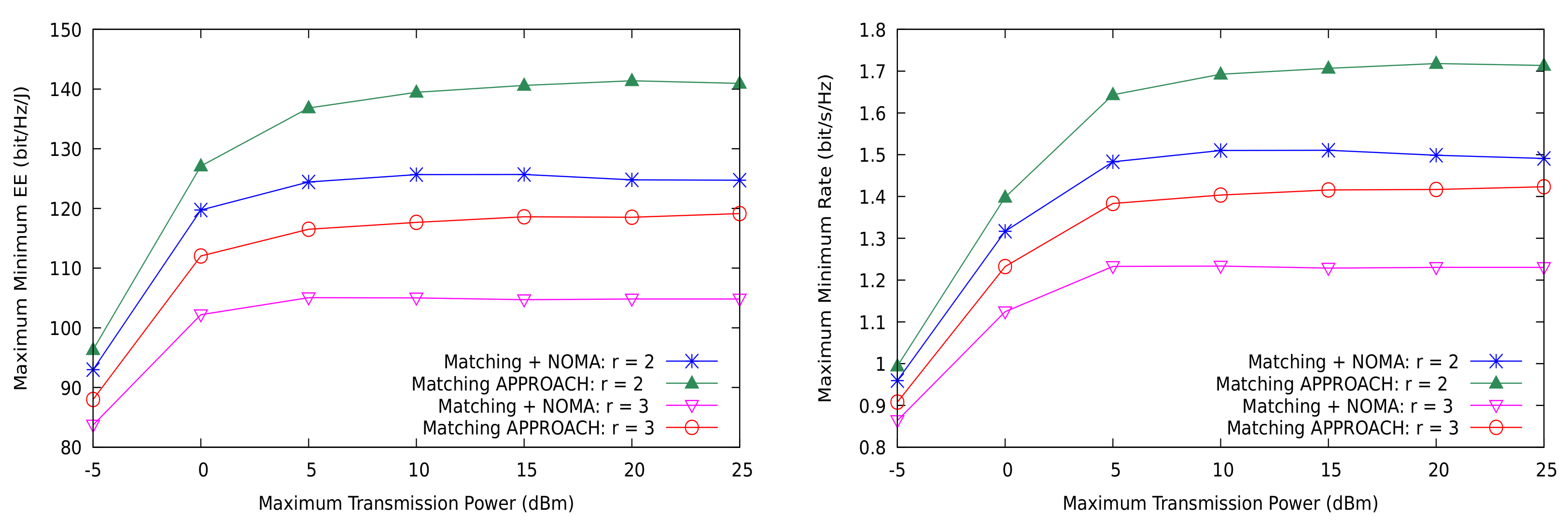
5.2. Comparison to Optimal Resource Allocation
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Agiwal, M.; Roy, A.; Saxena, N. Next generation 5G wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Meshgi, H.; Zhao, D.; Zheng, R. Optimal Resource Allocation in Multicast Device-to-Device Communications Underlaying LTE Networks. IEEE Trans. Veh. Technol. 2017, 66, 8357–8371. [Google Scholar] [CrossRef]
- Ye, Q.; Al-Shalash, M.; Caramanis, C.; Andrews, J.G. Distributed Resource Allocation in Device-to-Device Enhanced Cellular Networks. IEEE Trans. Commun. 2015, 63, 441–454. [Google Scholar] [CrossRef]
- Hmila, M.; Fernandez-Veiga, M.; Perez, M.R.; Herreria-Alonso, S. Distributed Energy Efficient Channel Allocation in Underlay Multicast D2D Communications. IEEE Trans. Mob. Comput. 2020. [Google Scholar] [CrossRef]
- Elnourani, M.; Deshmukh, S.; Beferull-Lozano, B. Distributed Resource Allocation in Underlay Multicast D2D Communications. IEEE Trans. Commun. 2021. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-lin, I.; Wang, Z. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.; Chih-Lin, I.; Poor, H.V. Application of Non-Orthogonal Multiple Access in LTE and 5G Networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Cover, T. Broadcast channels. IEEE Trans. Inf. Theory 1972, 18, 2–14. [Google Scholar] [CrossRef]
- Li, J.; Huang, S. Delay-Aware Power Control for D2D Communication With Successive Interference Cancellation and Hybrid Energy Source. IEEE Wirel. Commun. Lett. 2017, 6, 806–809. [Google Scholar] [CrossRef]
- Kazmi, S.M.A.; Tran, N.H.; Ho, T.M.; Manzoor, A.; Niyato, D.; Hong, C.S. Coordinated Device-to-Device Communication With Non-Orthogonal Multiple Access in Future Wireless Cellular Networks. IEEE Access 2018, 6, 39860–39875. [Google Scholar] [CrossRef]
- Ali, M.S.; Tabassum, H.; Hossain, E. Dynamic User Clustering and Power Allocation for Uplink and Downlink Non-Orthogonal Multiple Access (NOMA) Systems. IEEE Access 2016, 4, 6325–6343. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M. Joint Subchannel and Power Allocation for NOMA Enhanced D2D Communications. IEEE Trans. Commun. 2017, 65, 5081–5094. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal Multiple Access for 5G and Beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef]
- Shin, W.; Vaezi, M.; Lee, B.; Love, D.J.; Lee, J.; Poor, H.V. Non-Orthogonal Multiple Access in Multi-Cell Networks: Theory, Performance, and Practical Challenges. IEEE Commun. Mag. 2017, 55, 176–183. [Google Scholar] [CrossRef]
- Zeng, M.; Yadav, A.; Dobre, O.A.; Tsiropoulos, G.I.; Poor, H.V. Capacity Comparison Between MIMO-NOMA and MIMO-OMA With Multiple Users in a Cluster. IEEE J. Sel. Areas Commun. 2017, 35, 2413–2424. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, L.; Ng, D.W.K.; Yuan, J.; Hanzo, L. On the Performance Gain of NOMA Over OMA in Uplink Communication Systems. IEEE Trans. Commun. 2020, 68, 536–568. [Google Scholar] [CrossRef]
- Pan, Y.; Pan, C.; Yang, Z.; Chen, M. Resource allocation for D2D communications underlaying a NOMA-based cellular network. IEEE Wirel. Commun. Lett. 2017, 7, 130–133. [Google Scholar] [CrossRef]
- Baidas, M.W.; Bahbahani, M.S.; Alsusa, E.; Hamdi, K.A.; Ding, Z. Joint D2D Group Association and Channel Assignment in Uplink Multi-Cell NOMA Networks: A Matching-Theoretic Approach. IEEE Trans. Commun. 2019, 67, 8771–8785. [Google Scholar] [CrossRef]
- Hmila, M.; Fernández Veiga, M.; Rodríguez Pérez, M.; Herrería Alonso, S. Energy Efficient Power and Channel Allocation in Underlay Device to Multi Device Communications. IEEE Trans. Commun. 2019, 67, 5817–5832. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Denis, J.; Assaad, M. Interference Management in D2D. In Wiley 5G Ref: The Essential 5G Reference Online; Wiley: New York, NY, USA, 2019; pp. 1–20. [Google Scholar]
- Diao, X.; Zheng, J.; Wu, Y.; Cai, Y. Joint computing resource, power, and channel allocations for D2D-assisted and NOMA-based mobile edge computing. IEEE Access 2019, 7, 9243–9257. [Google Scholar] [CrossRef]
- Wang, J.; Song, X.; Dong, L. Resource Allocation and EE-SE Tradeoff for H-CRAN with NOMA-Based D2D Communications. KSII Trans. Internet Inf. Syst. 2020, 14. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Chai, K.K.; Chen, Y.; Elkashlan, M.; Alonso-Zarate, J. NOMA-based D2D communications: Towards 5G. In Proceedings of the 2016 IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Yoon, T.; Nguyen, T.H.; Nguyen, X.T.; Yoo, D.; Jang, B.; Nguyen, V.D. Resource allocation for NOMA-based D2D systems coexisting with cellular networks. IEEE Access 2018, 6, 66293–66304. [Google Scholar] [CrossRef]
- Alemaishat, S.; Saraereh, O.A.; Khan, I.; Choi, B.J. An efficient resource allocation algorithm for D2D communications based on NOMA. IEEE Access 2019, 7, 120238–120247. [Google Scholar] [CrossRef]
- Al-kahtani, M.S.; Ferdouse, L.; Karim, L. Energy Efficient Power Domain Non-Orthogonal Multiple Access Based Cellular Device-to-Device Communication for 5G Networks. Electronics 2020, 9, 237. [Google Scholar] [CrossRef]
- Dai, Y.; Sheng, M.; Liu, J.; Cheng, N.; Shen, X.; Yang, Q. Joint mode selection and resource allocation for D2D-enabled NOMA cellular networks. IEEE Trans. Veh. Technol. 2019, 68, 6721–6733. [Google Scholar] [CrossRef]
- Budhiraja, I.; Kumar, N.; Tyagi, S. Cross-Layer Interference Management Scheme for D2D Mobile Users Using NOMA. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Gu, W.; Zhu, Q. Stackelberg Game Based Social-Aware Resource Allocation for NOMA Enhanced D2D Communications. Electronics 2019, 8, 1360. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Dinkelbach, W. On Nonlinear Fractional Programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Zappone, A.; Bjornson, E.; Sanguinetti, L.; Jorswieck, E. Globally Optimal Energy-Efficient Power Control and Receiver Design in Wireless Networks. IEEE Trans. Signal Process. 2017, 65, 2844–2859. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, Y.; Pan, M.; Han, Z. Matching and cheating in device to device communications underlying cellular networks. IEEE J. Sel. Areas Commun. 2015, 33, 2156–2166. [Google Scholar] [CrossRef]
- Bayat, S.; Li, Y.; Song, L.; Han, Z. Matching theory: Applications in wireless communications. IEEE Signal Process. Mag. 2016, 33, 103–122. [Google Scholar] [CrossRef]
- Luo, F.L. Signal Processing for 5G; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ak, S.; Inaltekin, H.; Poor, H.V. Gaussian approximation for the downlink interference in heterogeneous cellular networks. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1611–1615. [Google Scholar] [CrossRef]
- Ak, S.; Inaltekin, H.; Poor, H.V. A Tractable Framework for the Analysis of Dense Heterogeneous Cellular Networks. IEEE Trans. Commun. 2018, 66, 3151–3171. [Google Scholar] [CrossRef]
- Hmila, M.; Fernández-Veiga, M. Energy-Efficient Power Control and Clustering in Underlay Device to Multi-device Communications. In Lecture Notes in Computer Science; Springer Nature Switzerland AG.: Cham, Switzerland, 2017; pp. 194–206. [Google Scholar] [CrossRef]
- Senel, K.; Cheng, H.V.; Bjornson, E.; Larsson, E.G. What Role can NOMA Play in Massive MIMO? IEEE J. Sel. Top. Signal Process. 2019, 13, 597–611. [Google Scholar] [CrossRef]
- Clerckx, B.; Mao, Y.; Schober, R.; Jorswieck, E.; Love, D.J.; Yuan, J.; Hanzo, L.; Li, G.Y.; Larsson, E.G.; Caire, G. Is NOMA Efficient in Multi-Antenna Networks? A Critical Look at Next Generation Multiple Access Techniques. arXiv 2021, arXiv:2101.04802. [Google Scholar]

| Ref. | Scenario | Approach | Model | Problem | Objective | NOMA |
|---|---|---|---|---|---|---|
| [17] | Dedicated CUs | Optimization | D2D pair | PC,RA | D2D sum rate | CU |
| [22] | Distributed Groups | Matching Theory | D2D group | PC,RA | Energy consumption, delay | CU |
| [25] | Distributed Groups | Optimization | D2D pair | RA,PC | Min transmission power | D2D + CUs |
| [26] | Dedicated CUs | Graph Theory | D2D group | PC,RA | D2D EE | D2D |
| [24] | Distributed Groups | Match Theory | D2D group | RA | Network sum rate | D2D + CUs |
| [28] | Dedicated CUs | Optimization | D2D pair | RA + | System sum rate | CU |
| Mode Selection | ||||||
| [29] | Dedicated CUs | Matching Theory | D2D group | RA | System sum rate | D2D |
| [30] | Dedicated CUs | Game Theory | D2D group | RA | CUs throughput | D2D |
| [18] | Dedicated CUs | Matching Theory | D2D group | PC,RA | Maximum users SINR | D2D |
| [27] | Dedicated CUs | Hungarian Algorithm | D2D pairs | PC,RA | D2D energy | D2D |
| Parameter | Value |
|---|---|
| Cell radius | 500 |
| Reuse factor (r) | |
| Network density | devices/cell |
| Split factor (s) | |
| Path loss exponent | |
| Minimum transmission rate | |
| Number of CU users (M) | |
| Maximum transmission powers | |
| Number of MD2D groups (K) | |
| Number of receivers | |
| Circuit power | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hmila, M.; Fernández-Veiga, M.; Rodríguez-Pérez, M.; Herrería-Alonso, S. Non-Orthogonal Multiple Access for Unicast and Multicast D2D: Channel Assignment, Power Allocation and Energy Efficiency. Sensors 2021, 21, 3436. https://doi.org/10.3390/s21103436
Hmila M, Fernández-Veiga M, Rodríguez-Pérez M, Herrería-Alonso S. Non-Orthogonal Multiple Access for Unicast and Multicast D2D: Channel Assignment, Power Allocation and Energy Efficiency. Sensors. 2021; 21(10):3436. https://doi.org/10.3390/s21103436
Chicago/Turabian StyleHmila, Mariem, Manuel Fernández-Veiga, Miguel Rodríguez-Pérez, and Sergio Herrería-Alonso. 2021. "Non-Orthogonal Multiple Access for Unicast and Multicast D2D: Channel Assignment, Power Allocation and Energy Efficiency" Sensors 21, no. 10: 3436. https://doi.org/10.3390/s21103436
APA StyleHmila, M., Fernández-Veiga, M., Rodríguez-Pérez, M., & Herrería-Alonso, S. (2021). Non-Orthogonal Multiple Access for Unicast and Multicast D2D: Channel Assignment, Power Allocation and Energy Efficiency. Sensors, 21(10), 3436. https://doi.org/10.3390/s21103436









