A Proposed Method to Assess the Mechanical Properties of Treadmill Surfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample
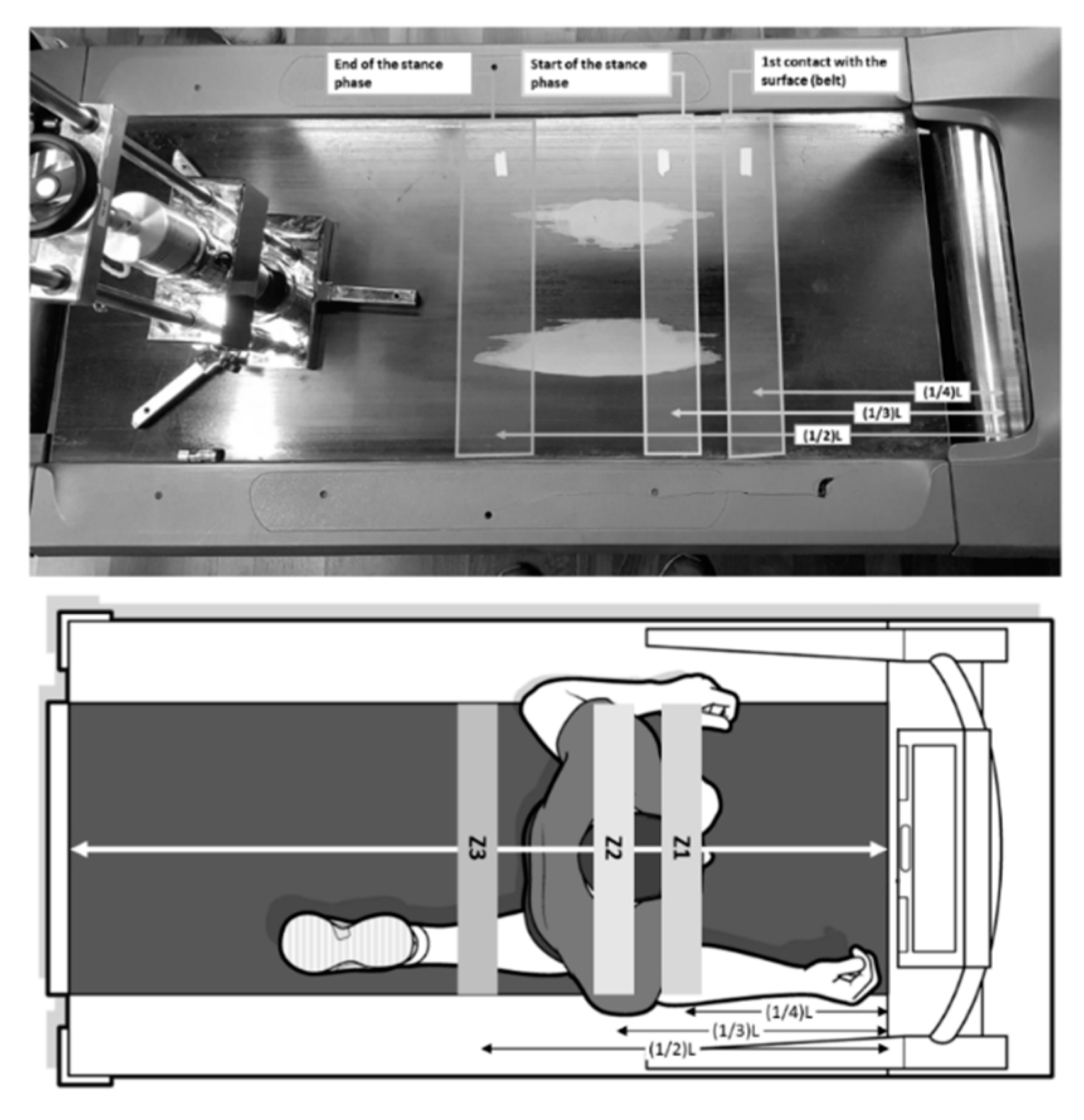
2.2. Procedures
- The apparatus was set vertically on the treadmill surface using a custom-made cart over which the AAA rested (Figure 2).
- The test foot was lowered smoothly onto the surface of the test specimen.
- A lift height of 55.00 ± 0.25 mm was set before hanging the falling mass back on the magnet, following EN 14,808 and the FIFA Handbook of Test Methods.
- First impact: After 30 (±5) seconds (to allow the test specimen to relax after removal of the test mass), the mass was dropped and the acceleration signal recorded. Within 10 s after the impact, lift height was checked before re-attaching the mass back on the magnet.
- Second impact: After 30 (±5) seconds, the mass was dropped, and the acceleration signal recorded again. Within 10 s after the impact, lift height was checked and the mass was re-attached on the magnet.
- Third impact: After 30 (±5) seconds, the mass was dropped, and the acceleration signal recorded.
2.3. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McMahon, T.A.; Greene, P.R. The influence of track compliance on running. J. Biomech. 1979, 12, 893–904. [Google Scholar] [CrossRef]
- Schrier, N.M.; Wannop, J.; Lewinson, R.T.; Worobets, J.; Stefanyshyn, D. Shoe traction and surface compliance affect performance of soccer-related movements. Footwear Sci. 2014, 6, 69–80. [Google Scholar] [CrossRef]
- Baroud, G.; Nigg, B.M.; Stefanyshyn, D. Energy storage and return in sport surfaces. Sports Eng. 1999, 2, 173–180. [Google Scholar] [CrossRef]
- Kerdok, A.E.; Biewener, A.A.; McMahon, T.A.; Weyand, P.G.; Herr, H.M. Energetics and mechanics of human running on surfaces of different stiffnesses. J. Appl. Physiol. 2002, 92, 469–478. [Google Scholar] [CrossRef]
- Van Hooren, B.; Fuller, J.T.; Buckley, J.D.; Miller, J.R.; Sewell, K.; Rao, G.; Barton, C.; Bishop, C.; Willy, R.W. Is Motorized Treadmill Running Biomechanically Comparable to Overground Running? A Systematic Review and Meta-Analysis of Cross-Over Studies. Sports Med. 2020, 50, 785–813. [Google Scholar] [CrossRef] [PubMed]
- Stefanyshyn, D.; Nigg, B. Energy and performance aspects in sports surfaces. In Sport Surfaces–Biomechanics, Injuries, Performance, Testing and Installation; Nigg, B., Cole, G., Stefanyshyn, D., Eds.; Topline Printing: Calgary, AB, Canada, 2003; pp. 31–46. [Google Scholar]
- Di Michele, R.; Di Renzo, A.M.; Ammazzalorso, S.; Merni, F. Comparison of Physiological Responses to an Incremental Running Test on Treadmill, Natural Grass, and Synthetic Turf in Young Soccer Players. J. Strength Cond. Res. 2009, 23, 939–945. [Google Scholar] [CrossRef] [PubMed]
- Sassi, A.; Stefanescu, A.; Menaspà, P.; Bosio, A.; Riggio, M.; Rampinini, E. The Cost of Running on Natural Grass and Artificial Turf Surfaces. J. Strength Cond. Res. 2011, 25, 606–611. [Google Scholar] [CrossRef] [PubMed]
- Farhang, B.; Araghi, F.R.; Bahmani, A.; Moztarzadeh, F.; Shafieian, M. Landing impact analysis of sport surfaces using three-dimensional finite element model. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2016, 230, 180–185. [Google Scholar] [CrossRef]
- McGhie, D.; Ettema, G. Biomechanical Analysis of Surface-Athlete Impacts on Third-Generation Artificial Turf. Am. J. Sports Med. 2012, 41, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Shorten, M.R.; Himmelsbach, J.A. In Shock attenuation of sports surfaces. In Proceedings of the 4th International Conference on the Engineering of Sport, Kyoto, Japan, 3–6 September 2002; Ujihashi, U., Haake, S.J., Eds.; Blackwell Science: Kyoto, Japan, 2002; pp. 152–159. [Google Scholar]
- CEN. EN 14877: 2013 Synthetic Surfaces for Outdoor Sports Areas—Specification; CEN: Brussels, Belgium, 2013. [Google Scholar]
- IAAF. IAAF Track and Runway Synthetic Surface Testing Specifications; IAAF: Stockholm, Sweden, 2016. [Google Scholar]
- CEN. EN 15330-1: 2014 Surfaces for Sports Areas—Synthetic Turf and Needle-Punched Surfaces Primarily Designed for Outdoor Use—Part 1: Specification for Synthetic Turf Surfaces for Football, Hockey, Rugby Union Training, Tennis and Multi-Sports Use; CEN: Brussels, Belgium, 2013. [Google Scholar]
- FIFA. FIFA Quality Programme for Football Turf. Handbook of Test Methods. V3.0; FIFA: Zürich, Switzerland, 2015. [Google Scholar]
- Running USA 2017 National Runner Survey. 2017. Available online: https://www.runningusa.org/RUSA/Research/Recent_Surveys/National_Runner_Survey.aspx?WebsiteKey=9842e655-a213-4bae-9401-5ff3ac06e6da (accessed on 10 May 2018).
- CEN. EN 957-6: 2010+A1:2014 Stationary Training Equipment—Part 6: Treadmills, Additional Specific Safety Requirements and Test Methods; CEN: Brussels, Belgium, 2014. [Google Scholar]
- Asmussen, M.J.; Kaltenbach, C.; Hashlamoun, K.; Shen, H.; Federico, S.; Nigg, B.M. Force measurements during running on different instrumented treadmills. J. Biomech. 2019, 84, 263–268. [Google Scholar] [CrossRef] [PubMed]
- Colino, E.; Garcia-Unanue, J.; Gallardo, L.; Foster, C.; Lucia, A.; Felipe, J.L. Mechanical Properties of Treadmill Surfaces and Their Effects on Endurance Running. Int. J. Sports Physiol. Perform. 2020, 15, 685–689. [Google Scholar] [CrossRef] [PubMed]
- Hardin, E.C.; Bogert, A.J.V.D.; Hamill, J. Kinematic Adaptations during Running: Effects of Footwear, Surface, and Duration. Med. Sci. Sports Exerc. 2004, 36, 838–844. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.M.; Doust, J.H. A 1% treadmill grade most accurately reflects the energetic cost of outdoor running. J. Sports Sci. 1996, 14, 321–327. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.; McKerrow, A.D.; Kohn, T.A. Metabolic cost of running is greater on a treadmill with a stiffer running platform. J. Sports Sci. 2016, 35, 1–6. [Google Scholar] [CrossRef] [PubMed]
- FIH. FIH Hockey Turf and Field Standards; Part 3. Requirements for Hockey Fields; FIH: Lausanne, Switzerland, 2017. [Google Scholar]
- World Rugby. Rugby Turf Performance Specification; World Rugby: Dublin, Ireland, 2016. [Google Scholar]
- Colino, E.; Sanchez-Sanchez, J.; Garcia-Unanue, J.; Ubago-Guisado, E.; Haxaire, P.; Le Blan, A.; Gallardo, L. Validity and reliability of two standard test devices in assessing mechanical properties of different sport surfaces. Polym. Test. 2017, 62, 61–67. [Google Scholar] [CrossRef]
- Buchheit, M.; Allen, A.; Poon, T.K.; Modonutti, M.; Gregson, W.; Di Salvo, V. Integrating different tracking systems in football: Multiple camera semi-automatic system, local position measurement and GPS technologies. J. Sports Sci. 2014, 32, 1844–1857. [Google Scholar] [CrossRef]
- Koo, T.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Nigg, B.M.; De Boer, R.W.; Fisher, V. A kinematic comparison of overground and treadmill running. Med. Sci. Sports Exerc. 1995, 27, 98–105. [Google Scholar] [CrossRef]
- Schache, A.G.; Blanch, P.D.; Rath, D.A.; Wrigley, T.V.; Starr, R.; Bennell, K.L. A comparison of overground and treadmill running for measuring the three-dimensional kinematics of the lumbo–pelvic–hip complex. Clin. Biomech. 2001, 16, 667–680. [Google Scholar] [CrossRef]
- Butler, R.J.; Crowell, H.P.; Davis, I.M. Lower extremity stiffness: Implications for performance and injury. Clin. Biomech. 2003, 18, 511–517. [Google Scholar] [CrossRef]
- Milgrom, C.; Finestone, A.S.; Segev, S.; Olin, C.; Arndt, T.; Ekenman, I. Are overground or treadmill runners more likely to sustain tibial stress fracture? Br. J. Sports Med. 2003, 37, 160–163. [Google Scholar] [CrossRef] [PubMed]
- Arampatzis, A.; Stafylidis, S.; Morey-Klapsing, G.; Bürggemann, G.-P. Interaction of the Human Body and Surfaces of Different Stiffness during Drop Jumps. Med. Sci. Sports Exerc. 2004, 36, 451–459. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.; MacIntosh, B.R. Running Economy from a Muscle Energetics Perspective. Front. Physiol. 2017, 8, 433. [Google Scholar] [CrossRef] [PubMed]
- Lejeune, T.M.; Willems, P.A.; Heglund, N.C. Mechanics and energetics of human locomotion on sand. J. Exp. Biol. 1998, 201, 2071–2080. [Google Scholar]
- Pinnington, H.C.; Dawson, B. The energy cost of running on grass compared to soft dry beach sand. J. Sci. Med. Sport 2001, 4, 416–430. [Google Scholar] [CrossRef]
- Sánchez-Sánchez, J.; Guerrero, A.M.G.; García-Gallart, A.; Sánchez-Sáez, J.A.; Felipe, J.L.; Encarnación-Martínez, A. Influence of the structural components of artificial turf systems on impact attenuation in amateur football players. Sci. Rep. 2019, 9, 7774. [Google Scholar] [CrossRef]
- Sanchez-Sanchez, J.; García-Unanue, J.; Jiménez-Reyes, P.; Gallardo, A.; Burillo, P.; Felipe, J.; Gallardo, L. Influence of the Mechanical Properties of Third-Generation Artificial Turf Systems on Soccer Players’ Physiological and Physical Performance and Their Perceptions. PLoS ONE 2014, 9, e111368. [Google Scholar] [CrossRef]
- Miller, J.R.; Van Hooren, B.; Bishop, C.; Buckley, J.D.; Willy, R.W.; Fuller, J.T. A Systematic Review and Meta-Analysis of Crossover Studies Comparing Physiological, Perceptual and Performance Measures Between Treadmill and Overground Running. Sports Med. 2019, 49, 763–782. [Google Scholar] [CrossRef]
- Shi, H.; Li, H.; Liu, H.; Yu, B. Effects of treadmill cushion and running speed on plantar force and metabolic energy consumption in running. Gait Posture 2019, 69, 79–84. [Google Scholar] [CrossRef]
- Dixon, S.J.; Collop, A.C.; Batt, M.E. Surface effects on ground reaction forces and lower extremity kinematics in running. Med. Sci. Sports Exerc. 2000, 32, 1919–1926. [Google Scholar] [CrossRef]
- Dixon, S.J.; Stiles, V. Impact absorption of tennis shoe-surface combinations. Sports Eng. 2003, 6, 1–9. [Google Scholar] [CrossRef]
- Nigg, B.M.; Yeadon, M.R. Biomechanical aspects of playing surfaces. J. Sports Sci. 1987, 5, 117–145. [Google Scholar] [CrossRef] [PubMed]
- Yukawa, H.; Aduma, R.; Kawamura, S.; Kobayashi, K. Shock attenuation properties of sports surfaces with two dimensional impact test. Procedia Eng. 2012, 34, 855–860. [Google Scholar] [CrossRef]


| T-Jog | T-Run | L-97T | L-DX | Total | ||
|---|---|---|---|---|---|---|
| Zone 1 | SA (%) | 61.5 ± 2.3 | 64.8 ± 1.0 | 67.9 ± 0.9 | 68.1 ± 0.6 | 65.6 ± 3.0 |
| VD (mm) | 7.8 ± 0.7 | 7.0 ± 0.4 | 9.8 ± 0.4 | 8.7 ± 0.2 | 8.3 ± 1.2 | |
| ER (%) | 39.9 ± 8.1 | 35.3 ± 4.6 | 54.1 ± 4.6 | 54.6 ± 2.3 | 45.5 ± 10.1 | |
| Zone 2 | SA (%) | 63.3 ± 1.5 | 65.3 ± 1.0 | 67.6 ± 0.9 | 68.3 ± 1.0 | 66.1 ± 2.2 |
| VD (mm) | 6.1 ± 0.3 | 6.7 ± 0.4 | 9.4 ± 0.3 | 8.5 ± 0.2 | 7.6 ± 1.4 | |
| ER (%) | 35.4 ± 4.8 | 42.1 ± 6.8 | 58.5 ± 3.3 | 50.3 ± 3.6 | 46.6 ± 10.0 | |
| Zone 3 | SA (%) | 62.0 ± 2.1 | 63.5 ± 1.8 | 66.0 ± 0.8 | 66.7 ± 1.4 | 64.5 ± 2.4 |
| VD (mm) | 5.7 ± 0.3 | 7.7 ± 0.6 | 9.6 ± 0.3 | 8.5 ± 0.2 | 7.9 ± 1.5 | |
| ER (%) | 42.5 ± 5.0 | 40.8 ± 3.9 | 62.0 ± 2.3 | 52.9 ± 5.2 | 49.3 ± 9.7 |
| Mean Difference | p-Value | SD of the Mean Difference | ICC | 95% CI | SEM | ||
|---|---|---|---|---|---|---|---|
| Lower | Upper | ||||||
| Zone 1 | |||||||
| SA (%) | −0.1 | 0.314 | 0.2 | 0.997 | 0.995 | 0.999 | 0.01 |
| VD (mm) | 0.0 | 0.057 | 0.1 | 0.997 | 0.994 | 0.998 | 0.00 |
| ER (%) | 0.2 | 1.000 | 1.2 | 0.993 | 0.988 | 0.996 | 0.10 |
| Zone 2 | |||||||
| SA (%) | 0.1 | 1.000 | 0.4 | 0.984 | 0.970 | 0.991 | 0.05 |
| VD (mm) | 0.0 | 0.020 | 0.1 | 0.998 | 0.996 | 0.999 | 0.00 |
| ER (%) | 0.0 | 1.000 | 0.8 | 0.997 | 0.995 | 0.998 | 0.04 |
| Zone 3 | |||||||
| SA (%) | 0.0 | 1.000 | 0.4 | 0.987 | 0.977 | 0.993 | 0.04 |
| VD (mm) | 0.0 | 0.052 | 0.1 | 0.998 | 0.995 | 0.999 | 0.00 |
| ER (%) | 0.0 | 1.000 | 1.3 | 0.992 | 0.985 | 0.996 | 0.11 |
| Mean Difference | p-Value | SD of the Mean Difference | ICC | 95% CI | SEM | ||
|---|---|---|---|---|---|---|---|
| Lower | Upper | ||||||
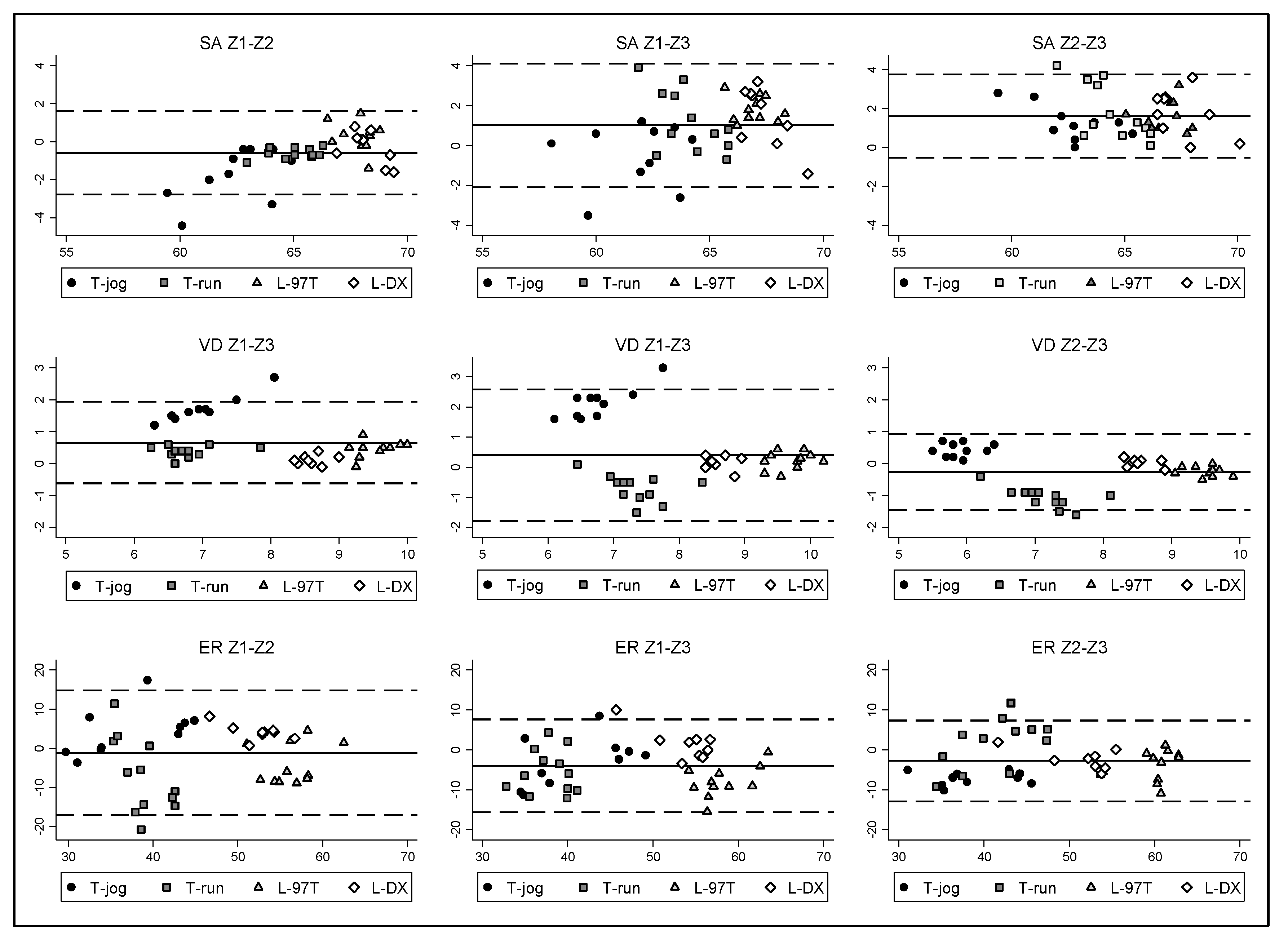
| SA (%) | |||||||
| Z1 vs. Z2 | −0.6 | 0.888 | 1.1 | 0.889 | 0.751 | 0.946 | 0.37 |
| Z1 vs. Z3 | 1.0 | 0.216 | 1.6 | 0.778 | 0.487 | 0.895 | 0.74 |
| Z2 vs. Z3 | 1.6 | 0.015 | 1.1 | 0.728 | −0.048 | 0.914 | 0.57 |
| VD (mm) | |||||||
| Z1 vs. Z2 | 0.7 | 0.082 | 0.7 | 0.771 | 0.186 | 0.915 | 0.31 |
| Z1 vs. Z3 | 0.4 | 0.533 | 1.1 | 0.630 | 0.400 | 0.784 | 0.68 |
| Z2 vs. Z3 | −0.3 | 1.000 | 0.6 | 0.898 | 0.796 | 0.947 | 0.19 |
| ER (%) | |||||||
| Z1 vs. Z2 | −1.2 | 1.000 | 8.1 | 0.673 | 0.468 | 0.809 | 4.64 |
| Z1 vs. Z3 | −4.0 | 0.201 | 5.9 | 0.763 | 0.439 | 0.890 | 2.89 |
| Z2 vs. Z3 | −2.8 | 0.598 | 5.2 | 0.834 | 0.641 | 0.918 | 2.11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colino, E.; Garcia-Unanue, J.; Van Hooren, B.; Gallardo, L.; Meijer, K.; Lucia, A.; Felipe, J.L. A Proposed Method to Assess the Mechanical Properties of Treadmill Surfaces. Sensors 2020, 20, 2724. https://doi.org/10.3390/s20092724
Colino E, Garcia-Unanue J, Van Hooren B, Gallardo L, Meijer K, Lucia A, Felipe JL. A Proposed Method to Assess the Mechanical Properties of Treadmill Surfaces. Sensors. 2020; 20(9):2724. https://doi.org/10.3390/s20092724
Chicago/Turabian StyleColino, Enrique, Jorge Garcia-Unanue, Bas Van Hooren, Leonor Gallardo, Kenneth Meijer, Alejandro Lucia, and Jose Luis Felipe. 2020. "A Proposed Method to Assess the Mechanical Properties of Treadmill Surfaces" Sensors 20, no. 9: 2724. https://doi.org/10.3390/s20092724
APA StyleColino, E., Garcia-Unanue, J., Van Hooren, B., Gallardo, L., Meijer, K., Lucia, A., & Felipe, J. L. (2020). A Proposed Method to Assess the Mechanical Properties of Treadmill Surfaces. Sensors, 20(9), 2724. https://doi.org/10.3390/s20092724










