A Subject-Specific Approach to Detect Fatigue-Related Changes in Spine Motion Using Wearable Sensors
Abstract
1. Introduction
2. Methods
2.1. Participants
2.2. Instrumentation
2.3. Fatiguing Protocol
2.4. Data Processing
2.5. Data Analysis
2.5.1. Continuous Relative Phase
2.5.2. Repetition Time
2.5.3. Orientation Range, Peak Orientation, Angular Velocity, and Angular Acceleration
2.5.4. Spine Motion Composite Index
2.5.5. Statistical Analyses
3. Results
3.1. Participants
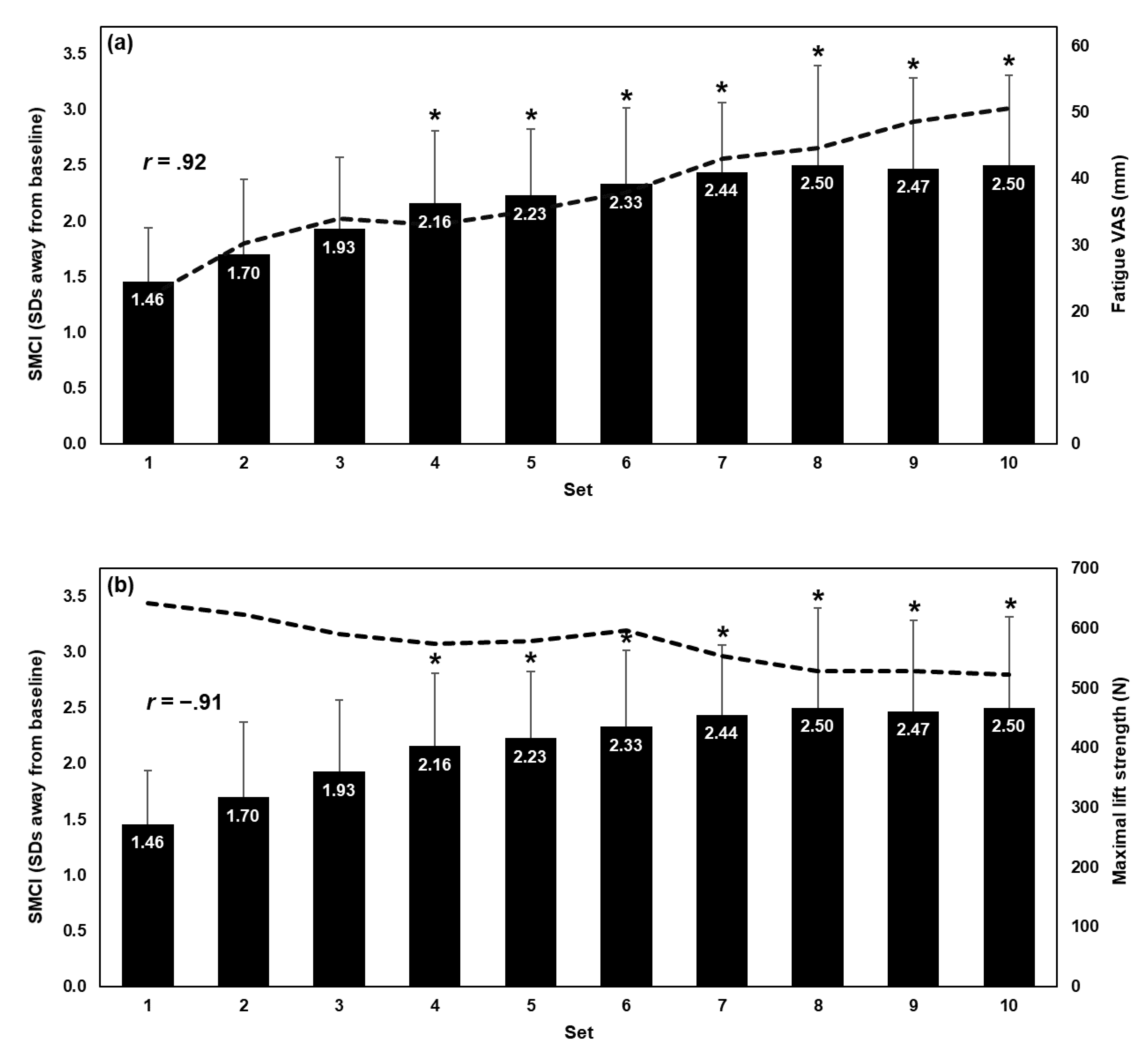
3.2. Influence of Fatiguing Set on Spine Motion Composite Index
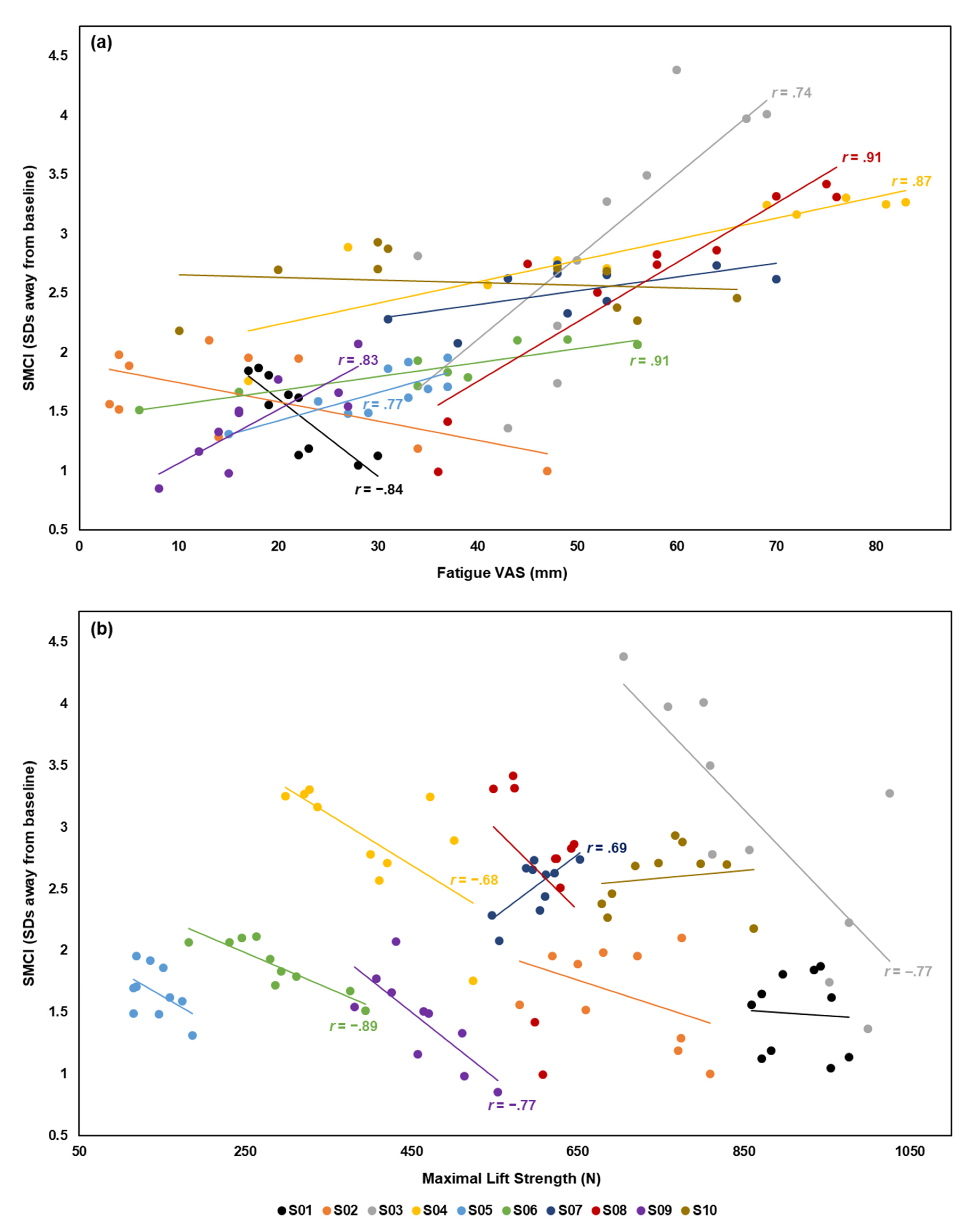
3.3. Correlation Between Spine Motion Composite Index and Fatigue Measures
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


References
- Vøllestad, N.K. Measurement of human muscle fatigue. J. Neurosci. Methods 1997, 74, 219–227. [Google Scholar] [CrossRef]
- Place, N.; Yamada, T.; Bruton, J.D.; Westerblad, H. Muscle fatigue: From observations in humans to underlying mechanisms studied in intact single muscle fibres. Eur. J. Appl. Physiol. 2010, 110, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Cowley, J.C.; Gates, D.H. Inter-joint coordination changes during and after muscle fatigue. Hum. Mov. Sci. 2017, 56, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Cowley, J.C.; Gates, D.H. Proximal and distal muscle fatigue differentially affect movement coordination. PLoS ONE 2017, 12, e0172835. [Google Scholar] [CrossRef] [PubMed]
- Asgari, N.; Sanjari, M.A.; Esteki, A. Local dynamic stability of the spine and its coordinated lower joints during repetitive Lifting: Effects of fatigue and chronic low back pain. Hum. Mov. Sci. 2017, 54, 339–346. [Google Scholar] [CrossRef] [PubMed]
- Gorelick, M.; Brown, J.M.M.; Groeller, H. Short-duration fatigue alters neuromuscular coordination of trunk musculature: Implications for injury. Appl. Ergon. 2003, 34, 317–325. [Google Scholar] [CrossRef]
- Dugan, S.A.; Frontera, W.R. Muscle fatigue and muscle injury. Phys. Med. Rehabil. Clin. 2000, 11, 385–403. [Google Scholar] [CrossRef]
- Antwi-Afari, M.F.; Li, H.; Edwards, D.J.; Pärn, E.A.; Seo, J.; Wong, A.Y.L. Biomechanical analysis of risk factors for work-related musculoskeletal disorders during repetitive lifting task in construction workers. Autom. Constr. 2017, 83, 41–47. [Google Scholar] [CrossRef]
- Younan, L.; Clinton, M.; Fares, S.; Jardali, F.E.; Samaha, H. The relationship between work-related musculoskeletal disorders, chronic occupational fatigue, and work organization: A multi-hospital cross-sectional study. J. Adv. Nurs. 2019, 75, 1667–1677. [Google Scholar] [CrossRef]
- Jovanović, J.; Šarac, I.; Đinđić, N.; Jovanović, S. The influence of working conditions, health status and characteristics of workers on the occurrence of workplace injuries. Acta Med. Median. 2017, 56, 17–24. [Google Scholar] [CrossRef]
- Mizrahi, J.; Verbitsky, O.; Isakov, E. Fatigue-related loading imbalance on the shank in running: A possible factor in stress fractures. Ann. Biomed. Eng. 2000, 28, 463–469. [Google Scholar] [CrossRef] [PubMed]
- Mehrdad, R.; Shams-Hosseini, N.S.; Aghdaei, S.; Yousefian, M. Prevalence of low back pain in health care workers and comparison with other occupational categories in Iran: A systematic review. Iran. J. Med. Sci. 2016, 41, 467–478. [Google Scholar]
- Oranye, N.O.; Bennett, J. Prevalence of work-related musculoskeletal and non-musculoskeletal injuries in health care workers: The implications for work disability management. Ergonomics 2018, 61, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Kassebaum, N.J.; Arora, M.; Barber, R.M.; Brown, J.; Carter, A.; Casey, D.C.; Charlson, F.J.; Coates, M.M.; Coggeshall, M.; Cornaby, L.; et al. Global, regional, and national disability-adjusted life-years (DALYs) for 315 diseases and injuries and healthy life expectancy (HALE), 1990–2015: A systematic analysis for the Global Burden of Disease Study 2015. Lancet 2016, 388, 1603–1658. [Google Scholar] [CrossRef]
- Aaronson, L.S.; Teel, C.S.; Cassmeyer, V.; Neuberger, G.B.; Pallikkathayil, L.; Pierce, J.; Press, A.N.; Williams, P.D.; Wingate, A. Defining and Measuring Fatigue. Image J. Nurs. Scholarsh. 1999, 31, 45–50. [Google Scholar] [CrossRef]
- Chiarotto, A.; Maxwell, L.J.; Ostelo, R.W.; Boers, M.; Tugwell, P.; Terwee, C.B. Measurement Properties of Visual Analogue Scale, Numeric Rating Scale, and Pain Severity Subscale of the Brief Pain Inventory in Patients With Low Back Pain: A Systematic Review. J. Pain 2019, 20, 245–263. [Google Scholar] [CrossRef]
- Zemková, E.; Poór, O.; Pecho, J. Peak Rate of Force Development and Isometric Maximum Strength of Back Muscles Are Associated With Power Performance During Load-Lifting Tasks. Am. J. Mens. Health 2019, 13. [Google Scholar] [CrossRef]
- González-Izal, M.; Malanda, A.; Gorostiaga, E.; Izquierdo, M. Electromyographic models to assess muscle fatigue. J. Electromyogr. Kinesiol. 2012, 22, 501–512. [Google Scholar] [CrossRef]
- Cortes, N.; Onate, J.; Morrison, S. Differential effects of fatigue on movement variability. Gait Posture 2014, 39, 888–893. [Google Scholar] [CrossRef]
- Reenalda, J.; Maartens, E.; Homan, L.; Buurke, J.H. (Jaap. Continuous three dimensional analysis of running mechanics during a marathon by means of inertial magnetic measurement units to objectify changes in running mechanics. J. Biomech. 2016, 49, 3362–3367. [Google Scholar] [CrossRef]
- Clermont, C.A.; Benson, L.C.; Edwards, W.B.; Hettinga, B.A.; Ferber, R. New considerations for wearable technology data: Changes in running biomechanics during a marathon. J. Appl. Biomech. 2019, 35, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Kobsar, D.; Ferber, R. Wearable sensor data to track subject-specific movement patterns related to clinical outcomes using a machine learning approach. Sensors 2018, 18, 2828. [Google Scholar] [CrossRef] [PubMed]
- Saisana, M.; Tarantola, S. State-of-the-Art Report on Current Methodologies and Practices for Composite Indicator Development; Joint Research Centre, European Commission: Ispra, Italy, 2002; pp. 1–72. [Google Scholar]
- Robertson, D.G.E.; Caldwell, G.E.; Hamill, J.; Kamen, G.; Whittlesey, S.N. Dynamical Systems Analysis of Coordination. In Research Methods in Biomechanics; Human Kinetics: Champaign, IL, USA, 2014; pp. 291–315. [Google Scholar]
- Seay, J.F.; Van Emmerik, R.E.A.; Hamill, J. Low back pain status affects pelvis-trunk coordination and variability during walking and running. Clin. Biomech. 2011, 26, 572–578. [Google Scholar] [CrossRef] [PubMed]
- Silfies, S.P.; Bhattacharya, A.; Biely, S.; Smith, S.S.; Giszter, S. Trunk control during standing reach: A dynamical system analysis of movement strategies in patients with mechanical low back pain. Gait Posture 2009, 29, 370–376. [Google Scholar] [CrossRef]
- Selles, R.W.; Wagenaarb, R.C.; Smit, T.H.; Wuismane, P.I.J.M. Disorders in trunk rotation during walking in patients with low back pain: A dynamical systems approach. Clin. Biomech. 2001, 16, 175–181. [Google Scholar] [CrossRef]
- Beaudette, S.M.; Zwambag, D.P.; Graham, R.B.; Brown, S.H.M. Discriminating spatiotemporal movement strategies during spine flexion-extension in healthy individuals. Spine J. 2019, 19, 1264–1275. [Google Scholar] [CrossRef]
- Sparto, P.J.; Parnianpour, M.; Reinsel, T.E.; Simon, S. The Effect of Fatigue on Multijoint Kinematics, Coordination, and Postural Stability During a Repetitive Lifting Test. J. Orthop. Sport. Phys. Ther. 1997, 25, 3–12. [Google Scholar] [CrossRef]
- Hu, B.; Ning, X. The influence of lumbar extensor muscle fatigue on lumbar–pelvic coordination during weightlifting. Ergonomics 2015, 58, 1424–1432. [Google Scholar] [CrossRef]
- Beange, K.H.E.; Chan, A.D.C.; Beaudette, S.M.; Graham, R.B. Concurrent validity of a wearable IMU for objective assessments of functional movement quality and control of the lumbar spine. J. Biomech. 2019, 97, 109356. [Google Scholar] [CrossRef]
- Baecke, J.A.H.; Burema, J.; Frijters, J.E. A short questionnaire for the measurement of habitual physical activity in epidemiological studies. Am. J. Clin. Nutr. 1982, 36, 936–942. [Google Scholar] [CrossRef]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors. XSens Technol. 2013, 1–9. [Google Scholar]
- Schepers, M.; Giuberti, M.; Bellusci, G. Xsens MVN: Consistent Tracking of Human Motion Using Inertial Sensing. Xsens Technol. B.V. 2018, 1–8. [Google Scholar]
- Zhang, J.T.; Novak, A.C.; Brouwer, B.; Li, Q. Concurrent validation of Xsens MVN measurement of lower limb joint angular kinematics. Physiol. Meas. 2013, 34, N63–N69. [Google Scholar] [CrossRef] [PubMed]
- Robert-Lachaine, X.; Mecheri, H.; Larue, C.; Plamondon, A. Validation of inertial measurement units with an optoelectronic system for whole-body motion analysis. Med. Biol. Eng. Comput. 2017, 55, 609–619. [Google Scholar] [CrossRef]
- Graham, R.B.; Oikawa, L.Y.; Ross, G.B. Comparing the local dynamic stability of trunk movements between varsity athletes with and without non-specific low back pain. J. Biomech. 2014, 47, 1459–1464. [Google Scholar] [CrossRef]
- Granata, K.P.; England, S.A. Stability of dynamic trunk movement. Spine (Phila. Pa. 1976). 2006, 31, E271–E276. [Google Scholar] [CrossRef]
- Howarth, S.J.; Graham, R.B. Sensor positioning and experimental constraints influence estimates of local dynamic stability during repetitive spine movements. J. Biomech. 2015, 48, 1219–1223. [Google Scholar] [CrossRef]
- Oddsson, L.I.E.; Giphart, J.E.; Buijs, R.J.C.; Roy, S.H.; Taylor, H.P.; De Luca, C.J. Development of new protocols and analysis procedures for the assessment of LBP by surface EMG techniques. J. Rehabil. Res. Dev. 1997, 34, 415–426. [Google Scholar]
- Winter, D.A. Three-Dimensional Kinematics and Kinetics. In Biomechanics and Motor Control of Human Movement; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 176–199. [Google Scholar]
- Graham, R.B.; Sadler, E.M.; Stevenson, J.M. Local dynamic stability of trunk movements during the repetitive lifting of loads. Hum. Mov. Sci. 2012, 31, 592–603. [Google Scholar] [CrossRef]
- Marras, W.S.; Lavender, S.A.; Leurgans, S.E.; Fathallah, F.A.; Ferguson, S.A.; Allread, W.G.; Rajulu, S.L. Biomechanical risk factors for occupationally related low back disorders. Ergonomics 1995, 38, 377–410. [Google Scholar] [CrossRef]
- Banks, A.D.; Aghazadeh, F. Progressive Fatigue Effects on Manual Lifting Factors. Hum. Factors Ergon. Manuf. 2009, 19, 361–377. [Google Scholar] [CrossRef]
- Chow, D.H.K.; Man, J.W.K.; Holmes, A.D.; Evans, J.H. Postural and trunk muscle response to sudden release during stoop lifting tasks before and after fatigue of the trunk erector muscles. Ergonomics 2004, 47, 607–624. [Google Scholar] [CrossRef] [PubMed]
- Peters, B.T.; Haddad, J.M.; Heiderscheit, B.C.; Van Emmerik, R.E.A.; Hamill, J. Limitations in the use and interpretation of continuous relative phase. J. Biomech. 2003, 36, 271–274. [Google Scholar] [CrossRef]
- Lamb, P.F.; Stöckl, M. On the use of continuous relative phase: Review of current approaches and outline for a new standard. Clin. Biomech. 2014, 29, 484–493. [Google Scholar] [CrossRef] [PubMed]
- Seay, J.F.; Sauer, S.G.; Patel, T.; Roy, T.C. A history of low back pain affects pelvis and trunk coordination during a sustained manual materials handling task. J. Sport Heal. Sci. 2016, 5, 52–60. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hamill, J.; Palmer, C.; Van Emmerik, R.E.A. Coordinative variability and overuse injury. Sports Med. Arthrosc. Rehabil. Ther. Technol. 2012, 4, 45. [Google Scholar] [CrossRef]
- Korkmaz, S.; Goksuluk, D.; Zararsiz, G. MVN: An R package for assessing multivariate normality. R J. 2014, 6, 151–162. [Google Scholar] [CrossRef]
- Bakdash, J.Z.; Marusich, L.R. Repeated measures correlation. Front. Psychol. 2017, 8, 456. [Google Scholar] [CrossRef]
- Cohen, J. Statistical power analysis for the behavioral sciences: Jacob Cohen. J. Am. Stat. Assoc. 1988, 84, 19–74. [Google Scholar]
- Graham, R.B.; Josan, G.P.K. Development of a novel wearable system for the clinical assessment of movement quality and control in low back pain. In Proceedings of the XXVI Congress of the International Society of Biomechanics, Brisbane, Australia, 23–27 July 2017; p. 407. [Google Scholar]
- Granata, K.P.; Gottipati, P. Fatigue influences the dynamic stability of the torso. Ergonomics 2008, 51, 1258–1271. [Google Scholar] [CrossRef]
- Monjo, F.; Terrier, R.; Forestier, N. Muscle fatigue as an investigative tool in motor control: A review with new insights on internal models and posture-movement coordination. Hum. Mov. Sci. 2015, 44, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Larson, D.J.; Pinto, B.L.; Brown, S.H.M. Differential effects of muscle fatigue on dynamic spine stability: Implications for injury risk. J. Electromyogr. Kinesiol. 2018, 43, 209–216. [Google Scholar] [CrossRef] [PubMed]
- Karg, M.; Venture, G.; Hoey, J.; Kulic, D. Human movement analysis as a measure for fatigue: A hidden markov-based approach. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 470–481. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.A. Correlation-Based Feature Selection for Discrete and Numeric Class Machine Learning; University of Waikato: Hamilton, New Zealand, 2000. [Google Scholar]

| Demographic | Male | Female |
|---|---|---|
| N | 5 | 5 |
| Age (years) | 29.6 (10.8) | 27 (3.3) |
| Mass (kg) | 78.46 (18.55) | 59.86 (9.20) |
| Height (cm) | 178.1 (11.3) | 173.3 (10.2) |
| Participant | Fatigue VAS (mm) | Maximal Lift Strength (N) | ||
|---|---|---|---|---|
| r | p Value | r | p Value | |
| S01 | −0.84 | < 0.001 * | −0.06 | 0.863 |
| S02 | −0.61 | 0.061 | −0.43 | 0.210 |
| S03 | 0.74 | 0.014 * | −0.77 | 0.009 * |
| S04 | 0.87 | 0.001 * | −0.68 | 0.029 * |
| S05 | 0.77 | 0.009 * | −0.48 | 0.156 |
| S06 | 0.91 | < 0.001 * | −0.89 | < 0.001 * |
| S07 | 0.59 | 0.072 | 0.69 | 0.027 * |
| S08 | 0.91 | < 0.001 * | −0.27 | 0.445 |
| S09 | 0.83 | 0.003 * | −0.77 | 0.009 * |
| S10 | −0.15 | 0.671 | 0.15 | 0.677 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, V.C.H.; Beaudette, S.M.; Smale, K.B.; Beange, K.H.E.; Graham, R.B. A Subject-Specific Approach to Detect Fatigue-Related Changes in Spine Motion Using Wearable Sensors. Sensors 2020, 20, 2646. https://doi.org/10.3390/s20092646
Chan VCH, Beaudette SM, Smale KB, Beange KHE, Graham RB. A Subject-Specific Approach to Detect Fatigue-Related Changes in Spine Motion Using Wearable Sensors. Sensors. 2020; 20(9):2646. https://doi.org/10.3390/s20092646
Chicago/Turabian StyleChan, Victor C.H., Shawn M. Beaudette, Kenneth B. Smale, Kristen H.E. Beange, and Ryan B. Graham. 2020. "A Subject-Specific Approach to Detect Fatigue-Related Changes in Spine Motion Using Wearable Sensors" Sensors 20, no. 9: 2646. https://doi.org/10.3390/s20092646
APA StyleChan, V. C. H., Beaudette, S. M., Smale, K. B., Beange, K. H. E., & Graham, R. B. (2020). A Subject-Specific Approach to Detect Fatigue-Related Changes in Spine Motion Using Wearable Sensors. Sensors, 20(9), 2646. https://doi.org/10.3390/s20092646






