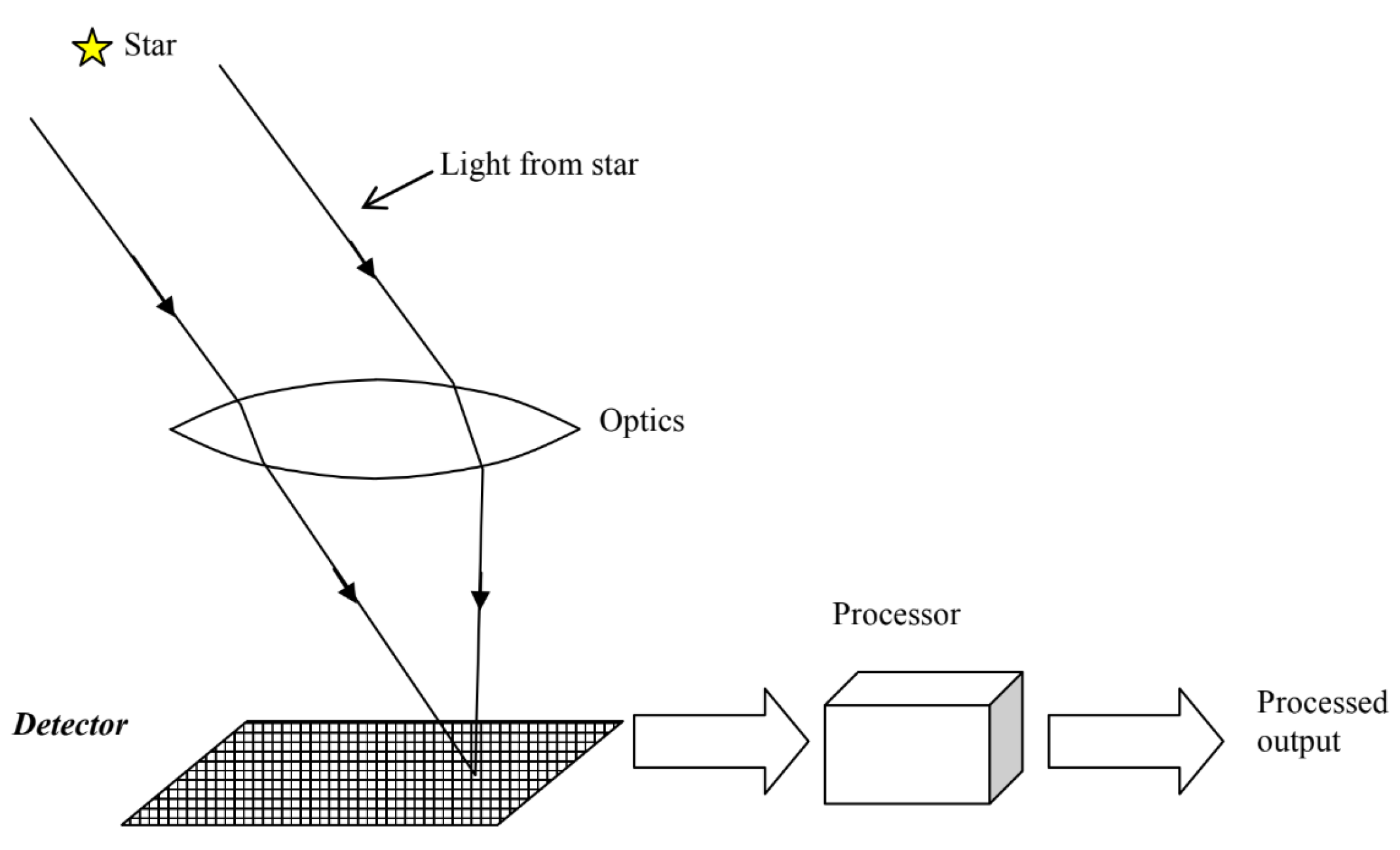
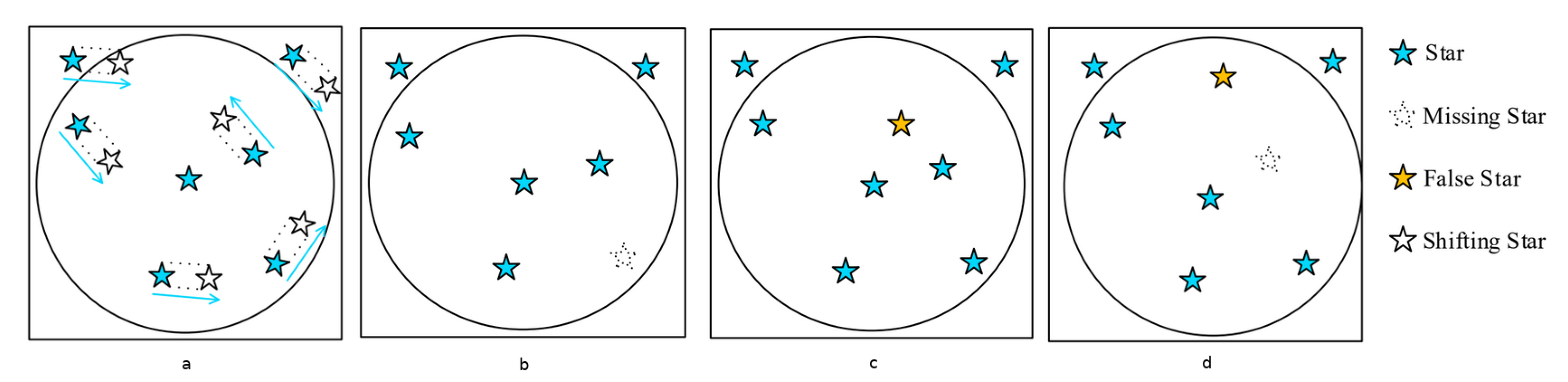
Multiple novel solutions have been proposed since 2009 and hardware has advanced significantly. In this section, we shall survey the relevant publications on star identification algorithms that are not covered by the Spratling and Mortari survey paper. The publications covered are published in a peer reviewed journal and improve performance significantly or have a novel, promising approach.
3.1. The Singular Value Method (SVM)
In 2003, Juang, Kim, and Junkins published their star pattern recognition algorithm method using singular value decomposition (SVD) [
14]. This novel approach does not need a separate attitude determination algorithm, but rather produces the attitude directly, eliminating the last block in the functional flow of
Figure 2. The algorithm uses a pattern association feature extraction. The pattern recognition is achieved recursively: the brightest star is selected as the boresight direction and four bright stars in the field of view are chosen. These vectors are decomposed and the singular values are compared with the database singular values. If the identification fails, another star is chosen as the boresight direction. If a match is found, the attitude is directly calculated from the singular values. In the original paper, testing is performed on only 10 real star images, achieving a matching rate of 70%. Even though Juang and Wang published a paper improving the algorithm in 2012 [
29] by using a sensitivity analysis method and eliminating the brightness ranking, the testing of the algorithm is not extended beyond the 10 images. Furthermore, for some images, the algorithm needs many iterations to find a match.
In 2019, Wei et al. published a paper using the oriented SVD transformation of triangles for the star identification algorithm [
30]. This algorithm also suffers from redundant matches and therefore requires a reliability evaluation using star voting. Wei et al. compare their algorithm against the grid algorithm by Padgett and Kreutz-Delgado [
13] and the SVM algorithm and report that their algorithm outperforms both in terms of robustness against magnitude and positional noise with respect to the SVM algorithm, with the grid algorithm performing significantly worse. The robustness against false stars is similar with respect to the grid algorithm at around 93.2% for three false stars versus 93.8%, while the SVM algorithm reaches only 70% with three false stars present in the image. The SVM algorithm outperforms both algorithms in terms of speed, while also outputting the attitude (skipping the need for an attitude determination algorithm and in effect reaching even better performance). This does come at a highly increased memory cost with respect to the other two algorithms. While the SVM paper does not specify a search method, it is reasonable to assume that the search time is
. The oriented singular value feature method uses a binary search for the initial matching, achieving
time while the original grid algorithm only achieves linear time
.
3.2. Modified Grid Algorithms
In 1997, Padgett and Kreutz-Delgado published a well-known paper on their grid algorithm, a lost-in-space type algorithm using a pattern recognition feature extraction [
13]. This algorithm has relatively poor performance in terms of magnitude and positional noise and recently attempts have been made to mitigate these shortcomings. In 2008, Na, Zheng, and Jia published a paper on their elastic grey grid algorithm which significantly improves the performance of the original algorithm [
31]. The grey grid algorithm eliminates the hard template matching of the original grid algorithm that caused it to be weakly robust to magnitude and positional noise. The hard template matching is replaced by a cost function that takes into account the difference between the measured pattern and the database pattern, and uses the relative magnitudes of the stars as a weight. This makes the pattern grey instead of binary, increasing the robustness to magnitude noise. The computational complexity increases with respect to the original algorithm to
, where b is the number of stars in a pattern. The authors simulate the algorithm against the original grid algorithm, and achieve a better recognition rate than the original grid algorithm under both magnitude and positional noise and false star presence. The algorithm is, however, slower than the grid algorithm by about 26.6% and does not address the issue the original grid algorithm has with respect to the low probability of selecting the right reference star and rotating the reference grid by selecting a neighbouring (pivot) star outside a certain radius. According to [
2], this probability can be as low as 50%.
In 2016, Aghaei and Moghaddam published a paper on an improved grid algorithm using a number of optimizations [
32]. These optimisations include forming radiometric clusters based on the relative brightness of the stars in an image. This reduces the probability of choosing a false pivot star. Another optimisation that is introduced is similar to the gray grid algorithm. While a larger cell size obviously makes the algorithm more robust to positional noise, it also reduces the pattern resolution. In order to solve this trade-off, the grid cell sizes are optimised as a function of the standard deviation of the positional noise. Lastly, the match classification error is reduced using ‘vetoing’ by only keeping the two matches with the highest vote scores and discarding all other matches for a certain orientation. This reduces the probability of false positive or negative matching. In combination with this, the optimum threshold for rejecting voting scores corresponding to false matches is calculated using Bayesian decision theory. The algorithm achieves
time, where
is the number of pivot stars. The authors compare the improved grid algorithm against the original grid algorithm, and conclude that it strongly improves the robustness against positional noise and the presence of uncatalogued stars. The authors do not address the robustness against false stars.
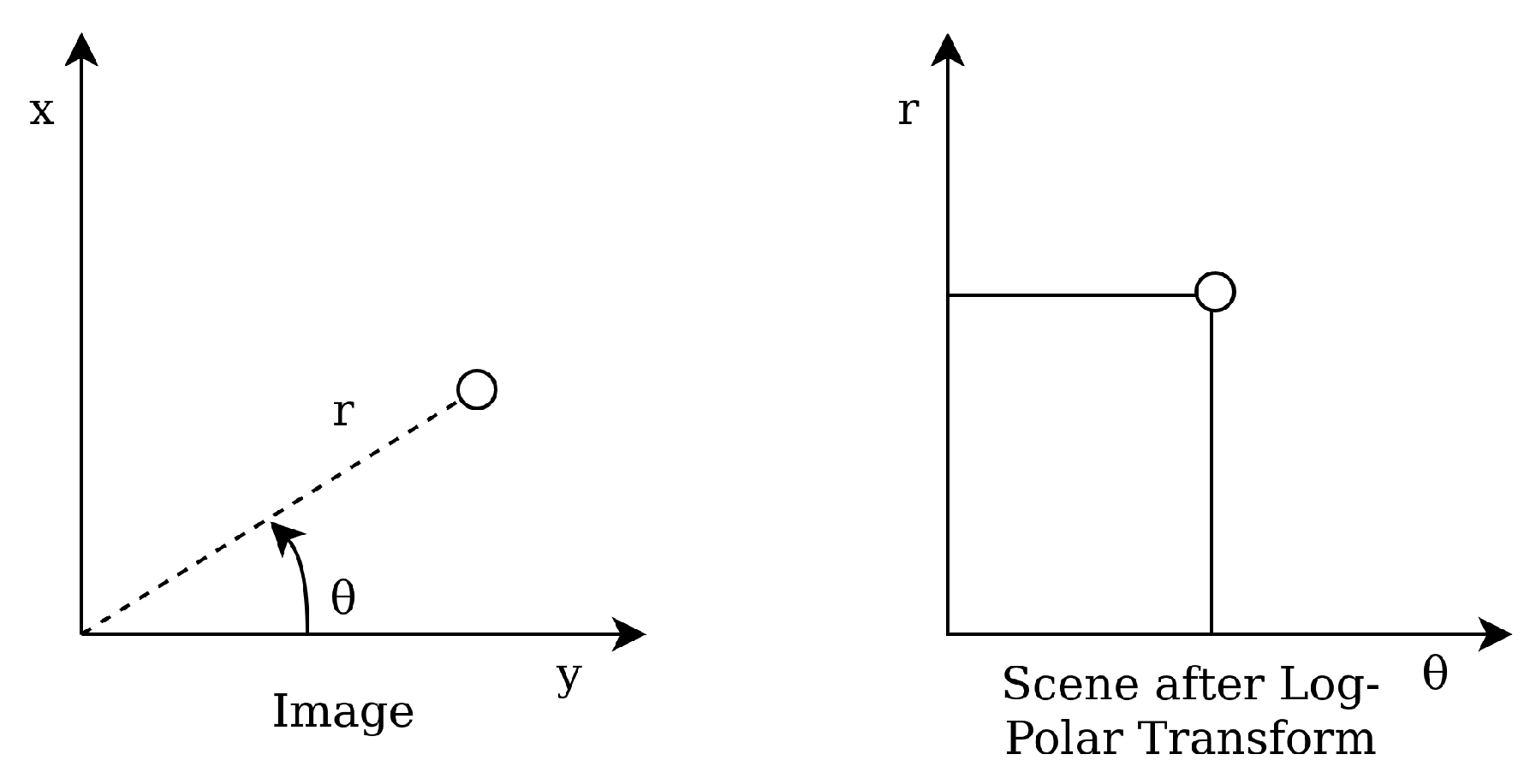
3.3. Star Identification Based on Log-Polar Transform (LPT)
Wei et al. presented their star identification algorithm based on the Log-Polar Transform (LPT) in 2009 [
15]. It is another lost in space algorithm with a pattern based feature extraction. The LPT transforms the star patterns from Cartesian coordinates to polar coordinates with logarithmic radius (see
Figure 4). The LPT properties are invariant to rotation and scale, and are calculated by shifting the star image such that guide star
t is located at the origin. Then, the coordinates are transformed by a LPT and digitised as a
m ×
n sparse matrix, with
m being the sampling points in
direction and
n the sampling points in
r direction. This result is projected on the
axis in order to make a one-dimensional 1 ×
m vector
lpt(t). The same procedure is performed on the catalog stars. The algorithm then encodes the patterns as strings while reducing the sparsity of the vector and matches these to the database stars.
By encoding the patterns as a string, searching for the right pattern in the database is analogous to searching for the most similar word in a dictionary. The LPT algorithm uses a modified string matching algorithm based on Knuth–Morris–Pratt (KMP), which keeps track of how many characters in a string match with the particular database section and how many are mismatched, while maintaining a search range limitation. KMP has complexity . If certain threshold conditions are met with respect to these values, a match is found. Otherwise, the algorithm is iterated on another star t in the image. If no star produces a match, the identification fails. Wei, Zhang, and Jiang note that their algorithm is very sensitive to the pattern radius R, which is dependent on the chosen FOV. The authors compare their algorithm to the grid algorithm and report better performance in terms of magnitude and positional noise, but fail to report the robustness against false stars or star dropout. The algorithm is relatively slow (about 50% slower than the grid algorithm) due to the computationally intensive string matching.
3.5. Image Based Identification Algorithms
In 2011, a new development emerged in the field of star identification algorithms. A new pattern based feature extraction approach by Yoon, Lim, and Bang proposed comparing the camera image to a database image by maximising a target cost function [
36]. This algorithm is called the Correlation Algorithm. After centroiding, the algorithm reconstructs the original image from the centroid coordinates. However, in order to do so, the algorithm uses the same approach as the grid algorithm (translating and rotating the image around a pivot star by putting the closest star to the pivot star on the
x-axis). Since this process is likely to fail, the algorithm essentially inherits the same problems as the original grid algorithm. Each star is modelled as a Gaussian distribution with a variance dependent on the system performance and star brightness. The correlation between both images is calculated by multiplying the camera image with a database image, yielding a higher magnitude if the images are more similar. Since this cost function is a cross-correlation of two functions, the authors solve it using a Fourier transform. This process has to be performed for all pivot stars in the database, making the search time linearly dependent on the amount of database entries (
).
Another image based star identification algorithm was proposed by Delabie, Durt, and Vandersteen in 2013 [
3]. The algorithm relies on an image processing technique called the Shortest Distance Transform. A distance transform of a binary image creates a map that colors each pixel according to the distance to the nearest star. This distance is defined as the Euclidean squared distance by the authors. The coordinates of the stars are binned by their pixels, which causes the distance transform map to consist of integers (see
Figure 6).
Since the algorithm relies on the comparison of images, the FOV for both the database and the camera needs to be equivalent. The authors generate images of equal sizes evenly distributed over the celestial sphere for the image database. Since the images taken by the star sensor are often rotated and translated with respect to the database images, the algorithm has to solve the same problem as the original grid algorithm: the image has to be rotated and translated in some consistent manner in order to match it to the database images. The authors solve this problem by using the ‘centroid method’. This method translates the database image by matching the centroid of a certain number of brightest stars and rotates it by the smallest angle between the centroid and the stars. This is done for all images in the database, but the authors state that the calculation time for this step is negligible compared to the comparison step. The comparison step () consists of creating a distance array consisting of the integer distances of the image stars and the database stars, where is the minimum number of database image and camera image stars. As decision criteria, the sum of the integer distances and the number of database stars within two pixels of the imaged stars are used. These two criteria express how similar the two images are, and the number of close stars divided by is used as an indication of the validity of a solution. Since it is not desirable to compare all the database images to the camera image, a threshold is used on the distance and angle features used in the centroid method to discard around 90% of the images. Furthermore, the centroid and angles are preprocessed and also saved in the database to reduce processing time. While the algorithm is not tested against other algorithms, it is tested for robustness to positional error, false stars and dropped stars. The algorithm is reported to be extremely robust to positional noise and false stars, correctly determining almost 99% of the images with 1000 arc seconds of positional error, and 98% with 650 false stars, respectively. It has to be noted here that the false stars that are added to the image have a magnitude higher than that of the third highest star in the image, which are favourable conditions for testing the algorithm and may not give fair comparisons to other tests. If the three brightest stars are dropped from an image, the algorithm still achieves a 90% matching rate.
The algorithm is implemented for an FOV of 20 degrees squared, which requires 1337 images in the database in order to achieve sufficient robustness. Even though there is a large image overlap in this case, a smaller FOV will lead to an exponentially increased database size. Since the search time is linearly dependent on the amount of images, this limits the algorithm to larger FOV’s.
3.6. Pole Star Algorithms Improved
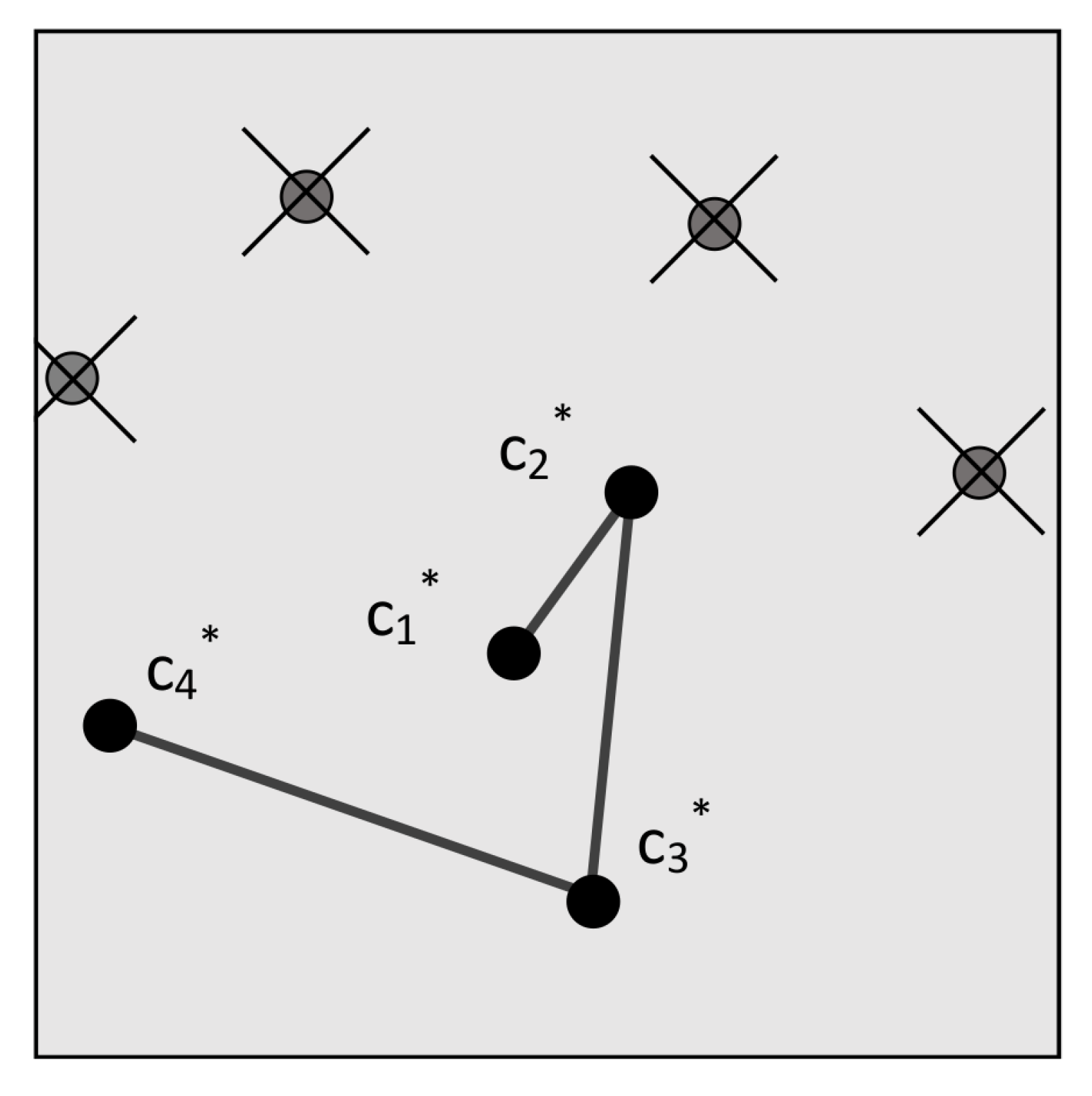
Another development has been the further advancement of algorithms based on the
Pole Star approach. These algorithms have in common that some form of a pole star pattern is used, similar to the original Group Match algorithm put forward by Kosik in 1991 [
11]. The algorithms find a pole star and define a number of pairs with the neighbouring stars. Originally, a subgraph isomorphism based feature extraction method, the angular distances are used to find all the matching sets for the star pairs. If there is a star present in all of the found sets, the pole star can be identified (see
Figure 7). However, the original approach is not robust to false stars and very storage intensive because it orders the database by angular distance [
2]. Attempts have been made to mitigate these shortcomings.
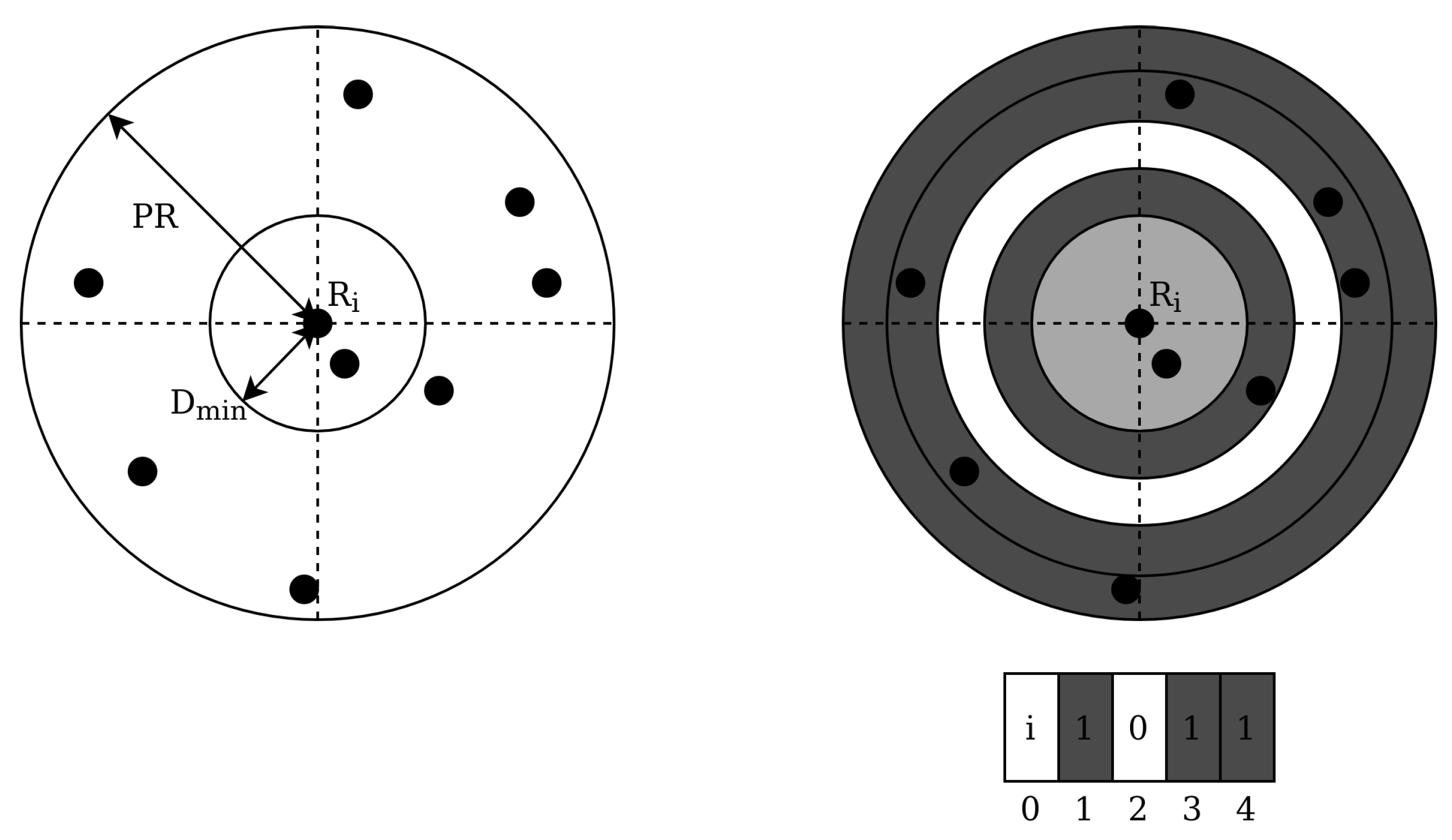
In 2006, Silani and Lovera introduced the Polestar algorithm [
37]. The authors define this algorithm as a mix between both feature extraction categories: using a pattern based approach for defining candidates and a subgraph isomorphism based approach for finding a match. The pattern generation scheme is as follows: first, a reference star
is chosen and the angular distance between this star and all stars outside of a certain radius
and inside the patter radius
are calculated. These angular distances are discretised in bins and a binary barcode is generated where a 1 indicates the presence of one or more stars in that bin (see
Figure 8).
A set of so-called pattern vectors is combined with all the selected reference stars and a database is generated that is indexed by the binary vector locations. At these index locations, a row constitutes all the stars that match the generated pattern, and a star counter is incremented for each star in the rows that are indexed by the pattern vector with a 1. If the counter is above a defined threshold, the star is considered a candidate. This process voting process is repeated for a number of patterns and has a
complexity. After the candidate selection step, a subgraph isomorphism feature extraction step is used by generating pairs, triangles and polygons iteratively using the candidate stars. If a match is found between a triangle of a candidate star and the sensor stars, but no match is found for a polygon with a greater number of edges, then an unambiguous identification is made. This step has a complexity of
, where k is the number of candidates. Otherwise, no identification is provided. The authors compare their algorithm to the grid algorithm and Liebe’s triangle algorithm [
9]. The Polestar algorithm outperforms both in terms of robustness to magnitude and positional noise, but the triangle algorithm outperforms it in terms of speed.
Shortly after, in 2008, Zhang, Wei and Jiang published their algorithm based on radial and cyclic features [
38]. This approach is similar to the Polestar algorithm, as the authors also used a binned radial feature pattern and a very similar database structure. However, the subgraph isomorphism step is replaced by a pattern based feature extraction, by generating a bit pattern based on binned cyclic sectors using the angles between the polestar and two other stars. The radial based matching is performed on every star in the image and has
complexity, where f is the average number of stars in the FOV. The cyclic patterns are generated for every imaged star and compared to the candidate stars achieving
. Similar to the Polestar algorithm, the algorithm is only compared to the older grid algorithm, which it outperforms. The cyclic pattern suffers from a similar issue as the original grid algorithm, namely that the selection of the starting side (the side of the smallest central angle) is easily affected by magnitude and positional noise, causing the matching to fail.
Li, Wei and Zhang proposed an iterative algorithm based on a voting mechanism in 2014 [
39]. Their subgraph isomorphism based approach consists of three steps: a single match process, an iterative search and verification. In the single match process, the distance between the pole star and one of its neighbours is calculated and used to find corresponding elements within a certain error margin in the database. For each measured star pair, a voting score is increased for both stars if a match is found. If a star counter is above the minimum matching threshold, the database star is considered a match. Generally, multiple candidate stars are found during this process and an iterative search is performed. The candidate stars are used as a reduced stair pair database in the next iteration of the matching process, where the minimum matching threshold is multiplied by the iteration number. If no match is found for a pole star, it is discarded as a false star for the next iteration. The analytical performance of this algorithm can be described as
, where
is the reduced star pair database fraction of the complete database. This analytical performance is equivalent to the analytical performance of the star identification method by Baldini et al. [
40] as defined by Spratling and Mortari [
1]. If more than two stars have a unique candidate star, a consistency check is performed on the other identified star pairs by checking if the error of the star pairs is within the limits (
). After this, a verification step is performed by checking if the number of matched stars is above 4. If this is not the case, the algorithm reports a failed identification. The algorithm is tested against the Group Match algorithm and the Geometric Voting algorithm [
41], outperforming both in terms of runtime, robustness against false stars, positional noise and magnitude noise.
In 2017, Schiattarella, Spiller and Curti introduced the Multi-Poles Algorithm (MPA) [
42]. This algorithm also uses a pole star pattern and is specifically designed to be robust against false stars. It uses a subgraph isomorphic feature extraction: the angular distances between the pole star and its neighbours are looked-up in an on-board database using the
k-vector technique [
43] and a list of candidate star sets is returned in
. Then, a process very similar to the original group match algorithm is used to ’accept’ the pole star and the neighbour stars, by finding the star that has the largest number of appearances in the sets of candidates. This acceptance phase runs at least twice on different stars in order to reduce the probability of accepting false stars. After this acceptance phase, the verification phase verifies the outcome by cross-checking the sets with each other. In order to mitigate the effects of false stars, a confirmation phase is implemented after the verification phase, which is similar to a method proposed by Xie et al. in 2012 [
44]. In this phase, a chain is generated by iteratively checking the angular distances between the pole star and its respective neighbours with the on-board database (see
Figure 9). This range search problem is again solved by using the
k-vector technique and the final output is a chain of confirmed stars that can be used for the attitude determination. The step takes
since the initial star is already known. While the authors do not compare MPA to other algorithms, they report a 100% identification rate with an input of 185 false stars and 33 cataloged stars.
In 2019, Wei et al. published an algorithm that uses dynamic cyclic patterns that mitigates this single point of failure that is the selection of the starting side [
45]. The algorithm uses the discretised centre angles to construct the pattern vector and give this vector a similarity score based on how similar it is to database vectors. While no search method is defined, we assume the search complexity to be
. After this, a confirmation phase is implemented using a chaining algorithm, similar to the Multi-Poles algorithm (
). The authors compare their algorithm to the grid algorithm, the radial and cyclic algorithm, the optimised grid algorithm and the multi-poles algorithm and report better performance in terms of robustness to noise and false stars. However, the performance of their implementation of the Multi-Poles algorithm is significantly worse than what the original authors report due to a different simulation environment.
3.7. Deep Learning Approach
Deep learning based approaches are not new to the field of star identification algorithms, but they have been limited by the massively parallel processor architecture needed to perform inference. Nevertheless, work continues to be published on this approach and advancements in edge-processing architectures will make deep learning algorithms in space a possibility in the near future. A recent deep learning based approach is RPNet, a star identification network based on representation learning. It was published in 2019 by Xu, Jiang and Liu [
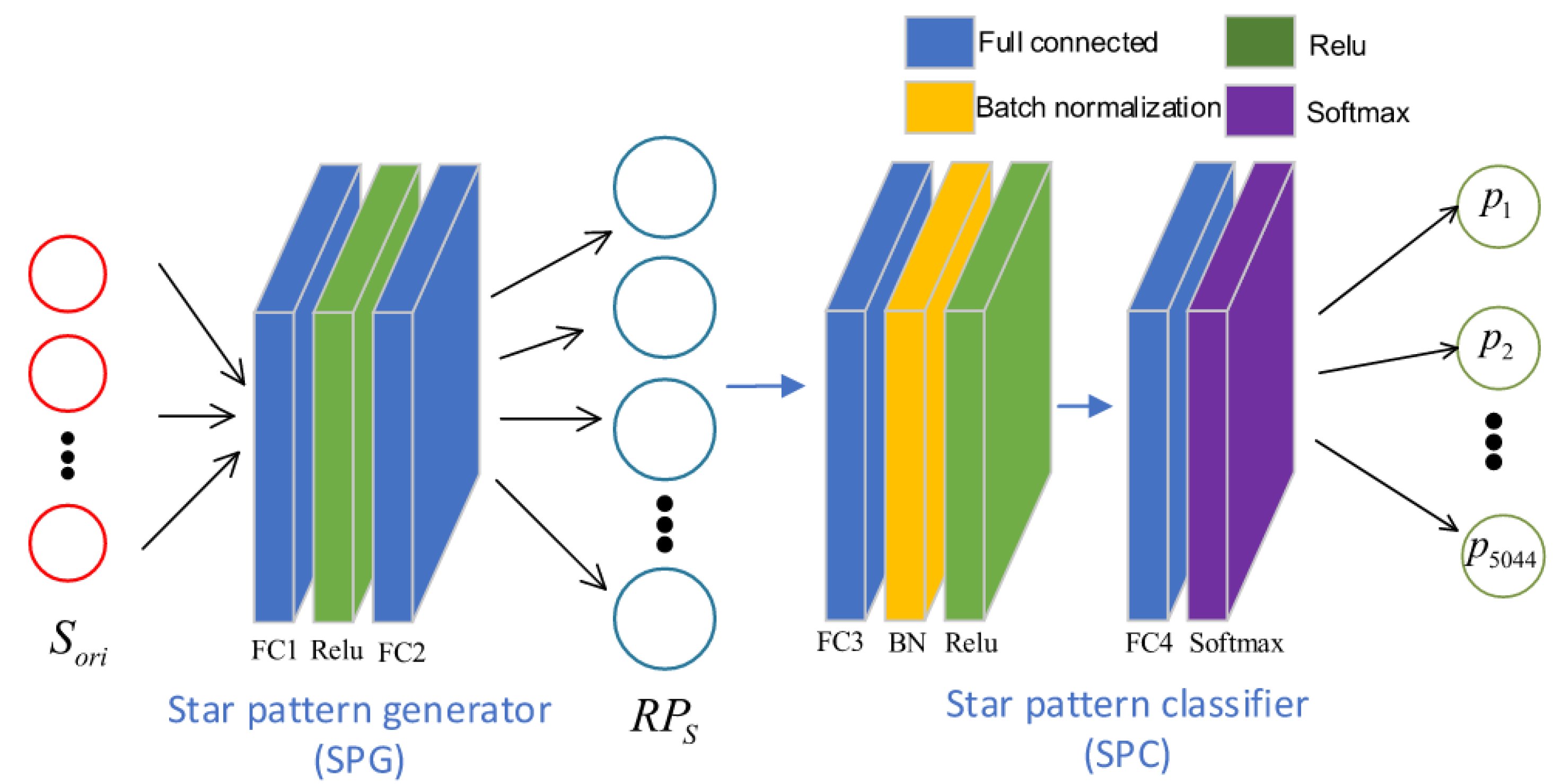
24]. RPNet uses a pattern based feature extraction method to construct its input, by selecting a guide star and its neighbour stars and discretizing the distances. Then, an encoder–decoder structure is employed (see
Figure 10): a pattern generator is used to create a pattern in a multidimensional space, which is classified using a star pattern classifier. Both the encoder and the decoder need to be trained using artificial star scenes. Once the encoder is trained, its output is used to train the classifier.
The authors compare the algorithm to the grid algorithm and report better robustness to position and magnitude noise and comparable performance in terms of false star robustness. However, the simulation environment has an FOV of 20∗20 degrees, which is relatively large and increases the amount of information the network receives. The algorithm is fast in terms of analytical performance, its inference phase achieves because the patterns are stored implicitly in the network. The storage size scales with as the algorithm still requires a lookup database. However, the neural network itself takes up a significant but constant amount of memory.
3.8. Summary of Recent Advancements of Lost-in-Space Star Identification Algorithms
In order to comprehensively show a representative view of the recent advancements in lost-in-space star identification algorithms, the covered algorithms are summarised in
Table 1. Furthermore, the application environment in terms of a signal-to-noise ratio is listed qualitatively based on the reported robustness to noise, required stars per image and use of verification steps. An algorithm that is able to deal with a lower signal-to-noise ratio can be employed in more challenging application environments. However, usually this does require a more complex solution involving iterative validation. A higher signal-to-noise ratio in a star sensor system may be achieved by a larger FOV, high detector sensitivity, etc. which limits the application environment. The search complexity and validation complexity are also listed since these two complexities are the most time critical and therefore a large driver in the performance of the algorithms.
Clearly a number of algorithms do not have an optimal search strategy which limits the time performance, resulting in linear complexity of the search or worse than linear complexity. The Adaptive Ant Colony and oriented SVD transformation method use a binary search which improves the database search time and greatly improves the performance. Even better is the Multi-Poles Algorithm, which has implemented the k-vector technique for the database search. However, this algorithm uses multiple iterations for identification essentially reducing the time performance slightly in favour of reliability. Analytically, the best search performance is achieved by deep learning solutions: because a search is eliminated, the complexity is constant regardless of the size of the problem. However, due to the nature of neural network, an answer is always produced no matter what the input is. This means that proper validation needs to be implemented in order to prevent false positive matching.
Many algorithms do not have a validation step. This is a trade-off in designing a star identification algorithm: while a validation step increases complexity, reliability also increases and the applicable signal-to-noise environment becomes less strict. This can be seen in
Table 1: every identification algorithm with a low signal-to-noise application environment has a validation step implemented. The complexity of the validation step is at best
, as implemented by Zhang et al. [
38]. This step is relatively simple since the search only covers a limited candidate list instead of the whole star database. While the chain validation algorithm requires multiple database searches, it is more robust. The Multi-Poles Algorithm implementation which uses the
k-vector technique for the searches is the fastest.