Detection of Atrial Fibrillation Using 1D Convolutional Neural Network
Abstract
1. Introduction
- We propose a simple, yet effective AF detection method based on end-to-end 1D CNN architecture to classify time-series 1D ECG signal directly without converting it to 2D data. Through exhaustive evaluation, we prove our method achieves better detection accuracy than the existing DL-based methods. In addition, the proposed method reduces network complexity significantly, as compared with the second-ranked method, CRNN.
- We study the effect of the batch normalization and pooling methods on detection accuracy, and then design the best network by combing the grid search method.
- We present a length normalization algorithm to solve variable length of ECG recordings.
2. Proposed AF Detection
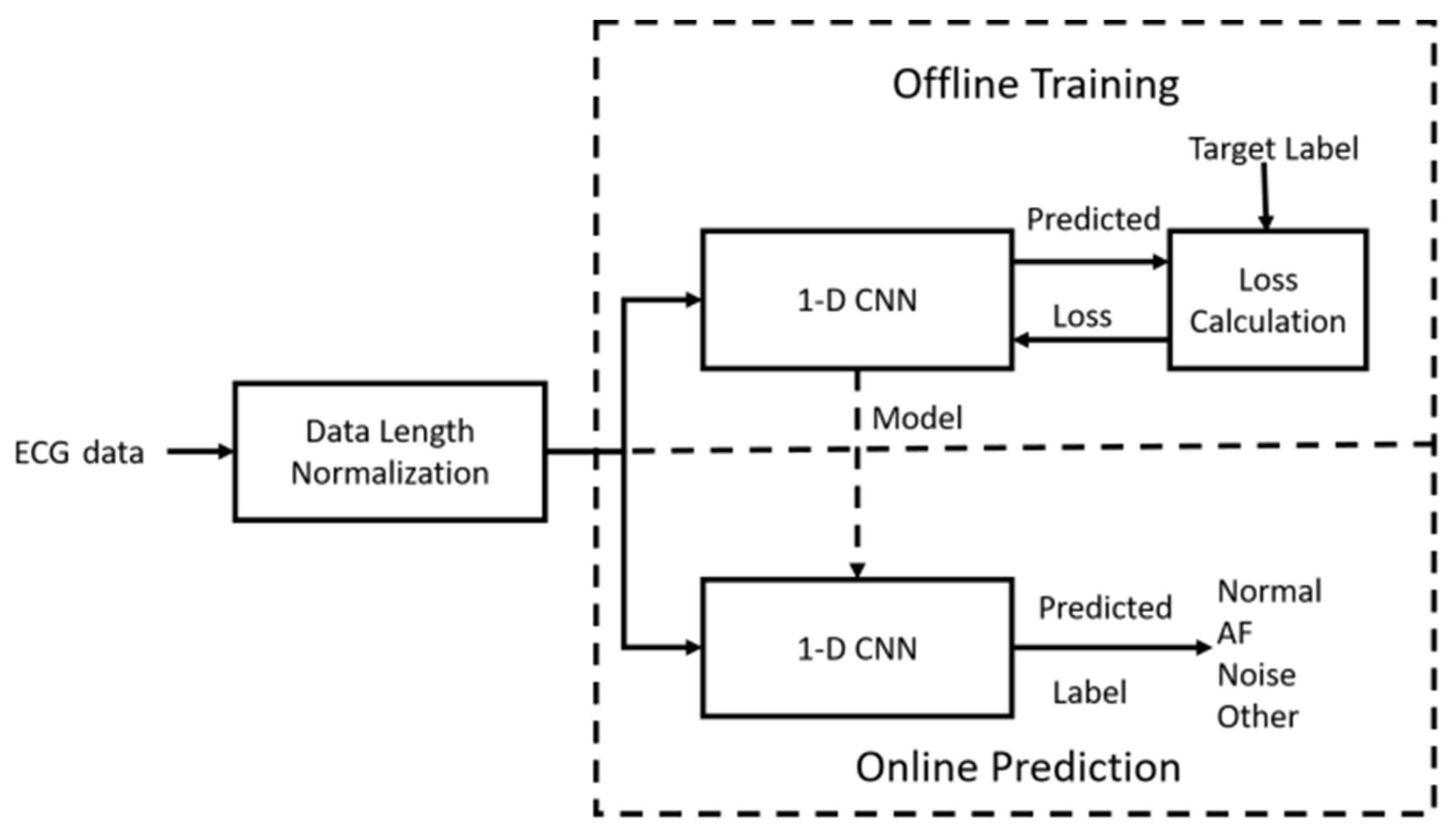
2.1. System Overview
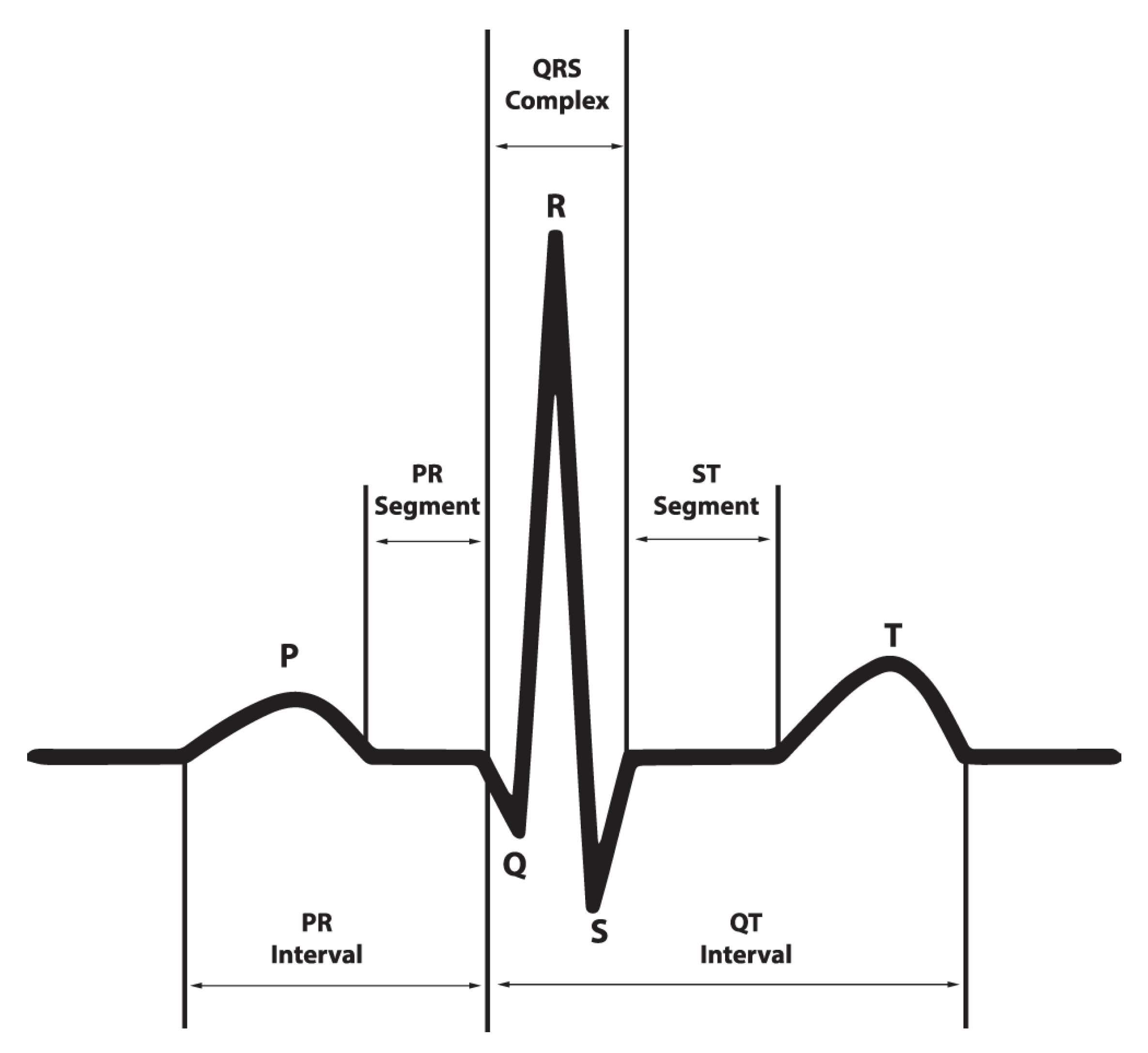
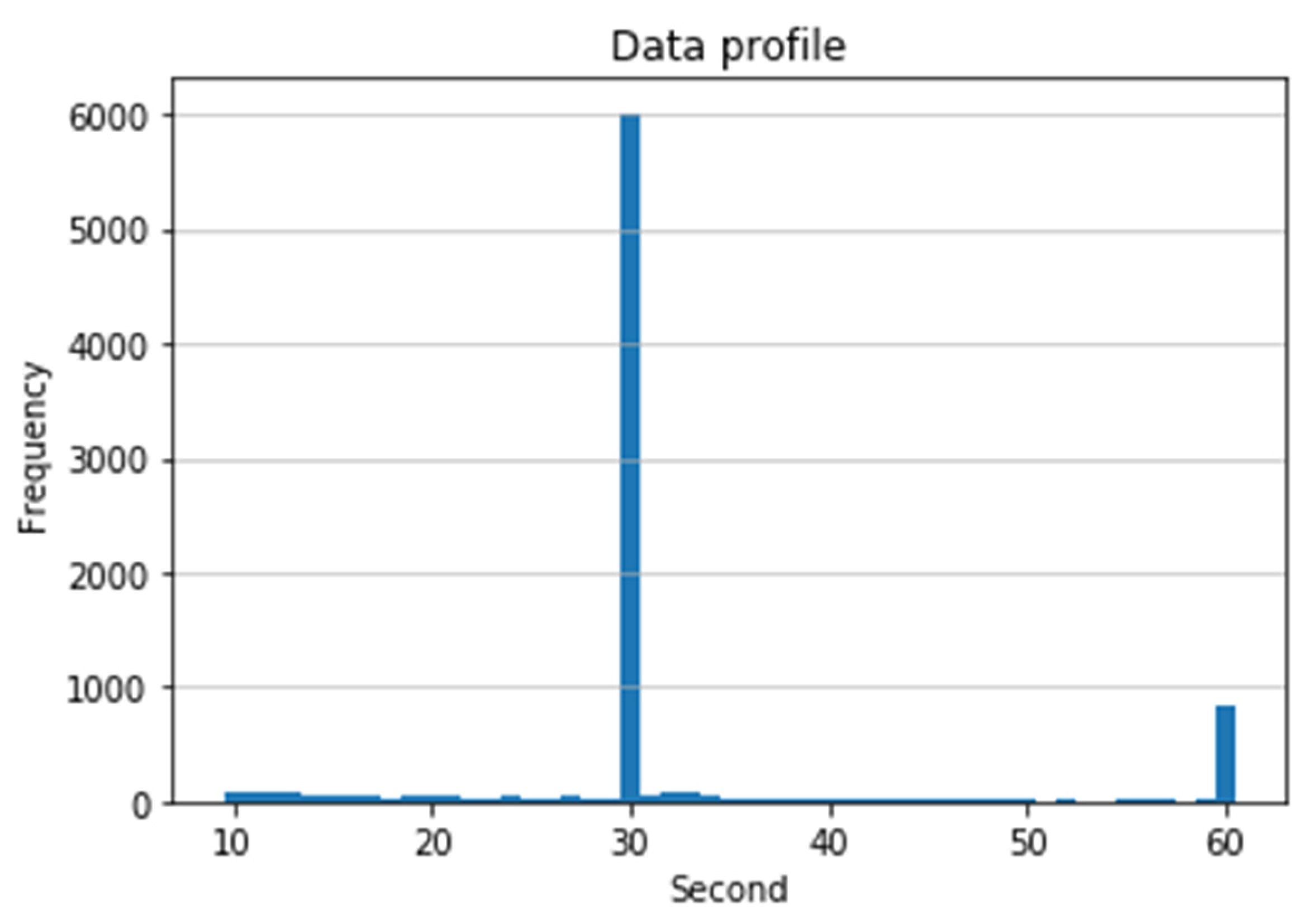
2.2. Data Length Normalization
| Algorithm 1. Pseudocode of data length normalization. |
| 1: IF the length of the recording is greater than 9000 samples |
| 2: Chop recording into 9000 samples with 50% overlap between segments |
| 3: IF the length of the recording is less than 9000 samples |
| 4: DATA: = copy the recording |
| 5: Append DATA in the back of the recording |
| 6: DO step 5 until the appended recording reaches 9000 samples |
| 7: IF the length of the recording is equal to 9000 samples |
| 8: Preserve the recording |
2.3. 1D CNN Design
2.3.1. CNN Architecture
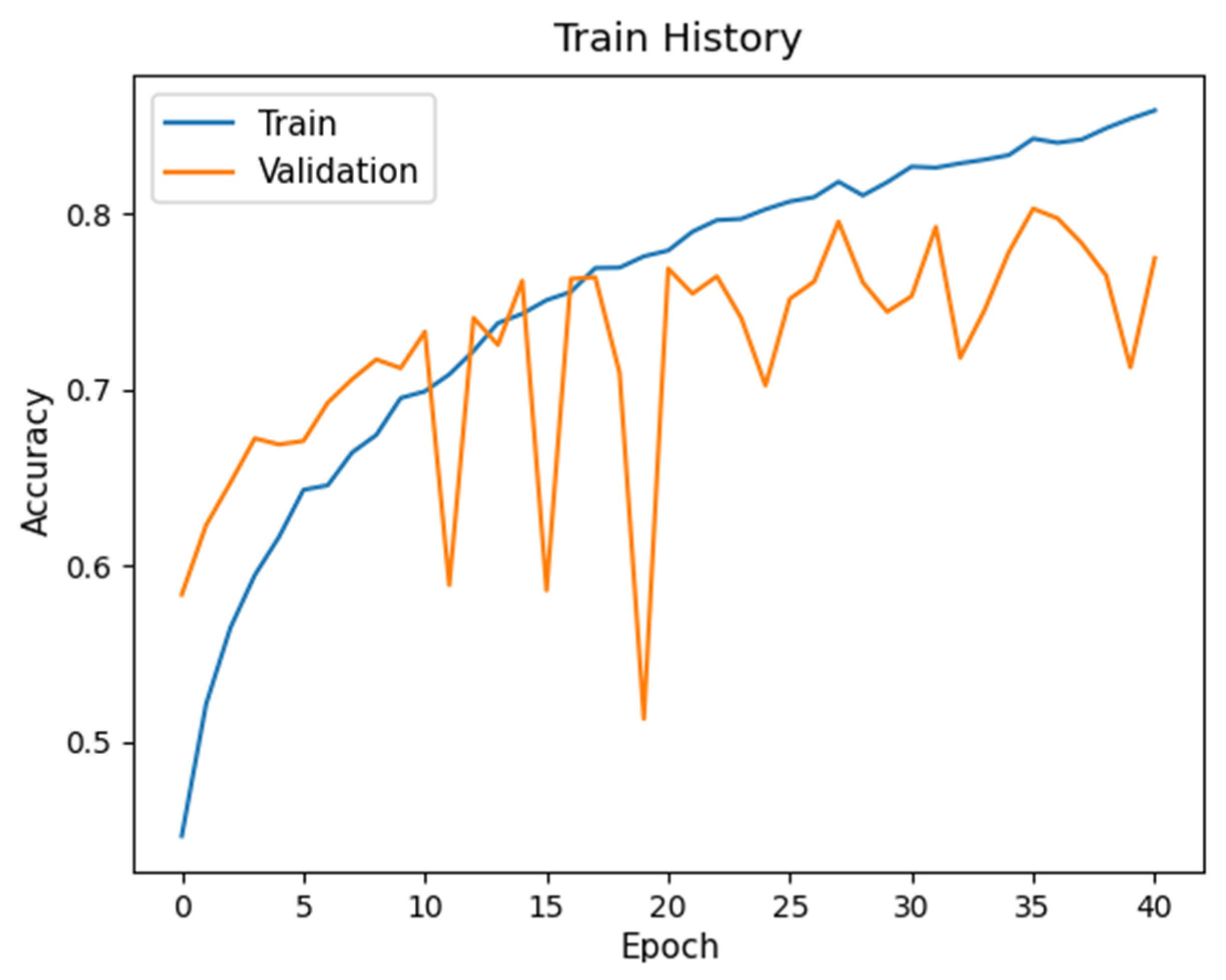
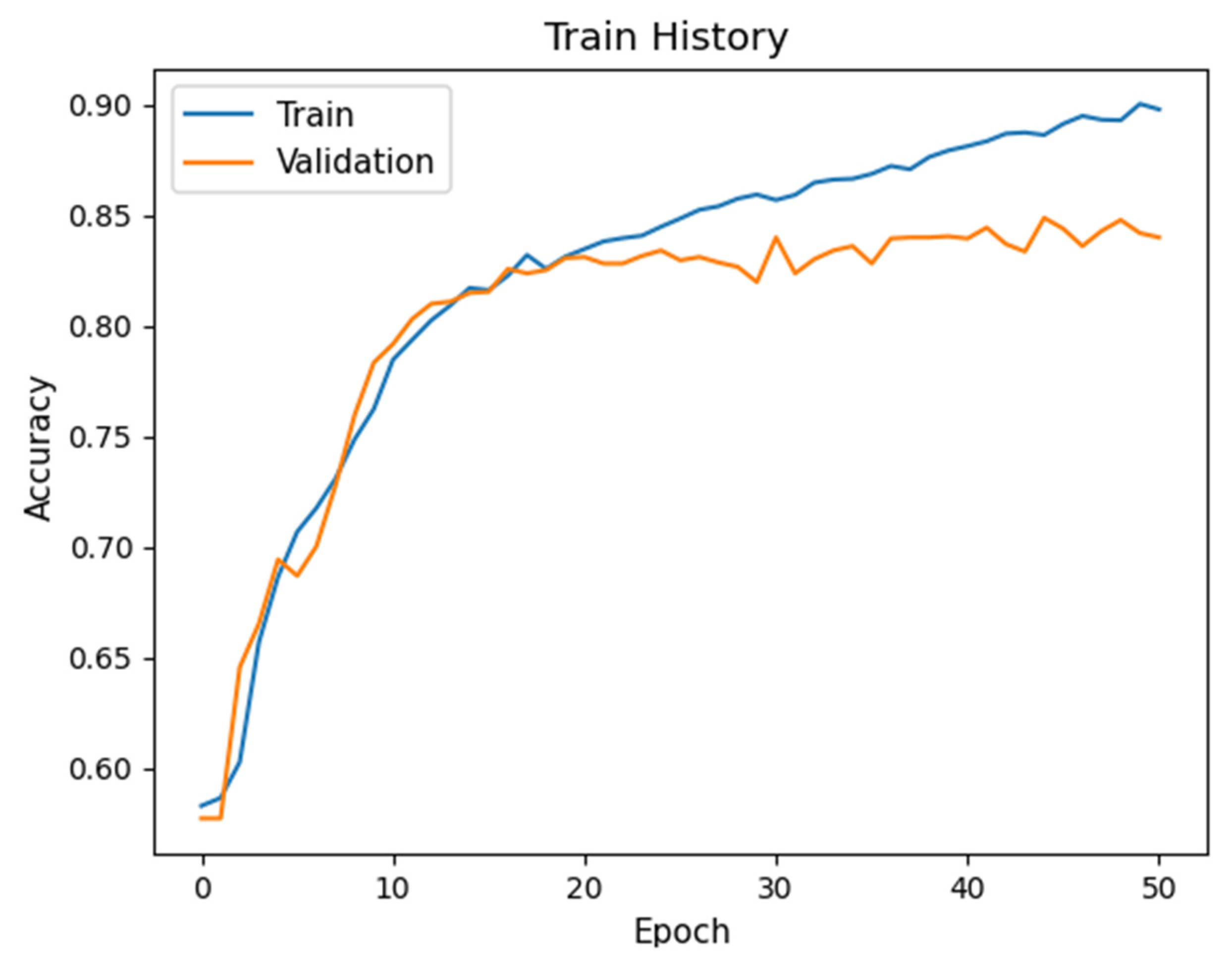
2.3.2. CNN Learning
3. Numerical Analysis
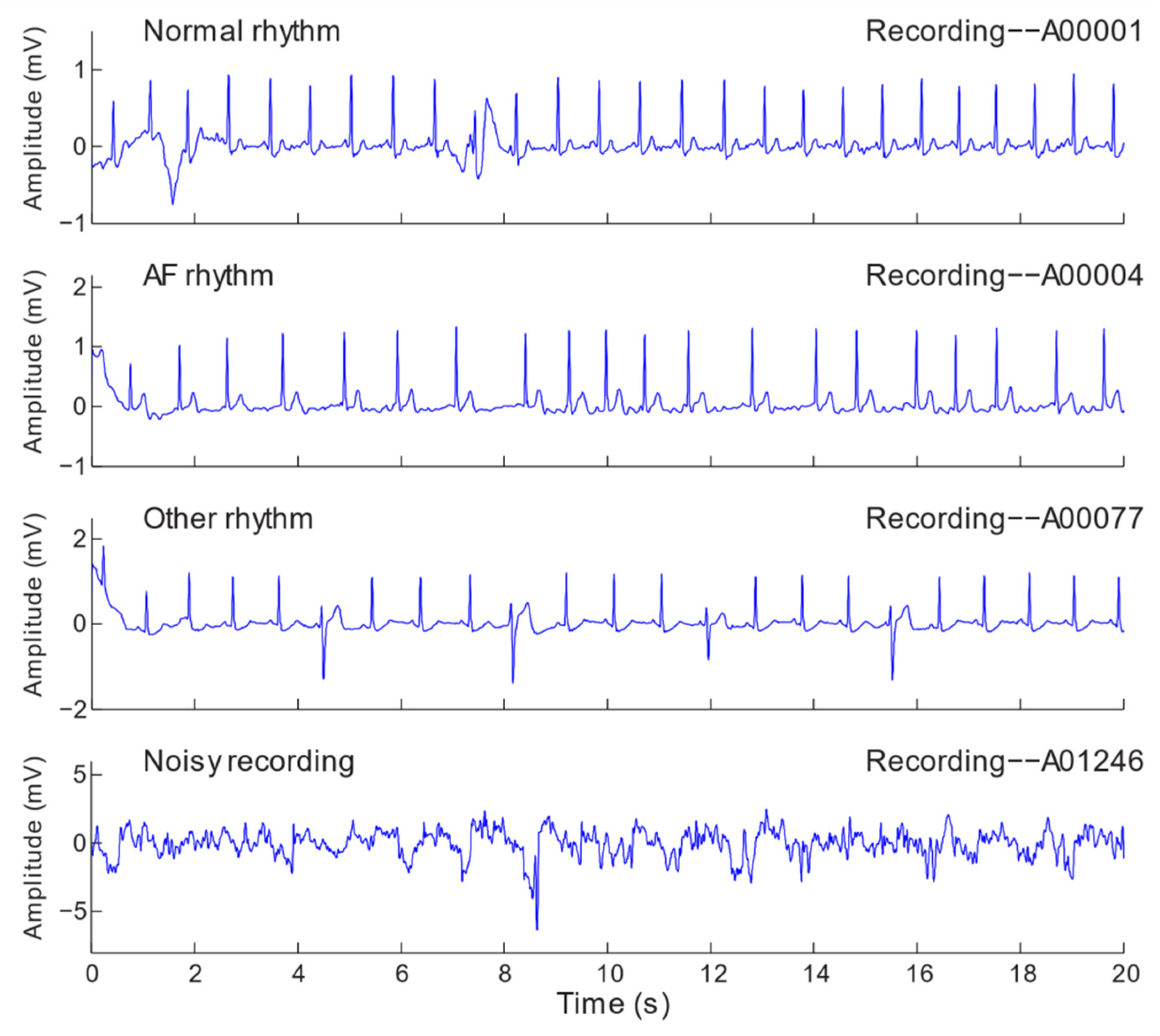
3.1. Dataset
3.2. Evaluation Metrics
3.3. K-Fold Cross-Validation
3.4. Hyperparameter Optimization
3.5. Results and Analysis
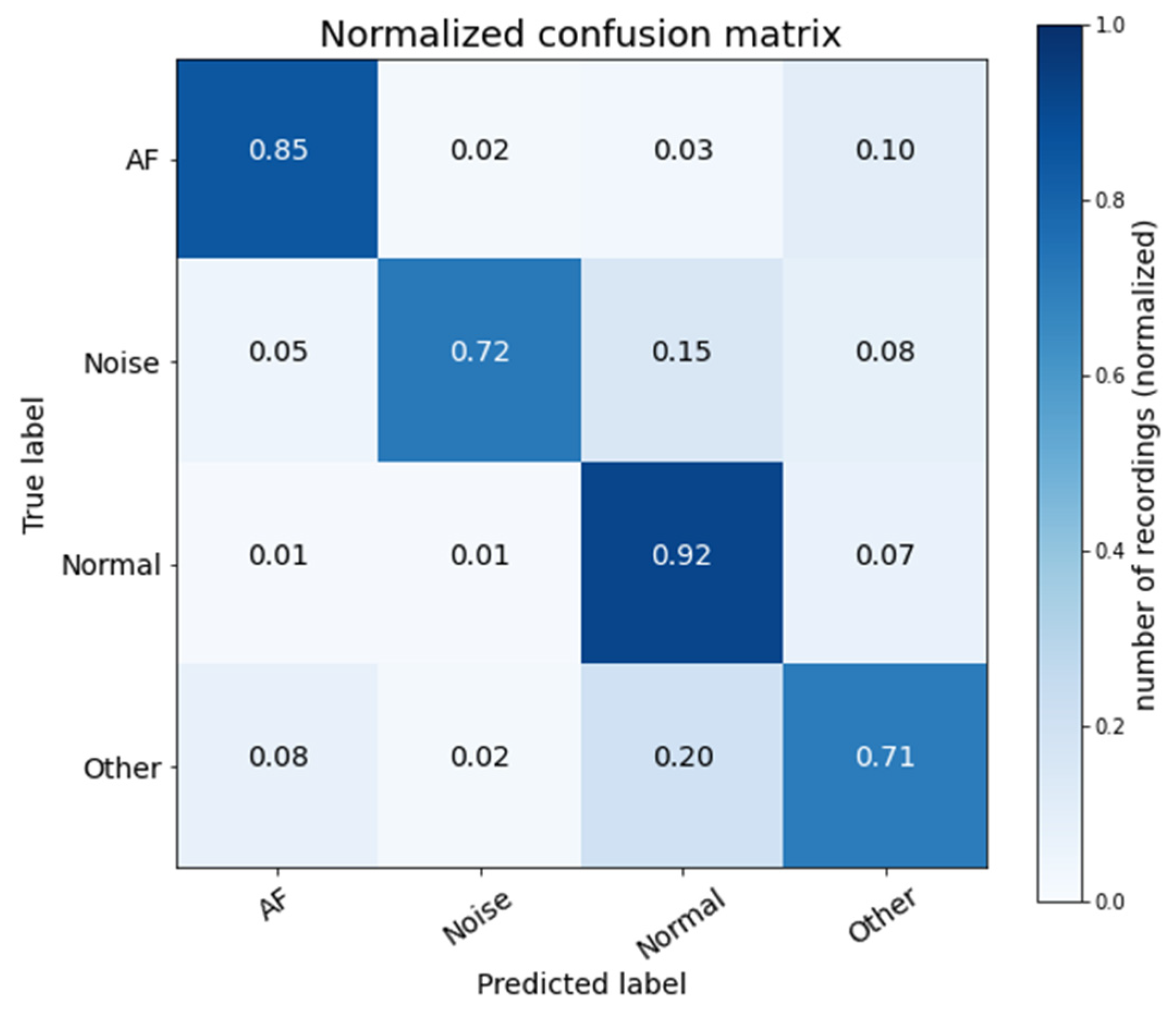
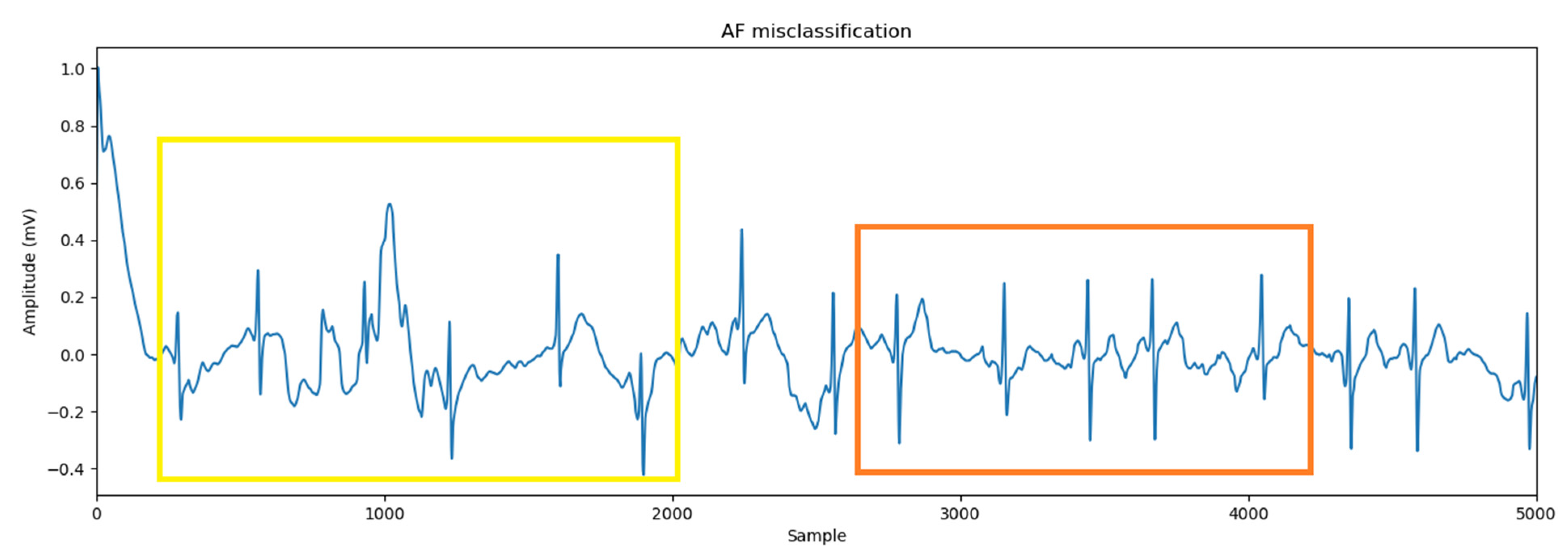
3.5.1. Prediction Accuracy
3.5.2. Network Architecture Analysis
3.5.3. Network Complexity Analysis
3.5.4. Comparison of Various Methods
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Atrial Fibrillation. Available online: https://www.mayoclinic.org/diseases-conditions/atrial-fibrillation/symptoms-causes/syc-20350624 (accessed on 18 October 2019).
- Conrad, N.; Judge, A.; Tran, J.; Mohseni, H.; Hedgecott, D.; Crespillo, A.P.; Allison, M.; Hemingway, H.; Cleland, J.G.; McMurray, J.J.V. Temporal trends and patterns in heart failure incidence: A population-based study of 4 million individuals. Lancet 2018, 391, 572–580. [Google Scholar] [CrossRef]
- Cook, C.; Cole, G.; Asaria, P.; Jabbour, R.; Francis, D.P. The annual global economic burden of heart failure. Int. J. Cardiol. 2014, 171, 368–376. [Google Scholar] [CrossRef] [PubMed]
- Mathew, S.T.; Patel, J.; Joseph, S. Atrial fibrillation: mechanistic insights and treatment options. Eur. J. Intern. Med. 2009, 20, 672–681. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Ding, H.; Ung, B.; Emma, P.M.; Zhang, Y. Automatic online detection of atrial fibrillation based on symbolic dynamics and Shannon entropy. Biomed. Eng. Online 2014, 13, 18. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, J.; Danioko, S.; Yao, H.; Guo, H.; Rakovski, C. A 12-lead electrocardiogram database for arrhythmia research covering more than 10,000 patients. Sci. Data 2020, 7, 48. [Google Scholar] [CrossRef]
- Clifford, G.D.; Liu, C.; Moody, B.; Lehman, L.H.; Silva, I.; Li, Q.; Johnson, A.E.; Mark, R.G. AF classification from a short single lead ECG recording: The PhysioNet Computing in Cardiology Challenge 2017. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; Volume 44, pp. 1–4. [Google Scholar]
- Tang, X.; Shu, L. Classification of electrocardiogram signals with RS and quantum neural networks. Int. J. Multimed. Ubiquitous Eng. 2014, 9, 363–372. [Google Scholar] [CrossRef]
- Osowski, S.; Linh, T.H. ECG beat recognition using fuzzy hybrid neural network. IEEE Trans. Biomed. Eng. 2001, 48, 1265–1271. [Google Scholar] [CrossRef]
- Linh, T.H.; Osowski, S.; Stodolski, M. On-line heartbeat recognition using Hermite polynomials and neuron-fuzzy network. IEEE Trans. Instrum. Meas. 2003, 52, 1224–1231. [Google Scholar] [CrossRef]
- Mitra, S.; Mitra, M.; Chaudhuri, B.B. A rough set-based inference engine for ECG classification. IEEE Trans. Instrum. Meas. 2006, 55, 2198–2206. [Google Scholar] [CrossRef]
- Melgani, F.; Bazi, Y. Classification of electrocardiogram signals with support vector machines and particle swarm optimization. IEEE Trans. Inf. Technol. Biomed. 2008, 12, 667–677. [Google Scholar] [CrossRef]
- Llamedo, M.; Martínez, J.P. Heartbeat classification using feature selection driven by database generalization criteria. IEEE Trans. Biomed. Eng. 2011, 58, 616–625. [Google Scholar] [CrossRef] [PubMed]
- Homaeinezhad, M.R.; Atyabi, S.A.; Tavakkoli, E.; Toosi, H.N.; Ghaffari, A.; Ebrahimpour, R. ECG arrhythmia recognition via a neuro-SVM–KNN hybrid classifier with virtual QRS image-based geometrical features. Expert Syst. Appl. 2012, 39, 2047–2058. [Google Scholar] [CrossRef]
- Rai, H.M.; Trivedi, A.; Shukla, S. ECG signal processing for abnormalities detection using multi-resolution wavelet transform and artificial neural network classifier. Measurement 2013, 46, 3238–3246. [Google Scholar] [CrossRef]
- Yeh, Y.C.; Wang, W.J.; Chiou, C.W. A novel fuzzy c-means method for classifying heartbeat cases from ECG signals. Measurement 2010, 43, 1542–1555. [Google Scholar] [CrossRef]
- Tantawi, M.M.; Revett, K.; Salem, A.B.M.; Tolba, M.F. Fiducial feature reduction analysis for electrocardiogram (ECG) based biometric recognition. J. Intell. Inf. Syst. 2013, 40, 17–39. [Google Scholar] [CrossRef]
- Gaetano, A.D.; Panunzi, S.; Rinaldi, F.; Risi, A.; Sciandrone, M. A patient adaptable ECG beat classifier based on neural networks. Appl. Math. Comput. 2009, 213, 243–249. [Google Scholar] [CrossRef]
- Datta, S.; Puri, C.; Mukherjee, A.; Banerjee, R.; Choudhury, A.D.; Singh, R.; Ukil, A.; Bandyopadhyay, S.; Pal, A.; Khandelwal, S. Identifying normal, AF and other abnormal ECG rhythms using a cascaded binary classifier. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; Volume 44, pp. 1–4. [Google Scholar]
- Luo, K.; Li, J.; Wang, Z.; Cuschieri, A. Patient-specific deep architectural model for ECG classification. J. Healthc. Eng. 2017, 2017, 4108720. [Google Scholar] [CrossRef]
- Andreotti, F.; Carr, O.; Pimentel, M.A.F.; Mahdi, A.; Vos, M.D. Comparing feature-based classifiers and convolutional neural networks to detect arrhythmia from short segments of ECG. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; Volume 44, pp. 1–4. [Google Scholar]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-Level Arrhythmia Detection with Convolutional Neural Networks. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- Warrick, P.; Homsi, M.N. Cardiac arrhythmia detection from ECG combining convolutional and long short-term memory networks. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; Volume 44, pp. 1–4. [Google Scholar]
- Zihlmann, M.; Perekrestenko, D.; Tschannen, M. Convolutional recurrent neural networks for electrocardiogram classification. In Proceedings of the 2017 Computing in Cardiology (CinC), Rennes, France, 24–27 September 2017; Volume 44, pp. 1–4. [Google Scholar]
- Hsieh, C.H.; Chen, J.Y.; Nien, B.H. Deep learning-based indoor localization using received signal strength and channel state information. IEEE Access 2019, 7, 33256–33267. [Google Scholar] [CrossRef]
- Zhou, Z.; Lin, Y.; Zhang, Z.; Wu, Y.; Johnson, P. Earthquake detection in 1-D time series data with feature selection and dictionary learning. Seismol. Res. Lett. 2019, 90, 563–572. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. In Proceedings of the 27th International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018, Part III; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sasaki, Y. The truth of the f-measure. In Teaching Tutorial Materials; University of Manchester: Manchester, UK, 2007. [Google Scholar]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. Components of a New Research Resource for Complex Physiologic Signals. Physiobank Physiotoolkit Physionet 2003, 101, 23. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2008. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 7th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2019, arXiv:1409.1556. [Google Scholar]
- Yang, G.; Pennington, J.; Rao, V.; Sohl-Dickstein, J.; Schoenholz, S.S. A Mean Field Theory of Batch Normalization. arXiv 2019, arXiv:1902.08129. [Google Scholar]
- Yu, D.; Wang, H.; Chen, P.; Wei, Z. Mixed pooling for convolutional neural networks. In Rough Sets and Knowledge Technology: 9th International Conference; Springer: Cham, Switzerland, 2014; pp. 364–375. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
| Layers | Parameters | Activation |
|---|---|---|
| Conv1D | Filter 32/kernel 5 | ReLU |
| BN | ||
| Maxpooling | 2 | |
| Conv1D | Filter 32/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Conv1D | Filter 64/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Conv1D | Filter 64/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Conv1D | Filter 128/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Conv1D | Filter 128/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Dropout | 0.5 | |
| Conv1D | Filter 256/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Conv1D | Filter 256/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Dropout | 0.5 | |
| Conv1D | Filter 512/kernel 5 | ReLU |
| Maxpooling | 2 | |
| Dropout | 0.5 | |
| Conv1D | Filter 512/kernel 5 | ReLU |
| Flatten | ||
| Dense | 128 | ReLU |
| Dropout | 0.5 | |
| Dense | 32 | ReLU |
| Dense | 4 | Softmax |
| Ground Truth | |||||
|---|---|---|---|---|---|
| AF (A) | Normal (N) | Noisy (~) | Other (O) | ||
| Predicted | AF (a) | Aa | Na | ~a | Oa |
| Normal (n) | An | Nn | ~n | On | |
| Noisy (~) | A~ | N~ | ~~ | O~ | |
| Other (o) | Ao | No | ~o | Oo | |
| Ground Truth | |||
|---|---|---|---|
| AF (A) | Non-AF (NA) | ||
| Predicted | AF (a) | Aa | NAa |
| Non-AF (na) | Ana | NAna | |
| Train/Test | AF | Normal | Noisy | Other | Average |
|---|---|---|---|---|---|
| 60:40 | 72.0 | 90.0 | 60.0 | 69.0 | 72.75 |
| 70:30 | 76.0 | 90.0 | 60.0 | 70.0 | 74.00 |
| 80:20 | 77.0 | 89.0 | 67.0 | 74.0 | 76.75 |
| 90:10 | 76.9 | 90.0 | 62.1 | 72.8 | 75.45 |
| Layer | Kernel Size | Batch Size | Learning Rate | Average F1 | σ | Total Number of Parameters |
|---|---|---|---|---|---|---|
| 8 | 3 | 50 | 0.001 | 69.4 | 12.5 | 2,558,340 |
| 5 | 50 | 0.001 | 72.2 | 12.9 | 2,687,428 | |
| 7 | 70 | 0.0005 | 73.6 | 11.4 | 2,816,516 | |
| 9 | 3 | 50 | 0.001 | 76.6 | 9.6 | 1,608,324 |
| 5 | 50 | 0.0001 | 77.2 | 9.9 | 1,868,484 | |
| 7 | 30 | 0.0005 | 76.8 | 11.4 | 2,128,644 | |
| 10 | 3 | 90 | 0.0005 | 77.0 | 9.4 | 2,428,292 |
| 5 | 30 | 0.0001 | 77.8 | 9.1 | 3,212,740 | |
| 7 | 50 | 0.001 | 76.4 | 10.6 | 3,997,188 | |
| 11 | 3 | 50 | 0.0005 | 77.1 | 9.9 | 2,625,412 |
| 5 | N/A | N/A | N/A | N/A | N/A | |
| 7 | N/A | N/A | N/A | N/A | N/A |
| Neural Networks | Average F1 Score | Total Number of Parameters |
|---|---|---|
| Proposed-1 | 77.8 | 3,212,740 |
| All-BN | 69.2 | 3,216,644 |
| No-BN | 76.2 | 3,212,676 |
| Maxpooling | 67.7 | 2,885,060 |
| Max-Average pooling | 75.6 | 2,885,060 |
| Proposed-2 | 78.2 | 3,212,740 |
| Extra-Average | 77.4 | 2,885,060 |
| Layer Type | Output Shape | Parameters |
|---|---|---|
| Conv1D | 8996 × 32 | 192 |
| Batch Normalization | 8996 × 32 | 128 |
| Conv1D | 4494 × 32 | 5152 |
| Conv1D | 2243 × 64 | 10,304 |
| Conv1D | 1117 × 64 | 20,544 |
| Conv1D | 554 × 128 | 41,088 |
| Conv1D | 273 × 128 | 82,048 |
| Conv1D | 132 × 256 | 164,096 |
| Conv1D | 62 × 256 | 327,936 |
| Conv1D | 27 × 512 | 655,872 |
| Conv1D | 9 × 512 | 1,311,232 |
| Dense | 128 | 589,952 |
| Dense | 32 | 4128 |
| Dense | 4 | 132 |
| Total number of network training parameters: 3,212,740 | ||
| Methods | AF (A) | Normal (N) | Noisy (~) | Other (O) |
|---|---|---|---|---|
| Proposed-1 | 79.1 | 90.7 | 65.3 | 76.0 |
| Proposed-2 | 80.8 | 90.4 | 66.2 | 75.3 |
| CRNN | 76.4 | 88.8 | 64.5 | 72.6 |
| ResNet-1 | 65.7 | 90.2 | 64.0 | 69.8 |
| ResNet-2 | 67.7 | 88.5 | 65.6 | 66.6 |
| CL3-I | 76.0 | 90.1 | 47.1 | 75.2 |
| Methods | Average F1 Score of A, N, ~, and O | Average F1 Score of A, N, and O | Total Number of Parameters |
|---|---|---|---|
| Proposed-1 | 77.8 | 81.9 | 3,212,740 |
| Proposed-2 | 78.2 | 82.2 | 3,212,740 |
| CRNN | 75.6 | 79.3 | 10,149,440 |
| ResNet-1 | 72.4 | 75.2 | 10,466,148 |
| ResNet-2 | 72.1 | 74.3 | 1,219,508 |
| CL3-I | 72.1 | 80.4 | 206,334 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, C.-H.; Li, Y.-S.; Hwang, B.-J.; Hsiao, C.-H. Detection of Atrial Fibrillation Using 1D Convolutional Neural Network. Sensors 2020, 20, 2136. https://doi.org/10.3390/s20072136
Hsieh C-H, Li Y-S, Hwang B-J, Hsiao C-H. Detection of Atrial Fibrillation Using 1D Convolutional Neural Network. Sensors. 2020; 20(7):2136. https://doi.org/10.3390/s20072136
Chicago/Turabian StyleHsieh, Chaur-Heh, Yan-Shuo Li, Bor-Jiunn Hwang, and Ching-Hua Hsiao. 2020. "Detection of Atrial Fibrillation Using 1D Convolutional Neural Network" Sensors 20, no. 7: 2136. https://doi.org/10.3390/s20072136
APA StyleHsieh, C.-H., Li, Y.-S., Hwang, B.-J., & Hsiao, C.-H. (2020). Detection of Atrial Fibrillation Using 1D Convolutional Neural Network. Sensors, 20(7), 2136. https://doi.org/10.3390/s20072136





