A Simple Condition Monitoring Method for Gearboxes Operating in Impulsive Environments
Abstract
1. Introduction
- SASE is sensitive to non-Gaussian noise.
- SASE is not capable of separating the synchronous and non-synchronous damaged components.
2. Gearbox Diagnostics
2.1. Synchronous Data Modelling
2.2. Estimating the Central Tendency of the Synchronous Data
- . This is a reasonable assumption because it is expected that the synchronous characteristics would be more representative than the non-synchronous data at a specific angular position.
- The distributions are non-overlapping. This assumption is made for mathematical convenience, but is also the most difficult case to consider. This is because the damage of the non-synchronous component is then very prominent in the data and would likely affect the estimated statistics.
2.3. Synchronous Statistics
2.4. Condition Indicators
3. Numerical Investigation
3.1. Modelling Impulsive Noise: -Stable Processes
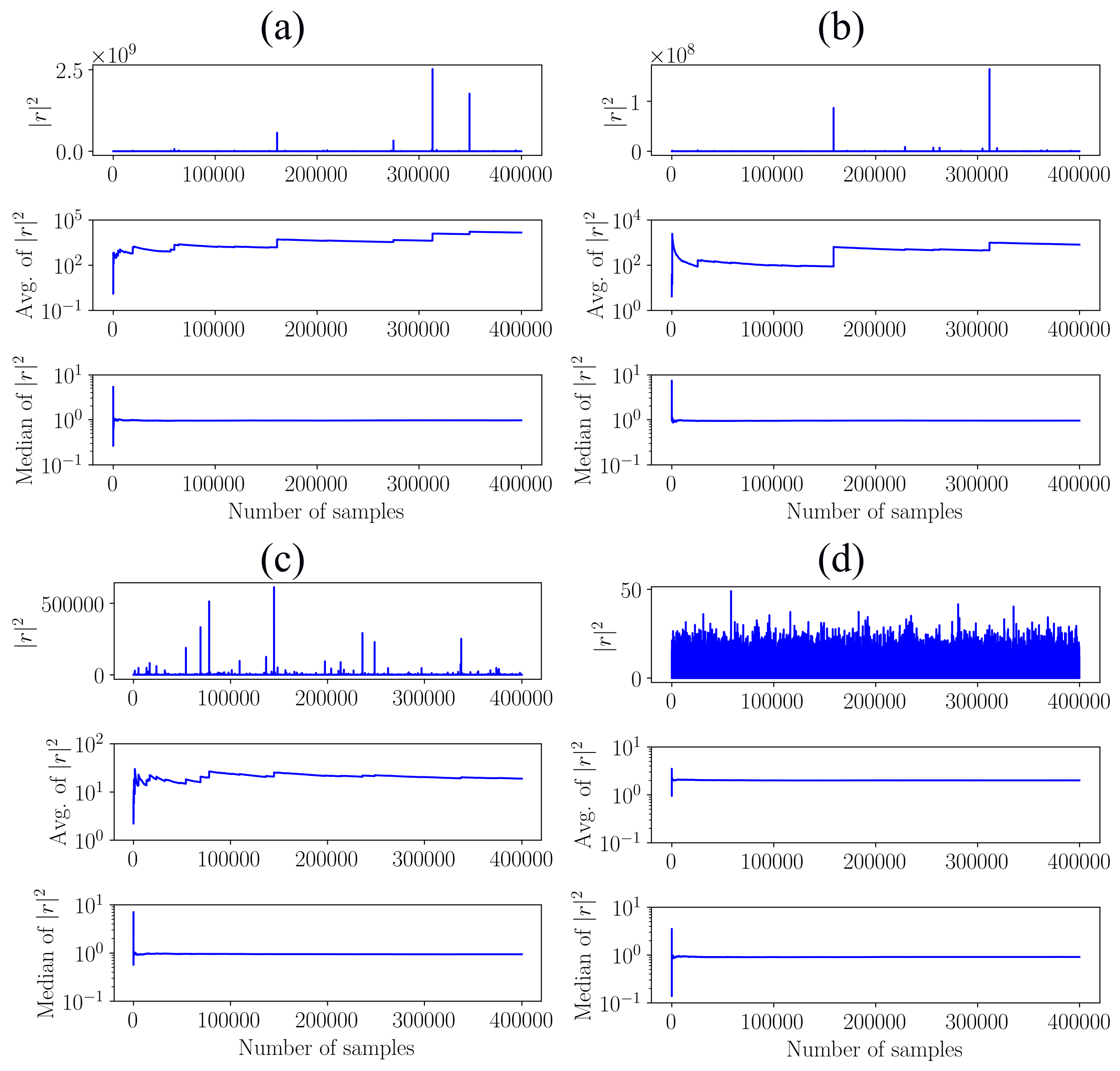
3.2. Convergence of the Average and Median Estimators
3.3. Performance of SMSE and SASE in Impulsive Noise
4. Experimental Investigation
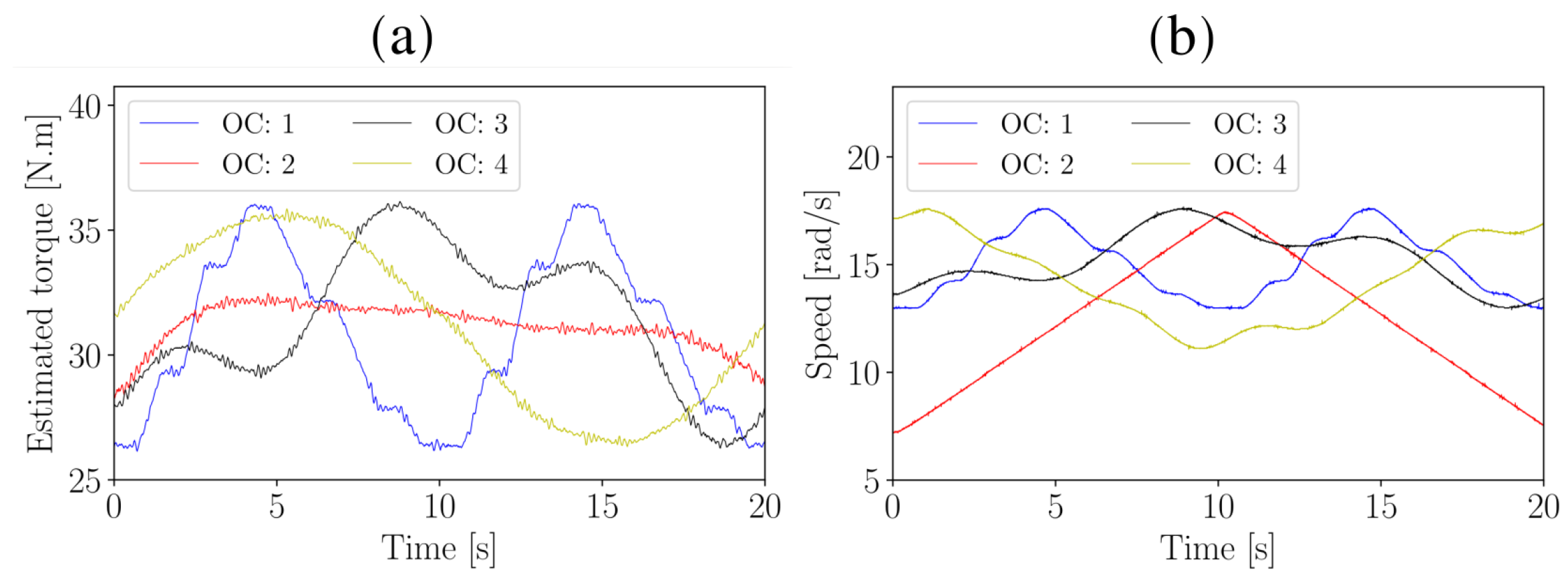
4.1. Overview of Experimental Setup
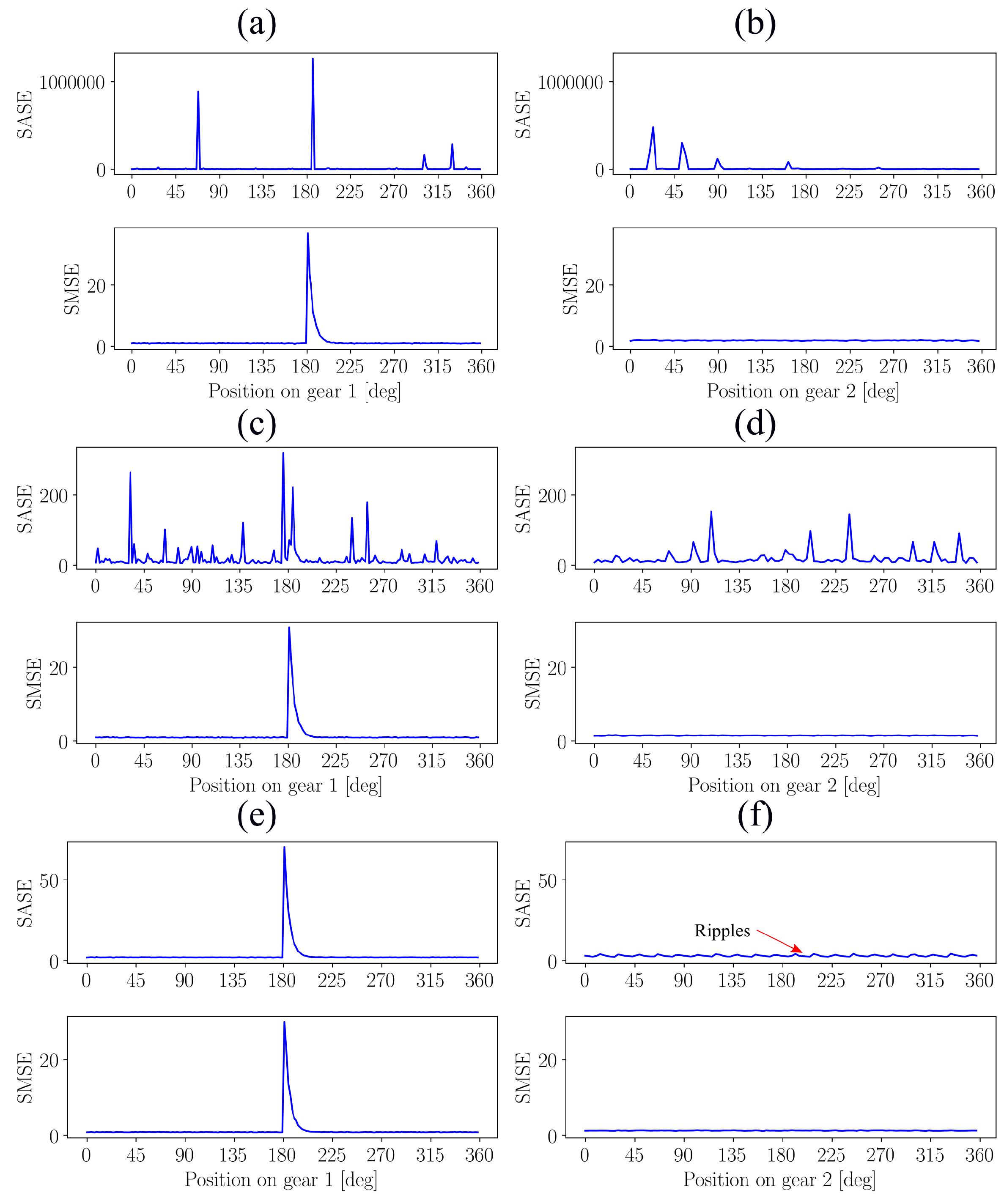
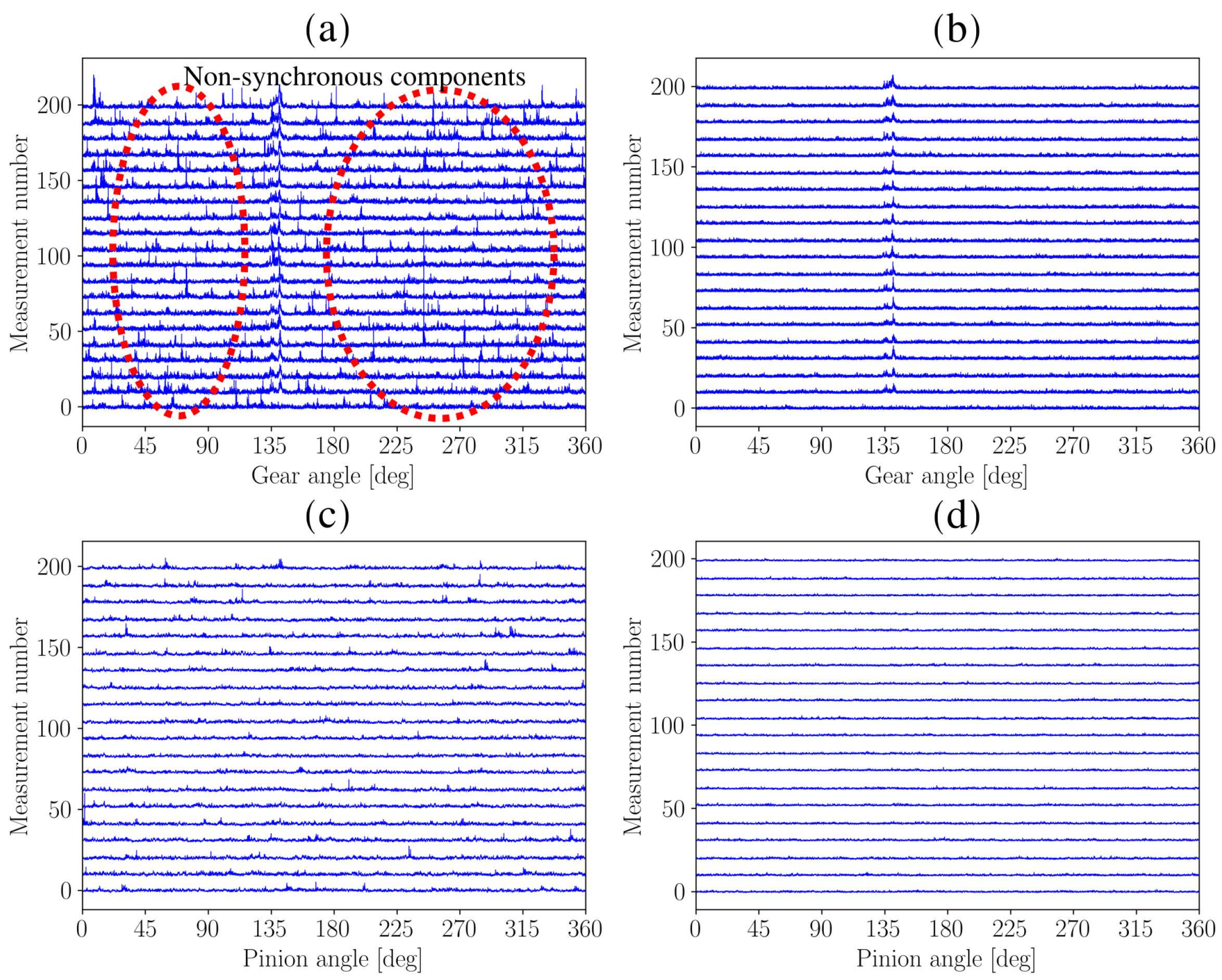
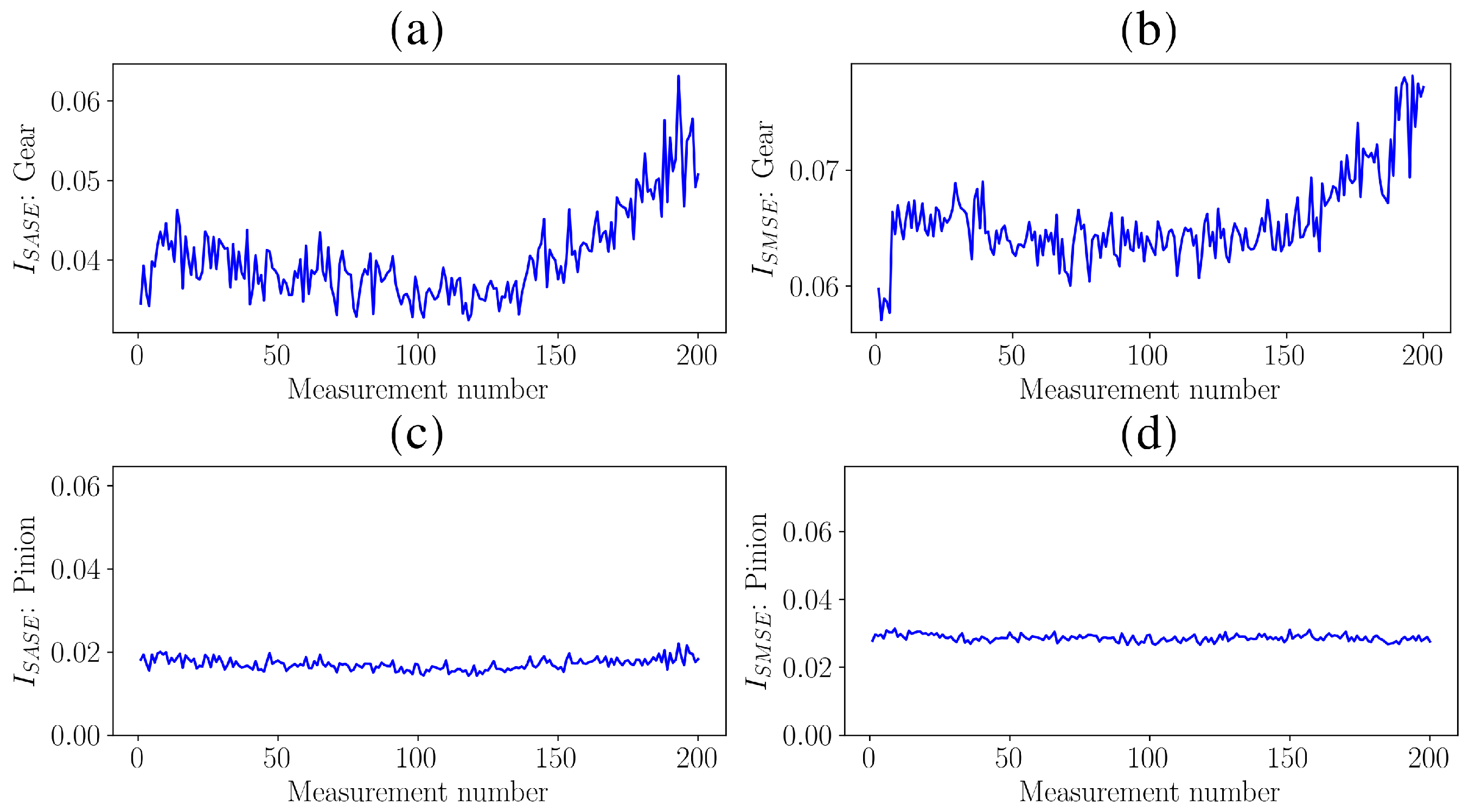
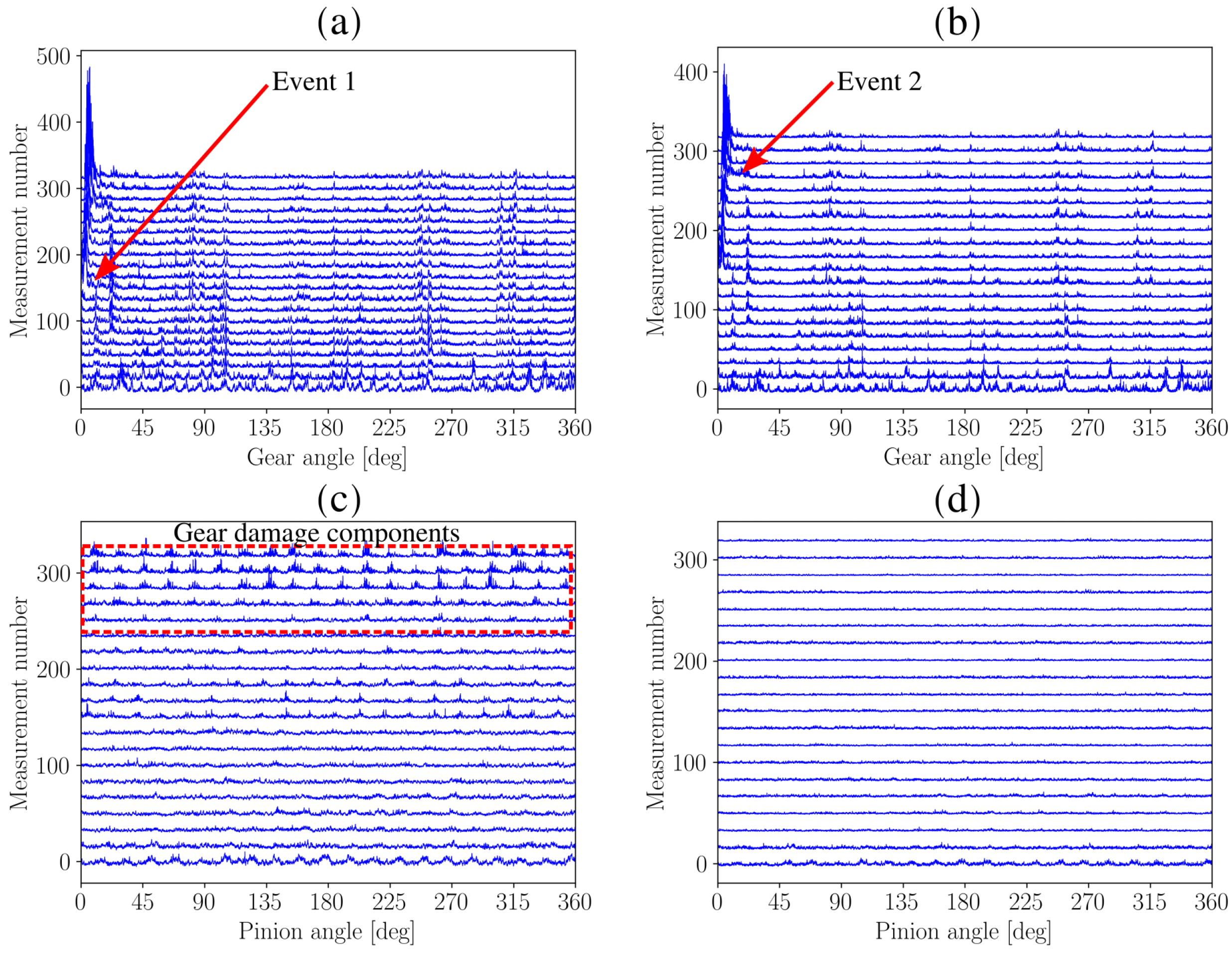
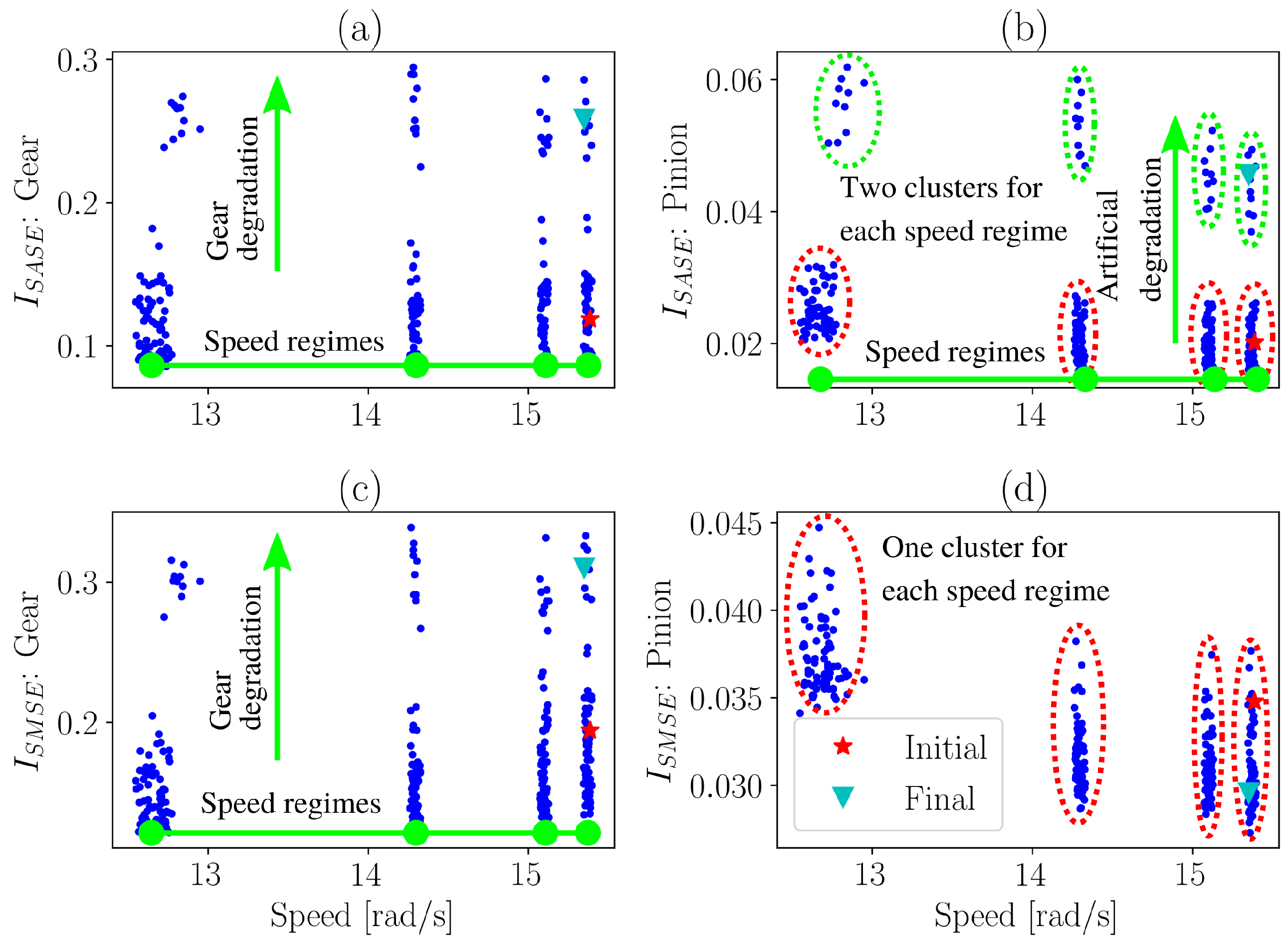
4.2. Localised Gear Damage Investigation
4.3. Distributed Gear Damage Investigation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
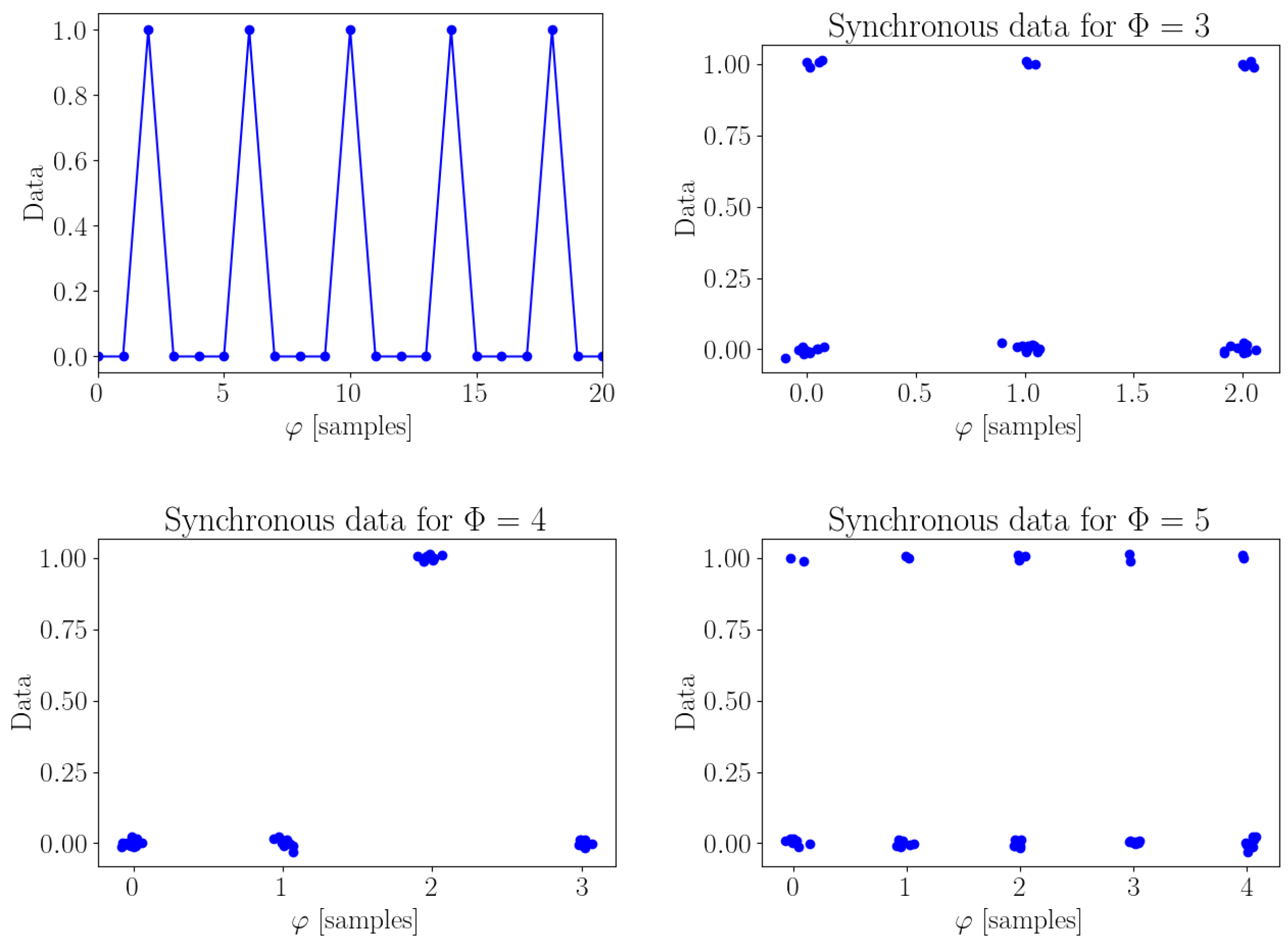
Appendix A. The Multimodality of Synchronous Data
References
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Zimroz, R.; Bartelmus, W.; Barszcz, T.; Urbanek, J. Diagnostics of bearings in presence of strong operating conditions non-stationarity—A procedure of load-dependent features processing with application to wind turbine bearings. Mech. Syst. Signal Process. 2014, 46, 16–27. [Google Scholar] [CrossRef]
- Bartelmus, W.; Zimroz, R. A new feature for monitoring the condition of gearboxes in non-stationary operating conditions. Mech. Syst. Signal Process. 2009, 23, 1528–1534. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- El-Thalji, I.; Liyanage, J.P. On the operation and maintenance practices of wind power asset. J. Qual. Maint. Eng. 2012, 18, 232–266. [Google Scholar] [CrossRef]
- Lin, Y.; Tu, L.; Liu, H.; Li, W. Fault analysis of wind turbines in China. Renew. Sustain. Energy Rev. 2016, 55, 482–490. [Google Scholar] [CrossRef]
- Obuchowski, J.; Wylomanska, A.; Zimroz, R. Selection of informative frequency band in local damage detection in rotating machinery. Mech. Syst. Signal Process. 2014, 48, 138–152. [Google Scholar] [CrossRef]
- Stander, C.J.; Heyns, P.S. Transmission path phase compensation for gear monitoring under fluctuating load conditions. Mech. Syst. Signal Process. 2006, 20, 1511–1522. [Google Scholar] [CrossRef]
- McFadden, P.D.; Toozhy, M.M. Application of synchronous averaging to vibration monitoring of rolling element bearings. Mech. Syst. Signal Process. 2000, 14, 891–906. [Google Scholar] [CrossRef]
- Wang, W. Early detection of gear tooth cracking using the resonance demodulation technique. Mech. Syst. Signal Process. 2001, 15, 887–903. [Google Scholar] [CrossRef]
- Schmidt, S.; Mauricio, A.; Heyns, P.S.; Gryllias, K.C. A methodology for identifying information rich frequency bands for diagnostics of mechanical components-of-interest under time-varying operating conditions. Mech. Syst. Signal Process. 2020, 142, 106739. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.S.; Gryllias, K.C. A pre-processing methodology to enhance novel information for rotating machine diagnostics. Mech. Syst. Signal Process. 2019, 124, 541–561. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.S. Localised gear anomaly detection without historical data for reference density estimation. Mech. Syst. Signal Process. 2019, 121, 615–635. [Google Scholar] [CrossRef]
- Abboud, D.; Antoni, J.; Sieg-Zieba, S.; Eltabach, M. Envelope analysis of rotating machine vibrations in variable speed conditions: A comprehensive treatment. Mech. Syst. Signal Process. 2017, 84, 200–226. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Smith, W.A.; Borghesani, P.; Ni, Q.; Wang, K.; Peng, Z. Optimal demodulation-band selection for envelope-based diagnostics: A comparative study of traditional and novel tools. Mech. Syst. Signal Process. 2019, 134, 106303. [Google Scholar] [CrossRef]
- Mauricio, A.; Qi, J.; Smith, W.A.; Sarazin, M.; Randall, R.B.; Janssens, K.; Gryllias, K. Bearing diagnostics under strong electromagnetic interference based on Integrated Spectral Coherence. Mech. Syst. Signal Process. 2020, 140, 106673. [Google Scholar] [CrossRef]
- Antoni, J.; Borghesani, P. A statistical methodology for the design of condition indicators. Mech. Syst. Signal Process. 2019, 114, 290–327. [Google Scholar] [CrossRef]
- Antoni, J.; Bonnardot, F.; Raad, A.; El Badaoui, M. Cyclostationary modelling of rotating machine vibration signals. Mech. Syst. Signal Process. 2004, 18, 1285–1314. [Google Scholar] [CrossRef]
- Fyfe, K.R.; Munck, E.D.S. Analysis of computed order tracking. Mech. Syst. Signal Process. 1997, 11, 187–205. [Google Scholar] [CrossRef]
- Leclère, Q.; André, H.; Antoni, J. A multi-order probabilistic approach for instantaneous angular speed tracking debriefing of the CMMNO’14 diagnosis contest. Mech. Syst. Signal Process. 2016, 81, 375–386. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.S. Normalisation of the amplitude modulation caused by time-varying operating conditions for condition monitoring. Measurement 2020, 149, 106964. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust statistics: Theory and Methods; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- El-Thalji, I.; Jantunen, E. A summary of fault modelling and predictive health monitoring of rolling element bearings. Mech. Syst. Signal Process. 2015, 60, 252–272. [Google Scholar] [CrossRef]
- Wang, W.; Forrester, B.D.; Frith, P.C. A unified approach to detecting and trending changes caused by mechanical faults in rotating machinery. Struct. Health Monit. 2016, 15, 204–222. [Google Scholar] [CrossRef]
- Schmidt, S.; Heyns, P.S.; De Villiers, J.P. A novelty detection diagnostic methodology for gearboxes operating under fluctuating operating conditions using probabilistic techniques. Mech. Syst. Signal Process. 2018, 100, 152–166. [Google Scholar] [CrossRef]
- Booyse, W.; Wilke, D.N.; Heyns, S. Deep digital twins for detection, diagnostics and prognostics. Mech. Syst. Signal Process. 2020, 140, 106612. [Google Scholar] [CrossRef]
- Liu, C.; Gryllias, K. A semi-supervised Support Vector Data Description-based fault detection method for rolling element bearings based on cyclic spectral analysis. Mech. Syst. Signal Process. 2020, 140, 106682. [Google Scholar] [CrossRef]
- Smith, W.A.; Fan, Z.; Peng, Z.; Li, H.; Randall, R.B. Optimised Spectral Kurtosis for bearing diagnostics under electromagnetic interference. Mech. Syst. Signal Process. 2016, 75, 371–394. [Google Scholar] [CrossRef]
- Sokołowski, J.; Obuchowski, J.; Wyłomańska, A.; Kruczek, P.; Zimroz, R. Multiple local damage detection method based on time-frequency representation and agglomerative hierarchical clustering of temporary spectral content. Appl. Acoust. 2019, 147, 44–55. [Google Scholar] [CrossRef]
- Wodecki, J.; Kruczek, P.; Bartkowiak, A.; Zimroz, R.; Wyłomańska, A. Novel method of informative frequency band selection for vibration signal using Nonnegative Matrix Factorization of spectrogram matrix. Mech. Syst. Signal Process. 2019, 130, 585–596. [Google Scholar] [CrossRef]
- Yu, G.; Li, C.; Zhang, J. A new statistical modeling and detection method for rolling element bearing faults based on alpha-stable distribution. Mech. Syst. Signal Process. 2013, 41, 155–175. [Google Scholar] [CrossRef]
- Żak, G.; Teuerle, M.; Wyłomańska, A.; Zimroz, R. Measures of dependence for alpha-stable distributed processes and its application to diagnostics of local damage in presence of impulsive noise. Shock Vib. 2017, 2017. [Google Scholar] [CrossRef]
- Wyłomańska, A.; Żak, G.; Kruczek, P.; Zimroz, R. Application of tempered stable distribution for selection of optimal frequency band in gearbox local damage detection. Appl. Acoust. 2017, 128, 14–22. [Google Scholar] [CrossRef]
- Peeters, C.; Leclère, Q.; Antoni, J.; Lindahl, P.; Donnal, J.; Leeb, S.; Helsen, J. Review and comparison of tacholess instantaneous speed estimation methods on experimental vibration data. Mech. Syst. Signal Process. 2019, 129, 407–436. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J.; Wang, X.; Lei, Y.; Cao, J. A tacho-less order tracking technique for large speed variations. Mech. Syst. Signal Process. 2013, 40, 76–90. [Google Scholar] [CrossRef]
- Urbanek, J.; Barszcz, T.; Antoni, J. A two-step procedure for estimation of instantaneous rotational speed with large fluctuations. Mech. Syst. Signal Process. 2013, 38, 96–102. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmidt, S.; Zimroz, R.; Chaari, F.; Heyns, P.S.; Haddar, M. A Simple Condition Monitoring Method for Gearboxes Operating in Impulsive Environments. Sensors 2020, 20, 2115. https://doi.org/10.3390/s20072115
Schmidt S, Zimroz R, Chaari F, Heyns PS, Haddar M. A Simple Condition Monitoring Method for Gearboxes Operating in Impulsive Environments. Sensors. 2020; 20(7):2115. https://doi.org/10.3390/s20072115
Chicago/Turabian StyleSchmidt, Stephan, Radoslaw Zimroz, Fakher Chaari, P. Stephan Heyns, and Mohamed Haddar. 2020. "A Simple Condition Monitoring Method for Gearboxes Operating in Impulsive Environments" Sensors 20, no. 7: 2115. https://doi.org/10.3390/s20072115
APA StyleSchmidt, S., Zimroz, R., Chaari, F., Heyns, P. S., & Haddar, M. (2020). A Simple Condition Monitoring Method for Gearboxes Operating in Impulsive Environments. Sensors, 20(7), 2115. https://doi.org/10.3390/s20072115





