Dynamic Hand Gesture Recognition Based on a Leap Motion Controller and Two-Layer Bidirectional Recurrent Neural Network
Abstract
1. Introduction
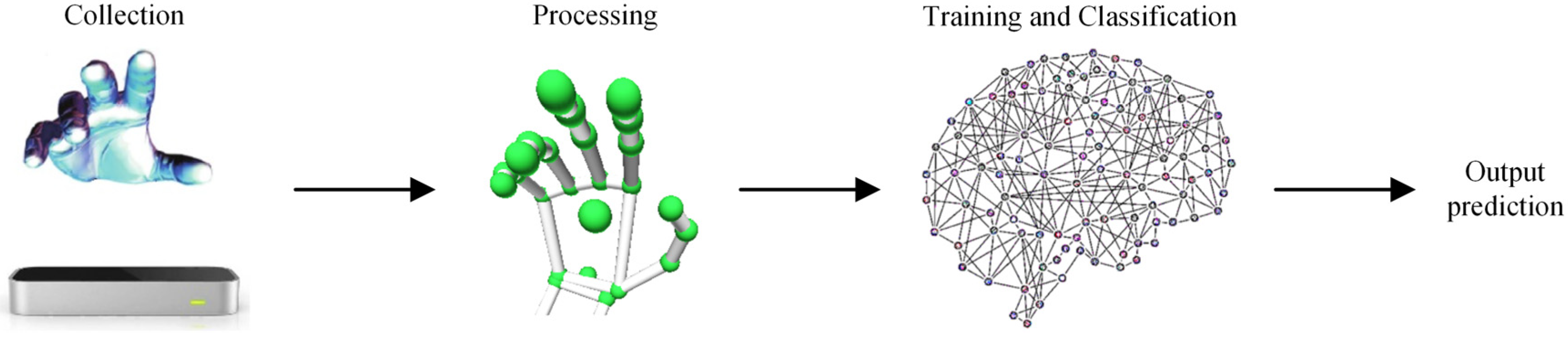
2. Materials and Methods
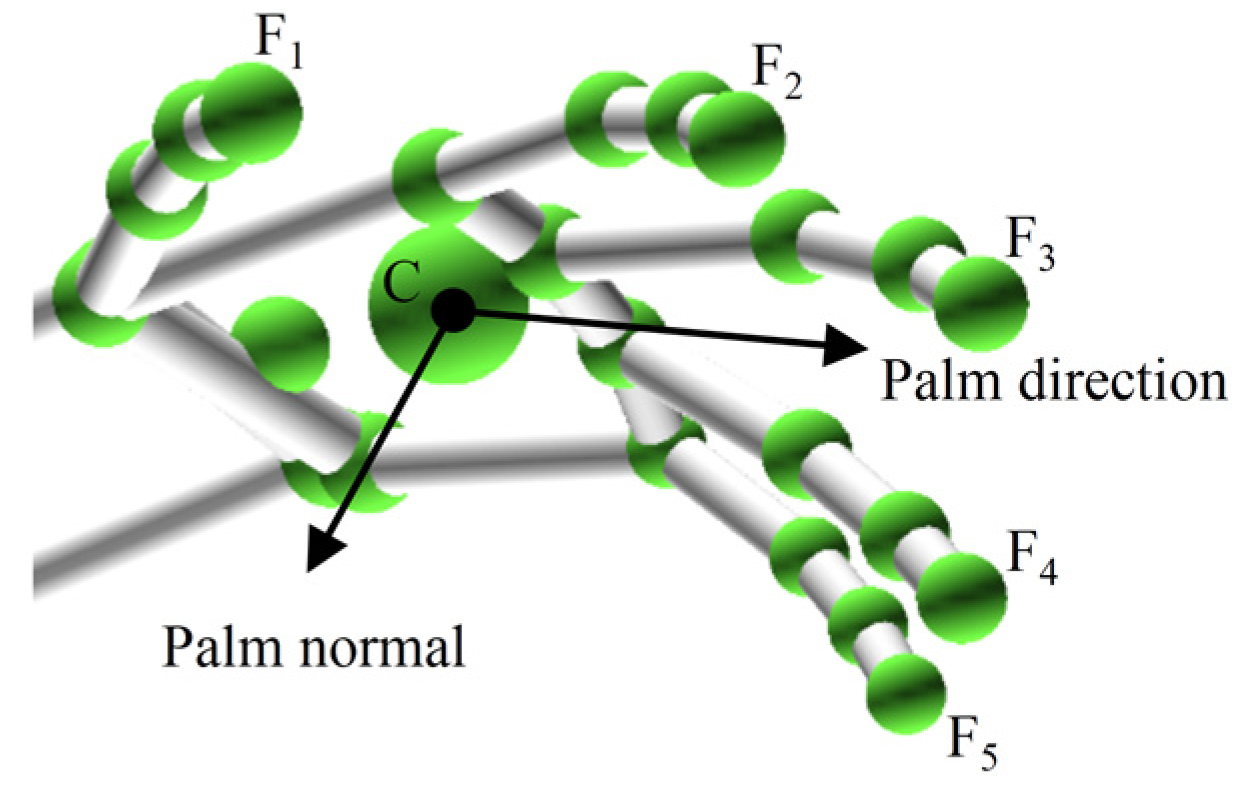
2.1. Feature Extraction
2.2. Data Collection and Processing
| Algorithm 1 |
| If(Hand is not empty) |
| { |
| If ( |
| sqrt (pow (frame. rotation Angle (last frame, x), 2)+ |
| pow (frame. rotation Angle (last frame, y), 2)+ |
| pow (frame. rotation Angle (last frame, z), 2)) |
| >threshold1 |
| or |
| fingertip. velocity > threshold2 |
| ) |
| Start collecting dynamic hand gestures |
| Else |
| Stop collecting dynamic hand gestures |
| } |
| Else |
| Stop collecting dynamic hand gestures |
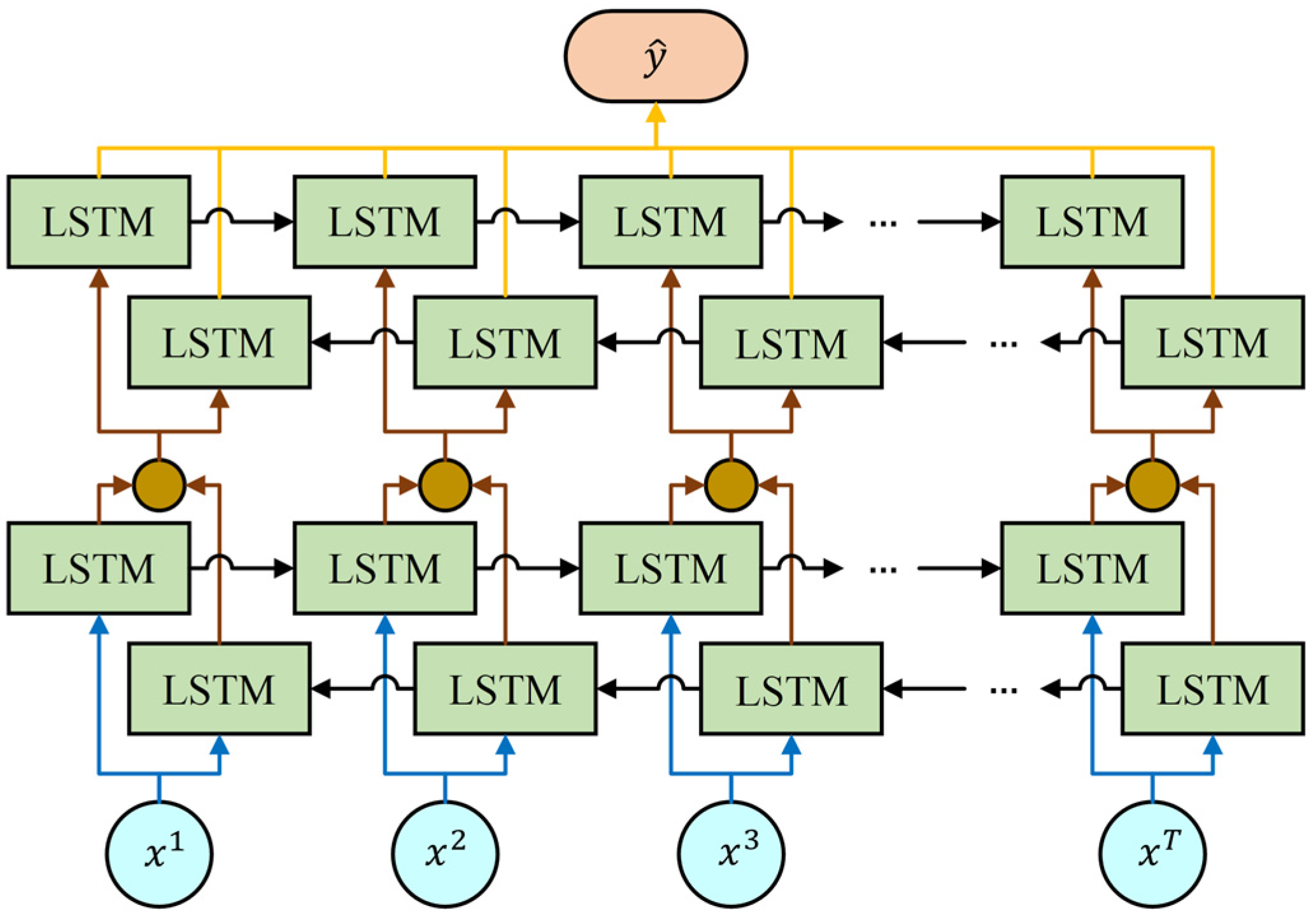
2.3. Two-Layer Bidirectional Recurrent Neural Network
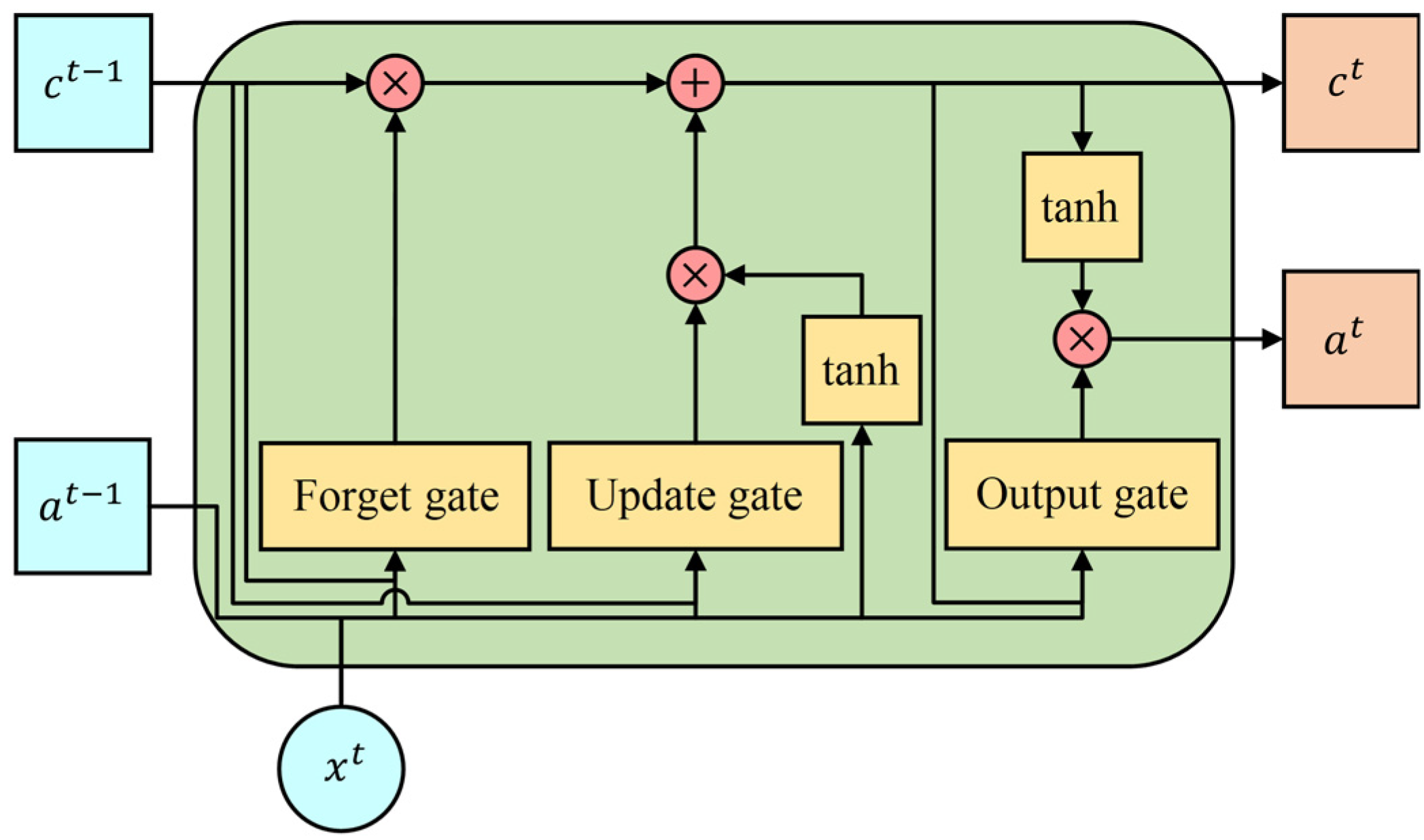
2.3.1. The Basic Long Short-Term Memory Unit
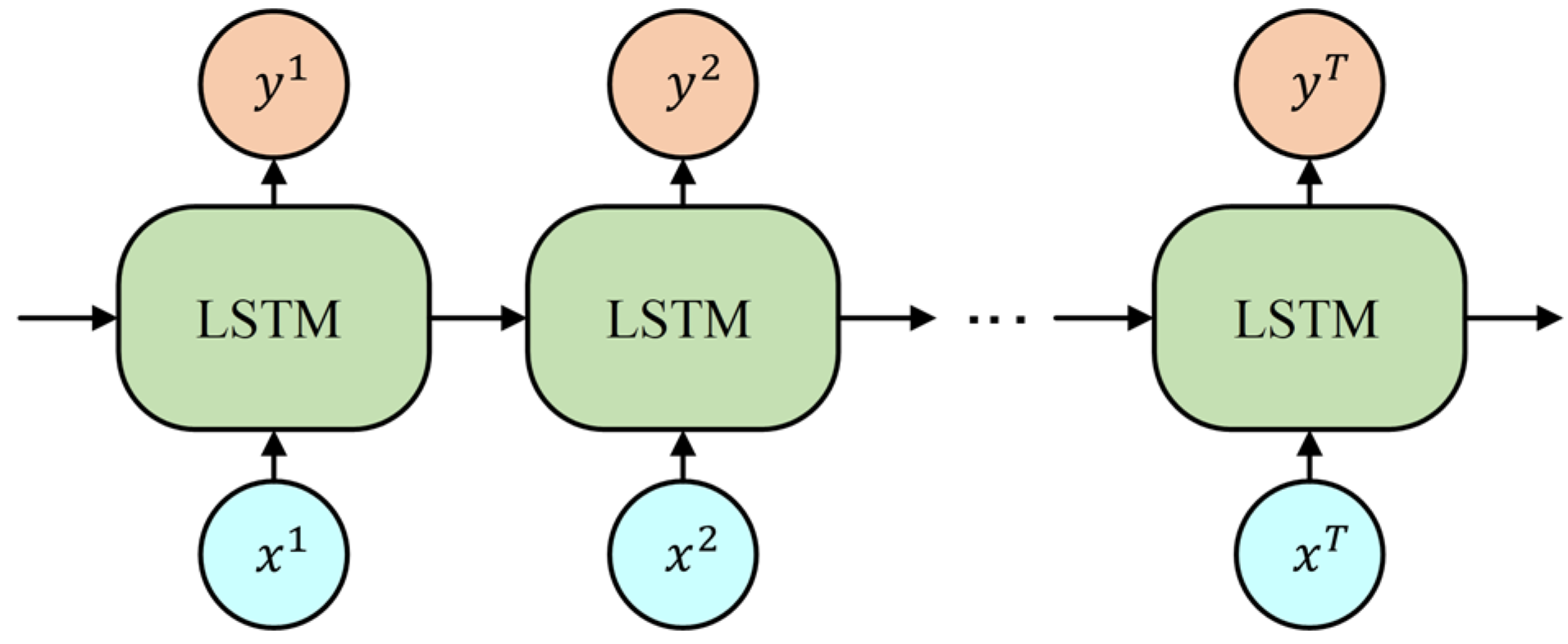
2.3.2. Bidirectional Recurrent Neural Network
2.4. Model Details
2.4.1. Loss Function
2.4.2. Learning Rate
3. Experimental Results and Discussion
3.1. Dynamic Gesture Datasets
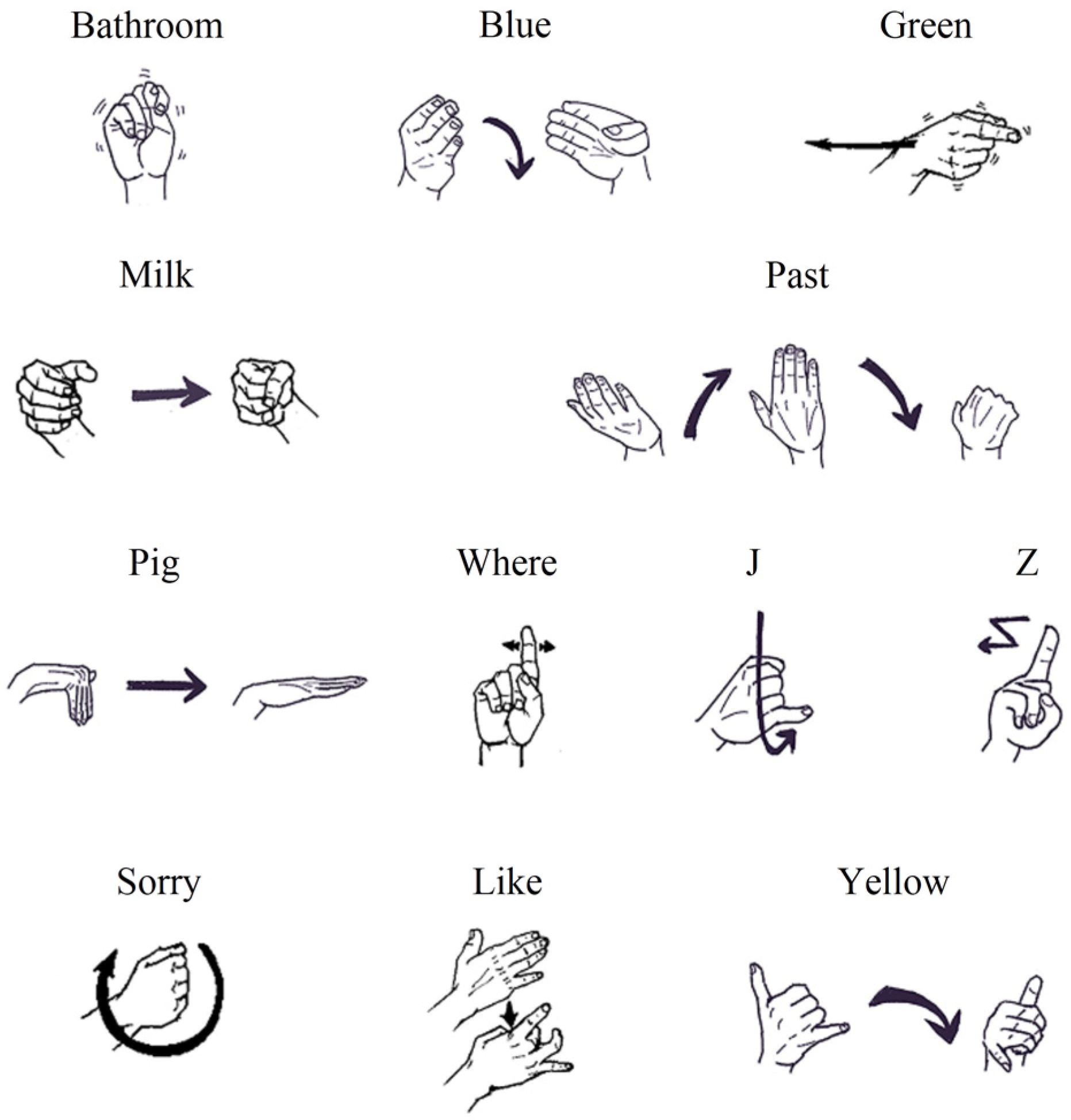
3.1.1. ASL Dataset
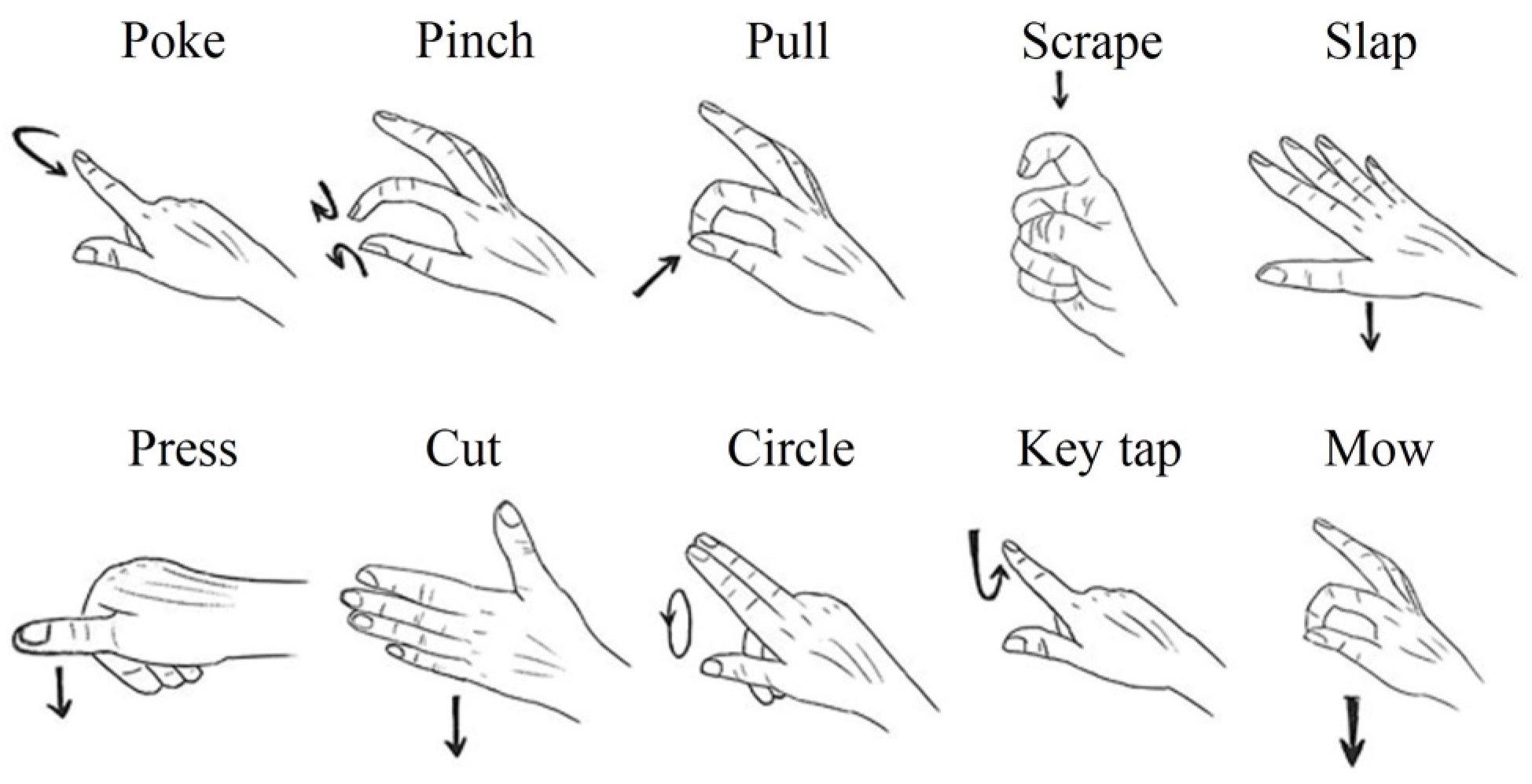
3.1.2. Handicraft-Gesture Dataset
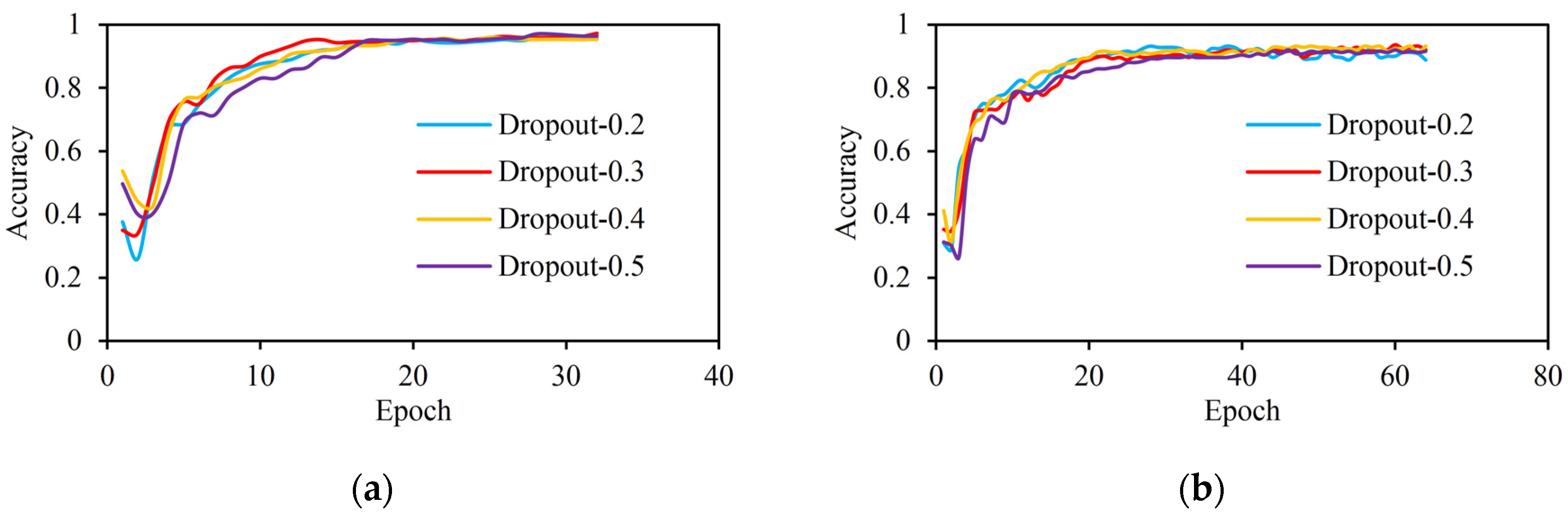
3.2. Selection of the Optimal Dropout Rate on Two Dataset
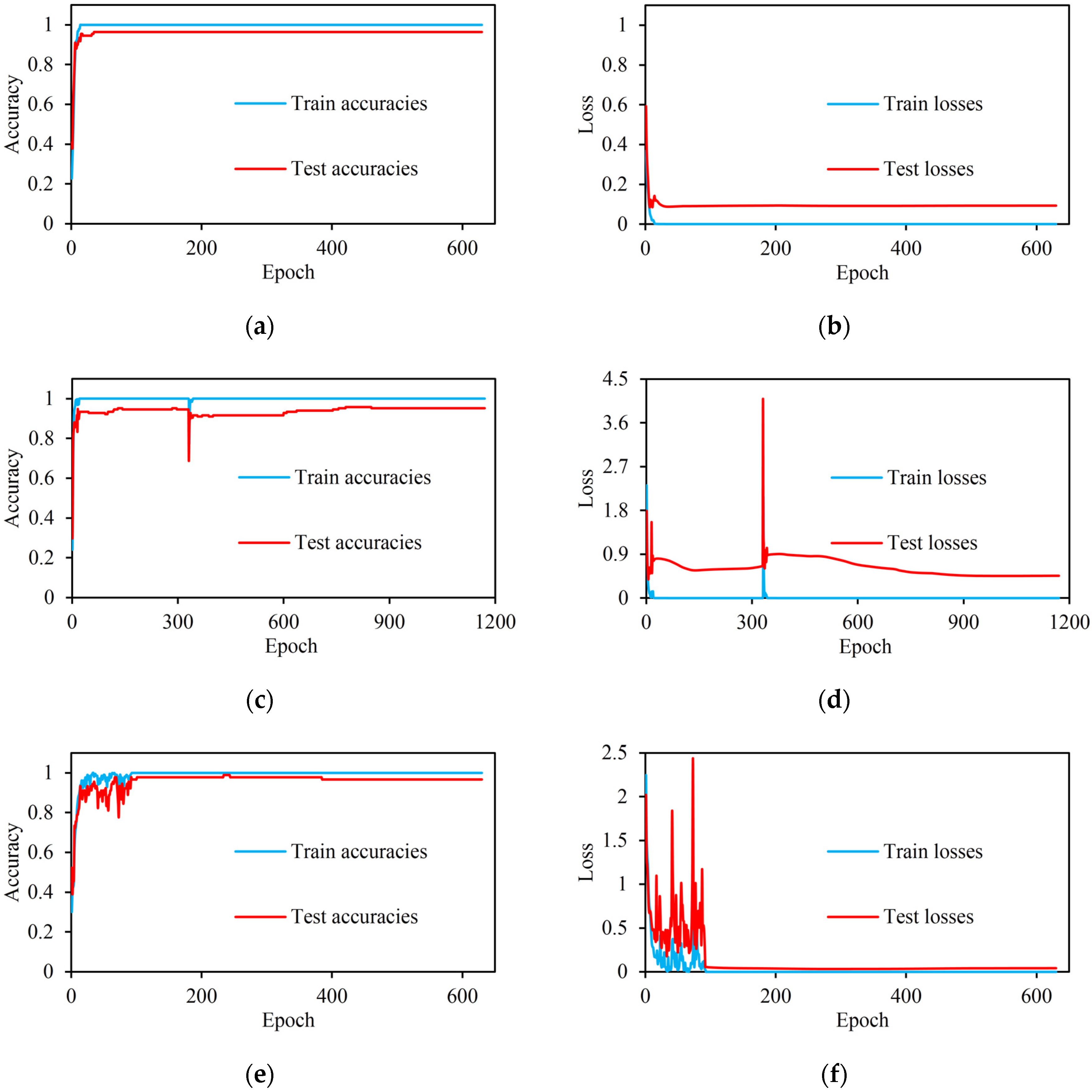
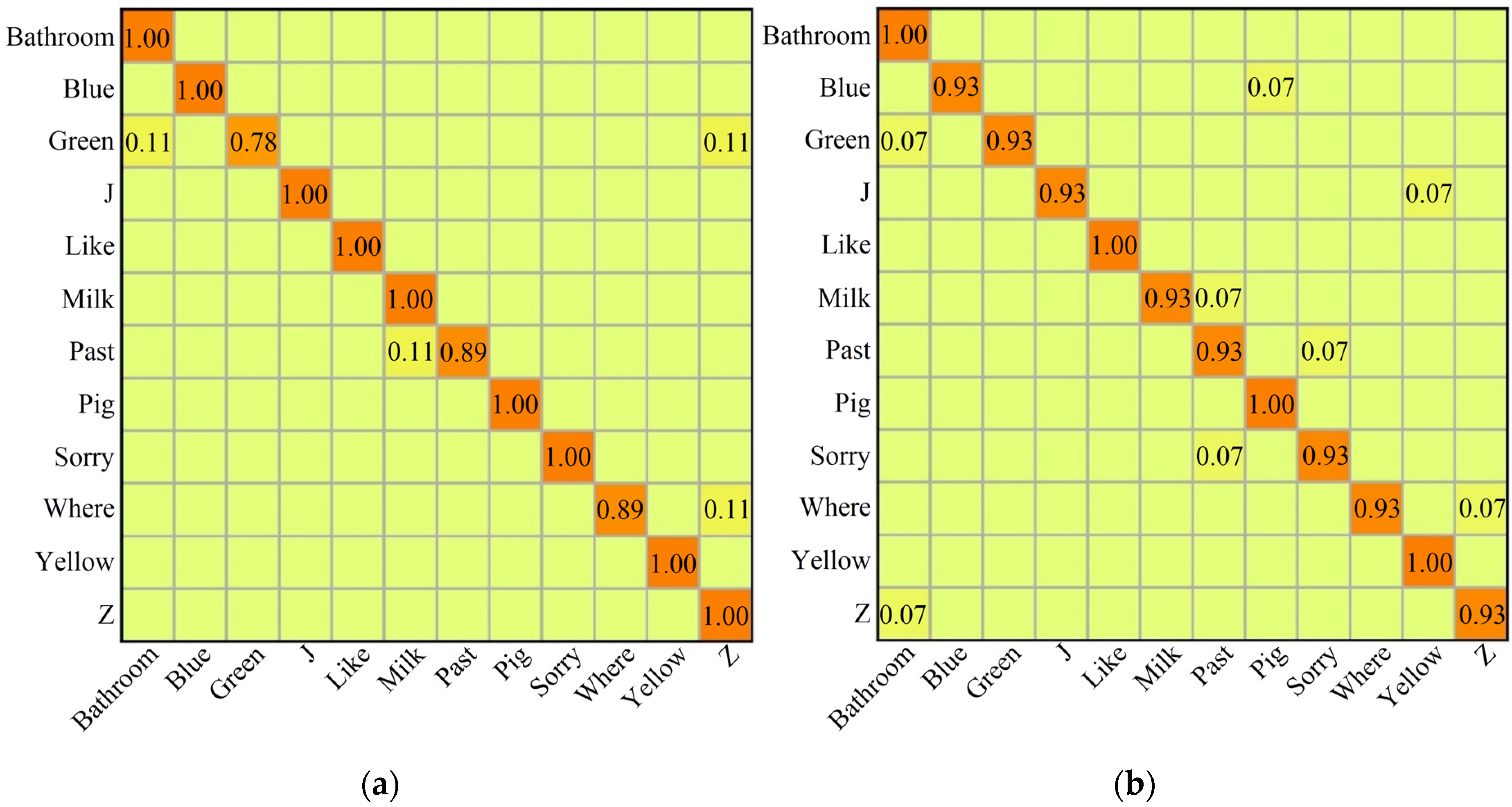
3.3. Experiment Results on ASL Dataset
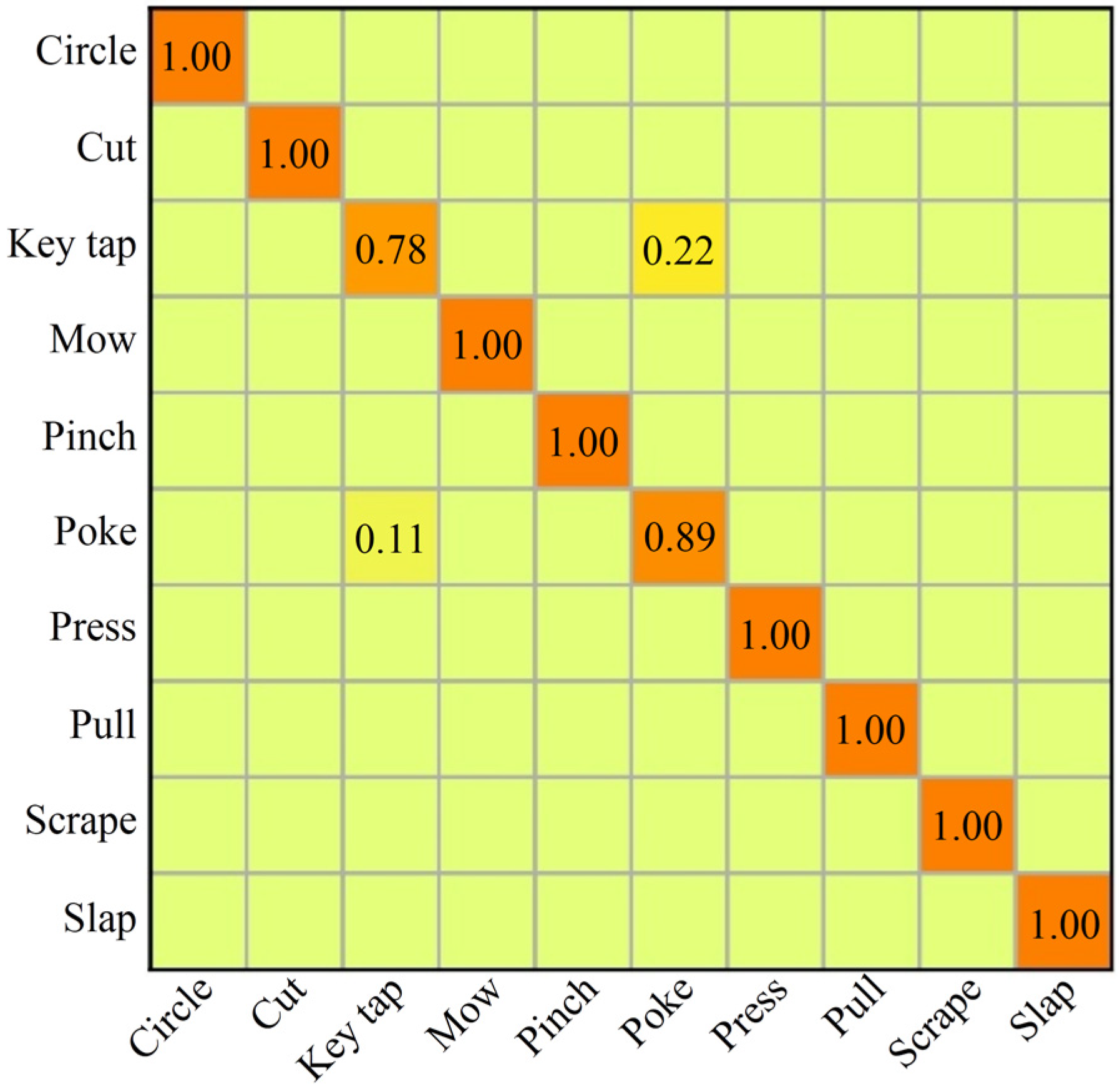
3.4. Experiment Results on Handicraft-Gesture Dataset
3.5. K-Fold and Leave-One-Out Cross-Validation
3.6. Comparisons
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Parimalam, A.; Shanmugam, A.; Raj, A.S.; Murali, N.; Murty, S.A.V.S. Convenient and elegant HCI features of PFBR operator consoles for safe operation. In Proceedings of the 4th International Conference on Intelligent Human Computer Interaction (IHCI), Kharagpur, India, 27–29 December 2012; pp. 1–9. [Google Scholar]
- Minwoo, K.; Jaechan, C.; Seongjoo, L.; Yunho, J. IMU Sensor-Based Hand Gesture Recognition for Human-Machine Interfaces. Sensors 2019, 19, 3827–3839. [Google Scholar]
- Cheng, H.; Yang, L.; Liu, Z.C. Survey on 3D hand gesture recognition. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 1659–1673. [Google Scholar] [CrossRef]
- Cheng, H.; Dai, Z.J.; Liu, Z.C. Image-to-class dynamic time warping for 3D hand gesture recognition. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), San Jose, CA, USA, 15–19 July 2013; pp. 1–6. [Google Scholar]
- Hachaj, T.; Piekarczyk, M. Evaluation of Pattern Recognition Methods for Head Gesture-Based Interface of a Virtual Reality Helmet Equipped with a Single IMU Sensor. Sensors 2019, 19, 5408. [Google Scholar] [CrossRef] [PubMed]
- Rautaray, S.S.; Agrawal, A. Real time hand gesture recognition system for dynamic applications. IJU 2012, 3, 21–31. [Google Scholar] [CrossRef]
- Hu, T.J.; Zhu, X.J.; Wang, X.Q. Human stochastic closed-loop behavior for master-slave teleoperation using multi-leap-motion sensor. Sci. China Tech. Sci. 2017, 60, 374–384. [Google Scholar] [CrossRef]
- Bergh, M.V.D.; Carton, D.; Nijs, R.D.; Mitsou, N.; Landsiedel, C.; Kuehnlenz, K.; Wollherr, D.; Gool, L.V.; Buss, M. Real-time 3D hand gesture interaction with a robot for understanding directions from humans. In Proceedings of the Ro-Man, Atlanta, GA, USA, 31 July–3 August 2011; pp. 357–362. [Google Scholar]
- Doe-Hyung, L.; Kwang-Seok, H. Game interface using hand gesture recognition. In Proceedings of the 5th International Conference on Computer Sciences and Convergence Information Technology (ICCIT), Seoul, Korea, 30 November–2 December 2010; pp. 1092–1097. [Google Scholar]
- Rautaray, S.S.; Agrawal, A. Interaction with virtual game through hand gesture recognition. In Proceedings of the International Conference on Multimedia, Signal Processing and Communication Technologies (IMPACT), Aligarh, India, 17–19 December 2011; pp. 244–247. [Google Scholar]
- Kim, T.; Shakhnarovich, G.; Livescu, K. Fingerspelling recognition with semi-Markov conditional random fields. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 1521–1528. [Google Scholar]
- Myoung-Kyu, S.; Sang-Heon, L.; Dong-Ju, K. A comparison of 3D hand gesture recognition using dynamic time warping. In Proceedings of the 27th Conference on Image and Vision Computing New Zealand (IVCNZ), Dunedin, New Zealand, 26–28 November 2012; pp. 418–422. [Google Scholar]
- Nobutaka, S.; Yoshiaki, S.; Yoshinori, K.; Juno, M. Hand gesture estimation and model refinement using monocular camera-ambiguity limitation by inequality constraints. In Proceedings of the 3rd IEEE International Conference on Automatic Face and Gesture Recognition (FG), Nara, Japan, 14–16 April 1998; pp. 268–273. [Google Scholar]
- Youngmo, H. A low-cost visual motion data glove as an input device to interpret human hand gestures. IEEE Trans. Consum. Electron. 2010, 56, 501–509. [Google Scholar]
- Guna, J.; Jakus, G.; Pogačnik, M.; Sašo, T.; Jaka, S. An analysis of the precision and reliability of the leap motion sensor and its suitability for static and dynamic tracking. Sensors 2014, 14, 3702–3720. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Y. Microsoft kinect sensor and its effect. IEEE Multimed. 2012, 19, 4–10. [Google Scholar] [CrossRef]
- Xu, Y.R.; Wang, Q.Q.; Bai, X.; Chen, Y.L.; Wu, X.Y. A novel feature extracting method for dynamic gesture recognition based on support vector machine. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 437–441. [Google Scholar]
- Karthick, P.; Prathiba, N.; Rekha, V.B.; Thanalaxmi, S. Transforming Indian sign language into text using leap motion. IJIRSET 2014, 3, 10906–10910. [Google Scholar]
- Schramm, R.; Jung, C.R.; Miranda, E.R. Dynamic time warping for music conducting gestures evaluation. IEEE Trans. Multimed. 2014, 17, 243–255. [Google Scholar] [CrossRef]
- Kumar, P.; Saini, R.; Roy, P.P.; Dogra, D.P. Study of text segmentation and recognition using leap motion sensor. IEEE Sens. J. 2016, 17, 1293–1301. [Google Scholar] [CrossRef]
- Lu, W.; Tong, Z.; Chu, J.H. Dynamic hand gesture recognition with leap motion controller. IEEE Signal Process. Lett. 2016, 23, 1188–1192. [Google Scholar] [CrossRef]
- Zhang, Q.X.; Deng, F. Dynamic gesture recognition based on leapmotion and HMM-CART model. In Proceedings of the 2017 International Conference on Cloud Technology and Communication Engineering (CTCE), Guilin, China, 18–20 August 2017; pp. 1–8. [Google Scholar]
- Avola, D.; Bernardi, M.; Cinque, L.; Foresti, G.L.; Massaroni, C. Exploiting recurrent neural networks and leap motion controller for the recognition of sign language and semaphoric hand gestures. IEEE Trans. Multimed. 2018, 21, 234–245. [Google Scholar] [CrossRef]
- Zeng, W.; Wang, C.; Wang, Q.H. Hand gesture recognition using Leap Motion via deterministic learning. Multimed. Tools Appl. 2018, 77, 28185–28206. [Google Scholar] [CrossRef]
- Mittal, A.; Kumar, P.; Roy, P.P.; Balasubramanian, R.; Chaudhuri, B.B. A Modified LSTM Model for Continuous Sign Language Recognition Using Leap Motion. IEEE Sens. J. 2019, 19, 7056–7063. [Google Scholar] [CrossRef]
- Deriche, M.; Aliyu, S.O.; Mohandes, M. An Intelligent Arabic Sign Language Recognition System Using a Pair of LMCs With GMM Based Classification. IEEE Sens. J. 2019, 19, 8067–8078. [Google Scholar] [CrossRef]
- Marin, G.; Dominio, F.; Zanuttigh, P. Hand gesture recognition with leap motion and kinect devices. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 1565–1569. [Google Scholar]
- Marin, G.; Dominio, F.; Zanuttigh, P. Hand gesture recognition with jointly calibrated leap motion and depth sensor. Multimed. Tools Appl. 2016, 75, 14991–15015. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; pp. 665–667. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 464–472. [Google Scholar]
- Semeniuta, S.; Severyn, A.; Barth, E. Recurrent dropout without memory loss. In Proceedings of the 26th International Conference on Computational Linguistics (COLING), Osaka, Japan, 11–16 December 2016; pp. 1757–1766. [Google Scholar]
- Gal, Y.; Ghahramani, Z. A theoretically grounded application of dropout in recurrent neural networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 1019–1027. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inform. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Liang, H.; Fu, W.L.; Yi, F.J. A Survey of Recent Advances in Transfer Learning. In Proceedings of the IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 1516–1523. [Google Scholar]
- Kurakin, A.; Zhang, Z.Y.; Liu, Z.C. A real time system for dynamic hand gesture recognition with a depth sensor. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 1975–1979. [Google Scholar]
- Wang, J.; Liu, Z.C.; Chorowski, J.; Chen, Z.Y.; Wu, Y. Robust 3d action recognition with random occupancy patterns. In Proceedings of the European Conference on Computer Vision (ECCV), Florence, Italy, 7–13 October 2012; pp. 872–885. [Google Scholar]
| Type | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| 360 samples | 96.2963% | 96.8182% | 96.2963% | 96.2674% |
| 480 samples | 95.238% | 95.546% | 95.238% | 95.274% |
| Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|
| 96.6667% | 96.75% | 96.6667% | 96.6563% |
| ASL Dataset (360 Samples) (%) | ASL Dataset (480 Samples) (%) | Handicraft-Gesture Dataset (%) | |
|---|---|---|---|
| 1 | 95.83 | 90.63 | 93.33 |
| 2 | 95.83 | 94.79 | 83.33 |
| 3 | 84.72 | 90.63 | 90 |
| 4 | 94.44 | 94.79 | 83.33 |
| 5 | 95.83 | 97.93 | 93.33 |
| Average: | 93.33 | 93.75 | 88.66 |
| ASL Dataset (360 Samples) (%) | ASL Dataset (480 Samples) (%) | Handicraft-Gesture Dataset (%) | |
|---|---|---|---|
| 1 | 94.44 | 97.92 | 100 |
| 2 | 88.89 | 93.75 | 93.33 |
| 3 | 91.67 | 95.83 | 96.67 |
| 4 | 91.67 | 89.53 | 86.67 |
| 5 | 97.2 | 91.67 | 86.67 |
| 6 | 97.2 | 87.5 | 83.33 |
| 7 | 86.1 | 91.67 | 76.67 |
| 8 | 100 | 97.92 | 96.67 |
| 9 | 97.2 | 97.92 | 86.67 |
| 10 | 97.2 | 91.67 | 93.33 |
| Average: | 94.1 | 93.5 | 90 |
| ASL Dataset (360 Samples) (%) | ASL Dataset (480 Samples) (%) | Handicraft-Gesture Dataset (%) | |
|---|---|---|---|
| Average: | 98.33 | 98.13 | 92 |
| Method | Dataset | Accuracy |
|---|---|---|
| This paper’s method | ASL (360 samples) | 96.3% |
| This paper’s method | ASL (480 samples) | 95.2% |
| Deep Recurrent Neural Network on Depth Features [23] | ASL (480 samples) | 95.2% |
| Hidden Conditional Neural Field on Depth Features [21] | ASL (360 samples) | 89.5% |
| Action Graph on Silhouette Features [37] | ASL (360 samples) | 87.7% |
| SVM on Random Occupancy Pattern Features [38] | ASL (334 samples) | 88.5% |
| Method | Dataset | Accuracy |
|---|---|---|
| This paper’s method | Handicraft-Gesture (300 samples) | 96.7% |
| Hidden Conditional Neural Field on Depth Features [21] | Handicraft-Gesture (300 samples) | 95% |
| Dataset | Item | Epoch | Time(h) |
|---|---|---|---|
| ASL dataset with 360 samples | single experiment (7:3) | 620 | 2 |
| 5-fold cross-validation (4:1) | 612 | 9.7 | |
| 10-fold cross-validation (9:1) | 612 | 29.52 | |
| Leave-One-Out cross-validation (359:1) | 5 | 5.4 | |
| ASL dataset with 480 samples | single experiment (13:7) | 1170 | 4.4 |
| 5-fold cross-validation (4;1) | 720 | 13.1 | |
| 10-fold cross-validation (9:1) | 810 | 31.3 | |
| Leave-One-Out cross-validation (479:1) | 5 | 9.5 | |
| Handicraft-Gesture dataset with 300 samples | single experiment (7:3) | 630 | 1.8 |
| 5-fold cross-validation (4:1) | 630 | 8.8 | |
| 10-fold cross-validation (9:1) | 810 | 24.9 | |
| Leave-One-Out cross-validation (299:1) | 5 | 3.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Chen, J.; Zhu, W. Dynamic Hand Gesture Recognition Based on a Leap Motion Controller and Two-Layer Bidirectional Recurrent Neural Network. Sensors 2020, 20, 2106. https://doi.org/10.3390/s20072106
Yang L, Chen J, Zhu W. Dynamic Hand Gesture Recognition Based on a Leap Motion Controller and Two-Layer Bidirectional Recurrent Neural Network. Sensors. 2020; 20(7):2106. https://doi.org/10.3390/s20072106
Chicago/Turabian StyleYang, Linchu, Ji’an Chen, and Weihang Zhu. 2020. "Dynamic Hand Gesture Recognition Based on a Leap Motion Controller and Two-Layer Bidirectional Recurrent Neural Network" Sensors 20, no. 7: 2106. https://doi.org/10.3390/s20072106
APA StyleYang, L., Chen, J., & Zhu, W. (2020). Dynamic Hand Gesture Recognition Based on a Leap Motion Controller and Two-Layer Bidirectional Recurrent Neural Network. Sensors, 20(7), 2106. https://doi.org/10.3390/s20072106







