Ultrahigh Resolution Thickness Measurement Technique Based on a Hollow Core Optical Fiber Structure
Abstract
1. Introduction
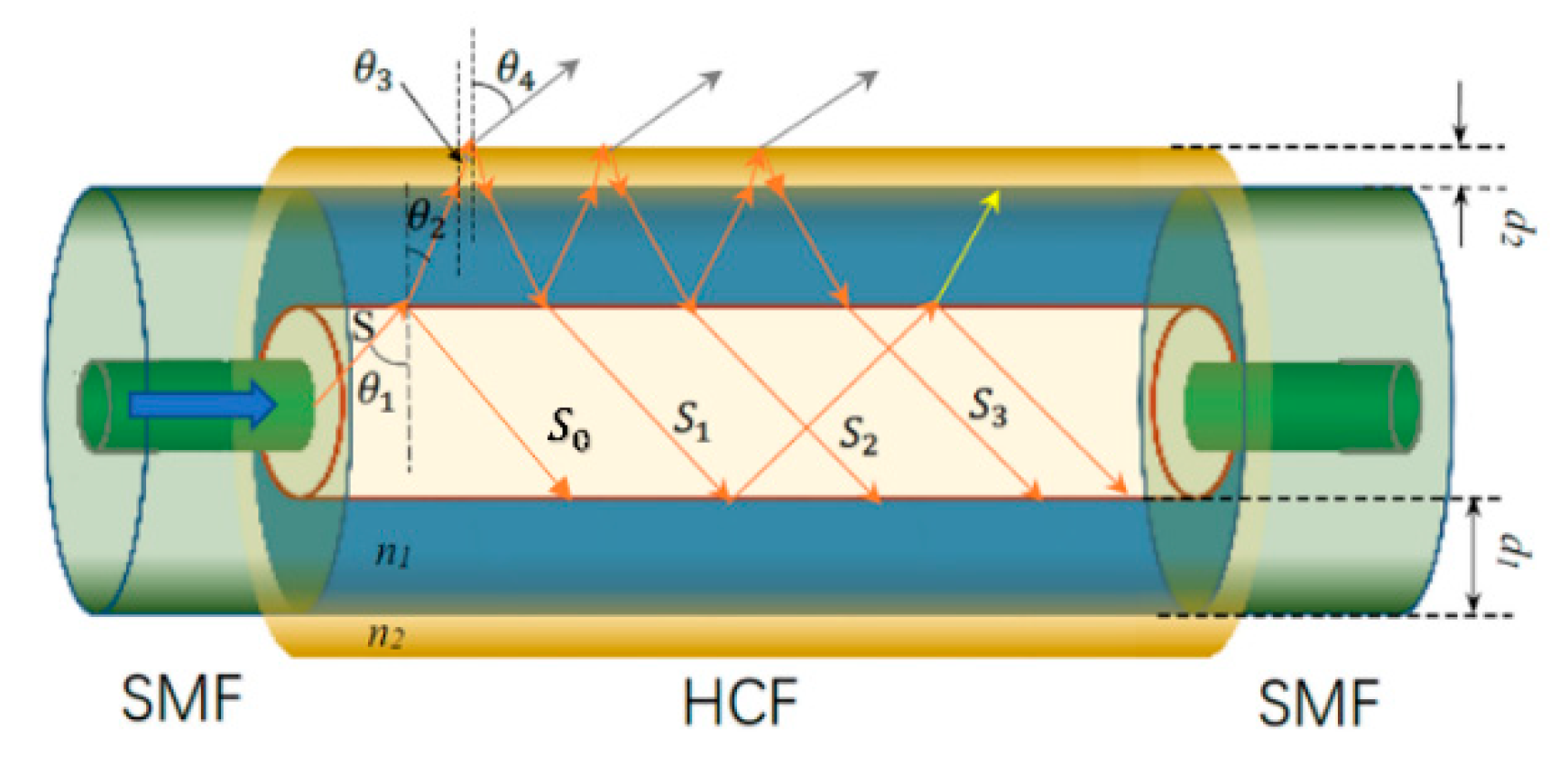
2. Theoretical Analysis
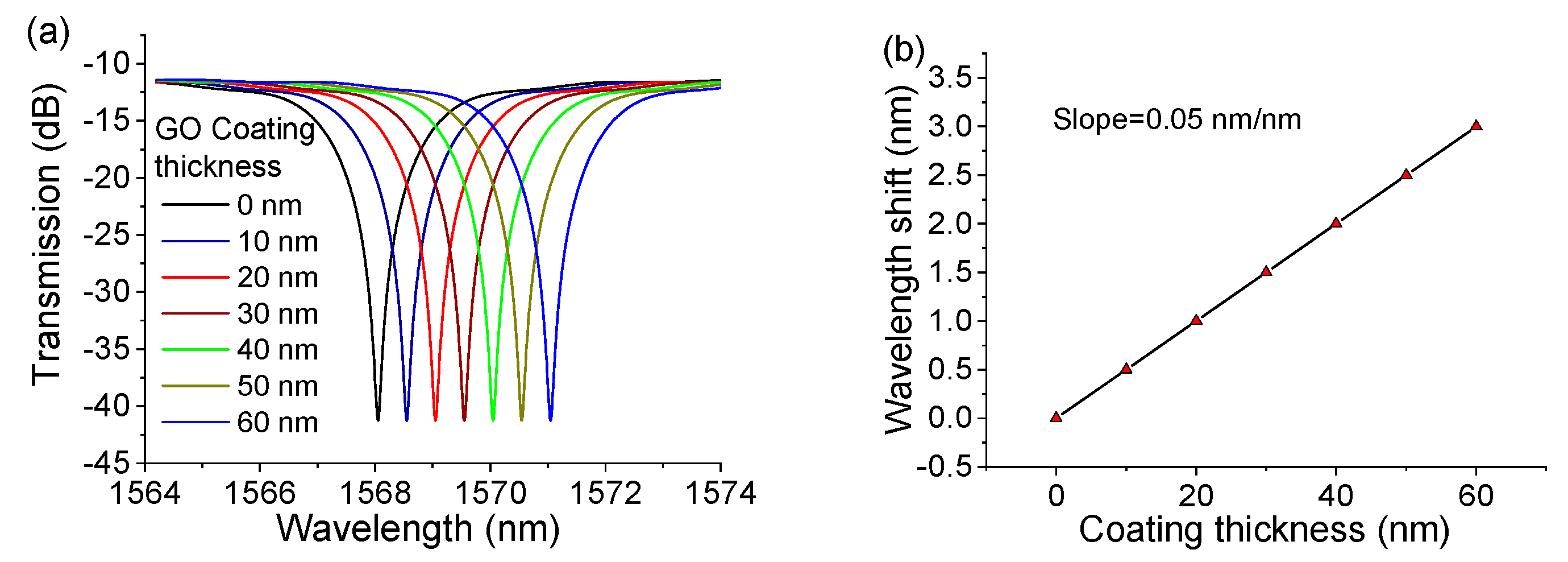
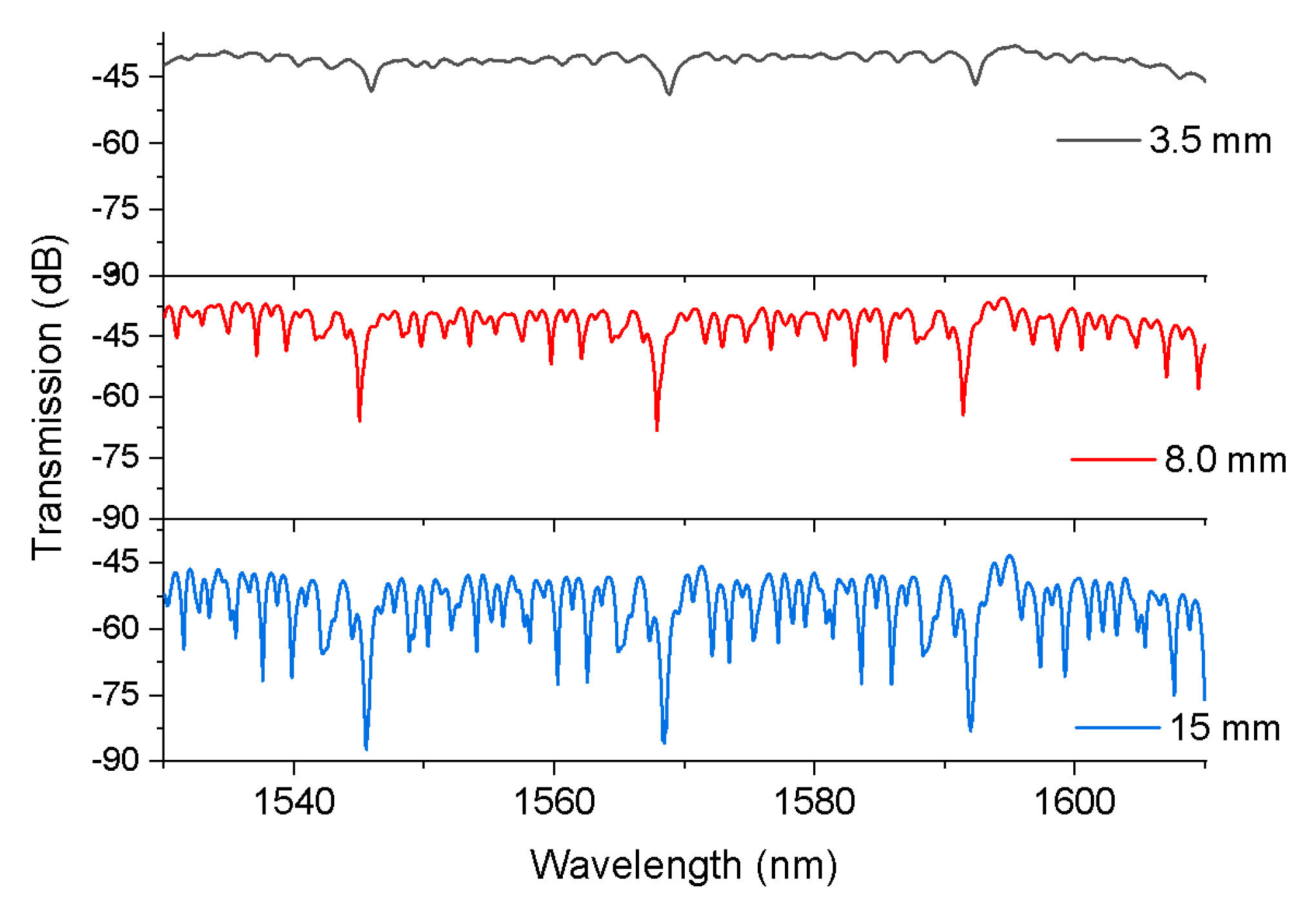
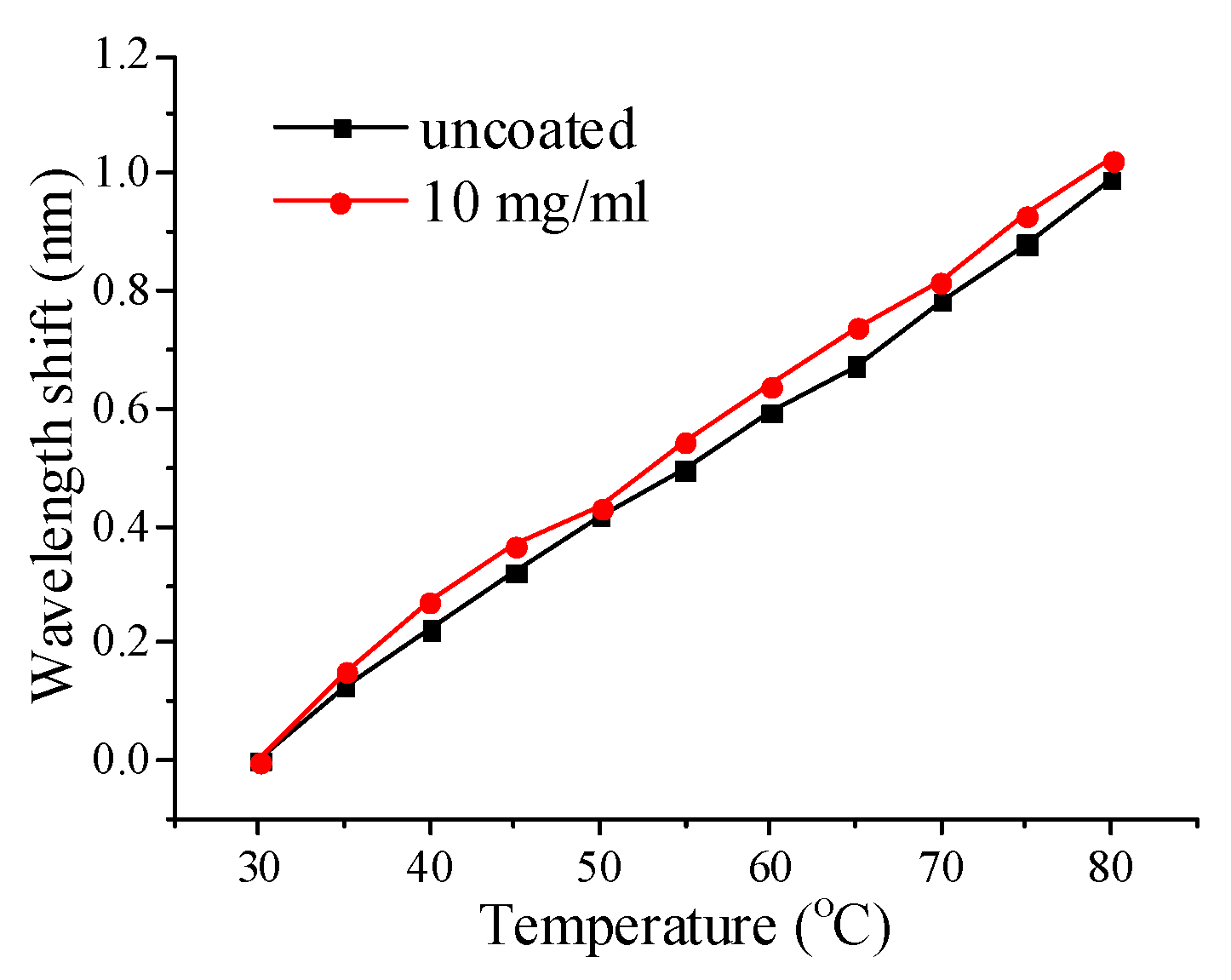
3. Experimental Results and Discussion
4. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Albert, J.; Liu, F.; Marquez-Cruz, V. Hypersensitivity and Applications of Cladding Modes of Optical Fibers Coated with Nanoscale Metal Layers. Sensors 2018, 18, 1518. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.P.; Chaurasia, S.K. Design Optimization of Pd-Coated Side-Polished Single Mode Optical Fiber Hydrogen Sensors. IEEE Sens. J. 2018, 18, 8389–8396. [Google Scholar] [CrossRef]
- Lei, X.; Dong, X.; Lu, C. Sensitive Humidity Sensor Based on a Special Dual-Mode Fiber. IEEE Sens. J. 2018, 19, 2587–2591. [Google Scholar] [CrossRef]
- Coelho, L.; Viegas, D.; Santos, J.L.; De Almeida, J.M.M.M. Characterization of zinc oxide coated optical fiber long period gratings with improved refractive index sensing properties. Sens. Actuators B Chem. 2016, 223, 45–51. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, L.; Du, X.; Yang, Y. Simultaneous measurements of thin film thickness using total internal reflection fluorescence microscopy and disjoining pressure using Scheludko cell. Rev. Sci. Instrum. 2019, 90, 045118. [Google Scholar] [CrossRef] [PubMed]
- Bobbitt, J.M.; Mendivelso-Pérez, D.; Smith, E.A. Scanning angle Raman spectroscopy: A nondestructive method for simultaneously determining mixed polymer fractional composition and film thickness. Polymer 2016, 107, 82–88. [Google Scholar] [CrossRef]
- Bobbitt, J.; Smith, E. Extracting interface locations in multilayer polymer waveguide films using scanning angle Raman spectroscopy. J. Raman Spectrosc. 2018, 49, 262–270. [Google Scholar] [CrossRef]
- Smith, R.; la Cavera, S.; Perez-cota, F.; Marques, L.; Clark, M. Thickness Measurement of Polymer Thin Films with High Frequency Ultrasonic Transducers. In Proceedings of the 45th Annual Review of Progress in Quantitative Nondestructive Evaluation, VT, USA, 15–19 July 2018; Volume 2102, p. 040015. [Google Scholar]
- Shupenev, A.; Pankova, N.; Korshunov, I.; Grigoriyants, A. An Analysis of Non-Destructive Methods for Thin Film Thickness Measurement. Izv. Vyss. Uchebnykh Zaved. Mashinostroenie 2019, 4, 18–27. [Google Scholar] [CrossRef]
- Whiteside, P.J.D.; Chininis, J.A.; Hunt, H.K. Techniques and Challenges for Characterizing Metal Thin Films with Applications in Photonics. Coatings 2016, 6, 35. [Google Scholar] [CrossRef]
- Xie, Z.; Tang, Y.; Liu, X.; Yang, K.; Hu, S. Fast thickness measurement of thin films using two-dimensional Fourier transform-based structured illumination microscopy. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies (Aomatt 2018): Meta-Surface-Wave And Planar Optics, Chengdu, China, 26–29 January 2018; Volume 10841. [Google Scholar]
- Xie, Z.; Tang, Y.; Liu, X.; Yang, K.; Hu, S. Surface and thickness measurement of transparent thin-film layers utilizing modulation-based structured-illumination microscopy. Opt. Express 2018, 26, 2944–2953. [Google Scholar] [CrossRef]
- Jasapara, J.; Wielandy, S. Characterization of coated optical fibers by Fourier-domain optical coherence tomography. Opt. Lett. 2005, 30, 1018–1020. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shao, H.; Yang, Y.; Pan, H.; Pang, F.; Wang, T. Refractometry With a Tailored Sensitivity Based on a Single-Mode-Capillary-Single-Mode Fiber Structure. IEEE Photon. J. 2017, 9, 1–8. [Google Scholar] [CrossRef]
- Lee, C.L.; Lee, L.H.; Hwang, H.E.; Hsu, J.M. Highly Sensitive Air-Gap Fiber Fabry–Pérot Interferometers Based on Polymer-Filled Hollow Core Fibers. IEEE Photon. Tech. Lett. 2012, 24, 149–151. [Google Scholar] [CrossRef]
- Lee, C.L.; Ho, H.Y.; Gu, J.H.; Yeh, T.Y.; Tseng, C.H. Dual hollow core fiber-based Fabry–Perot interferometer for measuring the thermo-optic coefficients of liquids. Opt. Lett. 2015, 40, 459–462. [Google Scholar] [CrossRef]
- Ferreira, M.S.; Coelho, L.; Schuster, K.; Kobelke, J.; Santos, J.L.; Frazao, O. Fabry–Perot cavity based on a diaphragm-free hollow-core silica tube. Opt. Lett. 2011, 36, 4029–4031. [Google Scholar] [CrossRef]
- Silverstone, J.W.; McFarlane, S.; Manchee, C.P.K.; Meldrum, A. Ultimate resolution for refractometric sensing with whispering gallery mode microcavities. Opt. Express 2012, 20, 8284–8295. [Google Scholar] [CrossRef][Green Version]
- Liu, D.; Wu, Q.; Mei, C.; Yuan, J.; Xin, X.; Mallik, A.K.; Wei, F.; Han, W.; Kumar, R.; Yu, C.; et al. Hollow Core Fiber Based Interferometer for High Temperature (1000 °C) Measurement. IEEE J. Lightwave Technol. 2018, 36, 1583–1590. [Google Scholar] [CrossRef]
- Lee, C.; Tsai, Y.; Chen, G.; Xiao, Y.; Hsu, J.; Horng, J. Refined Bridging of Microfiber Plugs in Hollow Core Fiber for Sensing Acoustic Vibrations. IEEE Photonics Technol. Lett. 2015, 27, 2403–2406. [Google Scholar] [CrossRef]
- Gao, R.; Lu, D.; Cheng, J.; Jiang, Y.; Jiang, L.; Qi, Z. Humidity sensor based on power leakage at resonance wavelengths of a hollow core fiber coated with reduced graphene oxide. Sens. Actuat. Biol. Chem. 2016, 222, 618–624. [Google Scholar] [CrossRef]
- Gao, R.; Lu, D.F.; Cheng, J.; Jiang, Y.; Jiang, L.; Qi, Z.M. Optical displacement sensor in a capillary covered hollow core fiber based on anti-resonant reflecting guidance. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 193–198. [Google Scholar] [CrossRef]
- Hou, M.; Zhu, F.; Wang, Y.; Wang, Y.; Liao, C.; Liu, S.; Lu, P. Antiresonant reflecting guidance mechanism in hollow-core fiber for gas pressure sensing. Opt. Express 2016, 24, 27890–27898. [Google Scholar] [CrossRef] [PubMed]
- Duguay, M.A.; Kokubun, Y.; Koch, T.L.; Pfeiffer, L. Antiresonant reflecting optical waveguides in SiO2-Si multilayer structures. Appl. Phys. Lett. 1986, 49, 13–15. [Google Scholar] [CrossRef]
- Litchinitser, N.M.; Abeeluck, A.K.; Headley, C.; Eggleton, B.J. Antiresonant reflecting photonic crystal optical waveguides. Opt. Lett. 2002, 27, 1592–1594. [Google Scholar] [CrossRef] [PubMed]
- Jung, I.; Vaupel, M.; Pelton, M.; Piner, R.; Stankovich, S.; Dikin, D.; Ruoff, R. Characterization of Thermally Reduced Graphene Oxide by Imaging Ellipsometry. J. Phys. Chem. C. 2008, 112, 8499–8506. [Google Scholar] [CrossRef]
- Liu, D.; Kumar, R.; Wei, F.; Han, W.; Mallik, A.K.; Yuan, J.; Yu, C.; Kang, Z.; Li, F.; Liu, Z.; et al. Highly sensitive twist sensor based on partially silver coated hollow core fiber structure. J. Lightwave Technol. 2018, 36, 3672–3677. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Liu, B.; Zhu, J.; Liu, J.; Wan, S.; Wu, T.; Sun, J. Ultrahigh Resolution Thickness Measurement Technique Based on a Hollow Core Optical Fiber Structure. Sensors 2020, 20, 2035. https://doi.org/10.3390/s20072035
Wu Z, Liu B, Zhu J, Liu J, Wan S, Wu T, Sun J. Ultrahigh Resolution Thickness Measurement Technique Based on a Hollow Core Optical Fiber Structure. Sensors. 2020; 20(7):2035. https://doi.org/10.3390/s20072035
Chicago/Turabian StyleWu, Zheyu, Bin Liu, Jiangfeng Zhu, Juan Liu, Shengpeng Wan, Tao Wu, and Jinghua Sun. 2020. "Ultrahigh Resolution Thickness Measurement Technique Based on a Hollow Core Optical Fiber Structure" Sensors 20, no. 7: 2035. https://doi.org/10.3390/s20072035
APA StyleWu, Z., Liu, B., Zhu, J., Liu, J., Wan, S., Wu, T., & Sun, J. (2020). Ultrahigh Resolution Thickness Measurement Technique Based on a Hollow Core Optical Fiber Structure. Sensors, 20(7), 2035. https://doi.org/10.3390/s20072035







