Abstract
In this paper, a data-driven optimal scheduling approach is investigated for continuous-time switched systems with unknown subsystems and infinite-horizon cost functions. Firstly, a policy iteration (PI) based algorithm is proposed to approximate the optimal switching policy online quickly for known switched systems. Secondly, a data-driven PI-based algorithm is proposed online solely from the system state data for switched systems with unknown subsystems. Approximation functions are brought in and their weight vectors can be achieved step by step through different data in the algorithm. Then the weight vectors are employed to approximate the switching policy and the cost function. The convergence and the performance are analyzed. Finally, the simulation results of two examples validate the effectiveness of the proposed approaches.
1. Introduction
Switched systems consisting of several subsystems and a switching policy ruling the switching among them [1,2] arise in certain application situations [3,4] such as a system which has to collect data sequentially from a number of sensory sources and switches its attention among the data sources [5,6]. The switching among subsystems complicates the control problems and many of the problems remain to be open such as the optimal control problems. Optimal control [7,8] problems of switched systems have attracted considerable attention over the past few years. Thereinto, the optimal scheduling problem of switched systems is investigated in this paper.
Multiple approaches have been introduced to solve the optimal control problems for switched systems. Gradient-based approaches are investigated to solve the optimal switching time problems [9] and optimal scheduling problems [10,11] directly, usually in a finite time horizon. By utilizing control inputs to represent the switching policy, embedding approaches transform the optimal control problems of switched systems to traditional optimal control problems to address [12,13,14]. Adaptive dynamic programming (ADP) [15] approaches are introduced to solve the optimal control problems for switched systems with different initial conditions directly [16,17,18,19,20,21,22]. For optimal scheduling of switched systems with infinite-horizon cost functions, ADP approaches perform well to provide approximate global optimal solutions directly.
Approximate global optimal solutions are derived in feedback forms through ADP for optimal scheduling of switched systems with discrete-time dynamics and finite-horizon cost functions [17] or infinite-horizon cost functions [18]. Then further research is conducted for problems with switching cost [19] or state jumps [20]. For optimal scheduling of switched systems with continuous-time dynamics, an approximate feedback solution is proposed based on policy iteration (PI) algorithm with its offline, online, and concurrent implementation [21]. Then, a PI algorithm with recursive least squares is proposed and modified into a single loop PI algorithm to reduce the computational burden [22].
The aforementioned optimal control approaches are deduced based on the a priori knowledge of system models. However, not all system models can be completed acquired so that approaches independent of system models [23,24,25] require investigated. For this purpose, some model-free optimal control approaches have been studied for switched systems. Adaptive dynamic programming approaches are presented respectively for a continuous-time switched system with an infinite-horizon cost function [26] and a discrete-time switched system with a finite-horizon cost function [27] under the assumption that dynamic equations can be evaluated at some sets. Gradient-decent approaches only employing state data are proposed to solve optimal switching problems for continuous-time switched systems with finite-horizon cost functions [28,29]. Data-driven research utilizes real-life data measured by sensory sources to achieve the intrinsic information of systems [30] and can solve the problems of switched systems with unknown subsystems, such as the data-driven framework for discovering cyber-physical systems directly from the data [31]. Thereinto, data-driven ADP approaches provide possible solutions for optimal control problems of switched systems [32,33,34] and based on that, the following approach is designed to adapt to the complexity of switched systems which is brought by switching. Then in this paper, the data-driven optimal scheduling approach is investigated for continuous-time switched systems with unknown subsystems. At first, an online PI-based algorithm inspired by the off-policy learning method [35,36] is proposed to approximate the optimal solution quickly for optimal scheduling problems with known system models first and based on that, a data-driven PI-based algorithm is formulated for optimal scheduling of continuous-time switched systems with infinite-horizon cost functions, which don’t require that dynamic equations can be evaluated or known at some sets. Moreover, common online algorithms usually keep collecting data with the updating switching policies applied to the system at each iteration while the online algorithms in this paper take advantages of the data produced only by the initial switching policy.
The contribution of this paper is stated as follows: (1) with the data produced by the initial switching policy, an online PI-based algorithm is proposed to approximate the optimal solution quickly for optimal scheduling of known switched systems. (2) A data-driven PI-based algorithm is designed to solve optimal scheduling problems for switched systems with infinite-horizon cost functions and unknown subsystems, solely from the data produced by the initial switching policy, which has not been achieved well in existing literature as far as we know. (3) The convergence is proved and the optimality is analyzed.
The remainder of the paper is organized as follows. In Section 2, the problem is stated and the classic PI approach is introduced for the optimal scheduling problem. In Section 3, online PI-based algorithms are proposed for switched systems with known subsystems and unknown subsystems. In Section 4, simulation results are shown to indicate the effectiveness of the algorithms. Finally, the conclusion is drawn in Section 5.
2. Preliminaries
Consider the switched system as follows:
where is the system state, represents the index of the active subsystem, is the index set of all subsystems, N is the number of subsystems, and denotes the unknown dynamics of subsystem v. is Lipschitz continuous in where including the origin is the region of interest and there exists such that .
In this paper, the problem to be addressed consists in seeking out the optimal switching policy to minimize the following cost function:
where is a positive definite function. During the time interval, the cost-to-go from the time t to infinity with the state at time t can be described as [37]:
and then
For the optimal problem, the admissible switching policy should be introduced and the relevant assumption is made as [22].
Definition 1.
Assumption 1.
There exists at least one admissible policy for the system.
According to the Bellman principle of optimality, the optimal cost-to-go can be represented by
and when , the corresponding optimal switching policy can be represented in a state-feedback form:
When , with first-order Taylor expansion of applied in (5) and (6), the HJB equation can be given as [21]:
where , when is a scalar and the corresponding optimal switching policy is given as [21]:
Then, a PI approach can be applied to solve the optimal scheduling problem. Given an admissible switching policy , the PI approach [21,22] is stated as follows:
where k is the iteration number. The cost-to-go is solved in policy evaluation (7) and the switching policy is updated in policy improvement (8) iteratively. The stability and convergence are stated in the following theorem which has been proved in [21,38].
Theorem 1.
3. Main Results
3.1. PI-Based Algorithm for Known Switched Systems
The offline, online and concurrent implementation of the aforementioned PI approach for switched systems with known dynamics has been investigated in references [21,22,38]. In this subsection, a novel online PI-based algorithm is proposed to approximate the optimal switching policy quickly.
Common online algorithms keep collecting data from the systems to evaluate and improve the switching policy. To be specific, once a new switching policy is produced at each iteration, it is applied to the system and the newly produced data is collected to calculate a new cost and a new switching policy. It entails considerable time to apply the new switching policy, collect new data and calculate a new cost and a new switching policy sequentially at each iteration. Aiming at this, inspired by the off-policy ADP methods for ordinary systems [36,39,40], an online PI-based algorithm is proposed to approximate the optimal switching policy quickly with only an initial switching policy applied and only the data produced by the initial switching policy is required. Next, the algorithm starts from the initial admissible switching policy.
With the initial admissible switching policy applied only, large amounts of data can be produced in the process and the state trajectory corresponding to the switching policy can be acquired which will be employed in the subsequent derivation. Along the acquired state trajectory , can be represented as
where is very small. To combine the policy iteration and the cost at the acquired state, integrating (7) along the acquired state trajectory and adding the integration to (9) yield
The cost is unknown. However, for all , it can be expressed by:
where is a vector concerning a set of linearly independent basis functions , is the weight vector and is the approximation error. is the number of the basis functions. A set of basis functions can constitute a particular basis of a function space and can almost approximate any function in the function space. With the approximation function (11) applied, Equation (10) can be transformed into
where when and is the approximation error. Then the estimation can be achieved:
where the estimate is achieved through substituting the estimate and the approximation (11) into (8) as follows:
with the initial switching policy estimate .
To employ the acquired state data corresponding to some selected instants, some data matrices can be defined as follows:
where are the selected instants, l is a positive integer, , , and . The following assumption concerning the data matrices is made as [40,41]:
Assumption 2.
There exist a positive integer and a positive number α such that for all , the following equality holds:
In optimal control of ordinary systems, this kind of assumption can be satisfied by exerting an exploration noise in the input [39,40]. In the case of the switched systems, according to [21,22], it can be satisfied through random switching.
Then based on Assumption 2, can be achieved with the data matrices as the following formula:
According to the analysis, the online PI-based algorithm for switched systems with known dynamics can be formulated in Algorithm 1.
| Algorithm 1 Online policy iteration (PI)-based Algorithm. |
| Step 1. Start with an initial admissible switching policy and set the iteration index . Step 2. Apply in the switched systems and acquire the state data. Set . Calculate and for according to their definition with the state data. Step 3. Calculate for according to its definition with the state data and then calculate from (15). Step 4. Update the switching policy as (14). Step 5. If , set and exit. Otherwise, set and go back to Step 3. |
In the algorithm, when the switching policy is applied, the corresponding system state data can be obtained. With multiple samples, multiple data matrix and will be calculated. Sufficient samples should be employed to satisfy that with a proper so that the sampling stage must be long enough to ensure that. Moreover, since the weight vector to be solved in Equation (15) has components, at least instants should be employed to solve so that r is no less than . Then through the algorithm, the approximate optimal cost function can be achieved as with the corresponding approximate optimal switching policy . It can be seen from Algorithm 1 that only the initial switching policy is applied and then Algorithm 1 can approximate the optimal switching policy quickly with the data produced by the initial switching policy.
3.2. Data-Driven PI-Based Algorithm for Unknown Switched Systems
In this subsection, based on the proposed PI approach dependent on system models, a data-driven PI-based algorithm is proposed for switched systems with unknown subsystems. The algorithm takes full advantage of data produced by an initial switching policy to approximate the optimal switching policy quickly.
From Section 3.1, with the initial admissible switching policy applied and along the acquired state trajectory , (10) can be achieved and the cost function can be represented by (11). In the process, can be represented by and solved with known system models. However, due to the unknown subsystem models, representing cannot work well as Section 3.1. So another approximation function is brought in to solve the problem. For all , the unknown variable can be expressed by:
where is a vector concerning a set of linearly independent basis functions , are the weight vectors and is the approximation error. is the number of the basis functions.
With the approximation functions (11) and (16) applied, Equation (10) can be transformed into
where is the approximation error. Since is very small, the values of and can be seen to be constant during the time interval so that and are constant during the time interval . Therefore, the estimation can be made as (18):
For the subsequent algorithm, in addition to the data matrices defined in Section 3.1, some more matrices are required which are defined as follows:
where , l is a positive integer, and .
At first, the following assumption concerning the data matrices is made as Assumption 2:
Assumption 3.
There exist a positive integer and a positive number α such that for all , the following equalities hold:
where the time instants satisfies the condition that ;
where the time instants satisfies the condition that for ;
where the time instants satisfies the conditions that and for .
Remark 1.
Since the vector changes as x changes, the weight vector and cannot be solved directly from (18) with the data matrices as Section 3.1. The difficulty in this problem is mainly calculating the weight vector and or achieve enough useful knowledge about the weight vectors through the state data.
Based on the above analysis, the following approach is designed to acquire useful knowledge about the weight vector and step by step through different state data. The weight vector is discussed firstly. The state data satisfying the condition that is selected from all the state data and then utilized in (18). It is obvious that when , and (18) can be simplified to:
Under Assumption 3, the estimate of the weight vector can be achieved from (19) with the data matrices defined in Section 3.1 concerning certain states as follows:
where the time instants satisfies the condition that .
Then, we concentrate on estimating the weight vector of . Along the acquired state trajectory produced by the switching policy , it can be obtained from (16) and (7) that when the following formula holds:
The estimation can be made as follows:
Under Assumption 3, the estimate of the weight vector can be easily achieved as follows:
where the time instants satisfies the condition that .
Though the weight vector is not easy to estimate, the estimate of can be easily achieved from (18) with the data matrices concerning certain states under Assumption 3 as follows:
where the time instants satisfies the conditions that and and .
For a certain state x, is constant and . Therefore, on the basis of (8), employing the estimate of (22) and (23), the switching policy is estimated by
with the initial switching policy estimate .
The approach utilizes different parts of the acquired state data to calculate the weight vector , and respectively. Then the weight vectors are employed to calculate the switching policy and the cost function.
According to the aforementioned analysis, the data-driven PI-based algorithm for switched systems can be formulated as follows:
Then, the approximate optimal cost function can be achieved as with the corresponding approximate optimal switching policy .
Remark 2.
In Algorithm 2, only the initial switching policy requires to be applied in the system and the produced state data is collected at the beginning. The data matrices , and are calculated once at the beginning and don’t require to be calculated repeatedly at each iteration. It is very convenient and timesaving to operate online according to Algorithm 2 and the calculation time is very short. Therefore, the optimal cost can be approximated rapidly in Algorithm 2. Moreover, Algorithm 2 is only based on data with no need for the knowledge of subsystems.
| Algorithm 2 Data-driven PI-based algorithm. |
| Step 1. Start with an initial admissible switching policy and set the iteration index . Step 2. Apply in the switched systems and acquire the state data. Set . Calculate , and for according to their definition with the state data. Step 3. Calculate for all from (22) and then calculate from (24). Set . Step 4. Calculate from (20) and then calculate from (23) for all . Step 5. Update the switching policy as (24). Step 6. If , set and exit. Otherwise, set and go back to Step 4. |
Next, the convergence of Algorithm 2 is analyzed. Based on Theorem 1, Theorem 2 is stated for the convergence analysis of Algorithm 2.
Theorem 2.
For system (1) with cost (2) under Assumptions 1 and 3, if the value function sequence and the switching policy sequence are generated through (7) and (8) initiating from an initial admissible policy , for and all , there exists such that for , when approaches to zero, the following inequalities hold:
where , , and are generated through (20) and (24) in Algorithm 2, and .
Proof of Theorem 2.
Mathematical induction is utilized to prove the convergence.
According to Assumption 3, it follows that
and then . The approximation theory [42] yields that for all , , then . Therefore, for and , there exists such that for , and then . It follows that and for . Then, it can be achieved from (21) and (22) that:
Similarly, the approximation theory [42] yields that for all , and then . Under Assumption 3, it can be deduced that for , . It implies that for .
Secondly, we consider the theorem when . When , . When is calculated, for and it can be achieved from (17) to (19) that:
where and thus for . Then it can be inferred that when
Under Assumption 3, it can be deduced that for all , , and . Then, it can be achieved from (17), (18) and (23) that:
Since it can be achieved that where , it can be inferred that
Since , and , under Assumption 3, it can be deduced that and then for . It implies that for .
Thirdly, we suppose the theorem holds when . That is to say, and for . When is calculated, it can be achieved from (17) to (19) that:
where and for . Then it can be inferred that
Under Assumption 3, it can be deduced that and for . Then, it can be achieved from (17), (18) and (23) that:
where . Since , and , under Assumption 3, it can be deduced that and then for . It implies that for . In brief, it can be deduced that the theorem holds when from the supposition that the theorem holds when .
The proof is completed through mathematical induction. □
It can be achieved from Theorem 2 that the value function generated through Algorithm 2 is an approximation of and the corresponding switching policy is if the preconditions are satisfied. Theorem 2 combined with Theorem 1 indicates that the value function is the approximate optimal cost function with the corresponding approximate optimal switching policy .
Remark 3.
In practice, the error of the approximation exists and the small parameter can not get infinitely close to zero so that the solution calculated from Algorithm 2 is suboptimal.
4. Example
In this section, two examples are illustrated to validate the effectiveness of the suboptimal scheduling approach of Algorithm 1 and the data-driven suboptimal scheduling approach of Algorithm 2 in this paper.
Example 1.
Consider a switched system as [21,38] consisting of the following subsystems:
with and .
The optimal switching policy can be known from [17] as
Choose the initial switching policy when and when . The basis functions are selected as [21]. Set the sample period s.
Apply Algorithm 1 and utilize the online state data from to s. Then after calculation in s, the approximate optimal cost is achieved with the corresponding approximate optimal switching policy through 3 iterations. The initial cost , the approximate optimal cost and the optimal cost are demonstrated in Figure 1. The largest error between and is 0.1621 and it is obvious that the approximate optimal cost is very close to the optimal cost of . The state trajectories with the initial switching policy , the approximate optimal switching policy and the optimal switching policy applied in the system after s are demonstrated in Figure 2, where the state trajectory corresponding to coincides with the one corresponding to and their largest error is zero while the largest error between the state trajectory corresponding to and the one corresponding to is 0.0563. The online trajectories are too close to show the superiority of the proposed algorithm so that the switching policies , and when are illustrated in Figure 3. Apparently, and are the same. The similarity rate of the schedules and is 100% while the similarity rate of the schedules and is 75.31%.
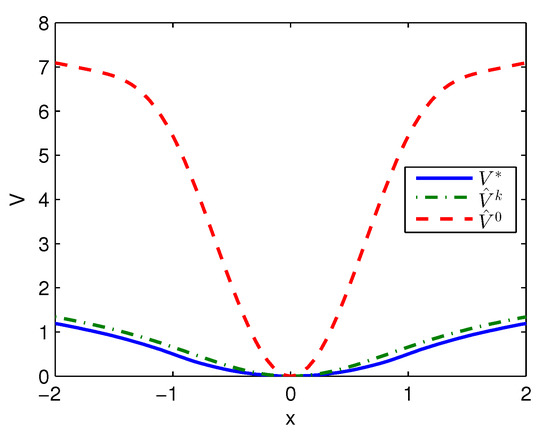
Figure 1.
Costs achieved by Algorithm 1 applied in Example 1.
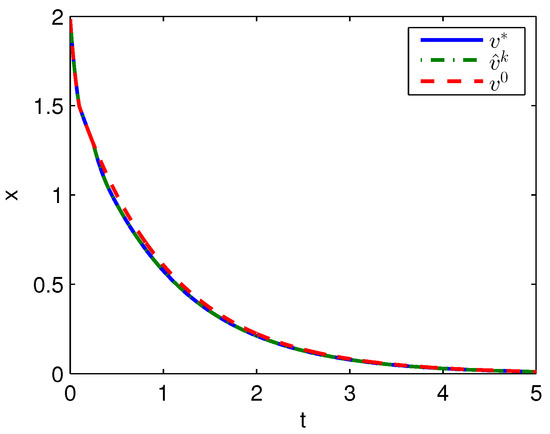
Figure 2.
State trajectories with Algorithm 1 applied in Example 1.
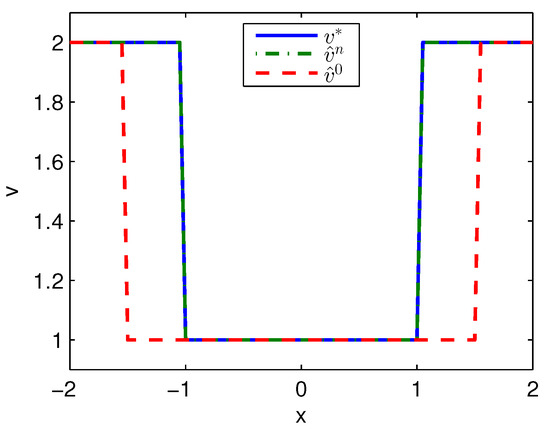
Figure 3.
Switching policies achieved by Algorithm 1 applied in Example 1.
Apply Algorithm 2 and utilize the online state data from to s. Then after calculation in s, the approximate optimal cost is achieved with the corresponding approximate optimal switching policy through 6 iterations. The costs , and are demonstrated in Figure 4. It can be obtained that compared with the initial cost of , the approximate optimal cost of is close to the optimal cost of . The state trajectories with , and applied in the system after s are demonstrated in Figure 5, where the state trajectory corresponding to coincides with the one corresponding to and their largest error is 0.0155 while the largest error between the state trajectory corresponding to and the one corresponding to is 0.0563. The online trajectories also are too close to show the superiority of the proposed algorithm so that the switching policies , and when are illustrated in Figure 6. It can be seen that is approximate to . The similarity rate of the schedules and is 95.06% while the similarity rate of the schedules and is 75.31%.
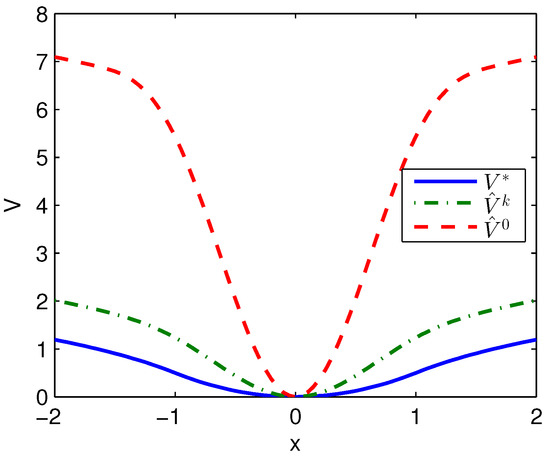
Figure 4.
Costs achieved by Algorithm 2 applied in Example 1.
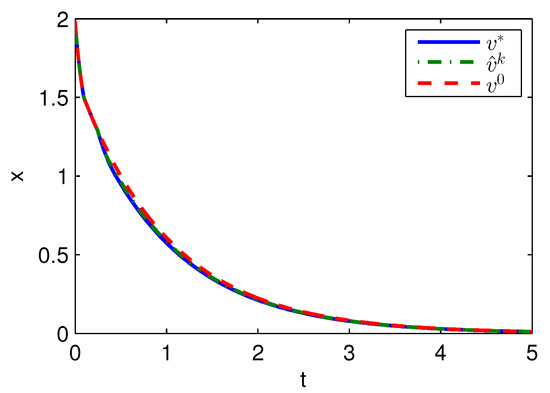
Figure 5.
State trajectories with Algorithm 2 applied in Example 1.
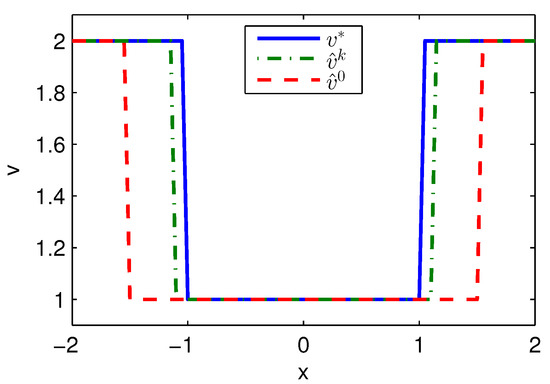
Figure 6.
Switching policies achieved by Algorithm 2 applied in Example 1.
Example 2.
Consider a mass-spring-damper system as [21,22]:
with , , and . Here, the state is the displacement of the mass measured from the relaxed length of the spring. is the external force acting on the mass. The initial state is and the function Q is
Choose the initial switching policy when , when and when . The basis functions are polynomials with all possible combinations of the state variables up to the 4th degree without repetitions selected as [21,22]. Set the sample period s.
Apply Algorithm 1 and utilize the online state data from to 23 s. Then after calculation in 7 s, the approximate optimal cost is achieved with the corresponding approximate optimal switching policy through 15 iterations. The initial cost and the approximate optimal cost are demonstrated in Figure 7. It can be seen that the approximate optimal cost is less than the initial cost . The state trajectories with the initial switching policy and the approximate optimal switching policy applied in the system after s are demonstrated in Figure 8, where the state trajectory corresponding to converges to the origin quickly after s while the trajectory corresponding to converges slowly with decreasing oscillation amplitude. The corresponding switching policies and are illustrated in Figure 9. It can be seen that which switches among three subsystems and finally stays at subsystem 3 results in that the trajectory corresponding to converges slowly with decreasing oscillation amplitude, while which switches between subsystem 1 and 2 results in that the state trajectory corresponding to converges to the origin quickly after s.
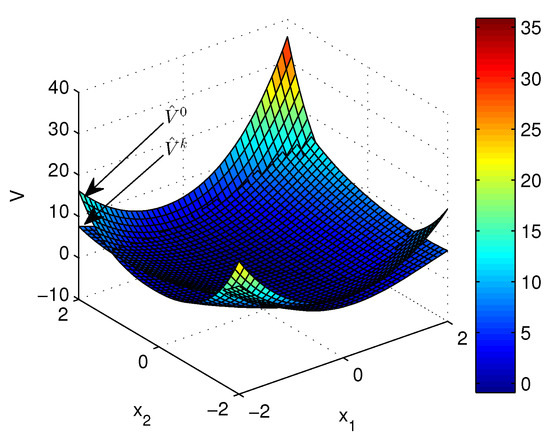
Figure 7.
Costs achieved by Algorithm 1 applied in Example 2.
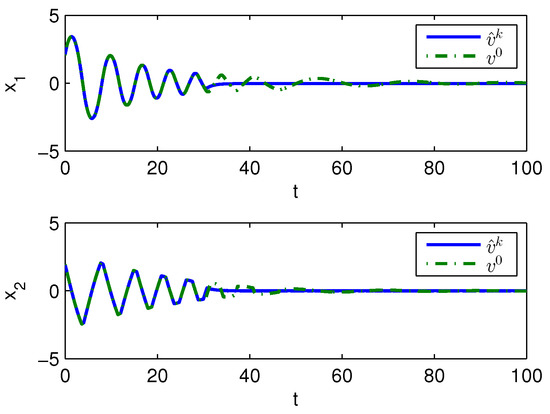
Figure 8.
State trajectories with Algorithm 1 applied in Example 2.
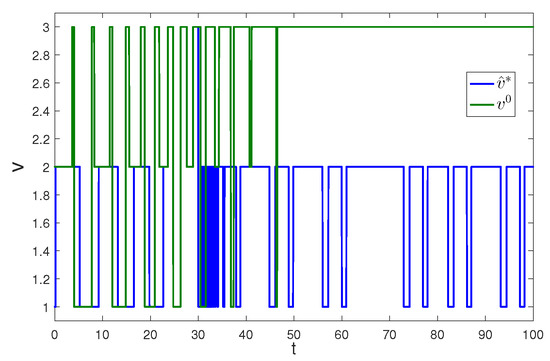
Figure 9.
Switching policies with Algorithm 1 applied in Example 2.
Apply Algorithm 2 and utilize the online state data from to 23 s. Then after calculation in 7 s, the approximate optimal cost is achieved with the corresponding approximate optimal switching policy through 21 iterations. The costs and are demonstrated in Figure 10. It can be seen that the approximate optimal cost is less than the initial cost . The state trajectories with and applied in the system after s are demonstrated in Figure 11, where the state trajectory corresponding to converges to the origin relatively quickly after s while the trajectory corresponding to converges slowly with decreasing oscillation amplitude. The corresponding switching policies and are illustrated in Figure 12. It can be seen that which switches among three subsystems and finally stays at subsystem three results in that the trajectory converges slowly with decreasing oscillation amplitude, while which switches between subsystem 1 and 2 results in that the state trajectory converges to the origin relatively quickly after s.
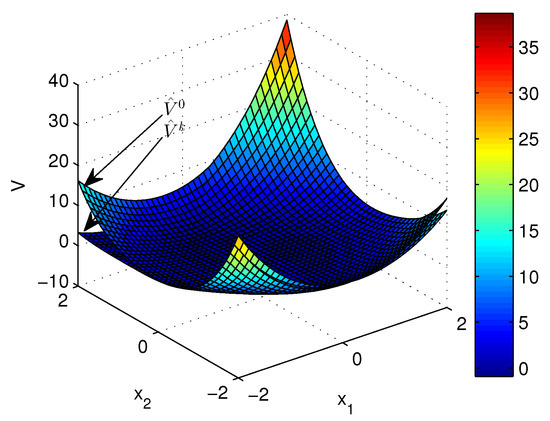
Figure 10.
Costs achieved by Algorithm 2 applied in Example 2.
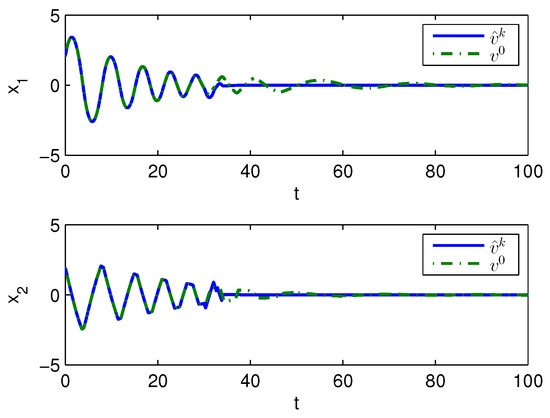
Figure 11.
State trajectories with Algorithm 2 applied in Example 2.
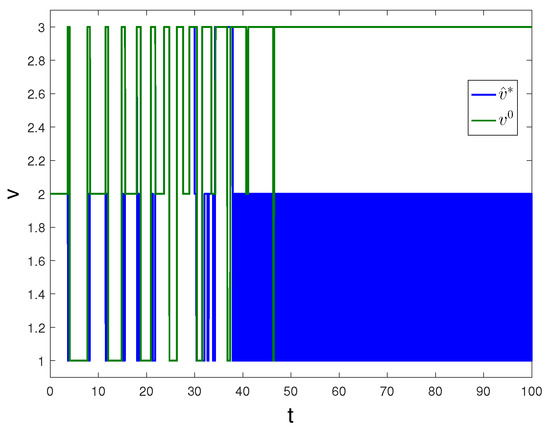
Figure 12.
Switching policies with Algorithm 2 applied in Example 2.
Remark 4.
In algorithm 2, the value of the initial switching policy should include every element of V and there should exist enough data to calculate for every so that the sampling stage must be long enough to ensure that.
Remark 5.
In the calculation, the fourth order Runge-Kutta algorithm is adopted to numerically evaluate the integrals which are necessary in certain terms such as and .
Remark 6.
In Example 1, the proposed algorithms converge in s while the online algorithm investigated in [38] requires more time. In Example 2, the proposed algorithms converge in 30 s while the online algorithms investigated in [21,22] require more time.
In the two examples, the effectiveness of Algorithm 2 has been validated. The superiority of Algorithm 2 lies in that it can work for switched systems with unknown subsystems while Algorithm 1 can not work if the subsystems of switched systems are unknown. Practical examples of this kind of switched systems appear in a wide range of applications such as cyber-physical systems which embed software into the physical world and have proved resistant to modeling due to their intrinsic complexity arising from the combination of physical and cyber components and the interaction between them in [31]. Thereinto, data-driven research has been conducted for some specific examples such as complex electronics switching among low-voltage, middle-voltage and high-voltage models, and smart grid switching between base configuration and changed configuration. These examples require the data-driven approaches of Algorithm 2 where Algorithm 1 is inapplicable.
Simulation results show that Algorithms 1 and 2 can approximate the optimal solution effectively and efficiently. Algorithm 2 achieves the approximate optimal solution for unknown switched systems with infinite-horizon cost function, which has not been achieved well in existing literature as far as we know.
5. Conclusions
In this paper, an online PI-based algorithm inspired by the off-policy learning method and based on that, a data-driven PI-based algorithm, are proposed to approximate the optimal solution quickly for optimal scheduling problems. Only data produced by an initial switching policy is necessary and the approximation time is relatively short. The data-driven algorithm acquires useful knowledge of the weight vectors step by step through different data and solves the optimal scheduling problem for switched systems with unknown subsystems, only taking advantage of data. However, the dwell-time problems, which are important in practical applications, are not incorporated in this paper. So, optimal scheduling problems with dwell-time constraints will be investigated in the future.
Author Contributions
Methodology, C.Z. and M.G.; formal analysis, C.Z. and J.Z.; validation, C.Z. and C.X.; writing—original draft preparation, C.Z.; supervision, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant number 61673065.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liberzon, D. Switching in Systems and Control; Springer Science & Business Media: Boston, MA, USA, 2003. [Google Scholar]
- Sun, Z. Switched Linear Systems: Control and Design; Springer Science & Business Media: London, UK, 2006. [Google Scholar]
- Zha, W.; Guo, Y.; Wu, H.; Sotelo, M.A.; Ma, Y.; Yi, Q.; Li, Z.; Sun, X. A new switched state jump observer for traffic density estimation in expressways based on hybrid-dynamic-traffic-network-model. Sensors 2019, 19, 3822. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhao, Y.; Zhu, J.; Wang, J.; Tang, B. A Switched-Element System Based Direction of Arrival (DOA) Estimation Method for Un-Cooperative Wideband Orthogonal Frequency Division Multi Linear Frequency Modulation (OFDM-LFM) Radar Signals. Sensors 2019, 19, 132. [Google Scholar] [CrossRef] [PubMed]
- Egerstedt, M.; Wardi, Y.; Axelsson, H. Transition-time optimization for switched-mode dynamical systems. IEEE Trans. Autom. Control 2006, 51, 110–115. [Google Scholar] [CrossRef]
- Axelsson, H.; Wardi, Y.; Egerstedt, M.; Verriest, E.I. Gradient Descent Approach to Optimal Mode Scheduling in Hybrid Dynamical Systems. J. Optim. Theory Appl. 2008, 136, 167–186. [Google Scholar] [CrossRef]
- Koksal, N.; Jalalmaab, M.; Fidan, B. Adaptive linear quadratic attitude tracking control of a quadrotor UAV based on IMU sensor data fusion. Sensors 2019, 19, 46. [Google Scholar] [CrossRef]
- Aranda-Escolástico, E.; Salt, J.; Guinaldo, M.; Chacón, J.; Dormido, S. Optimal control for aperiodic dual-rate systems with time-varying delays. Sensors 2018, 18, 1491. [Google Scholar] [CrossRef]
- Stellato, B.; Ober-Blobaum, S.; Goulart, P.J. Second-Order Switching Time Optimization for Switched Dynamical Systems. IEEE Trans. Autom. Control 2017, 62, 5407–5414. [Google Scholar] [CrossRef]
- Wardi, Y.; Egerstedt, M.; Hale, M. Switched-mode systems: Gradient-descent algorithms with Armijo step sizes. Discret. Event Dyn. Syst. 2015, 25, 571–599. [Google Scholar] [CrossRef]
- Ruffler, F.; Hante, F.M. Optimal switching for hybrid semilinear evolutions. Nonlinear Anal. Hybrid Syst. 2016, 22, 215–227. [Google Scholar] [CrossRef]
- Das, T.; Mukherjee, R. Optimally switched linear systems. Automatica 2008, 44, 1437–1441. [Google Scholar] [CrossRef]
- Zhang, W.; Hu, J.; Abate, A. Infinite-horizon switched LQR problems in discrete time: A suboptimal algorithm with performance analysis. IEEE Trans. Autom. Control 2012, 57, 1815–1821. [Google Scholar] [CrossRef]
- Caldwell, T.M.; Murphey, T.D. Projection-based iterative mode scheduling for switched systems. Nonlinear Anal. Hybrid Syst. 2016, 21, 59–83. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Wang, D. Data-based optimal control for weakly coupled nonlinear systems using policy iteration. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2016, 48, 511–521. [Google Scholar] [CrossRef]
- Heydari, A.; Balakrishnan, S.N. Optimal switching and control of nonlinear switching systems using approximate dynamic programming. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1106–1117. [Google Scholar]
- Heydari, A.; Balakrishnan, S. Optimal switching between autonomous subsystems. J. Frankl. Inst. 2014, 351, 2675–2690. [Google Scholar] [CrossRef]
- Heydari, A. Optimal scheduling for reference tracking or state regulation using reinforcement learning. J. Frankl. Inst. 2015, 352, 3285–3303. [Google Scholar] [CrossRef]
- Heydari, A. Feedback solution to optimal switching problems with switching cost. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 2009–2019. [Google Scholar] [CrossRef]
- Heydari, A. Optimal switching of DC–DC power converters using approximate dynamic programming. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 586–596. [Google Scholar] [CrossRef]
- Sardarmehni, T.; Heydari, A. Sub-optimal scheduling in switched systems with continuous-time dynamics: A gradient descent approach. Neurocomputing 2018, 285, 10–22. [Google Scholar] [CrossRef]
- Sardarmehni, T.; Heydari, A. Suboptimal Scheduling in Switched Systems With Continuous-Time Dynamics: A Least Squares Approach. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2167–2178. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D. Data-driven neuro-optimal temperature control of water–gas shift reaction using stable iterative adaptive dynamic programming. IEEE Trans. Ind. Electron. 2014, 61, 6399–6408. [Google Scholar] [CrossRef]
- Wei, Q.; Song, R.; Yan, P. Data-driven zero-sum neuro-optimal control for a class of continuous-time unknown nonlinear systems with disturbance using ADP. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 444–458. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Ma, H.; Zhang, X.; Li, Y. Compact Model-Free Adaptive Control Algorithm for Discrete-Time Nonlinear Systems. IEEE Access 2019, 7, 141062–141071. [Google Scholar] [CrossRef]
- Lu, W.; Ferrari, S. An approximate dynamic programming approach for model-free control of switched systems. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 3837–3844. [Google Scholar]
- Lu, W.; Zhu, P.; Ferrari, S. A Hybrid-Adaptive Dynamic Programming Approach for the Model-Free Control of Nonlinear Switched Systems. IEEE Trans. Autom. Control 2016, 61, 3203–3208. [Google Scholar] [CrossRef]
- Zhang, C.; Gan, M.; Zhao, J. Data-driven optimal control of switched linear autonomous systems. Int. J. Syst. Sci. 2019, 50, 1275–1289. [Google Scholar] [CrossRef]
- Gan, M.; Zhang, C.; Zhao, J. Data-driven optimal switching of switched systems. J. Frankl. Inst. 2019, 356, 5193–5221. [Google Scholar] [CrossRef]
- Kulin, M.; Fortuna, C.; De Poorter, E.; Deschrijver, D.; Moerman, I. Data-driven design of intelligent wireless networks: An overview and tutorial. Sensors 2016, 16, 790. [Google Scholar] [CrossRef]
- Yuan, Y.; Tang, X.; Zhou, W.; Pan, W.; Li, X.; Zhang, H.T.; Ding, H.; Goncalves, J. Data driven discovery of cyber physical systems. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]
- Wang, W.; Chen, X.; Fu, H.; Wu, M. Data-driven adaptive dynamic programming for partially observable nonzero-sum games via Q-learning method. Int. J. Syst. Sci. 2019, 50, 1338–1352. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Yu, R.; Xing, Z. H∞ Tracking Control of Discrete-Time System with Delays via Data-Based Adaptive Dynamic Programming. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2019. [Google Scholar] [CrossRef]
- Radac, M.B.; Precup, R.E. Data-Driven model-free tracking reinforcement learning control with VRFT-based adaptive actor-critic. Appl. Sci. 2019, 9, 1807. [Google Scholar] [CrossRef]
- Lagoudakis, M.G.; Parr, R. Least-squares policy iteration. J. Mach. Learn. Res. 2003, 4, 1107–1149. [Google Scholar]
- Jiang, Y.; Jiang, Z.P. Robust Adaptive Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Vrabie, D.; Pastravanu, O.; Abu-Khalaf, M.; Lewis, F.L. Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica 2009, 45, 477–484. [Google Scholar] [CrossRef]
- Sardarmehni, T.; Heydari, A. Policy iteration for optimal switching with continuous-time dynamics. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2016; pp. 3536–3543. [Google Scholar]
- Jiang, Y.; Jiang, Z.P. Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics. Automatica 2012, 48, 2699–2704. [Google Scholar] [CrossRef]
- Bian, T.; Jiang, Y.; Jiang, Z.P. Adaptive dynamic programming and optimal control of nonlinear nonaffine systems. Automatica 2014, 50, 2624–2632. [Google Scholar] [CrossRef]
- Bian, T.; Jiang, Z.P. Value iteration, adaptive dynamic programming, and optimal control of nonlinear systems. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 3375–3380. [Google Scholar]
- Powell, M.J.D. Approximation Theory and Methods; Cambridge University Press: London, UK, 1981. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).