Influence of Temperature Variation on the Vibrational Characteristics of Fused Silica Cylindrical Resonators for Coriolis Vibratory Gyroscopes
Abstract
1. Introduction
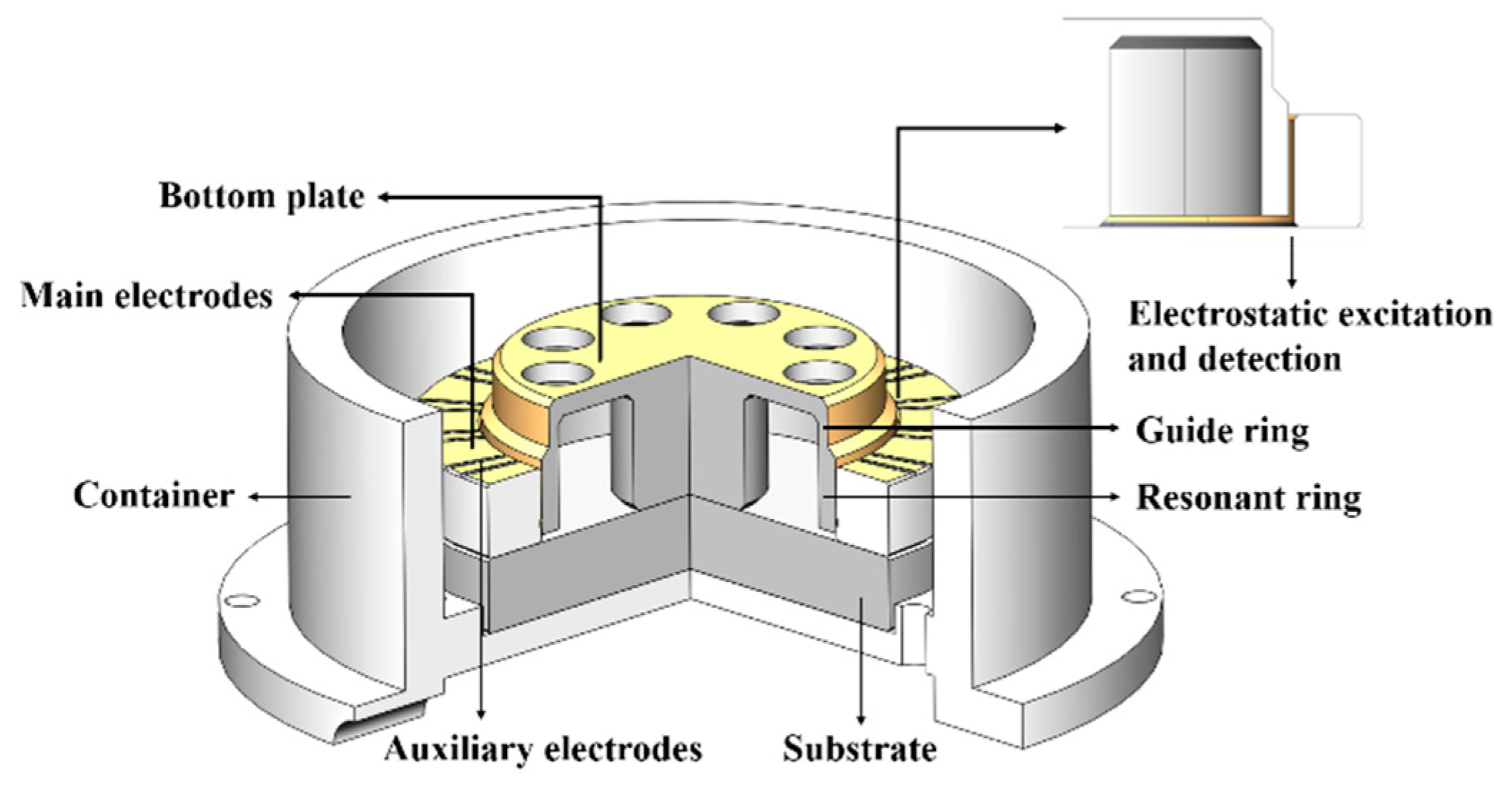
2. Experiments and Methods
2.1. Electrostatic Excitation and Detection
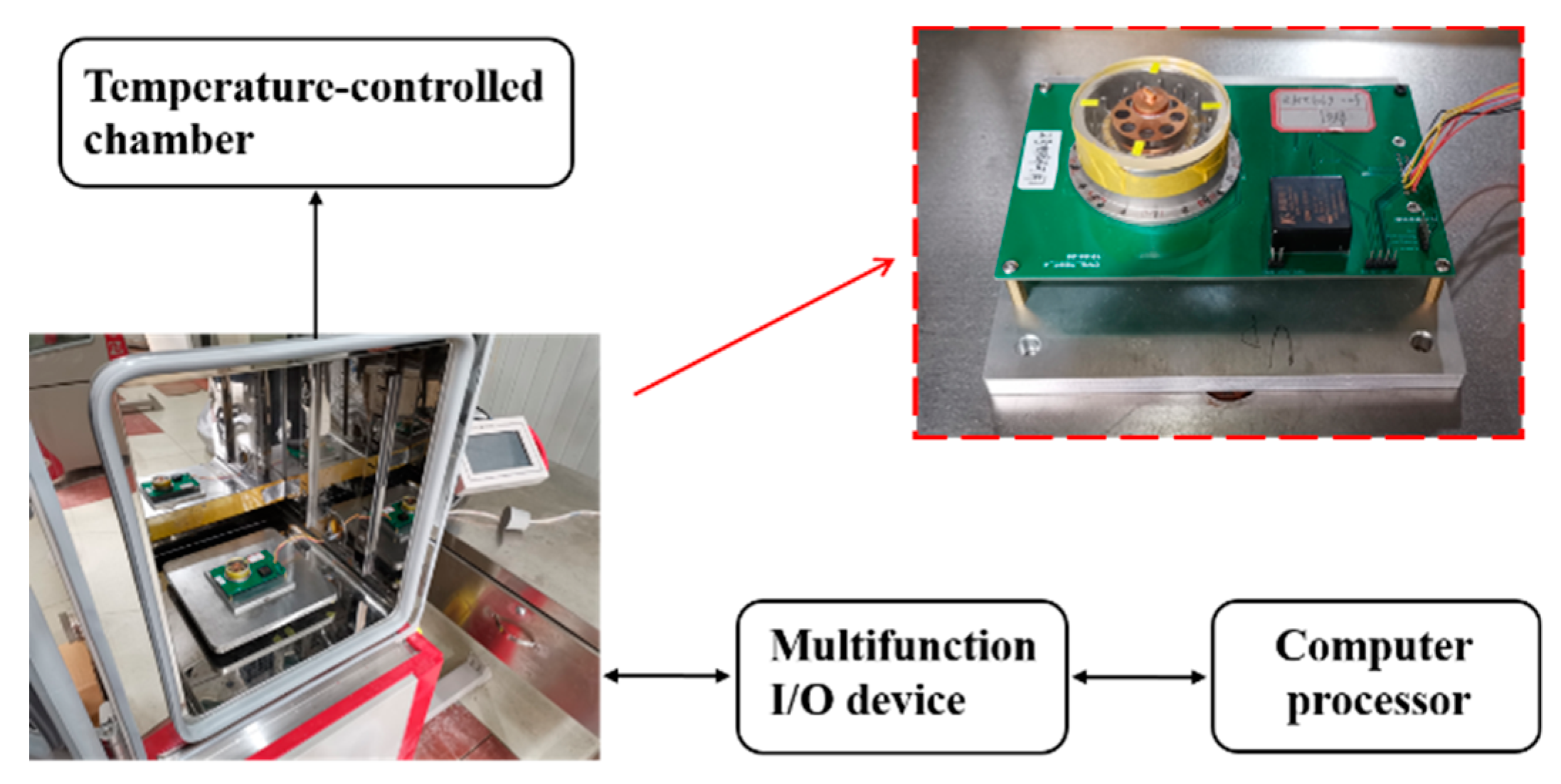
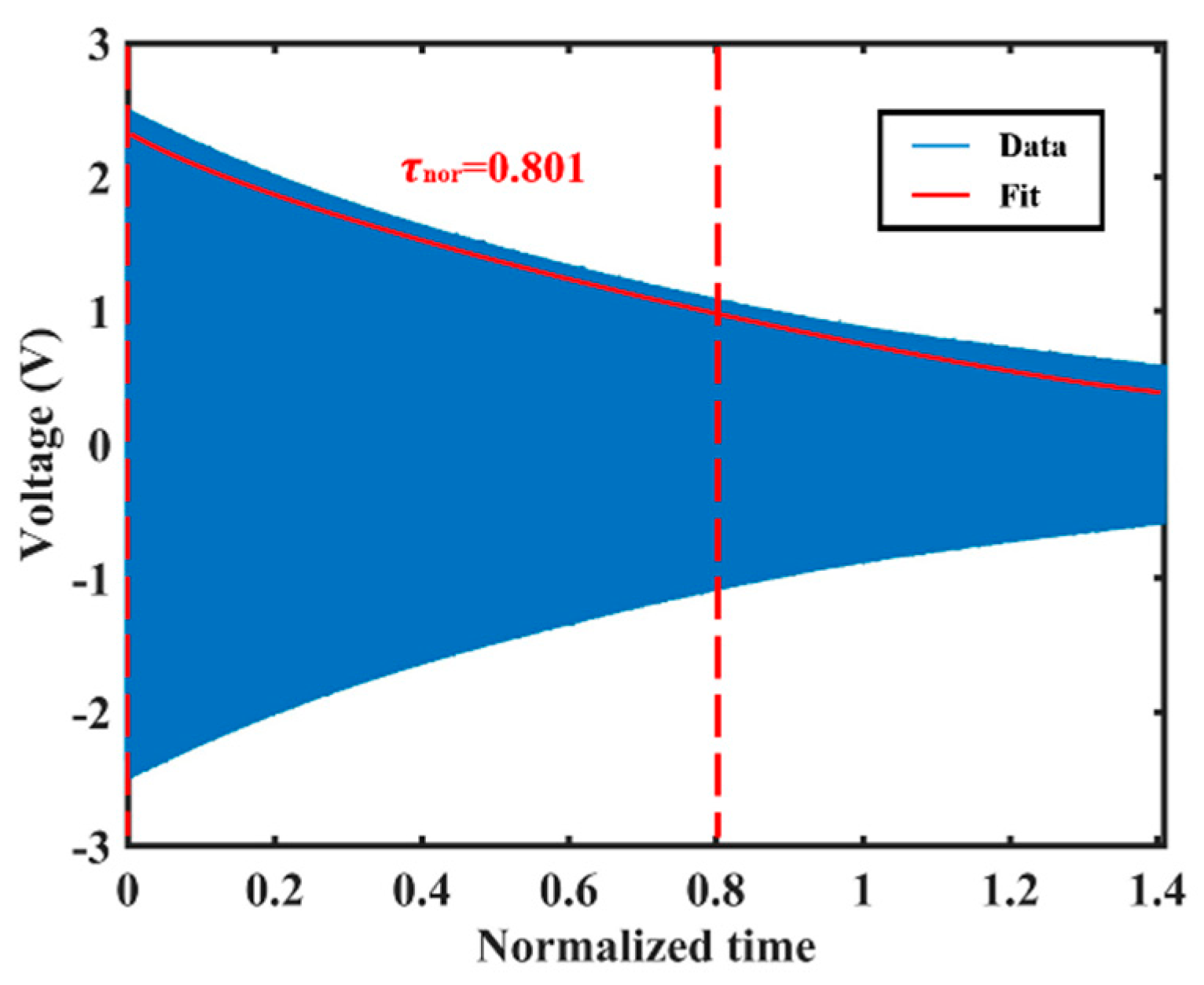
2.2. Measurement of Vibrational Characteristics
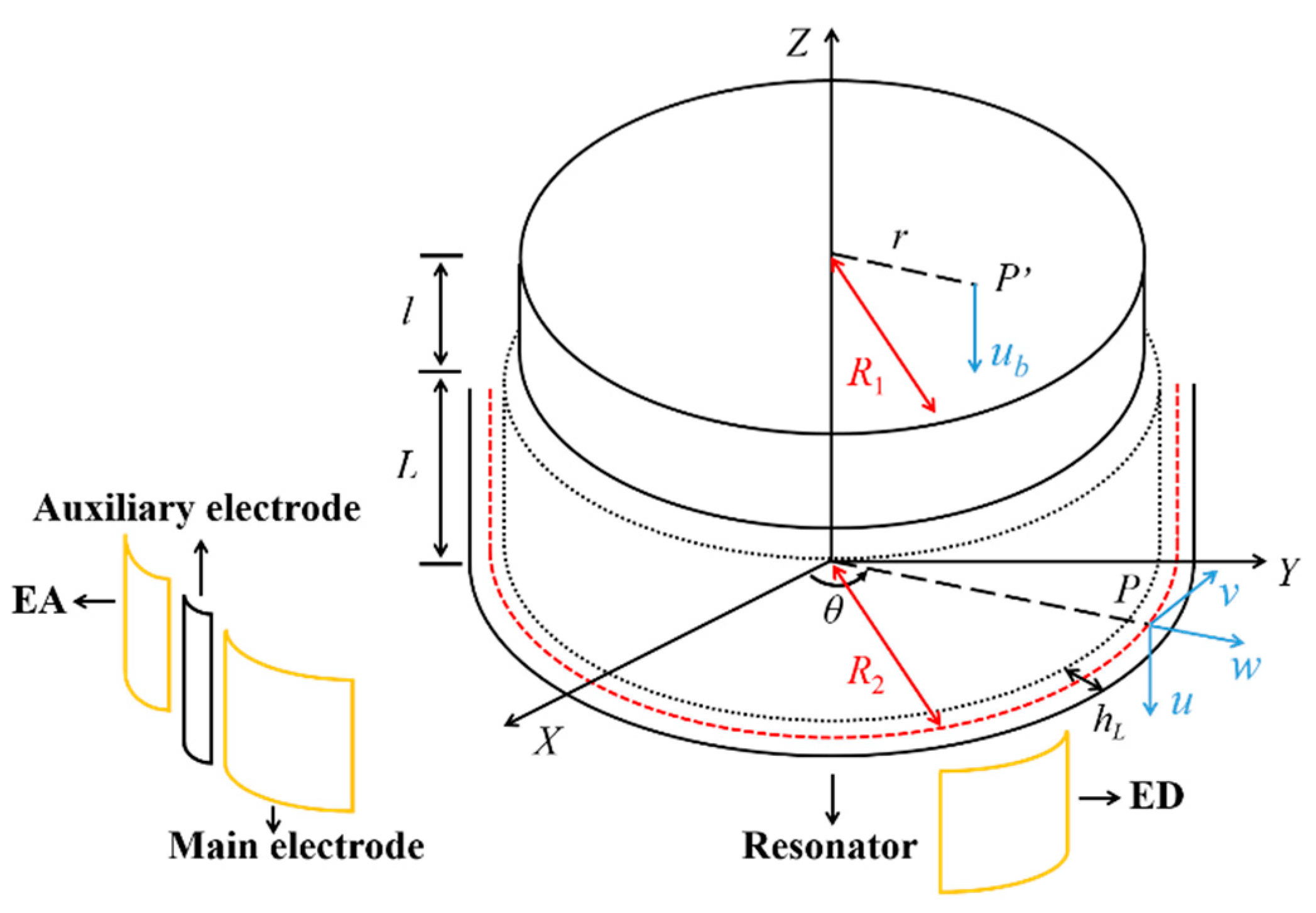
3. Theoretical Analysis
3.1. Theoretical Analysis
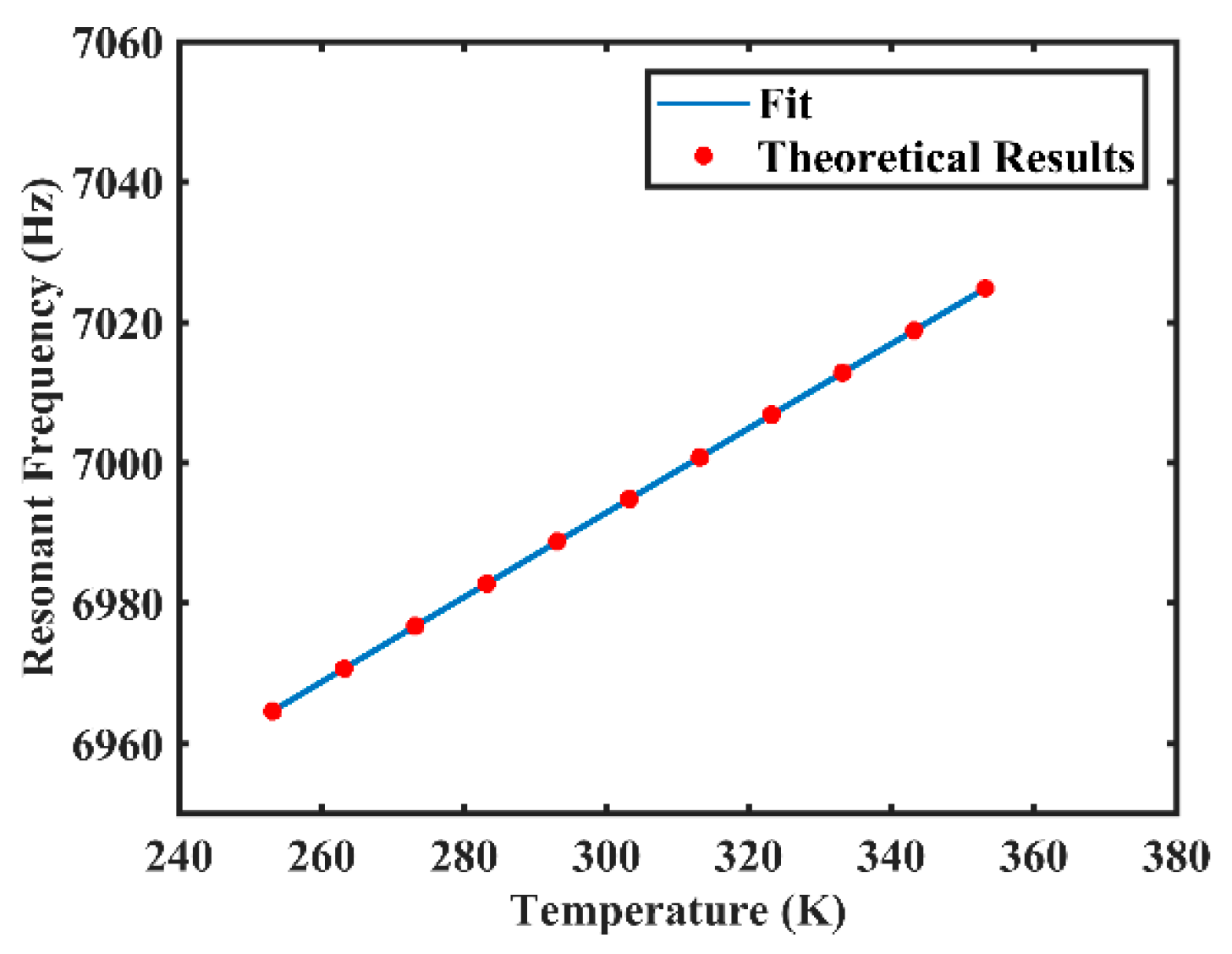
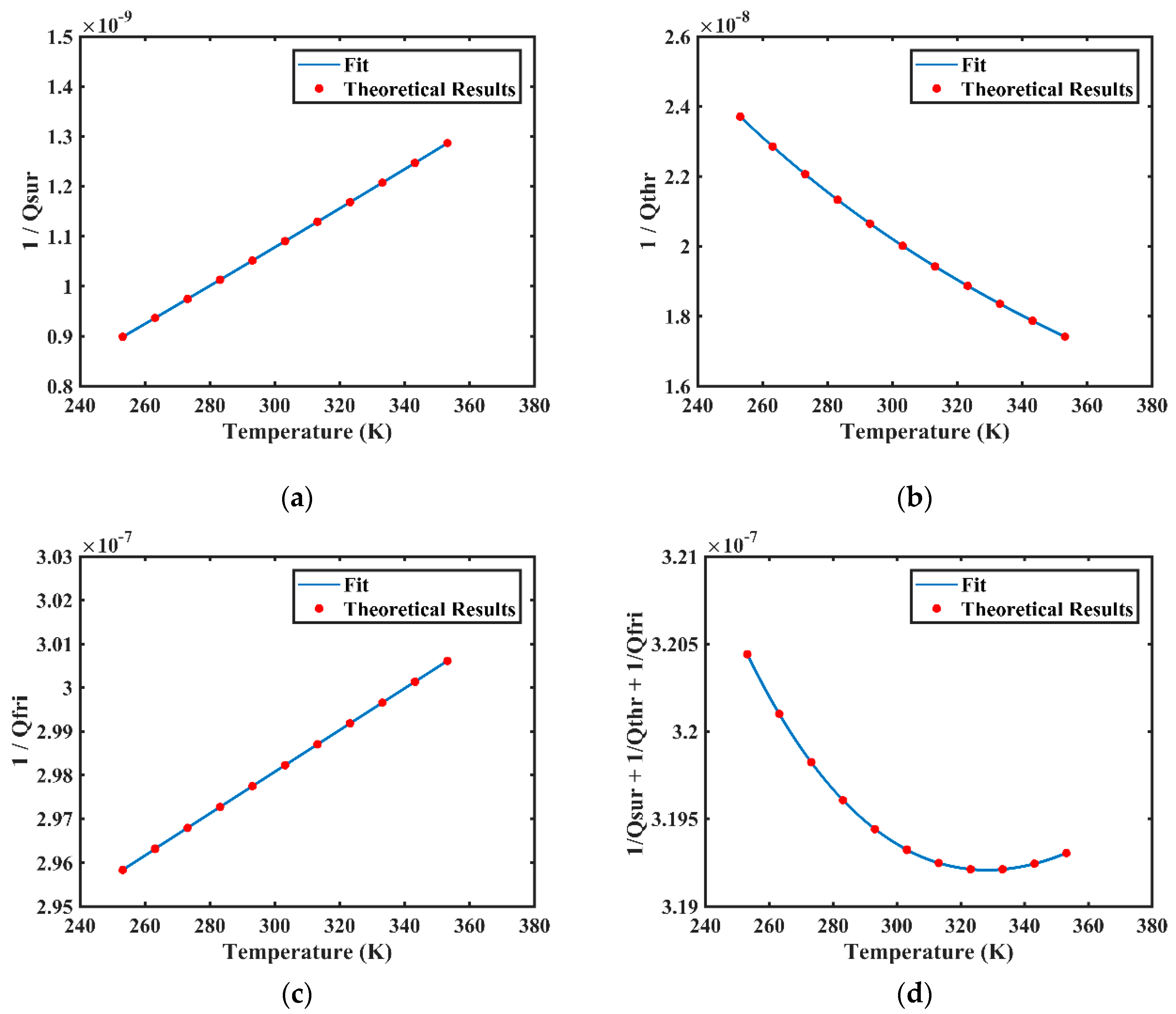
3.2. Numerical Calculations
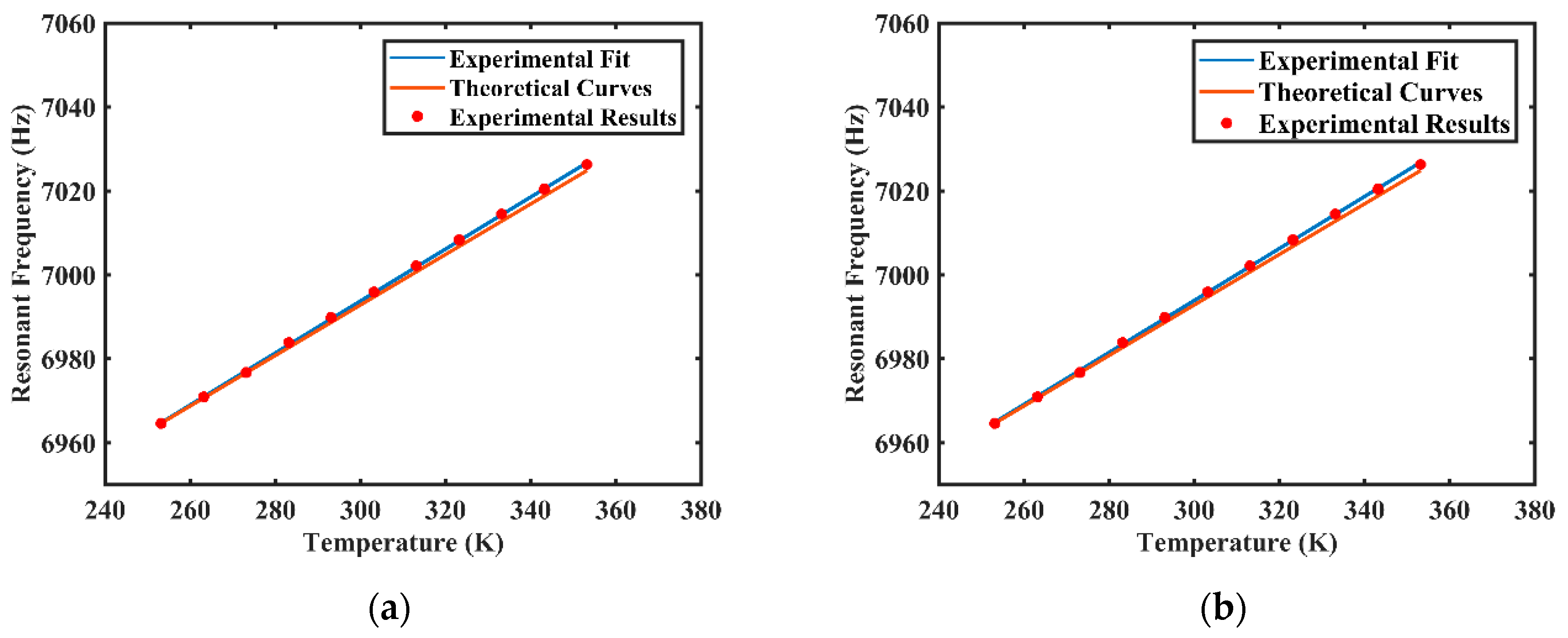
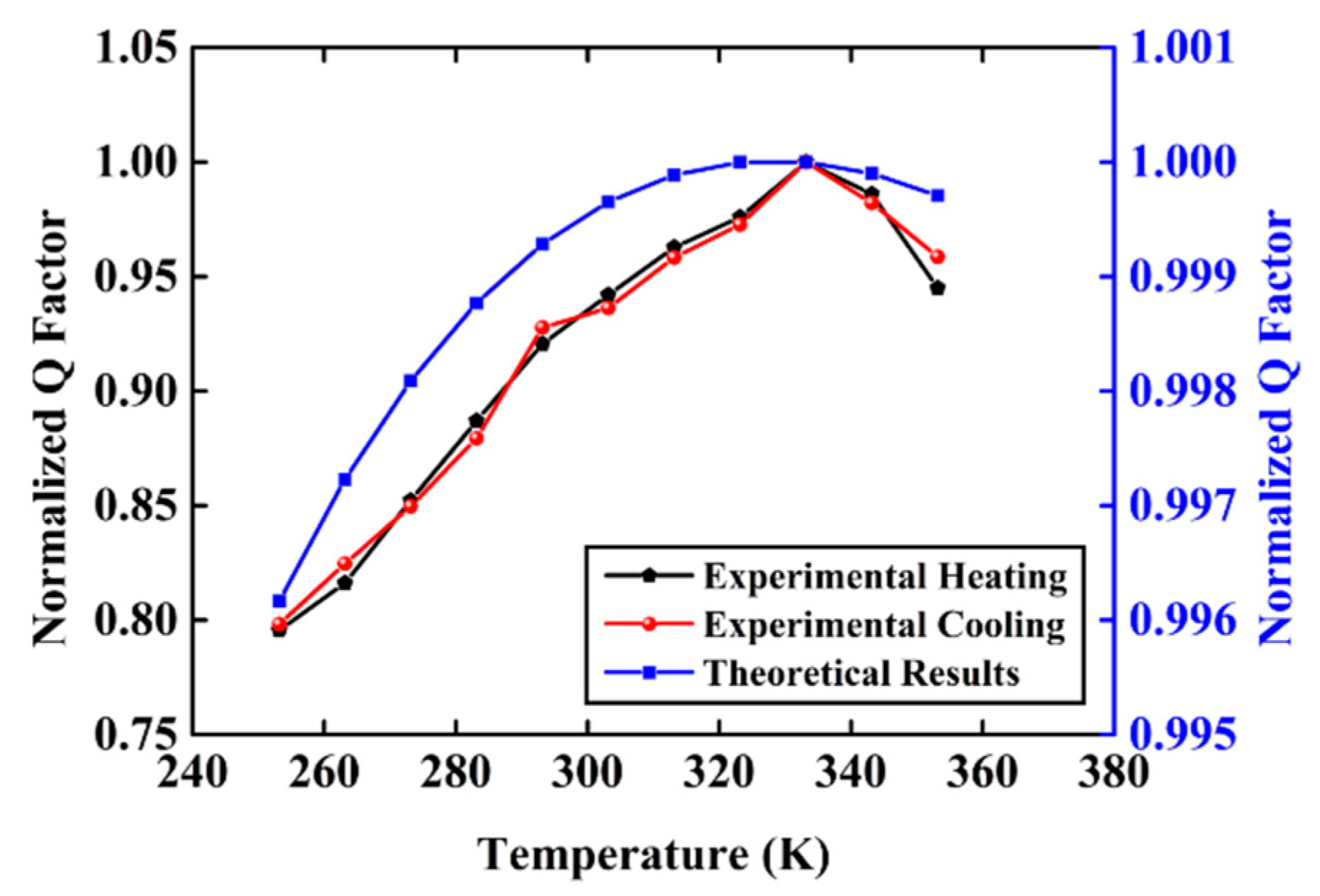
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chikovani, V.V.; Yatzenko, Y.A.; Kovalenko, V.A. Coriolis Force Gyroscope with High Sensitivity. U.S. Patent 7513156B2, 7 April 2009. [Google Scholar]
- Chikovani, V.; Yatsenko, Y.A.; Barabashov, A.; Marusyk, P.; Umakhanov, E.; Taturin, V.N. Improved accuracy metallic resonator CVG. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 40–43. [Google Scholar] [CrossRef]
- Chikovani, V.; Okon, I.; Barabashov, A.; Tewksbury, P. A set of high accuracy low cost metallic resonator CVG. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 238–243. [Google Scholar]
- Sarapuloff, S. Dynamics of Precise Solid-State Gyroscopes of HRG and CRG Types. In Proceedings of the V-th Brazilian Symposium on Inertial Engineering (V SBEIN), Rio de Janeiro, Brazil, 27–29 November 2007; pp. 27–29. [Google Scholar]
- Sarapuloff, S. Development and cost reduction of high-Q dielectric resonators of solid-state gyroscopes. In Proceedings of the 8 th Saint Petersburg International Conference on Integrated Navigation Systems, St. Petersburg, Russia, 28–30 May 2001; pp. 124–126. [Google Scholar]
- Yatsenko, Y.A.; Petrenko, S.; Vovk, V.; Chikovani, V. Technological aspects of manufacturing of compound hemispherical resonators for small-sized vibratory gyroscopes. In Proceedings of the 6 th Saint Petersburg International Conference on Integrated Navigation Systems, St. Petersburg, Russia, 24–26 May 1999. [Google Scholar]
- Watson, W.S. Vibratory gyro skewed pick-off and driver geometry. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 171–179. [Google Scholar]
- Rozelle, D.M. The hemispherical resonator gyro: From wineglass to the planets. In Proceedings of the 19th AAS/AIAA Space Flight Mechanics Meeting, Savannah, GA, USA, 8–12 February 2009; pp. 1157–1178. [Google Scholar]
- Luo, Y.; Qu, T.; Zhang, B.; Pan, Y.; Xiao, P. Simulations and Experiments on the Vibrational Characteristics of Cylindrical Shell Resonator Actuated by Piezoelectric Electrodes with Different Thicknesses. Shock Vib. 2017, 2017, 2314858. [Google Scholar] [CrossRef]
- Pan, Y.; Qu, T.; Wang, D.; Wu, S.; Liu, J.; Tan, Z.; Yang, K.; Luo, H. Observation and analysis of the quality factor variation behavior in a monolithic fused silica cylindrical resonator. Sens. Actuators A Phys. 2017, 260, 81–89. [Google Scholar] [CrossRef]
- Jeanroy, A.; Bouvet, A.; Remillieux, G. HRG and marine applications. Gyroscopy Navig. 2014, 5, 67–74. [Google Scholar] [CrossRef]
- Jeanroy, A.; Grosset, G.; Goudon, J.-C.; Delhaye, F. HRG by Sagem from laboratory to mass production. In Proceedings of the 2016 IEEE International Symposium on Inertial Sensors and Systems, Laguna Beach, CA, USA, 22–25 February 2016; pp. 1–4. [Google Scholar]
- Safran. Available online: https://www.safran-group.com/ (accessed on 13 February 2020).
- Beitia, J.; Fell, C.; O’Leary, J.; Okon, I.; Simonenko, D. High-grade CVG for Stabilisation Control Systems and Tactical Grade Systems. In Proceedings of the Inertial Sensors and Systems Symposium (ISS), Karlsruhe, Germany, 9 September 2013. [Google Scholar]
- Cho, J.Y.; Woo, J.-K.; He, G.; Yang, D.; Boyd, C.; Singh, S.; Darvishian, A.; Shiari, B.; Najafi, K. 1.5-Million Q-Factor Vacuum-Packaged Birdbath Resonator Gyroscope (BRG). In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS); Institute of Electrical and Electronics Engineers (IEEE), Seoul, Korea, 27–31 January 2019; pp. 210–213. [Google Scholar]
- Wu, Y.; Pan, Y.; Wang, D.; Qu, T.; Huang, Y. The Study on Temperature Characteristics of a Monolithic Fused Silica Cylindrical Resonator. In Proceedings of the 2016 Joint International Information Technology, Mechanical and Electronic Engineering Conference, Xi’an, China, 4–5 October 2016. [Google Scholar]
- Pan, Y.; Wang, D.; Wang, Y.; Liu, J.; Wu, S.; Qu, T.; Yang, K.; Luo, H. Monolithic Cylindrical Fused Silica Resonators with High Q Factors. Sensors 2016, 16, 1185. [Google Scholar] [CrossRef]
- Luo, Y.; Qu, T.; Cui, Y.; Pan, Y.; Yu, M.; Luo, H.; Jia, Y.; Tan, Z.; Liu, J.; Zhang, B. Cylindrical Fused Silica Resonators Driven by PZT Thin Film Electrodes with Q Factor Achieving 2.89 Million after Coating. Sci. Rep. 2019, 9, 9461. [Google Scholar] [CrossRef]
- Wang, X.; Wu, W.; Fang, Z.; Luo, B.; Li, Y.; Jiang, Q. Temperature Drift Compensation for Hemispherical Resonator Gyro Based on Natural Frequency. Sensors 2012, 12, 6434–6446. [Google Scholar] [CrossRef]
- Wu, Y.; Xi, X.; Tao, Y.; Wu, X.; Wu, X. A Study of the Temperature Characteristics of Vibration Mode Axes for Vibratory Cylinder Gyroscopes. Sensors 2011, 11, 7665–7677. [Google Scholar] [CrossRef]
- Green, E.I. The story of Q. Am. Sci. 1955, 43, 584–594. [Google Scholar]
- Li, B.; Ma, G.; Wang, C. Hemispherical Resonator Gyroscope Accuracy Analysis Under Temperature Influence. Sens. Transducers 2014, 173, 284. [Google Scholar]
- Tang, Q.; Wang, X.; Yang, Q.; Liu, C. Static temperature analysis and compensation of MEMS gyroscopes. Int. J. Metrol. Qual. Eng. 2013, 4, 209–214. [Google Scholar] [CrossRef]
- Shao, P. Microscale Hemispherical Shell Resonating Gyroscopes. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, Georgia, 2014. [Google Scholar]
- Zega, V.; Frangi, A.; Guercilena, A.; Gattere, G. Analysis of Frequency Stability and Thermoelastic Effects for Slotted Tuning Fork MEMS Resonators. Sensors 2018, 18, 2157. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Z.; Qu, T.; Pan, Y.; Jia, Y.; Fan, Z.; Yang, K.; Yuan, J.; Luo, H. Optical and Electrical Method Characterizing the Dynamic Behavior of the Fused Silica Cylindrical Resonator. Sensors 2019, 19, 2928. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Qiu, Z.; Pan, Y.; Li, S.; Qu, T.; Tan, Z.; Liu, J.; Yang, K.; Zhao, W.; Luo, H.; et al. Influence of Electrostatic Forces on the Vibrational Characteristics of Resonators for Coriolis Vibratory Gyroscopes. Sensors 2020, 20, 295. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Y.; Qu, T.; Jia, Y.; Yang, K.; Luo, H. Decreasing Frequency Splits of Hemispherical Resonators by Chemical Etching. Sensors 2018, 18, 3772. [Google Scholar] [CrossRef]
- Tao, Y.; Pan, Y.; Jin, S.; Jia, Y.; Yang, K.; Luo, H. Trimming of Imperfect Cylindrical Fused Silica Resonators by Chemical Etching. Sensors 2019, 19, 3596. [Google Scholar] [CrossRef]
- Zhang, M.; Llaser, N.; Rodes, F. High-Precision Time-Domain Measurement of Quality Factor. IEEE Trans. Instrum. Meas. 2011, 61, 842–844. [Google Scholar] [CrossRef]
- Warburton, G.B. Vibration of Thin Cylindrical Shells. J. Mech. Eng. Sci. 1965, 7, 399–407. [Google Scholar] [CrossRef]
- Loveday, P.; Rogers, C. Free vibration of elastically supported thin cylinders including gyroscopic effects. J. Sound Vib. 1998, 217, 547–562. [Google Scholar] [CrossRef]
- Xi, X.; Wu, X.; Zhang, Y.; Zhou, X.; Wu, X.; Wu, Y. A study on Q factor of the trimmed resonator for vibratory cupped gyroscopes. Sens. Actuators A Phys. 2014, 218, 23–32. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Hong, Y.U.; Huang, Q.A.; Liu, T.Q. Effect of Temperature on the Young’s Modulus of Silicon Nano-Films. Chin. J. Electron Devices 2007, 30, 755–758. [Google Scholar]
- Li, X.; Ono, T.; Wang, Y.; Esashi, M. Study on ultra-thin NEMS cantilevers—High yield fabrication and size-effect on Young’s modulus of silicon. In Proceedings of the Technical Digest. MEMS 2002 IEEE International Conference. Fifteenth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No.02CH37266), Las Vegas, NV, USA, 24–24 January 2002; pp. 427–430. [Google Scholar]
- Darvishian, A. Design and Analysis of Extremely Low-Noise MEMS Gyroscopes for Navigation. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2018. [Google Scholar]
- National Institute of Standards and Technology (NIST) Property Data Summaries. Available online: https://srdata.nist.gov/ (accessed on 13 February 2020).
- McSkimin, H.J. Measurement of Elastic Constants at Low Temperatures by Means of Ultrasonic Waves–Data for Silicon and Germanium Single Crystals, and for Fused Silica. J. Appl. Phys. 1953, 24, 988–997. [Google Scholar] [CrossRef]
- Uchiyama, T.; Tomaru, T.; Tobar, M.; Tatsumi, D.; Miyoki, S.; Ohashi, M.; Kuroda, K.; Suzuki, T.; Sato, N.; Haruyama, T.; et al. Mechanical quality factor of a cryogenic sapphire test mass for gravitational wave detectors. Phys. Lett. A 1999, 261, 5–11. [Google Scholar] [CrossRef]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago Press: Chicago, IL, USA, 1948. [Google Scholar]
- Lu, P.; Lee, H.; Lu, C.; Chen, H. Thermoelastic damping in cylindrical shells with application to tubular oscillator structures. Int. J. Mech. Sci. 2008, 50, 501–512. [Google Scholar] [CrossRef]
- Wong, S.; Fox, C.; McWilliam, S. Thermoelastic damping of the in-plane vibration of thin silicon rings. J. Sound Vib. 2006, 293, 266–285. [Google Scholar] [CrossRef]
- Sun, Y.; Tohmyoh, H. Thermoelastic damping of the axisymmetric vibration of circular plate resonators. J. Sound Vib. 2009, 319, 392–405. [Google Scholar] [CrossRef]
- Flügge, W. Statik Und Dynamik Der Schalen; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
| Component | Value | Units |
|---|---|---|
| Density, | 2.203 × 103 | Kg/m3 |
| Damaged layer depth, hdam | 100 | μm |
| Heat capacity, c | 772 | JKg−1 K−1 |
| Thermal conductivity, | 1.39 | W/mK−1 |
| Thermal expansion coefficient, | 5 × 10−7 | K−1 |
| Typical size of heat distribution, | 1 × 10−6 | m |
| Internal friction coefficient, | 1 × 10−11 |
| Component | Value | Units |
|---|---|---|
| Radius of the guide ring, R1 | 12.3 | mm |
| Radius of the resonant ring, R2 | 12.6 | mm |
| Height of the resonant ring, L | 5.7 | mm |
| Height of the guide ring, l | 3.1 | mm |
| Thickness of the resonant ring, hL | 1.2 | mm |
| Thickness of the guide ring, hl | 0.5 | mm |
| Thickness of the bottom plate, hb | 0.8 | mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Qiu, Z.; Luo, Y.; Pan, Y.; Qu, T.; Yang, K.; Luo, H.; Qin, S. Influence of Temperature Variation on the Vibrational Characteristics of Fused Silica Cylindrical Resonators for Coriolis Vibratory Gyroscopes. Sensors 2020, 20, 1032. https://doi.org/10.3390/s20041032
Xiao P, Qiu Z, Luo Y, Pan Y, Qu T, Yang K, Luo H, Qin S. Influence of Temperature Variation on the Vibrational Characteristics of Fused Silica Cylindrical Resonators for Coriolis Vibratory Gyroscopes. Sensors. 2020; 20(4):1032. https://doi.org/10.3390/s20041032
Chicago/Turabian StyleXiao, Pengbo, Zhinan Qiu, Yiming Luo, Yao Pan, Tianliang Qu, Kaiyong Yang, Hui Luo, and Shiqiao Qin. 2020. "Influence of Temperature Variation on the Vibrational Characteristics of Fused Silica Cylindrical Resonators for Coriolis Vibratory Gyroscopes" Sensors 20, no. 4: 1032. https://doi.org/10.3390/s20041032
APA StyleXiao, P., Qiu, Z., Luo, Y., Pan, Y., Qu, T., Yang, K., Luo, H., & Qin, S. (2020). Influence of Temperature Variation on the Vibrational Characteristics of Fused Silica Cylindrical Resonators for Coriolis Vibratory Gyroscopes. Sensors, 20(4), 1032. https://doi.org/10.3390/s20041032





