In-Plane and Out-of-Plane MEMS Piezoresistive Cantilever Sensors for Nanoparticle Mass Detection
Abstract
1. Introduction
2. Materials and Methods
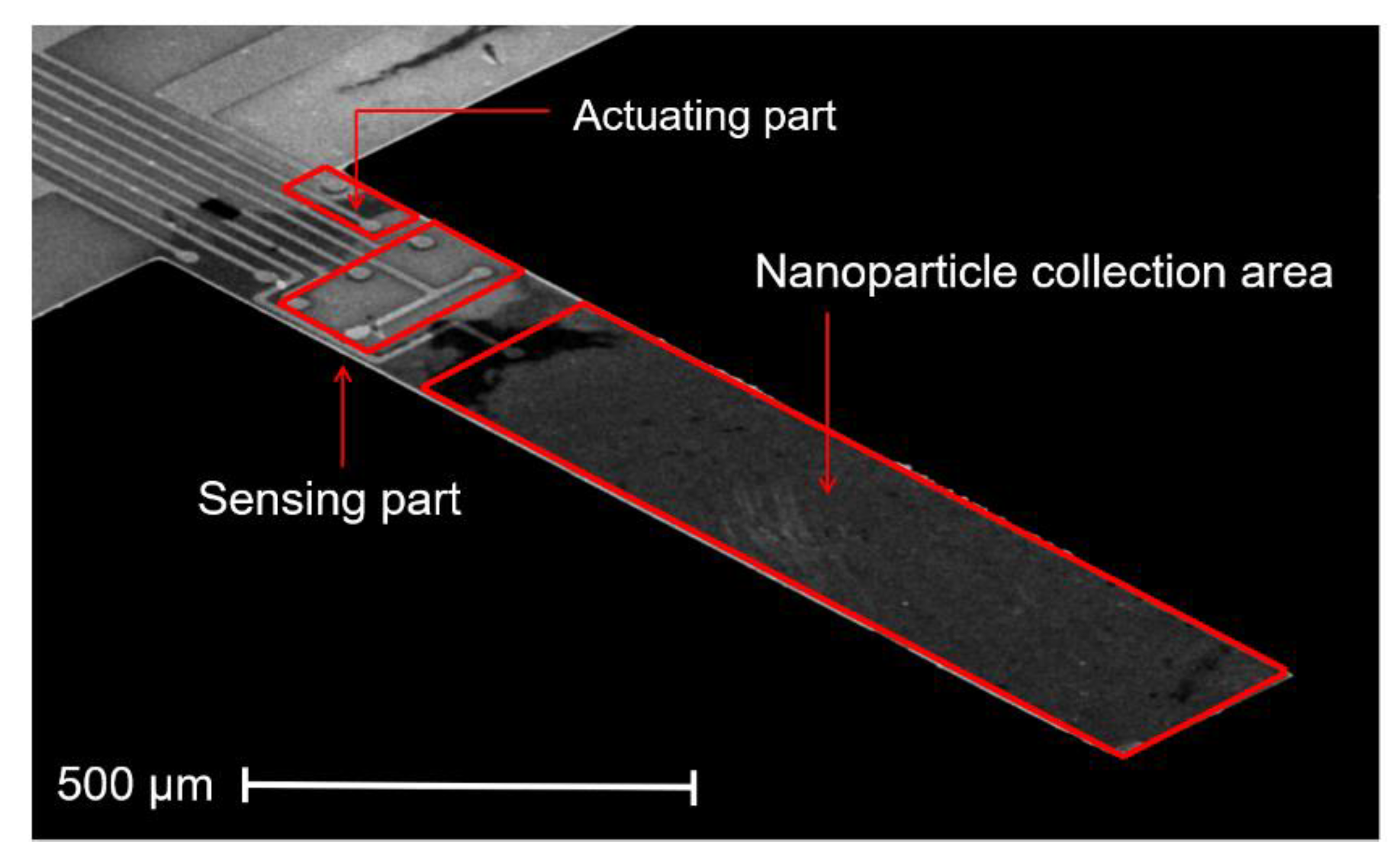
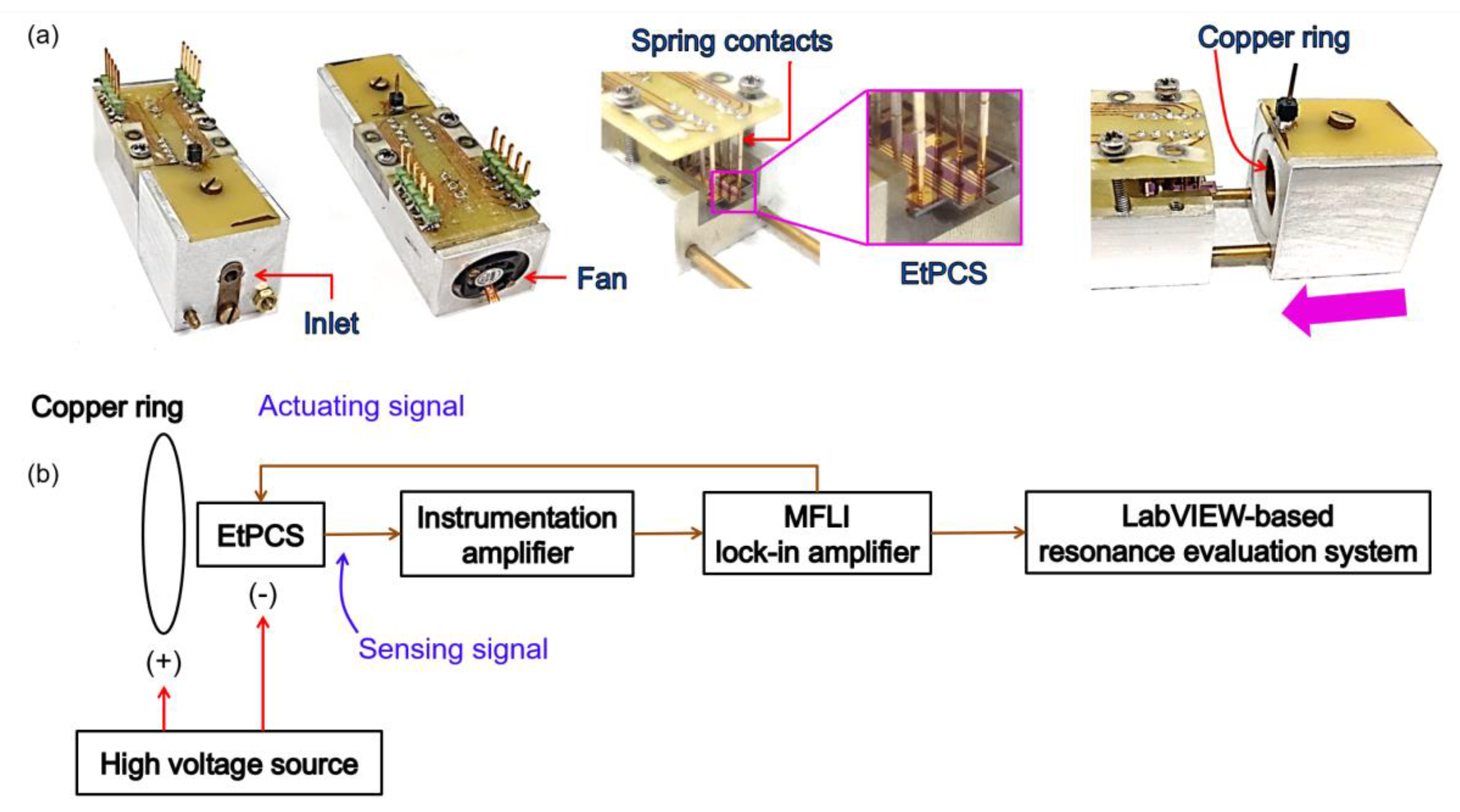
2.1. ElectroThermal Piezoresistive Cantilever Sensor (EtPCS)
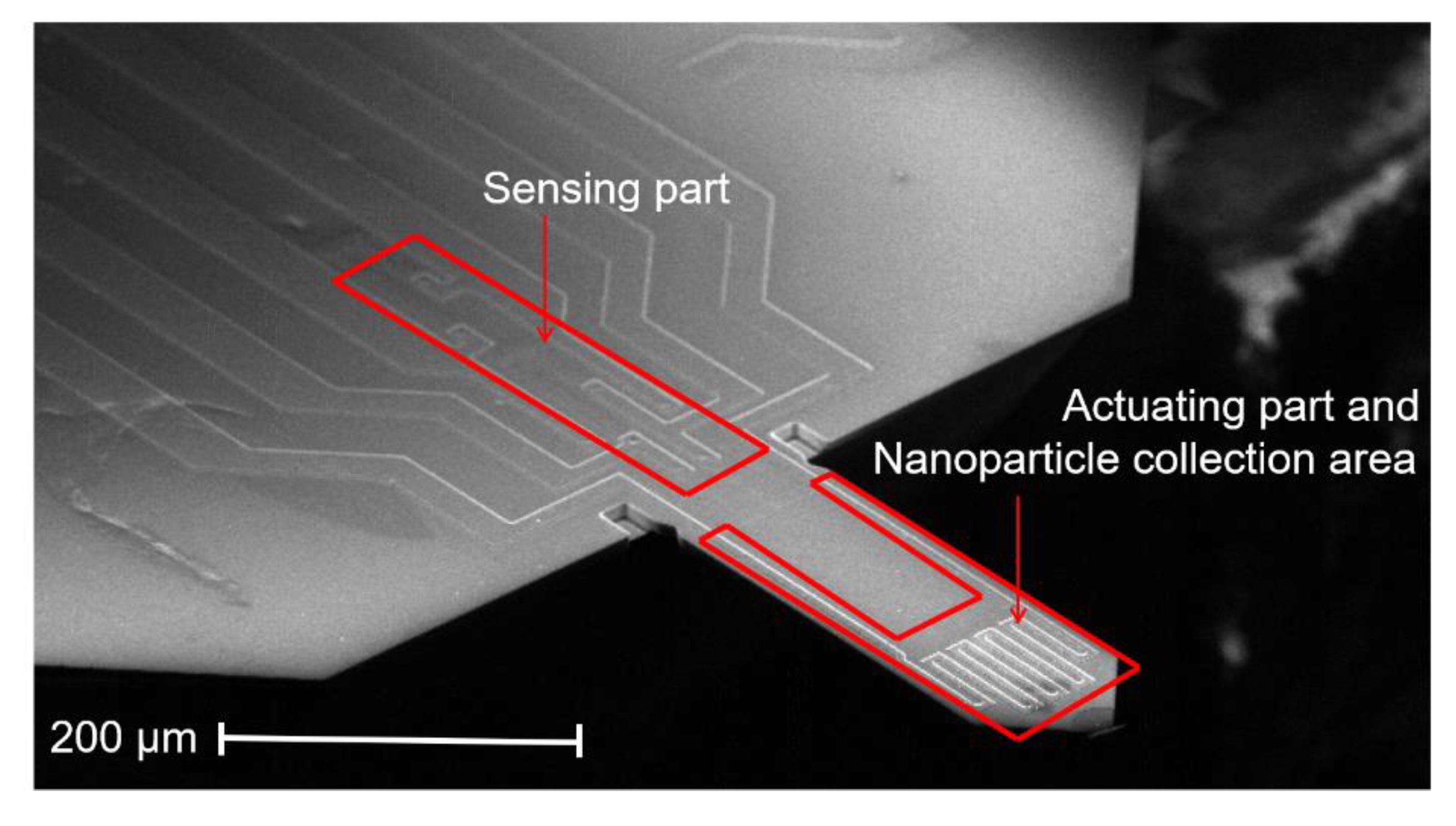
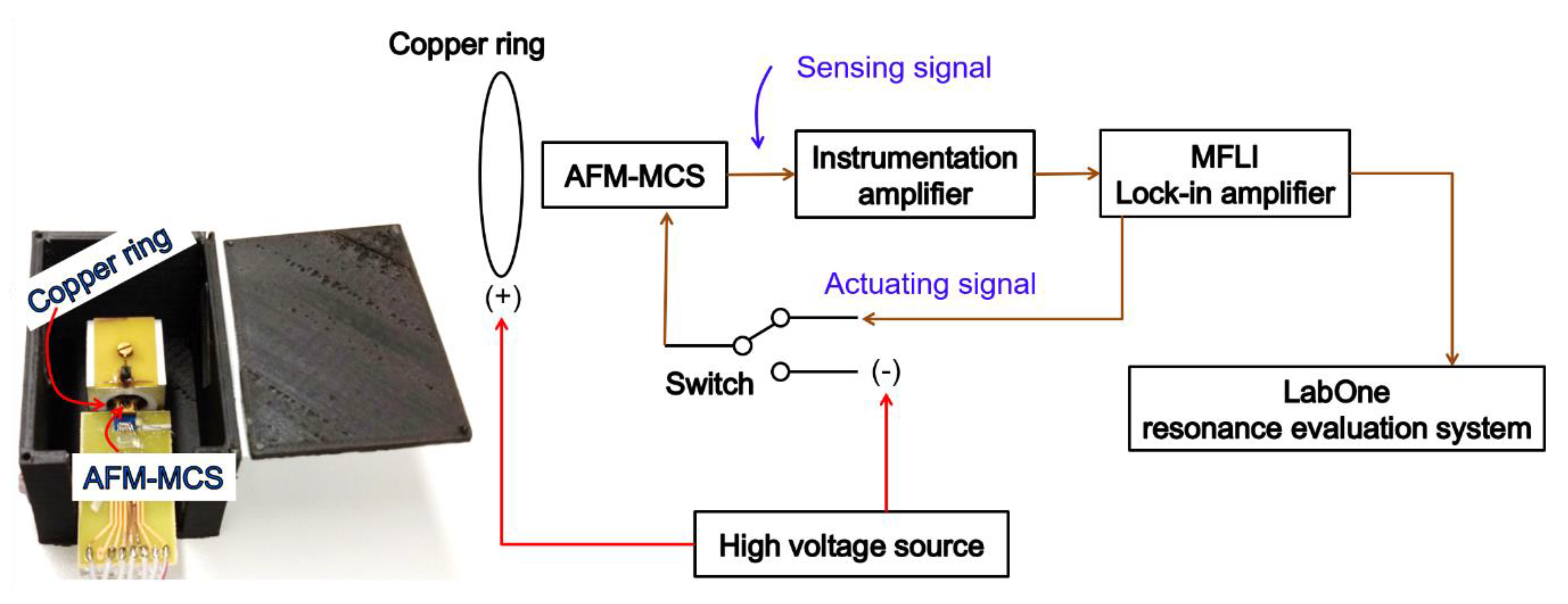
2.2. Atomic Force Microscopy Micro-Cantilever Sensor (AFM-MCS)
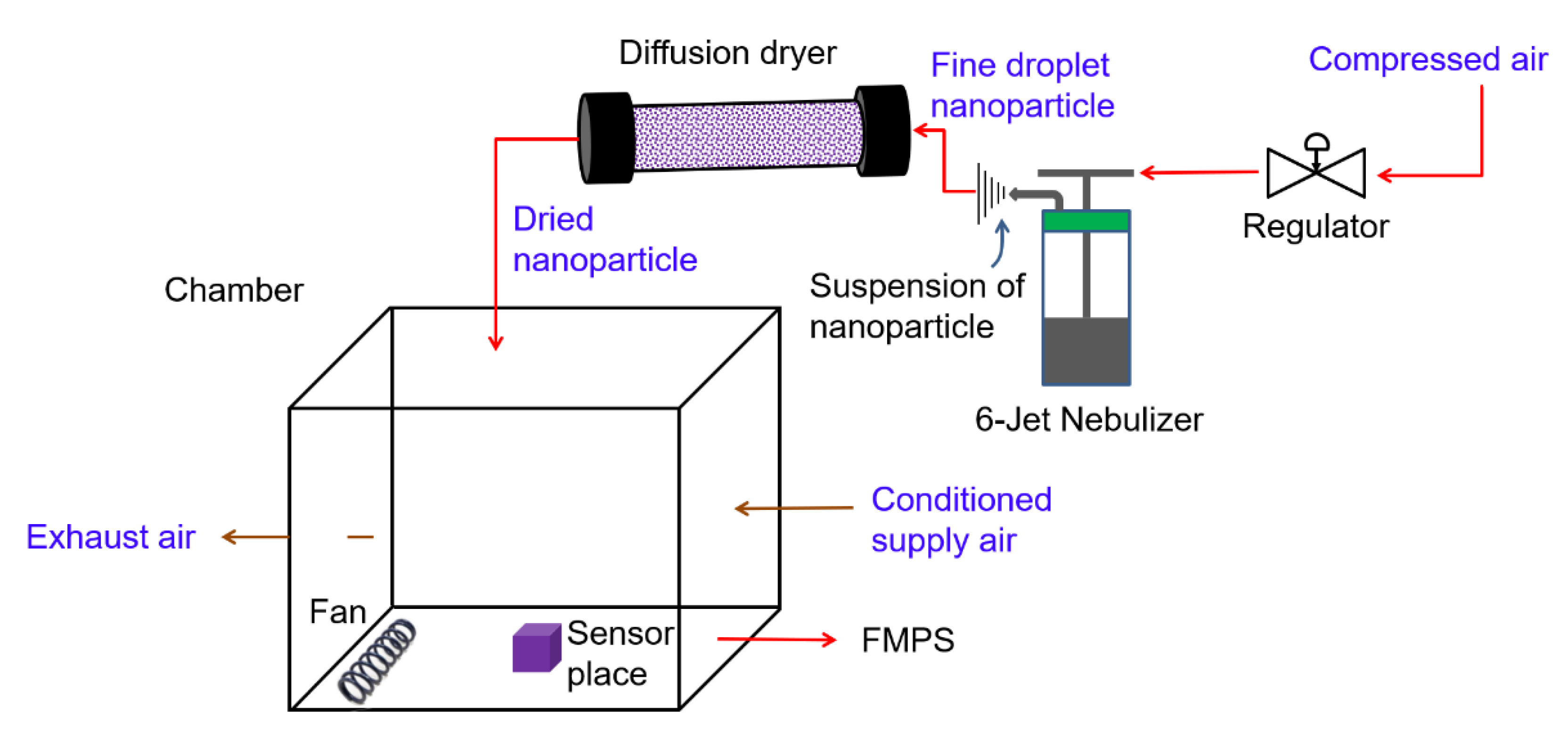
2.3. Nanoparticles Generation
3. Result and Discussion
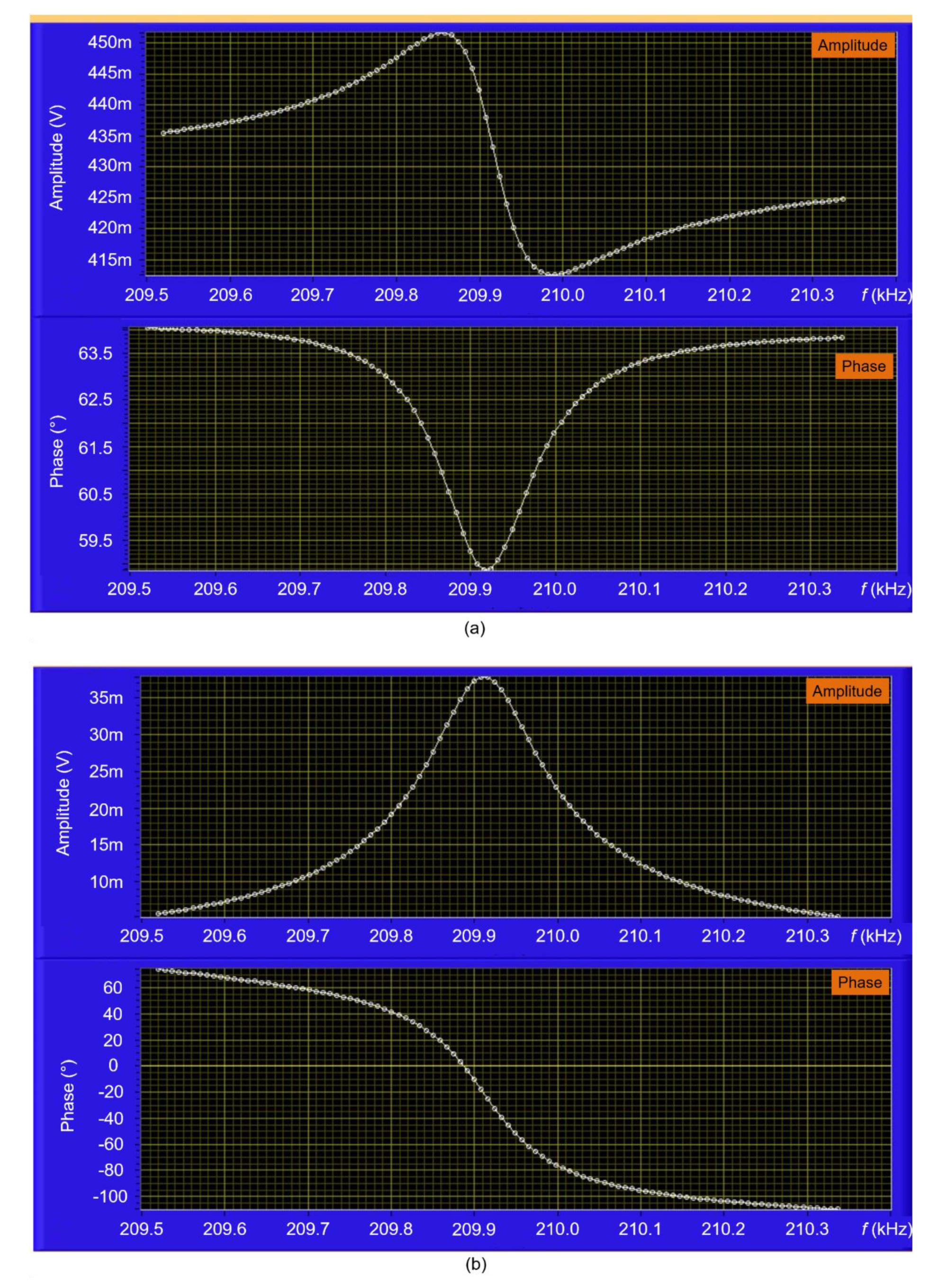
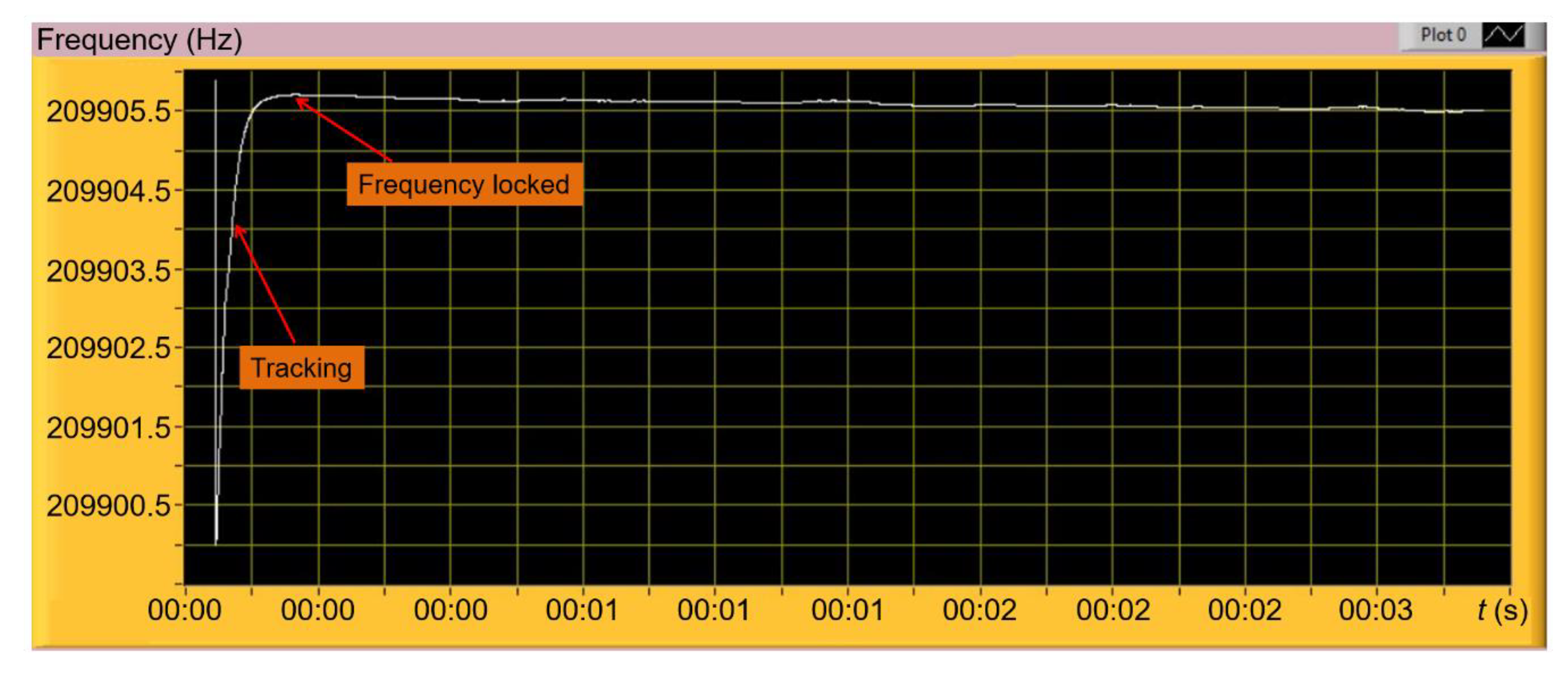
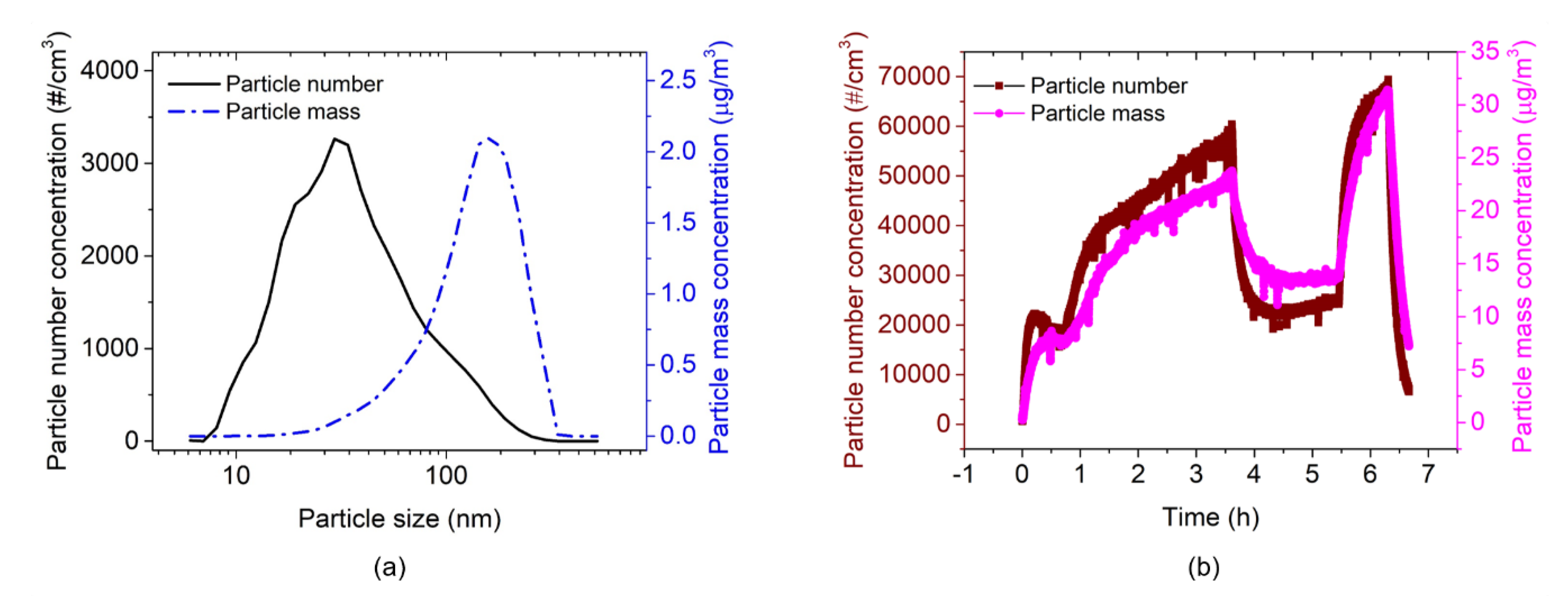
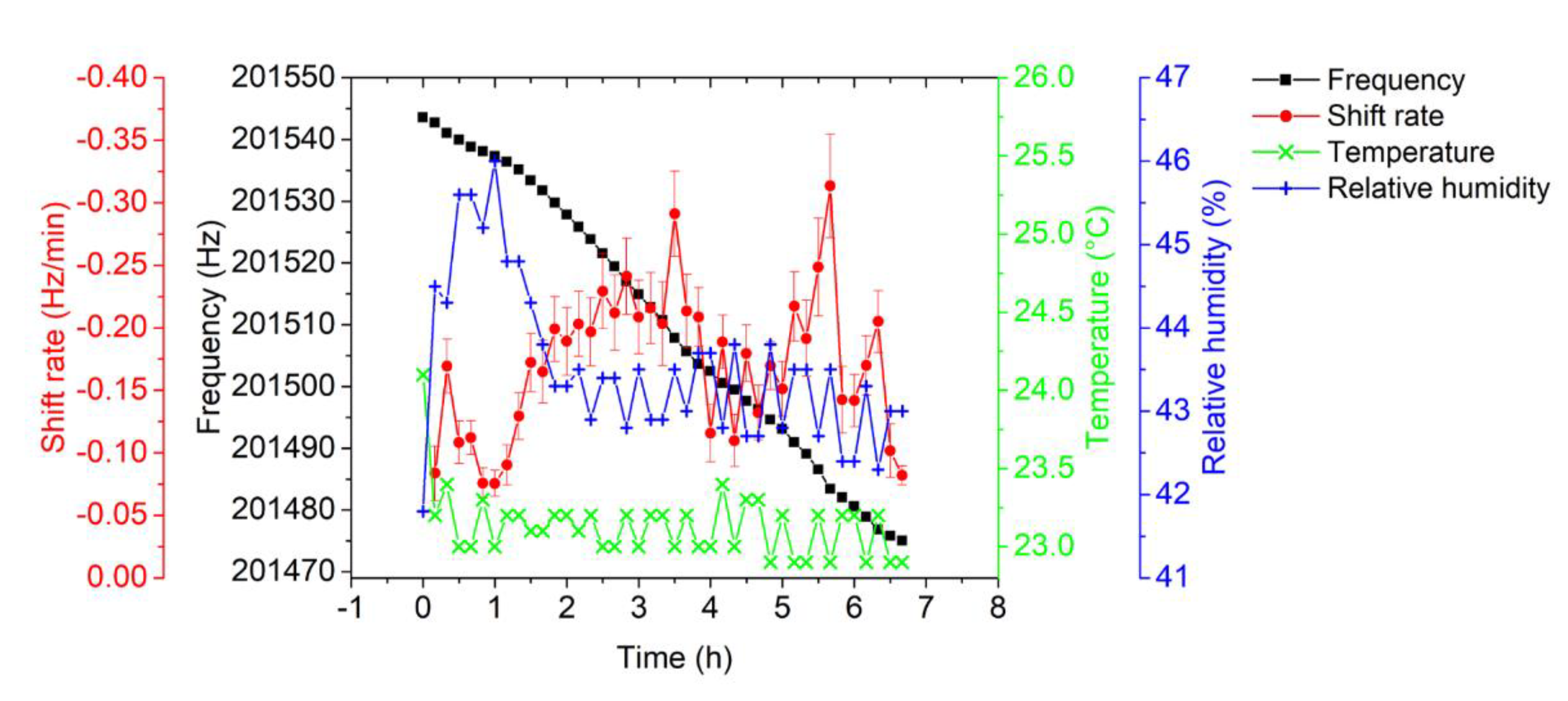
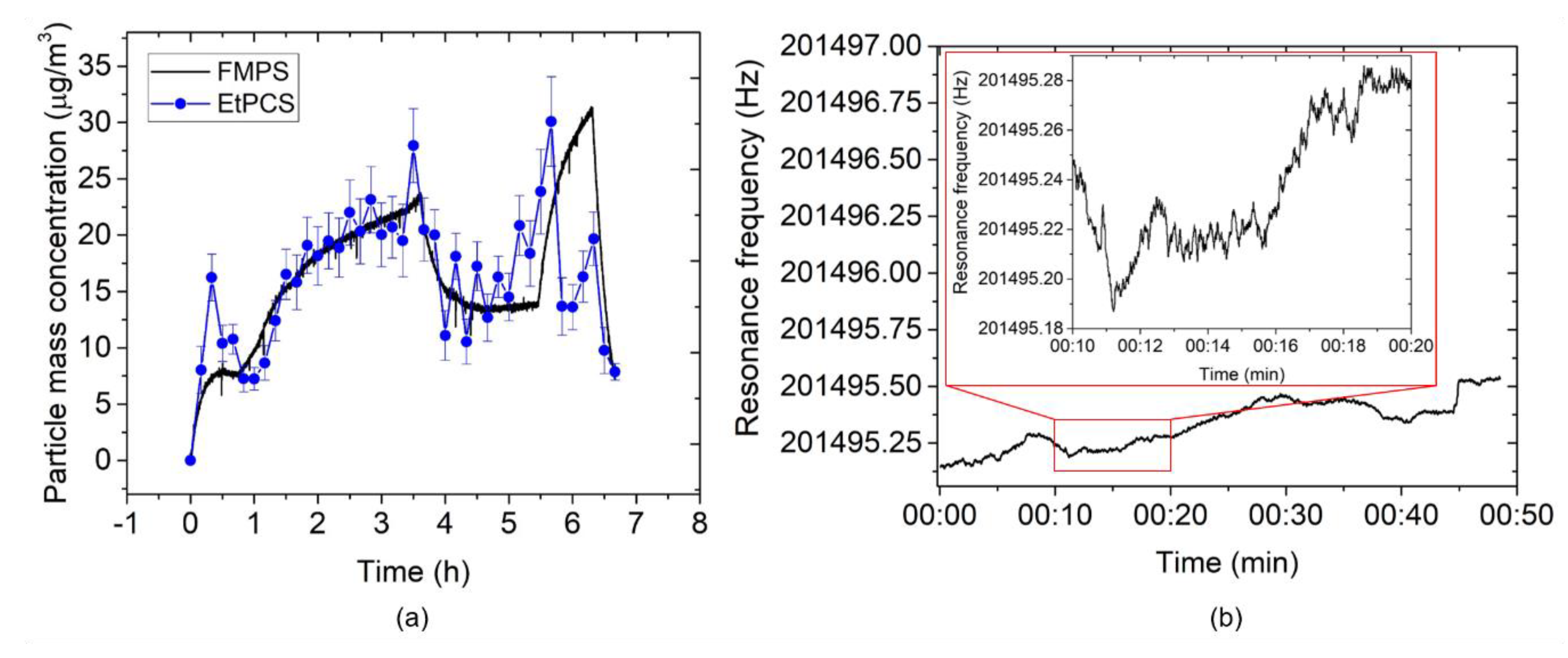
3.1. EtPCS Cantilever Performance
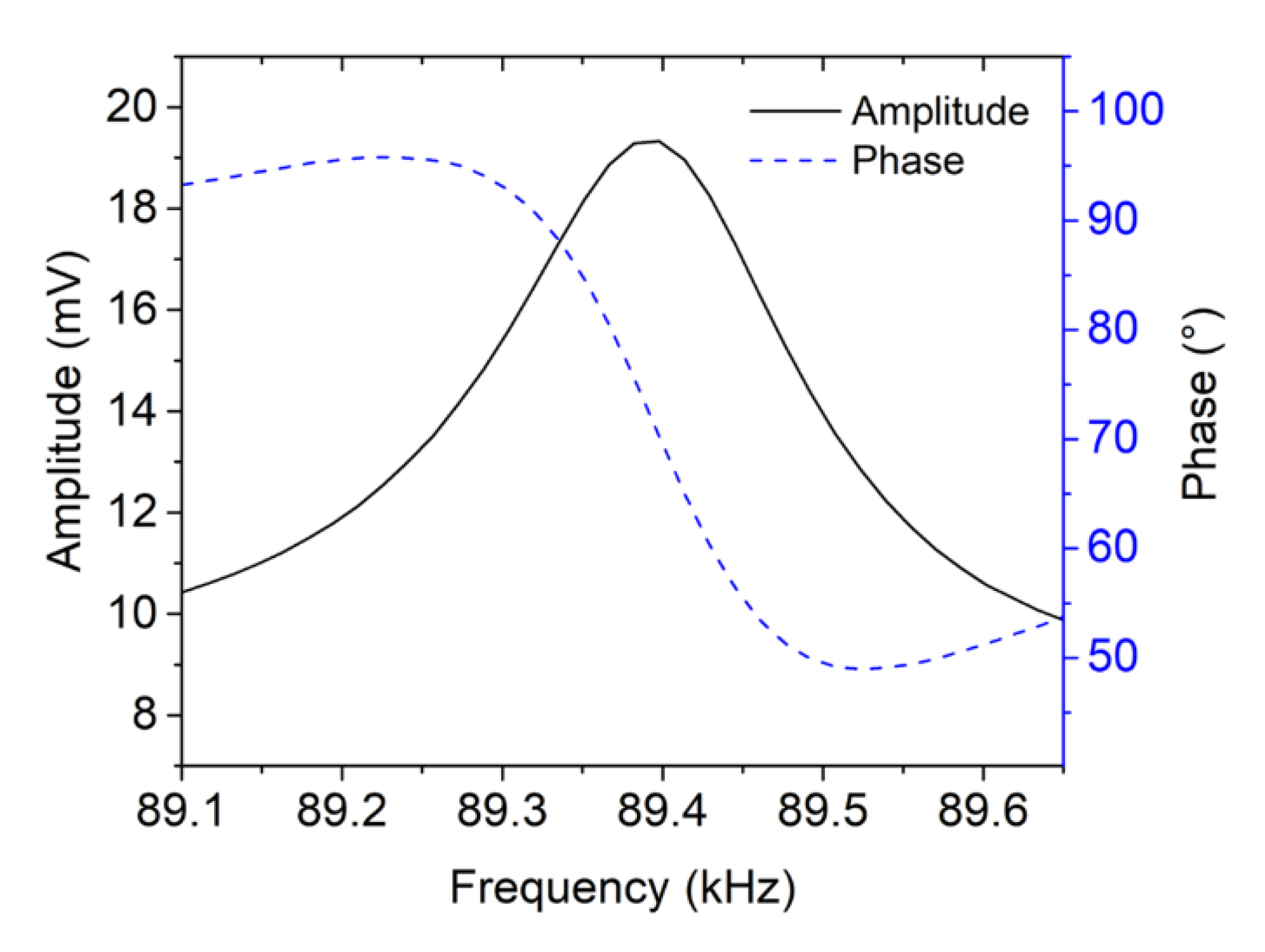
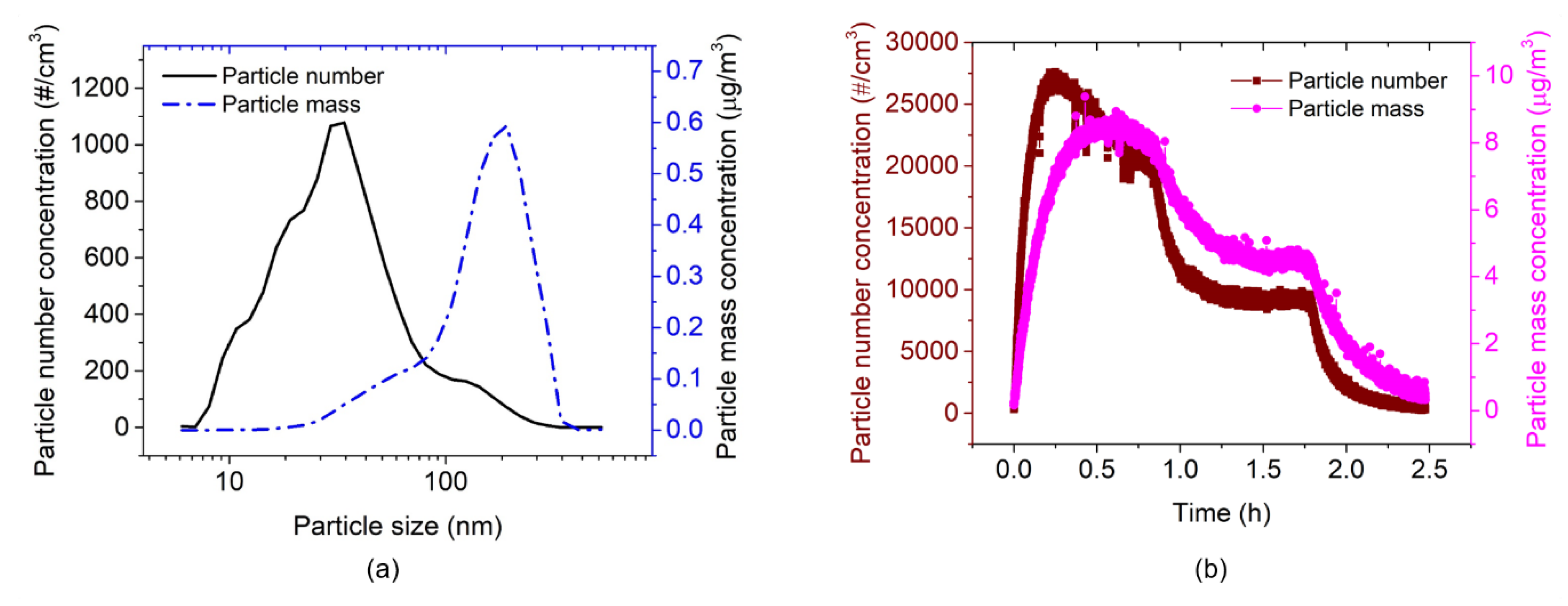
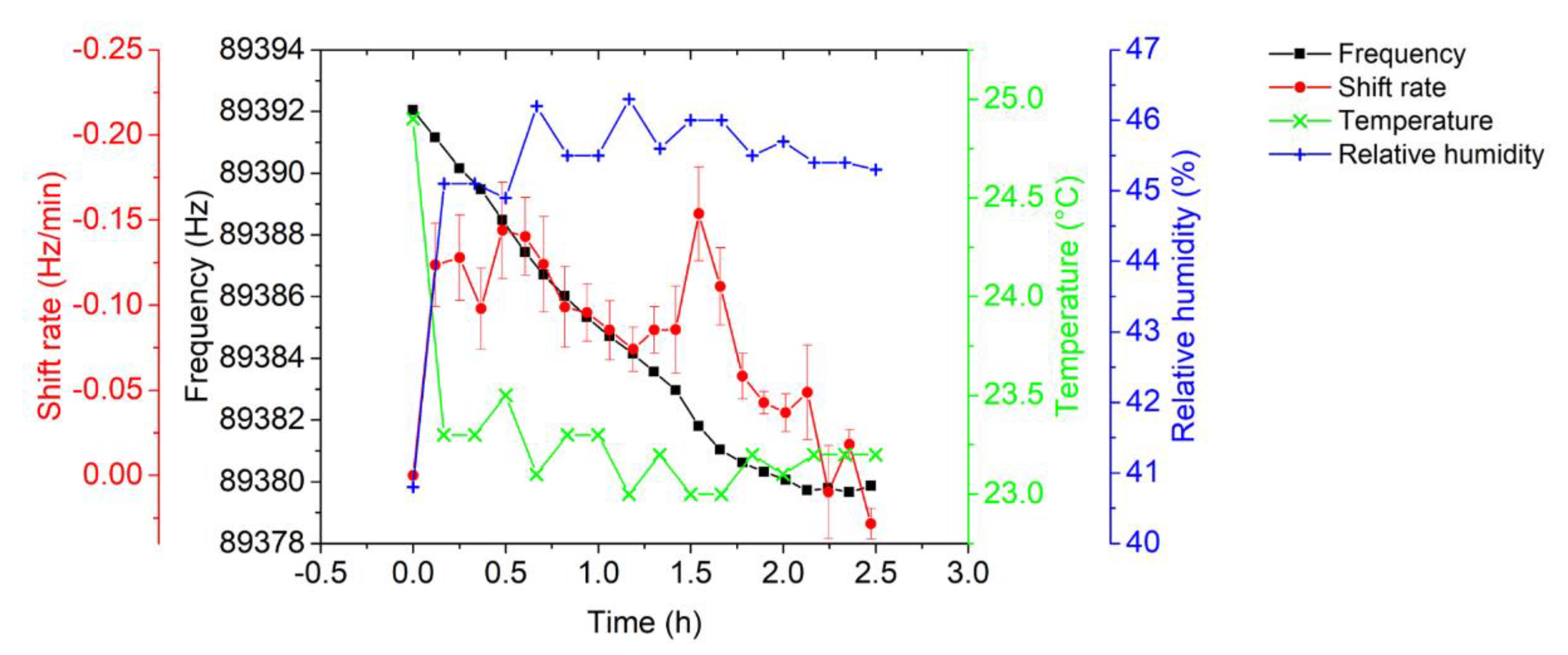
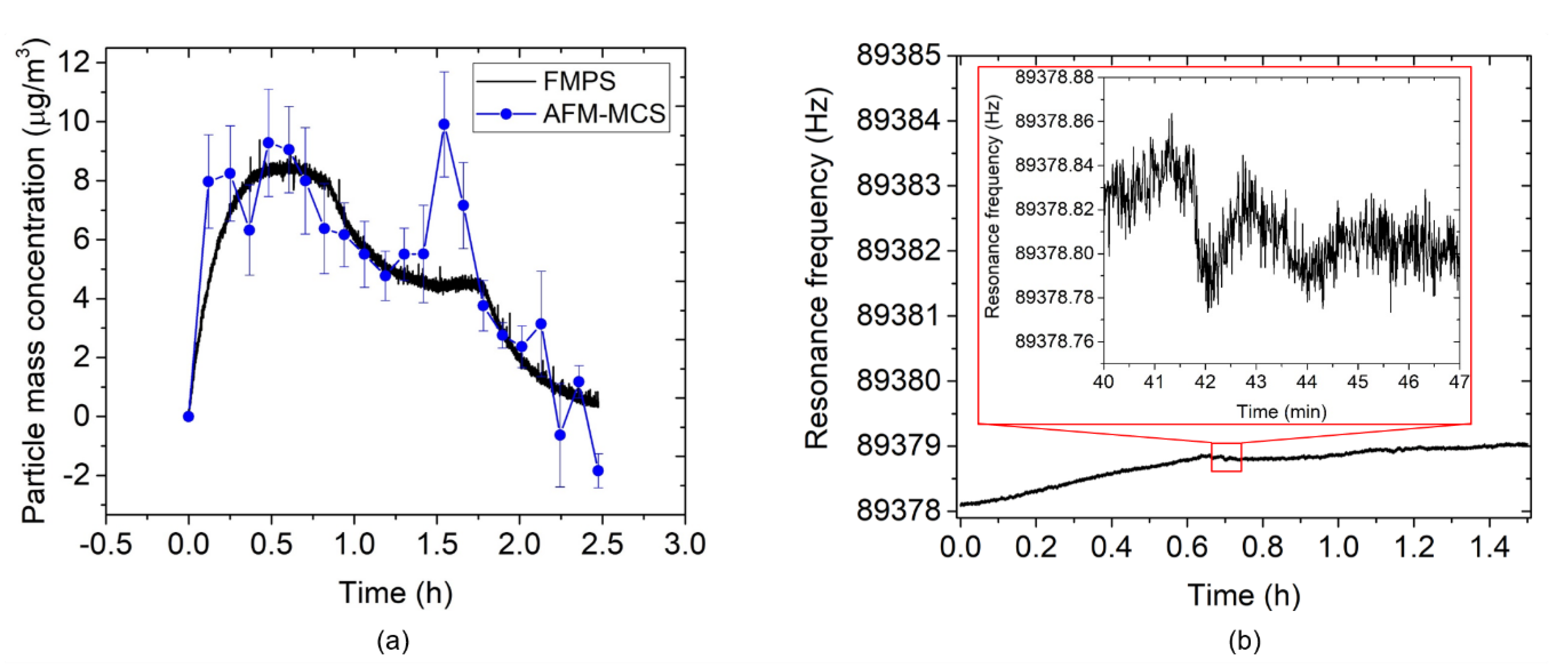
3.2. AFM-MCS Cantilever Performance
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qi, L.; Wang, S. Fossil fuel combustion and biomass burning sources of global black carbon from GEOS-Chem simulation and carbon isotope measurements. Atmos. Chem. Phys. 2019, 19, 11545–11557. [Google Scholar] [CrossRef]
- Niranjan, R.; Thakur, A.K. The Toxicological Mechanisms of Environmental Soot (Black Carbon) and Carbon Black: Focus on Oxidative Stress and Inflammatory Pathways. Front. Immunol. 2017, 8, 763. [Google Scholar] [CrossRef]
- Riediker, M.; Zink, D.; Kreyling, W.; Oberdörster, G.; Elder, A.; Graham, U.; Lynch, I.; Duschl, A.; Ichihara, G.; Ichihara, S.; et al. Particle toxicology and health—where are we? Part. Fibre Toxicol. 2019, 16, 19. [Google Scholar] [CrossRef]
- Stone, V.; Miller, M.R.; Clift, M.J.D.; Elder, A.; Mills, N.L.; Møller, P.; Schins, R.P.F.; Vogel, U.; Kreyling, W.G.; Alstrup Jensen, K.; et al. Nanomaterials Versus Ambient Ultrafine Particles: An Opportunity to Exchange Toxicology Knowledge. Environ. Health Perspect. 2017, 125, 106002. [Google Scholar] [CrossRef] [PubMed]
- Mazaheri, M.; Lin, W.; Clifford, S.; Yue, D.; Zhai, Y.; Xu, M.; Rizza, V.; Morawska, L. Characteristics of school children’s personal exposure to ultrafine particles in Heshan, Pearl River Delta, China—A pilot study. Environ. Int. 2019, 132, 105134. [Google Scholar] [CrossRef] [PubMed]
- Nowack, B.; Bucheli, T.D. Occurrence, behavior and effects of nanoparticles in the environment. Environ. Pollut. 2007, 150, 5–22. [Google Scholar] [CrossRef]
- Gao, X.; Zou, H.; Xu, X.; Zhou, L.; Tang, S.; Yuan, W.; Zhang, M. Developing a guideline for measuring the total number concentration of engineering nanomaterials in workplaces in China. J. Occup. Health 2019, 61, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Joe, Y.-H.; Shim, J.; Shin, I.-K.; Yook, S.-J.; Park, H.-S. A Study on Electrical Charge Distribution of Aerosol Using Gerdien Ion Counter. Aerosol Air Qual. Res. 2018, 18, 2922–2928. [Google Scholar] [CrossRef]
- Marra, J.; Voetz, M.; Kiesling, H.-J. Monitor for detecting and assessing exposure to airborne nanoparticles. J. Nanopart. Res. 2010, 12, 21–37. [Google Scholar] [CrossRef]
- Stetefeld, J.; McKenna, S.A.; Patel, T.R. Dynamic light scattering: A practical guide and applications in biomedical sciences. Biophys. Rev. 2016, 8, 409–427. [Google Scholar] [CrossRef]
- Ross Hallett, F. Particle size analysis by dynamic light scattering. Food Res. Int. 1994, 27, 195–198. [Google Scholar] [CrossRef]
- Agranovski, I. Aerosols. Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 978-3-527-32660-0. [Google Scholar]
- Wang, Y.; Wang, Y.; Chen, D.; Liu, X.; Wu, C.; Xie, J. A Miniature System for Separation and Detection of PM Based on 3-D Printed Virtual Impactor and QCM Sensor. IEEE Sens. J. 2018, 18, 6130–6137. [Google Scholar] [CrossRef]
- Triyana, K.; Rianjanu, A.; Nugroho, D.B.; As’ari, A.H.; Kusumaatmaja, A.; Roto, R.; Suryana, R.; Wasisto, H.S. A highly sensitive safrole sensor based on polyvinyl acetate (PVAc) nanofiber-coated QCM. Sci. Rep. 2019, 9, 15407. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Bertke, M.; Wasisto, H.S.; Peiner, E. Piezoresistive microcantilevers for humidity sensing. J. Micromech. Microeng. 2019, 29, 53003. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Airborne engineered nanoparticle mass sensor based on a silicon resonant cantilever. Sens. Actuators B Chem. 2013, 180, 77–89. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Stranz, A.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Silicon resonant nanopillar sensors for airborne titanium dioxide engineered nanoparticle mass detection. Sens. Actuators B Chem. 2013, 189, 146–156. [Google Scholar] [CrossRef]
- Schlur, L.; Hofer, M.; Ahmad, A.; Bonnot, K.; Holz, M.; Spitzer, D. Cu(OH)2 and CuO Nanorod Synthesis on Piezoresistive Cantilevers for the Selective Detection of Nitrogen Dioxide. Sensors 2018, 18, 1108. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Y.; Hebibul, R.; Ding, J.; Wang, T.; Xu, T.; Liu, X.; Zhao, Y.; Jiang, Z. A Novel Slope Method for Measurement of Fluid Density with a Micro-cantilever under Flexural and Torsional Vibrations. Sensors 2016, 16, 1471. [Google Scholar] [CrossRef]
- Fras, L.J.; Dziekonski, C.; Dera, W.; Jarząbek, D.M. Piezoelectric bimorph as a high-sensitivity viscosity resonant sensor to test the anisotropy of magnetorheological fluid. Rev. Sci. Instrum. 2018, 89, 105111. [Google Scholar] [CrossRef]
- Bertke, M.; Fahrbach, M.; Hamdana, G.; Xu, J.; Wasisto, H.S.; Peiner, E. Contact resonance spectroscopy for on-the-machine manufactory monitoring. Sens. Actuators A Phys. 2018, 279, 501–508. [Google Scholar] [CrossRef]
- Jarzabek, D.M.; Rymuza, Z.; Horiba, A.; Hirai, Y. Development of an experimental technique for testing rheological properties of ultrathin polymer films used in nanoimprint lithography. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. 2011, 29, 61603. [Google Scholar] [CrossRef]
- Brand, O.; Dufour, I.; Heinrich, S.; Josse, F.; Fedder, G.K.; Hierold, C.; Korvink, J.G.; Tabata, O. Resonant MEMS. Fundamentals, Implementation, and Application; Wiley: Hoboken, NJ, USA, 2015; ISBN 9783527676361. [Google Scholar]
- Setiono, A.; Nyang’au, W.O.; Fahrbach, M.; Xu, J.; Bertke, M.; Wasisto, H.S.; Peiner, E. Improvement of frequency responses of an in-plane electro-thermal cantilever sensor for real-time measurement. J. Micromech. Microeng. 2019, 29, 124006. [Google Scholar] [CrossRef]
- Wasisto, H.S. Direct-Reading Personal Airborne Nanoparticle Detector Based on Micromechanical Silicon Cantilever Resonators; 1 Aufl.; Verl. Dr. Hut: München, Germany, 2014; ISBN 3843916802. [Google Scholar]
- Nyang’au, W.O.; Setiono, A.; Bertke, M.; Bosse, H.; Peiner, E. Cantilever-Droplet-Based Sensing of Magnetic Particle Concentrations in Liquids. Sensors 2019, 19, 4758. [Google Scholar] [CrossRef] [PubMed]
- Wasisto, H.S.; Merzsch, S.; Uhde, E.; Waag, A.; Peiner, E. Handheld personal airborne nanoparticle detector based on microelectromechanical silicon resonant cantilever. Microelectron. Eng. 2015, 145, 96–103. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Uhde, E.; Waag, A.; Peiner, E. Partially integrated cantilever-based airborne nanoparticle detector for continuous carbon aerosol mass concentration monitoring. J. Sens. Sens. Syst. 2015, 4, 111–123. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Portable cantilever-based airborne nanoparticle detector. Sens. Actuators B: Chem. 2013, 187, 118–127. [Google Scholar] [CrossRef]
- Bertke, M.; Hamdana, G.; Wu, W.; Wasisto, H.S.; Uhde, E.; Peiner, E. Analysis of asymmetric resonance response of thermally excited silicon micro-cantilevers for mass-sensitive nanoparticle detection. J. Micromech. Microeng. 2017, 27, 64001. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Andrej, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Femtogram aerosol nanoparticle mass sensing utilising vertical silicon nanowire resonators. Micro Nano Lett. 2013, 8, 554–558. [Google Scholar] [CrossRef]
- Merzsch, S.; Steib, F.; Wasisto, H.S.; Stranz, A.; Hinze, P.; Weimann, T.; Peiner, E.; Waag, A. Production of vertical nanowire resonators by cryogenic-ICP–DRIE. Microsyst. Technol. 2014, 20, 759–767. [Google Scholar] [CrossRef]
- Setiono, A.; Xu, J.; Fahrbach, M.; Bertke, M.; Nyang’au, W.O.; Wasisto, H.S.; Peiner, E. Real-Time Frequency Tracking of an Electro-Thermal Piezoresistive Cantilever Resonator with ZnO Nanorods for Chemical Sensing. Chemosensors 2019, 7, 2. [Google Scholar] [CrossRef]
- Setiono, A.; Fahrbach, M.; Xu, J.; Bertke, M.; Nyang’au, W.O.; Hamdana, G.; Wasisto, H.S.; Peiner, E. Phase optimization of thermally actuated piezoresistive resonant MEMS cantilever sensors. J. Sens. Sens. Syst. 2019, 8, 37–48. [Google Scholar] [CrossRef]
- SCL-Sensor. Tech. Fabrication GmbH. PRSA 300 × 100 µm TL Probes. Available online: https://www.sclsensortech.com/portfolio-item/prsa-l300-f506080-tl-pcbchp-probes-2/ (accessed on 21 January 2020).
- Badarlis, A.; Pfau, A.; Kalfas, A. Measurement and Evaluation of the Gas Density and Viscosity of Pure Gases and Mixtures Using a Micro-Cantilever Beam. Sensors 2015, 15, 24318–24342. [Google Scholar] [CrossRef] [PubMed]
- Bertke, M.; Xu, J.; Setiono, A.; Kirsch, I.; Uhde, E.; Peiner, E. Fabrication of a microcantilever-based aerosol detector with integrated electrostatic on-chip ultrafine particle separation and collection. J. Micromech. Microeng. 2020, 30, 14001. [Google Scholar] [CrossRef]
- Maierhofer, P.; Röhrer, G.; Bainschab, M.; Bergmann, A. On the Inherent Variability of Particulate Matter Concentrations on Small Scales and the Consequences for Miniaturized Particle Sensors. Aerosol Air Qual. Res. 2019. [Google Scholar] [CrossRef]
- Seo, Y.H.; Kim, B.H. A self-resonant micro flow velocity sensor based on a resonant frequency shift by flow-induced vibration. J. Micromech. Microeng. 2010, 20, 75024. [Google Scholar] [CrossRef]
- Graczyk, H.; Bryan, L.C.; Lewinski, N.; Suarez, G.; Coullerez, G.; Bowen, P.; Riediker, M. Physicochemical characterization of nebulized superparamagnetic iron oxide nanoparticles (SPIONs). J. Aerosol Med. Pulm. Drug Deliv. 2015, 28, 43–51. [Google Scholar] [CrossRef]
- Maldonado-Garcia, M.; Kumar, V.; Wilson, J.C.; Pourkamali, S. Chip-Scale Implementation and Cascade Assembly of Particulate Matter Collectors with Embedded Resonant Mass Balances. IEEE Sens. J. 2017, 17, 1617–1625. [Google Scholar] [CrossRef]
- Liu, T.-Y.; Sung, C.-A.; Weng, C.-H.; Chu, C.-C.; Zope, A.A.; Pillai, G.; Li, S.-S. Gated CMOS-MEMS Thermal-Piezoresistive Oscillator-Based PM2.5 Sensor with Enhanced Particle Collection Efficiency. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, North Ireland, 21–25 January 2018; pp. 75–78. [Google Scholar]


| Reference | EtPCS Cantilever (This Work) | AFM-MCS Cantilever (This Work) | DP-TPR [41] | TPO [42] |
|---|---|---|---|---|
| Particle sampling | electrophoresis (−115 V), continuous | electrophoresis (−115 V), intermittent with frequency sweeping | chip-scale single inertial impactor | inertial impactor, intermittent with frequency tracking |
| Air-flow rate | 680 mL/min | 0 | <0.1–0.25 mL/min | − |
| Resonance frequency | 201.54 kHz | 89.38 kHz | 5.26 MHz | ~950 kHz |
| Mass sensitivity | 0.013 Hz/pg | 0.14 Hz/pg | 42 Hz/pg | 1.946 Hz/pg |
| Particle collection efficiency | 0.12% | − (no air-flow) | 100% * | − |
| Collecting time | 10 min | 7 min | 60 min | 5 min |
| LOD | 1.4 µg/m3 | 0.7 µg/m3 | 0.01–0.2 µg/m3 ** | 50 µg/m3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setiono, A.; Bertke, M.; Nyang’au, W.O.; Xu, J.; Fahrbach, M.; Kirsch, I.; Uhde, E.; Deutschinger, A.; Fantner, E.J.; Schwalb, C.H.; et al. In-Plane and Out-of-Plane MEMS Piezoresistive Cantilever Sensors for Nanoparticle Mass Detection. Sensors 2020, 20, 618. https://doi.org/10.3390/s20030618
Setiono A, Bertke M, Nyang’au WO, Xu J, Fahrbach M, Kirsch I, Uhde E, Deutschinger A, Fantner EJ, Schwalb CH, et al. In-Plane and Out-of-Plane MEMS Piezoresistive Cantilever Sensors for Nanoparticle Mass Detection. Sensors. 2020; 20(3):618. https://doi.org/10.3390/s20030618
Chicago/Turabian StyleSetiono, Andi, Maik Bertke, Wilson Ombati Nyang’au, Jiushuai Xu, Michael Fahrbach, Ina Kirsch, Erik Uhde, Alexander Deutschinger, Ernest J. Fantner, Christian H. Schwalb, and et al. 2020. "In-Plane and Out-of-Plane MEMS Piezoresistive Cantilever Sensors for Nanoparticle Mass Detection" Sensors 20, no. 3: 618. https://doi.org/10.3390/s20030618
APA StyleSetiono, A., Bertke, M., Nyang’au, W. O., Xu, J., Fahrbach, M., Kirsch, I., Uhde, E., Deutschinger, A., Fantner, E. J., Schwalb, C. H., Wasisto, H. S., & Peiner, E. (2020). In-Plane and Out-of-Plane MEMS Piezoresistive Cantilever Sensors for Nanoparticle Mass Detection. Sensors, 20(3), 618. https://doi.org/10.3390/s20030618








