An Improved Calibration Method for Photonic Mixer Device Solid-State Array Lidars Based on Electrical Analog Delay
Abstract
1. Introduction
- (1)
- This paper proposed a self-adaptive grayscale correlation based depth calibration method (SA-GCDCM) for PMD solid-state array Lidar. Due to its special structure, the PMD Lidar has the ability to obtain a grayscale image and depth image simultaneously. Meanwhile, the amplitude of grayscale image has a close relationship with ambient light. Based on this, the grayscale image was used to estimate the parameters of ambient light compensation in depth calibration in this method. Through SA-GCDCM, the disturbance of ambient light could be effectively eliminated. Traditional joint calibration methods always need an extra RGB camera to cooperate with the ToF camera. The inconformity of the parameters of the two cameras, such as the image resolution and the field of view, can introduce extra errors to the system, leading to low calibration accuracy and efficiency. Compared with the traditional methods, this method has no requirement of coordinate transformation and feature matching, leading to better data consistency and self-adaptability.
- (2)
- This paper proposed a grayscale calibration method based on integration time simulating. Firstly, the raw grayscale images were acquired under multiple ambient light levels through setting the integration time in several values. Then the spatial variances were calculated from the images to estimate the dark signal non-uniformity (DSNU) and photo response non-uniformity (PRNU). At last the influence of DSNU and PRNU were eliminated by a correction algorithm.
- (3)
- Based on the electrical analog delay method, a comprehensive, multiscene adaptive multifactor calibration model was established through combining the SA-GCDCM with raw distance demodulation compensation, distance response non-uniformity (DRNU) compensation and temperature drift compensation. Compared with the prior methods, the established model is more adaptive to multiscenes with targets of different reflectivities, which significantly improves the ranging accuracy and adaptability of PMD Lidar.
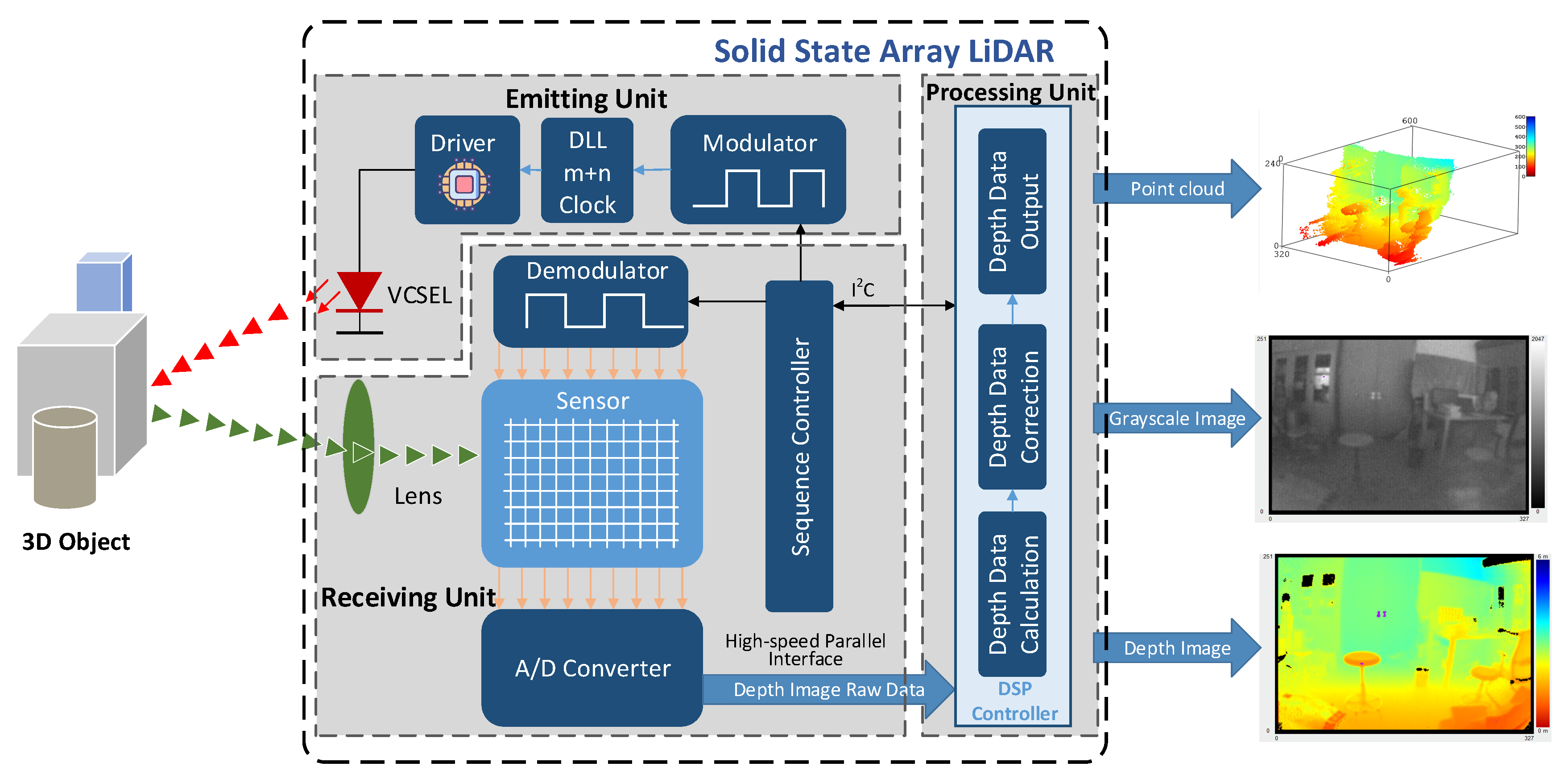
2. System Introduction
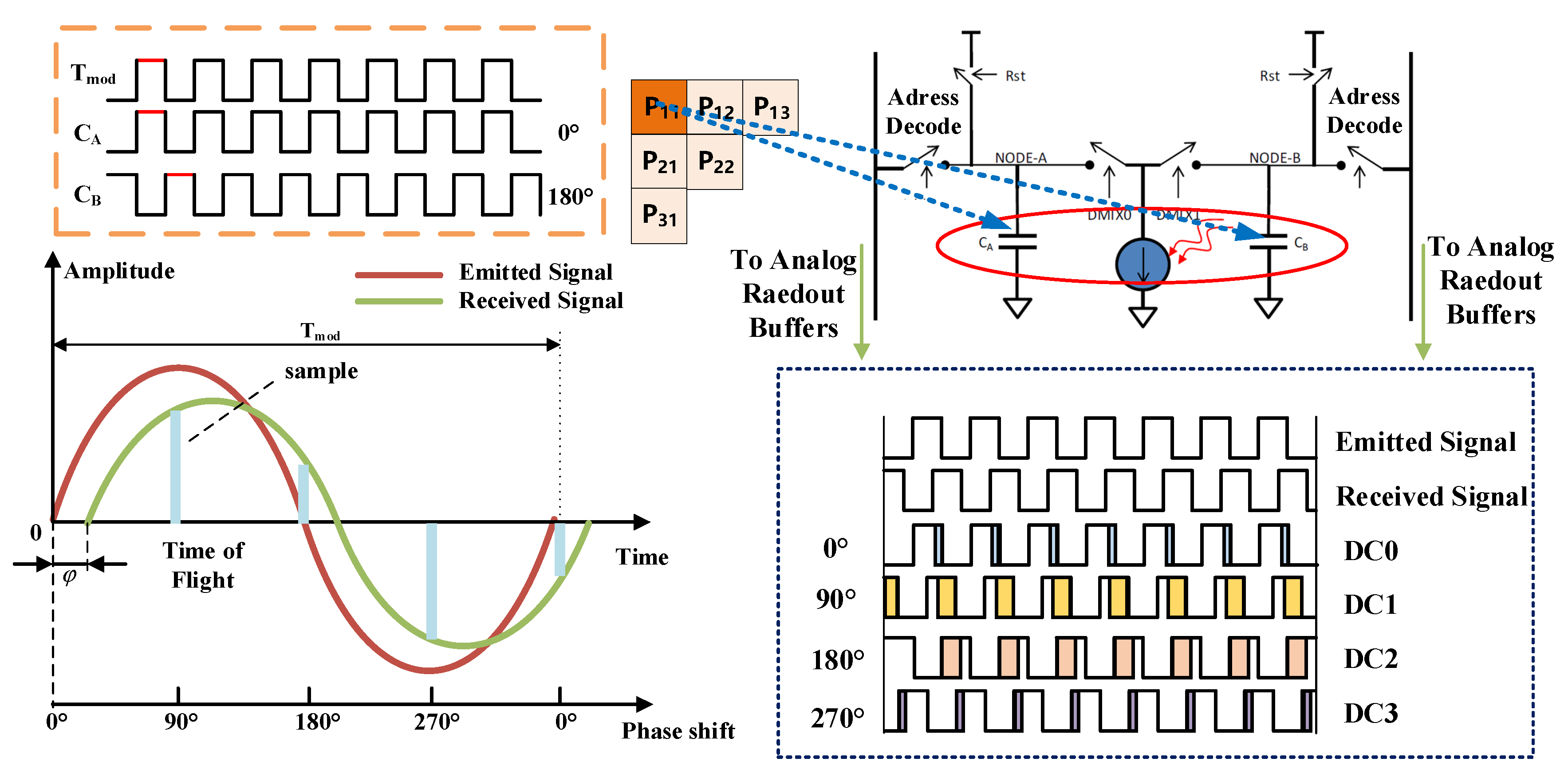
2.1. Principle of PMD Solid-State Array Lidar
2.2. Analysis of Error Sources of PMD Solid-State Array Lidar
2.2.1. Integration Time
2.2.2. Temperature Drift
2.2.3. Distance Response Non-Uniformity (DRNU)
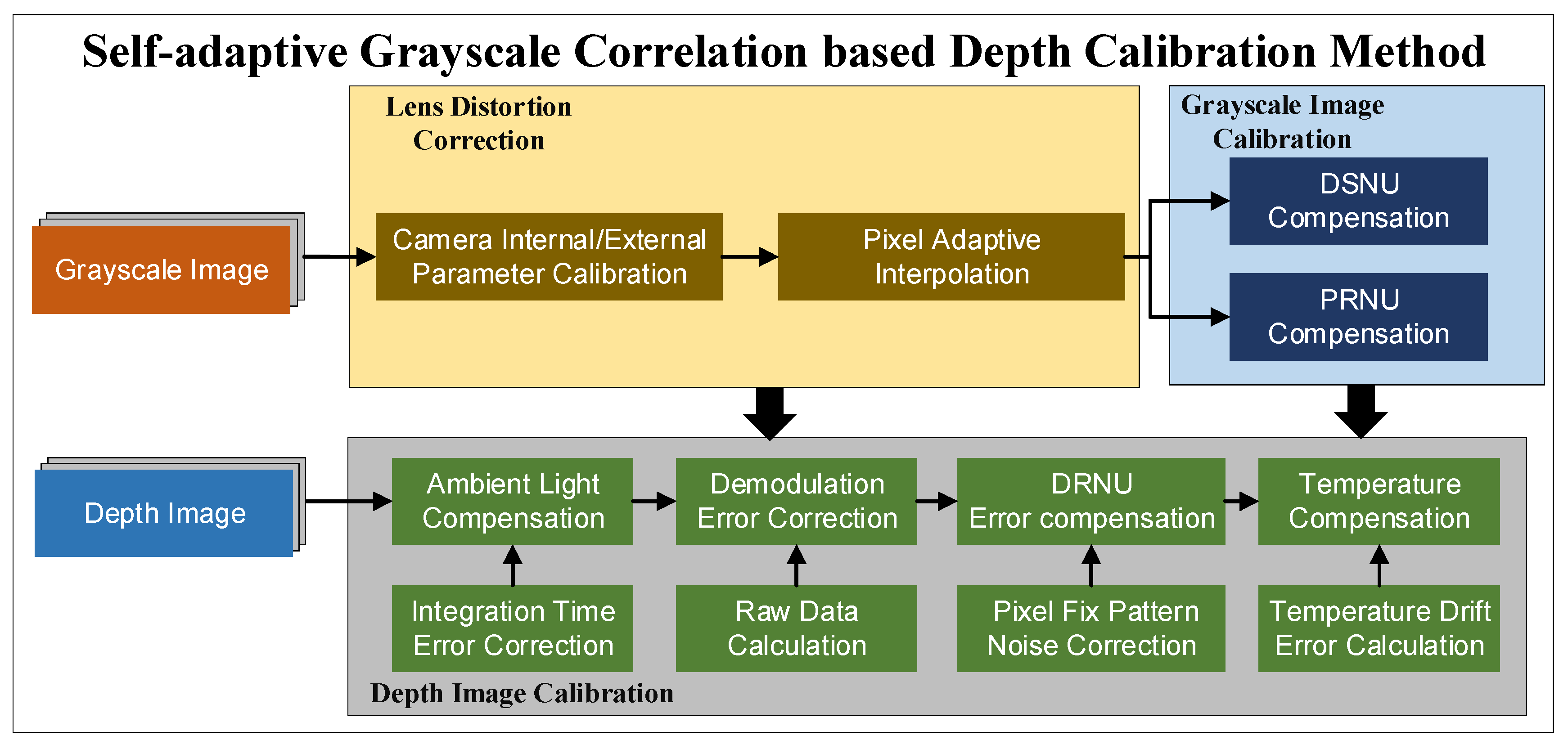
3. Methodology
3.1. Lens Distortion Correction
3.2. Grayscale Image Calibration
- (1)
- Set the integration time to 0 μs to simulate the dark condition. Collect N = 100 frames of grayscale images and calculate the mean value.
- (2)
- Change the integration time to simulate different ambient light levels. Collect N = 100 frames of grayscale images under amplitudes of 10%, 30%, 50% and 80% respectively. Similarly, the mean values with different amplitudes are obtained.
- (3)
- Calculate the spatial variances under different ambient levels. Spatial variance is simply an overall measure of the spatial nonuniformity, which is helpful to estimate DSNU and PRNU.
- (4)
- Calculate the correction values of DSNU and PRNU.
- (5)
- The grayscale compensation of pixel is calculated by Equation (10).where is the mean value of grayscale images under the dark condition, is the mean value of grayscale images under ambient light, N means the number of frames, and are spatial variances under dark and ambient light conditions, respectively, is the offset of DSNU, is the gain of PRNU and is the compensation value of grayscale image after calibration.
3.3. Depth Image Calibration
3.3.1. Ambient Light Compensation
- (1)
- Turn the ambient light on and record the amplitude of the grayscale image as Qgray.
- (2)
- Change the amplitude of the grayscale image to 0.5 times that of Qgray by adjusting the integration time. Measure the DC0/2 and record as DC0setting1 and DC2setting1, respectively.
- (3)
- Change the amplitude of the grayscale image to 1.5 times that of Qgray by adjusting the integration time. Measure the DC0/2 and record as DC0setting2 and DC2setting2, respectively.
- (4)
- Turn the ambient light off and measure the DC0/2, which are recorded as DC0no and DC2no, respectively.
- (5)
- Calculate four measurements, Q01, Q02, Q21 and Q22.
- (6)
- Correct the errors generated in the sampling. There inevitably exists internal noise and external error. The internal noise mainly comes from the internal circuit and can be eliminated by subtracting two samples at the same phase. The external error mainly comes from the instability of the environment. It can be suppressed by calculating the mean value of the samples.
- (7)
- The ambient light correction factor KAL is calculated by Equation (13):where DC0/1/2/3 are the sample values acquired at 0°, 90°, 180° and 270° respectively. KAL is used to compensate the ambient light error during the demodulation process as Equation (14):where represents the corrected value of .
3.3.2. Demodulation Error Correction
3.3.3. DRNU Error Compensation
3.3.4. Temperature Compensation
4. Experiments and Discussions
4.1. Experimental Settings
- (1)
- Clamp the PMD Lidar on the clamping device.
- (2)
- Adjust the clamping device to a proper location where the checkerboard is suitable in size and position in the field of view of the PMD Lidar.
- (3)
- Calibrate the grayscale image based on integration time simulating.
- (4)
- Obtain several grayscale images with checkerboard in different directions to calibrate the lens distortion.
- (5)
- Utilize the pixel adaptive interpolation strategy to fill the holes.
- (1)
- Install the cylinder on the PMD Lidar and clamp the PMD Lidar on the clamping device.
- (2)
- Adjust the clamping device to a proper location where the quality of the light spot projected on the reflecting plate is optimized.
- (3)
- Change the distance with the electrical analog delay method to perform the depth calibration. Multiple error compensation is included in this step.
- (4)
- Change the reflecting board to adjust the method with objects of different reflectivities.
- (5)
- Conduct the interpolation on the data to obtain the continuous offset curves.
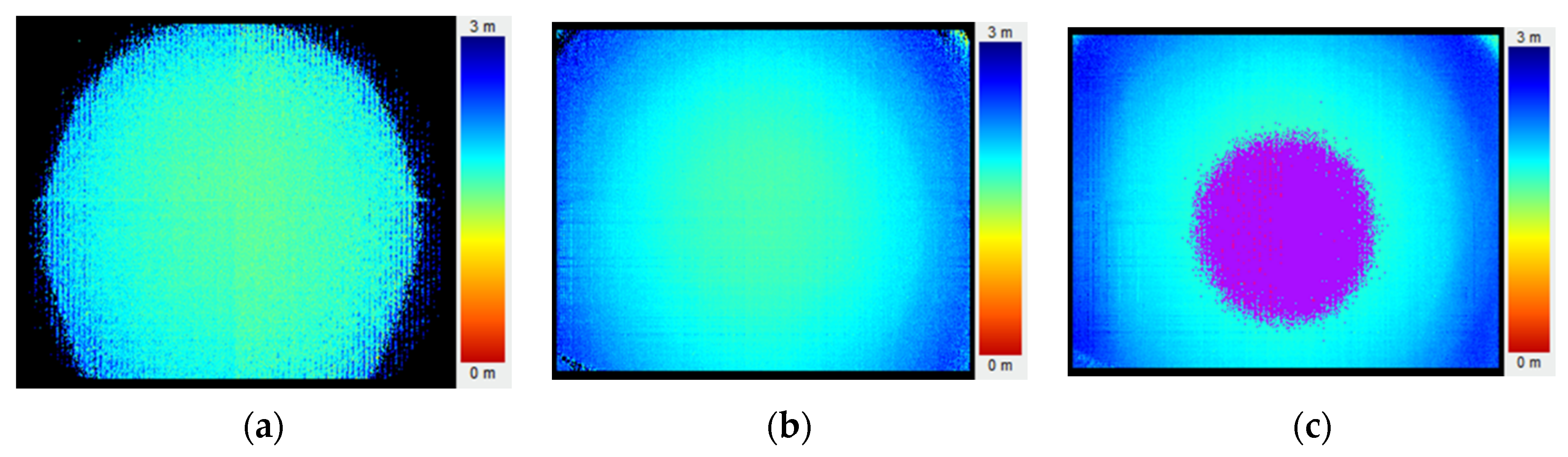
4.2. Results with Grayscale Image Calibration
4.2.1. Lens Distortion Correction
4.2.2. DSNU and PRNU
4.3. Result with Depth Image Calibration
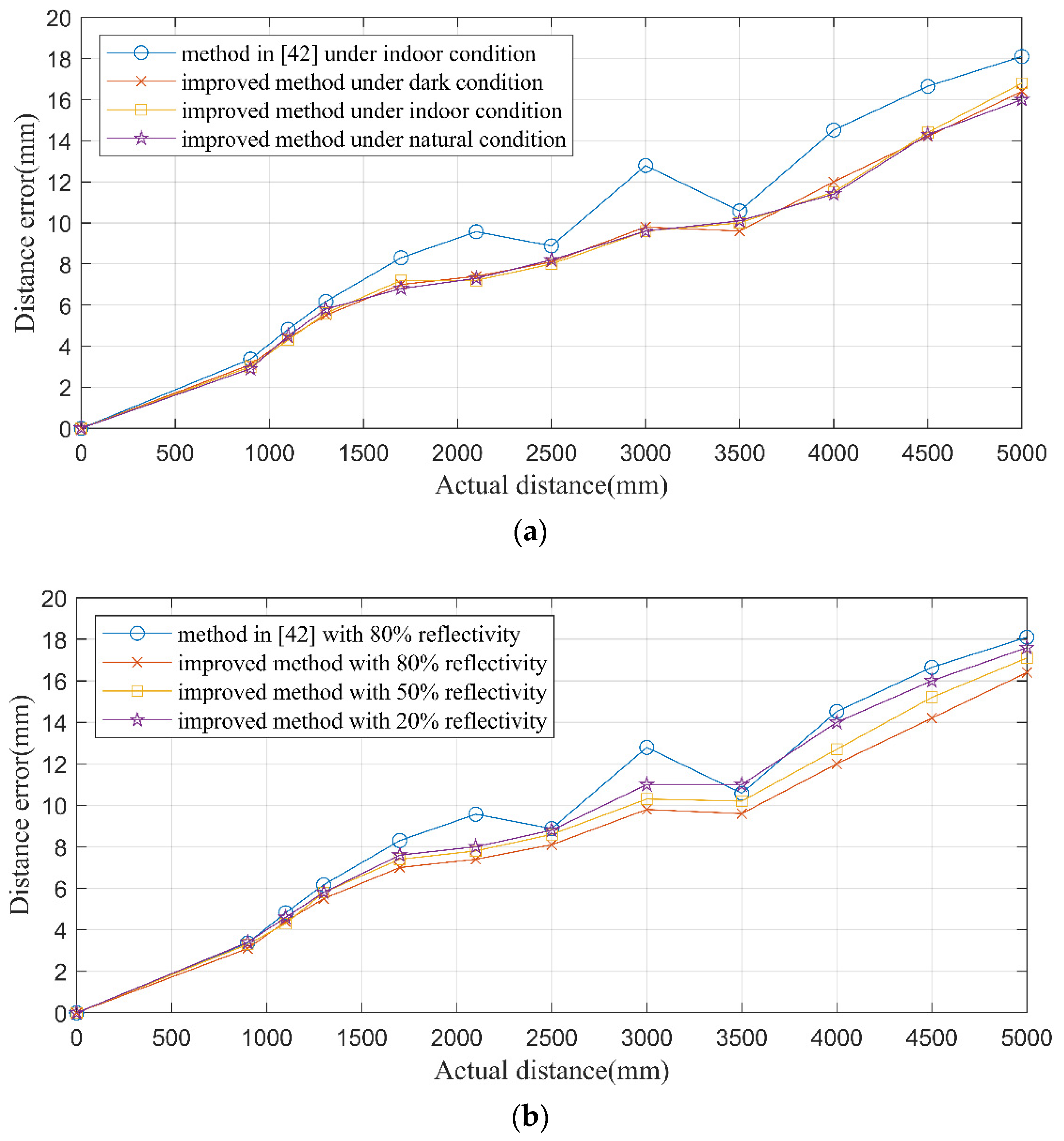
4.4. Ranging Accuracy Verification under Real Environment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sansoni, G.; Trebeschi, M.; Docchio, F. State-of-The-Art and Applications of 3D Imaging Sensors in Industry, cultural heritage, medicine, and criminal investigation. Sensors 2009, 9, 568–601. [Google Scholar] [CrossRef] [PubMed]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using kinect-style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef]
- Okada, K.; Inaba, M.; Inoue, H. Integration of real-time binocular stereo vision and whole body information for dynamic walking navigation of humanoid robot. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, (MFI 2003), Tokyo, Japan, 1 August 2003; pp. 131–136. [Google Scholar]
- Scharstein, D.; Szeliski, R. High-accuracy stereo depth maps using structured light. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 195–202. [Google Scholar]
- Sun, M.J.; Edgar, M.P.; Gibson, G.M.; Sun, B.; Radwell, N.; Lamb, R.; Padgett, M.J. Single-pixel three-dimensional imaging with time-based depth resolution. Nat. Commun. 2016, 7, 12010. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Schuon, S.; Chan, D.; Thrun, S.; Theobalt, C. 3D shape scanning with a time-of-flight camera. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1173–1180. [Google Scholar]
- He, Y.; Chen, S.Y. Recent advances in 3D Data acquisition and processing by Time-of-Flight camera. IEEE Access. 2019, 7, 12495–12510. [Google Scholar] [CrossRef]
- Horaud, R.; Hansard, M.; Evangelidis, G.; Ménier, C. An overview of depth cameras and range scanners based on time-of-flight technologies. Mach. Vis. Appl. 2016, 27, 1005–1020. [Google Scholar] [CrossRef]
- Rueda, H.; Fu, C.; Lau, D.L.; Arce, G.R. Single aperture spectral+ToF compressive camera: Toward hyperspectral+depth imagery. IEEE J. Sel. Top. Signal Process. 2017, 11, 992–1003. [Google Scholar] [CrossRef]
- Rueda-Chacon, H.; Florez, J.F.; Lau, D.L.; Arce, G.R. Snapshot compressive ToF+Spectral imaging via optimized color-coded apertures. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2346–2360. [Google Scholar]
- Lindner, M.; Schiller, I.; Kolb, A.; Koch, R. Time-of-Flight sensor calibration for accurate range sensing. Comput. Vis. Image Underst. 2010, 114, 1318–1328. [Google Scholar] [CrossRef]
- Lindner, M.; Kolb, A. Lateral and depth calibration of PMD-distance sensors. advances in visual computing. In Advance of Visual Computing, Proceedings of the Second International Symposium on Visual Computing, Lake Tahoe, NV, USA, 6–8 November 2006; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2006; Volume 4292, pp. 524–533. [Google Scholar]
- Lindner, M.; Kolb, A. Calibration of the intensity-related distance error of the PMD TOF-camera. In Intelligent Robots and Computer Vision XXV: Algorithms, Techniques, and Active Vision, Proceedings of Optics East, Boston, MA, USA, 9–12 September 2007; Casanent, D.P., Hall, E.L., Röning, R., Eds.; SPIE: Bellingham, WA, USA, 2007; Volume 6764, p. 67640W. [Google Scholar]
- Lindner, M.; Lambers, M.; Kolb, A. Sub-pixel data fusion and edge-enhanced distance refinement for 2d/3d images. Int. J. Intell. Syst. Technol. Appl. 2008, 5, 344–354. [Google Scholar] [CrossRef]
- Kahlmann, T.; Remondino, F.; Ingensand, H. Calibration for increased accuracy of the range imaging camera SwissRanger. In Proceedings of the ISPRS Commission V Symposium “Image Engineering and Vision Metrology”, Dresden, Germany, 25–27 September 2006; Volume 36, pp. 136–141. [Google Scholar]
- Kahlmann, T.; Ingensand, H. Calibration and development for increased accuracy of 3D range imaging cameras. J. Appl. Geodesy. 2008, 2, 1–11. [Google Scholar] [CrossRef]
- Steiger, O.; Felder, J.; Weiss, S. Calibration of time-of-flight range imaging cameras. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1968–1971. [Google Scholar]
- Swadzba, A.; Beuter, N.; Schmidt, J.; Sagerer, G. Tracking objects in 6D for reconstructing static scenes. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–7. [Google Scholar]
- Schiller, I.; Beder, C.; Koch, R. Calibration of a PMD-camera using a planar calibration pattern together with a multicamera setup. ISPRS Int. J. Geo-Inf. 2008, 21, 297–302. [Google Scholar]
- Fuchs, S.; May, S. Calibration and registration for precise surface reconstruction with time of flight cameras. Int. J. Int. Syst. Technol. App. 2008, 5, 274–284. [Google Scholar] [CrossRef]
- Fuchs, S.; Hirzinger, G. Extrinsic and depth calibration of ToF-cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar]
- Chiabrando, F.; Chiabrando, R.; Piatti, D.; Rinaudo, F. Sensors for 3D Imaging: Metric Evaluation and Calibration of a CCD/CMOS Time-of-Flight Camera. Sensors 2009, 9, 10080–10096. [Google Scholar] [CrossRef] [PubMed]
- Christian, B.; Reinhard, K. Calibration of focal length and 3D pose based on the reflectance and depth image of a planar object. Int. J. Intell. Syst. Technol. Appl. 2008, 5, 285–294. [Google Scholar]
- Kuhnert, K.D.; Stommel, M. Fusion of stereo-camera and PMD-camera data for real-time suited precise 3D environment reconstruction. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 4780–4785. [Google Scholar]
- Schmidt, M. Analysis, Modeling and Dynamic Optimization of 3d Time-of-Flight Imaging Systems. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 20 July 2011; pp. 1–158. [Google Scholar]
- Huang, T.; Qian, K.; Li, Y. All Pixels Calibration for ToF Camera. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Ordos, China, 28–29 April 2018; IOP Publishing: Bristol, UK, 2018; Volume 170, p. 022164. [Google Scholar]
- Ying, H.; Bin, L.; Yu, Z.; Jin, H.; Jun, Y. Depth errors analysis and correction for Time-of-Flight (ToF) cameras. Sensors 2017, 17, 92. [Google Scholar]
- Radmer, J.; Fuste, P.M.; Schmidt, H.; Kruger, J. Incident light related distance error study and calibration of the PMD-range imaging camera. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–6. [Google Scholar]
- Frank, M.; Plaue, M.; Rapp, H.; Köthe, U.; Jähne, B.; Hamprecht, F.A. Theoretical and experimental error analysis of continuous-wave time-of-flight range cameras. Opt. Eng. 2009, 48, 013602. [Google Scholar]
- Schiller, I.; Bartczak, B.; Kellner, F.; Kollmann, J.; Koch, R. Increasing realism and supporting content planning for dynamic scenes in a mixed reality system incorporating a Time-of-Flight camera. In Proceedings of the IET 5th European Conference on Visual Media Production (CVMP 2008), London, UK, 26–27 November 2008; IET: Stevenage, UK, 2008; Volume 7, p. 11. [Google Scholar] [CrossRef]
- Foix, S.; Alenya, G.; Torras, C. Lock-in time-of-flight (ToF) cameras: A survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Piatti, D.; Rinaudo, F. SR-4000 and CamCube3.0 time of flight (ToF) cameras: Tests and comparison. Remote Sens. 2012, 4, 1069–1089. [Google Scholar] [CrossRef]
- Lee, S. Time-of-flight depth camera accuracy enhancement. Opt. Eng. 2012, 51, 083203. [Google Scholar] [CrossRef]
- Lee, C.; Kim, S.Y.; Kwon, Y.M. Depth error compensation for camera fusion system. Opt. Eng. 2013, 52, 073103. [Google Scholar] [CrossRef]
- Fürsattel, P.; Placht, S.; Balda, M.; Schaller, C.; Hofmann, H.; Maier, A.; Riess, C. A Comparative error analysis of current Time-of-Flight sensors. IEEE Trans. Comput. Imaging 2017, 2, 27–41. [Google Scholar] [CrossRef]
- Karel, W. Integrated range camera calibration using image sequences from hand-held operation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 945–952. [Google Scholar]
- Gao, J.; Jia, B.; Zhang, X.; Hu, L. PMD camera calibration based on adaptive bilateral filter. In Proceedings of the 2011 Symposium on Photonics and Optoelectronics (SOPO), Wuhan, China, 16–18 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–4. [Google Scholar]
- Park, Y.; Yun, S.; Won, C.S.; Cho, K.; Um, K.; Sim, S. Calibration between color camera and 3D LIDAR instruments with a polygonal planar board. Sensors 2014, 14, 5333–5353. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Lee, J.-Y.; Jeong, Y.; Kweon, I.S. Time-of-flight sensor calibration for a color and depth camera pair. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1501–1513. [Google Scholar] [CrossRef]
- Villena-Martínez, V.; Fuster-Guilló, A.; Azorín-López, J.; Saval-Calvo, M.; Mora-Pascual, J.; Garcia-Rodriguez, J.; Garcia-Garcia, A. A quantitative comparison of calibration methods for RGB-D sensors using different technologies. Sensors 2017, 17, 243. [Google Scholar] [CrossRef]
- Zeng, Y.; Yu, H.; Dai, H.; Song, S.; Lin, M.; Sun, B.; Jiang, W.; Meng, M.Q. An improved calibration method for a rotating 2D LiDAR system. Sensors 2018, 18, 497. [Google Scholar] [CrossRef]
- Zhai, Y.; Song, P.; Chen, X. A fast calibration method for photonic mixer device solid-state array lidars. Sensors 2019, 19, 822. [Google Scholar] [CrossRef]
- Fujioka, I.; Ho, Z.; Gu, X.; Koyama, F. Solid State LiDAR with Sensing Distance of over 40m using a VCSEL Beam Scanner. In Proceedings of the 2020 Conference on Lasers and Electro-Optics, San Jose, CA, USA, 10–15 May 2020; OSA Publishing: Washington, DC, USA, 2020; p. SM2M.4. [Google Scholar]
- Prafulla, M.; Marshall, T.D.; Zhu, Z.; Sridhar, C.; Eric, P.F.; Blair, M.K.; John, W.M. VCSEL Array for a Depth Camera. U.S. Patent US20150229912A1, 27 September 2016. [Google Scholar]
- Seurin, J.F.; Zhou, D.; Xu, G.; Miglo, A.; Li, D.; Chen, T.; Guo, B.; Ghosh, C. High-efficiency VCSEL arrays for illumination and sensing in consumer applications. In Vertical-Cavity Surface-Emitting Lasers XX, Proceedings of the SPIE OPTO, San Francisco, CA, USA, 4 March 2016; SPIE: Bellingham, WA, USA, 2016; Volume 9766, p. 97660D. [Google Scholar]
- Tatum, J. VCSEL proliferation. In Vertical-Cavity Surface-Emitting Lasers XI, Proceedings of the Integrated Optoelectronic Devices 2007, San Jose, CA, USA; SPIE: Bellingham, WA, USA, 2007; Volume 6484, p. 648403. [Google Scholar]
- Kurtti, S.; Nissinen, J.; Kostamovaara, J. A wide dynamic range CMOS laser radar receiver with a time-domain walk error compensation scheme. IEEE Trans. Circuits Syst. I-Regul. Pap. 2016, 64, 550–561. [Google Scholar] [CrossRef]
- Kadambi, A.; Whyte, R.; Bhandari, A.; Streeter, L.; Barsi, C.; Dorrington, A.; Raskar, R. Coded time of flight cameras: Sparse deconvolution to address multipath interference and recover time profiles. ACM Trans. Graph. 2013, 32, 167. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- EMVA. European Machine Vision Association: Downloads. Available online: www.emva.org/standards-technology/emva-1288/emva-standard-1288-downloads/ (accessed on 30 December 2016).
- Pappas, T.N.; Safranek, R.J.; Chen, J. Perceptual Criteria for Image Quality Evaluation. In Handbook of Image and Video Processing, 2nd ed.; Elsevier: Houston, TX, USA, 2005; pp. 939–959. [Google Scholar]








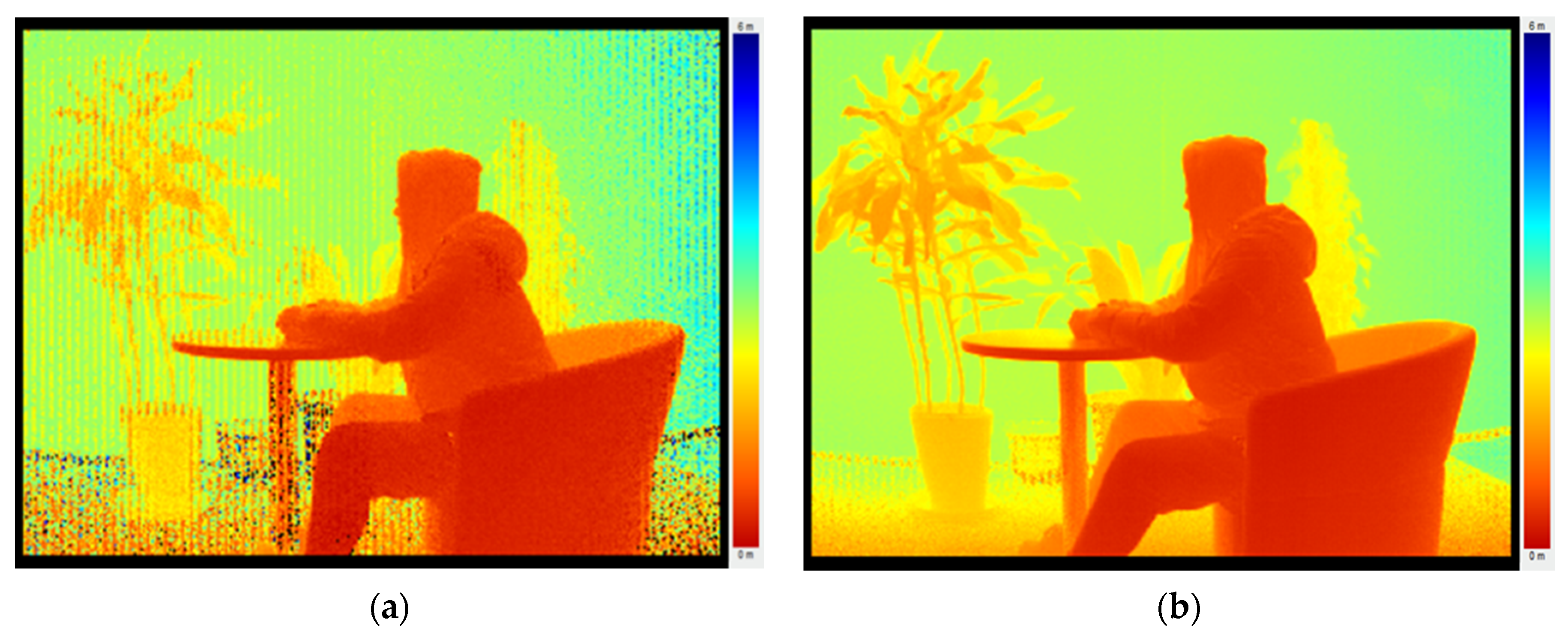

| Case | Pixel Adaptive Interpolation Strategy |
|---|---|
 | |
 | |
 | |
 | |
 | |
 |
| Internal Parameters | fx | fy | cx | cy |
| 208.915 | 209.647 | 159.404 | 127.822 | |
| Distortion Coefficients | k1 | k2 | p1 | p2 |
| −0.37917 | 0.17410 | 0.00021 | 0.00124 |
| Flat White Board | Real Scene 1 | Real Scene 2 | ||||
|---|---|---|---|---|---|---|
| Before | After | Before | After | Before | After | |
| Mean value | 913.98 | 915.73 | 559.85 | 571.83 | 278.91 | 305.03 |
| RMSE | 168.22 | 12.89 | 291.30 | 221.23 | 256.65 | 192.86 |
| PSNR | 43.97 | 55.13 | 41.58 | 42.78 | 42.13 | 43.37 |
| Comparison Items | Maximal Error (mm) | Average Error (mm) | RMSE (mm) |
|---|---|---|---|
| The proposed method | 16.4 | 8.13 | 4.47 |
| Reference [42] method | 20.5 | 9.68 | 5.56 |
| Distance Error (mm) | Calibration Time | Scene Scope | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 900 | 1100 | 1300 | 1700 | 2100 | 2500 | 3000 | 3500 | 4000 | |||
| Lindner et al. [13] | 19.4 | 28.2 | 21.0 | 28.9 | 13.5 | 17.3 | 15.9 | 21.8 | 26.7 | About dozens of minutes | About 4 m × 0.6 m × 0.4 m |
| Steiger et al. [17] | NaN | 3(at 1207) | 25 | 57 | NaN | NaN | NaN | NaN | About dozens of minutes | Not mentioned | |
| Schiller et al. [19] (Automatic feature detection) | 7.45 (mean) | NaN | NaN | About dozens of minutes | About 3 m × 0.6 m × 0.4 m | ||||||
| Schiller et al. [19] (Some manual feature selection) | 7.51 (mean) | NaN | NaN | About dozens of minutes | About 3 m × 0.6 m × 0.4 m | ||||||
| Huang et al. [26] | 42 | 23 | 18 | 24 | 46 | 60 | 58 | 76 | NaN | Not mentioned | About 1.5 m × 1.5 m × 2 m |
| The proposed method | 3.1 | 4.4 | 5.5 | 7 | 7.4 | 8.1 | 9.8 | 9.6 | 12 | 90 s(calculation) 10 min (calculation, scene setup and initialization) | About 1.0 m × 1.0 m × 1.5 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Song, P.; Zhang, W. An Improved Calibration Method for Photonic Mixer Device Solid-State Array Lidars Based on Electrical Analog Delay. Sensors 2020, 20, 7329. https://doi.org/10.3390/s20247329
Wang X, Song P, Zhang W. An Improved Calibration Method for Photonic Mixer Device Solid-State Array Lidars Based on Electrical Analog Delay. Sensors. 2020; 20(24):7329. https://doi.org/10.3390/s20247329
Chicago/Turabian StyleWang, Xuanquan, Ping Song, and Wuyang Zhang. 2020. "An Improved Calibration Method for Photonic Mixer Device Solid-State Array Lidars Based on Electrical Analog Delay" Sensors 20, no. 24: 7329. https://doi.org/10.3390/s20247329
APA StyleWang, X., Song, P., & Zhang, W. (2020). An Improved Calibration Method for Photonic Mixer Device Solid-State Array Lidars Based on Electrical Analog Delay. Sensors, 20(24), 7329. https://doi.org/10.3390/s20247329





