Wavefront Shaping Concepts for Application in Optical Coherence Tomography—A Review
Abstract
:1. Introduction
2. Principles of Wavefront Shaping
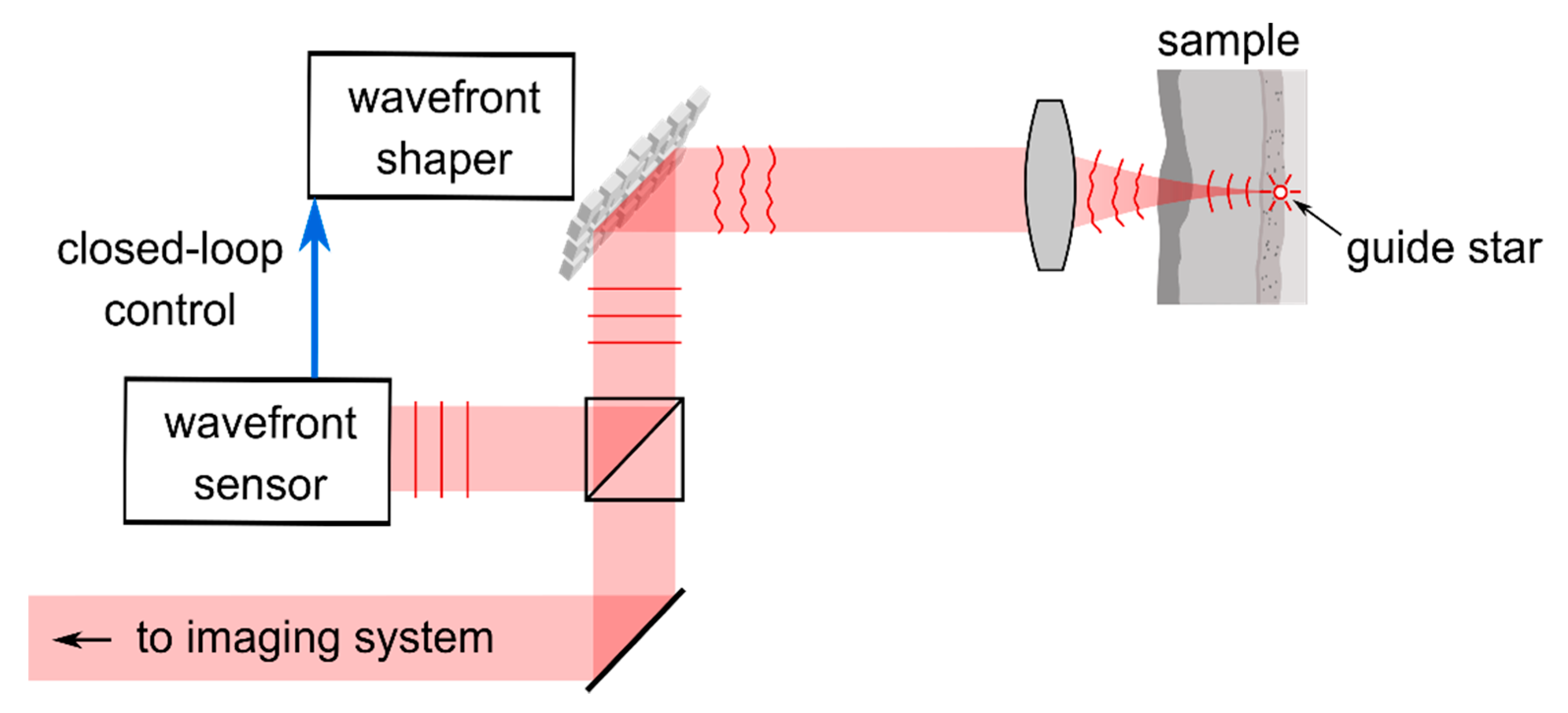
2.1. Adaptive Optics
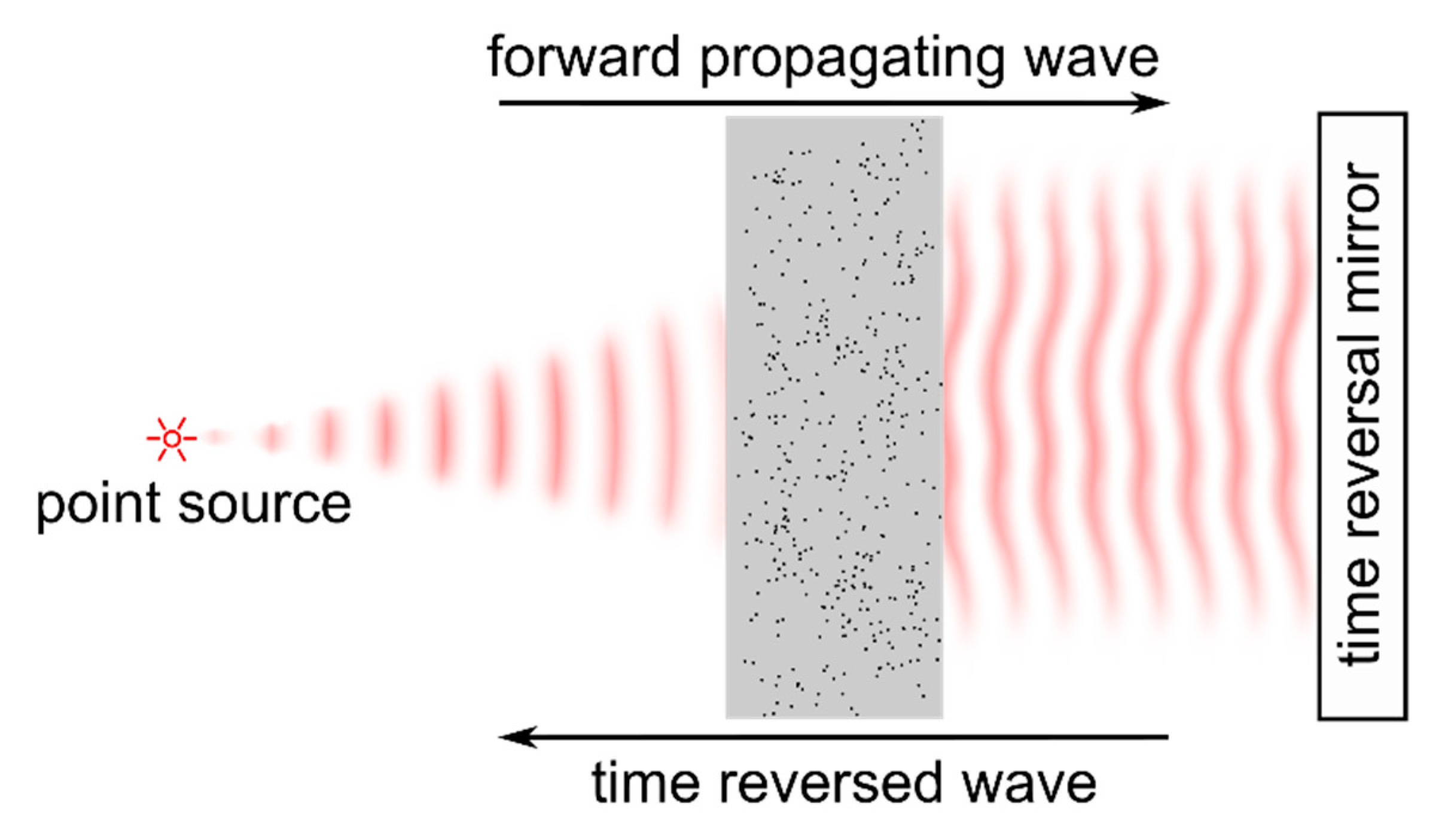
2.2. Time Reversal and Phase Conjugation
2.2.1. Imaging and the Optical Memory Effect
2.3. Iterative Wavefront Shaping
2.3.1. Principles of Iterative Wavefront Shaping
2.3.2. Feedback Types and Implementation for Imaging
2.3.3. Algorithms
2.3.4. Acquisition Time
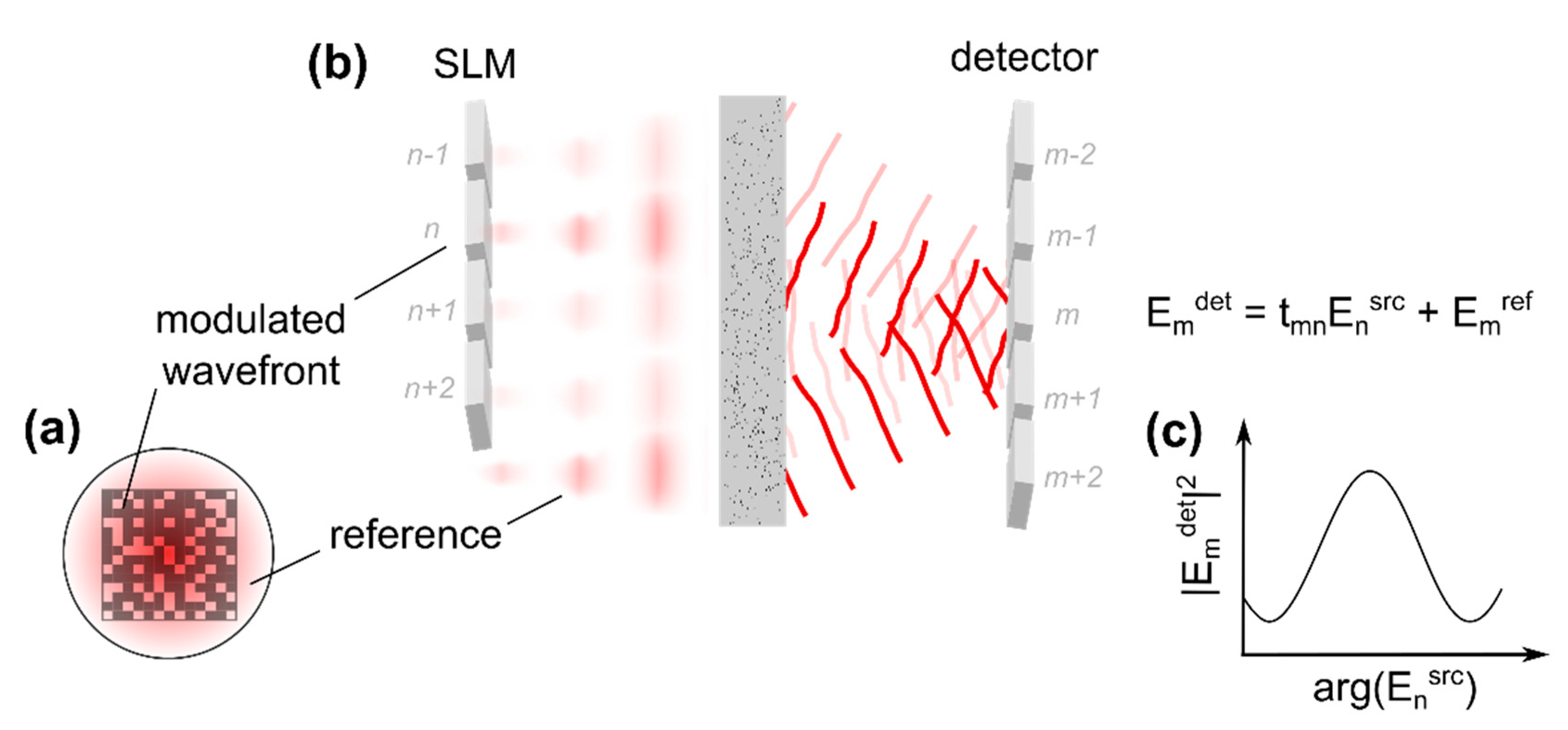
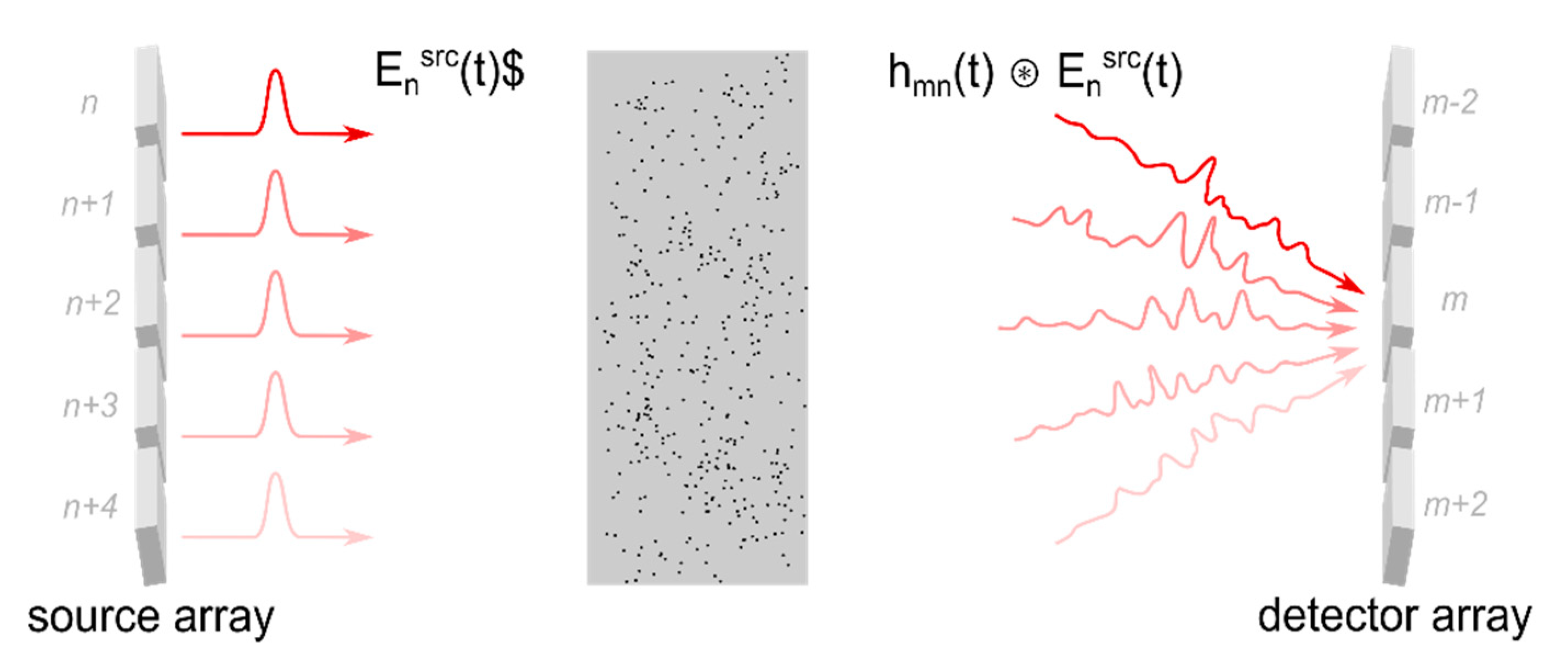
2.4. Transmission Matrix Approaches
2.4.1. Principles of Transmission Matrix-Based Concepts
2.4.2. Single-Point Focusing
2.4.3. Imaging Using Transmission Matrix Approach
2.4.4. Singular Value Decomposition
2.4.5. Acquisition Speed Enhancement
3. Applications of Wavefront Shaping to Optical Coherence Tomography
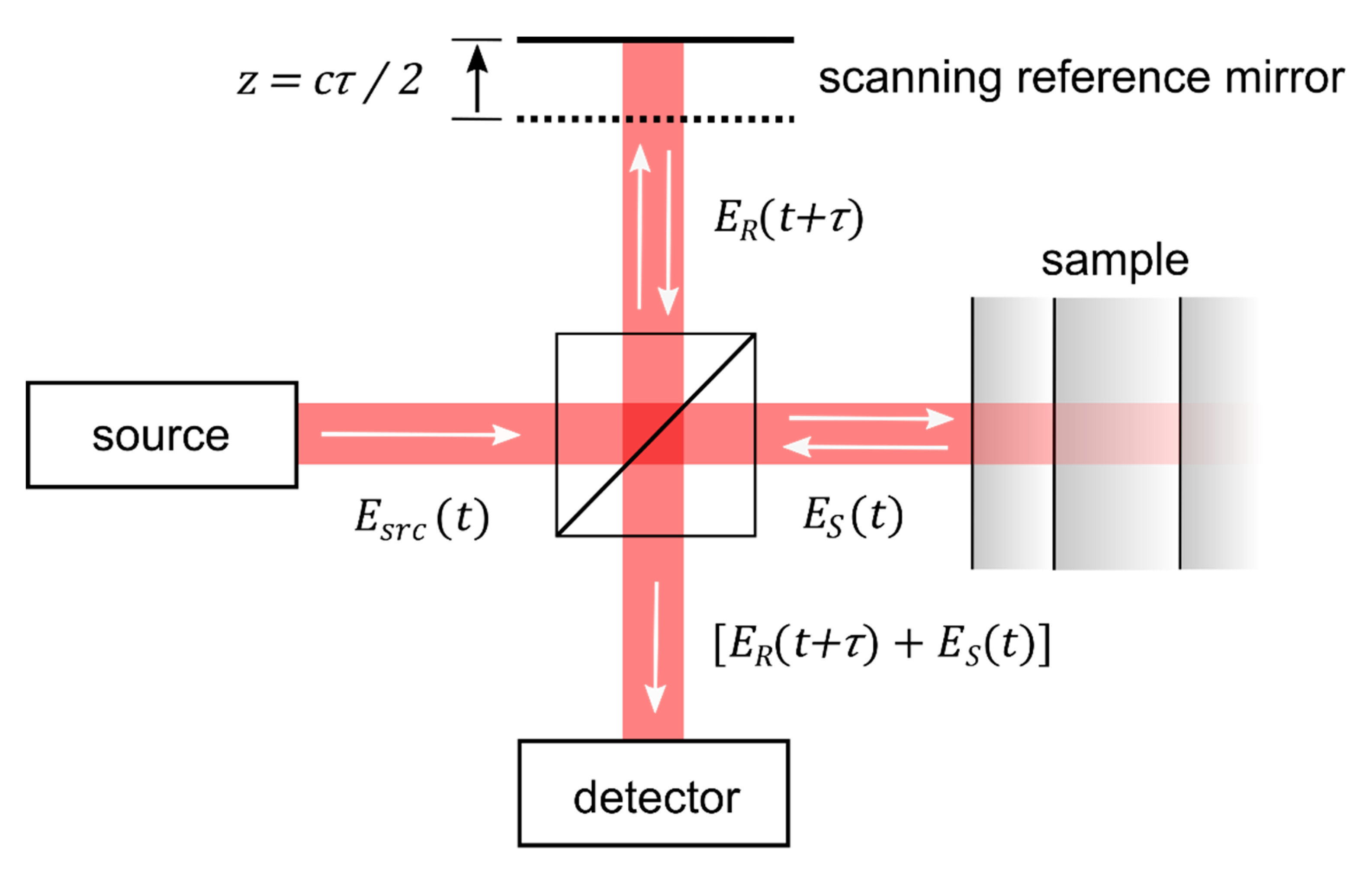
3.1. OCT Implementations
3.2. Exploiting the Reflection Matrix to Suppress Multiple-scattered Light
3.3. Spectral and Temporal Shaping of Scattered Light
3.4. Wavefront Shaping Techniques for Direct OCT Signal Enhancement
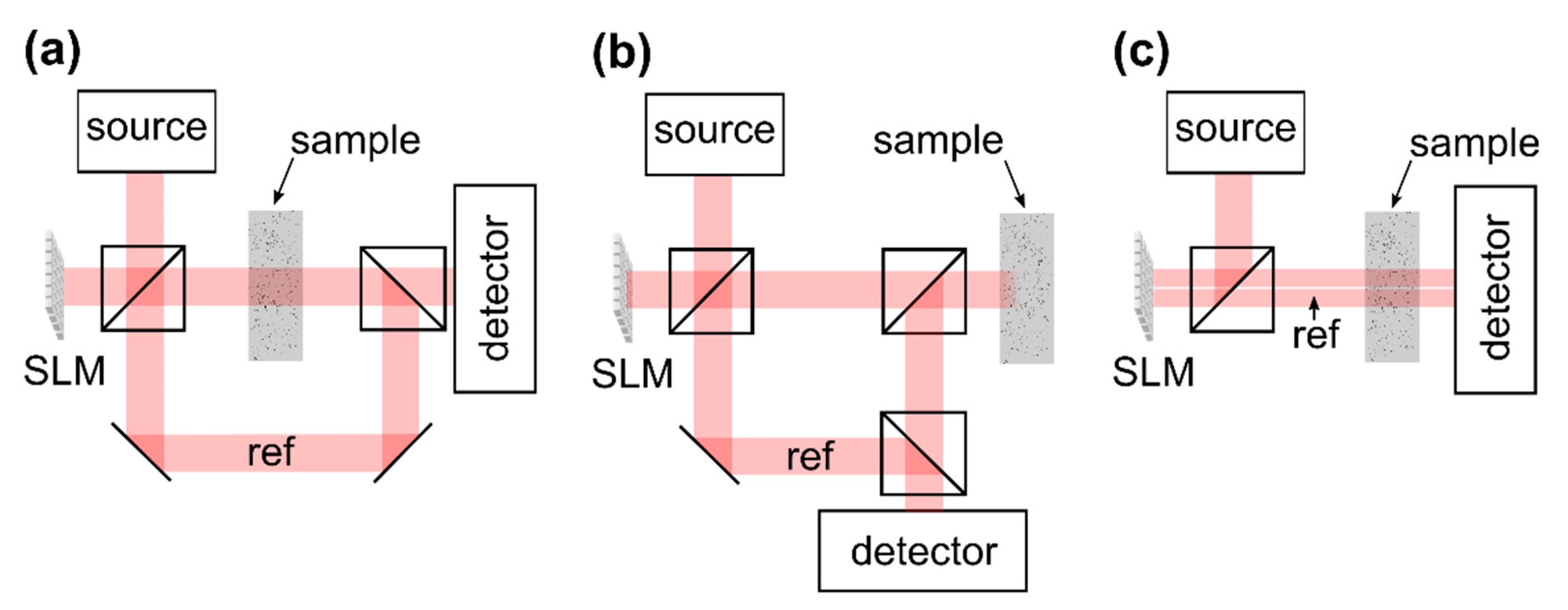
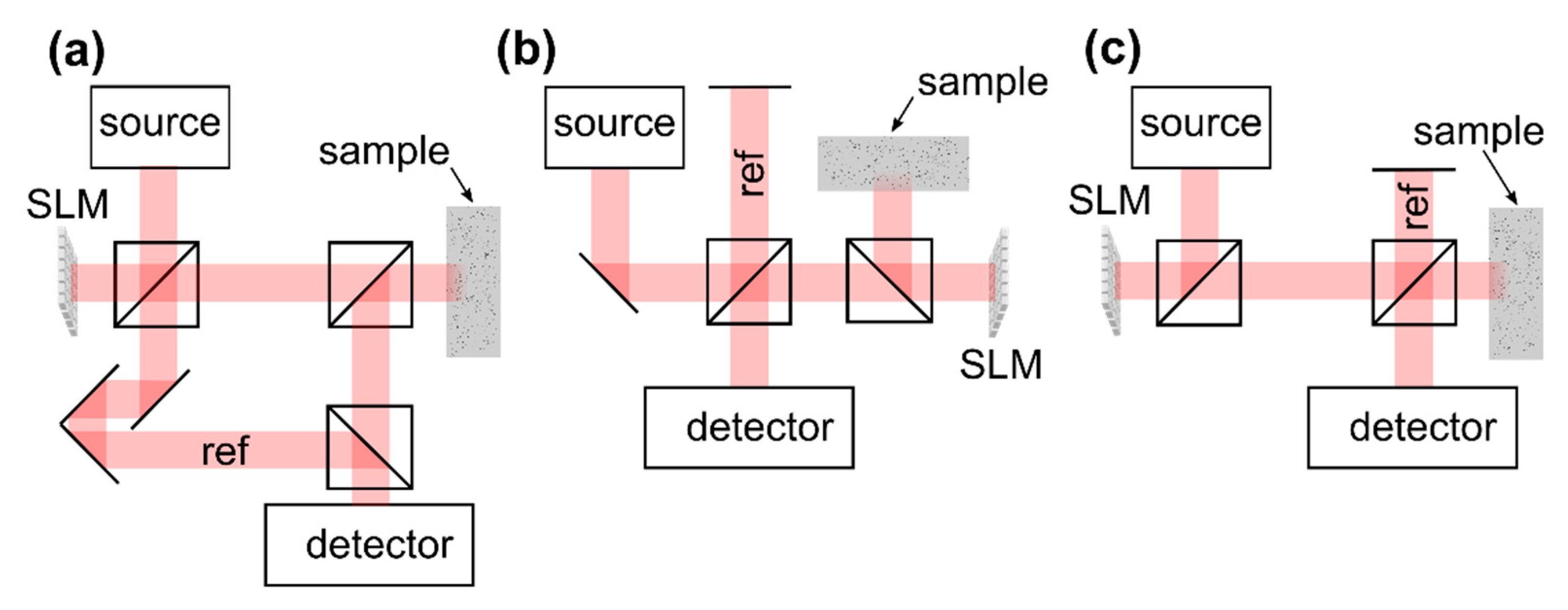
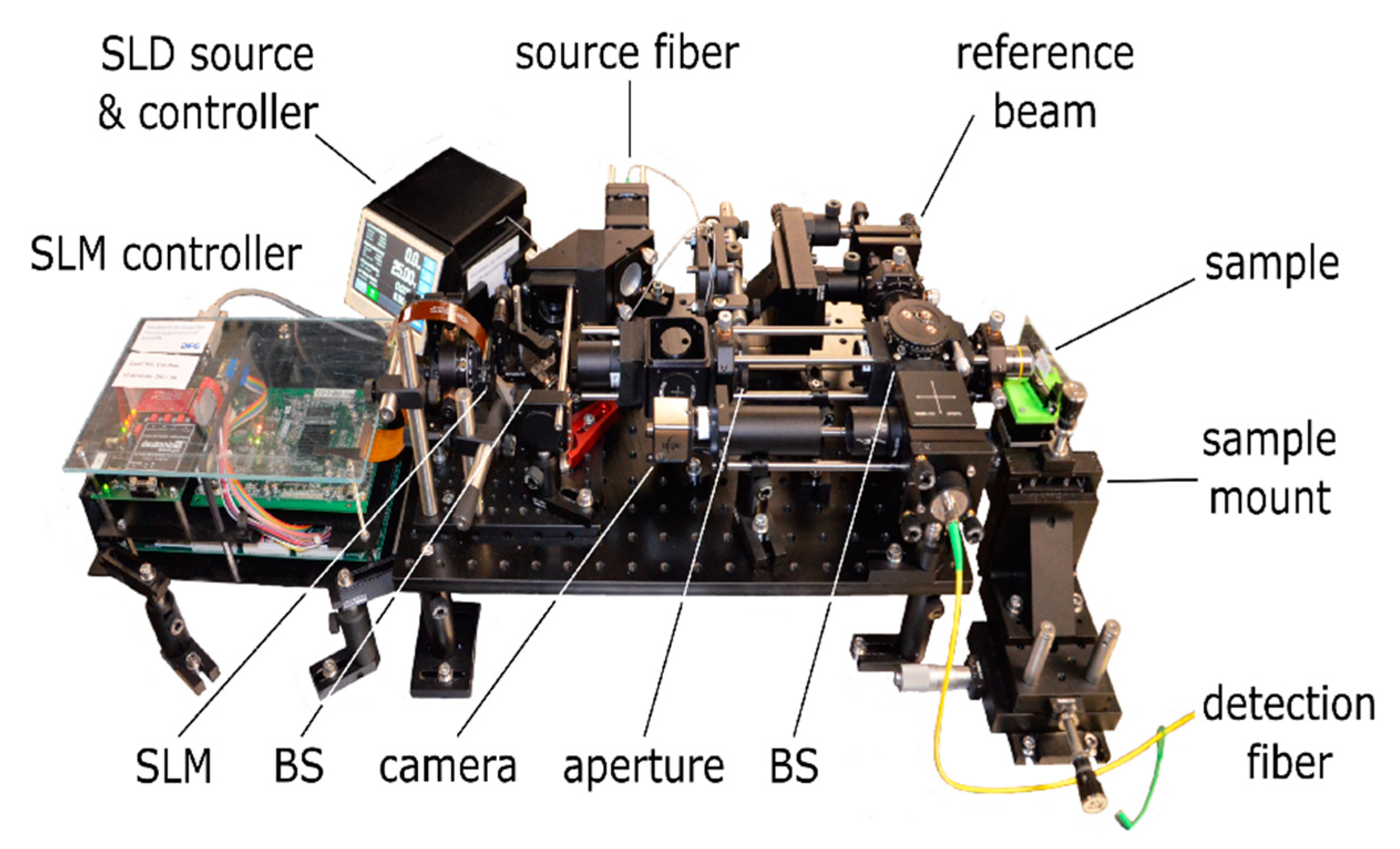
3.4.1. Technical Implementation
3.4.2. Non-Invasive Focusing Approaches
3.4.3. Depth-Enhanced Imaging
4. Remaining Problems
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Youngquist, R.C.; Carr, S.; Davies, D.E.N. Optical coherence-domain refectometry: A new optical evaluation technique. Opt. Lett. 1987, 12, 158–160. [Google Scholar] [CrossRef]
- Takada, K.; Yokohama, I.; Chida, K.; Noda, J. New measurement system for fault location in optical waveguide devices based on an interferometric technique. Appl. Opt. 1987, 26, 1603–1606. [Google Scholar] [CrossRef] [PubMed]
- Fercher, A.F.; Mengedoht, K.; Werner, W. Eye-length measurement by interferometry with partially coherent light. Opt. Lett. 1988, 13, 186–188. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Wang, J.; Lin, C.P.; Puliafito, C.A.; Fujimoto, J.G. Micronresolution ranging of cornea anterior chamber by optical reectometry. Lasers Surg. Med. 1991, 11, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Swanson, E.A.; Lin, C.P.; Schuman, J.S.; Stinson, W.G.; Chang, W.; Hee, M.R.; Flotte, T.; Gregory, K.; Puliafito, C.A.; et al. Optical coherence tomography. Science 1991, 254, 1178–1181. [Google Scholar] [CrossRef] [Green Version]
- Fercher, A.F.; Hitzenberger, C.K.; Drexler, W.; Kamp, G.; Sattmann, H. In vivo optical coherence tomography. Am. J. Ophthalmol. 1993, 116, 113–115. [Google Scholar] [CrossRef]
- Swanson, E.A.; Izatt, J.A.; Hee, M.R.; Huang, D.; Lin, C.P.; Schuman, J.S.; Puliafito, C.A.; Fujimoto, J.G. In vivo retinal imaging by optical coherence tomography. Opt. Lett. 1993, 18, 1864–1866. [Google Scholar] [CrossRef]
- Kanngiesser, J. Wavefront Shaping Approaches for Spectral Domain Optical Coherence Tomography. Ph.D. Thesis, Leibniz University Hannover, Hannover, Germany, 2020. [Google Scholar]
- Lauterborn, W.; Kurz, T. Coherent Optics, Fundamentals and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Demtröder, W. Laser Spectroscopy, Basic Concepts and Instrumentation; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Schmitt, J.M. Optical coherence tomography (OCT): A review. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 1205–1215. [Google Scholar] [CrossRef] [Green Version]
- Fercher, A.F.; Drexler, W.; Hitzenberger, C.K.; Lasser, T. Optical coherence tomography-principles and applications. Rep. Prog. Phys. 2003, 66, 239–303. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics, 1st ed.; Wiley-Interscience: New York, NY, USA, 2000. [Google Scholar]
- Leitgeb, R.A.; Hitzenberger, C.K.; Fercher, A.F. Performance of fourier domain vs. time domain optical coherence tomography. Opt. Express 2003, 11, 889–894. [Google Scholar] [CrossRef]
- Choma, M.A.; Sarunic, M.V.; Yang, C.; Izatt, J.A. Sensitivity advantage of swept source and Fourier domain optical coherence tomography. Opt. Express 2003, 11, 2183–2189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Boer, J.F.; Park, B.H.; Pierce, M.C.; Tearney, G.J.; Bouma, B.E. Improved signal-to-noise ratio in spectral-domain compared with time-domain optical coherence tomography. Opt. Lett. 2003, 28, 2067–2069. [Google Scholar] [CrossRef] [PubMed]
- Roddier, F. (Ed.) Adaptive Optics in Astronomy; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Tyson, R.K. Principles of Adaptive Optics, 4th ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Pircher, M.; Zawadzki, R.J. Combining adaptive optics with optical coherence tomography: Unveiling the cellular structure of the human retina in vivo. Expert Rev. Ophthalmol. 2014, 2, 1019–1035. [Google Scholar] [CrossRef]
- Booth, M.J. Adaptive optics in microscopy. Philos. Trans. R. Soc. A 2007, 365, 2829–2843. [Google Scholar] [CrossRef]
- Miller, D.T.; Kocaoglu, O.P.; Wang, Q.; Lee, S. Adaptive optics and the eye (super resolution OCT). Eye 2011, 25, 321–330. [Google Scholar] [CrossRef] [Green Version]
- Booth, M.J. Adaptive optical microscopy: The ongoing quest for a perfect image. Light Sci. Appl. 2014, 3, e165. [Google Scholar] [CrossRef]
- Jonnal, R.S.; Kocaoglu, O.P.; Zawadzki, R.J.; Liu, Z.; Miller, D.T.; Werner, J.S. A review of adaptive optics optical coherence tomography: Technical advances, scientific applications, and the future. Investig. Ophthalmol. Vis. Sci. 2016, 57, OCT51–OCT68. [Google Scholar] [CrossRef]
- Pircher, M.; Zawadzki, R.J. Review of adaptive optics OCT (AO-OCT): Principles and applications for retinal imaging. Biomed. Opt. Express 2017, 8, 2536–2562. [Google Scholar] [CrossRef]
- Derode, A.; Roux, P.; Fink, M. Robust acoustic time reversal with high-order multiple scattering. Phys. Rev. Lett. 1995, 75, 4206–4210. [Google Scholar] [CrossRef]
- Derode, A.; Tourin, A.; Fink, M. Random multiple scattering of ultrasound. II. Is time reversal a self-averaging process? Phys. Rev. E 2001, 64, 36606. [Google Scholar] [CrossRef]
- Lemoult, F.; Lerosey, G.; de Rosny, J.; Fink, M. Manipulating spatiotemporal degrees of freedom of waves in random media. Phys. Rev. Lett. 2009, 103, 173902. [Google Scholar] [CrossRef] [PubMed]
- Leith, E.N.; Upatnieks, J. Holographic imagery through diffusing media. J. Opt. Soc. Am. 1966, 56, 523. [Google Scholar] [CrossRef]
- Yaqoob, Z.; Psaltis, D.; Feld, M.S.; Yang, C. Optical phase conjugation for turbidity suppression in biological samples. Nat. Photonics 2008, 2, 110–115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hillman, T.R.; Yamauchi, T.; Choi, W.; Dasari, R.R.; Feld, M.S.; Park, Y.; Yaqoob, Z. Digital optical phase conjugation for delivering two-dimensional images through turbid media. Sci. Rep. 2013, 3, 1909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsieh, C.-L.; Pu, Y.; Grange, R.; Laporte, G.; Psaltis, D. Imaging through turbid layers by scanning the phase conjugated second harmonic radiation from a nanoparticle. Opt. Express 2010, 18, 20723–20731. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, C.-L.; Pu, Y.; Grange, R.; Psaltis, D. Digital phase conjugation of second harmonic radiation emitted by nanoparticles in turbid media. Opt. Express 2010, 18, 12283–12290. [Google Scholar] [CrossRef] [Green Version]
- Cui, M.; Yang, C. Implementation of a digital optical phase conjugation system and its application to study the robustness of turbidity suppression by phase conjugation. Opt. Express 2010, 18, 3444–3455. [Google Scholar] [CrossRef] [Green Version]
- Jang, M.; Ruan, H.; Vellekoop, I.M.; Judkewitz, B.; Chung, E.; Yang, C. Relation between speckle decorrelation and optical phase conjugation (OPC)-based turbidity suppression through dynamic scattering media: A study on in vivo mouse skin. Biomed. Opt. Express 2015, 6, 72–85. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, E.H.; Brake, J.; Ruan, H.; Jang, M.; Yang, C. Focusing through dynamic tissue with millisecond digital optical phase conjugation. Optica 2015, 2, 728–735. [Google Scholar] [CrossRef]
- Cui, M.; McDowell, E.J.; Yang, C. An in vivo study of turbidity suppression by optical phase conjugation (TSOPC) on rabbit ear. Opt. Express 2010, 18, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Judkewitz, B.; Horstmeyer, R.; Vellekoop, I.M.; Papadopoulos, I.N.; Yang, C. Translation correlations in anisotropically scattering media. Nat. Phys. 2015, 11, 684–689. [Google Scholar] [CrossRef]
- Kong, L.; Tang, J.; Cui, M. In vivo volumetric imaging of biological dynamics in deep tissue via wavefront engineering. Opt. Express 2016, 24, 1214–1221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kong, L.; Cui, M. In vivo fluorescence microscopy via iterative multi-photon adaptive compensation technique. Opt. Express 2014, 22, 23786–23794. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Kane, C.; Lee, P.A.; Stone, A.D. Correlations and fluctuations of coherent wave transmission through disordered media. Phys. Rev. Lett. 1988, 61, 834–837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freund, I. Looking through walls and around corners. Physica A 1990, 168, 49–65. [Google Scholar] [CrossRef]
- Zhou, E.H.; Ruan, H.; Yang, C.; Judkewitz, B. Focusing on moving targets through scattering samples. Optica 2014, 1, 227–232. [Google Scholar] [CrossRef] [Green Version]
- Judkewitz, B.; Wang, Y.M.; Horstmeyer, R.; Mathy, A.; Yang, C. Speckle-scale focusing in the diffusive regime with time-reversal of variance-encoded light (TROVE). Nat. Photonics 2013, 7, 300–305. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Wang, L.V. Time-reversed ultrasonically encoded optical focusing into scattering media. Nat. Photonics 2011, 5, 154–157. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Lai, P.; Ma, C.; Xu, X.; Grabar, A.A.; Wang, L.V. Optical focusing deep inside dynamic scattering media with near-infrared time-reversed ultrasonically encoded (TRUE) light. Nat. Commun. 2015, 6, 5904. [Google Scholar] [CrossRef]
- Si, K.; Fiolka, R.; Cui, M. Fluorescence imaging beyond the ballistic regime by ultrasound-pulse-guided digital phase conjugation. Nat. Photonics 2012, 6, 657–661. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.M.; Judkewitz, B.; DiMarzio, C.A.; Yang, C. Deep-tissue focal fluorescence imaging with digitally time-reversed ultrasound-encoded light. Nat. Commun. 2012, 3, 928. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vellekoop, I.M.; Mosk, A.P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 2007, 32, 2309–2311. [Google Scholar] [CrossRef] [PubMed]
- Mahmud, M.S.; Cadotte, D.W.; Vuong, B.; Sun, C.; Luk, T.W.H.; Mariampillai, A.; Yang, V.X.D. Review of speckle and phase variance optical coherence tomography to visualize microvascular networks. J. Biomed. Opt. 2013, 18, 050901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vellekoop, I.M.; Lagendijk, A.; Mosk, A.P. Exploiting disorder for perfect focusing. Nat. Photonics 2010, 4, 320–322. [Google Scholar] [CrossRef] [Green Version]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Effect of experimental parameters on optimal reflection of light from opaque media. Phys. Rev. A 2016, 93, 13813. [Google Scholar] [CrossRef] [Green Version]
- Anderson, B.R.; Gunawidjaja, R.; Eilers, H. Effect of experimental parameters on optimal transmission of light through opaque media. Phys. Rev. A 2014, 90, 53826. [Google Scholar] [CrossRef] [Green Version]
- Vellekoop, I.M.; van Putten, E.G.; Lagendijk, A.; Mosk, A.P. Demixing light paths inside disordered metamaterials. Opt. Express 2008, 16, 67–80. [Google Scholar] [CrossRef] [Green Version]
- Akbulut, D.; Huisman, T.J.; van Putten, E.G.; Vos, W.L.; Mosk, A.P. Focusing light through random photonic media by binary amplitude modulation. Opt. Express 2011, 19, 4017–4029. [Google Scholar] [CrossRef] [Green Version]
- Popoff, S.M.; Lerosey, G.; Fink, M.; Boccara, A.C.; Gigan, S. Controlling light through optical disordered media: Transmission matrix approach. New J. Phys. 2011, 13, 123021. [Google Scholar] [CrossRef]
- Tang, J.; Germain, R.N.; Cui, M. Superpenetration optical microscopy by iterative multiphoton adaptive compensation technique. Proc. Natl. Acad. Sci. USA 2012, 109, 8434–8439. [Google Scholar] [CrossRef] [Green Version]
- Katz, O.; Small, E.; Bromberg, Y.; Silberberg, Y. Focusing and compression of ultrashort pulses through scattering media. Nat. Photonics 2011, 5, 372–377. [Google Scholar] [CrossRef]
- Katz, O.; Small, E.; Guan, Y.; Silberberg, Y. Noninvasive nonlinear focusing and imaging through strongly scattering turbid layers. Optica 2014, 1, 170–174. [Google Scholar] [CrossRef] [Green Version]
- Tay, J.W.; Lai, P.; Suzuki, Y.; Wang, L.V. Ultrasonically encoded wavefront shaping for focusing into random media. Sci. Rep. 2014, 4, 3918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, P.; Wang, L.; Tay, J.W.; Wang, L.V. Photoacoustically guided wavefront shaping for enhanced optical focusing in scattering media. Nat. Photonics 2015, 9, 126–132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conkey, D.B.; Caravaca-Aguirre, A.M.; Dove, J.D.; Ju, H.; Murray, T.W.; Piestun, R. Super-resolution photoacoustic imaging through a scattering wall. Nat. Commun. 2015, 6, 7902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caravaca-Aguirre, A.M.; Conkey, D.B.; Dove, J.D.; Ju, H.; Murray, T.W.; Piestun, R. High contrast three-dimensional photoacoustic imaging through scattering media by localized optical fluence enhancement. Opt. Express 2013, 21, 26671–26676. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Silverman, R.H.; Liu, L.; Chitnis, P.V.; Lee, K.K.; Chen, Y.-C. Photoacoustic-guided convergence of Light through optically diffusive media. Opt. Lett. 2011, 36, 2053–2055. [Google Scholar] [CrossRef] [Green Version]
- Conkey, D.B.; Brown, A.N.; Caravaca-Aguirre, A.M.; Piestun, R. Genetic algorithm optimization for focusing through turbid media in noisy environments. Opt. Express 2012, 20, 4840–4849. [Google Scholar] [CrossRef]
- Tzang, O.; Niv, E.; Caravaca-Aguirre, A.M.; Piestun, R. Thermal expansion feedback for wave-front shaping. Opt. Express 2017, 25, 6122–6131. [Google Scholar] [CrossRef]
- Vellekoop, I.M.; Mosk, A.P. Phase control algorithms for focusing light through turbid media. Opt. Commun. 2008, 281, 3071–3080. [Google Scholar] [CrossRef] [Green Version]
- Cui, M. Parallel wavefront optimization method for focusing light through random scattering media. Opt. Lett. 2011, 36, 870–872. [Google Scholar] [CrossRef]
- Choi, Y.; Hillman, T.R.; Choi, W.; Lue, N.; Dasari, R.R.; So, P.T.C.; Choi, W.; Yaqoob, Z. Measurement of the time-resolved reflection matrix for enhancing light energy delivery into a scattering medium. Phys. Rev. Lett. 2013, 111, 243901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blochet, B.; Bourdieu, L.; Gigan, S. Focusing light through dynamical samples using fast continuous wavefront optimization. Opt. Lett. 2017, 42, 4994–4997. [Google Scholar] [CrossRef] [PubMed]
- Fiolka, R.; Si, K.; Cui, M. Complex wavefront corrections for deep tissue focusing using low coherence backscattered light. Opt. Express 2012, 20, 16532–16543. [Google Scholar] [CrossRef]
- Jang, J.; Lim, J.; Yu, H.; Choi, H.; Ha, J.; Park, J.-H.; Oh, W.-Y.; Jang, W.; Lee, S.; Park, Y. Complex wavefront shaping for optimal depth-selective focusing in optical coherence tomography. Opt. Express 2013, 21, 2890–2902. [Google Scholar] [CrossRef] [PubMed]
- Hemphill, A.S.; Tay, J.W.; Wang, L.V. Hybridized wavefront shaping for high-speed, high-efficiency focusing through dynamic diffusive media. J. Biomed. Opt. 2016, 21, 121502. [Google Scholar] [CrossRef] [Green Version]
- Feldkhun, D.; Tzang, O.; Wagner, K.H.; Piestun, R. Focusing and scanning through scattering media in microseconds. Optica 2019, 6, 72–75. [Google Scholar] [CrossRef]
- Popoff, S.M.; Lerosey, G.; Carminati, R.; Fink, M.; Boccara, A.C.; Gigan, S. Measuring the transmission matrix in optics: An approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 2010, 104, 100601. [Google Scholar] [CrossRef]
- Cizmar, T.; Mazilu, M.; Dholakia, K. In situ wavefront correction and its application to micromanipulation. Nat. Photonics 2010, 4, 388–394. [Google Scholar] [CrossRef]
- Chaigne, T.; Katz, O.; Boccara, A.C.; Fink, M.; Bossy, E.; Gigan, S. Controlling light in scattering media non-invasively using the photoacoustic transmission matrix. Nat. Photonics 2014, 8, 58–64. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.; Yang, T.D.; Fang-Yen, C.; Kang, P.; Lee, K.J.; Dasari, R.R.; Feld, M.S.; Choi, W. Overcoming the diffraction limit using multiple light scattering in a highly disordered medium. Phys. Rev. Lett. 2011, 107, 23902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popoff, S.M.; Lerosey, G.; Fink, M.; Boccara, A.C.; Gigan, S. Image transmission through an opaque material. Nat. Commun. 2010, 1, 81. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Park, J.-H.; Park, Y. Measuring large optical reflection matrices of turbid media. Opt. Commun. 2015, 352, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Popoff, S.M.; Aubry, A.; Lerosey, G.; Fink, M.; Boccara, A.C.; Gigan, S. Exploiting the time-reversal operator for adaptive optics, selective focusing, and scattering pattern analysis. Phys. Rev. Lett. 2011, 107, 263901. [Google Scholar] [CrossRef] [Green Version]
- Prada, C.; Manneville, S.; Spoliansky, D.; Fink, M. Decomposition of the time reversal operator: Detection and selective focusing on two scatterers. J. Acoust. Soc. Am. 1996, 99, 2067–2076. [Google Scholar] [CrossRef]
- Badon, A.; Li, D.; Lerosey, G.; Boccara, A.C.; Fink, M.; Aubry, A. Smart optical coherence tomography for ultra-deep imaging through highly scattering media. Sci. Adv. 2016, 2, e1600370. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Miao, Y.; Huo, T.; Li, Y.; Heidari, E.; Zhu, J.; Chen, Z. Deep imaging in highly scattering media by combining reflection matrix measurement with Bessel-like beam based optical coherence tomography. Appl. Phys. Lett. 2018, 113, 11106. [Google Scholar] [CrossRef]
- Kang, S.; Kang, P.; Jeong, S.; Kwon, Y.; Yang, T.D.; Hong, J.H.; Kim, M.; Song, K.-D.; Park, J.H.; Lee, J.H.; et al. High-resolution adaptive optical imaging within thick scattering media using closed-loop accumulation of single scattering. Nat. Commun. 2017, 8, 2157. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.; Jeong, S.; Choi, W.; Ko, H.; Yang, T.D.; Joo, J.H.; Lee, J.-S.; Lim, Y.-S.; Park, Q.-H.; Choi, W. Imaging deep within a scattering medium using collective accumulation of single-scattered waves. Nat. Photonics 2015, 9, 253–258. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, Y.-R.; Choi, W.; Kang, S.; Hong, J.H.; Park, J.-S.; Lim, Y.-S.; Park, H.-G.; Choi, W. Focusing of light energy inside a scattering medium by controlling the time-gated multiple light scattering. Nat. Photonics 2018, 12, 277–283. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Lee, P.; Lee, K.; Jang, J.; Lim, J.; Jang, W.; Jeong, Y.; Park, Y. In vivo deep tissue imaging using wavefront shaping optical coherence tomography. J. Biomed. Opt. 2016, 21, 101406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.; Lee, P.; Jo, Y.; Lee, K.; Tuchin, V.V.; Jeong, Y.; Park, Y. Collaborative effects of wavefront shaping and optical clearing agent in optical coherence tomography. J. Biomed. Opt. 2016, 21, 121510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.; Jang, J.; Lim, J.; Park, J.-H.; Jang, W.; Kim, J.-Y.; Park, Y. Depth-enhanced 2-D optical coherence tomography using complex wavefront shaping. Opt. Express 2014, 22, 7514–7523. [Google Scholar] [CrossRef] [PubMed]
- Badon, A.; Barolle, V.; Irsch, K.; Boccara, A.C.; Fink, M.; Aubry, A. Distortion matrix concept for deep imaging in optical coherence microscopy. arXiv 2019, arXiv:1910.07252. [Google Scholar]
- McCabe, D.J.; Tajalli, A.; Austin, D.R.; Bondareff, P.; Walmsley, I.A.; Gigan, S.; Chatel, B. Spatio-temporal focusing of an ultrafast pulse through a multiply scattering medium. Nat. Commun. 2011, 2, 447. [Google Scholar] [CrossRef]
- Small, E.; Katz, O.; Guan, Y.; Silberberg, Y. Spectral control of broadband light through random media by wavefront shaping. Opt. Lett. 2012, 37, 3429–3431. [Google Scholar] [CrossRef] [Green Version]
- Aulbach, J.; Gjonaj, B.; Johnson, P.M.; Mosk, A.P.; Lagendijk, A. Control of light transmission through opaque scattering media in space and time. Phys. Rev. Lett. 2011, 106, 103901. [Google Scholar] [CrossRef]
- Mounaix, M.; Defienne, H.; Gigan, S. Deterministic light focusing in space and time through multiple scattering media with a time-resolved transmission matrix approach. Phys. Rev. A 2016, 94, 41802. [Google Scholar] [CrossRef] [Green Version]
- Mounaix, M.; Ta, D.M.; Gigan, S. Transmission matrix approaches for nonlinear fluorescence excitation through multiple scattering media. Opt. Lett. 2018, 43, 2831–2834. [Google Scholar] [CrossRef]
- Mounaix, M.; Andreoli, D.; Defienne, H.; Volpe, G.; Katz, O.; Grésillon, S.; Gigan, S. Spatiotemporal coherent control of light through a multiple scattering medium with the multispectral transmission matrix. Phys. Rev. Lett. 2016, 116, 253901. [Google Scholar] [CrossRef]
- Andreoli, D.; Volpe, G.; Popoff, S.M.; Katz, O.; Grésillon, S.; Gigan, S. Deterministic control of broadband light through a multiply scattering medium via the multispectral transmission matrix. Sci. Rep. 2015, 5, 10347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van Beijnum, F.; van Putten, E.G.; Lagendijk, A.; Mosk, A.P. Frequency bandwidth of light focused through turbid media. Opt. Lett. 2011, 36, 373–375. [Google Scholar] [CrossRef] [PubMed]
- Park, J.-H.; Park, C.; Yu, H.; Cho, Y.-H.; Park, Y. Active spectral filtering through turbid media. Opt. Lett. 2012, 37, 3261–3263. [Google Scholar] [CrossRef] [PubMed]
- Paudel, H.P.; Stockbridge, C.; Mertz, J.; Bifano, T. Focusing polychromatic light through strongly scattering media. Opt. Express 2013, 21, 17299–17308. [Google Scholar] [CrossRef] [PubMed]
- Kanngiesser, J.; Rahlves, M.; Roth, B. Double interferometer design for independent wavefront manipulation in spectral domain optical coherence tomography. Sci. Rep. 2019, 9, 14651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanngiesser, J.; Rahlves, M.; Roth, B. Iterative wavefront correction for complex spectral domain optical coherence tomography. Opt. Lett. 2019, 44, 1347–1350. [Google Scholar] [CrossRef]
- Fiolka, R.; Cui, M. High speed phase distortion measurement and compensation for focusing in space and time. In Proceedings of the Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing XX, San Francisco, CA, USA, 2–7 February 2013; Volume 8589, p. 85890V. [Google Scholar]
- Choi, W.; Kim, M.; Kim, D.; Yoon, C.; Fang-Yen, C.; Park, Q.-H.; Choi, W. Preferential coupling of an incident wave to reflection eigenchannels of disordered media. Sci. Rep. 2015, 5, 11393. [Google Scholar] [CrossRef] [Green Version]
- Jeong, S.; Kim, D.-Y.; Lee, Y.-R.; Choi, W.; Choi, W. Iterative optimization of time-gated reflectance for the efficient light energy delivery within scattering media. Opt. Express 2019, 27, 10936. [Google Scholar] [CrossRef]
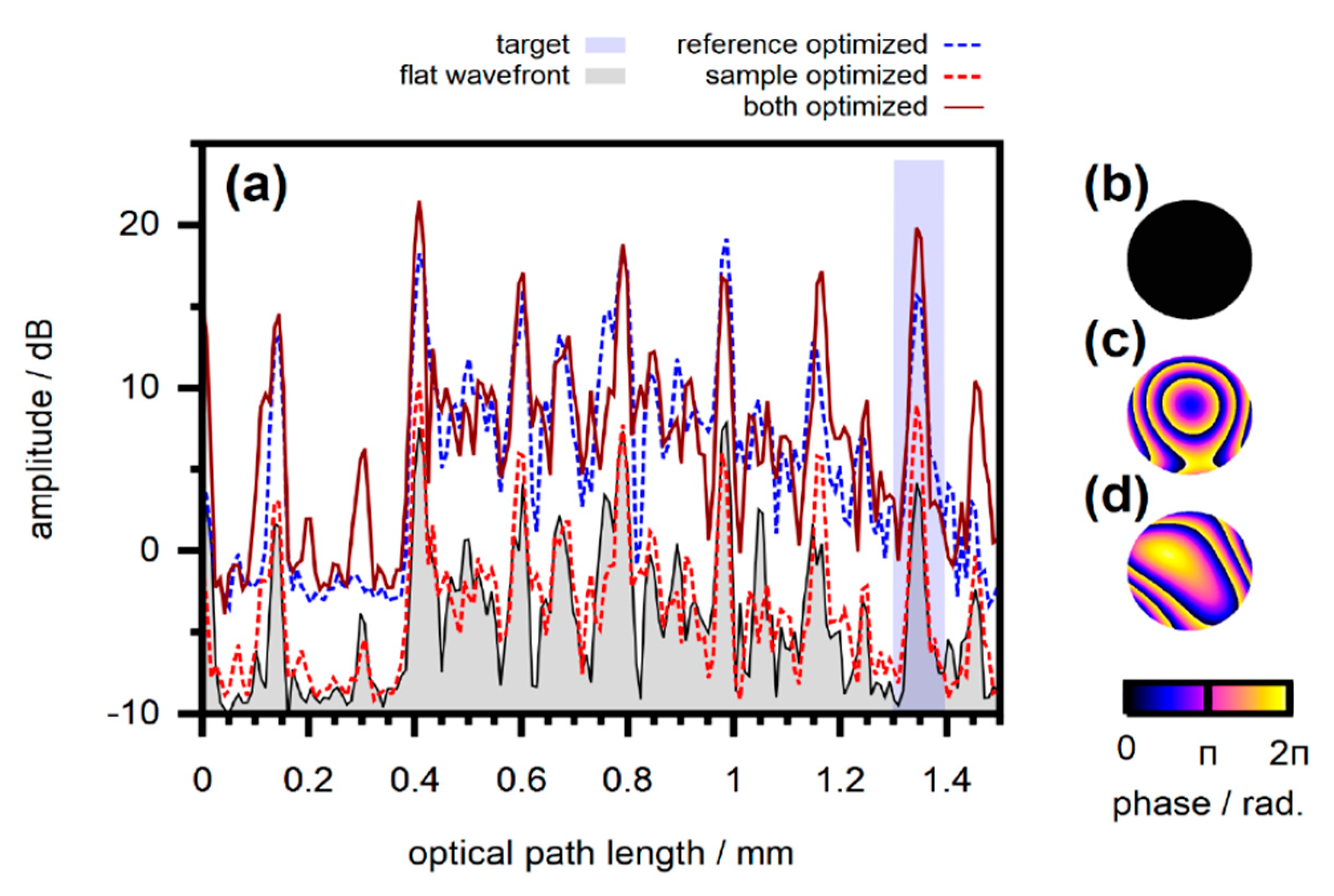
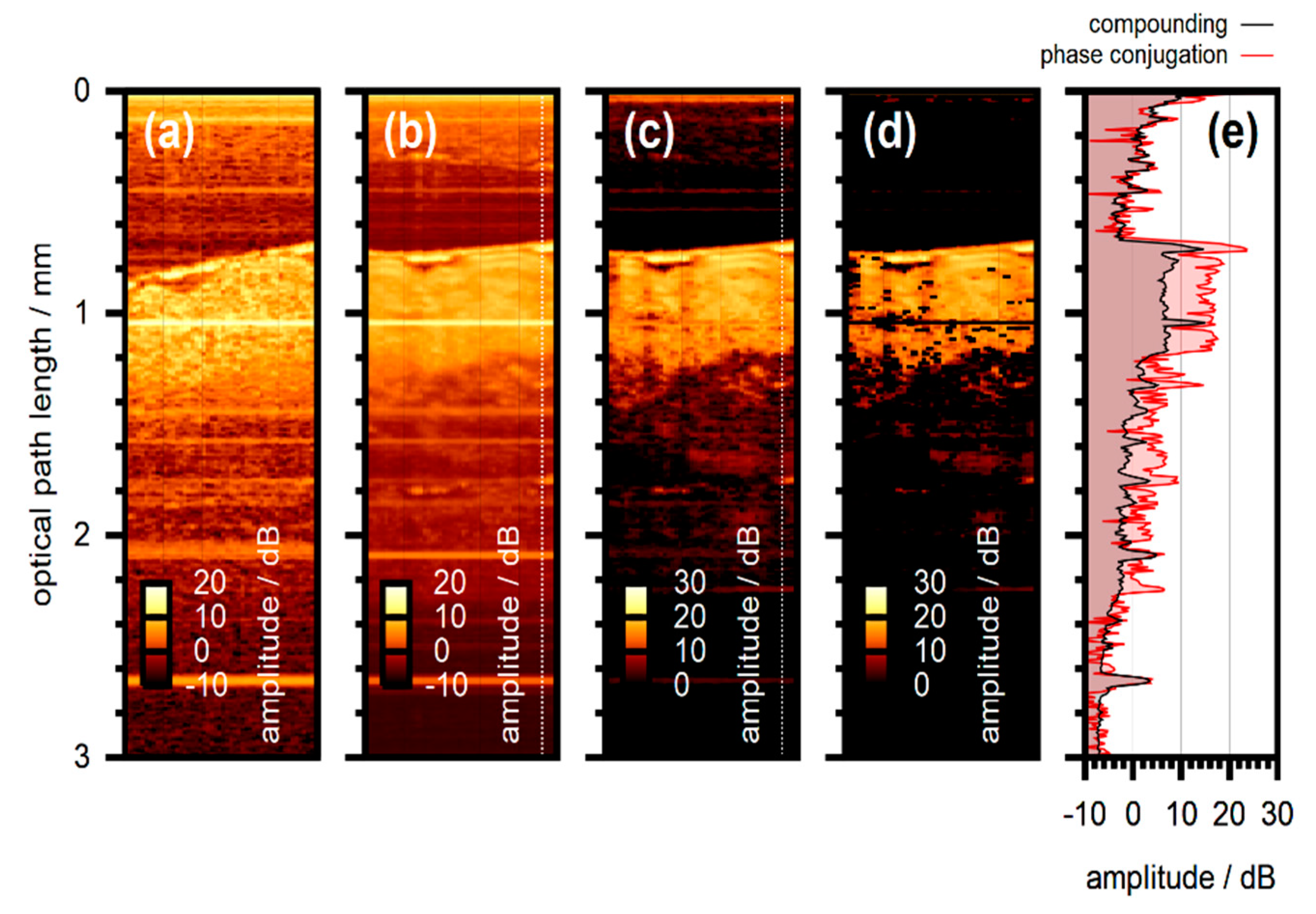
- Kanngiesser, J.; Roth, B. Effect of image artefacts on phase conjugation with spectral domain optical coherence tomography. Opt. Express 2020, 28, 18224–18240. [Google Scholar] [CrossRef]
- Varkentin, A.; Mazurenka, M.; Blumenroether, E.; Meinhardt-Wollweber, M.; Rahlves, M.; Broekaert, S.M.C.; Schäd-Trcka, S.; Emmert, S.; Morgner, U.; Roth, B. Comparative study of presurgical skin infiltration depth measurements of melanocytic lesions with OCT and high frequency ultrasound. J. Biophotonics 2017, 10, 854–861. [Google Scholar] [CrossRef]
- Mazurenka, M.; Behrendt, L.; Meinhardt-Wollweber, M.; Morgner, U.; Roth, B. Development of a combined OCT-Raman probe for the prospective in vivo clinical melanoma skin cancer screening. Rev. Sci. Instrum. 2017, 88, 105103. [Google Scholar] [CrossRef] [PubMed]
- Varkentin, A.; Mazurenka, M.; Blumenroether, E.; Behrendt, L.; Rahlves, M.; Meinhardt-Wollweber, M.; Morgner, U.; Roth, B. Trimodal system for in vivo skin cancer screening with combined optical coherence tomography-Raman and co-localized optoacoustic measurements. J. Biophotonics 2018, 11, e201700288. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanngiesser, J.; Roth, B. Wavefront Shaping Concepts for Application in Optical Coherence Tomography—A Review. Sensors 2020, 20, 7044. https://doi.org/10.3390/s20247044
Kanngiesser J, Roth B. Wavefront Shaping Concepts for Application in Optical Coherence Tomography—A Review. Sensors. 2020; 20(24):7044. https://doi.org/10.3390/s20247044
Chicago/Turabian StyleKanngiesser, Jonas, and Bernhard Roth. 2020. "Wavefront Shaping Concepts for Application in Optical Coherence Tomography—A Review" Sensors 20, no. 24: 7044. https://doi.org/10.3390/s20247044
APA StyleKanngiesser, J., & Roth, B. (2020). Wavefront Shaping Concepts for Application in Optical Coherence Tomography—A Review. Sensors, 20(24), 7044. https://doi.org/10.3390/s20247044





