Assessing Effects of Salinity on the Performance of a Low-Cost Wireless Soil Water Sensor
Abstract
1. Introduction
2. Materials and Methods
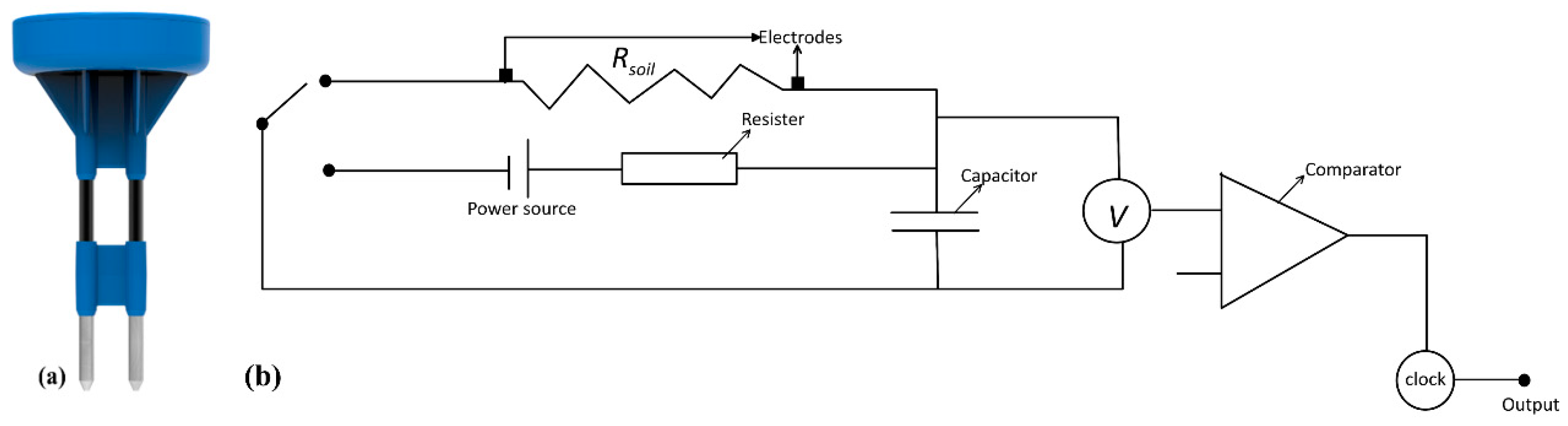
2.1. Sensor Description
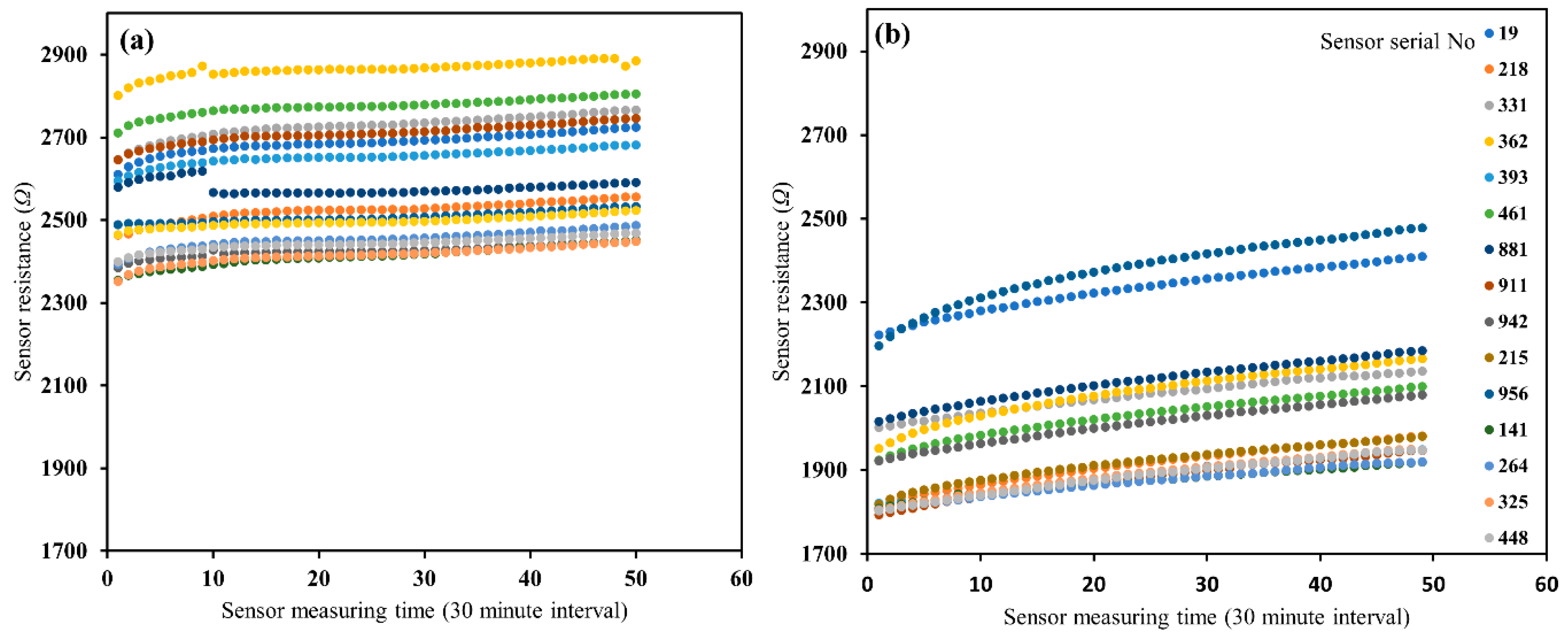
2.2. Assessing Sensor-to-Sensor Variability
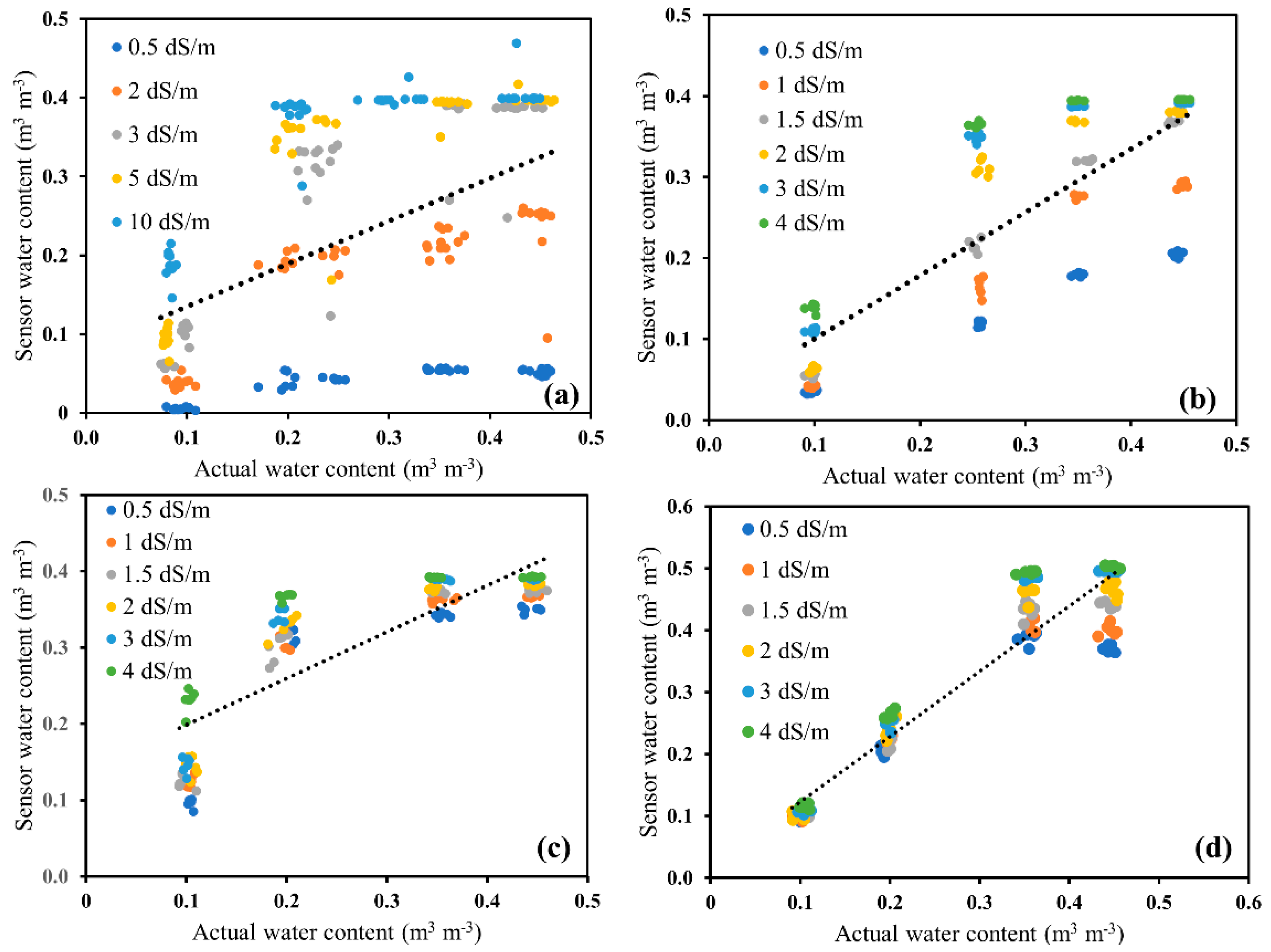
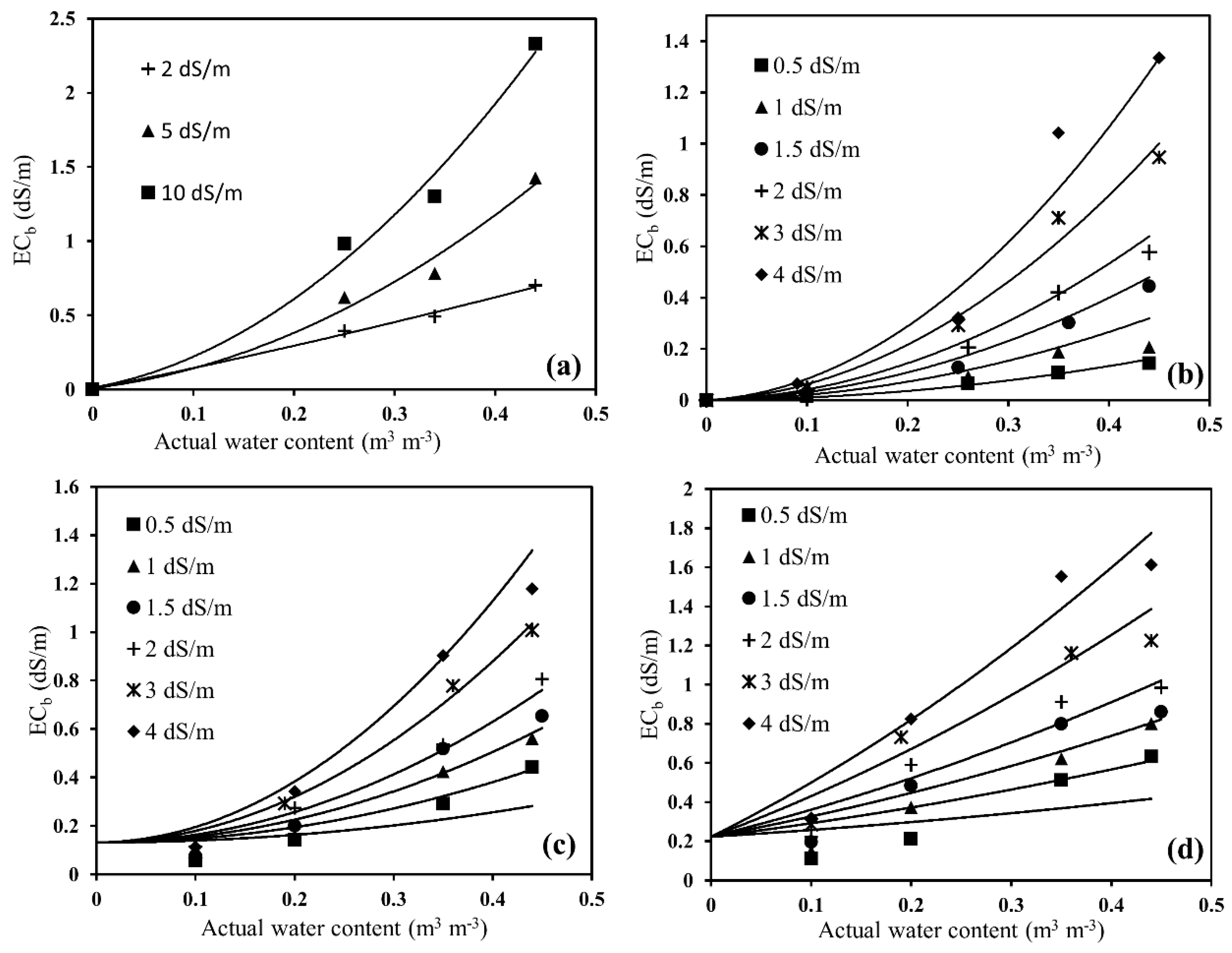
2.3. Effect of Soil Type and Solution Electrical Conductivity on Sensor Performance
2.4. Assessing Sensor Sensitivity to Variations in Temperature
3. Results and Discussion
3.1. Sensor-to-Sensor Variability
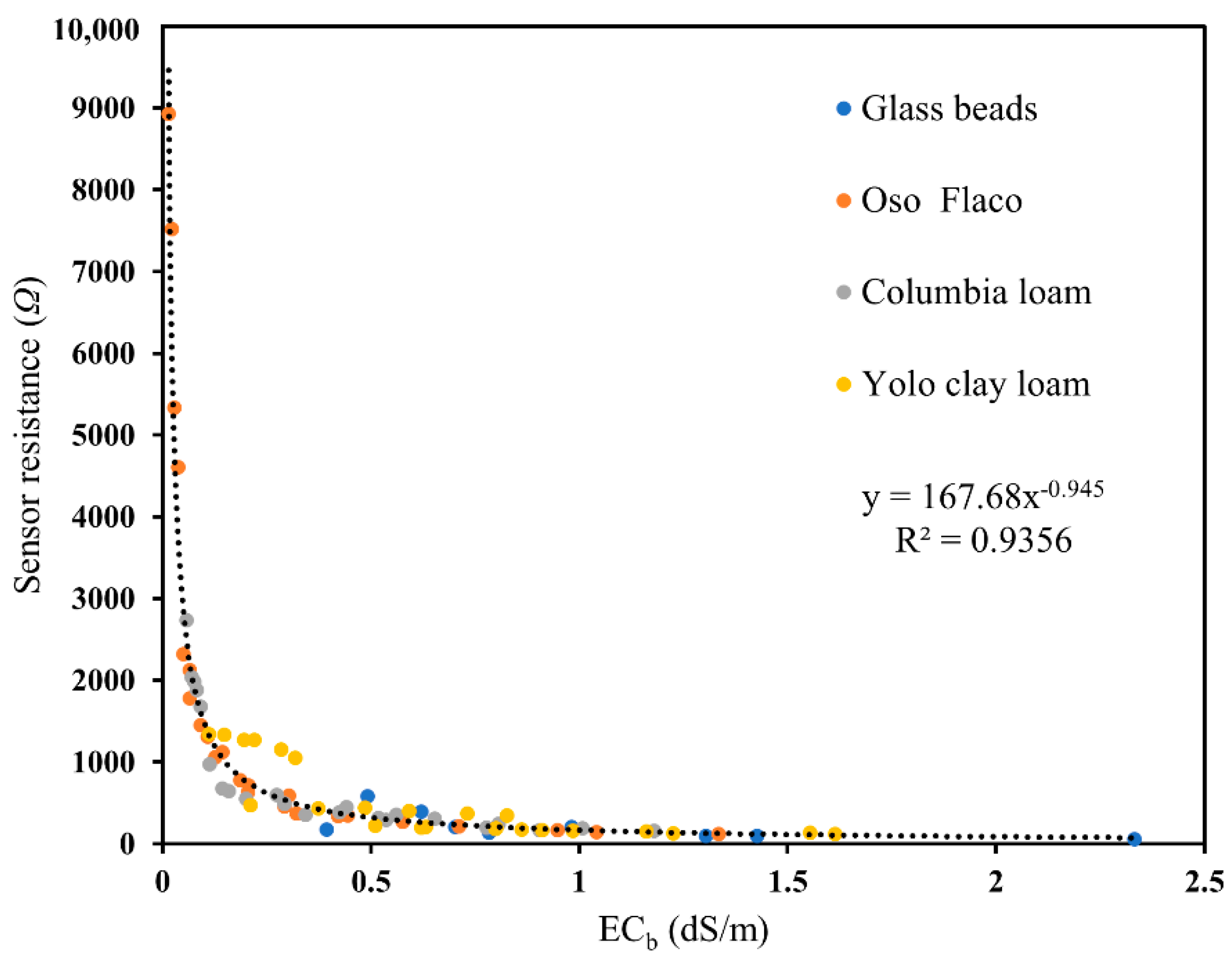
3.2. Effect of Soil Type and Solution Electrical Conductivity on Sensor Performance
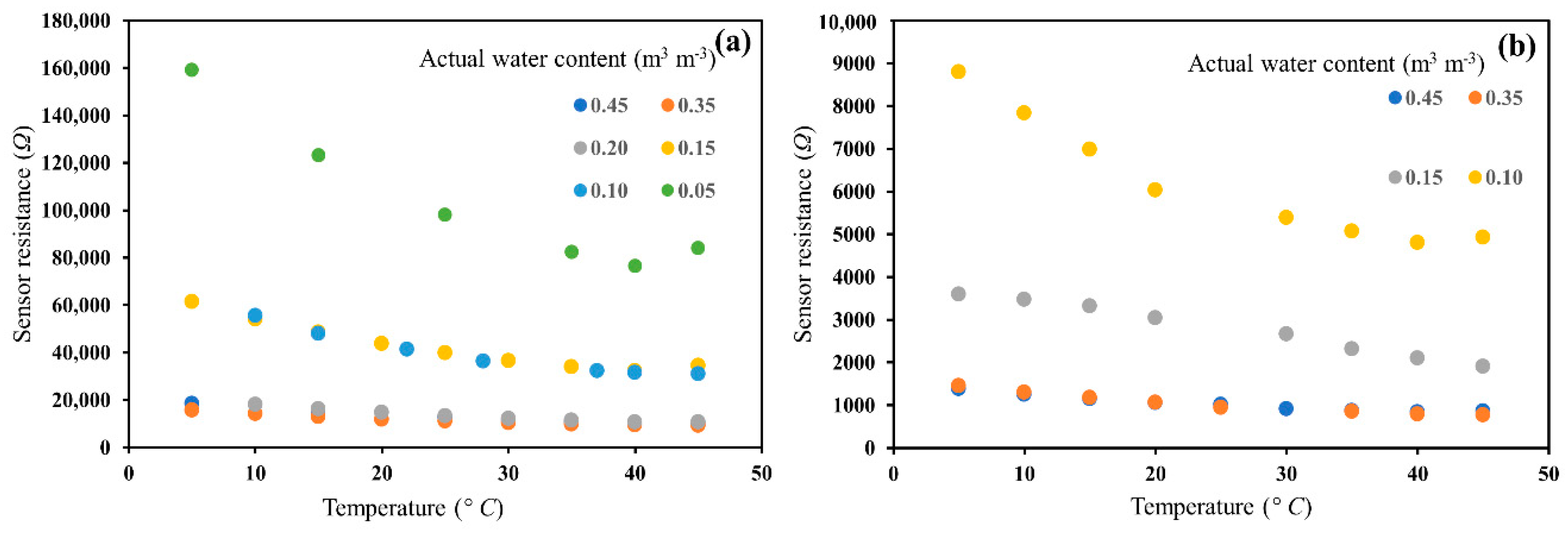
3.3. Temperature Effect on Sensor Water Content Measurements
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Lara, A.; Longchamps, L.; Khosla, R. Soil water content and high-resolution imagery for precision irrigation: Maize yield. Agronomy 2019, 9, 174. [Google Scholar] [CrossRef]
- Kisekka, I.; Migliaccio, K.W.; Muñoz-Carpena, R.; Schaffer, B.; Khare, Y. Modelling soil water dynamics considering measurement uncertainty. Hydrol. Process. 2015, 29, 692–711. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Oberdörster, C.; Vereecken, H. Evaluation of a low-cost soil water content sensor for wireless network applications. J. Hydrol. 2007, 344, 32–42. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil Moisture Measurement for Ecological and Hydrological Watershed-Scale Observatories: A Review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Castillo, V.M.; Gómez-Plaza, A.; Martínez-Mena, M. The role of antecedent soil water content in the runoff response of semiarid catchments: A simulation approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.; Li, C.; Wang, H.; Liu, J.; Mu, W. Investigation of rainfall-runoff processes and soil moisture dynamics in grassland plots under simulated rainfall conditions. Water 2014, 6, 2671–2689. [Google Scholar] [CrossRef]
- Kendy, E.; Gérard-Marchant, P.; Walter, M.T.; Zhang, Y.; Liu, C.; Steenhuis, T.S. A soil-water-balance approach to quantify groundwater recharge from irrigated cropland in the North China Plain. Hydrol. Process. 2003, 7, 2011–2031. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. Evaluation of three complementary relationship evapotranspiration models by water balance approach to estimate actual regional evapotranspiration in different climatic regions. J. Hydrol. 2005, 308, 105–121. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Change 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Granier, A.; Reichstein, M.; Bréda, N.; Janssens, I.A.; Falge, E.; Ciais, P.; Grünwald, T.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; et al. Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agric. For. Meteorol. 2007, 143, 123–145. [Google Scholar] [CrossRef]
- Yunus, I.S.; Harwin; Kurniawan, A.; Adityawarman, D.; Indarto, A. Nanotechnologies in water and air pollution treatment. Environ. Technol. Rev. 2012, 1, 136–148. [Google Scholar] [CrossRef]
- Bristow, K.L.; Campbell, G.S.; Calissendorff, K. Test of a Heat-Pulse Probe for Measuring Changes in Soil Water Content. Soil Sci. Soc. Am. J. 1993, 57, 930–934. [Google Scholar] [CrossRef]
- Mori, Y.; Hopmans, J.W.; Mortensen, A.P.; Kluitenberg, G.J. Multi-Functional Heat Pulse Probe for the Simultaneous Measurement of Soil Water Content, Solute Concentration, and Heat Transport Parameters. Vadose Zone J. 2003, 2, 561–571. [Google Scholar] [CrossRef]
- Rowlandson, T.L.; Berg, A.A.; Bullock, P.R.; Ojo, E.R.T.; McNairn, H.; Wiseman, G.; Cosh, M.H. Evaluation of several calibration procedures for a portable soil moisture sensor. J. Hydrol. 2013, 498, 335–344. [Google Scholar] [CrossRef]
- Kowalsky, M.B.; Finsterle, S.; Peterson, J.; Hubbard, S.; Rubin, Y.; Majer, E.; Ward, A.; Gee, G. Estimation of field-scale soil hydraulic and dielectric parameters through joint inversion of GPR and hydrological data. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Reynolds, S.G. The gravimetric method of soil moisture determination Part I A study of equipment, and methodological problems. J. Hydrol. 1970, 11, 258–273. [Google Scholar] [CrossRef]
- Peddinti, S.R.; Kambhammettu, B.V.N.P.; Ranjan, S.; Suradhaniwar, S.; Badnakhe, M.R.; Adinarayana, J.; Gade, R.M. Modeling Soil-Water-Disease Interactions of Flood-Irrigated Mandarin Orange Trees: Role of Root Distribution Parameters. Vadose Zone J. 2018, 17, 1–13. [Google Scholar] [CrossRef]
- Huth, N.I.; Poulton, P.L. An electromagnetic induction method for monitoring variation in soil moisture in agroforestry systems. Aust. J. Soil Res. 2007, 45, 63–72. [Google Scholar] [CrossRef]
- Klotzsche, A.; Lärm, L.; Vanderborght, J.; Cai, G.; Morandage, S.; Zörner, M.; Vereecken, H.; Kruk, J. Monitoring Soil Water Content Using Time-Lapse Horizontal Borehole GPR Data at the Field-Plot Scale. Vadose Zone J. 2019, 18, 190044. [Google Scholar] [CrossRef]
- Adla, S.; Rai, N.K.; Karumanchi, S.H.; Tripathi, S.; Disse, M.; Pande, S. Laboratory calibration and performance evaluation of low-cost capacitive and very low-cost resistive soil moisture sensors. Sensors 2020, 20, 363. [Google Scholar] [CrossRef] [PubMed]
- Bogena, H.R.; Bol, R.; Borchard, N.; Brüggemann, N.; Diekkrüger, B.; Drüe, C.; Groh, J.; Gottselig, N.; Huisman, J.A.; Lücke, A.; et al. A terrestrial observatory approach to the integrated investigation of the effects of deforestation on water, energy, and matter fluxes. Sci. China Earth Sci. 2015, 58, 61–75. [Google Scholar] [CrossRef]
- Kizito, F.; Campbell, C.S.; Campbell, G.S.; Cobos, D.R.; Teare, B.L.; Carter, B.; Hopmans, J.W. Frequency, electrical conductivity and temperature analysis of a low-cost capacitance soil moisture sensor. J. Hydrol. 2008, 352, 367–378. [Google Scholar] [CrossRef]
- Bogena, H.R.; Huisman, J.A.; Schilling, B.; Weuthen, A.; Vereecken, H. Effective calibration of low-cost soil water content sensors. Sensors 2017, 17, 208. [Google Scholar] [CrossRef]
- Ruys, J.; Zanen, E.; Roethof, D.; Boedhoe, R. Measuring Probe for Measuring in Ground a Parameter and a Method for Making Such a Probe. Sensoterra Bv, 2020. U.S. Patent Application No. 16/472,599, 14 May 2020. [Google Scholar]
- Peddinti, S.R.; Kisekka, I.; Hopmans, J.W. Soil Specific Sensoterra Soil Moisture Sensor Calibration; Febuary 2020 Report; University of California Davis: Davis, CA, USA, 2020. [Google Scholar]
- Peddinti, S.R.; Kisekka, I.; Hopmans, J.W. Soil Specific Sensoterra Soil Moisture Sensor Calibration; May 2020 Report; University of California Davis: Davis, CA, USA, 2020. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Al-Shammary, A.A.G.; Kouzani, A.Z.; Kaynak, A.; Khoo, S.Y.; Norton, M.; Gates, W. Soil Bulk Density Estimation Methods: A Review. Pedosphere 2018, 28, 581–596. [Google Scholar] [CrossRef]
- Casanova, M.; Tapia, E.; Seguel, O.; Salazar, O. Direct measurement and prediction of bulk density on alluvial soils of central Chile. Chil. J. Agric. Res. 2016, 76, 105–113. [Google Scholar] [CrossRef]
- Fares, A.; Safeeq, M.; Awal, R.; Fares, S.; Dogan, A. Temperature and Probe-to-Probe Variability Effects on the Performance of Capacitance Soil Moisture Sensors in an Oxisol. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Rhoades, J.D.; Raats, P.A.C.; Prather, R.J. Effects of Liquid-phase Electrical Conductivity, Water Content, and Surface Conductivity on Bulk Soil Electrical Conductivity. Soil Sci. Soc. Am. J. 1976, 40, 651–655. [Google Scholar] [CrossRef]
- Tuli, A.; Hopmans, J.W. Effect of degree of fluid saturation on transport coefficients in disturbed soils. Eur. J. Soil Sci. 2004, 55, 147–164. [Google Scholar] [CrossRef]
- Saito, T.; Fujimaki, H.; Yasuda, H.; Inoue, M. Empirical Temperature Calibration of Capacitance Probes to Measure Soil Water. Soil Sci. Soc. Am. J. 2009, 73, 1931–1937. [Google Scholar] [CrossRef]
- Rosenbaum, U.; Huisman, J.A.; Weuthen, A.; Vereecken, H.; Bogena, H.R. Sensor-to-Sensor Variability of the ECHO EC-5, TE, and 5TE Sensors in Dielectric Liquids. Vadose Zone J. 2010, 9, 181. [Google Scholar] [CrossRef]
- Peddinti, S.R.; Kisekka, I.; Hopmans, J.W. Soil Specific Sensoterra Soil Moisture Sensor Calibration; August 2020 Report; University of California Davis: Davis, CA, USA, 2020. [Google Scholar]
- Zhang, N.; Fan, G.; Lee, K.H.; Kluitenberg, G.J.; Loughin, T.M. Simultaneous Measurement of Soil Water Content and Salinity Using a Frequency-Response Method. Soil Sci. Soc. Am. J. 2004, 68, 1515–1525. [Google Scholar] [CrossRef]
- Szerement, J.; Saito, H.; Furuhata, K.; Yagihara, S.; Szyplowska, A.; Lewandowski, A.; Kafarski, M.; Wilczek, A.; Majcher, J.; Woszczyk, A.; et al. Dielectric properties of glass beads with talc as a reference material for calibration and verification of dielectric methods and devices for measuring soil moisture. Materials 2020, 13, 1968. [Google Scholar] [CrossRef] [PubMed]
- Hendrickx, J.M.H.; Wraith, J.M.; Corwin, D.L.; Kachanoski, R.G. Solute Content and Concentration. In Methods of Soil Analysis, Part 4: Physical Methods; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America: Madison, WI, USA, 2002; pp. 1253–1322. [Google Scholar]


| Soil | Sand | Silt | Clay | ECw | Dry Bulk Density |
|---|---|---|---|---|---|
| % | dS/m | (g/cm3) | |||
| Glass beads | 100 | 0 | 0 | 0 | 1.31 ± 0.02 |
| Oso Flaco sand | 100 | 0 | 0 | 0 | 1.35 ± 0.01 |
| Columbia silt loam | 54 | 30.9 | 15.1 | 0.41 | 1.25 ± 0.02 |
| Yolo clay loam | 32.4 | 36.8 | 30.8 | 0.48 | 1.26 ± 0.02 |
| Glass Beads | Oso Flaco Sand | ||||||||
| θ/EC | 0.45 | 0.35 | 0.25 | 0.1 | θ/EC | 0.45 | 0.35 | 0.25 | 0.1 |
| 0 | 4.9 | 12.4 | 10.9 | 8.5 | 0.5 | 2.2 | 1.3 | 3.5 | 0.4 |
| 0.5 | 8 | 2.5 | 15.2 | 8.8 | 1 | 2.1 | 1.2 | 7.4 | 3.9 |
| 1 | 1.4 | 7.9 | 6.4 | 12 | 1.5 | 2.7 | 0.9 | 3.7 | 5.4 |
| 2 | 2.9 | 3.9 | 14.2 | 32.1 | 2 | 2.1 | 1.7 | 5.9 | 6.5 |
| 5 | 8.4 | 6.2 | 18.5 | 9.8 | 3 | 4 | 1.4 | 5.5 | 2.2 |
| 10 | 14 | 24.2 | 18.1 | 11.8 | 4 | 1 | 3.7 | 4.4 | 4 |
| Columbia Loam | Yolo Clay Loam | ||||||||
| θ/EC | 0.45 | 0.35 | 0.2 | 0.1 | θ/EC | 0.45 | 0.35 | 0.2 | 0.1 |
| 0.5 | 3.81 | 2.27 | 6.27 | 7.31 | 0.5 | 3.09 | 1.77 | 6.32 | 7.21 |
| 1 | 2.54 | 3.61 | 6.08 | 7.59 | 1 | 2.59 | 3.14 | 4.39 | 4.48 |
| 1.5 | 4.34 | 3.68 | 10.57 | 8.06 | 1.5 | 1.22 | 3.85 | 8.05 | 3.28 |
| 2 | 5.45 | 6.31 | 10.07 | 10.22 | 2 | 3.08 | 3.19 | 6.73 | 7.73 |
| 3 | 3.75 | 3.34 | 9.04 | 8.11 | 3 | 1.99 | 1.86 | 4.22 | 6.79 |
| 4 | 4.18 | 2.87 | 6.24 | 7.61 | 4 | 4.83 | 2.61 | 2.92 | 4.67 |
| Source | Sum of Squares | df | Mean Square | F Value | p-Value | F Crit |
|---|---|---|---|---|---|---|
| Glass beads | 73,879,231.21 | 15 | 4,925,282.08 | 128.089 | 0.000001 | 1.67915 |
| Oso Flaco | 18,616,279.45 | 15 | 1,329,734.24 | 600.183 | 0.0000001 | 1.70552 |
| Soil | b0 | b1 | R2 | RMSE |
|---|---|---|---|---|
| Glass beads | 0.081 | 0.543 | 0.25 | 0.124 |
| Oso Flaco sand | 0.022 | 0.781 | 0.65 | 0.091 |
| Columbia silt loam | 0.138 | 0.608 | 0.68 | 0.082 |
| Yolo clay loam | 0.017 | 1.053 | 0.89 | 0.058 |
| Soil | Regression Coefficients (dS/m) | RMSE (dS/m) | |||
|---|---|---|---|---|---|
| R2 | |||||
| Glass beads | 0.89 | 0.15 | - | 0.96 | 0.051 |
| Oso Flaco sand | 1.52 | 0.06 | - | 0.97 | 0.063 |
| Columbia silt loam | 1.54 | 0.06 | 0.13 | 0.94 | 0.071 |
| Yolo clay loam | 0.56 | 0.64 | 0.22 | 0.90 | 0.121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peddinti, S.R.; Hopmans, J.W.; Abou Najm, M.; Kisekka, I. Assessing Effects of Salinity on the Performance of a Low-Cost Wireless Soil Water Sensor. Sensors 2020, 20, 7041. https://doi.org/10.3390/s20247041
Peddinti SR, Hopmans JW, Abou Najm M, Kisekka I. Assessing Effects of Salinity on the Performance of a Low-Cost Wireless Soil Water Sensor. Sensors. 2020; 20(24):7041. https://doi.org/10.3390/s20247041
Chicago/Turabian StylePeddinti, Srinivasa Rao, Jan W. Hopmans, Majdi Abou Najm, and Isaya Kisekka. 2020. "Assessing Effects of Salinity on the Performance of a Low-Cost Wireless Soil Water Sensor" Sensors 20, no. 24: 7041. https://doi.org/10.3390/s20247041
APA StylePeddinti, S. R., Hopmans, J. W., Abou Najm, M., & Kisekka, I. (2020). Assessing Effects of Salinity on the Performance of a Low-Cost Wireless Soil Water Sensor. Sensors, 20(24), 7041. https://doi.org/10.3390/s20247041







