Magnetic Position System Design Method Applied to Three-Axis Joystick Motion Tracking
Abstract
1. Introduction
2. Methods
2.1. General Formalism
- the observables of interest , where P is the parameter space of interest. Typical observables can be the lever position in a gear shift or the tilt angle of a joystick. The parameter space P then simply corresponds to the allowed range of mechanical motion.
- the system design parameters describe a specific MPO system implementation attempting to realize . The system parameters include all quantities that can be varied within an allowed system parameter space S in a design process. They include magnet and sensor choice and placement within the system, component geometries, or material parameters. The parameter range S can be for instance the result of limited construction space.
- the sensor outputs that correspond to single or multiple components of the magnetic field at the sensor positions. Although linear sensing technology is considered in this work, the formalism can be easily extended to include arbitrary sensor transfer functions. Hereafter, the sensor output and the magnetic field will be treated the same, and therefore, will simply denote the set of all possible sensor outputs.
- a set of constraints that must be fulfilled in the design process. They can for example describe weighted sensing resolutions, maximal cost limitations, or the influence of system fabrication tolerances and external stray fields.
2.2. Field Shaping and Shape Variation
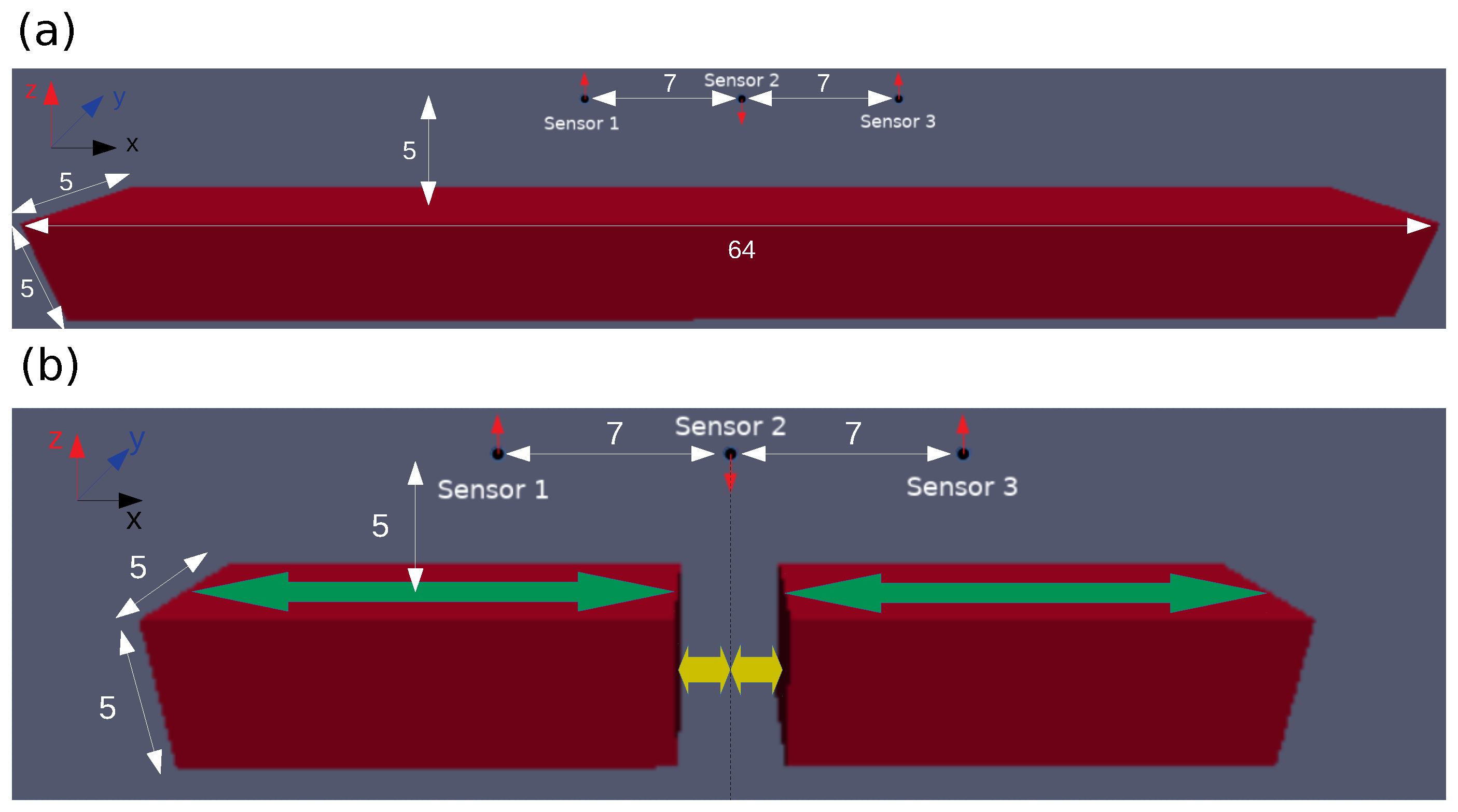
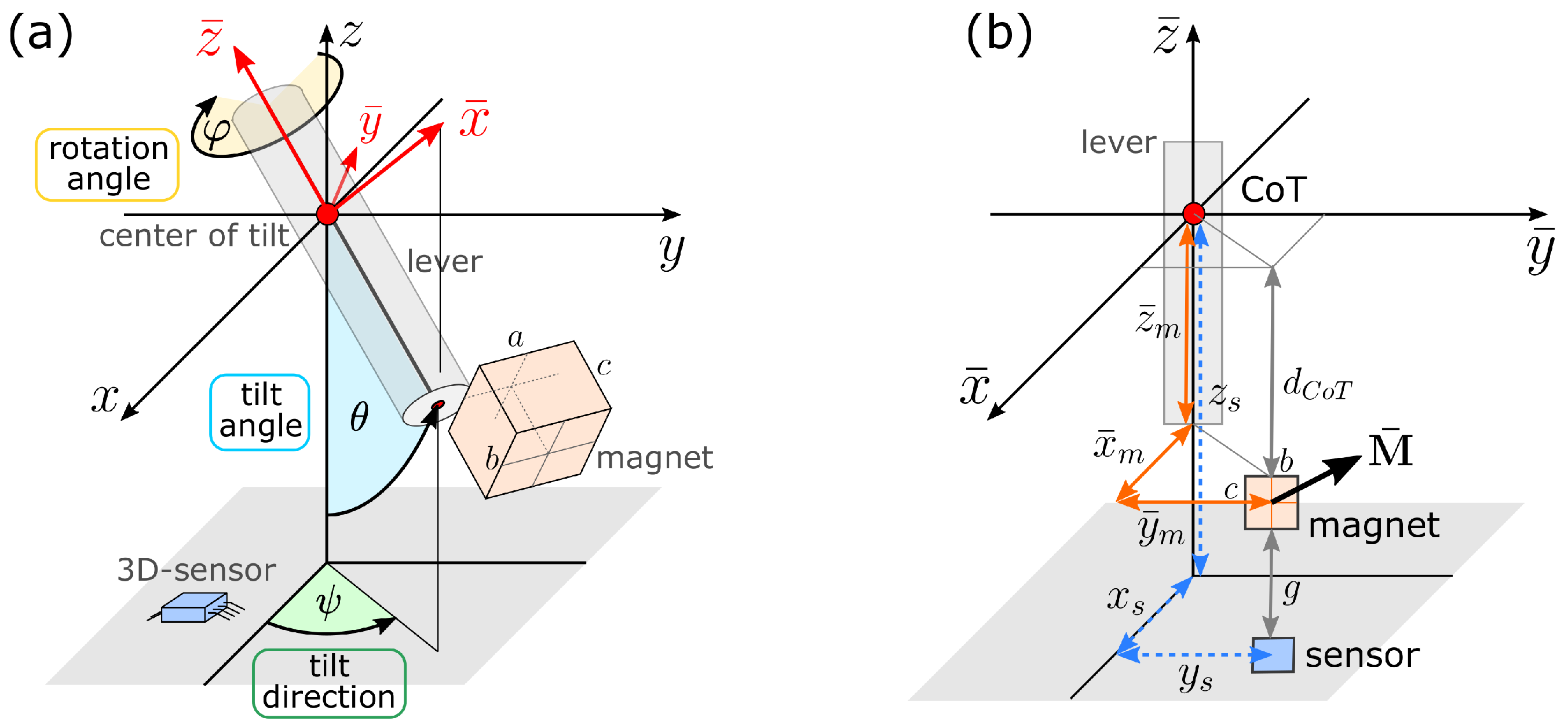
2.3. The Three-Axis Joystick System
- the position of a 3D magnetic field sensor . The sensor output is the magnetic field vector .
- the magnet position in the LCS. The lengths and indicate lateral displacement of the magnet from the lever axis, while is the distance of the magnet from the center of tilt.
- the magnet magnetization vector defined in the LCS, assuming uniform magnetization.
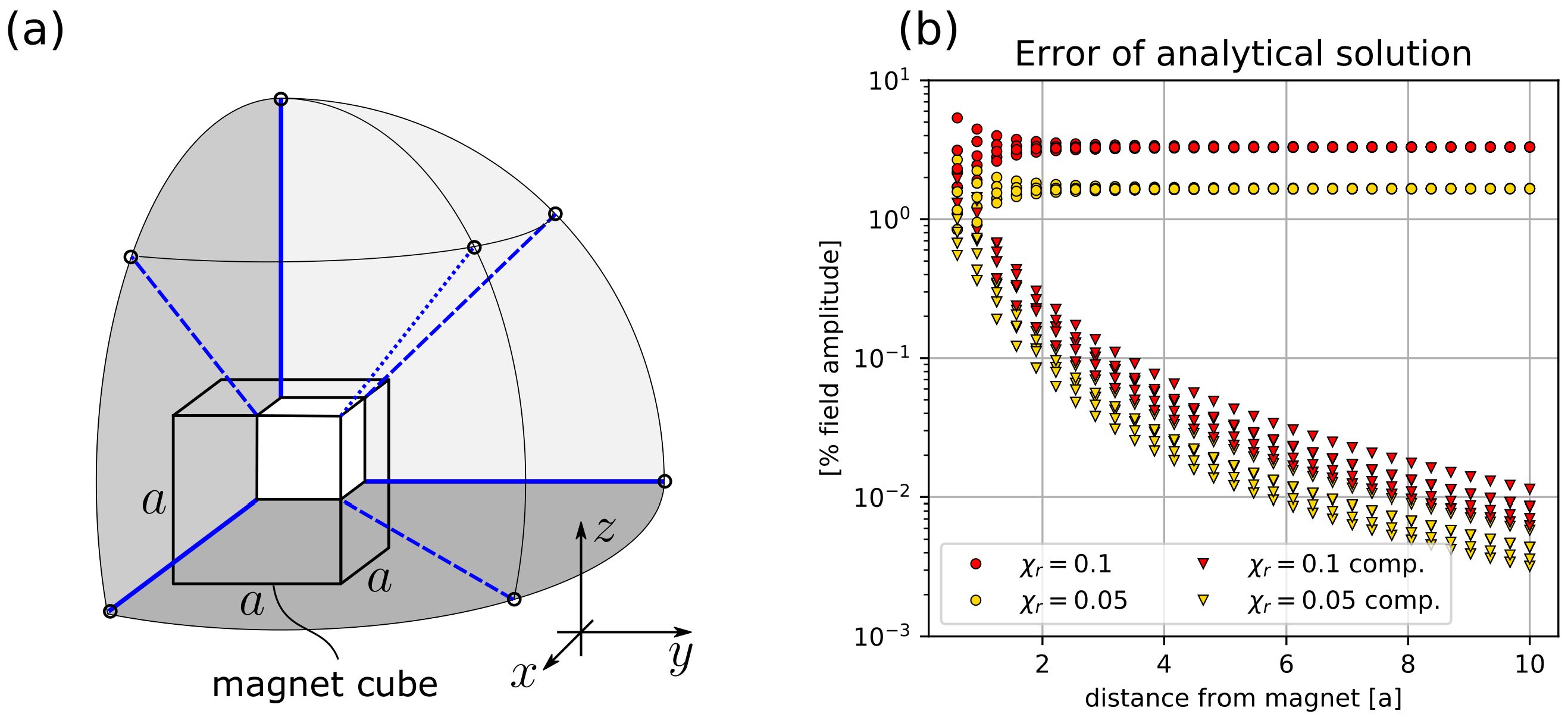
- the size of the magnet given by its side lengths , considering a cuboid magnet shape with orientation in the LCS. The cuboid magnet shape is chosen for computational reasons; see Section 2.4.
2.4. Magnetic Field Computation
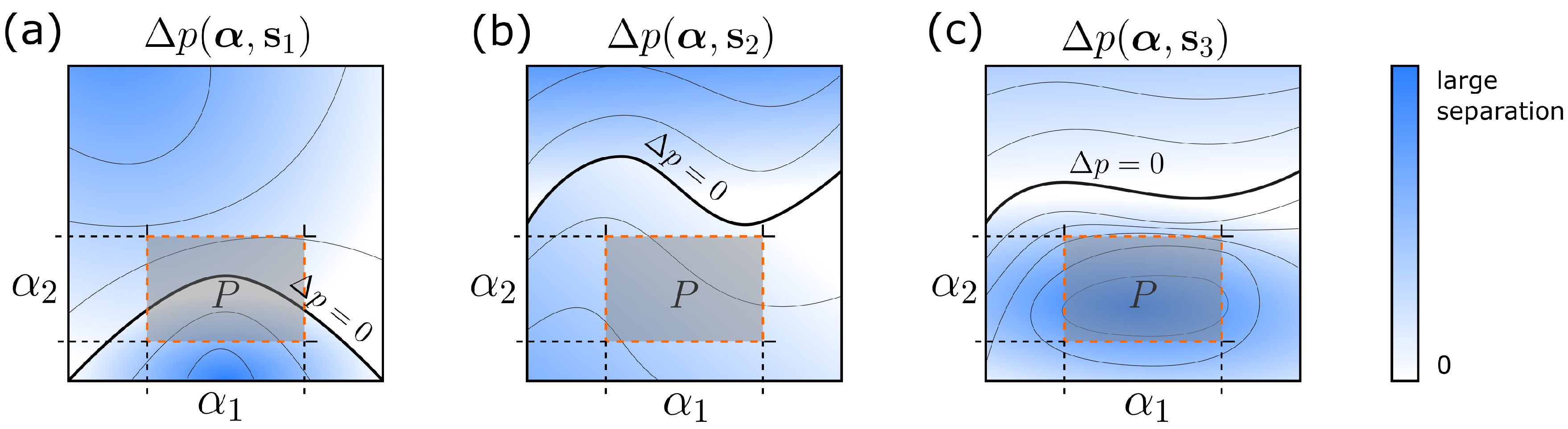
2.5. Optimization Algorithm
3. Results
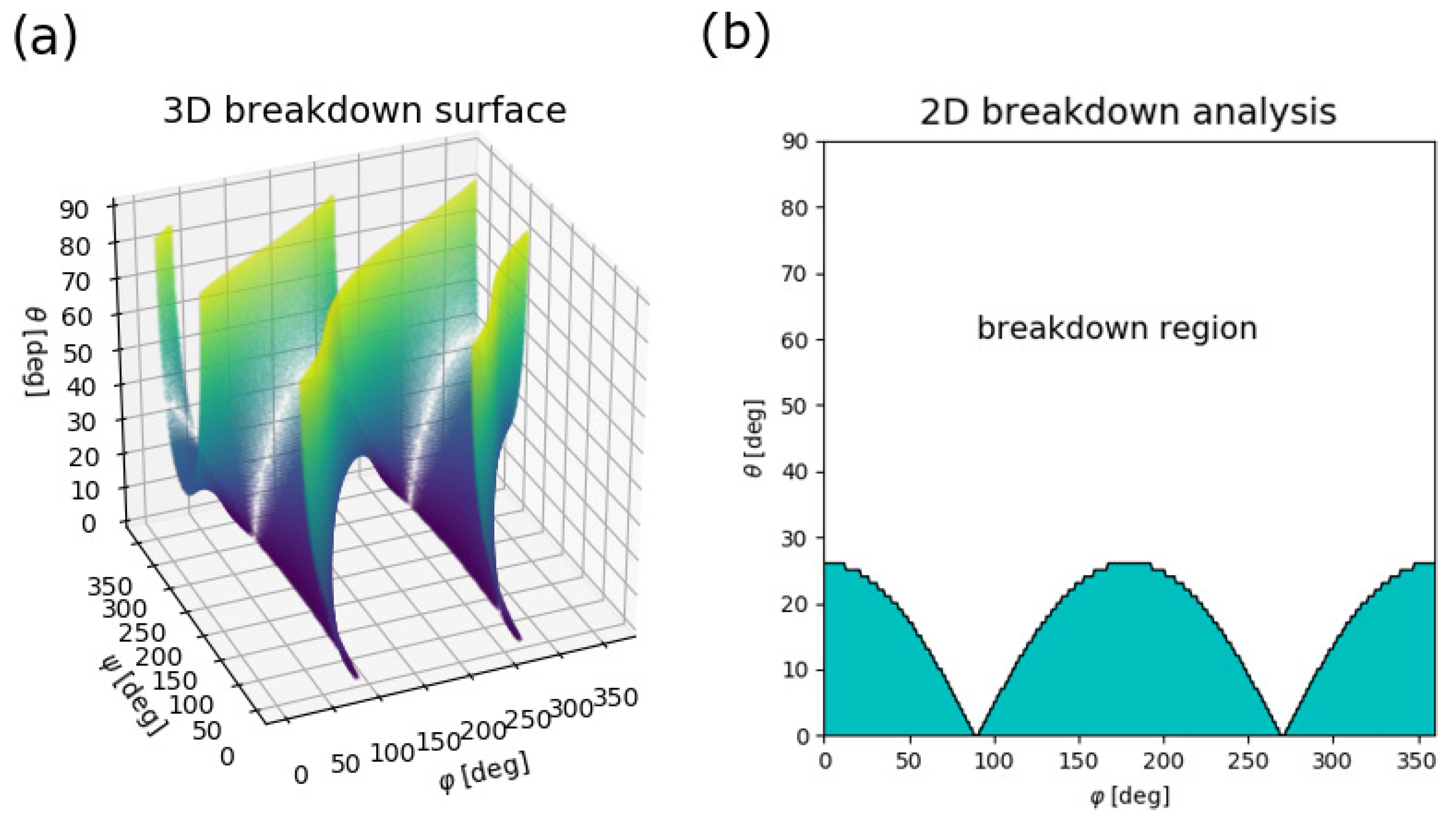
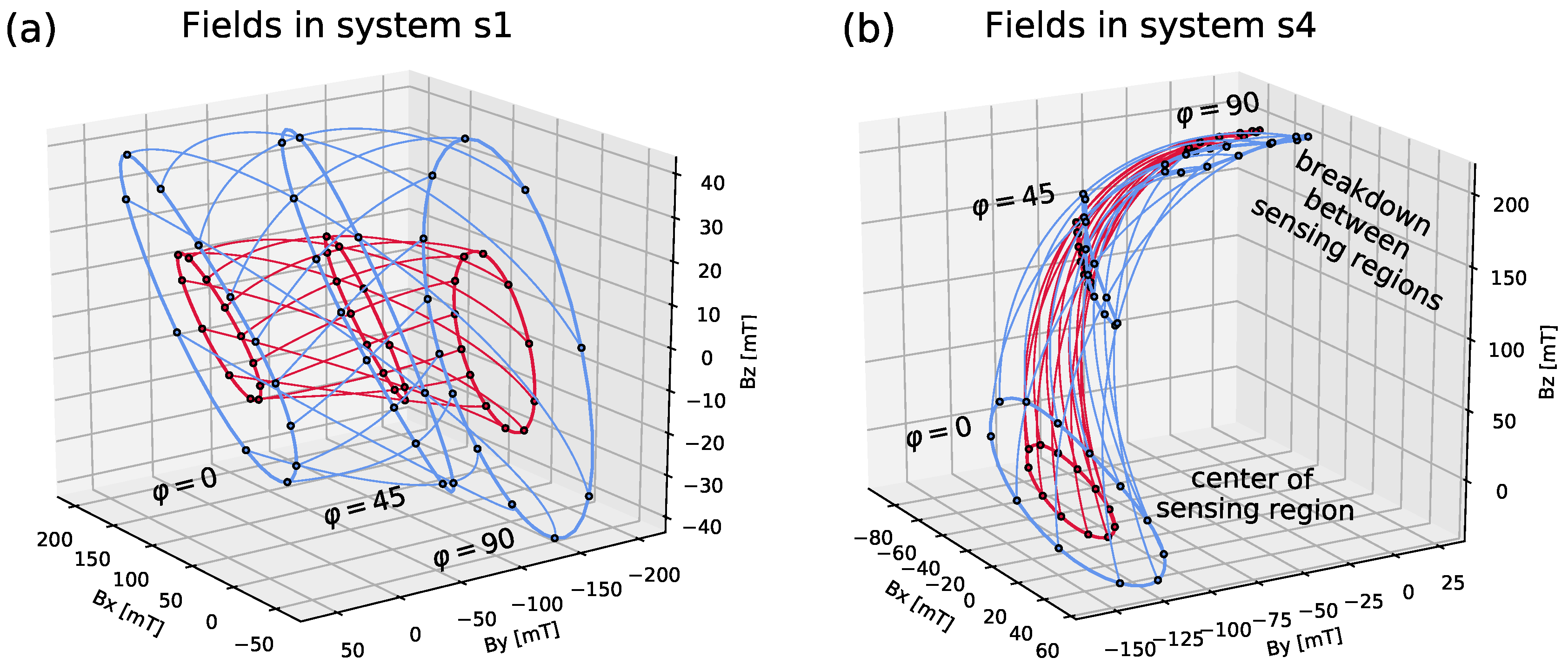
3.1. Feasibility Analysis
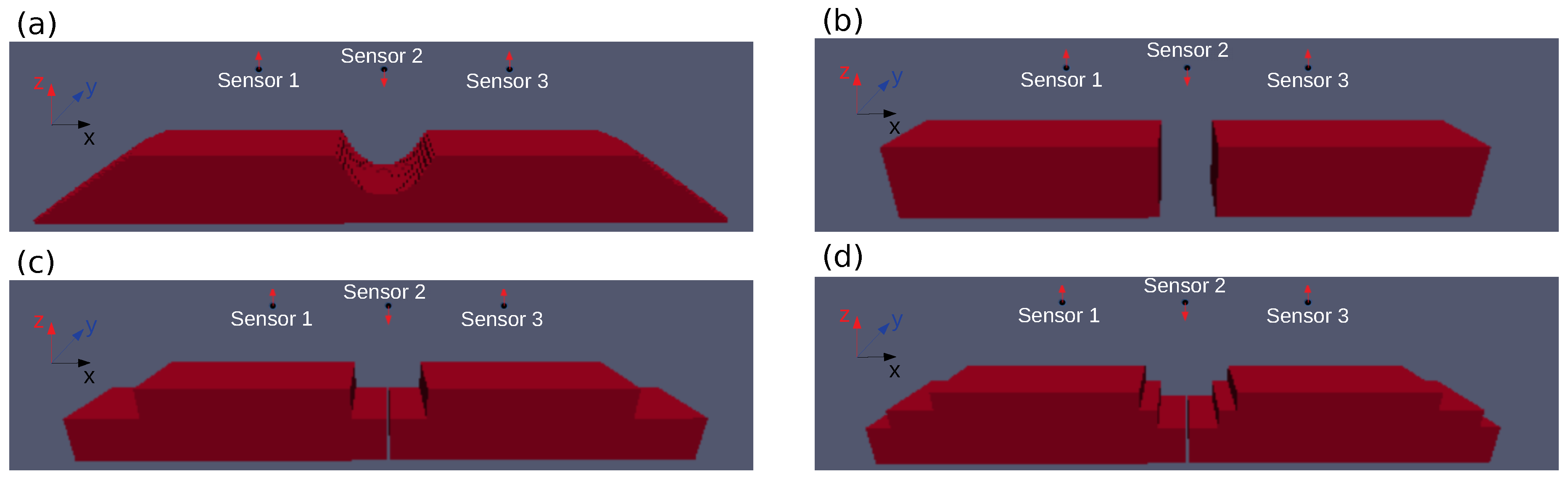
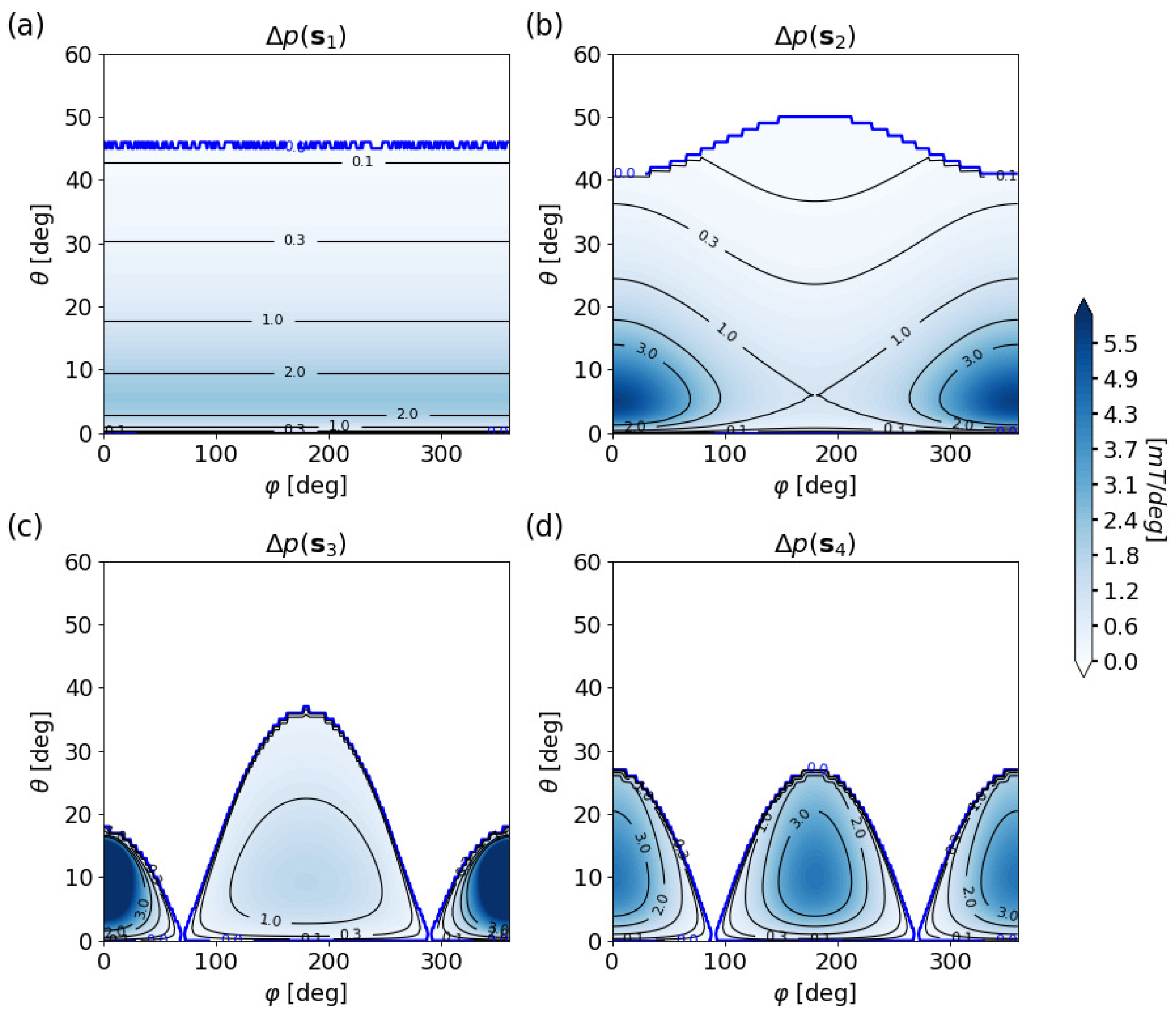
- system type sensor in the center, magnet displaced (),
- system type sensor and magnet displaced, magnet further out (),
- system type sensor and magnet displaced, sensor further out (),
- system type magnet in center, sensor displaced ().
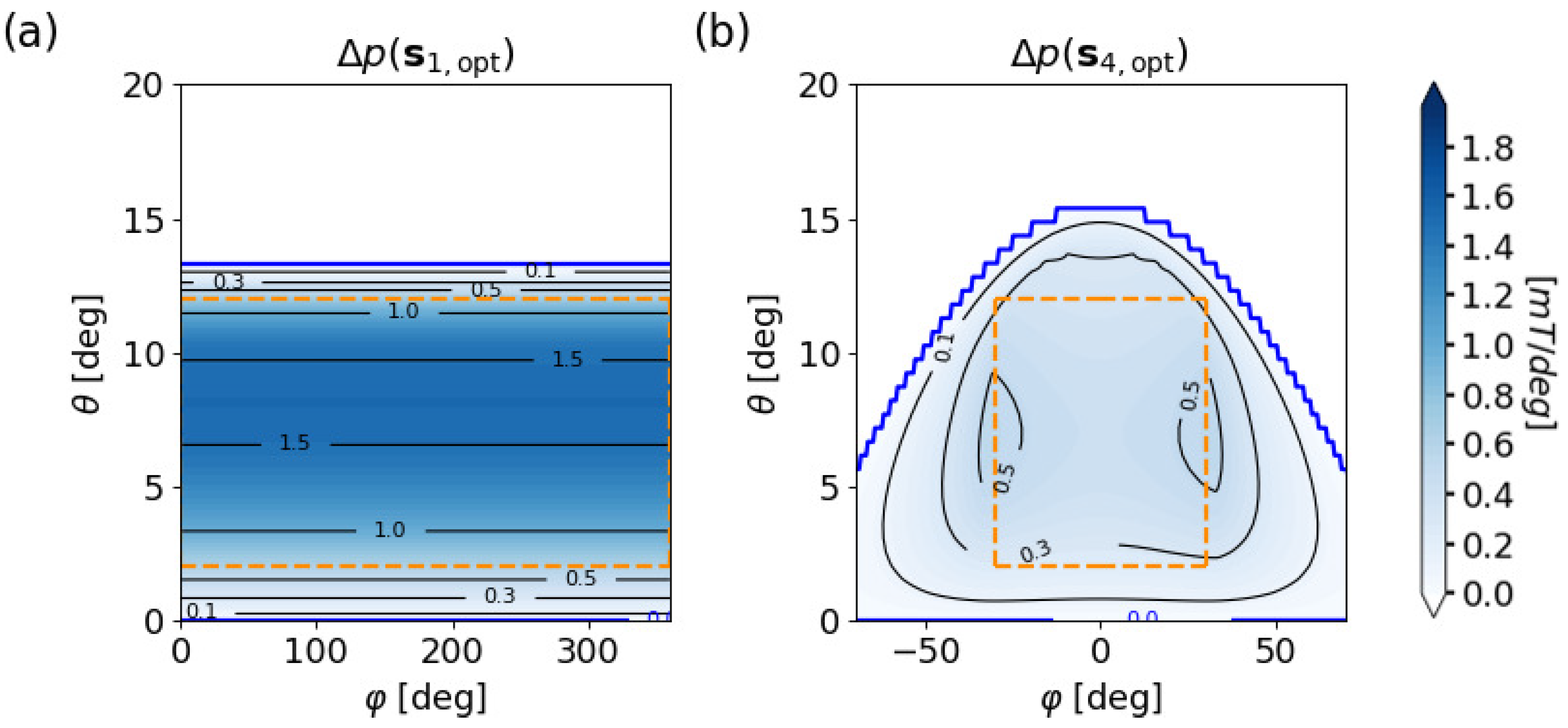
3.2. Quality Analysis
3.3. Optimized Systems with Cuboid Magnets
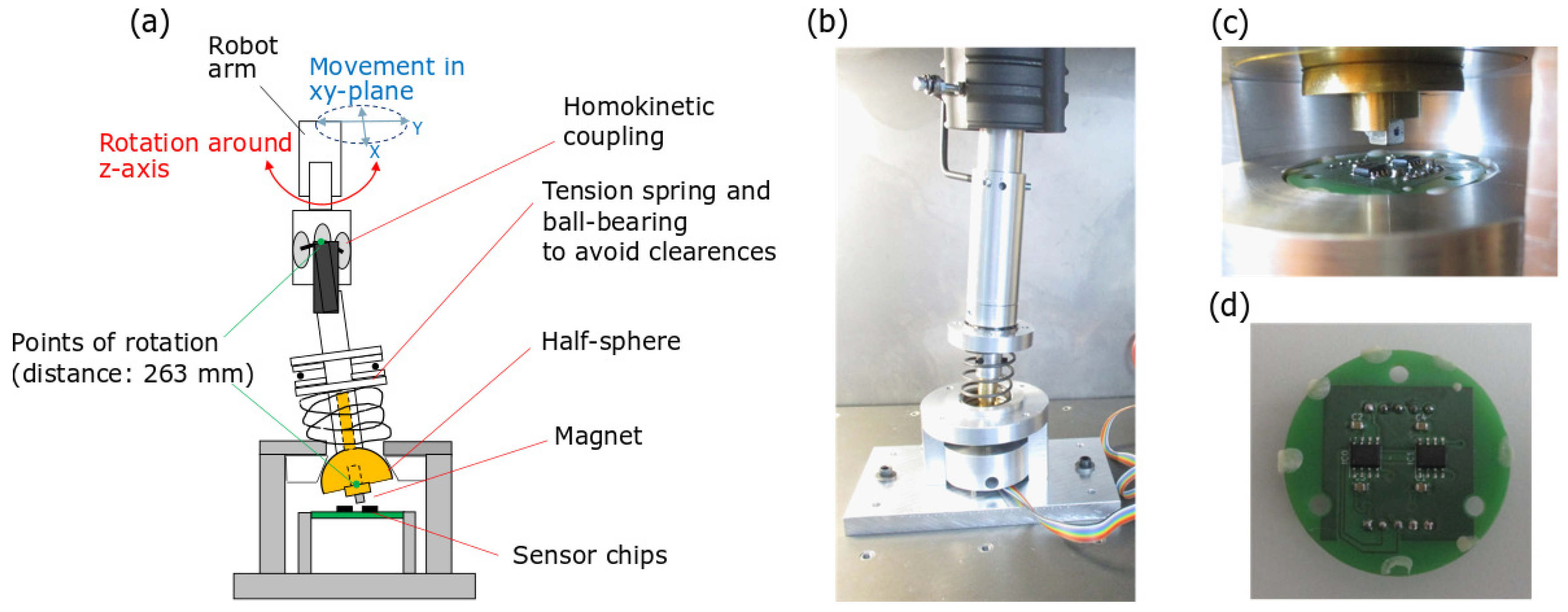
3.4. Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MPO | Magnetic position and orientation |
| DoF | Degree(s) of freedom |
| ABS | Anti-lock braking system |
| CCTV | Closed-circuit television |
| DOS | Density of states |
| LCS | Local coordinate system |
| FE | Finite element |
| DE | Differential evolution |
| PCB | Printed circuit board |
Appendix A. Connectedness Requirement
Appendix B. Field Shaping with Topology Optimization (Adjoint Method) and Shape Variation
| Layers | DoF | Deviation from [%] |
|---|---|---|
| 1 | 2 | 3.35 |
| 2 | 5 | 0.79 |
| 3 | 8 | 0.49 |
| Topology Optimization | Shape Variation | |
|---|---|---|
| number DoF | large | small |
| optimization algorithm | gradient based (local) | function evaluation based (global) |
| quality factor | requires derivation | requires fast evaluation |
| optimum (magnet shape) | very accurate, but possibly local | inaccurate, depending on choice of DoF |
| optimum (magnetic field) | very accurate, but possibly local | possibly very accurate, depending on DoF choice |
| application case | theoretical optimum solutions | good practical solutions |
Appendix C. Computation of the Rotation Matrix
Appendix D. Magpylib Code

Appendix E. Demagnetization
References
- Treutler, C. Magnetic sensors for automotive applications. Sens. Actuators Phys. 2001, 91, 2–6. [Google Scholar] [CrossRef]
- Granig, W.; Hartmann, S.; Köppl, B. Performance and technology comparison of GMR versus commonly used angle sensor principles for automotive applications. SAE Trans. 2007, 116, 29–41. [Google Scholar]
- Ortner, M.; Ribeiro, M.; Spitzer, D. Absolute Long-Range Linear Position System With a Single 3-D Magnetic Field Sensor. IEEE Trans. Magn. 2018, 55, 1–4. [Google Scholar] [CrossRef]
- Hohe, H.; Sauerer, J. Robuste Positionsmessung in Hydraulik-und Pneumatikzylindern. Mechatronik 2008, 11, 60–63. [Google Scholar]
- Ausserlechner, U. Magnetic Angle Sensors. In Magnetic Sensors and Devices: Technologies and Applications; CRC Press: Boca Raton, FL, USA, 2017; p. 201. [Google Scholar]
- Huber, S.; Burssens, J.W.; Dupré, N.; Dubrulle, O.; Bidaux, Y.; Close, G.; Schott, C. A gradiometric magnetic sensor system for stray-field-immune rotary position sensing in harsh environment. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 809. [Google Scholar] [CrossRef]
- Bandorf, R.; Ortner, K.; Krau, M. PVD-Abscheidung von CoSm-Schichten für magnetische Maßstäbe: Hohlkathoden-Gasfluss-Sputtern (GFS) für hochwertige Hartmagnetschichten. Vak. Forsch. Und Prax. 2020, 32, 28–32. [Google Scholar] [CrossRef]
- Cichon, D.; Psiuk, R.; Brauer, H.; Töpfer, H. A Hall-sensor-based localization method with six degrees of freedom using unscented Kalman filter. IEEE Sens. J. 2019, 19, 2509–2516. [Google Scholar] [CrossRef]
- Popek, K.M.; Schmid, T.; Abbott, J.J. Six-degree-of-freedom localization of an untethered magnetic capsule using a single rotating magnetic dipole. IEEE Robot. Autom. Lett. 2016, 2, 305–312. [Google Scholar] [CrossRef]
- Infineon Technologies AG, “XENSIV—Sensing the world”, Product catalog, B142-I0675-V2-7600-EU-EC-P. 2020. Available online: https://www.infineon.com/dgdl/Infineon-SensorSelectionGuide-ProductSelectionGuide-v01_00-EN.pdf?fileId=5546d462636cc8fb0164229c09f51bbe (accessed on 30 November 2020).
- Suchy, J.; Paces, P. BMW iDrive automotive hid device in EFIS control. In Proceedings of the 2014 IEEE/AIAA 33rd Digital Avionics Systems Conference (DASC), Colorado Springs, CO, USA, 5–9 October 2014; p. 2D3-1. [Google Scholar]
- Danfoss-Heavy-Duty Joysticks. Available online: https://www.danfoss.com/en-us/products/electronic-controls/dps/plus1-joysticks-and-pedals/plus1-joysticks/js1-h/#tab-overview (accessed on 30 November 2020).
- ZF Products for Marine Propulsion Systems—Joystick Maneuvering System. Available online: https://www.zf.com/products/en/marine/products_29109.html#products_anchor_link_c0150d0cc891-3713-b6e7-018d91295758 (accessed on 30 November 2020).
- Volvo Penta—Easy Boat Maneuvering. Available online: https://www.volvopenta.com/marine/products/easy-boating-solutions/maneuvering/ (accessed on 30 November 2020).
- Megatron Precision for Your Design—Joysticks for Industrial and Medical Applications. Available online: https://www.megatron.de/en/category/joysticks.html (accessed on 30 November 2020).
- Sidestick Airbus Edition. Available online: https://www.thrustmaster.com/en_US/products/tcasidestick-airbus-edition (accessed on 30 November 2020).
- Arcade Xpress—Mag-Stick. Available online: https://www.arcadexpress.com/en/arcade-joysticks/90-396-joystick-magnetico-industrias-lorenzo.html (accessed on 30 November 2020).
- Lemken—Joystick Box. Available online: https://lemken.com/en/iqblue/implement-control/auxiliaries/ (accessed on 30 November 2020).
- Ermakova, A.; Ribeiro, M.; Spitzer, D.; Ortner, M. Analytical Development of a Four-Axis Magnetic Multimedia Control Element. IEEE Sens. J. 2018, 18, 7819–7825. [Google Scholar] [CrossRef]
- Ortner, M. Magnetic Multimedia Control Element. US Patent 10,048,091, 14 August 2018. [Google Scholar]
- Lumetti, S.; Malagò, P.; Spitzer, D.; Ortner, M. Computationally efficient calibration of a magnetic position system. Eng. Proc. 2020, 1, 5. [Google Scholar]
- Infineon TLV493D-A1B6 3D Magnetic Sensor Datasheet. Available online: https://www.infineon.com/dgdl/Infineon-TLV493D-A1B6-DataSheet-v01_10-EN.pdf?fileId=5546d462525dbac40152a6b85c760e80 (accessed on 30 November 2020).
- Perlepe, P.; Oyarzabal, I.; Mailman, A.; Yquel, M.; Platunov, M.; Dovgaliuk, I.; Rouzières, M.; Négrier, P.; Mondieig, D.; Suturina, E.A.; et al. Metal-organic magnets with large coercivity and ordering temperatures up to 242 °C. Science 2020, 370, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Bruckner, F.; Abert, C.; Wautischer, G.; Huber, C.; Vogler, C.; Hinze, M.; Suess, D. Solving large-scale inverse magnetostatic problems using the adjoint method. Sci. Rep. 2017, 7, 40816. [Google Scholar] [CrossRef] [PubMed]
- Balaban, A.L.; Bakhvalov, Y.A.; Denisov, P.A. Review of methods for solving inverse problems in identifying permanent magnets of executive elements in dynamic devices. MATEC Web Conf. 2018, 226, 04022. [Google Scholar] [CrossRef][Green Version]
- Ortner, M. Improving magnetic linear position measurement by field shaping. In Proceedings of the 2015 9th International Conference on Sensing Technology (ICST), Auckland, New Zealand, 8–10 December 2015; pp. 359–364. [Google Scholar]
- Ortner, M.; Huber, C.; Vollert, N.; Pilz, J.; Süss, D. Application of 3D-printed magnets for magnetic position detection systems. In Proceedings of the 2017 IEEE Sensors, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Huber, C.; Abert, C.; Bruckner, F.; Groenefeld, M.; Schuschnigg, S.; Teliban, I.; Vogler, C.; Wautischer, G.; Windl, R.; Suess, D. 3D printing of polymer-bonded rare-earth magnets with a variable magnetic compound fraction for a predefined stray field. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- Gordon, W.B. On the Diffeomorphisms of Euclidean Space. Am. Math. Mon. 1972, 79, 755–759. [Google Scholar] [CrossRef]
- Abert, C.; Huber, C.; Bruckner, F.; Vogler, C.; Wautischer, G.; Suess, D. A fast finite-difference algorithm for topology optimization of permanent magnets. J. Appl. Phys. 2017, 122, 113904. [Google Scholar] [CrossRef]
- Huber, C.; Abert, C.; Bruckner, F.; Pfaff, C.; Kriwet, J.; Groenefeld, M.; Teliban, I.; Vogler, C.; Suess, D. Topology optimized and 3D printed polymer-bonded permanent magnets for a predefined external field. J. Appl. Phys. 2017, 122, 053904. [Google Scholar] [CrossRef]
- Hinze, M.; Pinnau, R.; Ulbrich, M.; Ulbrich, S. Mathematical Modelling: Theory and Applications. In Optimization with PDE Constraints; Springer: New York, NY, USA, 2009; p. xii+270. [Google Scholar]
- ANSYS Electronics Desktop. Available online: https://www.ansys.com/products/electronics/ansyselectronics-desktop (accessed on 30 November 2020).
- COMSOL Multiphysics Software. Available online: https://www.comsol.de/ (accessed on 30 November 2020).
- Abert, C.; Exl, L.; Bruckner, F.; Drews, A.; Suess, D. magnum. fe: A micromagnetic finite-element simulation code based on FEniCS. J. Magn. Magn. Mater. 2013, 345, 29–35. [Google Scholar] [CrossRef]
- Meeker, D. Finite Element Method Magnetics Software. 2010. Available online: http://www.femm.info/Archives/doc/manual42.pdf (accessed on 30 November 2020).
- Furlani, E.P. Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications; Academic Press: Waltham, MA, USA, 2001. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Camacho, J.M.; Sosa, V. Alternative method to calculate the magnetic field of permanent magnets with azimuthal symmetry. Rev. Mex. Física 2013, 59, 8–17. [Google Scholar]
- Yang, Z.; Johansen, T.; Bratsberg, H.; Helgesen, G.; Skjeltorp, A. Potential and force between a magnet and a bulk Y1Ba2Cu3O7-δ superconductor studied by a mechanical pendulum. Supercond. Sci. Technol. 1990, 3, 591. [Google Scholar] [CrossRef]
- Ortner, M.; Bandeira, L.G.C. Magpylib: A free Python package for magnetic field computation. SoftwareX 2020, 11, 100466. [Google Scholar] [CrossRef]
- Huber, C.; Goertler, M.; Abert, C.; Bruckner, F.; Groenefeld, M.; Teliban, I.; Suess, D. Additive manufactured and topology optimized passive shimming elements for permanent magnetic systems. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Dupré, N.; Dubrulle, O.; Huber, S.; Burssens, J.W.; Schott, C.; Close, G. Experimental demonstration of stray-field immunity beyond 5 mt for an automotive-grade rotary position sensor. Multidiscip. Digit. Publ. Inst. Proc. 2018, 2, 763. [Google Scholar] [CrossRef]
- Grambichler, K.; Binder, G.; Hainz, S.; Köck, H. GMR-basierter, störfeldrobuster Kurbelwellensensor für Hybridfahrzeuge. In Automobil-Sensorik 2; Springer: Berlin, Germany, 2018; pp. 177–198. [Google Scholar]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996; pp. 519–523. [Google Scholar]
- Rocca, P.; Oliveri, G.; Massa, A. Differential evolution as applied to electromagnetics. IEEE Antennas Propag. Mag. 2011, 53, 38–49. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python. arXiv 2019, arXiv:1907.10121. [Google Scholar] [CrossRef]
- Farhadi Machekposhti, D.; Tolou, N.; Herder, J. A review on compliant joints and rigid-body constant velocity universal joints toward the design of compliant homokinetic couplings. J. Mech. Des. 2015, 137, 032301. [Google Scholar] [CrossRef]
- Okamoto, Y.; Takahashi, N. A Novel Topology Optimization of Nonlinear Magnetic Circuit Using ON/OFF Method. IEEJ Trans. Fundam. Mater. 2005, 125, 549–553. [Google Scholar] [CrossRef]
- Nielsen, K.K.; Bjørk, R. The magnetic field from a homogeneously magnetized cylindrical tile. J. Magn. Magn. Mater. 2020, 507, 166799. [Google Scholar] [CrossRef]
- Caciagli, A.; Baars, R.J.; Philipse, A.P.; Kuipers, B.W. Exact expression for the magnetic field of a finite cylinder with arbitrary uniform magnetization. J. Magn. Magn. Mater. 2018, 456, 423–432. [Google Scholar] [CrossRef]
- Rubeck, C.; Yonnet, J.P.; Allag, H.; Delinchant, B.; Chadebec, O. Analytical calculation of magnet systems: Magnetic field created by charged triangles and polyhedra. IEEE Trans. Magn. 2012, 49, 144–147. [Google Scholar] [CrossRef]
- Hirosawa, S.; Nishino, M.; Miyashita, S. Perspectives for high-performance permanent magnets: Applications, coercivity, and new materials. Adv. Nat. Sci. Nanosci. Nanotechnol. 2017, 8, 013002. [Google Scholar] [CrossRef]
- Chadebec, O.; Coulomb, J.L.; Janet, F. A review of magnetostatic moment method. IEEE Trans. Magn. 2006, 42, 515–520. [Google Scholar] [CrossRef]
- Aharoni, A. Demagnetizing factors for rectangular ferromagnetic prisms. J. Appl. Phys. 1998, 83, 3432–3434. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malagò, P.; Slanovc, F.; Herzog, S.; Lumetti, S.; Schaden, T.; Pellegrinetti, A.; Moridi, M.; Abert, C.; Suess, D.; Ortner, M. Magnetic Position System Design Method Applied to Three-Axis Joystick Motion Tracking. Sensors 2020, 20, 6873. https://doi.org/10.3390/s20236873
Malagò P, Slanovc F, Herzog S, Lumetti S, Schaden T, Pellegrinetti A, Moridi M, Abert C, Suess D, Ortner M. Magnetic Position System Design Method Applied to Three-Axis Joystick Motion Tracking. Sensors. 2020; 20(23):6873. https://doi.org/10.3390/s20236873
Chicago/Turabian StyleMalagò, Perla, Florian Slanovc, Stefan Herzog, Stefano Lumetti, Thomas Schaden, Andrea Pellegrinetti, Mohssen Moridi, Claas Abert, Dieter Suess, and Michael Ortner. 2020. "Magnetic Position System Design Method Applied to Three-Axis Joystick Motion Tracking" Sensors 20, no. 23: 6873. https://doi.org/10.3390/s20236873
APA StyleMalagò, P., Slanovc, F., Herzog, S., Lumetti, S., Schaden, T., Pellegrinetti, A., Moridi, M., Abert, C., Suess, D., & Ortner, M. (2020). Magnetic Position System Design Method Applied to Three-Axis Joystick Motion Tracking. Sensors, 20(23), 6873. https://doi.org/10.3390/s20236873







