An Indoor Robust Localization Algorithm Based on Data Association Technique
Abstract
1. Introduction
- NLOS identification was performed through hypothesis testing, and some NLOS transmissions were eliminated, effectively reducing the effect of NLOS.
- The algorithm established the corresponding clustering probability matrix for the position estimation through hypothesis testing with the improved method to calculate the probability, where the positioning accuracy was higher.
- If the hypothesis testing failed continuously when there was no position estimation obtained from the subgroup that fell into the verification gate, the NLOS tracking method was used to avoid positioning errors.
2. Related Works
3. Signal Model
4. Proposed Algorithm
4.1. General Concept
4.2. Grouping and Hypothesis Testing
4.2.1. Kalman Prediction
4.2.2. NLOS Identification
4.3. Association Probability Updating
- The LOS environment and the NLOS environment from the target node to the anchor node had position estimates;
- Each position estimation was from LOS or NLOS environments.
4.4. NLOS Tracking
- (1)
- Let , getting the initial position estimate .
- (2)
- Calculate the residual:
- (3)
- Use the to estimate the range of
- (4)
- Update the and :
- (5)
- Calculate , if the value is less than the set previously, the loop is stopped to obtain the final position estimation value. Otherwise, go to the second step and continue the cycle until it stops:where
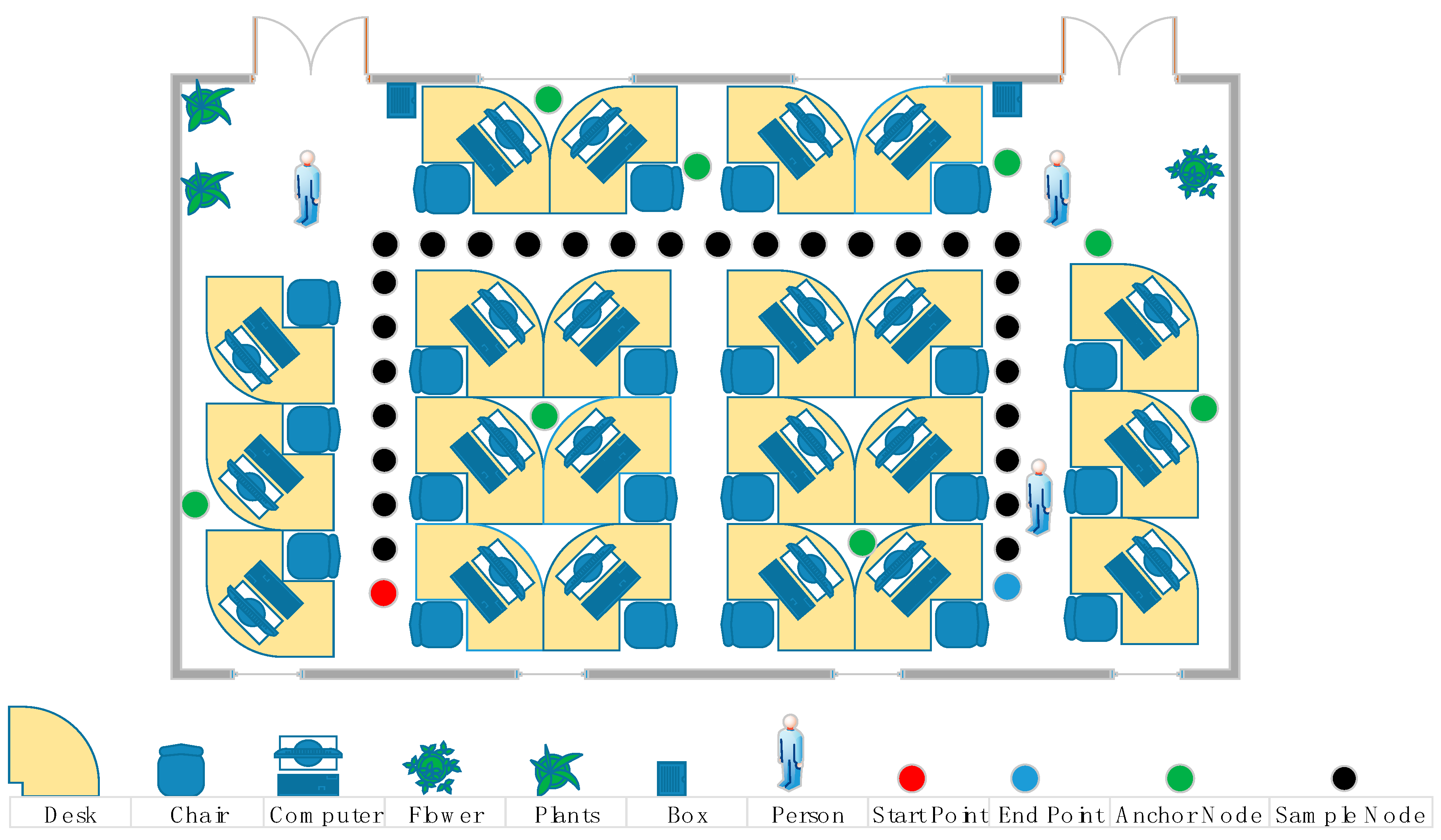
5. Experiment Simulation
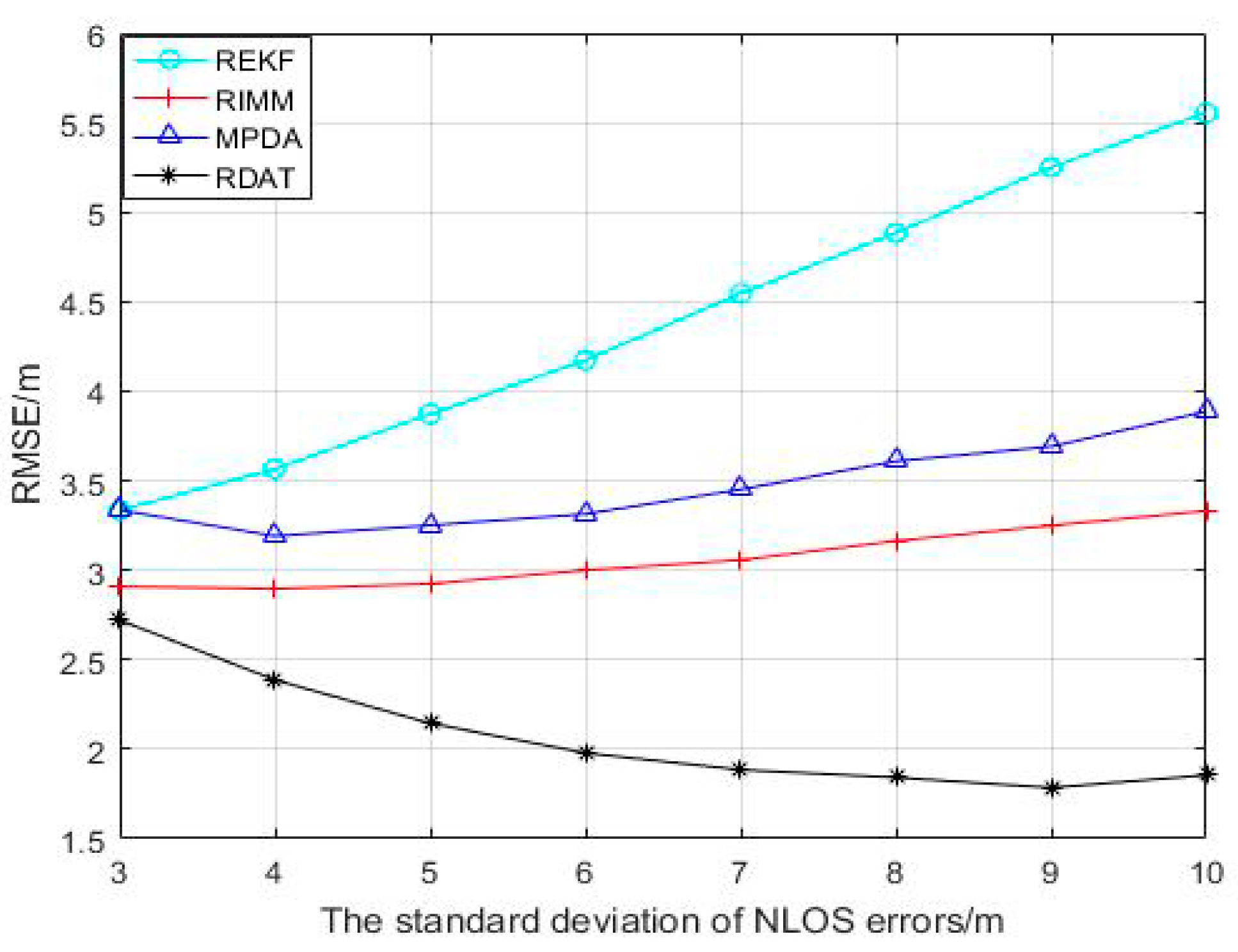
5.1. The NLOS Errors Obeys Gaussian Distribution
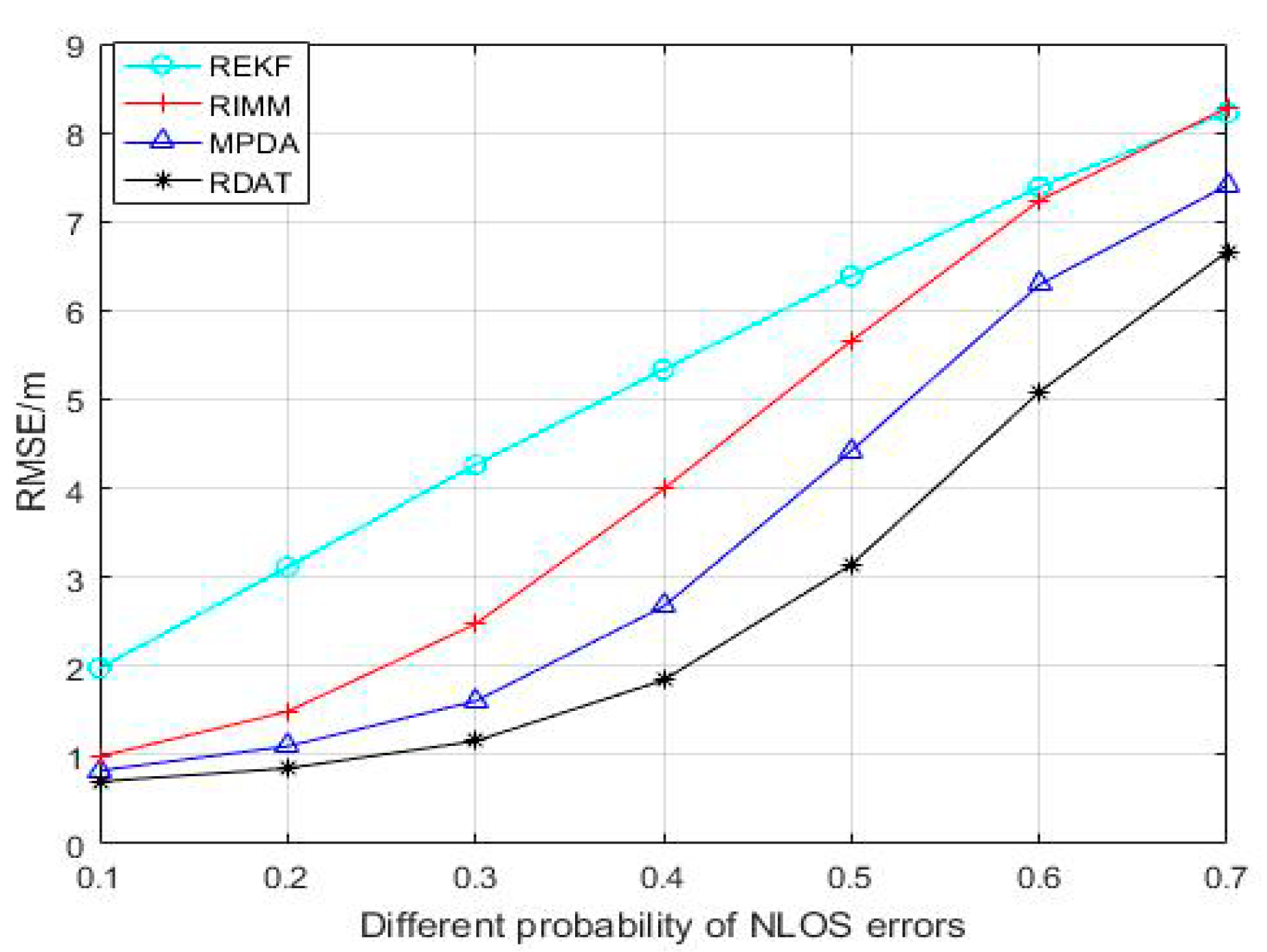
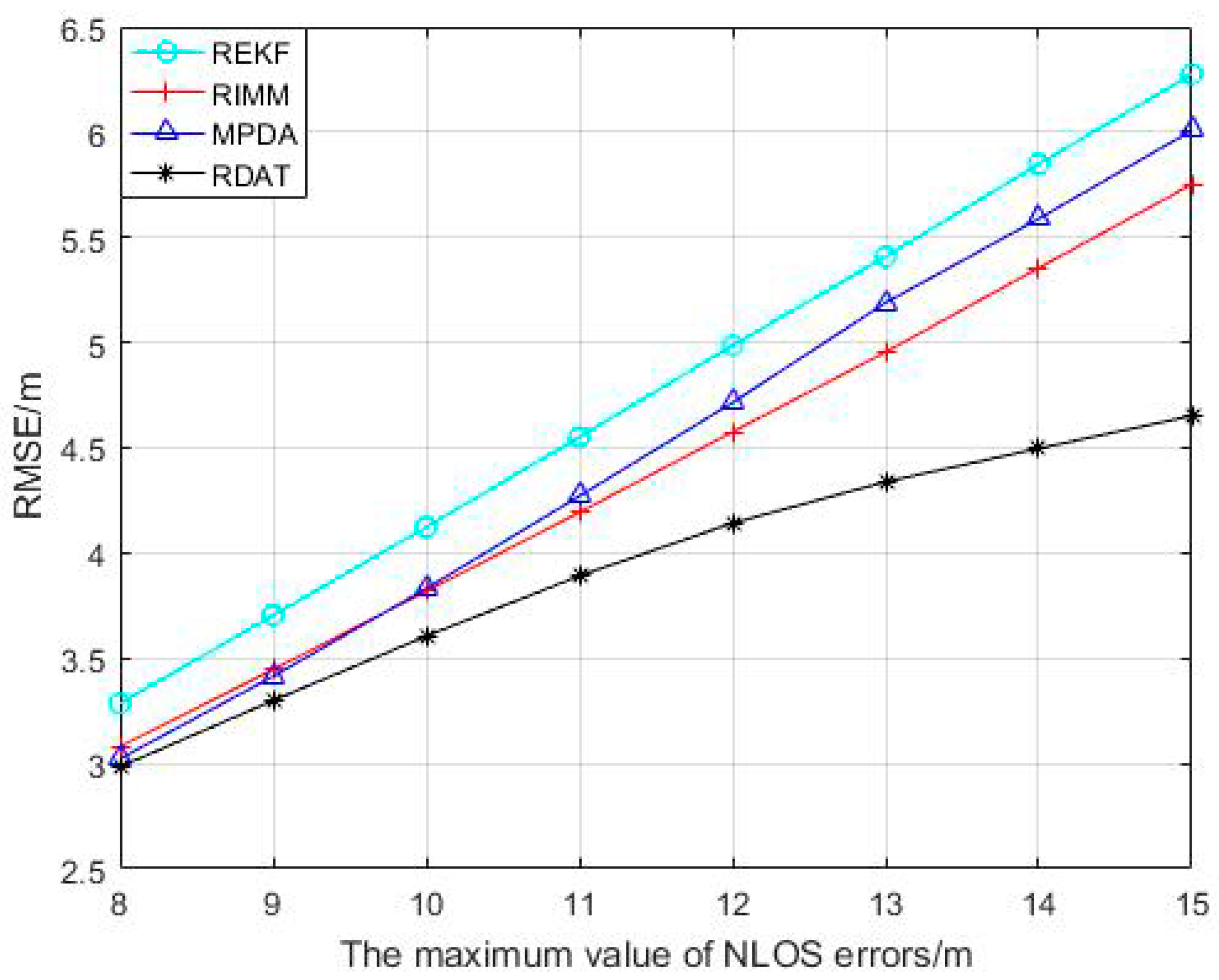
5.2. The NLOS Errors Obey Uniform Distribution
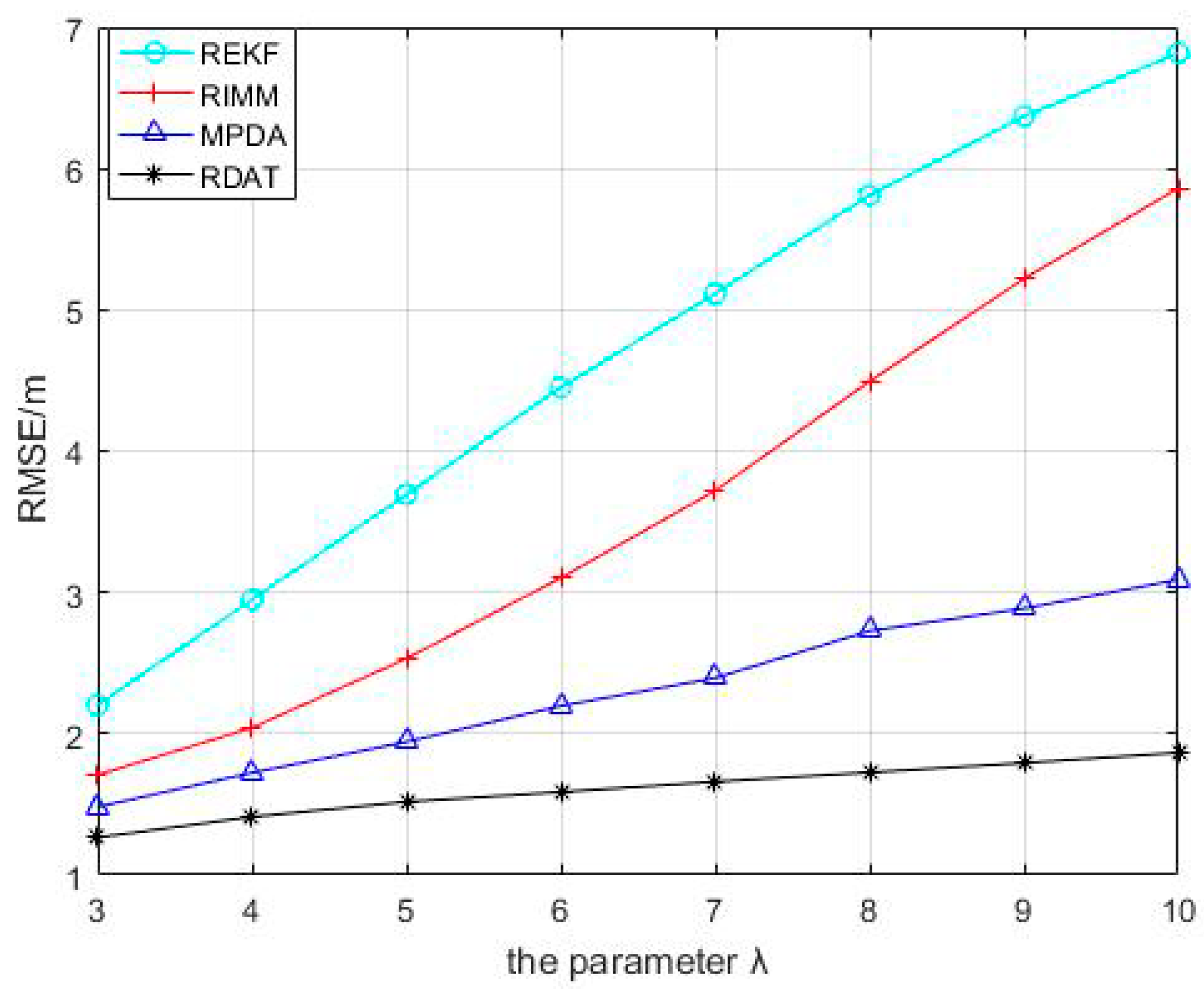
5.3. The NLOS Errors Obey Index Distribution
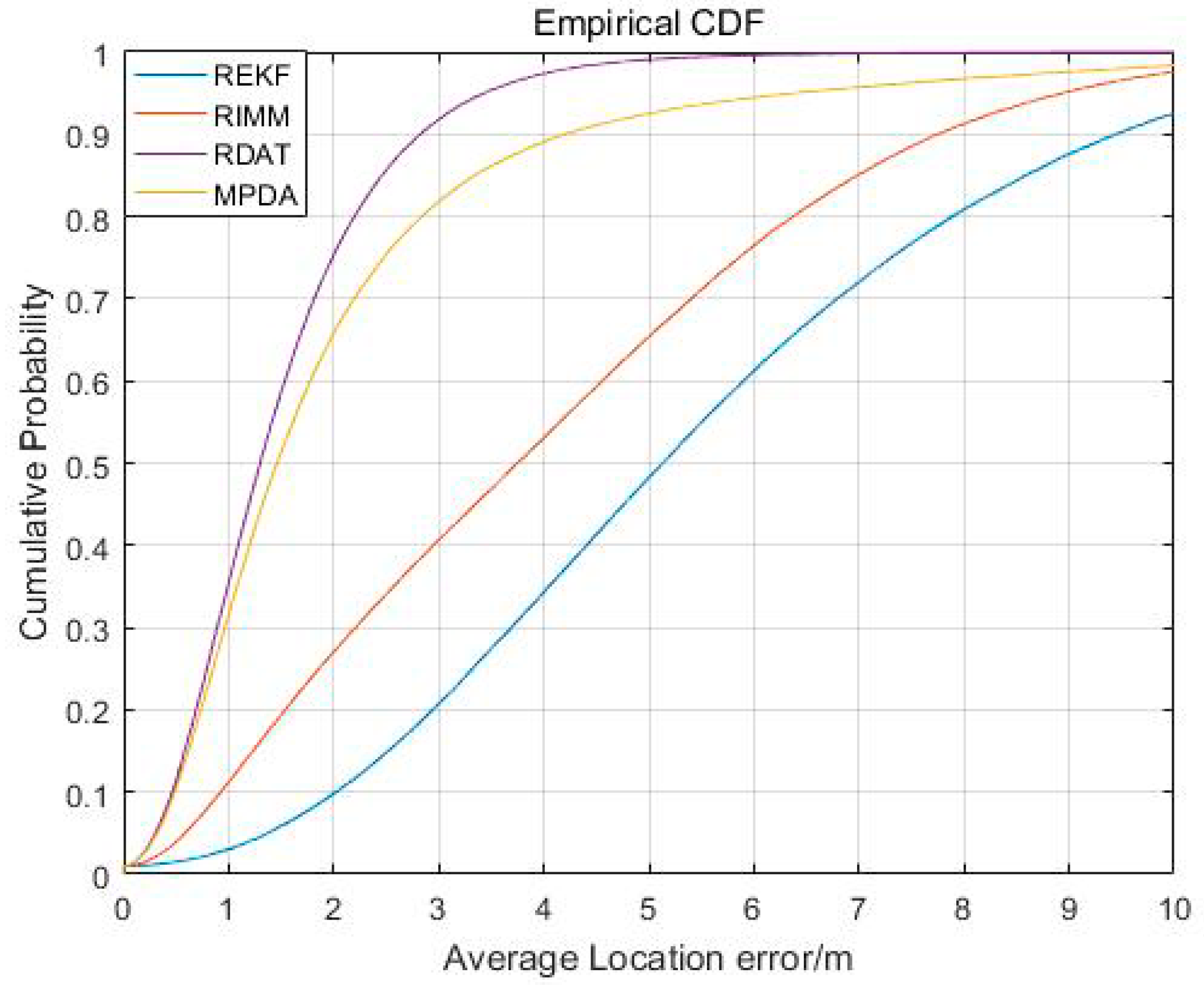
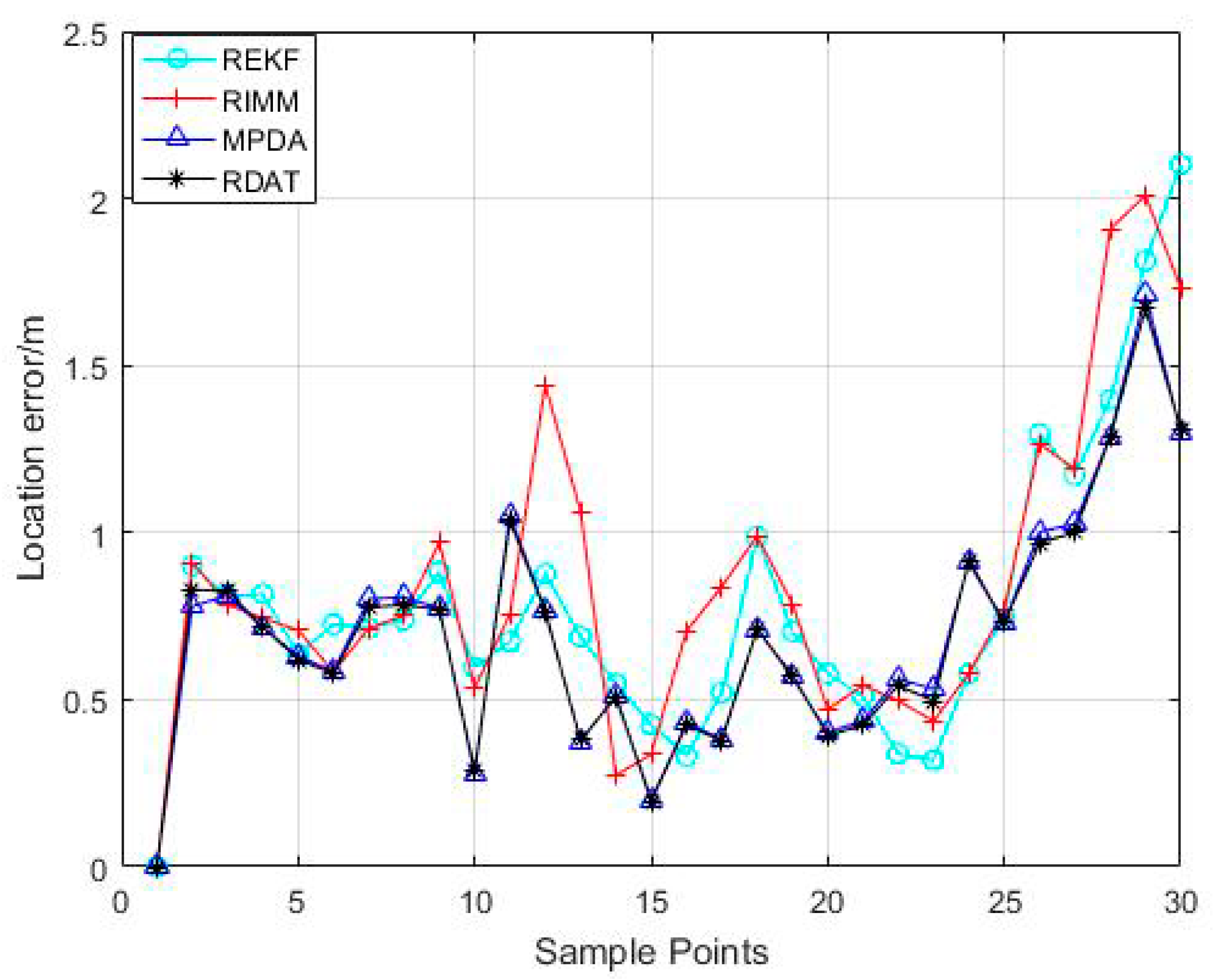
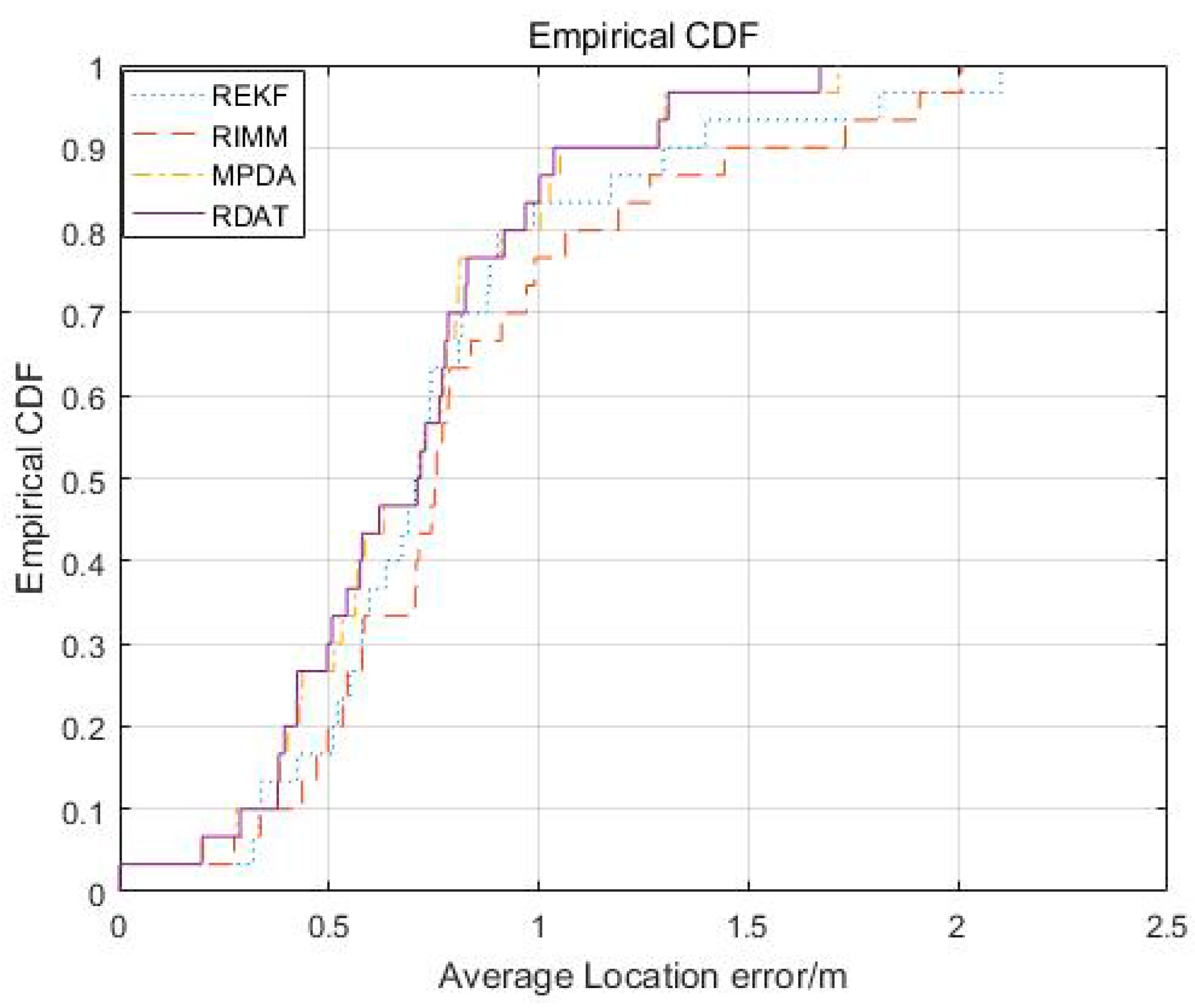
5.4. Experimental Result
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shi, Q.; Cui, X.; Zhao, S.; Lu, M. Sequential TOA-Based Moving Target Localization in Multi-Agent Networks. IEEE Commun. Lett. 2020, 24, 1719–1723. [Google Scholar] [CrossRef]
- Cao, S.; Chen, X.; Zhang, X.; Chen, X. Combined Weighted Method for TDOA-Based Localization. IEEE Trans. Instrum. Meas. 2019, 69, 1962–1971. [Google Scholar] [CrossRef]
- Yang, B.; Guo, L.; Guo, R.; Zhao, M.; Zhao, T. A Novel Trilateration Algorithm for RSSI-Based Indoor Localization. IEEE Sens. J. 2020, 20, 8164–8172. [Google Scholar] [CrossRef]
- Zheng, Y.; Sheng, M.; Liu, J.; Li, J. Exploiting AoA Estimation Accuracy for Indoor Localization: A Weighted AoA-Based Approach. IEEE Wirel. Commun. Lett. 2018, 8, 65–68. [Google Scholar] [CrossRef]
- Gui, L.; Val, T.; Wei, A.; Dalce, R. Improvement of range-free localization technology by a novel DV-hop protocol in wireless sensor networks. Ad Hoc Netw. 2015, 24, 55–73. [Google Scholar] [CrossRef]
- Haigh, S.; Kulon, J.; Partlow, A.; Rogers, P.; Gibson, C. A Robust Algorithm for Classification and Rejection of NLOS Signals in Narrowband Ultrasonic Localization Systems. IEEE Trans. Instrum. Meas. 2018, 68, 646–655. [Google Scholar] [CrossRef]
- Tian, X.; Wei, G.; Wang, J.; Zhang, D. A Localization and Tracking Approach in NLOS Environment Based on Distance and Angle Probability Model. Sensors 2019, 19, 4438. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zawodniok, M. New Theoretical Limit Analysis of LoS and RSS Based Positioning Methods for Ricean Fading Channel in RF Systems. IEEE Trans. Mob. Comput. 2019, 18, 2401–2414. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.J.; García-Naya, J.A.; Maneiro-Catoira, R. NLOS Identification and Mitigation Using Low-Cost UWB Devices. Sensors 2019, 19, 3464. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Deng, Z.; Wen, L.; Ge, L.; Ke, H.; Jiao, J. An UWB Location Algorithm for Indoor NLOS Environment. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA; pp. 1–6. [Google Scholar]
- Yuan, Y.; Li, Y.; Liu, Z.; Chan, K.Y.; Zhu, S.; Guan, X. A three dimensional tracking scheme for underwater non-cooperative objects in mixed LOS and NLOS environment. Peer-to-Peer Netw. Appl. 2018, 12, 1369–1384. [Google Scholar] [CrossRef]
- Wang, Y.; Jie, H.; Cheng, L. A Fusion Localization Method based on a Robust Extended Kalman Filter and Track-Quality for Wireless Sensor Networks. Sensors 2019, 19, 3638. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, W. Hyperbolic-Weighted Centroid Indoor Location Algorithm based on Kalman Filter. In Proceedings of the 2018 IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 October 2018; pp. 2520–2523. [Google Scholar]
- Dwek, N.; Birem, M.; Geebelen, K.; Hostens, E.; Mishra, A.; Steckel, J.; Yudanto, R. Improving the Accuracy and Robustness of Ultra-Wideband Localization Through Sensor Fusion and Outlier Detection. IEEE Robot. Autom. Lett. 2020, 5, 32–39. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. A Robust NLOS Bias Mitigation Technique for RSS-TOA-Based Target Localization. IEEE Signal Process. Lett. 2019, 26, 64–68. [Google Scholar] [CrossRef]
- Chang, S.; Li, Y.; Yang, X.; Wang, H.; Hu, W.; Wu, Y. A Novel Localization Method Based on RSS-AOA Combined Measurements by Using Polarized Identity. IEEE Sens. J. 2019, 19, 1463–1470. [Google Scholar] [CrossRef]
- Chen, H.; Wang, G.; Ansari, N. Improved Robust TOA-Based Localization via NLOS Balancing Parameter Estimation. IEEE Trans. Veh. Technol. 2019, 68, 6177–6181. [Google Scholar] [CrossRef]
- Yang, M.N.; Jackson, D.R.; Chen, J.; Xiong, Z.B. A TDOA Localization Method for NLOS Scenarios. IEEE Trans. Antennas Propag. 2019, 67, 2666–2676. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, W.; Ansari, N. Robust TDOA-Based Localization for IoT via Joint Source Position and NLOS Error Estimation. IEEE Internet Things J. 2019, 6, 8529–8541. [Google Scholar] [CrossRef]
- Xiong, W.; So, H.C. TOA-Based Localization with NLOS Mitigation via Robust Multidimensional Similarity Analysis. IEEE Signal Process. Lett. 2019, 26, 1334–1338. [Google Scholar] [CrossRef]
- Cheng, L.; Hang, J.; Wang, Y.; Bi, Y. A Fuzzy C-Means and Hierarchical Voting Based RSSI Quantify Localization Method for Wireless Sensor Network. IEEE Access 2019, 7, 47411–47422. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Y.; Wang, Y.; Bi, Y.; Feng, L.; Xue, M. A Triple-Filter NLOS Localization Algorithm Based on Fuzzy C-means for Wireless Sensor Networks. Sensors 2019, 19, 1215. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hang, J.; Cheng, L.; Li, C.; Song, X. A Hierarchical Voting Based Mixed Filter Localization Method for Wireless Sensor Network in Mixed LOS/NLOS Environments. Sensors 2018, 18, 2348. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Xu, Z.; Sadler, B.M. Geolocation Performance with Biased Range Measurements. IEEE Trans. Sinal Process. 2012, 60, 2315–2329. [Google Scholar] [CrossRef]
- Li, D.; Sun, J. Robust Interacting Multiple Model Filter Based on Student’s t-Distribution for Heavy-Tailed Measurement Noises. Sensors 2019, 19, 4830. [Google Scholar] [CrossRef] [PubMed]
- Hammes, U.; Zoubir, A.M. Robust MT Tracking Based on M-Estimation and Interacting Multiple Model Algorithm. IEEE Trans. Signal Process. 2011, 59, 3398–3409. [Google Scholar] [CrossRef]
- Hammes, U.; Zoubir, A.M. Robust Mobile Terminal Tracking in NLOS Environments Based on Data Association. IEEE Trans. Signal Process. 2010, 58, 5872–5882. [Google Scholar] [CrossRef]

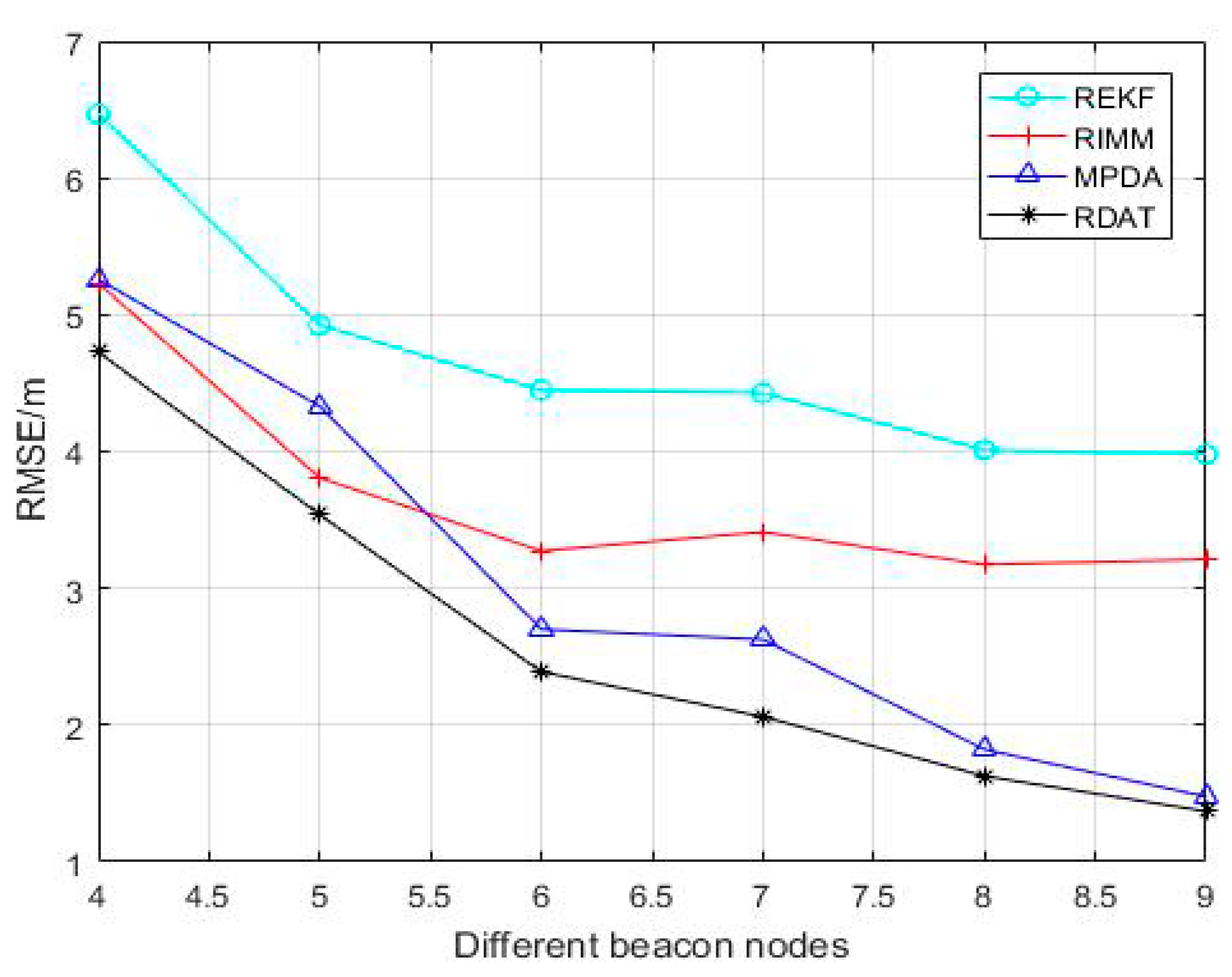
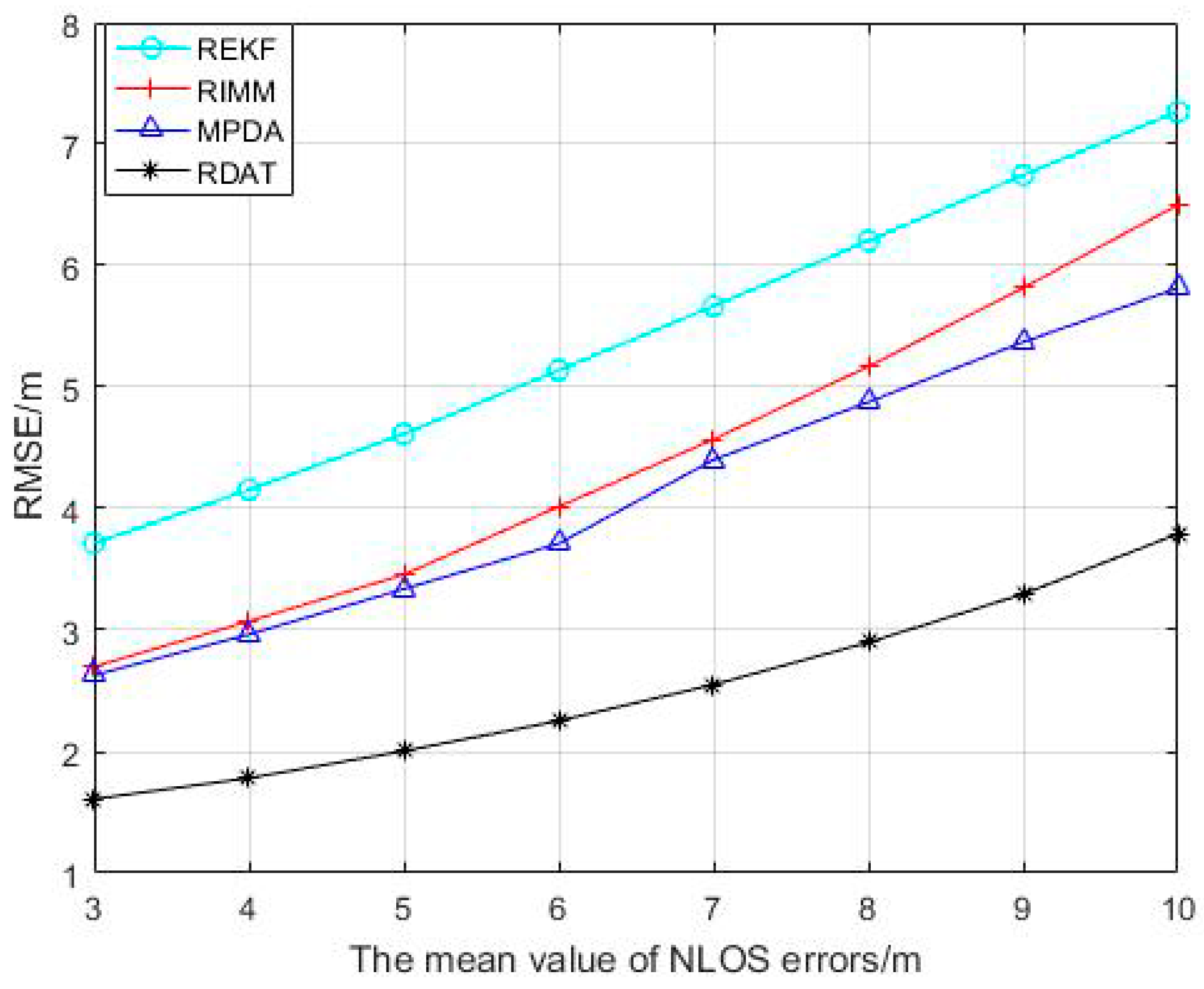
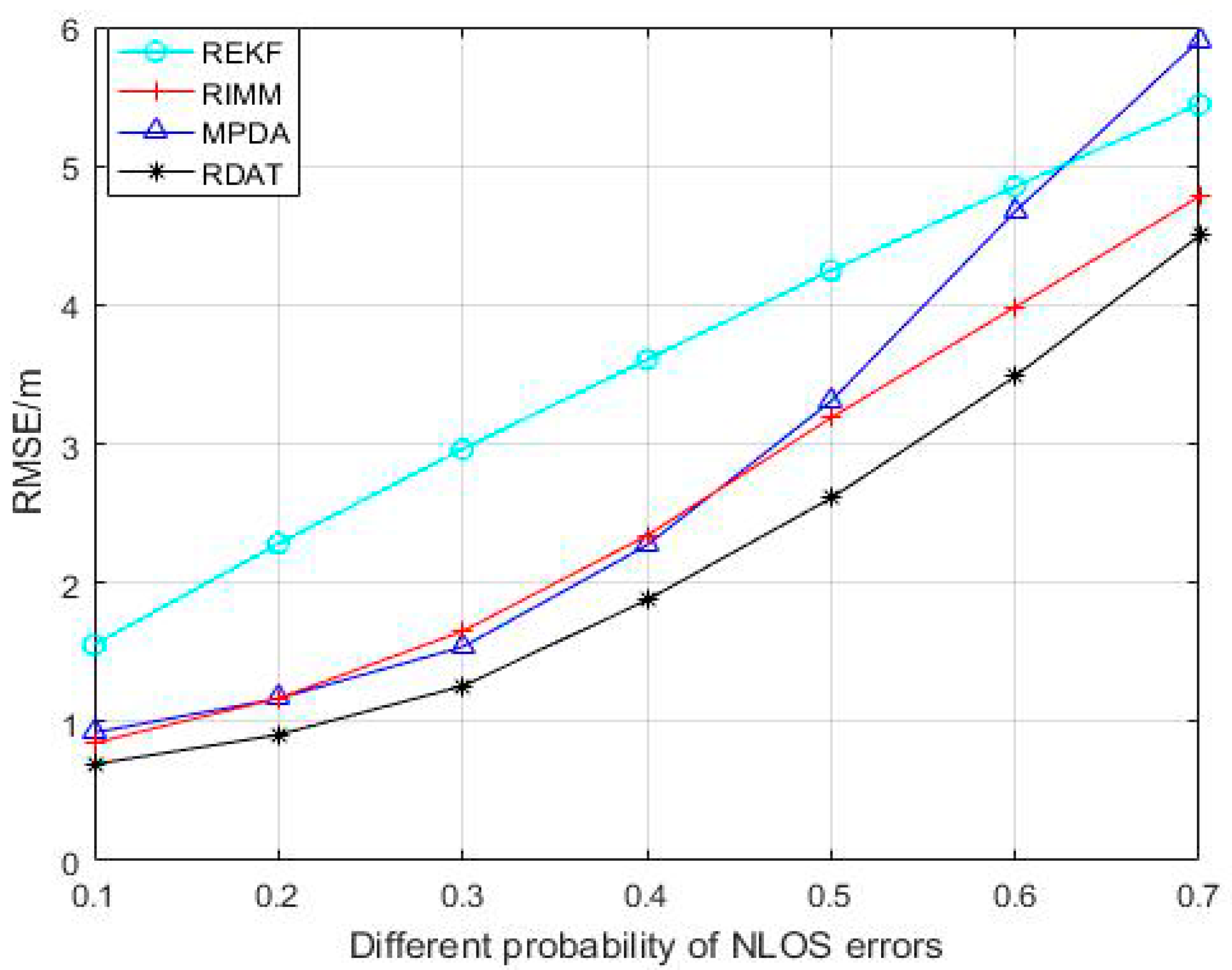
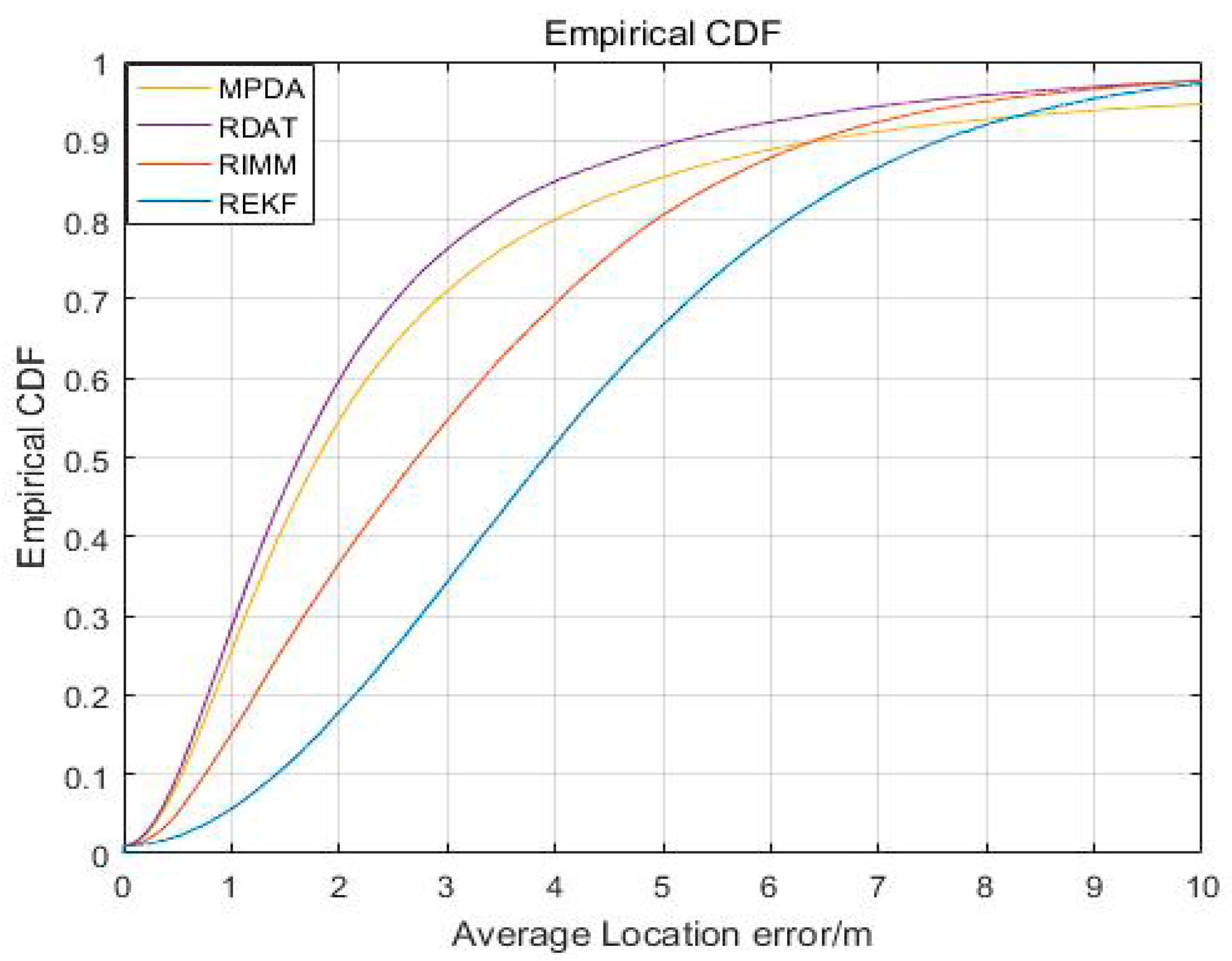
| Parameter | Sign | Values |
|---|---|---|
| The number of anchor nodes | 6 | |
| NLOS error probability | 0.5 | |
| The measurement noise | ||
| The NLOS errors |
| Parameter | Sign | Values |
|---|---|---|
| The number of anchor nodes | 6 | |
| NLOS error probability | 0.5 | |
| The measurement noise | ||
| The NLOS errors |
| Parameter | Sign | Values |
|---|---|---|
| The number of anchor nodes | 6 | |
| NLOS error probability | 0.5 | |
| The measurement noise | ||
| The NLOS errors |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, L.; Wang, Y.; Xue, M.; Bi, Y. An Indoor Robust Localization Algorithm Based on Data Association Technique. Sensors 2020, 20, 6598. https://doi.org/10.3390/s20226598
Cheng L, Wang Y, Xue M, Bi Y. An Indoor Robust Localization Algorithm Based on Data Association Technique. Sensors. 2020; 20(22):6598. https://doi.org/10.3390/s20226598
Chicago/Turabian StyleCheng, Long, Yong Wang, Mingkun Xue, and Yangyang Bi. 2020. "An Indoor Robust Localization Algorithm Based on Data Association Technique" Sensors 20, no. 22: 6598. https://doi.org/10.3390/s20226598
APA StyleCheng, L., Wang, Y., Xue, M., & Bi, Y. (2020). An Indoor Robust Localization Algorithm Based on Data Association Technique. Sensors, 20(22), 6598. https://doi.org/10.3390/s20226598




