Effect of Surface and Interfacial Tension on the Resonance Frequency of Microfluidic Channel Cantilever
Abstract
1. Introduction
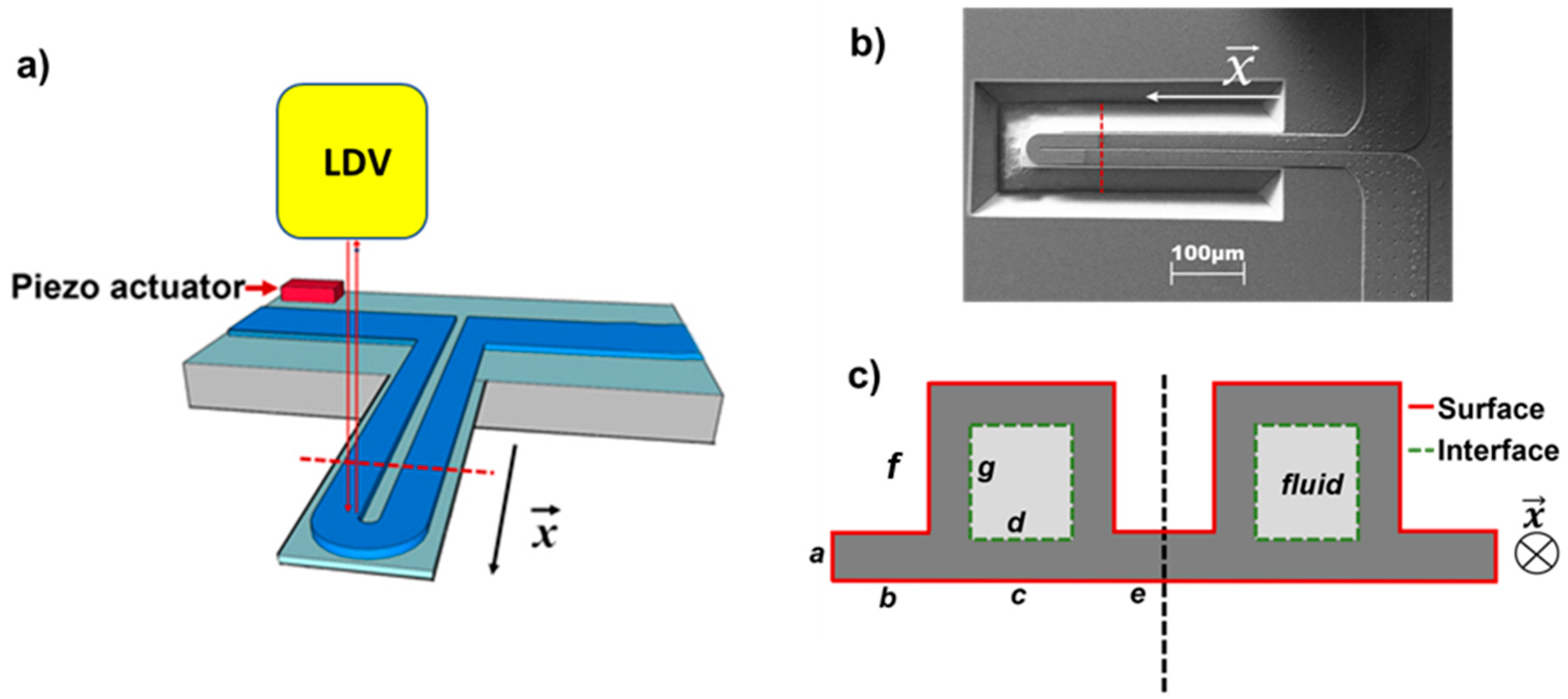
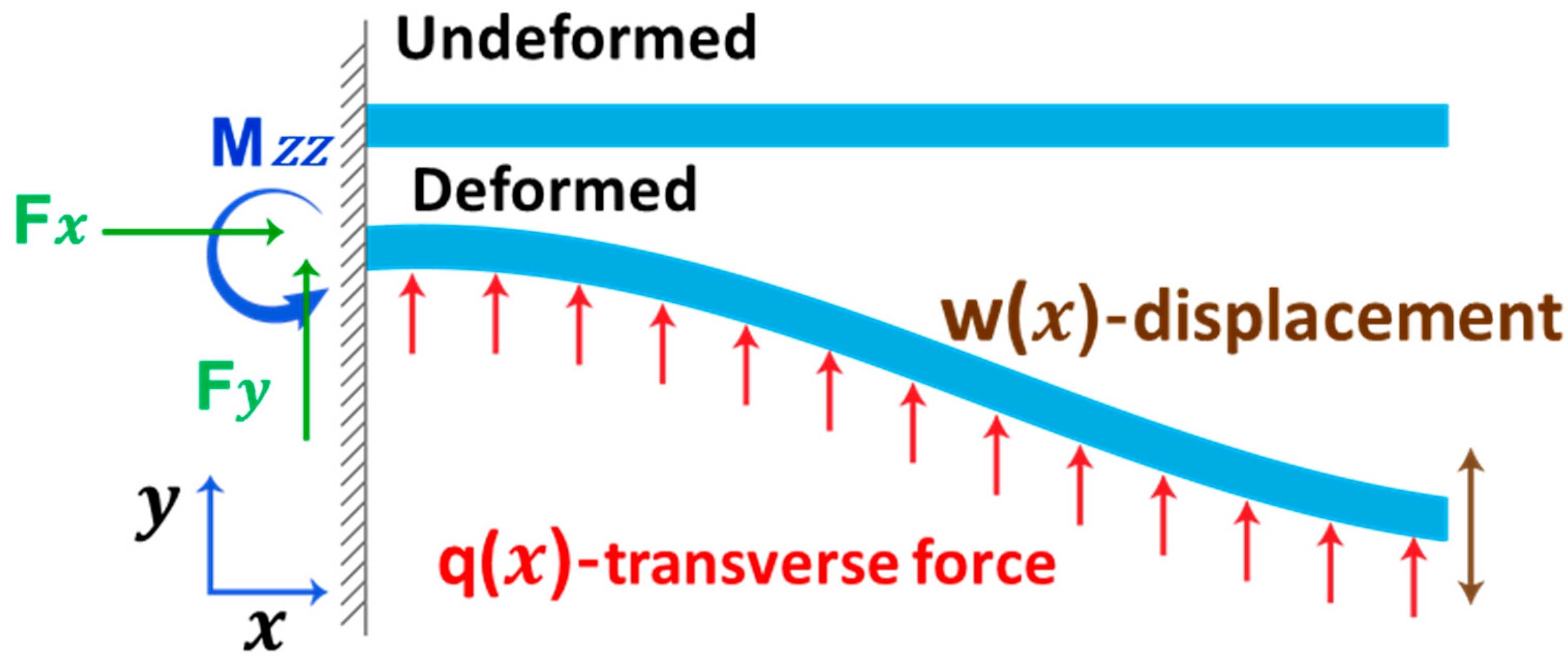
2. Analytical Model Incorporating Surface Pressure
- (1)
- The length-to-width ratio of the channel is greater than the order of 100.
- (2)
- The amplitude of the beam vibration is smaller than the any beam dimension.
- (3)
- The fluid inside the channel is considered a homogeneous media and incompressible and the beam is a linearly elastic solid.
- (4)
- The deformed beam is in equilibrium considering that all the internal forces are balanced within.
- (5)
- The cross section of beam is uniform over its entire length.
3. Estimating Interfacial Tension
4. Experimental Details
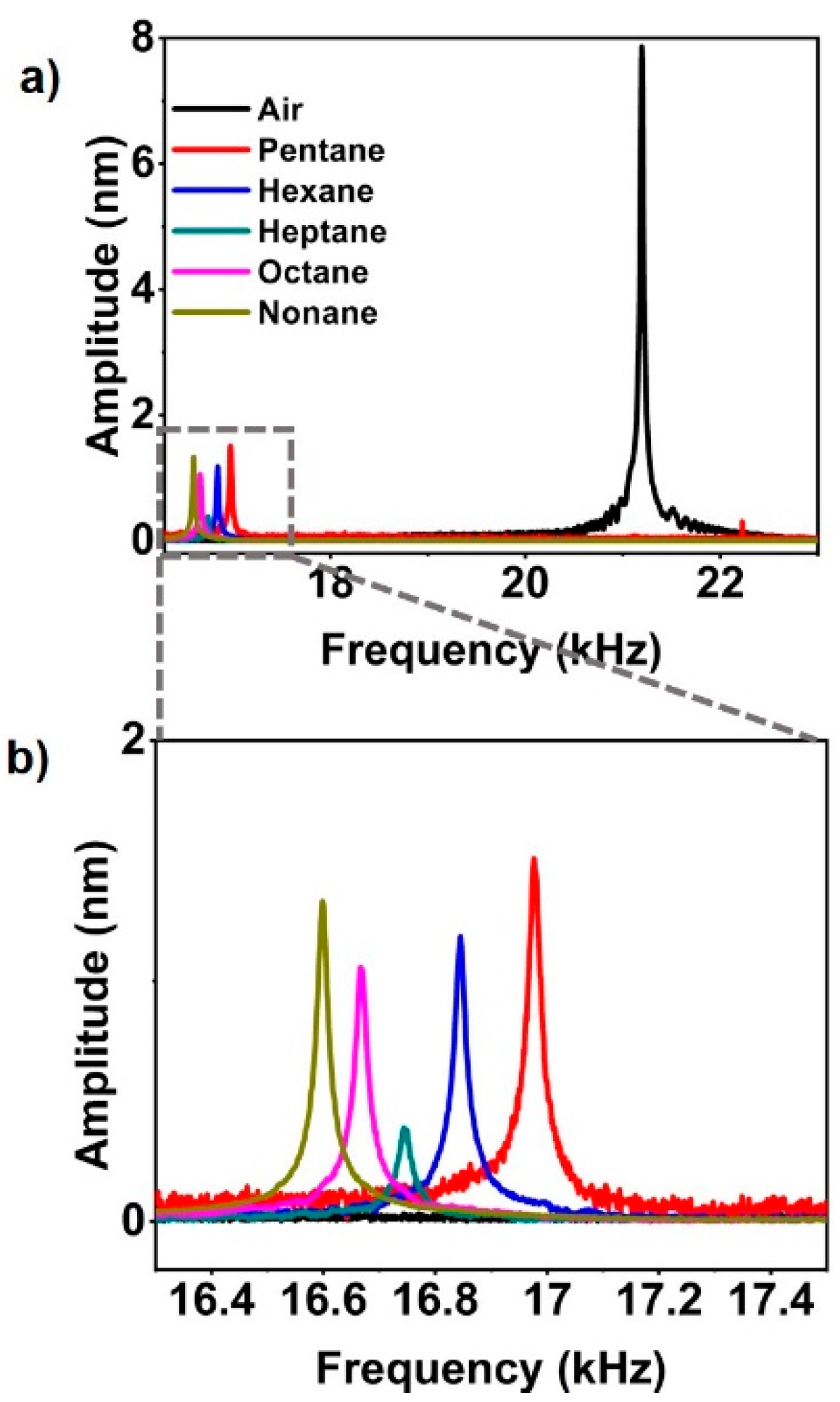
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Data Availability Statement
References
- Goeders, K.M.; Colton, J.S.; Bottomley, L.A. Microcantilevers: Sensing Chemical Interactions via Mechanical Motion. Chem. Rev. 2008, 108, 522–542. [Google Scholar] [CrossRef] [PubMed]
- Lavrik, N.V.; Sepaniak, M.J.; Datskos, P.G. Cantilever transducers as a platform for chemical and biological sensors. Rev. Sci. Instrum. 2004, 75, 2229–2253. [Google Scholar] [CrossRef]
- Alvarez, M.; Lechuga, L.M. Microcantilever-based platforms as biosensing tools. Analyst 2010, 135, 827–836. [Google Scholar] [CrossRef] [PubMed]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nat. Cell Biol. 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
- Olcum, S.; Cermak, N.; Wasserman, S.C.; Christine, K.S.; Atsumi, H.; Payer, K.R.; Shen, W.; Lee, J.; Belcher, A.M.; Bhatia, S.N.; et al. Weighing nanoparticles in solution at the attogram scale. Proc. Natl. Acad. Sci. USA 2014, 111, 1310–1315. [Google Scholar] [CrossRef] [PubMed]
- Wachter, E.A.; Thundat, T. Micromechanical sensors for chemical and physical measurements. Rev. Sci. Instrum. 1995, 66, 3662–3667. [Google Scholar] [CrossRef]
- Tamayo, J.; Ramos, D.; Mertens, J.; Calleja, M. Effect of the adsorbate stiffness on the resonance response of microcantilever sensors. Appl. Phys. Lett. 2006, 89, 224104. [Google Scholar] [CrossRef]
- Datar, R.; Kim, S.; Jeon, S.; Hesketh, P.; Manalis, S.R.; Boisen, A.; Thundat, T. Cantilever Sensors: Nanomechanical Tools for Diagnostics. MRS Bull. 2009, 34, 449–454. [Google Scholar] [CrossRef]
- Ruz, J.J.; Pini, V.; Malvar, O.; Kosaka, P.M.; Calleja, M.; Tamayo, J. Effect of surface stress induced curvature on the eigenfrequencies of microcantilever plates. AIP Adv. 2018, 8, 105213. [Google Scholar] [CrossRef]
- Gurtin, E.M.; Markenscoff, X.; Thurston, R.N. Effect of surface stress on the natural frequency of thin crystals. Appl. Phys. Lett. 1976, 29, 529–530. [Google Scholar] [CrossRef]
- Butt, H.-J. A Sensitive Method to Measure Changes in the Surface Stress of Solids. J. Colloid Interface Sci. 1996, 180, 251–260. [Google Scholar] [CrossRef]
- Lagowski, J.; Gatos, H.C.; Sproles, E.S. Surface stress and the normal mode of vibration of thin crystals: GaAs. Appl. Phys. Lett. 1975, 26, 493–495. [Google Scholar] [CrossRef]
- Chen, G.Y.; Thundat, T.; Wachter, E.A.; Warmack, R.J. Adsorption-induced surface stress and its effects on resonance frequency of microcantilevers. J. Appl. Phys. 1995, 77, 3618–3622. [Google Scholar] [CrossRef]
- Cherian, S.; Thundat, T. Determination of adsorption-induced variation in the spring constant of a microcantilever. Appl. Phys. Lett. 2002, 80, 2219–2221. [Google Scholar] [CrossRef]
- Wang, D.F.; Ono, T.; Esashi, M. Thermal treatments and gas adsorption influences on nano mechanics of ultra-thin silicon resonators for ultimate sensing. Nanotechnology 2004, 15, 1851. [Google Scholar] [CrossRef]
- Hwang, K.S.; Eom, K.; Lee, J.H.; Chun, D.W.; Cha, B.H.; Yoon, D.S.; Kim, T.S.; Park, J.-H. Dominant surface stress driven by biomolecular interactions in the dynamical response of nanomechanical microcantilevers. Appl. Phys. Lett. 2006, 89, 173905. [Google Scholar] [CrossRef]
- Malvar, O.; Ruz, J.J.; Kosaka, P.M.; Domínguez, C.M.; Gil-Santos, E.; Calleja, M.; Tamayo, J. Mass and stiffness spectrometry of nanoparticles and whole intact bacteria by multimode nanomechanical resonators. Nat. Commun. 2016, 7, 13452. [Google Scholar] [CrossRef]
- Stachiv, I.; Gan, L.; Kuo, C.-Y.; Sittner, P.; Sevecek, O. Mass spectrometry of heavy analytes and large biological aggregates by monitoring changes in quality factor of nanomechanical resonator in air. ACS Sens. 2020, 5, 2128–2135. [Google Scholar] [CrossRef]
- McFarland, A.W.; Poggi, M.A.; Doyle, M.J.; Bottomley, L.A.; Colton, J.S. Influence of surface stress on the resonance behavior of microcantilevers. Appl. Phys. Lett. 2005, 87, 053505. [Google Scholar] [CrossRef]
- Ren, Q.; Zhao, Y.-P. Influence of surface stress on frequency of microcantilever-based biosensors. Microsyst. Technol. 2004, 10, 307–314. [Google Scholar] [CrossRef]
- Huang, G.-Y.; Gao, W.; Yu, S.-W. Model for the adsorption-induced change in resonance frequency of a cantilever. Appl. Phys. Lett. 2006, 89, 043506. [Google Scholar] [CrossRef]
- Dorignac, J.; Kalinowski, A.; Erramilli, S.; Mohanty, P. Dynamical Response of Nanomechanical Oscillators in Immiscible Viscous Fluid for In Vitro Biomolecular Recognition. Phys. Rev. Lett. 2006, 96, 186105. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.-F.; Feng, X.-Q. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Appl. Phys. Lett. 2007, 90, 231904. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.; Lu, C.; O’Shea, S.J. Surface stress effects on the resonance properties of cantilever sensors. Phys. Rev. B 2005, 72, 085405. [Google Scholar] [CrossRef]
- Lachut, M.J.; Sader, J.E. Effect of Surface Stress on the Stiffness of Cantilever Plates. Phys. Rev. Lett. 2007, 99, 206102. [Google Scholar] [CrossRef] [PubMed]
- Sader, J.E. Surface stress induced deflections of cantilever plates with applications to the atomic force microscope: Rectangular plates. J. Appl. Phys. 2001, 89, 2911–2921. [Google Scholar] [CrossRef]
- Karabalin, R.B.; Villanueva, L.G.; Matheny, M.H.; Sader, J.E.; Roukes, M.L. Stress-induced variations in the stiffness of micro- and nanocantilever beams. Phys. Rev. Lett. 2012, 108, 236101. [Google Scholar] [CrossRef]
- He, J.; Lilley, C.M. Surface stress effect on bending resonance of nanowires with different boundary conditions. Appl. Phys. Lett. 2008, 93, 263108. [Google Scholar] [CrossRef]
- Sohi, A.N.; Nieva, P. Frequency response of curved bilayer microcantilevers with applications to surface stress measurement. J. Appl. Phys. 2016, 119, 044503. [Google Scholar] [CrossRef]
- Sohi, A.N.; Nieva, P.M. Size-dependent effects of surface stress on resonance behavior of microcantilever-based sensors. Sens. Actuators A Phys. 2018, 269, 505–514. [Google Scholar] [CrossRef]
- Stachiv, I. Impact of surface and residual stresses and electro-/magnetostatic axial loading on the suspended nanomechanical based mass sensors: A theoretical study. J. Appl. Phys. 2014, 115, 214310. [Google Scholar] [CrossRef]
- Stachiv, I.; Fang, T.-H.; Chen, T.-H. Micro-/nanosized cantilever beams and mass sensors under applied axial tensile/compressive force vibrating in vacuum and viscous fluid. AIP Adv. 2015, 5, 117140. [Google Scholar] [CrossRef]
- Kong, S.; Zhou, S.; Nie, Z.; Wang, K. The size-dependent natural frequency of Bernoulli–Euler micro-beams. Int. J. Eng. Sci. 2008, 46, 427–437. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, S.; Wang, B.; Wang, X. Nonlinear microbeam model based on strain gradient theory. Appl. Math. Model. 2012, 36, 2674–2686. [Google Scholar] [CrossRef]
- Javili, A.; Dell’Isola, F.; Steinmann, P. Geometrically nonlinear higher-gradient elasticity with energetic boundaries. J. Mech. Phys. Solids 2013, 61, 2381–2401. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Seppecher, P.; Madeo, A. How contact interactions may depend on the shape of Cauchy cuts in Nth gradient continua: Approach “à la D’Alembert. ” Z. Angew. Math. Phys. 2012, 63, 1119–1141. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Della Corte, A.; Giorgio, I. Higher-gradient continua: The legacy of Piola, Mindlin, Sedov and Toupin and some future research perspectives. Math. Mech. Solids 2016, 22, 852–872. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Germain, P. The Method of Virtual Power in Continuum Mechanics. Part 2: Microstructure. SIAM J. Appl. Math. 1973, 25, 556–575. [Google Scholar] [CrossRef]
- Spencer, A.M.; Soldatos, K. Finite deformations of fibre-reinforced elastic solids with fibre bending stiffness. Int. J. Non-Linear Mech. 2007, 42, 355–368. [Google Scholar] [CrossRef]
- Alibert, J.-J.; Seppecher, P.; Dell’Isola, F. Truss Modular Beams with Deformation Energy Depending on Higher Displacement Gradients. Math. Mech. Solids 2003, 8, 51–73. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Giorgio, I.; Pawlikowski, M.; Rizzi, N.L. Large deformations of planar extensible beams and pantographic lattices: Heuristic homogenization, experimental and numerical examples of equilibrium. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150790. [Google Scholar] [CrossRef]
- Bolouri, S.E.S.; Kim, C.I.; Yang, S. Linear theory for the mechanics of third-gradient continua reinforced with fibers resistance to flexure. Math. Mech. Solids 2019, 25, 937–960. [Google Scholar] [CrossRef]
- Kim, C.I.; Islam, S. Mechanics of third-gradient continua reinforced with fibers resistant to flexure in finite plane elastostatics. Contin. Mech. Thermodyn. 2020, 32, 1595–1617. [Google Scholar] [CrossRef]
- Kim, C.I. Strain-Gradient Elasticity Theory for the Mechanics of Fiber Composites Subjected to Finite Plane Deformations: Comprehensive Analysis. Multiscale Sci. Eng. 2019, 1, 150–160. [Google Scholar] [CrossRef]
- Zeidi, M.; Kim, C.I. Mechanics of fiber composites with fibers resistant to extension and flexure. Math. Mech. Solids 2017, 24, 3–17. [Google Scholar] [CrossRef]
- Kim, C.I.; Zeidi, M. Gradient elasticity theory for fiber composites with fibers resistant to extension and flexure. Int. J. Eng. Sci. 2018, 131, 80–99. [Google Scholar] [CrossRef]
- Zeidi, M.; Kim, C.I. Finite plane deformations of elastic solids reinforced with fibers resistant to flexure: Complete solution. Arch. Appl. Mech. 2018, 88, 819–835. [Google Scholar] [CrossRef]
- Zeidi, M.; Kim, C.I. Mechanics of an elastic solid reinforced with bidirectional fiber in finite plane elastostatics: Complete analysis. Contin. Mech. Thermodyn. 2018, 30, 573–592. [Google Scholar] [CrossRef]
- Kim, C.I. Superposed Incremental Deformations of an Elastic Solid Reinforced with Fibers Resistant to Extension and Flexure. Adv. Mater. Sci. Eng. 2018, 2018, 6501985. [Google Scholar] [CrossRef]
- Liu, C.; Rajapakse, N. Continuum Models Incorporating Surface Energy for Static and Dynamic Response of Nanoscale Beams. IEEE Trans. Nanotechnol. 2009, 9, 422–431. [Google Scholar] [CrossRef]
- Bukhari, S.A.M.; Khan, M.F.; Goswami, A.; McGee, R.; Thundat, T. Thermomechanical analysis of picograms of polymers using a suspended microchannel cantilever. RSC Adv. 2017, 7, 8415–8420. [Google Scholar] [CrossRef]
- Gimzewski, J.; Gerber, C.; Meyer, E.; Schlittler, R. Observation of a chemical reaction using a micromechanical sensor. Chem. Phys. Lett. 1994, 217, 589–594. [Google Scholar] [CrossRef]
- Jiang, K.; Khan, F.; Thomas, J.; Desai, P.R.; Phani, A.; Das, S.; Thundat, T. Thermomechanical responses of microfluidic cantilever capture DNA melting and properties of DNA premelting states using picoliters of DNA solution. Appl. Phys. Lett. 2019, 114, 173703. [Google Scholar] [CrossRef]
- Khan, F.; Schmid, S.; Larsen, P.E.; Davis, Z.J.; Yan, W.; Stenby, E.H.; Boisen, A. Online measurement of mass density and viscosity of pL fluid samples with suspended microchannel resonator. Sens. Actuators B Chem. 2013, 185, 456–461. [Google Scholar] [CrossRef]
- Etayash, H.; Khan, M.F.; Kaur, K.; Thundat, T. Microfluidic cantilever detects bacteria and measures their susceptibility to antibiotics in small confined volumes. Nat. Commun. 2016, 7, 12947. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Weissmuller, J.; Larche, F. A general theory of curved deformable interface in solids at equilibrium. Philos. Mag. A 1998, 78, 1093–1109. [Google Scholar] [CrossRef]
- Prak, D.J.L.; Cowart, J.S.; Trulove, P.C. Density, Viscosity, Speed of Sound, Bulk Modulus, and Surface Tension of Binary Mixtures ofn-Heptane + 2,2,4-Trimethylpentane at (293.15 to 338.15) K and 0.1 MPa. J. Chem. Eng. Data 2014, 59, 3842–3851. [Google Scholar] [CrossRef]
- Mougin, P.; Rasaolofosaon, P.; Zinszer, B. Petroacoustics of poorly consolidated reservoir rocks saturated with co2/methane/brine mixtures. In SACS2 European Research Project. Available online: https://www.sintef.no/globalassets/project/ik23430000-sacs/other_reports/mougin_etal_2002_ifp_final_report_wp7.pdf (accessed on 29 March 2020).
- Zapoměl, J.; Stachiv, I.; Ferfecki, P. A novel method combining Monte Carlo–FEM simulations and experiments for simultaneous evaluation of the ultrathin film mass density and Young׳s modulus. Mech. Syst. Signal Process. 2016, 66, 223–231. [Google Scholar] [CrossRef]
- Park, S.J.; Seo, M.K. Interface Science and Composites, 1st ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Grigoryev, B.A.; Nemzer, B.V.; Kurumov, D.S.; Sengers, J.V. Surface tension of normal pentane, hexane, heptane, and octane. Int. J. Thermophys. 1992, 13, 453–464. [Google Scholar] [CrossRef]
- Sadegh-Cheri, M.; Latifi, H.; Sadeghi, J.; Moghaddam, M.S.; Shahraki, H.; Hajghassem, H. Real-time measurement of flow rate in microfluidic devices using a cantilever-based optofluidic sensor. Analyst 2014, 139, 431–438. [Google Scholar] [CrossRef] [PubMed]
- Hajesfandiari, A.; Sukhotskiy, V.; Alodhayb, A.; Khan, M.; Thundat, T.; Furlani, E. Microfluidic microcantilever as a sensitive platform to measure evaporation rate of picoliters of ethanol. Measurement 2020, 108617. [Google Scholar] [CrossRef]

| Alkane | |||
|---|---|---|---|
| Pentane | 15.82 | 15.82 | 46.9817 |
| Hexane | 18.4 | 18.4 | 46.2004 |
| Heptane | 19.9 | 19.9 | 45.8542 |
| Octane | 21.3 | 21.3 | 45.5929 |
| Nonane | 23 | 23 | 45.3473 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abraham, R.; Khan, F.; Bukhari, S.A.; Liu, Q.; Thundat, T.; Chung, H.-J.; Kim, C.I. Effect of Surface and Interfacial Tension on the Resonance Frequency of Microfluidic Channel Cantilever. Sensors 2020, 20, 6459. https://doi.org/10.3390/s20226459
Abraham R, Khan F, Bukhari SA, Liu Q, Thundat T, Chung H-J, Kim CI. Effect of Surface and Interfacial Tension on the Resonance Frequency of Microfluidic Channel Cantilever. Sensors. 2020; 20(22):6459. https://doi.org/10.3390/s20226459
Chicago/Turabian StyleAbraham, Rosmi, Faheem Khan, Syed A. Bukhari, Qingxia Liu, Thomas Thundat, Hyun-Joong Chung, and Chun Il Kim. 2020. "Effect of Surface and Interfacial Tension on the Resonance Frequency of Microfluidic Channel Cantilever" Sensors 20, no. 22: 6459. https://doi.org/10.3390/s20226459
APA StyleAbraham, R., Khan, F., Bukhari, S. A., Liu, Q., Thundat, T., Chung, H.-J., & Kim, C. I. (2020). Effect of Surface and Interfacial Tension on the Resonance Frequency of Microfluidic Channel Cantilever. Sensors, 20(22), 6459. https://doi.org/10.3390/s20226459







